An Analytical Method for Elastic Seismic Response of Structures Considering the Effect of Ground Motion Duration

Abstract

The response to earthquake ground motion is composed of three basic elements, namely, amplitude, frequency, and duration. The seismic response of a structure is controlled by the particular combination of these three elements. The seismic response spectra reflect the earthquake ground motion’s frequency-domain features and provide the maximum response amplitude of a single-degree-of-freedom system to a given earthquake ground motion but do not consider the duration factor. However, the analysis of post-earthquake damage shows that the seismic response duration has a strong impact on the damage to structures. Therefore, it is necessary to develop a simple and practical analytical method to account for the seismic response duration. The present study was conducted based on the response spectra theory. We introduce an analytical method of elastic seismic response, which considers its duration by adding the time-domain dimension of earthquakes. The time-domain spectral matrix is used to solve the time-dependent seismic response through the vibration mode decomposition method. The time-domain vibration mode decomposition reaction spectrum not only takes into account the maximum seismic reaction of each vibration mode but also considers the seismic reaction of different vibration modes occurring at the same time, at each moment. The dynamic time duration of the structure’s seismic reaction is quantified by the time-domain seismic reaction spectrum to obtain a more accurate analysis method for the seismic reaction of the structure.

1. Introduction

The object of the time-domain analysis of the elastic seismic response is to obtain the response of a single-degree-of-freedom [1,2] (initial static state) system to the earthquake ground motion. This coincides with that of the general response spectra analysis and considers the duration effect on the ground motion input process [3]. The elastic system as a research object is illustrated in Figure 1.

According to the d’Alembert principle, the external forces acting on an object at any moment are in balance with the inertial forces of the object [4,5,6]. Thus, the differential motion equation of a single-degree-of-freedom system has the following form:

$$-m\cdot \left[\stackrel{\dot{}\dot{}}{x_0}(t)+\stackrel{\dot{}\dot{}}{x}(t)\right]-k\cdot x(t)-c\cdot \dot{x}(t)=0$$

(1)

where m is the mass of the system’s mass point, k is the stiffness of the elastic straight bar supporting the mass point, and c is the damping coefficient.

After shifting the known term to the right part of Equation (1) and dividing both sides by m, we obtain

$$\stackrel{\dot{}\dot{}}{x}(t)+\frac{c}{m}\cdot \dot{x}(t)+\frac{k}{m}\cdot x(t)=-\stackrel{\dot{}\dot{}}{x_0}(t)$$

(2)

or

$$\stackrel{\dot{}\dot{}}{x}(t)+2\cdot \xi \cdot \omega \cdot \dot{x}(t)+{\omega }^2\cdot x(t)=-\stackrel{\dot{}\dot{}}{x_0}(t)$$

Considering the values of $\stackrel{\dot{}\dot{}}{x_0}(t)$, the time interval between adjacent acceleration responses is generally small, resulting in a high density of values. The point positions expressed in numbers can reflect the main features of the acceleration responses. Therefore, it is assumed that the intermediate values between the two accelerations are linearly distributed. Thus, the distribution of $\stackrel{\dot{}\dot{}}{x_0}(t)$ within the range t_i ≤ t ≤ t _{i + 1} is given by Equation (3):

$${\stackrel{\dot{}\dot{}}{x}}_0(t)={\stackrel{\dot{}\dot{}}{x}}_0(t_i)+\frac{\stackrel{\dot{}\dot{}}{x_0}(t_{i+1})-\stackrel{\dot{}\dot{}}{x_0}(t_i)}{t_{i+1}-t_i}(t-t_i)$$

(3)

By substituting Equation (3) into Equation (2), we obtain

$$\stackrel{\dot{}\dot{}}{x}(t)+2\cdot \xi \cdot \omega \cdot \dot{x}(t)+{\omega }^2\cdot x(t)=-{\stackrel{\dot{}\dot{}}{x}}_0(t_i)-\frac{\stackrel{\dot{}\dot{}}{x_0}(t_{i+1})-\stackrel{\dot{}\dot{}}{x_0}(t_i)}{t_{i+1}-t_i}(t-t_i)$$

(4)

where $t_i\le t\le t_{i+1}$. The above formula yields the solution at time $t_i\le t\le t_{i+1}$ as follows:

$$x=e^{-\xi \cdot \omega (t-t_i)}\lfloor c_1\sin \omega \sqrt{1-{\xi }^2}(t-t_i)+c_2\cos \omega \sqrt{1-{\xi }^2}(t-t_i)\rfloor -$$

$$\frac{{\stackrel{\dot{}\dot{}}{x}}_0(t_i)}{{\omega }^2}+\frac{2\xi }{{\omega }^3}\frac{\stackrel{\dot{}\dot{}}{x_0}(t_{i+1})-\stackrel{\dot{}\dot{}}{x_0}(t_i)}{t_{i+1}-t_i}-\frac{1}{{\omega }^2}\frac{\stackrel{\dot{}\dot{}}{x_0}(t_{i+1})-\stackrel{\dot{}\dot{}}{x_0}(t_i)}{t_{i+1}-t_i}(t-t_i)$$

(5)

where $c_1$ and $c_2$ are integration constants, which can be calculated according to the boundary conditions (i.e., initial value conditions) $x=x(t_0)$ and $\dot{x}=\dot{x}(t_0)$ as follows:

$$c_1=\frac{1}{\omega \sqrt{1-{\xi }^2}}(\xi \omega x(t_0)+\dot{x}(t_0)-\frac{2{\xi }^2-1}{{\omega }^2}\cdot \frac{\stackrel{\dot{}\dot{}}{x_0}(t_1)-\stackrel{\dot{}\dot{}}{x_0}(t_0)}{t_1-t_0}+\frac{\xi }{\omega }\stackrel{\dot{}\dot{}}{x_0}(t_0))$$

$$c_2=x(t_0)-\frac{2\xi }{{\omega }^3}\cdot \frac{\stackrel{\dot{}\dot{}}{x_0}(t_1)-\stackrel{\dot{}\dot{}}{x_0}(t_0)}{t_1-t_0}+\frac{\stackrel{\dot{}\dot{}}{x_0}(t_0)}{\omega }$$

To evaluate the response value at $t_{i+1}$, we substitute the values of $c_1,c_2,t=t_{i+1}$ into Equation (5) and provide its time derivative, which yields

$$x(t_{i+1})=a_{11}\cdot x(t_i)+a_{12}\cdot \stackrel{\dot{}\dot{}}{x}(t_i)+b_{11}\cdot {\stackrel{\dot{}\dot{}}{x}}_0(t_i)+b_{12}\cdot {\stackrel{\dot{}\dot{}}{x}}_0(t_{i+1})$$

(6)

$$\dot{x}(t_{i+1})=a_{21}\cdot x(t_i)+a_{22}\cdot \stackrel{\dot{}\dot{}}{x}(t_i)+b_{21}\cdot {\stackrel{\dot{}\dot{}}{x}}_0(t_i)+b_{22}\cdot {\stackrel{\dot{}\dot{}}{x}}_0(t_{i+1})$$

(7)

where the coefficients $a_{11}$, $a_{12}$, $a_{21}$, $a_{22}$, $b_{11}$, $b_{12}$, $b_{21}$, and $b_{22}$ are the constants of Equation (5) after differentiating with respect to time, and are extracted for the convenience of later program design and use. They are derived as follows:

$$a_{11}=e^{-\xi \omega \Delta t_i}\cdot \frac{\xi }{\sqrt{1-{\xi }^2}}\cdot \sin \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i+\cos \omega \cdot \sqrt{1-{\xi }^2}$$

$$a_{12}=e^{-\xi \omega \Delta t_i}\cdot \frac{\sin \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i}{\omega \cdot \sqrt{1-{\xi }^2}}$$

$$a_{21}=-\frac{\omega }{\sqrt{1-{\xi }^2}}\cdot e^{-\xi \omega \Delta t_i}\cdot \sin \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i$$

$$a_{22}=e^{-\xi \omega \Delta t_i}\cdot (\cos \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i-\frac{\xi }{\sqrt{1-{\xi }^2}}\sin \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i$$

$$b_{11}=e^{-\xi \omega \Delta t_i}\cdot \left[\left(\frac{2{\xi }^2-1}{{\omega }^2\Delta t_i}+\frac{\xi }{\omega }\right)\frac{\sin \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i}{\omega \sqrt{1-{\xi }^2}}+(\frac{2\xi }{{\omega }^3\Delta t_i}+\frac{1}{{\omega }^2})\cos \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i\right]-\frac{2\xi }{{\omega }^3\Delta t_i}$$

$$b_{12}=-e^{-\xi \omega \Delta t_i}\cdot \left[\left(\frac{2{\xi }^2-1}{{\omega }^2\Delta t_i}+\frac{\xi }{\omega }\right)\frac{\sin \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i}{\omega \sqrt{1-{\xi }^2}}+\frac{2\xi }{{\omega }^3\Delta t_i}\cos \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i\right]-\frac{1}{{\omega }^2}+\frac{2\xi }{{\omega }^3\Delta t_i}$$

$$b_{21}=e^{-\xi \omega \Delta t_i}\cdot [(\frac{2{\xi }^2-1}{{\omega }^2\Delta t_i}+\frac{\xi }{\omega })\cos \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i-\frac{\xi }{\sqrt{1-{\xi }^2}}\sin \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i-$$

$$(\frac{2\xi }{{\omega }^3\Delta t_i}+\frac{1}{{\omega }^2})\cdot (\omega \sqrt{1-{\xi }^2}\sin \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i+\xi \omega \cdot \cos \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i)]+\frac{1}{{\omega }^2\Delta t_i}$$

$$b_{22}=-e^{-\xi \omega \Delta t_i}\cdot [\frac{2{\xi }^2-1}{{\omega }^2\Delta t_i}(\cos \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i-\frac{\xi }{\sqrt{1-{\xi }^2}}\sin \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i)-$$

$$\frac{2\xi }{{\omega }^3\Delta t_i}\cdot (\omega \sqrt{1-{\xi }^2}\sin \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i+\xi \omega \cdot \cos \omega \cdot \sqrt{1-{\xi }^2}\Delta t_i)]-\frac{1}{{\omega }^2\Delta t_i}$$

If the given seismic acceleration numerical values are recorded at equal time intervals, the above coefficients are fixed values. Then, the single-degree-of-freedom system displacement and velocity responses at time t_i+1 can be calculated via Equations (6) and (7) from the displacement and velocity values at instant t_i and the seismic acceleration values at instants t_i and t_i+1. The absolute acceleration of the system can be directly obtained from the following differential motion equation:

$${\stackrel{\dot{}\dot{}}{x}}_0(t_{i+1})+\stackrel{\dot{}\dot{}}{x}(t_{i+1})=-\left[2\cdot \xi \cdot \omega \cdot \dot{x}(t_{i+1})+{\omega }^2\cdot x(t_{i+1})\right]$$

(8)

For any seismic wave, the displacement, velocity, and acceleration responses of the single-degree-of-freedom system with a certain self-oscillation period at any time in the time domain can be calculated via Equations (6)–(8).

2. Method

Via the above calculation, we can obtain the acceleration responses of the single-degree-of-freedom (initial static state) system with different natural vibration periods, due to the fact that the earthquake influence coefficient of the time-domain response spectrum is two-dimensional, and hence a two-dimensional matrix can effectively be introduced into the digital records.

2.1. Method of Recording

The time-domain seismic response spectrum in Figure 2 shows the single-degree-of-freedom system seismic influence coefficient corresponding to the natural vibration period $T_c$ at time $t$. The natural vibration period $T_c$ is plotted on the Y-axis, time t is plotted on the X-axis, and the seismic influence coefficient α(x, y) on the Z-axis, where x represents time t_x. If the time interval is $\Delta t$, then t_x = x · Δt; y is the periodic point of the natural vibration period $T_y$. If the periodic interval is $\Delta T$, $T_y=y\cdot \Delta T$.

2.2. Physical Meaning

The time-domain spectrum of the seismic response in Figure 2 can be represented by a matrix:

$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdot \cdot \cdot & a_{1n}\\ a_{21}& a_{22}& \cdot \cdot \cdot & a_{2n}\\ \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot \\ a_{m1}& a_{m2}& \cdot \cdot \cdot & a_{mn}\end{array}\right]$$

where $a_{xy}$ is the maximum value of the seismic influence coefficient, from time t_x−1 to t_x, of the single-degree-of-freedom system under the natural vibration period T_y. The periodic interval of T_y is $\Delta T$, thus $T_y=T_1+(y-1)\cdot \Delta T$; the time interval of t_x is $\Delta t$, thus $t_x=t_1+(x-1)\cdot \Delta t$.

3. Data Preparation Process

The following describes the specific operation of the process of forming the response spectrum surface (response spectrum matrix) for any seismic wave data, according to the principles in Section 1 and Section 2.

First, the seismic record data need to be processed. Any seismic wave is split into equal time intervals, as shown in Figure 3. Then, the full-period seismic response spectra are calculated for each time interval after splitting.

The physical meaning and generation process of the rows of the time-domain seismic response spectrum are as follows. As illustrated in Figure 2, the maximum values of the seismic influence coefficient at each periodic point from time t_m−1 to t_m are α_m1, α_m2, …, and α_mn. The physical meaning and the generation process of the columns of the time-domain seismic response spectrum are the maximum values of the seismic influence coefficient at time intervals 0–t₁, t₁–t₂, …, t_m−1–t_m, i.e., α_1n, α_2n, …, and α_mn, respectively. According to the physical meaning of the time-domain response spectral matrix, the projection of the curved surface of the time-domain response spectrum on the α_0T plane is the seismic response curve in the ordinary sense.

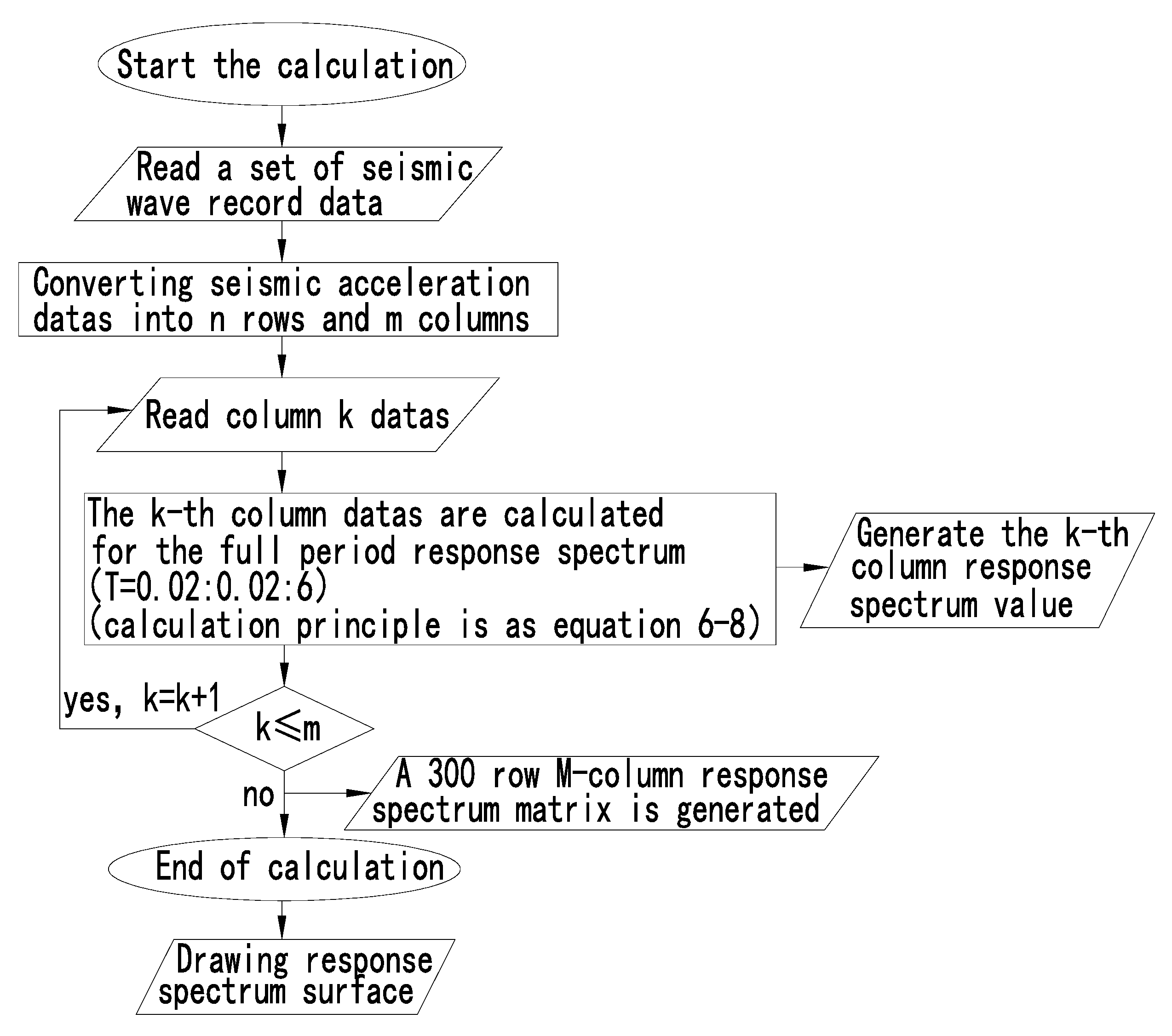
4. Program Implementation Process

Through the introduction in the first three sections, we can understand the formation principle, process, and required seismic record data of the time-domain response spectrum. However, a large number of calculations must be completed by the program. The following describes the specific process of program implementation for obtaining the response spectrum surface (response spectrum matrix) according to the above principle.

In this study, the elastic seismic response analysis was performed on a concrete structure with a damping ratio $\xi$ of 0.05. The seismic wave data used for the analysis were recorded by a high-precision digital seismograph in the Japanese seismic network (the seismic records in the east–west direction at the AOM021 seismic station during the Great East Japan Earthquake on 11 March 2011). The time interval for the seismic acceleration data was 0.01 s, the total recording duration was 300 s, and the period response spectrum calculation ranged from 0 to 6 s. In the row–column conversion processing method for seismic acceleration data, the number of rows is the segmentation time interval divided by 0.01, as shown in Figure 3, and the number of columns is the total length of the seismic records divided by $\Delta t$; The number of rows of the produced response spectrum matrix is divided by the cycle interval of the calculated response spectrum (such as 0.02 s in Figure 4, “T = 0.02:0.02:6“), and the number of columns is the same as the number of columns converted from the seismic acceleration records. The block diagram of the calculation program for the time-domain seismic response spectral matrix (response spectral surface) is shown in Figure 4.

The acceleration response spectra were calculated using a self-developed program based on the seismic records in the east–west direction at the AOM021 seismic station during the Great East Japan Earthquake on 11 March 2011 (with a recording duration of 300 s, the peak acceleration amplitude-modulated to 35 cm/s², and a damping ratio $\xi$ of 0.05. Note that an estimation of the epicentral location of the Great East Japan Earthquake could be achieved a few months in advance by means of natural time analysis of the Japanese seismicity). Figure 5 shows the time interval of 10 s selected for the time-domain seismic response spectra. The seismic wave data had to be converted to 1000 rows and 30 columns, and the generated response spectral matrix consisted of 300 rows and 30 columns.

Using the projection of the time-domain response spectrum’s curved surface on the α_0T plane, the constructed curve is shown in Figure 5.

The physical meaning of the seismic influence coefficient curve in Figure 5 is consistent with that in the seismic code. Since the seismic influence coefficient is generated by projection onto the axis representing the period, the seismic response’s temporal effect is lost, compared to the seismic influence coefficient’s curved surface. It represents only the maximum seismic response at each periodic point. The response spectrum matrix can be used to analyze the time-domain response of the building structure because the response spectrum surface increases in the time dimension compared with the response spectrum curve.

The time interval for calculating the seismic influence coefficient in the time domain was 0.01 s. Figure 6 and Figure 7 depict the curved surfaces of the seismic influence coefficient generated via the recorded seismic data acceleration and absolute acceleration responses, respectively.

The same seismic acceleration records were used in Figure 6 and Figure 7, which present the time-domain curved surfaces of the seismic influence coefficient generated from the accelerations and absolute accelerations, respectively, within the time interval of 0.01 s and the periodic interval of 0.01 s. A comparative analysis of the above figures shows that the maximum absolute values of the positive or negative seismic influence coefficients in Figure 6 are consistent with those in Figure 7. However, Figure 6 reflects the structure’s acceleration response’s cyclic process, which is the cyclic motion of the structure under the excitation of earthquake ground motion. Thus, the seismic response of the structure can be more realistically characterized. Figure 6 reflects the same positive and negative changes in the seismic influence coefficient during the seismic acceleration data history at different periodic points.

Figure 5 and Figure 7 are the time-domain curved surfaces of the seismic influence coefficient of absolute acceleration, using the same seismic acceleration records but different time intervals. A comparison of the two figures indicates that the occurrence periods and times of the peak of the seismic influence coefficient are consistent. The time interval in Figure 7 is very short, and more abundant changes are shown in the time domain, with more peaks in the curved surface. The time-domain seismic force analysis using this curved surface of the response spectrum can be considered exact within the time interval of 0.01 s. However, the calculation workload is undeniably huge. When mode decomposition is applied to the response spectral matrix using the above seismic records, the number of seismic forces in the time domain reaches 30,000 per vibration mode. The total number of seismic forces in the time domain is n, where n is the number of vibration modes. These n seismic forces are then combined with the vibration modes, and the huge calculation workload inevitably results in a low calculation efficiency. Therefore, it is recommended to use time intervals of 1, 5, and 10 s, depending on each stage’s design requirements, to generate the time-domain response spectral matrix for seismic force analysis. For example, the time interval of 10 s was used in Figure 5. The number of seismic forces in each vibration mode’s time domain was only 30 in the corresponding elastic response spectral matrix. Although the seismic force’s variation trend within 10 s could not be properly reflected, the seismic force peaks within 10 s were preserved. Therefore, the seismic force variation in the time domain can be characterized by seismic records over 300 s.

5. Application

After the response spectrum surface is calculated by the program, it can be used to analyze the time-domain response of the building structure. Previous studies only used the maximum value of the acceleration response [7,8,9,10,11], and could not use the response spectrum for time-domain analysis, which is reflected in the seismic codes of various countries that use the response spectrum curve. Therefore, this study used the response spectrum for time-domain analysis of building structures after extending the response spectrum to the time domain. The standard spectrum can only calculate the maximum response of the building structure within the earthquake time history, which is the difference between, and the advantage of, the response spectrum surface over the standard response spectrum curve.

With regard to the response spectrum matrix, this section introduces the specific calculation method of the dynamic time-history analysis of building structures by using the response spectrum matrix through mode decomposition (response spectrum method of time-domain mode decomposition). Some simplification is needed when performing a dynamic analysis of structures. Structures with a significant mass concentration, high stiffness in the upper part, and small inter-story displacement are simplified to single-mass-point systems for seismic response analysis. Structures with a scattered mass distribution, low stiffness in the upper part, and large inter-story displacement are reduced to multiple-mass-points systems and subjected to seismic response analysis using the time-domain seismic response spectra specific to the multiple-mass-points systems.

Before deriving the standard values of the seismic response in the time domain, the multiple-mass-points system’s basic vibration modes must first be determined. On this basis, the natural vibration periods of different vibration modes and the displacement of each mass point for each vibration mode can be determined [12,13,14,15]. During the basic vibration modes calculation, the mass points undergo purely translational motion with no rotation. Therefore, the shear stiffness is used to calculate the natural vibration period $T_i$ and the displacement $X_{ji}$ for each vibration mode.

The seismic response of each mass point within the seismic duration is calculated by the time-domain mode decomposition reaction spectroscopy method [16,17,18,19,20]. For a multiple-mass-point system, the i-th mass point’s standard value for the j-th vibration mode is expressed as follows:

$$F_{ji}={\alpha }_{tx j}{\gamma }_j{X}_{ji}{G}_i$$

(9)

where ${\alpha }_{tx j}=\left\{\begin{array}{c}{\alpha }_{t1 j}\\ {\alpha }_{t2 j}\\ ....\\ {\alpha }_{tm j}\end{array}\right\}$ is the seismic influence coefficient matrix in the time domain for the j-th vibration mode under the corresponding natural vibration period, ${\gamma }_j$ is the modal participation factor of the j-th vibration mode, $X_{ji}$ is the displacement of the i-th mass point for the j-th vibration mode, and $G_i$ is the representative value of the gravity load concentrated at the i-th mass point.

Hence, the seismic response of each point in the time domain has the following form:

$$F_{ji}=\left\{\begin{array}{c}{\alpha }_{t1 j}\\ {\alpha }_{t2 j}\\ ....\\ {\alpha }_{tm j}\end{array}\right\}{\gamma }_j{X}_{ji}{G}_i=\left\{\begin{array}{c}{F}_{t1 ji}\\ F_{t2 ji}\\ ....\\ F_{tm ji}\end{array}\right\}$$

(10)

From the above, the standard value of the seismic shear force at time t_x at the i-th mass point for the j-th vibration mode is derived as follows:

$$V_{ji tx}=\sum _{y=i}^p{F}_{jy tx}$$

(11)

The standard value of the horizontal seismic force at t_x at the i-th mass point is obtained by extracting the square root of the sum of squares, which yields $V_{i tx}$. Here, the physical meaning of the horizontal seismic forces combination is more explicit than in the conventional mode decomposition. The combination consists of the seismic forces occurring at each time point for different vibration modes. However, with the conventional mode decomposition, the maximum seismic force is taken for each vibration mode, although the maximum seismic forces for different vibration modes do not occur simultaneously.

Hence, the standard value of the seismic response of each mass point in the time domain is expressed as:

$$V_i=\left\{\begin{array}{c}{V}_{i t1}\\ V_{i t2}\\ \cdot \cdot \cdot \\ V_{i tm}\end{array}\right\}$$

(12)

In this paper, the base shear of a concrete frame structure (the structure has five horizontal and vertical spans, with a span of 5 m; there are eight vertical stories, each of 3 m; the slab thickness of each story is 120 mm; cross sections of all frame beams are 250 mm × 500 mm; cross sections of all frame columns are 500 mm × 500 mm; the concrete strength of each member is C30; the dead and live loads of each story of the slab surface are 2 kN/m², apart from their own weight) was calculated by using the code response spectrum, time-domain mode decomposition response spectrum, and elastic dynamic time-history method, respectively, under the condition that the Chinese seismic code intensity was 7 and the seismic site was class II. The time-domain mode decomposition response spectrum method and the elastic dynamic time method both used the above seismic record data, the peak acceleration being amplitude-modulated to 35 cm/s², matching an intensity of 7 in the code. The main results were as follows:

Considering the comparison of the maximum base shear values given in

Table 1. Calculation and analysis of base shear force for a frame structure.

	Methods	Standard Mode Decomposition Response Spectrum Method	Time-Domain Mode Decomposition Response Spectrum Method	Elastic Dynamic Time Method
Results
Maximum horizontal base seismic shear		1242.7 kN	1236.4 kN	1268.9 kN
Time when the maximum value occurs			at the 122nd second	at the 142nd second
Calculation duration		1 min 12 s	2 min 42 s	8 min 53 s

, it can be seen that the calculation results of the three methods were basically consistent, but the calculation efficiency of the time-domain mode decomposition response spectrum was significantly higher than that of elastic dynamic time-history method.

Compared with the conventional mode decomposition of the response spectra, the mode decomposition in the time domain considers the maximum seismic response of each mode and the seismic response of different vibration modes at each time point. This quantifies the dynamic time history of the structure’s seismic response through the seismic response’s time-domain spectra. The maximum values of seismic forces for each vibration mode are combined with the conventional mode decomposition. However, in fact, the maximum values of seismic forces for different vibration modes do not occur simultaneously. Therefore, the conventional mode decomposition has some theoretical deficiencies. Time-domain mode decomposition splits the seismic responses occurring simultaneously within the time duration. As long as the time interval is sufficiently small, the above theoretical deficiency of the conventional mode decomposition, i.e., the fact that the maximum values of seismic forces for each vibration mode cannot occur simultaneously, can be overcome. Therefore, the time-domain decomposition of the seismic response spectra can yield a more detailed and precise seismic response of the structures.

6. Conclusions

In this study, the physical meaning of the time-domain elastic seismic response spectra was analyzed, and the generation process of the response spectra was described. First, we analyzed the research object and the calculation principle of time-domain elastic seismic response spectra. The time-domain seismic response spectrum was transformed into the time-domain seismic response spectral matrix. We described the specific process of the matrix formation and the self-developed calculation program for the time-domain elastic seismic response matrix for any seismic wave (curved surface of the response spectrum). Finally, the calculation method for the dynamic seismic response of the structure was introduced by applying time-domain mode decomposition to the response spectral matrix. The results obtained made it possible to draw the following conclusions.

(1)

The time-domain seismic response spectra are the values of the seismic influence coefficient at the time t of an earthquake for a single-degree-of-freedom and natural vibration period T_c. The natural vibration period T_c is plotted on the Y-axis, time t is plotted on the X-axis, and the seismic influence coefficient α(x,y) on the Z-axis. The seismic response analysis based on the time-domain seismic response spectra yielded the maximum response of the structure and the seismic response simultaneously occurring for different vibration modes at each time point.

(2)

The time-domain mode decomposition not only considered the maximum seismic response of each vibration mode but also included the seismic response of different vibration modes at each time point. Thus, it quantified the dynamic time history of the structure’s seismic response through the seismic response’s time-domain spectra.

(3)

Through comparative analysis, the calculation accuracy of the time-domain response spectrum can meet the engineering requirements, and the calculation efficiency is significantly higher than that of the elastic dynamic time-history method.