Hydraulic Fracture Propagation Near the Cavity in a Poroelastic Media
Abstract
:1. Introduction
- existing possibility of natural and artificial cracks emerging into the working, which can disrupt its integrity and possibly stop the underground activity;
- carbonate oil and gas reservoirs, which contain abundant natural fractures and cavities and have great potential for development via hydraulic fracturing.
2. Basic Equations of the Model
3. Numerical Test Results and Discussion
3.1. Formulation of the Problem
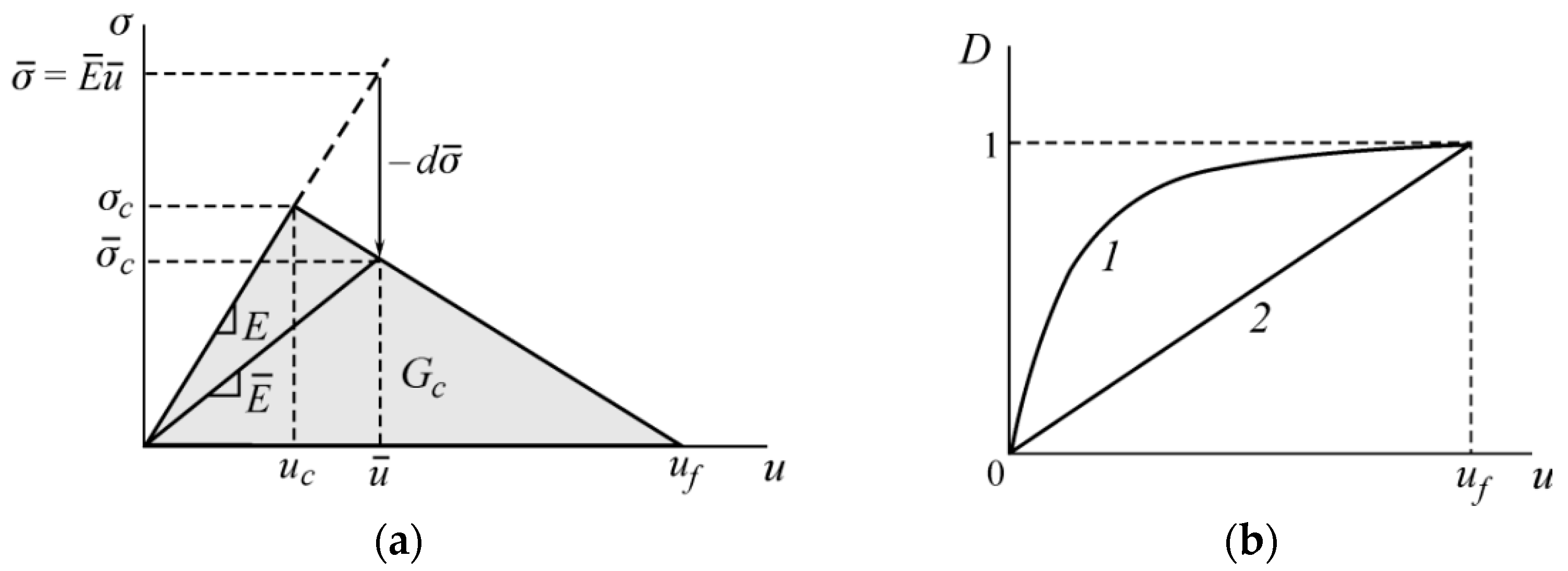
3.2. Uncoupled Problem
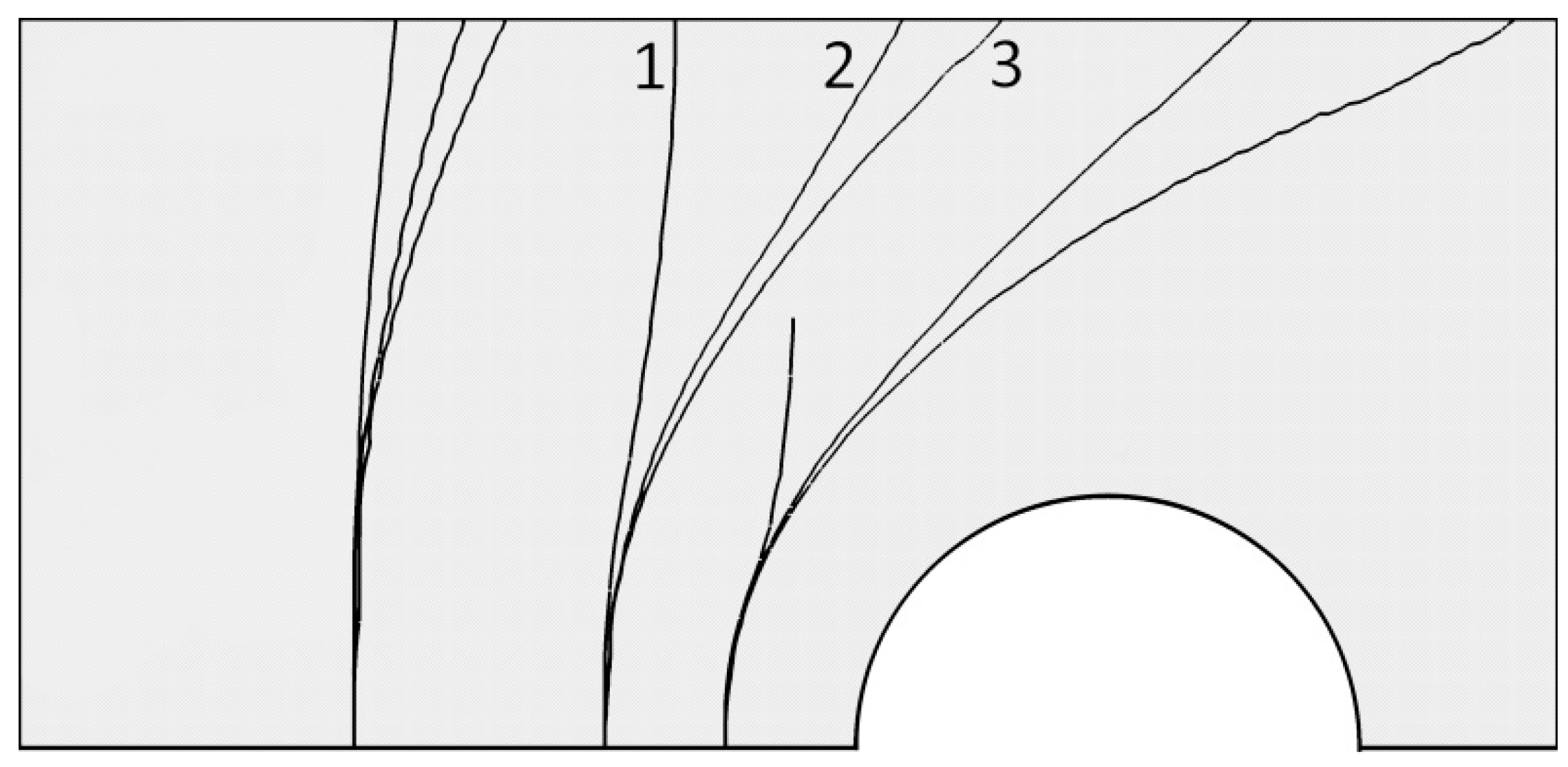
3.3. Influence of Poroelastic Parameters on Hydraulic Fracturing
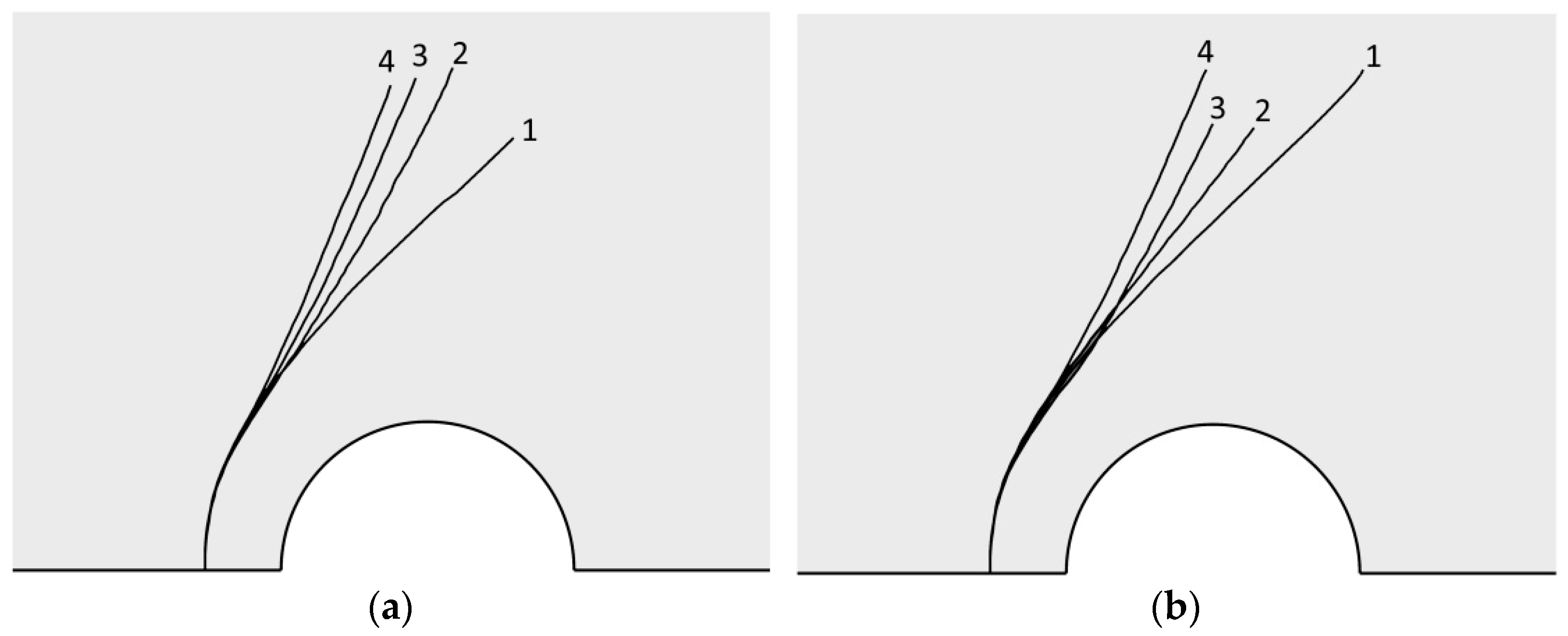
3.4. Influence of s and P on the Hydraulic Fracturing Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yoo, H.; Park, S.; Xie, L.; Kim, K.I.; Min, K.B.; Rutqvist, J.; Rinaldi, A.P. Hydro-mechanical modeling of the first and second hydraulic stimulations in a fractured geothermal reservoir in Pohang, South Korea. Geothermics 2021, 89, 101982. [Google Scholar] [CrossRef]
- AbuAisha, M.; Loret, B.; Eaton, D. Enhanced Geothermal Systems (EGS): Hydraulic fracturing in a thermo-poroelastic framework. J. Pet. Sci. Eng. 2016, 146, 1179–1191. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, G.; Luo, T.; Jiang, Y.; Ning, S. Hydraulic fracturing in high-temperature granite characterized by acoustic emission. J. Pet. Sci. Eng. 2019, 178, 475–484. [Google Scholar] [CrossRef]
- Cladouhos, T.; Petty, S.; Larson, B.; Iovenitti, J.; Livesay, B.; Baria, R. Toward more efficient heat mining: A planned enhanced geothermal system demonstration project. GRC Trans. 2009, 33, 165–170. [Google Scholar]
- Eshiet, K.I.; Sheng, Y. Carbon dioxide injection and associated hydraulic fracturing of reservoir formations. Environ. Earth Sci. 2014, 72, 1011–1024. [Google Scholar] [CrossRef] [Green Version]
- Fu, P.; Settgast, R.R.; Hao, Y.; Morris, J.P.; Ryerson, F.J. The influence of hydraulic fracturing on carbon storage performance. J. Geophys. Res. Solid Earth 2017, 122, 9931–9949. [Google Scholar] [CrossRef] [Green Version]
- Fu, P.; Ju, X.; Huang, J.; Settgast, R.R.; Morris, J.P. THM modeling of poroelastic sustainability of hydraulic fracture in CO2 storage reservoirs. In Proceedings of the 53rd US Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019; pp. 4369–4374. [Google Scholar]
- Schlüter, R.; Mischo, H. In-situ underground bioleaching—Novel conditioning technologies. In Proceedings of the 2015 SME Annual Meeting and Conference, Denver, CO, USA, 15–18 February 2015; pp. 299–303. [Google Scholar]
- Werner, A.; Haseneder, R.; Repke, J.U. Design and conception of a membrane pilot plant for the in situ treatment of bioleaching solutions. Chem. Ing. Tech. 2019, 91, 145–150. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Geehan, T.; Ovalle, A.P. Increased assurance of drill cuttings re-injection-challenges, recent advances and case studies. SPE Drill. Complet. 2007, 22, 99–105. [Google Scholar] [CrossRef]
- Gaurina-Međimurec, N.; Pašić, B.; Mijić, P.; Medved, I. Deep underground injection of waste from drilling activities—An overview. Minerals 2020, 10, 303. [Google Scholar] [CrossRef] [Green Version]
- Jeffrey, R.; Mills, K.; Zhang, X. Experience and results from using hydraulic fracturing in coal mining. In Proceedings of the 3rd International Workshop on Mine Hazards Prevention and Control, Brisbane, Australia, 19–21 November 2013; pp. 110–116. [Google Scholar]
- Plaksin, M.S.; Rodin, R.I. Improvement of degasification efficiency by pulsed injection of water in coal seam. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Novokuznetsk, Russia, 4–7 June 2019; Volume 377, p. 012052. [Google Scholar] [CrossRef]
- Guanhua, N.; Hongchao, X.; Zhao, L.; Lingxun, Z.; Yunyun, N. Improving the permeability of coal seam with pulsating hydraulic fracturing technique: A case study in Changping coal mine, China. Process Saf. Environ. Prot. 2018, 117, 565–572. [Google Scholar] [CrossRef]
- Shilova, T.; Patutin, A.; Serdyukov, S. Sealing quality increasing of coal seam gas drainage wells by barrier screening method. In Proceedings of the International Multidisciplinary Scientific GeoConference SGEM, Albena, Bulgaria, 16–22 June 2013; Volume 1, pp. 701–708. [Google Scholar] [CrossRef]
- Shilova, T.; Patutin, A.; Rybalkin, L.; Serdyukov, S.; Hutornoy, V. Development of the impermeable membranes using directional hydraulic fracturing. Procedia Eng. 2017, 191, 520–524. [Google Scholar] [CrossRef]
- Lekontsev, Y.M.; Sazhin, P.V. Directional hydraulic fracturing in difficult caving roof control and coal degassing. J. Min. Sci. 2014, 50, 914–917. [Google Scholar] [CrossRef]
- Huang, B.; Wang, Y. Roof weakening of hydraulic fracturing for control of hanging roof in the face end of high gassy coal longwall mining: A Case study. Arch. Min. Sci. 2016, 61, 601–615. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Liu, B.; Bian, W.; Chen, K.; Wang, H.; Cao, C. Application Cumulative Tensile Explosions for Roof Cutting in Chinese Underground Coal Mines. Arch. Min. Sci. 2021, 66, 421–435. [Google Scholar] [CrossRef]
- Kang, H.; Zhang, X.; Si, L.; Wu, Y.; Gao, F. In-situ stress measurements and stress distribution characteristics in underground coal mines in China. Eng. Geol. 2010, 116, 333–345. [Google Scholar] [CrossRef]
- Rubtsova, E.V.; Skulkin, A.A. Hydraulic fracturing stress measurement in underground salt rock mines at Upper Kama Deposit. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Novosibirsk, Russia, 2–6 October 2017; Volume 134, p. 012049. [Google Scholar] [CrossRef] [Green Version]
- Serdyukov, S.V.; Kurlenya, M.V.; Patutin, A.V. Hydraulic fracturing for in situ stress measurement. J. Min. Sci. 2016, 52, 1031–1038. [Google Scholar] [CrossRef]
- Khristianovic, S.A.; Zheltov, Y.P. Formation of vertical fractures by means of highly viscous liquid. In Proceedings of the World Petroleum Congress Proceedings, Rome, Italy, 6–15 June 1955; pp. 579–586. [Google Scholar]
- Geertsma, J.; de Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Pet. Technol. 1969, 21, 1571–1581. [Google Scholar] [CrossRef]
- Perkins, T.K.; Kern, L.R. Widths of hydraulic fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Nordgren, R.P. Propagation of a vertical hydraulic fracture. SPE J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Zhang, X.; Jeffrey, R.G.; Thiercelin, M. Deflection and propagation of fluid-driven fractures at frictional bedding interfaces: A numerical investigation. J. Struct. Geol. 2007, 29, 396–410. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, W.; Chen, J.; Xiao, X.; Li, Y.; Zhao, X. Simulation of hydraulic fracturing using particle flow method and application in a coal mine. Int. J. Coal Geol. 2014, 121, 1–13. [Google Scholar] [CrossRef]
- Olovyanny, A.G. Mathematical modeling of hydraulic fracturing in coal seams. J. Min. Sci. 2005, 41, 61–67. [Google Scholar] [CrossRef]
- Yan, X.; Huang, Z.; Yao, J.; Zhang, Z.; Liu, P.; Li, Y.; Fan, D. Numerical simulation of hydro-mechanical coupling in fractured vuggy porous media using the equivalent continuum model and embedded discrete fracture model. Adv. Water Resour. 2019, 126, 137–154. [Google Scholar] [CrossRef]
- Bubshait, A.; Jha, B. Coupled poromechanics-damage mechanics modeling of fracturing during injection in brittle rocks. Int. J. Numer. Methods Eng. 2020, 121, 256–276. [Google Scholar] [CrossRef]
- Yun, K.; Kim, T.J.; Jang, P.S.; Wang, Z.; Ronald, S. An improved crack tracking algorithm with self-correction ability of the crack path and its application in a continuum damage model. Int. J. Numer. Methods Eng. 2019, 117, 249–269. [Google Scholar] [CrossRef]
- Xia, B.; Zhang, X.; Yu, B.; Jia, J. Weakening effects of hydraulic fracture in hard roof under the influence of stress arch. Int. J. Min. Sci. Technol. 2018, 28, 951–958. [Google Scholar] [CrossRef]
- Cherdantsev, N.V. Approach to constructing a hydraulic fracture trajectory in a rock mass near a mine working. Mech. Solids 2020, 55, 1372–1391. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, Q.; Sun, Y.; Tang, X.; Shao, Z.; Weng, Z. Investigation of the Influence of Natural Cavities on Hydraulic Fracturing Using Phase Field Method. Arab. J. Sci. Eng. 2019, 44, 10481–10501. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Dusseault, M.B.; Weng, L. Effect of excavation stress condition on hydraulic fracture behaviour. Eng. Fract. Mech. 2020, 226, 106871. [Google Scholar] [CrossRef]
- Azarov, A.V.; Serdyukov, S.V.; Patutin, A.V. Investigation of hydraulic fracture growth near a mine opening. J. Fundam. Appl. Min. Sci. 2019, 6, 26–31. [Google Scholar] [CrossRef]
- Zhao, H.; Xie, Y.; Zhao, L.; Liu, Z.; Li, Y.; Li, N. Simulation of mechanism of hydraulic fracture propagation in fracture-cavity reservoirs. Chem. Technol. Fuels Oils 2020, 55, 814–827. [Google Scholar] [CrossRef]
- Golovin, S.V.; Baykin, A.N. Influence of pore pressure on the development of a hydraulic fracture in poroelastic medium. Int. J. Rock Mech. Min. Sci. 2018, 108, 198–208. [Google Scholar] [CrossRef] [Green Version]
- Azarov, A.V.; Kurlenya, M.V.; Serdyukov, S.V.; Patutin, A.V. Features of hydraulic fracturing propagation near free surface in isotropic poroelastic medium. J. Min. Sci. 2019, 55, 1–8. [Google Scholar] [CrossRef]
- Feng, Y.; Gray, K.E. Modeling of curving hydraulic fracture propagation from a wellbore in a poroelastic medium. J. Nat. Gas Sci. Eng. 2018, 53, 83–93. [Google Scholar] [CrossRef]
- Wang, H.; Marongiu-Porcu, M.; Economides, M.J. Poroelastic and poroplastic modeling of hydraulic fracturing in brittle and ductile formations. SPE Prod. Oper. 2016, 31, 47–59. [Google Scholar] [CrossRef]
- Zeng, Q.D.; Yao, J.; Shao, J. Study of hydraulic fracturing in an anisotropic poroelastic medium via a hybrid EDFM-XFEM approach. Comput. Geotech. 2019, 105, 51–68. [Google Scholar] [CrossRef]
- Bruno, M.S.; Nakagawa, F.M. Pore pressure influence on tensile fracture propagation in sedimentary rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, 261–273. [Google Scholar] [CrossRef]
- Wang, S.Y.; Sloan, S.W.; Fityus, S.G.; Griffiths, D.V.; Tang, C.A. Numerical modeling of pore pressure influence on fracture evolution in brittle heterogeneous rocks. Rock Mech. Rock Eng. 2013, 46, 1165–1182. [Google Scholar] [CrossRef]
- He, B.; Zhuang, X. Modeling hydraulic cracks and inclusion interaction using XFEM. Undergr. Space 2018, 3, 218–228. [Google Scholar] [CrossRef]
- Yang, T.; Zhu, W.; Yu, Q.; Liu, H. The role of pore pressure during hydraulic fracturing and implications for groundwater outbursts in mining and tunnelling. Hydrogeol. J. 2011, 19, 995–1008. [Google Scholar] [CrossRef]
- Ortiz, M.; Pandolfi, A. Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int. J. Numer. Methods Eng. 1999, 44, 1267–1282. [Google Scholar] [CrossRef]
- Irwin, G.R. Analysis of stresses and strains near the end of a crack traversing a plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Martynyuk, P.A.; Sher, E.N. Development of a crack close to a circular opening with an external field of compressive stresses. J. Min. Sci. 1996, 32, 453–463. [Google Scholar] [CrossRef]
- Cheng, W.; Lu, C.; Zhou, Z. Modeling of borehole hydraulic fracture initiation and propagation with pre-existing cracks using the displacement discontinuity method. Geotech. Geol. Eng. 2020, 38, 2903–2912. [Google Scholar] [CrossRef]
- Shi, F.; Wang, D.; Chen, X. A numerical study on the propagation mechanisms of hydraulic fractures in fracture-cavity carbonate reservoirs. CMES 2021, 127, 575–598. [Google Scholar] [CrossRef]
- Cheng, L.; Luo, Z.; Yu, Y.; Zhao, L.; Zhou, C. Study on the interaction mechanism between hydraulic fracture and natural karst cave with the extended finite element method. Eng. Fract. Mech. 2019, 222, 106680. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azarov, A.; Patutin, A.; Serdyukov, S. Hydraulic Fracture Propagation Near the Cavity in a Poroelastic Media. Appl. Sci. 2021, 11, 11004. https://doi.org/10.3390/app112211004
Azarov A, Patutin A, Serdyukov S. Hydraulic Fracture Propagation Near the Cavity in a Poroelastic Media. Applied Sciences. 2021; 11(22):11004. https://doi.org/10.3390/app112211004
Chicago/Turabian StyleAzarov, Anton, Andrey Patutin, and Sergey Serdyukov. 2021. "Hydraulic Fracture Propagation Near the Cavity in a Poroelastic Media" Applied Sciences 11, no. 22: 11004. https://doi.org/10.3390/app112211004
APA StyleAzarov, A., Patutin, A., & Serdyukov, S. (2021). Hydraulic Fracture Propagation Near the Cavity in a Poroelastic Media. Applied Sciences, 11(22), 11004. https://doi.org/10.3390/app112211004





