Multiscale Compact Modelling of UTC-Photodiodes Enabling Monolithic Terahertz Communication Systems Design
Abstract
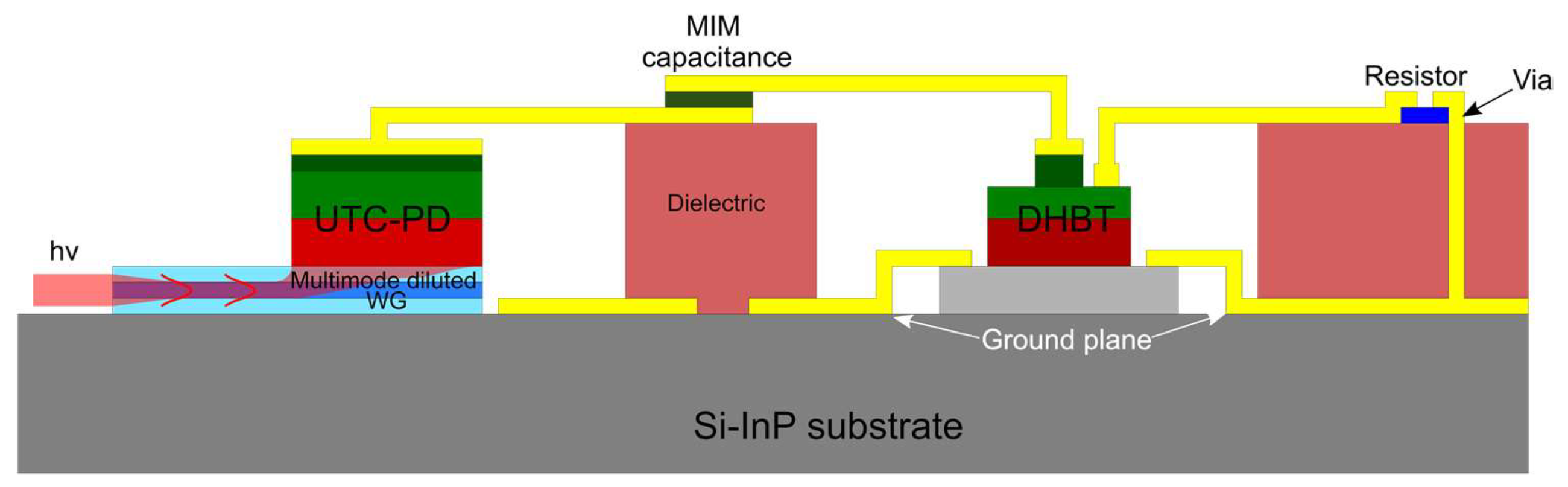
:1. Introduction
2. Compact Model Development
2.1. Model Description
2.2. Model Formulation
2.3. Parameter Extraction Methodology
3. Compact Model Validation
3.1. De-Embedding Procedure
3.1.1. InGaAs/InGaAsP UTC-PD De-Embedding
3.1.2. GaInAsSb/InP UTC-PD De-Embedding
3.1.3. InGaAs/InP UTC-PD De-Embedding
3.2. Validation of RF Characteristics
3.2.1. Intrinsic Junction Capacitance Extraction
3.2.2. Intrinsic Series Resistance Extraction
3.3. Validation of DC Characteristics
3.4. Bandwidth Validation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Akyildiz, I.F.; Kak, A.; Nie, S. 6G and Beyond: The Future of Wireless Communications Systems. IEEE Access 2020, 8, 133995–134030. [Google Scholar] [CrossRef]
- Nagatsuma, T.; Ducournau, G.; Renaud, C.C. Advances in terahertz communications accelerated by photonics. Nat. Photon. 2016, 10, 371–379. [Google Scholar] [CrossRef]
- Mukherjee, C.; Deng, M.; Nodjiadjim, V.; Riet, M.; Mismer, C.; Guendouz, D.; Caillaud, C.; Bertin, H.; Vaissiere, N.; Luisier, M.; et al. Towards Monolithic Indium Phosphide (InP)-Based Electronic Photonic Technologies for beyond 5G Communication Systems. Appl. Sci. 2021, 11, 2393. [Google Scholar] [CrossRef]
- Koch, U.; Uhl, C.; Hettrich, H.; Fedoryshyn, Y.; Hoessbacher, C.; Heni, W.; Baeuerle, B.; Bitachon, B.I.; Josten, A.; Ayata, M.; et al. A Monolithic Bipolar CMOS Electronic–Plasmonic High-Speed Transmitter. Nat. Electron. 2020, 6, 338–345. [Google Scholar] [CrossRef]
- Sorace-Agaskar, C.; Leu, J.; Watts, M.R.; Stojanovic, V. Electro-Optical Co-Simulation for Integrated CMOS Photonic Circuits with VerilogA. Opt. Express 2015, 23, 27180. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, C.; Ardouin, B.; Dupuy, J.Y.; Nodjiadjim, V.; Riet, M.; Zimmer, T.; Marc, F.; Maneux, M. Reliability-Aware Circuit Design Methodology for beyond-5g Communication Systems. IEEE Trans. Device Mater. Reliab. 2017, 17, 490–506. [Google Scholar] [CrossRef] [Green Version]
- Shawon, M.J.; Saxena, V. Rapid Simulation of Photonic Integrated Circuits Using Verilog-A Compact Models. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 3331–3341. [Google Scholar] [CrossRef]
- Song, H.J.; Nagatsuma, T. Handbook of Terahertz Technologies: Devices and Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Ishibashi, T.; Shimizu, N.; Kodama, S.; Ito, H.; Nagatsuma, T.; Furata, H. Uni-Travelling-Carrier Photodiodes. Tech. Dig., Ultrafast Electronics and Optoelectronics. In Proceedings of the OSA Spring Topical Meeting, Lake Tahoe, NV, USA, 17–21 March 1997; pp. 166–168. [Google Scholar]
- Ito, H.; Nagatsuma, T.; Hirata, A.; Minotani, T.; Sasaki, A.; Hirota, Y.; Ishibashi, T. High-Power Photonic Millimetre Wave Generation at 100GHz Using Matching-Circuit-Integrated Uni-Travelling-Carrier Photodiodes. IEEE Proc. Optoelectron. 2003, 150, 138–142. [Google Scholar] [CrossRef]
- Mukherjee, C.; Natrella, M.; Seddon, J.; Graham, C.; Mounaix, P.; Renaud, C.C.; Maneux, C. Efficient compact modelling of UTC-photodiode towards terahertz communication system design. Solid-State Electron. 2020, 170, 107836. [Google Scholar] [CrossRef]
- Schroter, M.; Pawlak, A.; Sakalas, P.; Krause, J.; Nardmann, T. SiGeC and InP HBT Compact Modeling for Mm-Wave and THz Applications. In Proceedings of the Technical Digest—IEEE Compound Semiconductor Integrated Circuit Symposium (CSIC), Waikoloa, HI, USA, 16–19 October 2011. [Google Scholar] [CrossRef]
- Mukherjee, C.; Raya, C.; Ardouin, B.; Deng, M.; Frégonèse, S.; Zimmer, T.; Nodjiadjim, V.; Riet, M.; Dupuy, J.Y.; Luisier, M.; et al. Scalable Compact Modeling of III–V DHBTs: Prospective Figures of Merit Toward Terahertz Operation. IEEE Trans. Electron Devices 2018, 65, 5357–5364. [Google Scholar] [CrossRef]
- Ishibashi, T.; Ito, H. Uni-Traveling-Carrier Photodiodes. J. Appl. Phys. 2020, 127, 031101. [Google Scholar] [CrossRef]
- Banáš, S.; Divín, J.; Dobeš, J.; Paňko, V. Accurate Diode Behavioral Model with Reverse Recovery. Solid-State Electron. 2018, 139, 31–38. [Google Scholar] [CrossRef]
- Brinson, M.E.; Jahn, S. Qucs: A GPL Software Package for Circuit Simulation, Compact Device Modelling and Circuit Macromodelling from DC to RF and Beyond. Int. J. Numer. Model. Electron. Netw. Devices Fields 2009, 22, 297–319. [Google Scholar] [CrossRef] [Green Version]
- Scholten, A.J.; Smit, G.D.J.; Durand, M.; Van Langevelde, R.; Klaassen, D.B.M. The Physical Background of JUNGAP2. IEEE Trans. Electron Devices 2006, 53, 2098–2107. [Google Scholar] [CrossRef]
- Schroter, M.; Pawlak, A.; Mukherjee, A. HICUM/L2 A Geometry Scalable Physics-Based Compact Bipolar Transistor Model. 2017. Available online: http://www.iee.et.tudresden.de/iee/eb/forsch/Hicum_PD/Hicum23/hicum_L2_manual.pdf (accessed on 18 September 2021).
- Eastman, L.F.; Tiwari, S.; Shur, M.S. Design Criteria for GaAs MESFETs Related to Stationary High Field Domains. Solid State Electron. 1980, 23, 383–389. [Google Scholar] [CrossRef]
- Verdun, M.; Beaudoin, G.; Portier, B.; Bardou, N.; Dupuis, C.; Sagnes, I.; Haïdar, R.; Pardo, F.; Pelouard, J.L. Dark Current Investigation in Thin P-i-N InGaAs Photodiodes for Nano-Resonators. J. Appl. Phys. 2016, 120, 084501. [Google Scholar] [CrossRef] [Green Version]
- Milnes, A.G.; Feucht, D.L. Heterojunctions and Metal Semiconductor Junctions; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar] [CrossRef]
- Anagnosti, M.; Caillaud, C.; Blache, F.; Jorge, F.; Angelini, P.; Paret, J.F.; Achouche, M. Optimized High Speed UTC Photodiode for 100 Gbit/s Applications. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 29–35. [Google Scholar] [CrossRef]
- Arabhavi, A.M.; Chaudhary, R.; Fluckiger, R.; Marti, D.; Hamzeloui, S.; Ciabattini, F.; Quan, W.; Leich, M.; Ostinelli, O.; Bolognesi, C.R. Type-II GaInAsSb/InP Uniform Absorber High Speed Uni-Traveling Carrier Photodiodes. J. Lightwave Technol. 2021, 39, 2171–2176. [Google Scholar] [CrossRef]
- Xu, H.; Kasper, E. A De-Embedding Procedure for One-Port Active Mm-Wave Devices. In Proceedings of the 2010 Topical Meeting on Silicon Monolithic Integrated Circuits in RF Systems (SiRF), New Orleans, LA, USA, 11–13 January 2010; pp. 37–40. [Google Scholar] [CrossRef]
- Konstantinou, D.; Caillaud, C.; Rommel, S.; Johannsen, U.; Tafur Monroy, I. Investigation of De-Embedding Techniques Applied on Uni-Traveling Carrier Photodiodes. Int. J. Microw. Wirel. Technol. 2021, 13, 569–581. [Google Scholar] [CrossRef]
- Guendouz, D.; Deng, M.; Mukherjee, C.; Caillaud, C.; Mounaix, P.; De Matos, M.; Maneux, C. Access Modelling-Based De-Embedding Method for High-Frequency Characterization of Uni-Traveling Carrier Photodiodes. In Proceedings of the 51st European Microwave Conference (EuMC), London, UK, 13–18 February 2021. [Google Scholar]
- Davidson, A.; Jones, K.; Strid, E. LRM and LRRM Calibrations with Automatic Determination of Load Inductance. In Proceedings of the 36th ARFTG Conference Digest—Fall, Monterey, CA, USA, 29–30 November 1990. [Google Scholar] [CrossRef]
- Ehsan, M.A.; Zhou, Z.; Yi, Y. Development of an Equivalent Circuit Model of a Finite Ground Coplanar Waveguide Interconnect in MIS System for Ultra-Broadband Monolithic ICs. Prog. Electromagn. Res. 2015, 56, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011; Available online: https://scholar.google.fr/scholar?q=microwave+engineeing+pozar+2011+google+scholar&hl=fr&as_sdt=0&as_vis=1&oi=scholart (accessed on 18 September 2021).













| UTC-PD Technology | Drawn Active Area (µm2) | |
|---|---|---|
| UTC-PD type I | InGaAs/InGaAsP | 100, 125 and 150 |
| InGaAs/InP | 13 | |
| UTC-PD type II | GaInAsSb/InP | 64, 79 and 100 |
| 18.0 pH | 15.0 fF | 0.83 Ω | 28.0 pH | 11.0 fF | 5.0 pH | 5.0 fF |
| 0.19 Ω | 47.55 pH | 11.49 fF |
| 1.5 Ω | 106.74 pH | 48.06 fF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guendouz, D.; Mukherjee, C.; Deng, M.; De Matos, M.; Caillaud, C.; Bertin, H.; Bobin, A.; Vaissière, N.; Mekhazni, K.; Mallecot, F.; et al. Multiscale Compact Modelling of UTC-Photodiodes Enabling Monolithic Terahertz Communication Systems Design. Appl. Sci. 2021, 11, 11088. https://doi.org/10.3390/app112311088
Guendouz D, Mukherjee C, Deng M, De Matos M, Caillaud C, Bertin H, Bobin A, Vaissière N, Mekhazni K, Mallecot F, et al. Multiscale Compact Modelling of UTC-Photodiodes Enabling Monolithic Terahertz Communication Systems Design. Applied Sciences. 2021; 11(23):11088. https://doi.org/10.3390/app112311088
Chicago/Turabian StyleGuendouz, Djeber, Chhandak Mukherjee, Marina Deng, Magali De Matos, Christophe Caillaud, Hervé Bertin, Antoine Bobin, Nicolas Vaissière, Karim Mekhazni, Franck Mallecot, and et al. 2021. "Multiscale Compact Modelling of UTC-Photodiodes Enabling Monolithic Terahertz Communication Systems Design" Applied Sciences 11, no. 23: 11088. https://doi.org/10.3390/app112311088
APA StyleGuendouz, D., Mukherjee, C., Deng, M., De Matos, M., Caillaud, C., Bertin, H., Bobin, A., Vaissière, N., Mekhazni, K., Mallecot, F., Arabhavi, A. M., Chaudhary, R., Ostinelli, O., Bolognesi, C., Mounaix, P., & Maneux, C. (2021). Multiscale Compact Modelling of UTC-Photodiodes Enabling Monolithic Terahertz Communication Systems Design. Applied Sciences, 11(23), 11088. https://doi.org/10.3390/app112311088






