A Tunable Metamaterial Joint for Mechanical Shock Applications Inspired by Carbon Nanotubes
Abstract
:1. Introduction
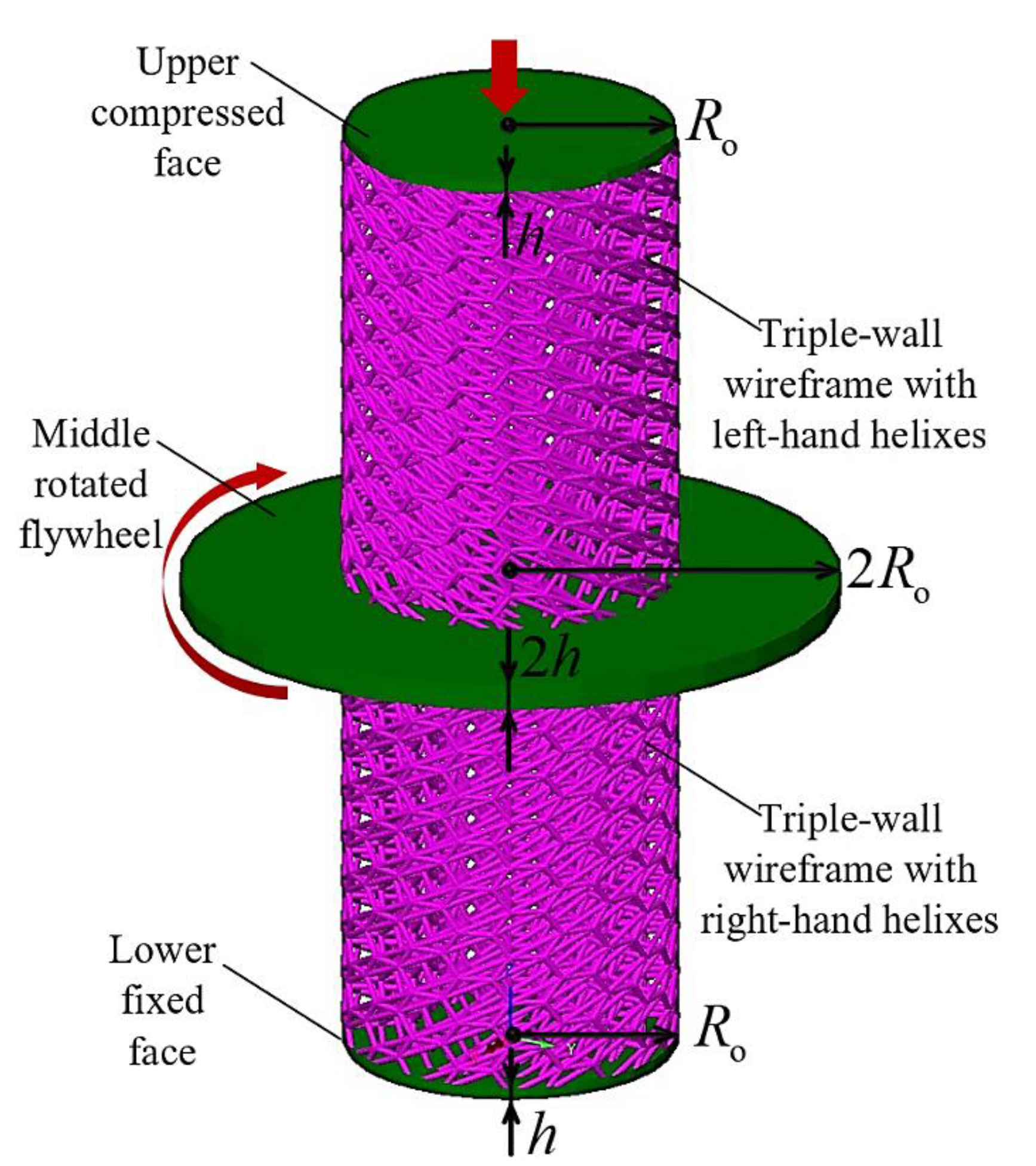
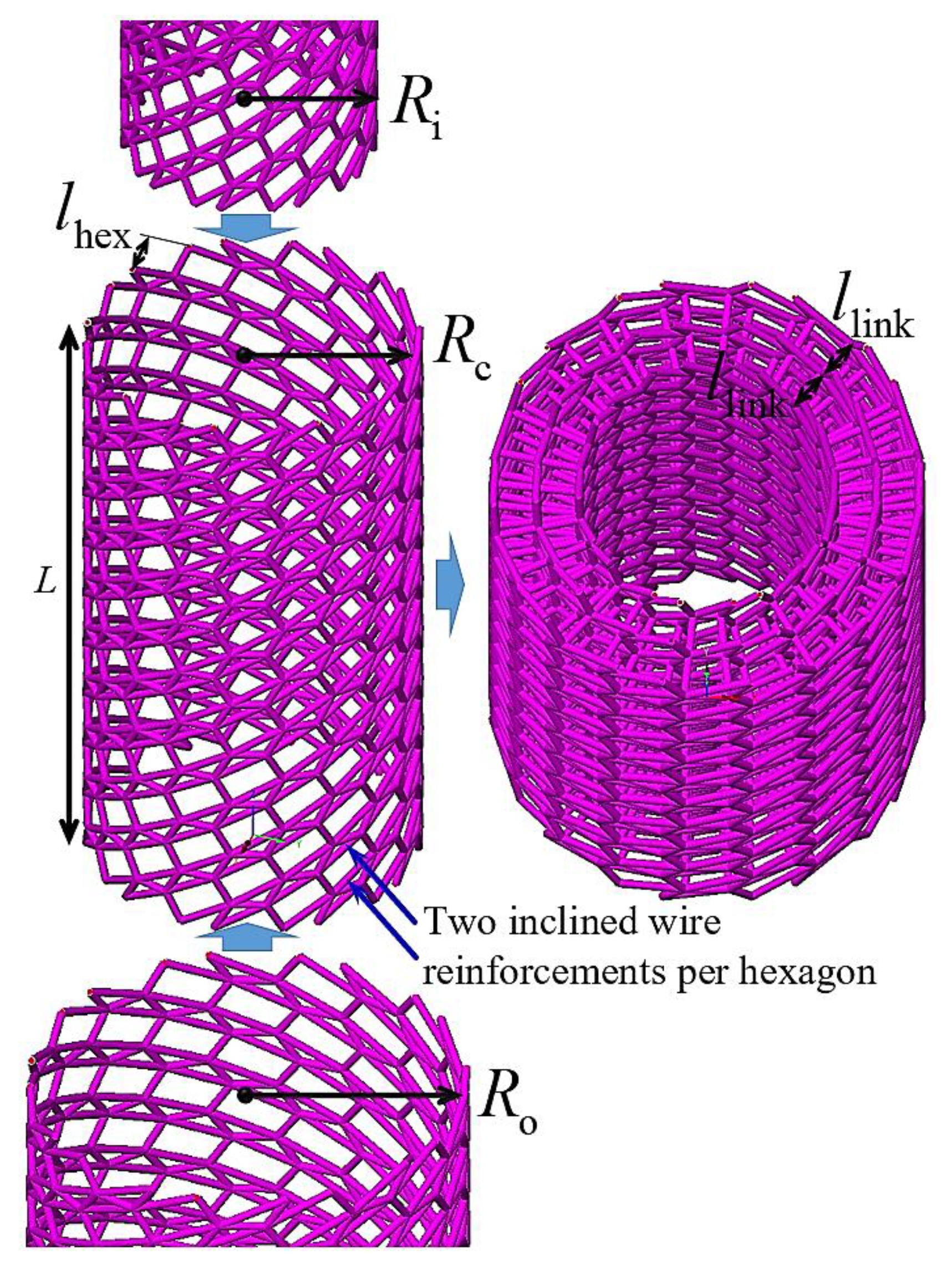
2. Design and Microstructure of the Joint
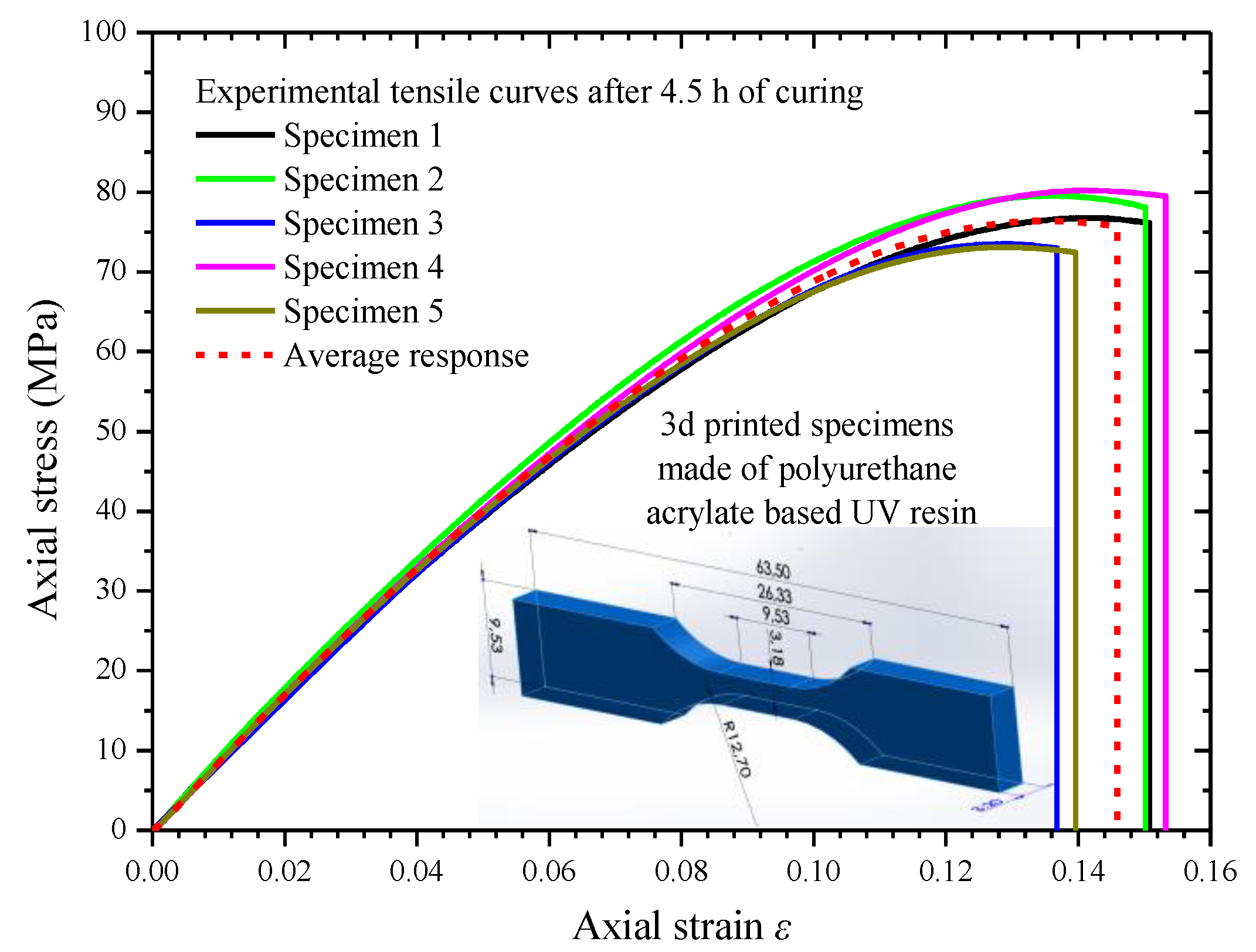
3. Experimental Characterization of the UV Resin After-Curing Mechanical Behavior
4. Results
4.1. Fundamental Equations and Numerical Process
4.2. Mesh, Material Properties, and Boundary Conditions
5. Evaluation and Characterization of the Compressive Behavior of the Joint
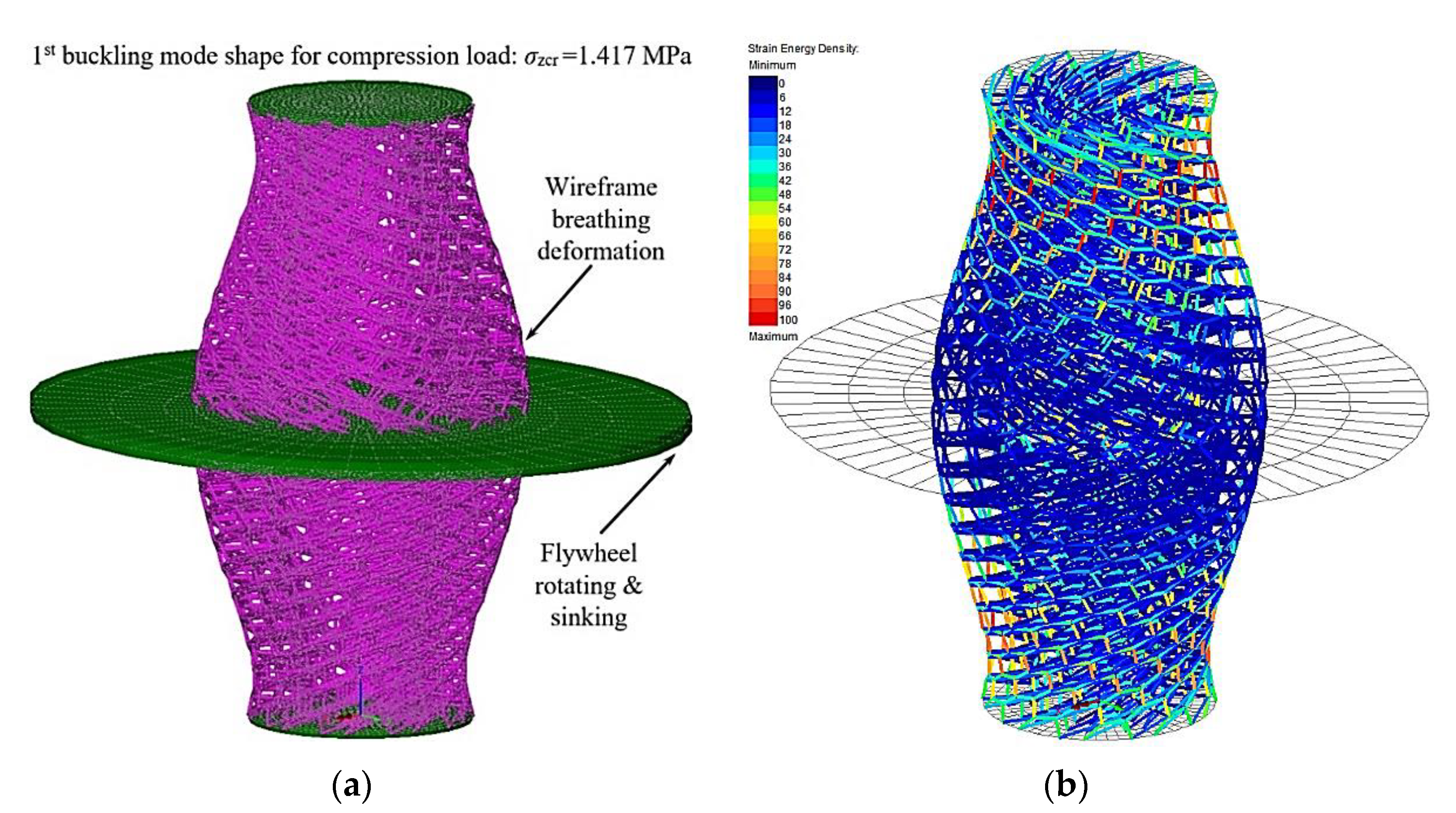
5.1. Linear Elastic Buckling Analysis
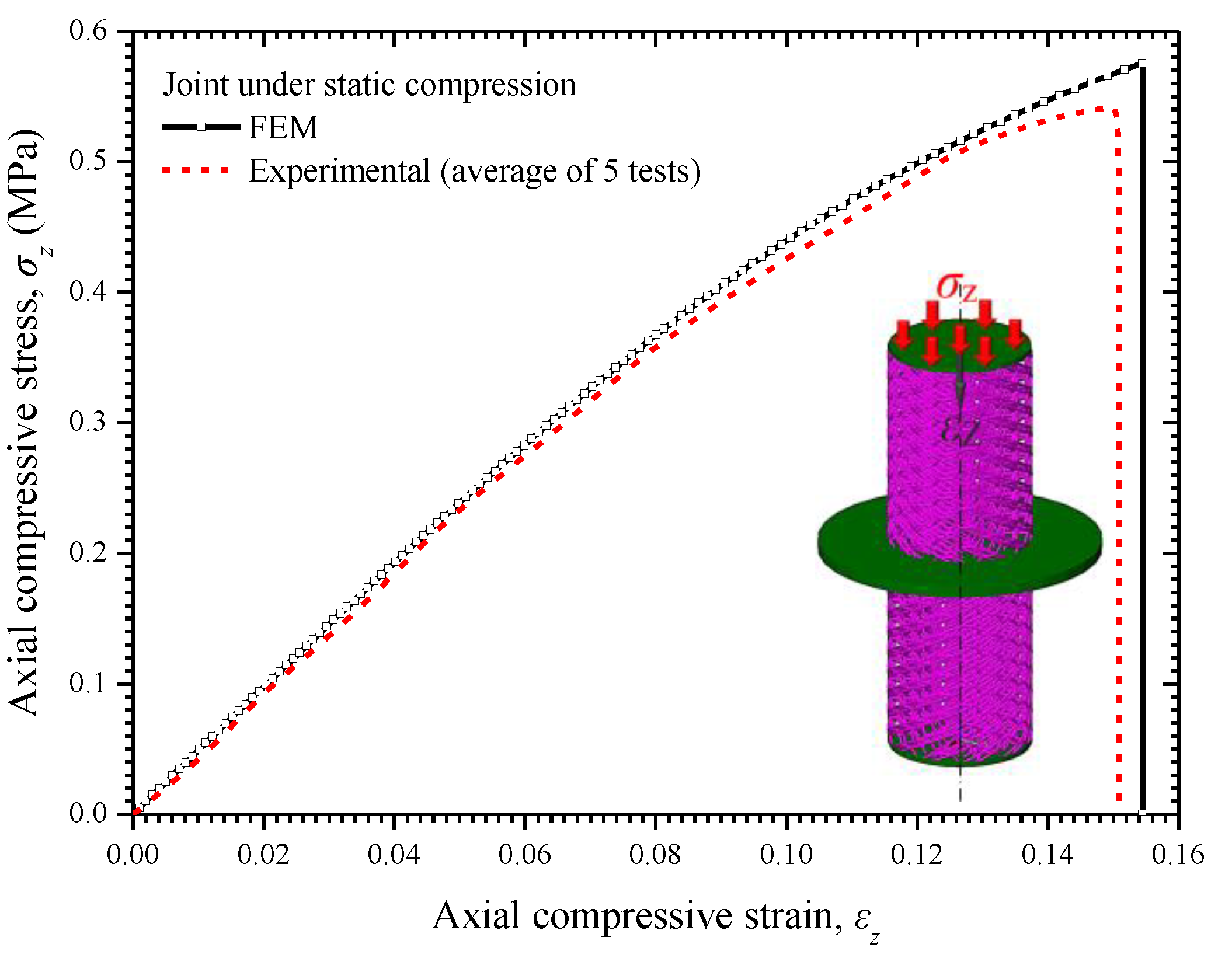
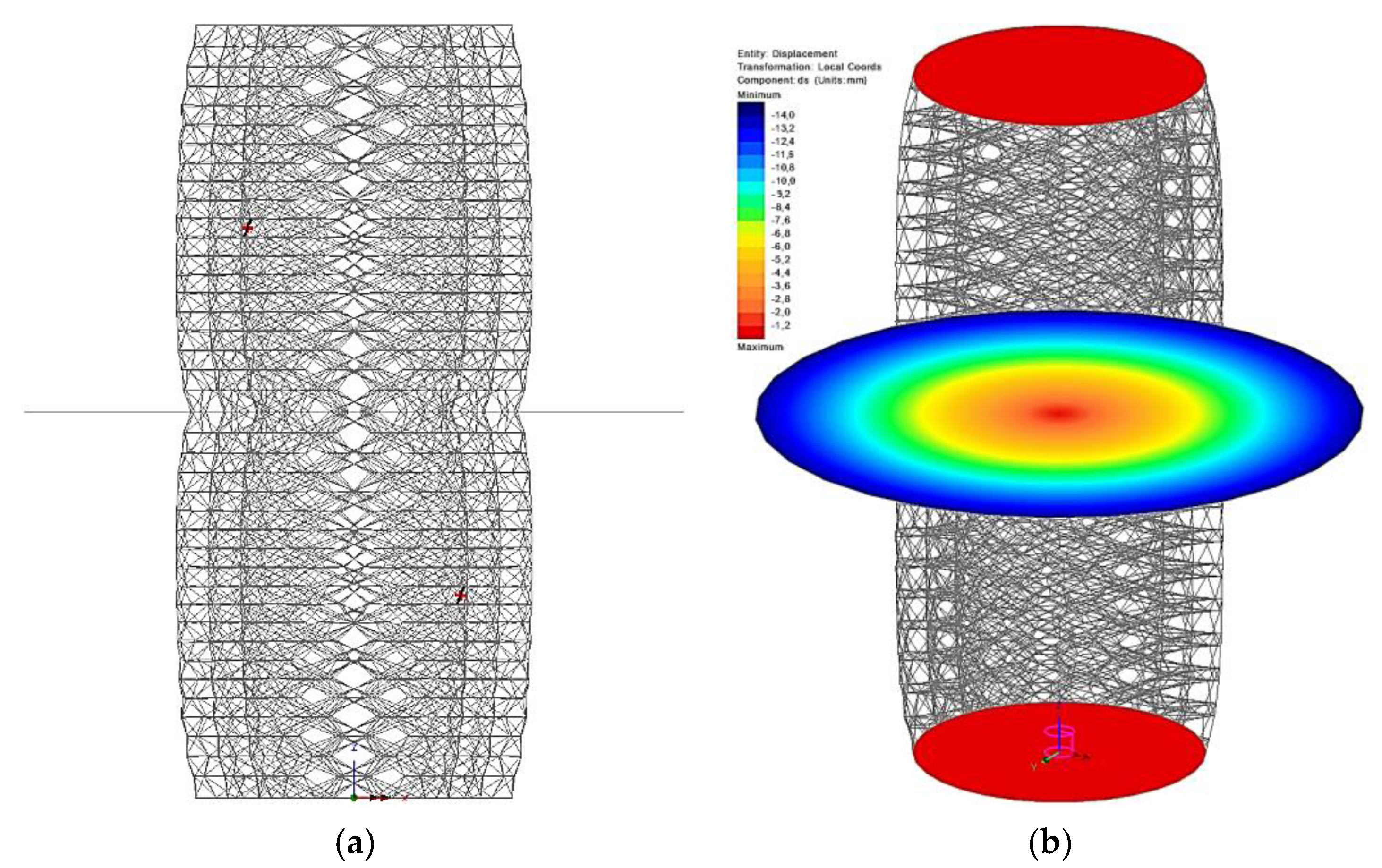
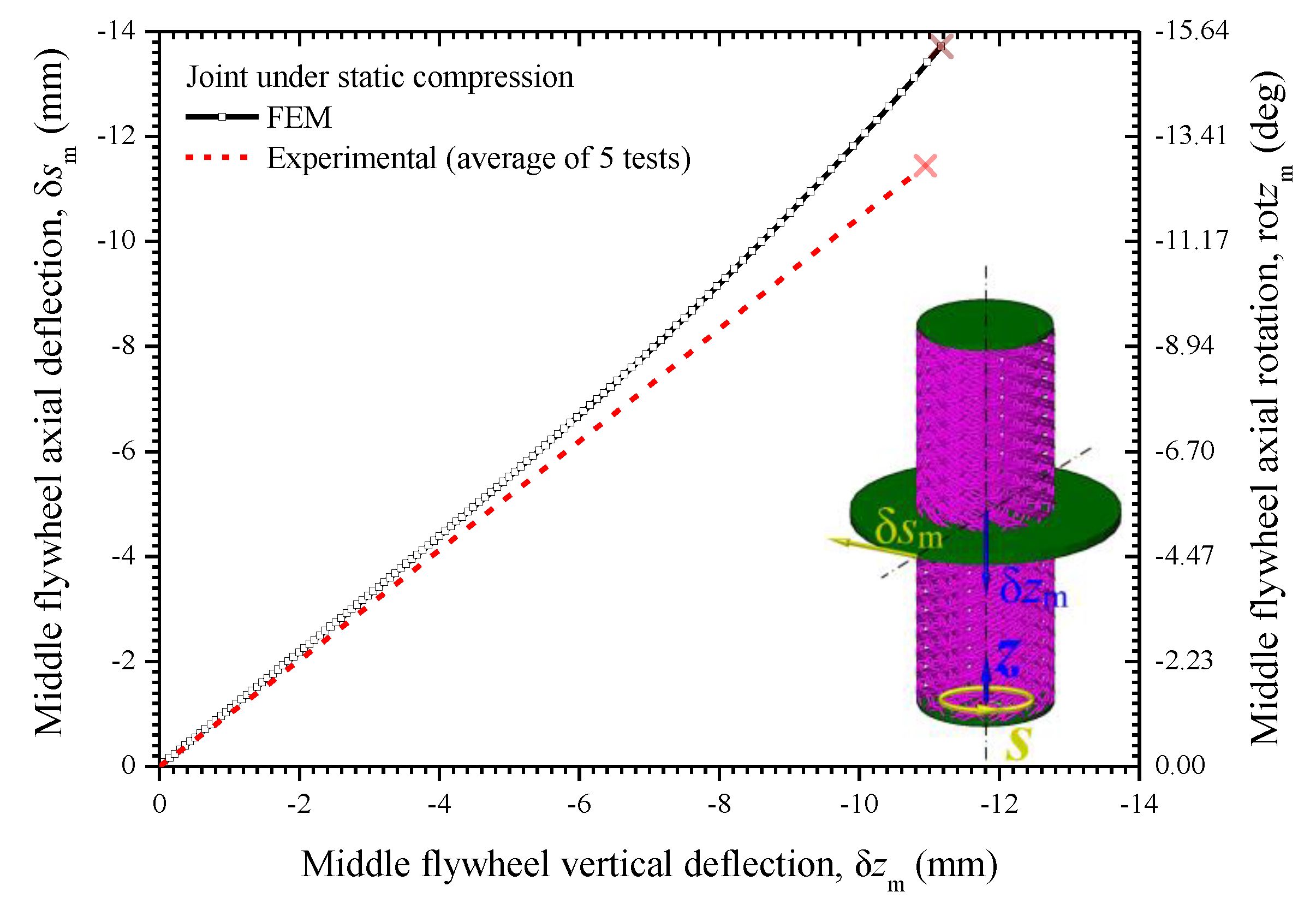
5.2. Static Elastoplastic Analysis
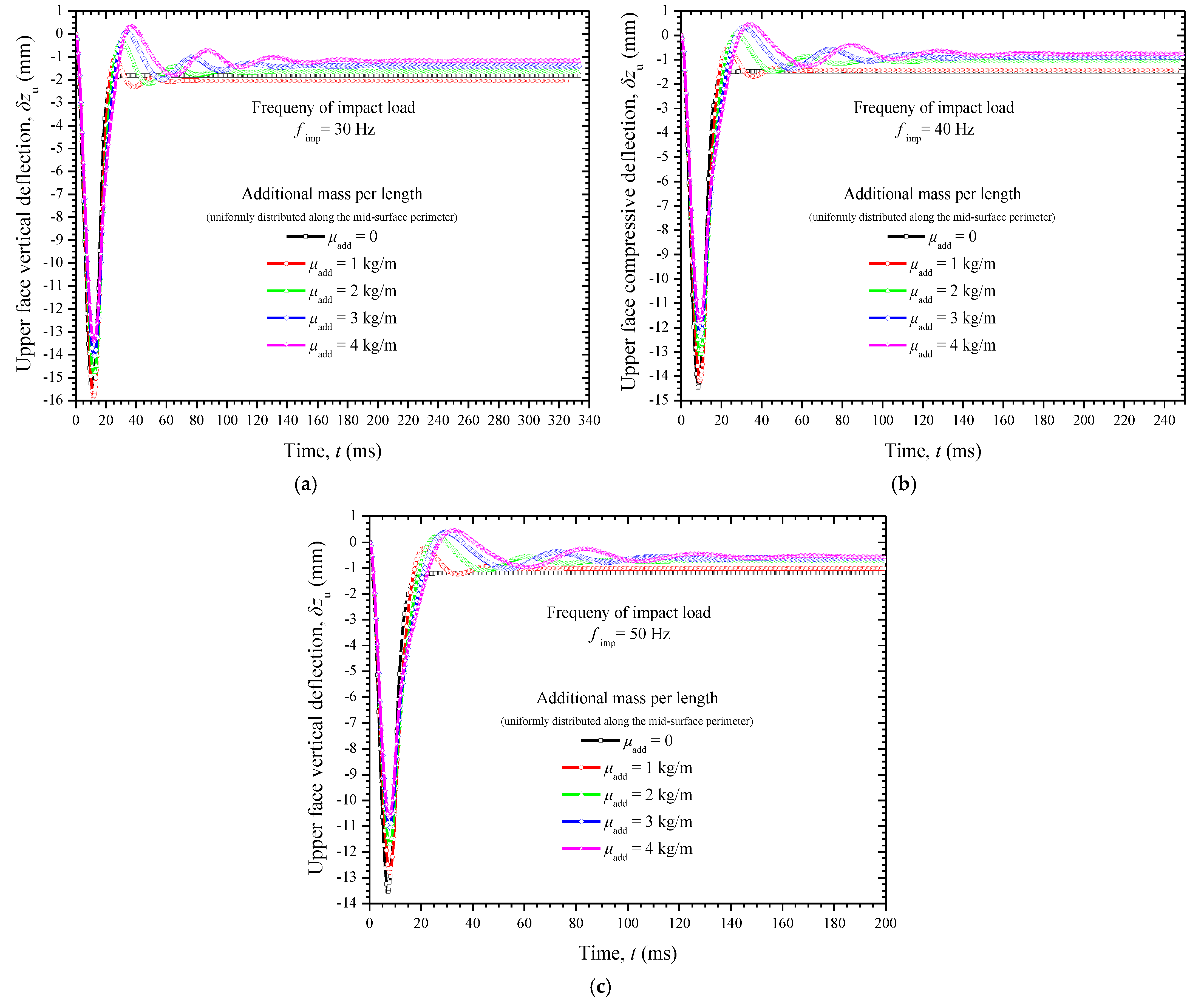
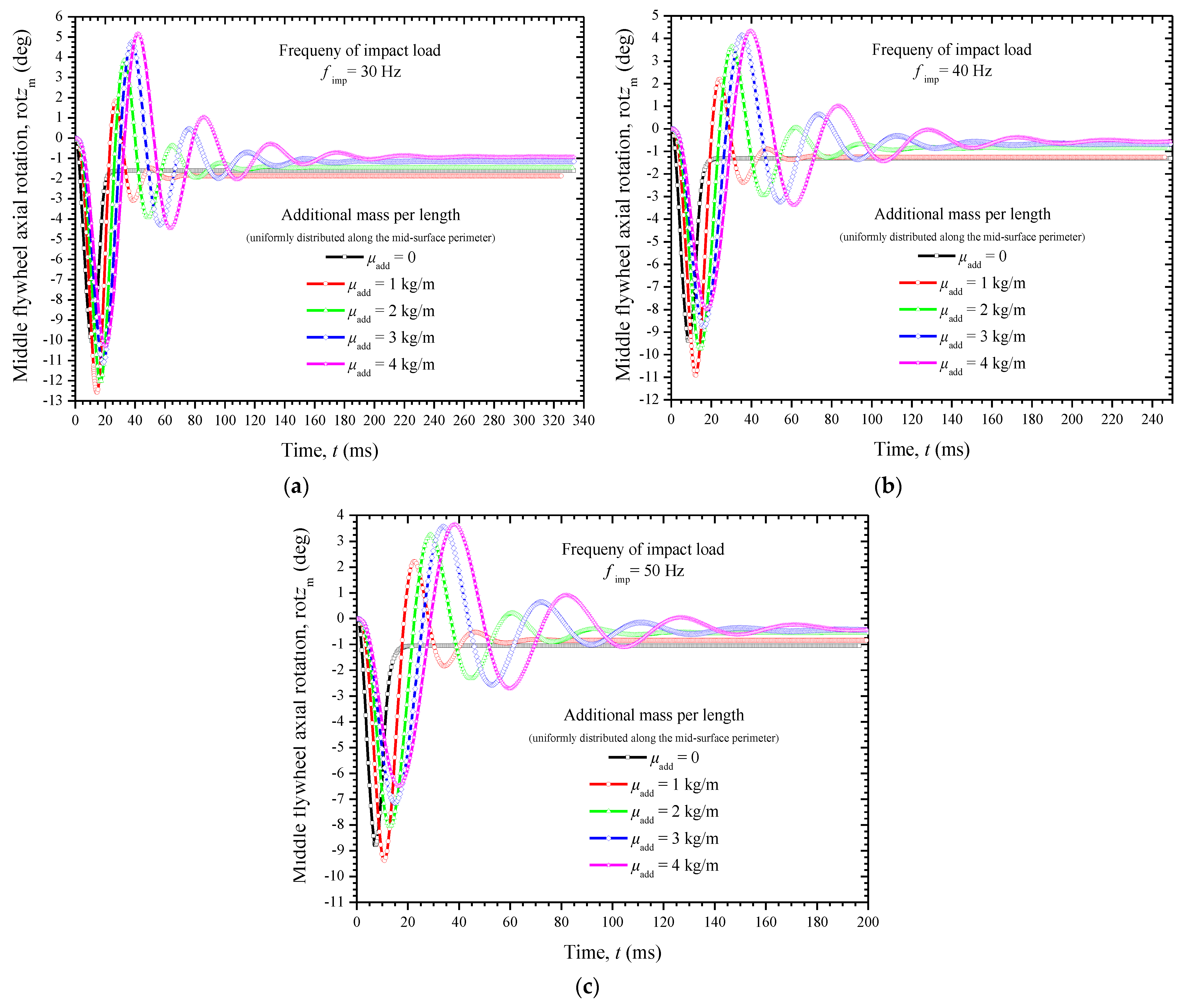
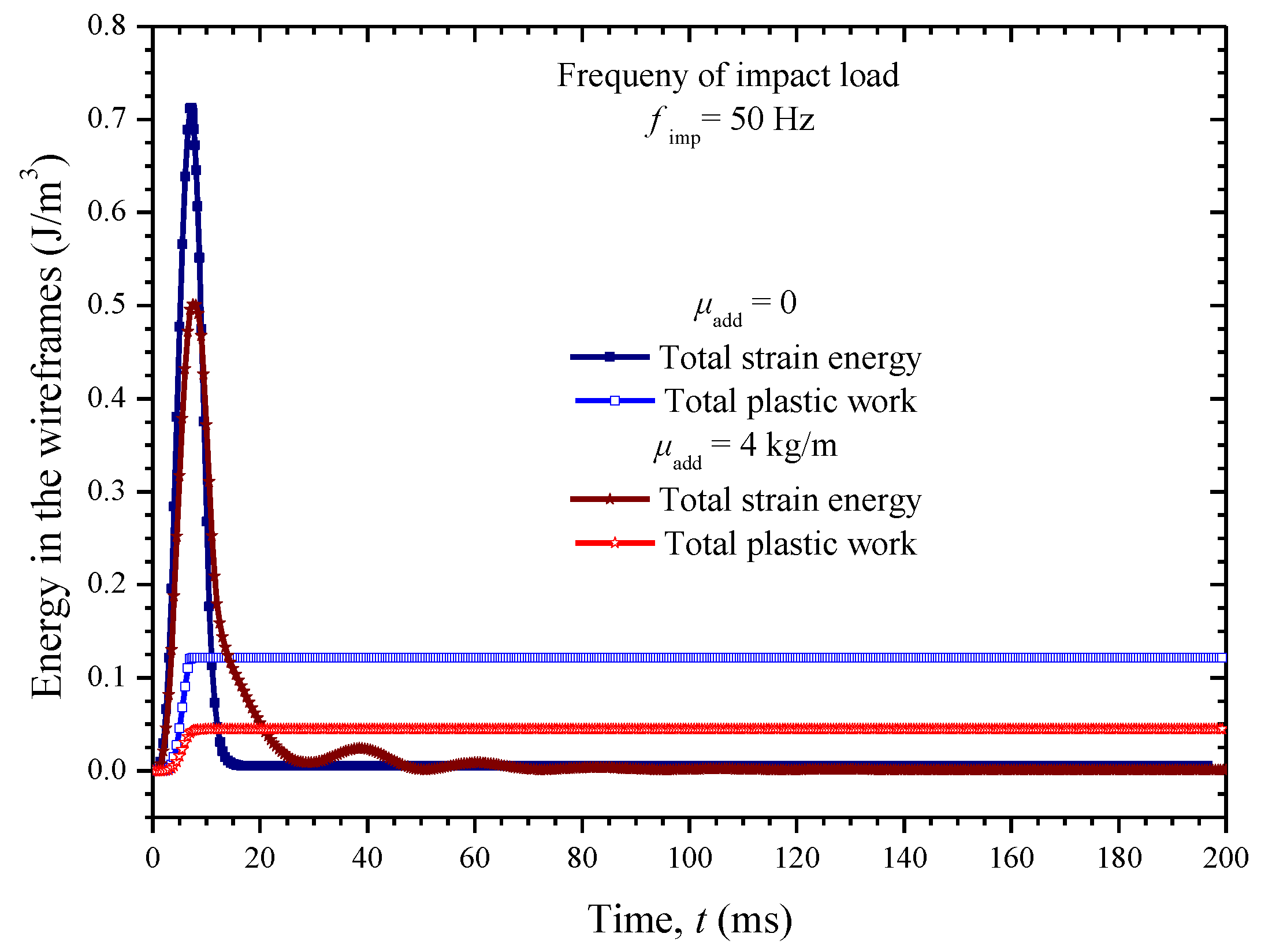
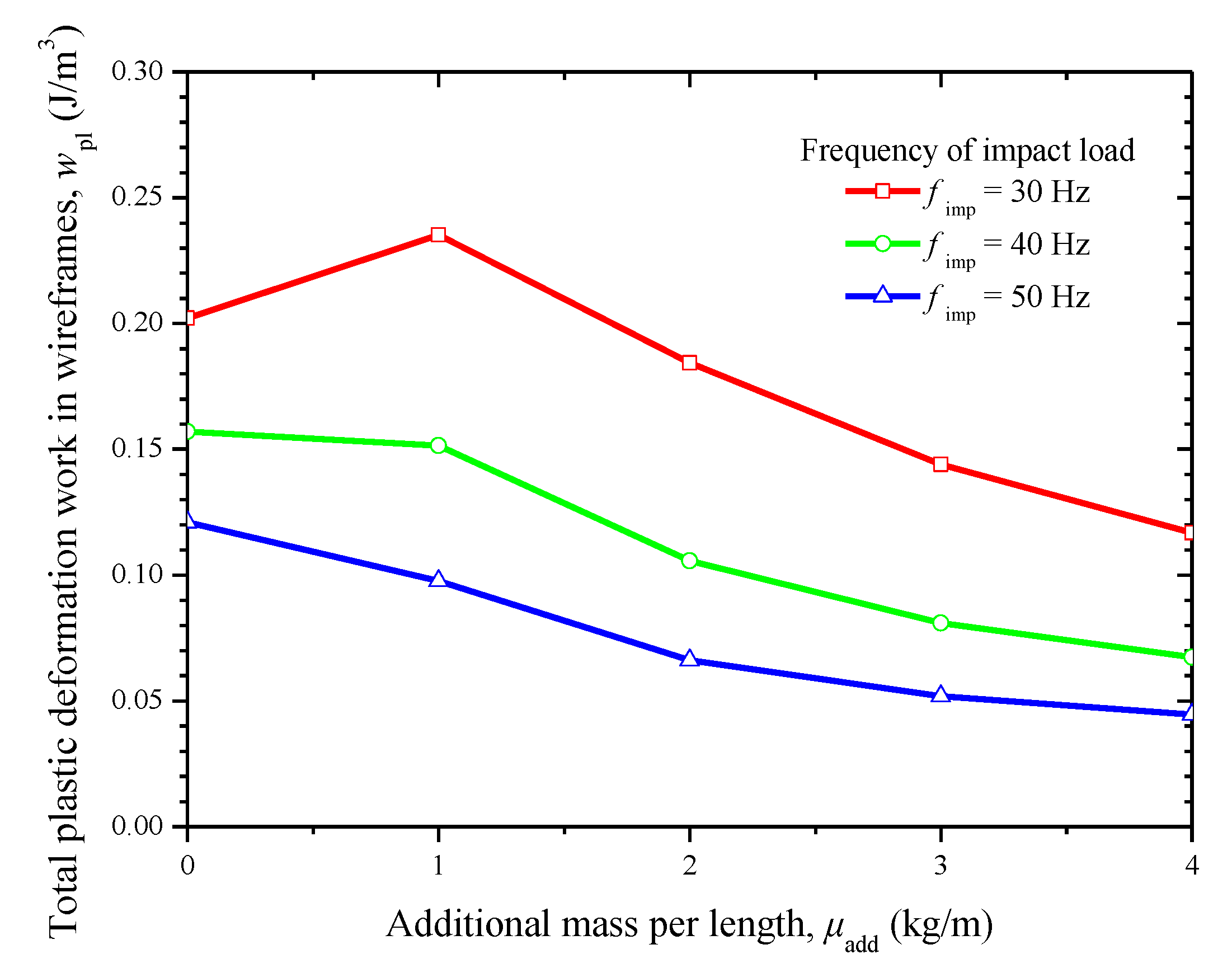
5.3. Dynamic Impact Analysis
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Huang, J.-Q.; Qian, W.-Z.; Zhang, Y.; Wei, F. The Road for Nanomaterials Industry: A Review of Carbon Nanotube Production, Post-Treatment, and Bulk Applications for Composites and Energy Storage. Small 2013, 9, 1237–1265. [Google Scholar] [CrossRef] [PubMed]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 2019, 21, 1800864. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Miao, W.-S.; Zhang, Y.-D.; Gao, H.-J.; Hui, D. Mechanical properties of nanomaterials: A review. Nanotechnol. Rev. 2020, 9, 259–273. [Google Scholar] [CrossRef]
- Gouadec, G.; Colomban, P. Raman Spectroscopy of nanomaterials: How spectra relate to disorder, particle size and mechanical properties. Prog. Cryst. Growth Charact. Mater. 2007, 53, 1–56. [Google Scholar] [CrossRef] [Green Version]
- Guz, I.; Rodger, A.; Guz, A.; Rushchitsky, J. Developing the mechanical models for nanomaterials. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1234–1250. [Google Scholar] [CrossRef]
- Ariga, K.; Mori, T.; Hill, J.P. Mechanical Control of Nanomaterials and Nanosystems. Adv. Mater. 2012, 24, 158–176. [Google Scholar] [CrossRef]
- Tang, Q.; Zhou, Z.; Chen, Z. Graphene-related nanomaterials: Tuning properties by functionalization. Nanoscale 2013, 5, 4541–4583. [Google Scholar] [CrossRef]
- Baimova, Y.A.; Murzaev, R.T.; Dmitriev, S. Mechanical properties of bulk carbon nanomaterials. Phys. Solid State 2014, 56, 2010–2016. [Google Scholar] [CrossRef]
- Zaeri, M.; Ziaei-Rad, S.; Vahedi, A.; Karimzadeh, F. Mechanical modelling of carbon nanomaterials from nanotubes to buckypaper. Carbon 2010, 48, 3916–3930. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, F.; Li, N.; Qu, N.; Gou, H.; Hao, X. Density functional theory study of hexagonal carbon phases. J. Phys. Condens. Matter 2009, 21, 235401. [Google Scholar] [CrossRef]
- Liarte, D.B.; Stenull, O.; Lubensky, T.C. Multifunctional twisted kagome lattices: Tuning by pruning mechanical metamaterials. Phys. Rev. E 2020, 101, 063001. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Xu, X.; Shi, J.; Huang, G. A 3D Mechanism-driven Hexagonal Metamaterial: Evaluation of Auxetic Behavior. Int. J. Mech. Sci. 2021, 209, 106699. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Ghaedizadeh, A.; Tian, H.; Xie, Y.M. Experiments and parametric studies on 3D metallic auxetic metamaterials with tuneable mechanical properties. Smart Mater. Struct. 2015, 24, 095016. [Google Scholar] [CrossRef]
- Cui, H.; Hensleigh, R.; Chen, H.; Zheng, X. Additive Manufacturing and size-dependent mechanical properties of three-dimensional microarchitected, high-temperature ceramic metamaterials. J. Mater. Res. 2018, 33, 360–371. [Google Scholar] [CrossRef] [Green Version]
- Dragoni, E.; Ciace, V.A. Mechanical design and modelling of lightweight additively manufactured lattice structures evolved from regular three-dimensional tessellations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1759–1773. [Google Scholar] [CrossRef]
- Wickeler, A.L.; Naguib, H.E. Novel origami-inspired metamaterials: Design, mechanical testing and finite element modelling. Mater. Des. 2020, 186, 108242. [Google Scholar] [CrossRef]
- Mizzi, L.; Attard, D.; Gatt, R.; Dudek, K.K.; Ellul, B.; Grima, J.N. Implementation of periodic boundary conditions for loading of mechanical metamaterials and other complex geometric microstructures using finite element analysis. Eng. Comput. 2020, 37, 1765–1779. [Google Scholar] [CrossRef]
- Ghaedizadeh, A.; Shen, J.; Ren, X.; Xie, Y.M. Tuning the Performance of Metallic Auxetic Metamaterials by Using Buckling and Plasticity. Materials 2016, 9, 54. [Google Scholar] [CrossRef]
- Coulais, C. As the extension, so the twist. Science 2017, 358, 994–995. [Google Scholar] [CrossRef]
- Cheng, L.; Tang, T.; Yang, H.; Hao, F.; Wu, G.; Lyu, F.; Bu, Y.; Zhao, Y.; Zhao, Y.; Liu, G.; et al. The Twisting of Dome-Like Metamaterial from Brittle to Ductile. Adv. Sci. 2021, 8, 2002701. [Google Scholar] [CrossRef]
- Ji, J.; Luo, Q.; Ye, K. Vibration control based metamaterials and origami structures: A state-of-the-art review. Mech. Syst. Signal Process. 2021, 161, 107945. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Wang, X.-T.; Ma, L. Damping mechanisms of CFRP three-dimensional double-arrow-head auxetic metamaterials. Polym. Test. 2020, 81, 106189. [Google Scholar] [CrossRef]
- Qiao, J.; Chen, C. Impact resistance of uniform and functionally graded auxetic double arrowhead honeycombs. Int. J. Impact Eng. 2015, 83, 47–58. [Google Scholar] [CrossRef]
- Ma, L.; Chen, Y.-L.; Yang, J.-S.; Wang, X.-T.; Ma, G.-L.; Schmidt, R.; Schröder, K.-U. Modal characteristics and damping enhancement of carbon fiber composite auxetic double-arrow corrugated sandwich panels. Compos. Struct. 2018, 203, 539–550. [Google Scholar] [CrossRef]
- Miniaci, M.; Krushynska, A.; Bosia, F.; Pugno, N.M. Large scale mechanical metamaterials as seismic shields. New J. Phys. 2016, 18, 083041. [Google Scholar] [CrossRef]
- Van Belle, L.; Claeys, C.; Deckers, E.; Desmet, W. On the impact of damping on the dispersion curves of a locally resonant metamaterial: Modelling and experimental validation. J. Sound Vib. 2017, 409, 1–23. [Google Scholar] [CrossRef]
- Rebelo, H.; Lecompte, D.; Cismasiu, C.; Jonet, A.; Belkassem, B.; Maazoun, A. Experimental and numerical investigation on 3D printed PLA sacrificial honeycomb cladding. Int. J. Impact Eng. 2019, 131, 162–173. [Google Scholar] [CrossRef]
- Santos, F.; Rebelo, H.; Coutinho, M.; Sutherland, L.; Cismasiu, C.; Farina, I.; Fraternali, F. Low velocity impact response of 3D printed structures formed by cellular metamaterials and stiffening plates: PLA vs. PETg. Compos. Struct. 2021, 256, 113128. [Google Scholar] [CrossRef]
- Chen, X.; Ji, Q.; Wei, J.; Tan, H.; Yu, J.; Zhang, P.; Laude, V.; Kadic, M. Light-weight shell-lattice metamaterials for mechanical shock absorption. Int. J. Mech. Sci. 2020, 169, 105288. [Google Scholar] [CrossRef]
- Brecher, C.; Fey, M.; Bäumler, S. Damping models for machine tool components of linear axes. CIRP Ann. 2013, 62, 399–402. [Google Scholar] [CrossRef]
- Kołoczek, J.; Kwon, Y.-K.; Burian, A. Characterization of spatial correlations in carbon nanotubes-modelling studies. J. Alloys Compd. 2001, 328, 222–225. [Google Scholar] [CrossRef]
- Shan, J.; Yang, Z.; Chen, G.; Hu, Y.; Luo, Y.; Dong, X.; Zheng, W.; Zhou, W. Design and Synthesis of Free-Radical/Cationic Photosensitive Resin Applied for 3D Printer with Liquid Crystal Display (LCD) Irradiation. Polymers 2020, 12, 1346. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, K.W.H.; Mohamad, Z.; Othman, N.; Man, S.H.C.; Jusoh, M. The mechanical properties of photopolymer prepared via 3d stereolithography printing: The effect of uv curing time and anisotropy. Chem. Eng. Trans. 2020, 78, 565–570. [Google Scholar]
- LUSAS Version 15.0: Theory Volume Manual 1 and 2; LUSAS: Kingston Upon Thames: Surrey, UK, 2013.
- Chowdhury, I.; Dasgupta, S.P. Computation of Rayleigh damping coefficients for large systems. Electron. J. Geotech. Eng. 2003, 8, 1–11. [Google Scholar]
- Liao, F.; Zeng, X.-R.; Li, H.-Q.; Lai, X.-J.; Zhao, F.-C. Synthesis and properties of UV curable polyurethane acrylates based on two different hydroxyethyl acrylates. J. Central South Univ. 2012, 19, 911–917. [Google Scholar] [CrossRef]
- Malas, A.; Isakov, D.; Couling, K.; Gibbons, G.J. Fabrication of High Permittivity Resin Composite for Vat Photopolymerization 3D Printing: Morphology, Thermal, Dynamic Mechanical and Dielectric Properties. Materials 2019, 12, 3818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McLaskey, G.C.; Glaser, S.D. Hertzian impact: Experimental study of the force pulse and resulting stress waves. J. Acoust. Soc. Am. 2010, 128, 1087–1096. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Creality LD-002H UV Resin 3D Printer | ASTM Standardized 3D Printed Specimens | ||
|---|---|---|---|
| Specification | Value | Property | Value |
| Modeling Technology: | LCD | Layer Height: | 0.05 mm |
| Print Size: | 130 mm × 82 mm × 160 mm | Bottom Layer Count: | 8 |
| Print Speed: | 1–4 s/layer | Exposure Time: | 6 s |
| Screen: | 3.5-inch touch screen | Bottom Exposure Time: | 50 s |
| Machine Size: | 221 mm × 221 mm × 403 mm | Light-off Delay: | 0 |
| Package Size: | 295 mm × 295 mm × 540 mm | Bottom Light-off Delay: | 0 |
| Machine Weight: | 8.3 kg | Bottom Lift Distance: | 5 mm |
| Layer Height: | 0.03–0.05 mm | Lifting Distance: | 5 mm |
| XY axis Precision: | 0.051 mm | Bottom Lift Speed: | 20 mm/min |
| Lifting Speed: | 65 mm/min | ||
| Retract Speed: | 100 mm/min | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannopoulos, G.I.; Georgantzinos, S.K. A Tunable Metamaterial Joint for Mechanical Shock Applications Inspired by Carbon Nanotubes. Appl. Sci. 2021, 11, 11139. https://doi.org/10.3390/app112311139
Giannopoulos GI, Georgantzinos SK. A Tunable Metamaterial Joint for Mechanical Shock Applications Inspired by Carbon Nanotubes. Applied Sciences. 2021; 11(23):11139. https://doi.org/10.3390/app112311139
Chicago/Turabian StyleGiannopoulos, Georgios I., and Stylianos K. Georgantzinos. 2021. "A Tunable Metamaterial Joint for Mechanical Shock Applications Inspired by Carbon Nanotubes" Applied Sciences 11, no. 23: 11139. https://doi.org/10.3390/app112311139
APA StyleGiannopoulos, G. I., & Georgantzinos, S. K. (2021). A Tunable Metamaterial Joint for Mechanical Shock Applications Inspired by Carbon Nanotubes. Applied Sciences, 11(23), 11139. https://doi.org/10.3390/app112311139







