Influence of Concrete Strength Class on the Long-Term Static and Dynamic Elastic Moduli of Concrete
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results and Discussions
3.1. Static Modulus of Elasticity
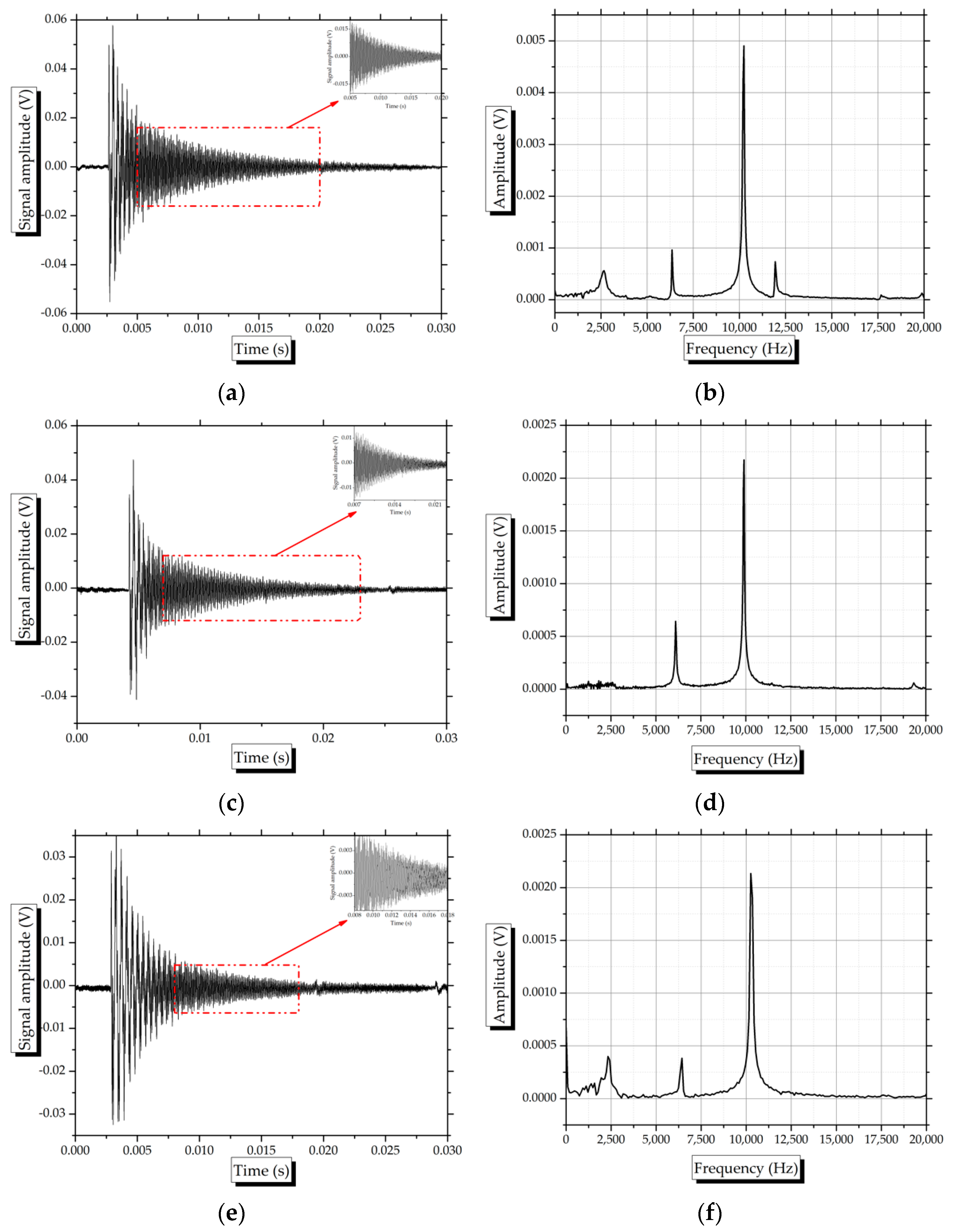
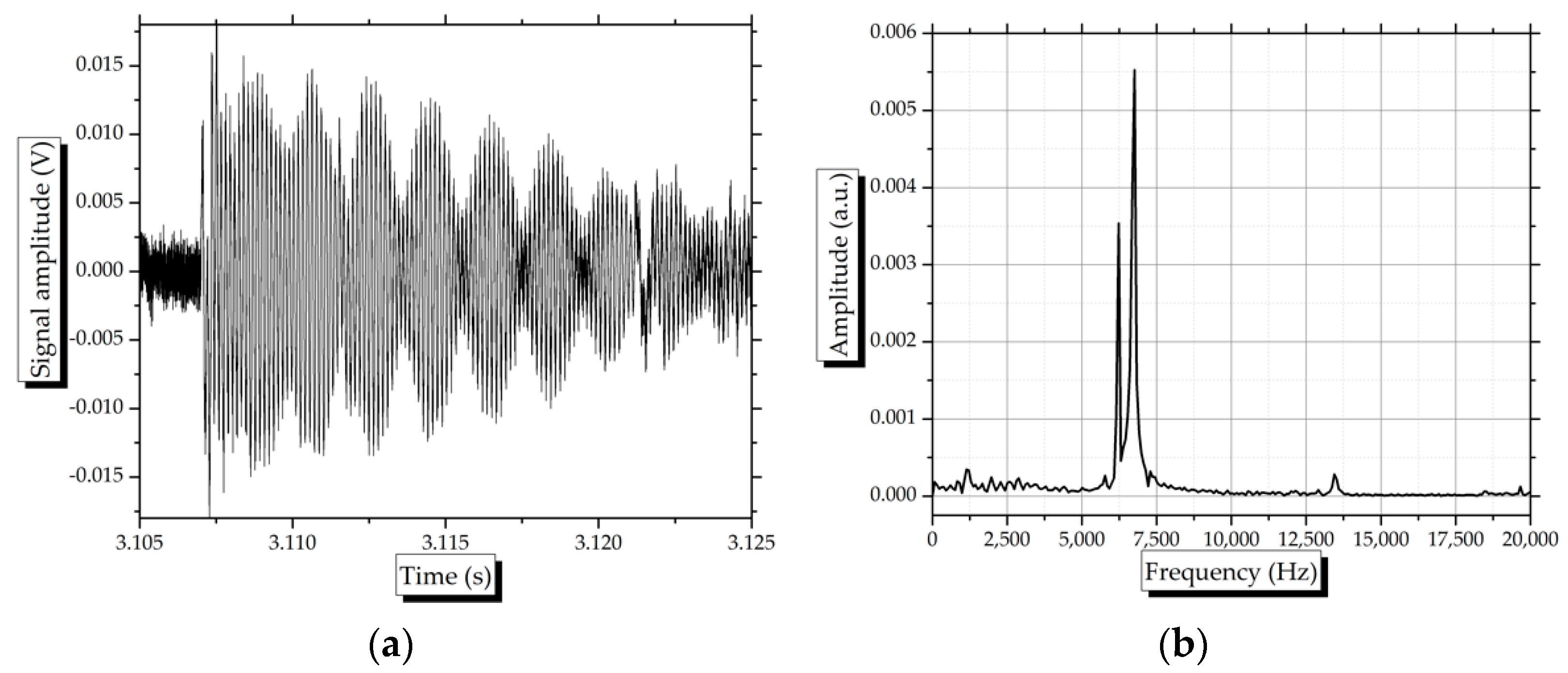
3.2. Dynamic Longitudinal Modulus of Elasticity
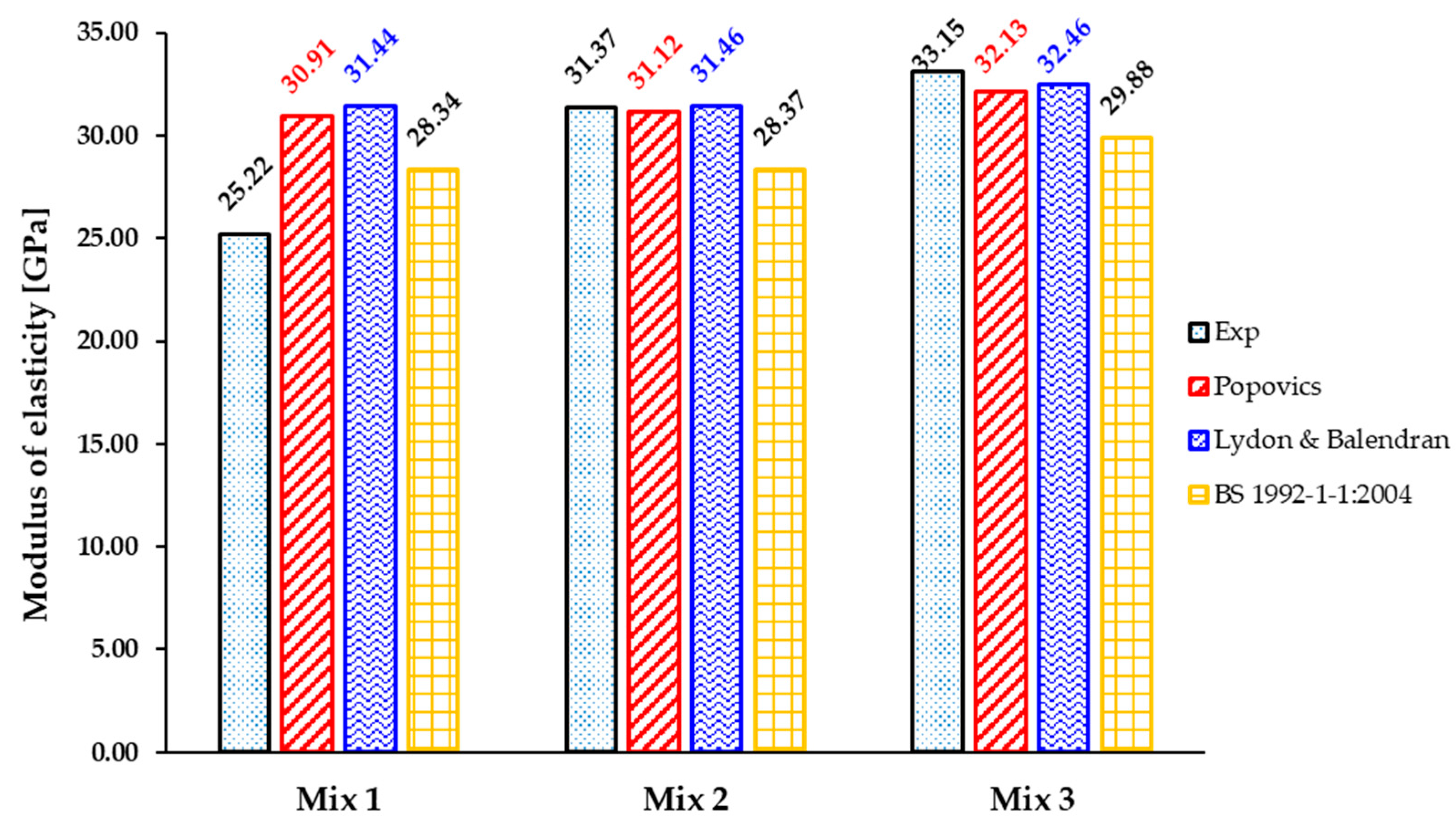
3.3. Conversion Equations from Dynamic to Static Modulus of Elasticity
3.4. Dynamic Shear Modulus of Elasticity
3.5. Dynamic Poisson’s Ratio
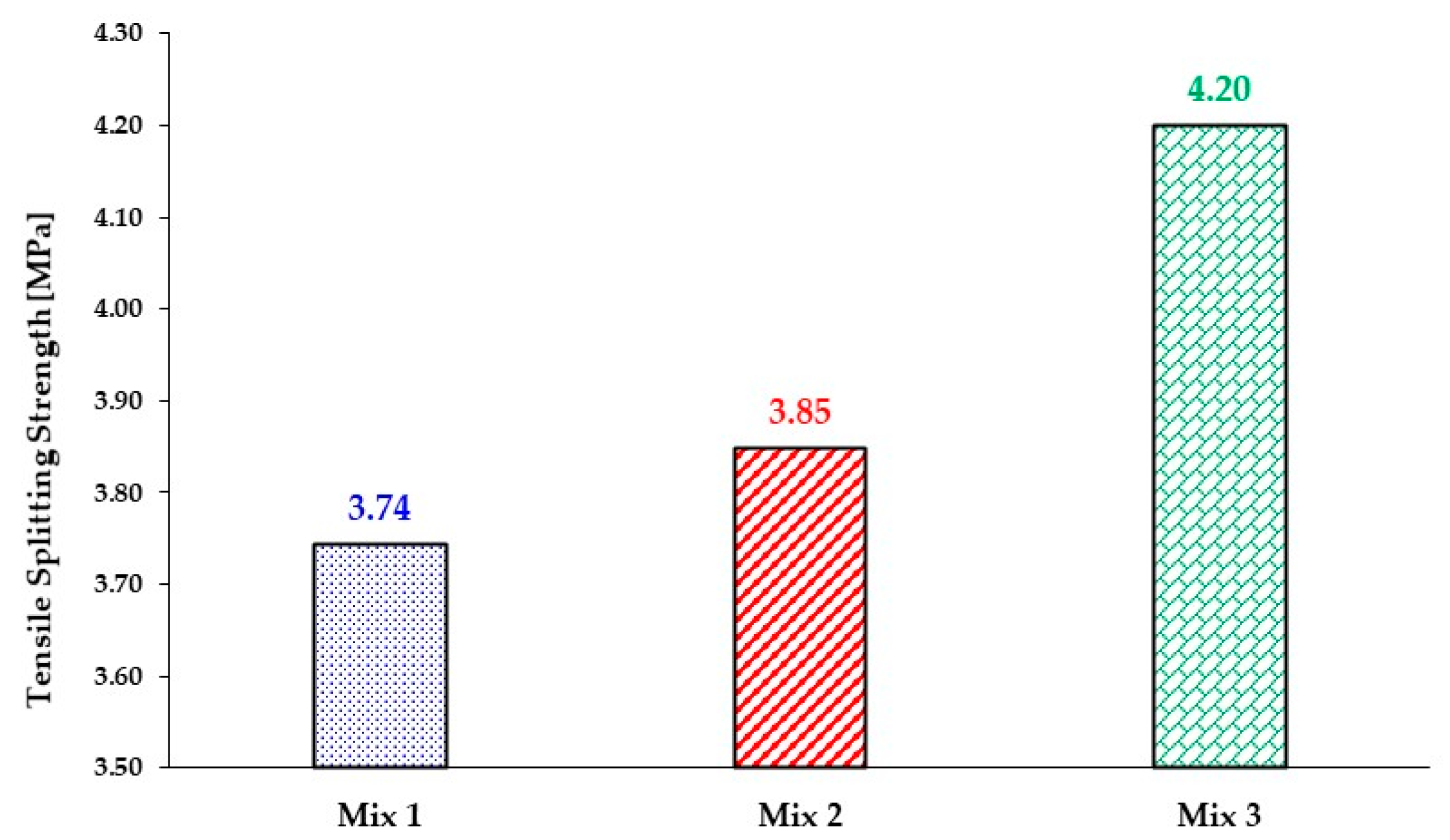
3.6. Compressive and Tensile Splitting Strengths
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nasseralshariati, E.; Mohammadzadeh, D.; Karballaeezadeh, N.; Mosavi, A.; Reuter, U.; Saatcioglu, M. The Effect of Incorporating Industrials Wastewater on Durability and Long-Term Strength of Concrete. Materials 2021, 14, 4088. [Google Scholar] [CrossRef] [PubMed]
- Terzijski, I.; Kocáb, D.; Štěpánek, P.; Strnad, J.; Girgle, F.; Šimůnek, P. Development of Variants of High-Performance Self-Compacting Concrete with Improved Resistance to the Attack of Sulfates. Appl. Sci. 2021, 11, 5945. [Google Scholar] [CrossRef]
- Asaad, M.; Morcous, G. Evaluating Prediction Models of Creep and Drying Shrinkage of Self-Consolidating Concrete Containing Supplementary Cementitious Materials/Fillers. Appl. Sci. 2021, 11, 7345. [Google Scholar] [CrossRef]
- Sanjuán, M.; Andrade, C. Reactive Powder Concrete: Durability and Applications. Appl. Sci. 2021, 11, 5629. [Google Scholar] [CrossRef]
- Borosnyói, A. Long term durability performance and mechanical properties of high performance concretes with combined use of supplementary cementing materials. Constr. Build. Mater. 2016, 112, 307–324. [Google Scholar] [CrossRef]
- Al Menhosh, A.; Wang, Y.; Wang, Y.; Nelson, L.A. Long term durability properties of concrete modified with metakaolin and polymer admixture. Constr. Build. Mater. 2018, 172, 41–51. [Google Scholar] [CrossRef]
- Shi, J.; Liu, B.; Shen, S.; Tan, J.; Dai, J.; Ji, R. Effect of curing regime on long-term mechanical strength and transport properties of steam-cured concrete. Constr. Build. Mater. 2020, 255, 119407. [Google Scholar] [CrossRef]
- Dey, A.; Vastrad, A.V.; Bado, M.F.; Sokolov, A.; Kaklauskas, G. Long-Term Concrete Shrinkage Influence on the Performance of Reinforced Concrete Structures. Materials 2021, 14, 254. [Google Scholar] [CrossRef] [PubMed]
- Kliukas, R.; Jaras, A.; Lukoševičienė, O. The Impact of Long-Term Physical Salt Attack and Multicycle Temperature Gradient on the Mechanical Properties of Spun Concrete. Materials 2021, 14, 4811. [Google Scholar] [CrossRef] [PubMed]
- Bradu, A.; Mihai, P.; Budescu, M.; Banu, O.-M.; Taranu, N.; Florea, N. The Comparative Study of the Self-Compacting Concrete and of Vibrated Concrete Properties Including the Complete Characteristic Curve under Compression. Rev. Rom. Mater. J. Mater. 2017, 47, 379–386. [Google Scholar]
- European Committee for Standardization. EN1992-1-1:2004 Eurocode 2: Design of Concrete structures—Part 1-1: General Rules and Rules for Buildings 2004; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Romanian Standards Association (ASRO). SR EN 197-1: Cement. Part I: Composition, Specifications and Conformity Criteria for Normal Use Cements 2011; Romanian Standards Association (ASRO): Bucharest, Romania, 2011. [Google Scholar]
- Romanian Standards Association (ASRO). SR EN 12390-13/2013, Testing Hardened Concrete. Part 13: Determination of Secant Modulus of Elasticity in Compression 2013; Romanian Standards Association (ASRO): Bucharest, Romania, 2011. [Google Scholar]
- Romanian Standards Association (ASRO). SR EN 12390-3/2009, Testing Hardened Concrete. Part 3: Compressive Strength of Test Specimens 2009; Romanian Standards Association (ASRO): Bucharest, Romania, 2011. [Google Scholar]
- Romanian Standards Association (ASRO). SR EN 12390-6/2010—Testing Hardened Concrete. Part 6: Tensile Splitting Strength of Test Specimens 2010; Romanian Standards Association (ASRO): Bucharest, Romania, 2011. [Google Scholar]
- ASTM International. ASTM C215-14—Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens 2014; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Toma, I.-O.; Alexa-Stratulat, S.-M.; Mihai, P.; Toma, A.-M.; Taranu, G. Experimental Investigations on the Long Term Material Properties of Rubberized Portland Cement Concrete. Appl. Sci. 2021, 11, 10868. [Google Scholar] [CrossRef]
- Kou, S.-C.; Poon, C.S. Long-term mechanical and durability properties of recycled aggregate concrete prepared with the incorporation of fly ash. Cem. Concr. Compos. 2013, 37, 12–19. [Google Scholar] [CrossRef]
- Obayes, O.; Gad, E.; Pokharel, T.; Lee, J.; Abdouka, K. Evaluation of Concrete Material Properties at Early Age. Civil Eng. 2020, 1, 326–350. [Google Scholar] [CrossRef]
- Mead, D.J. A general theory of harmonic wave propagation in linear periodic systems with multiple coupling. J. Sound Vib. 1973, 27, 235–260. [Google Scholar] [CrossRef]
- Popovics, S. Verification of relationships between mechanical properties of concrete-like materials. Mater. Struct. 1975, 8, 183–191. [Google Scholar] [CrossRef]
- Lydon, F.D.; Balendran, R.V. Some observations on elastic properties of plain concrete. Cem. Concr. Res. 1986, 16, 314–324. [Google Scholar] [CrossRef]
- British Standards Institute (BSI). BS EN 1992-1-1—Structural use of concrete. In Code of Practice for Special Circumstances; British Standards Institute (BSI): London, UK, 2004; ISBN 0 580 14490 9. [Google Scholar]
- Leon, G.; Chen, H.-L. (Roger) Direct Determination of Dynamic Elastic Modulus and Poisson’s Ratio of Timoshenko Rods. Vibration 2019, 2, 157–173. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, L. Dynamic Measurements for Determining Poisson’s Ratio of Young Concrete. Nord. Concr. Res. 2018, 58, 95–106. [Google Scholar] [CrossRef] [Green Version]
- Pal, P. Dynamic poisson’s ratio and modulus of elasticity of pozzolana Portland cement concrete. Int. J. Eng. Technol. Innov. 2019, 9, 131–144. [Google Scholar]
- Mhaya, A.M.; Huseien, G.F.; Abidin, A.R.Z.; Ismail, M. Long-term mechanical and durable properties of waste tires rubber crumbs replaced GBFS modified concretes. Constr. Build. Mater. 2020, 256, 119505. [Google Scholar] [CrossRef]
- American Concrete Institute (ACI). ACI CODE-318-14: Building Code Requirements for Structural Concrete and Commentary 2014; American Concrete Institute (ACI): Farmington Hills, MI, USA, 2014. [Google Scholar]



| Mix Designation | Cement (C) | Water (W) | W/C | Aggregates | Super-Plasticizer | ||
|---|---|---|---|---|---|---|---|
| Sand | Sort 4–8 mm | Sort 8–16 mm | |||||
| [kg/m3] | [kg/m3] | - | [kg/m3] | [kg/m3] | [kg/m3] | [kg/m3] | |
| Mix1 | 320 | 160 | 0.5 | 799 | 309 | 796 | 1.6 |
| Mix 2 | 340 | 170 | 756 | 302 | 810 | 1.7 | |
| Mix 3 | 360 | 180 | 739 | 294 | 788 | 1.8 | |
| Mix Designation | Static Modulus of Elasticity | Standard Deviation | Coefficient of Variation |
|---|---|---|---|
| [MPa] | [MPa] | [%] | |
| Mix 1 | 25,214 | 2461.7 | 9.76 |
| Mix 2 | 31,369 | 1563.1 | 4.98 |
| Mix 3 | 33,147 | 1838.3 | 5.55 |
| Mix Designation | Dynamic Modulus of Elasticity, Ed | Standard Deviation | Coefficient of Variation |
|---|---|---|---|
| [MPa] | [MPa] | [%] | |
| Mix 1 | 37,874 | 1071.14 | 2.83 |
| Mix 2 | 37,900 | 1221.27 | 3.22 |
| Mix 3 | 39,106 | 685.01 | 1.75 |
| Mix Designation | Dynamic Shear Modulus, Gd | Standard Deviation | Coefficient of Variation |
|---|---|---|---|
| [MPa] | [MPa] | [%] | |
| Mix 1 | 14,386 | 450.61 | 3.13 |
| Mix 2 | 14,540 | 581.81 | 4.00 |
| Mix 3 | 15,088 | 384 | 2.55 |
| Mix Designation | Dynamic Poisson’s Ratio, μd | Standard Deviation | Coefficient of Variation |
|---|---|---|---|
| - | - | [%] | |
| Mix 1 | 0.303 | 0.0202 | 6.68 |
| Mix 2 | 0.316 | 0.0111 | 3.51 |
| Mix 3 | 0.296 | 0.0147 | 4.95 |
| Mix Designation | Ec (Eurocode 2, Equation (9)) | Exp/Ec, Equation (9) | Ec (ACI 318-14, Equation (10)) | Exp/Ec, Equation (10) |
|---|---|---|---|---|
| [MPa] | - | [MPa] | - | |
| Mix 1 | 31,840 | 0.79 | 28,883 | 0.87 |
| Mix 2 | 33,122 | 0.95 | 30,252 | 1.04 |
| Mix 3 | 36,107 | 0.92 | 35,223 | 0.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexa-Stratulat, S.-M.; Mihai, P.; Toma, A.-M.; Taranu, G.; Toma, I.-O. Influence of Concrete Strength Class on the Long-Term Static and Dynamic Elastic Moduli of Concrete. Appl. Sci. 2021, 11, 11671. https://doi.org/10.3390/app112411671
Alexa-Stratulat S-M, Mihai P, Toma A-M, Taranu G, Toma I-O. Influence of Concrete Strength Class on the Long-Term Static and Dynamic Elastic Moduli of Concrete. Applied Sciences. 2021; 11(24):11671. https://doi.org/10.3390/app112411671
Chicago/Turabian StyleAlexa-Stratulat, Sergiu-Mihai, Petru Mihai, Ana-Maria Toma, George Taranu, and Ionut-Ovidiu Toma. 2021. "Influence of Concrete Strength Class on the Long-Term Static and Dynamic Elastic Moduli of Concrete" Applied Sciences 11, no. 24: 11671. https://doi.org/10.3390/app112411671
APA StyleAlexa-Stratulat, S.-M., Mihai, P., Toma, A.-M., Taranu, G., & Toma, I.-O. (2021). Influence of Concrete Strength Class on the Long-Term Static and Dynamic Elastic Moduli of Concrete. Applied Sciences, 11(24), 11671. https://doi.org/10.3390/app112411671








