A Novel Method for Predicting Local Site Amplification Factors Using 1-D Convolutional Neural Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Geological Condition
2.2. Preparation of the Data
2.2.1. Amplification Factor
2.2.2. Surface Amplification Factors at Lower Hutt Valley
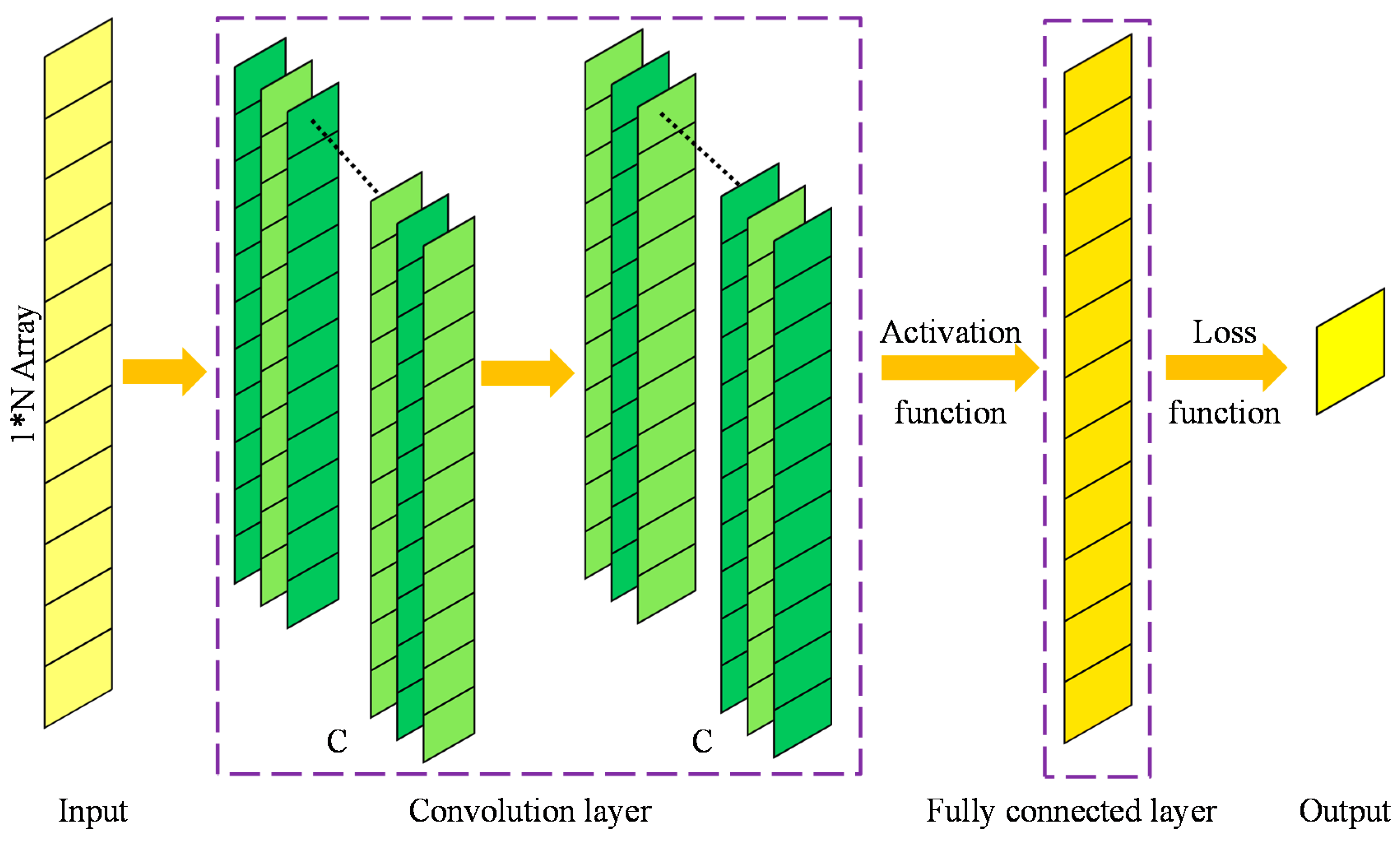
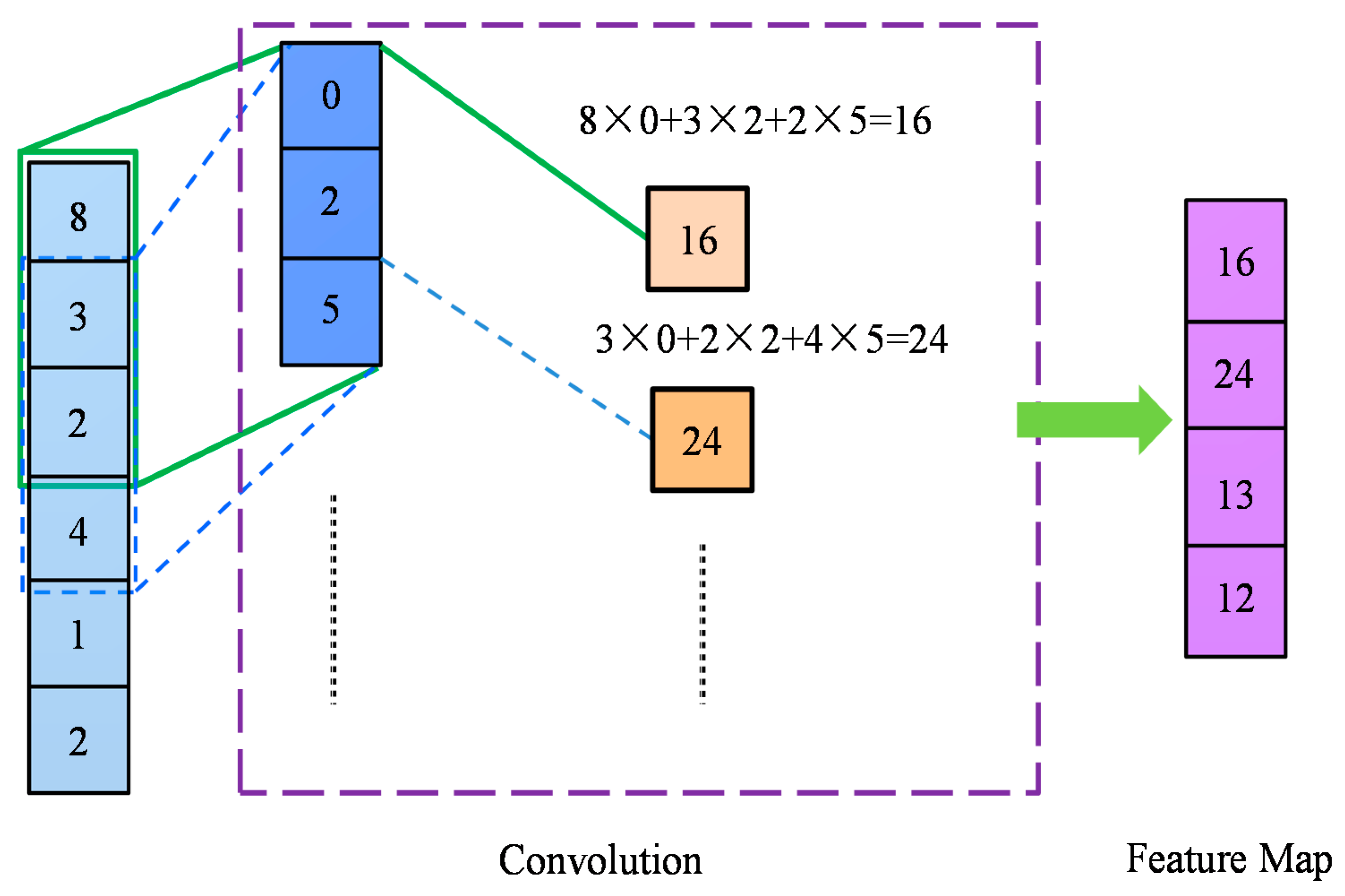
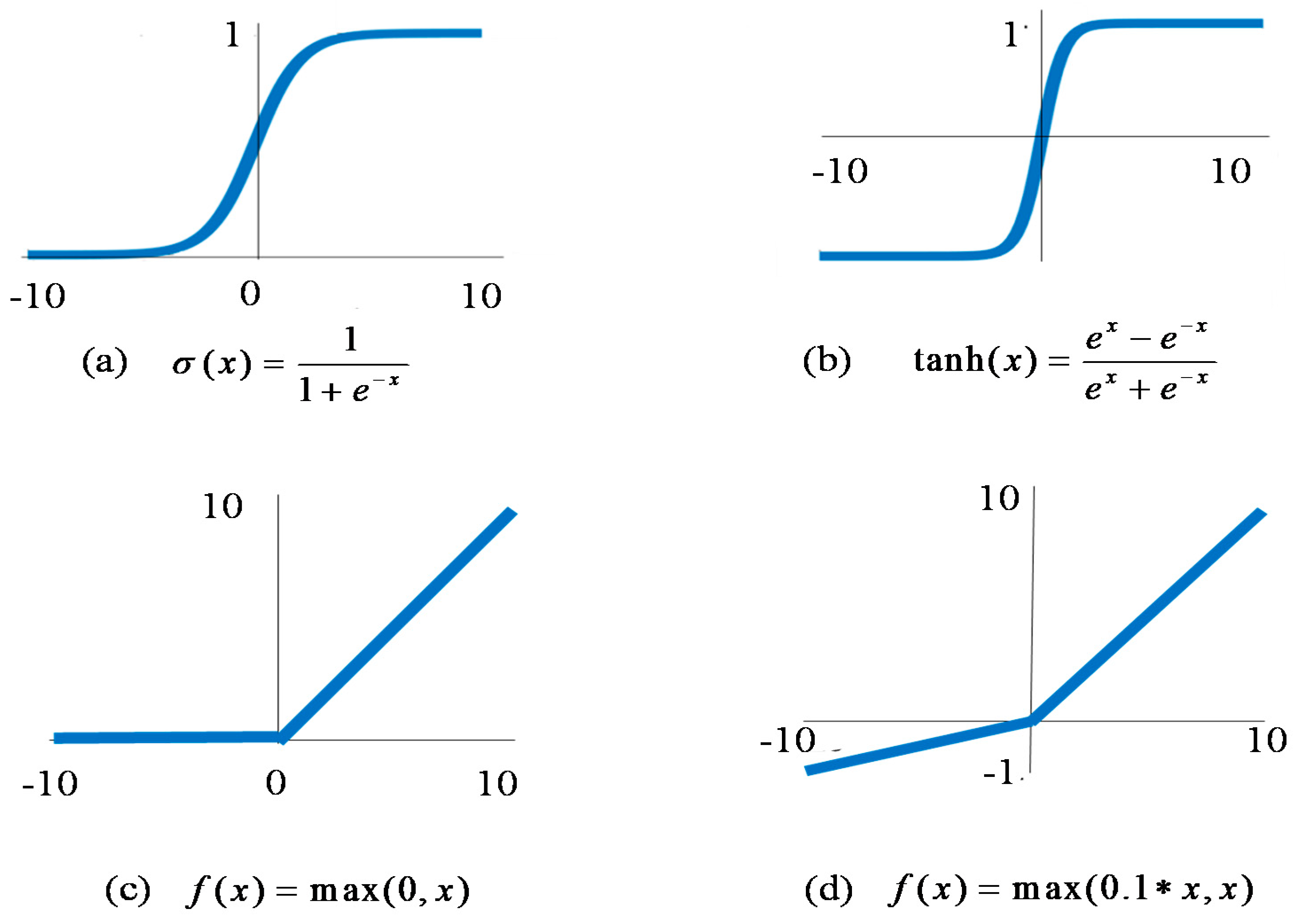
2.3. 1-D Convolutional Neural Network
Loss Function
2.4. Design of the Models
2.4.1. Parameters of the Models
2.4.2. Description of the Models
3. Results and Discussion
3.1. Comparisons with BPNN Models
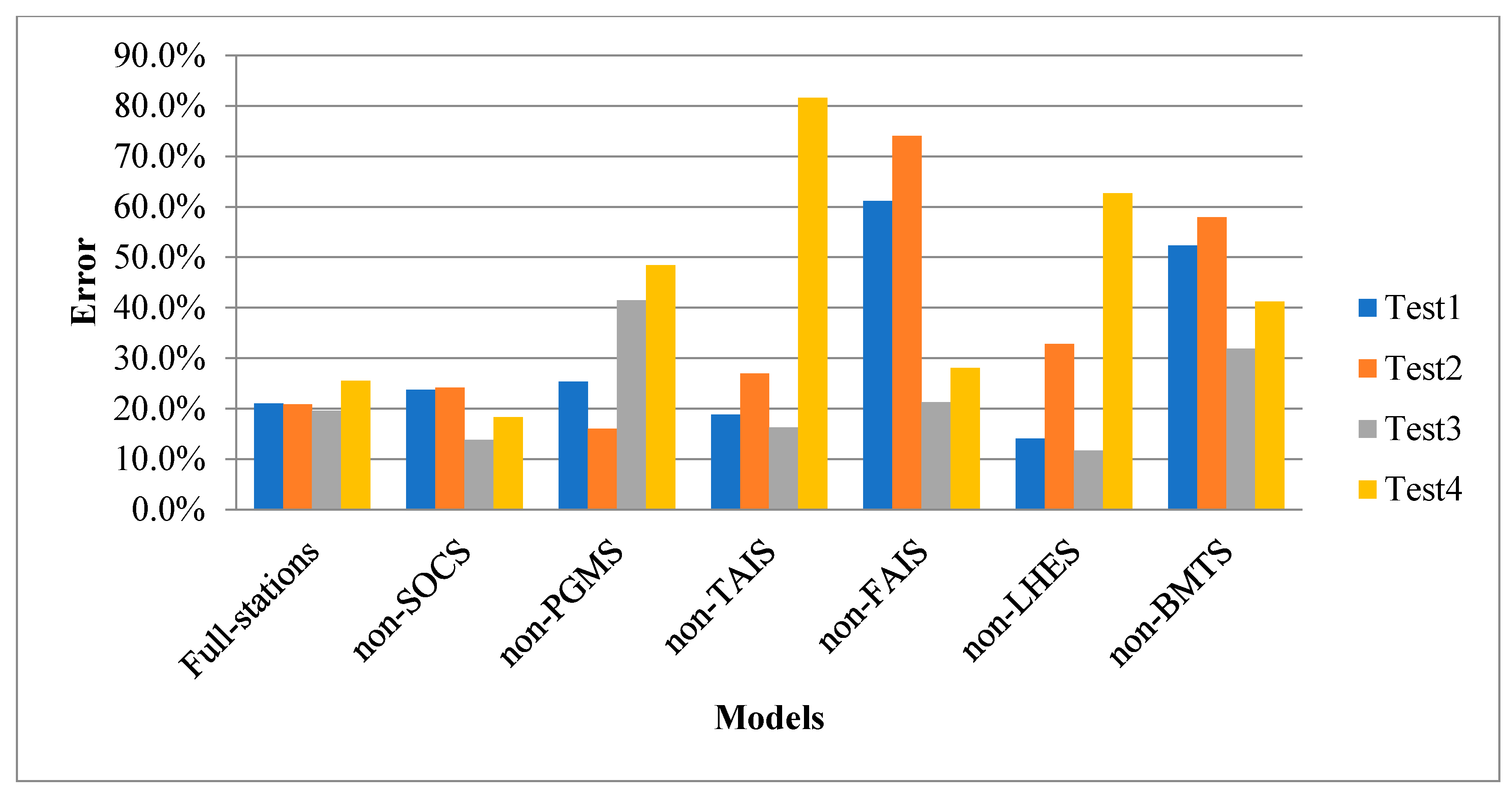
3.1.1. Effect of Parameters on Different Models
3.1.2. Comparisons of Prediction Results
3.2. Prediction Results of the CNN-FSPA Model
3.2.1. Testing of Different Parameters
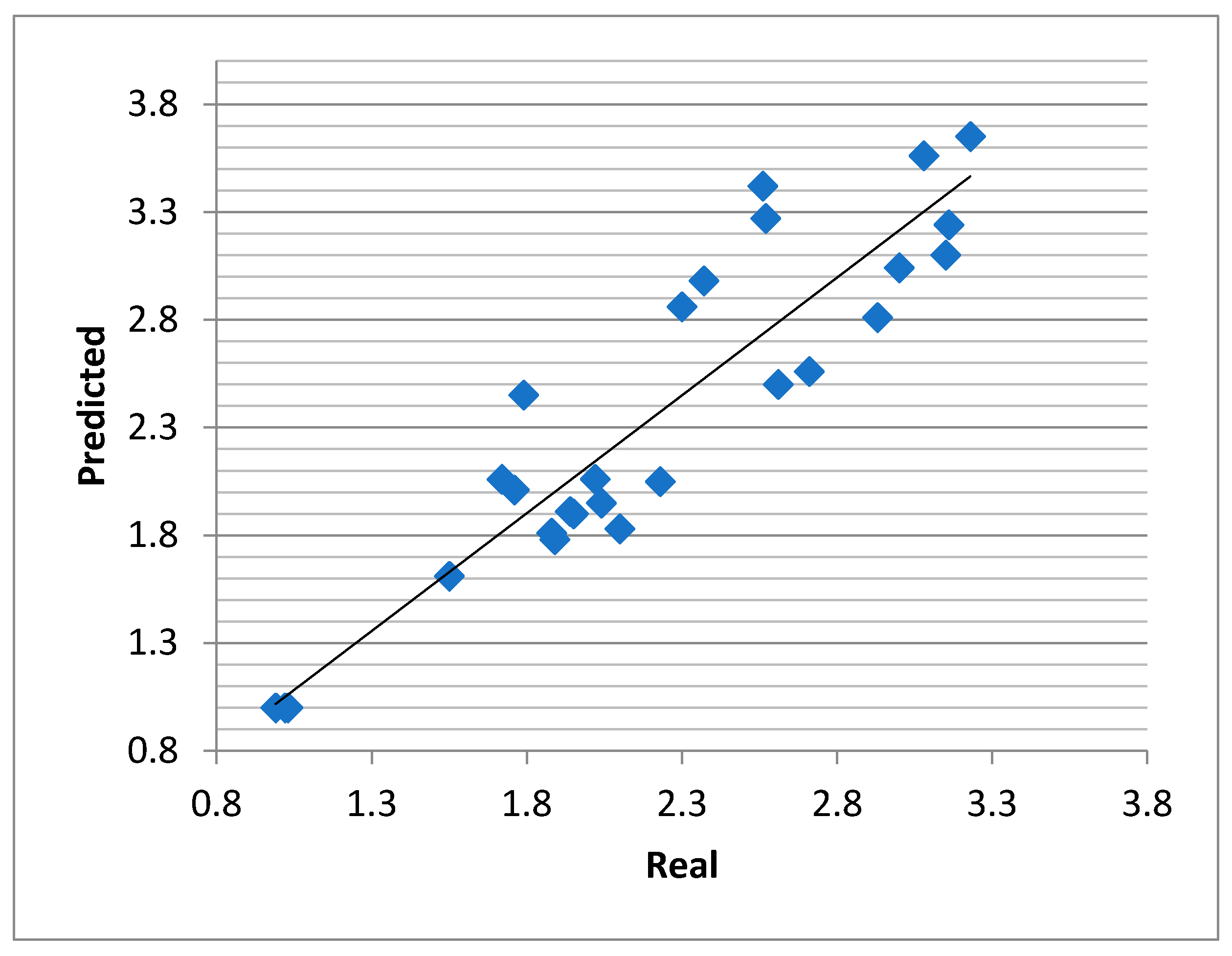
3.2.2. Comparisons with Recorded Results
3.3. Prediction Results of CNN-PSPA Models
3.3.1. Optimal Parameters for CNN-PSPA Models
3.3.2. Comparisons with Observed Results
3.3.3. Comparison with CNN-FSPA Model
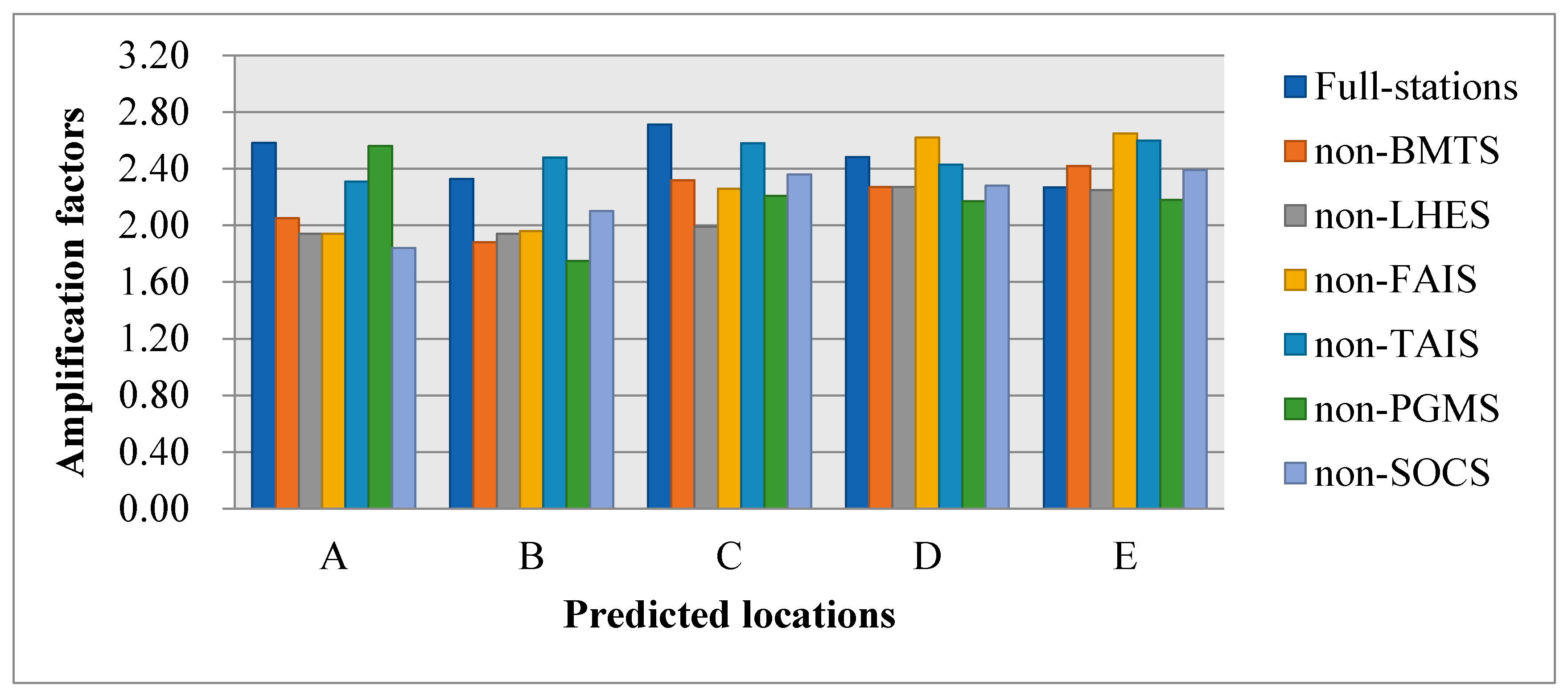
3.4. Comparisons of Unrecorded Locations
4. Conclusions
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sánchez-Sesma, F.; Crouse, C.B. Effects of site geology on seismic ground motion: Early history. Earthq. Eng. Struct. Dyn. 2015, 44, 1099–1113. [Google Scholar] [CrossRef]
- Trifunac, M.D. Site conditions and earthquake ground motion–A review. Soil Dyn. Earthq. Eng. 2016, 90, 88–100. [Google Scholar] [CrossRef]
- Markham, C.S.; Bray, J.D.; Macedo, J.; Luque, R. Evaluating nonlinear effective stress site response analyses using records from the Canterbury earthquake sequence. Soil Dyn. Earthq. Eng. 2016, 82, 84–98. [Google Scholar] [CrossRef] [Green Version]
- Harmsen, S.C. Determination of site amplification in the Los Angeles urban area from inversion of strong-motion records. Bull. Seismol. Soc. Am. 1997, 87, 866–887. [Google Scholar]
- Hartzell, S. Variability in nonlinear sediment response during the 1994 Northridge, California, earthquake. Bull. Seismol. Soc. Am. 1998, 88, 1426–1437. [Google Scholar]
- Kaveh, A.; Bakhshpoori, T.; Hamzeh-Ziabari, S.M. Derivation of New Equations for Prediction of Principal Ground-Motion Parameters using M5’ Algorithm. J. Earthq. Eng. 2016, 20, 910–930. [Google Scholar] [CrossRef]
- Pezzo, E.D.; Martino, S.D.; Parrinello, M.T.; Sabbarese, C. Seismic site amplification factors in Campi Flegrei, Southern Italy. Phys. Earth Planet. Inter. 1993, 78, 105–117. [Google Scholar] [CrossRef]
- Sandikkaya, M.A.; Akkar, S.; Bard, P.Y. A Nonlinear Site-Amplification Model for the Next Pan-European Ground-Motion Prediction Equations. Bull. Seismol. Soc. Am. 2013, 103, 19–32. [Google Scholar] [CrossRef]
- Yu, J. The Choice of Reference Sites for Seismic Ground Amplification Analyses: Case Study at Parkway, New Zealand. Bull. Seismol. Soc. Am. 2003, 93, 713–723. [Google Scholar] [CrossRef]
- Zaslavsky, Y.; Shapira, A. Experimental study of topographic amplification using the Israel Seismic Network. J. Earthq. Eng. 2000, 4, 43–65. [Google Scholar] [CrossRef]
- Ferrari, R.D.; Ferretti, G.; Barani, S.; Pepe, G.; Cevasco, A. On the role of stiff soil deposits on seismic ground shaking in western Liguria, Italy: Evidences from past earthquakes and site response. Eng. Geol. 2017, 226, 172–183. [Google Scholar] [CrossRef]
- Kanai, K.; Tanaka, T. On Microtremors. VIII. Bull. Earthq. Res. Inst. 1961, 39, 97–114. [Google Scholar]
- Nakamura, Y.A. Method for Dynamic Characteristics Estimation of Subsurface Using Microtremor on Ground Surface. Q. Rep. Rtri. 1989, 30, 25–33. [Google Scholar]
- Sadiq, M.T.; Yu, X.; Yuan, Z.; Fan, Z.; Rehman, A.U.; Li, G.; Xiao, G. Motor imagery EEG signals classification based on mode amplitude and frequency components using empirical wavelet transform. IEEE Access 2019, 7, 127678–127692. [Google Scholar] [CrossRef]
- Sadiq, M.T.; Yu, X.; Yuan, Z.; Aziz, M.Z. Motor imagery BCI classification based on novel two-dimensional modelling in empirical wavelet transform. Electron. Lett. 2020, 56, 1367–1369. [Google Scholar] [CrossRef]
- Sadiq, M.T.; Yu, X.; Yuan, Z.; Zeming, F.; Rehman, A.U.; Ullah, I.; Li, G.; Xiao, G. Motor imagery EEG signals decoding by multivariate empirical wavelet transform-based framework for robust brain–computer interfaces. IEEE Access 2019, 7, 171431–171451. [Google Scholar] [CrossRef]
- Bernal, D. Amplification factors for inelastic dynamic p–Δ effects in earthquake analysis. Earthq. Eng. Struct. Dyn. 1987, 15, 635–651. [Google Scholar] [CrossRef]
- Tropeano, G.; Soccodato, F.M.; Silvestri, F. Re-evaluation of code-specified stratigraphic amplification factors based on Italian experimental records and numerical seismic response analyses. Soil Dyn. Earthq. Eng. 2018, 110, 262–275. [Google Scholar] [CrossRef]
- Glinsky, N.; Bertrand, E.; Régnier, J. Numerical simulation of topographical and geological site effects. Applications to canonical topographies and Rognes hill, South East France. Soil Dyn. Earthq. Eng. 2019, 116, 620–636. [Google Scholar] [CrossRef]
- Kamai, R.; Abrahamson, N.A.; Silva, W.J. Nonlinear Horizontal Site Amplification for Constraining the NGA-West2 GMPEs. Earthq. Spectra 2014, 30, 1223–1240. [Google Scholar] [CrossRef]
- Athanasopoulos, G.A.; Pelekis, P.C.; Leonidou, E.A. Effects of surface topography on seismic ground response in the Egion (Greece) 15 June 1995 earthquake. Soil Dyn. Earthq. Eng. 1999, 18, 135–149. [Google Scholar] [CrossRef]
- Riga, E.; Makra, K.; Pitilakis, K. Aggravation factors for seismic response of sedimentary basins: A code-oriented parametric study. Soil Dyn. Earthq. Eng. 2016, 91, 116–132. [Google Scholar] [CrossRef]
- Wald, D.J.; Graves, R.W. The seismic response of the Los Angeles basin, California. Bull. Seism. Soc. Am. 1998, 88, 337–356. [Google Scholar]
- Khanbabazadeh, H.; Iyisan, R.; Ansal, A.; Hasal, M.E. 2D non-linear seismic response of the Dinar basin, TURKEY. Soil Dyn. Earthq. Eng. 2016, 89, 5–11. [Google Scholar] [CrossRef]
- Stamati, O.; Klimis, N.; Lazaridis, T. Evidence of complex site effects and soil non-linearity numerically estimated by 2D vs 1D seismic response analyses in the city of Xanthi. Soil Dyn. Earthq. Eng. 2016, 87, 101–115. [Google Scholar] [CrossRef]
- Semblat, J.F.; Duval, A.M.; Dangla, P. Numerical analysis of seismic wave amplification in Nice (France) and comparisons with experiments. Soil Dyn. Earthq. Eng. 2000, 19, 347–362. [Google Scholar] [CrossRef] [Green Version]
- Meza-Fajardo, K.C.; Varone, C.; Lenti, L.; Martino, S.; Semblat, J.F. Surface wave quantification in a highly heterogeneous alluvial basin: Case study of the Fosso di Vallerano valley, Rome, Italy. Soil Dyn. Earthq. Eng. 2019, 120, 292–300. [Google Scholar] [CrossRef]
- Abdullah, S.M. On linear site amplification behavior of crustal and subduction interface earthquakes in Japan: (1) regional effects, (2) best proxy selection. Bull. Earthq. Eng. 2018, 17, 119–139. [Google Scholar]
- Kim, S.; Hwang, Y.; Seo, H.; Kim, B. Ground motion amplification models for Japan using machine learning techniques. Soil Dyn. Earthq. Eng. 2020, 132, 106095. [Google Scholar] [CrossRef]
- Yuen, K.V.; Ortiz, G.A.; Huang, K. Novel nonparametric modeling of seismic attenuation and directivity relationship. Comput. Methods Appl. Mech. Eng. 2016, 311, 537–555. [Google Scholar] [CrossRef]
- Güllü, H.; Erçelebi, E. A neural network approach for attenuation relationships: An application using strong ground motion data from Turkey. Eng. Geol. 2007, 93, 65–81. [Google Scholar] [CrossRef]
- Yaghmaei-Sabegh, S.; Rupakhety, R. A new method of seismic site classification using HVSR curves: A case study of the 12 November 2017 Mw 7.3 Ezgeleh earthquake in Iran. Eng. Geol. 2020, 270, 105574. [Google Scholar] [CrossRef]
- Yaghmaei-Sabegh, S.; Tsang, H.-H. A new site classification approach based on neural networks. Soil Dyn. Earthq. Eng. 2011, 31, 974–981. [Google Scholar] [CrossRef]
- Mu, H.Q.; Yuen, K.V. Ground Motion Prediction Equation Development by Heterogeneous Bayesian Learning. Comput. Civ. Infrastruct. Eng. 2016, 116, 761–776. [Google Scholar] [CrossRef]
- Sadiq, M.T.; Yu, X.; Yuan, Z. Exploiting dimensionality reduction and neural network techniques for the development of expert brain–computer interfaces. Expert Syst. Appl. 2021, 164, 114031. [Google Scholar] [CrossRef]
- Hough, S.E.; Altidor, J.R.; Anglade, D.; Given, D.; Yong, A. Localized damage caused by topographic amplification during the 2010 M7.0 Haiti earthquake. Nat. Geosci. 2010, 3, 778–782. [Google Scholar] [CrossRef]

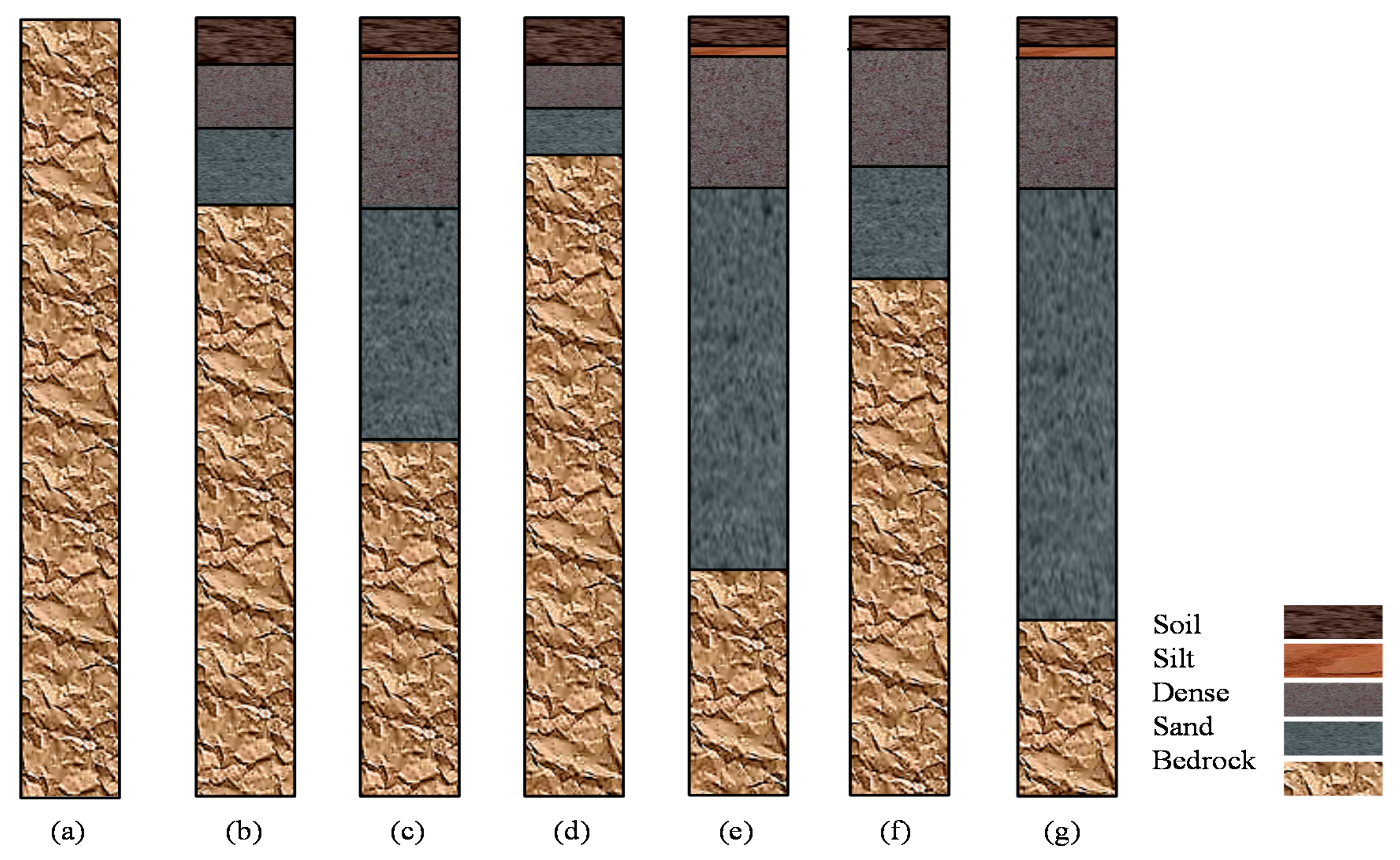
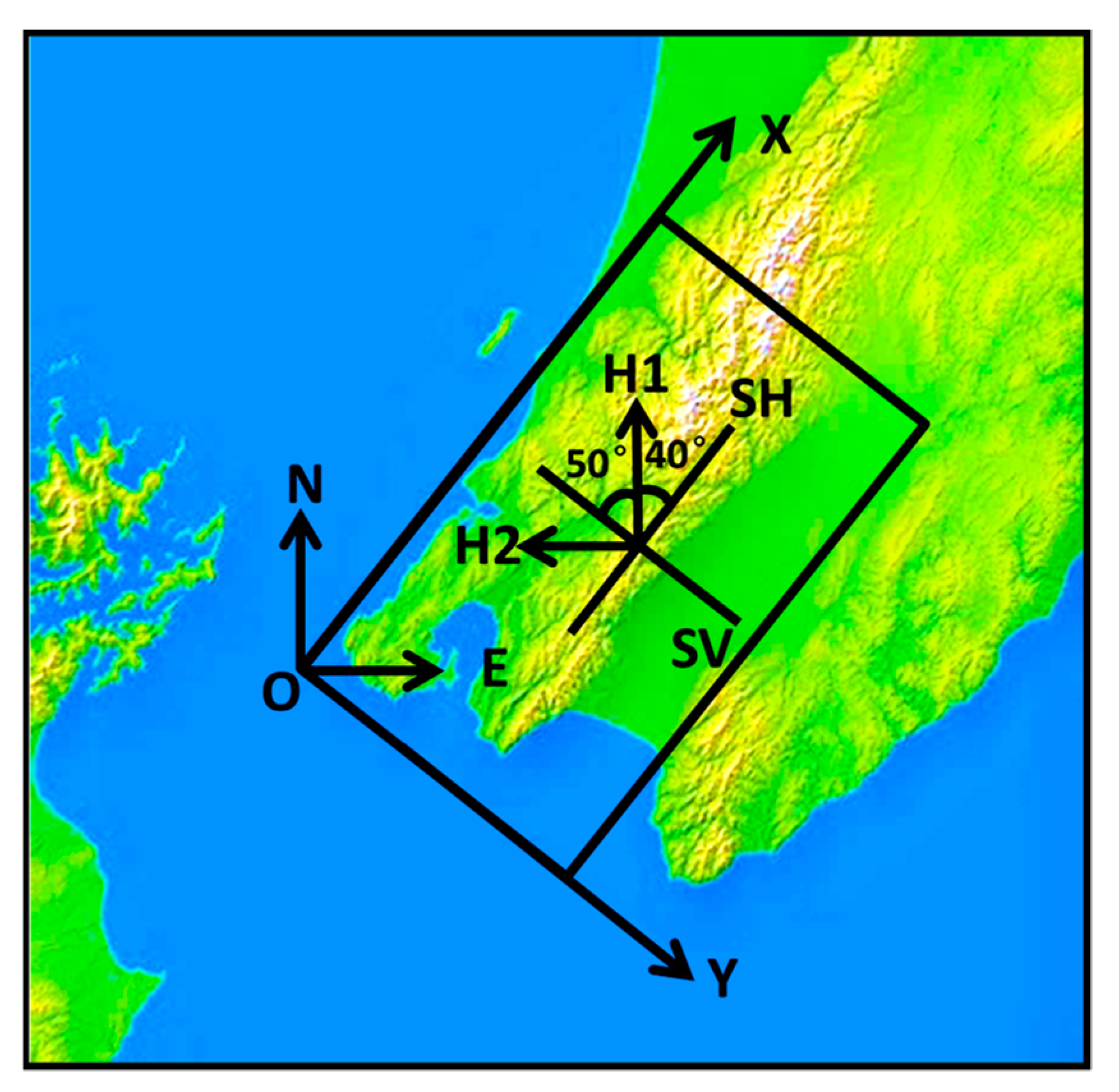

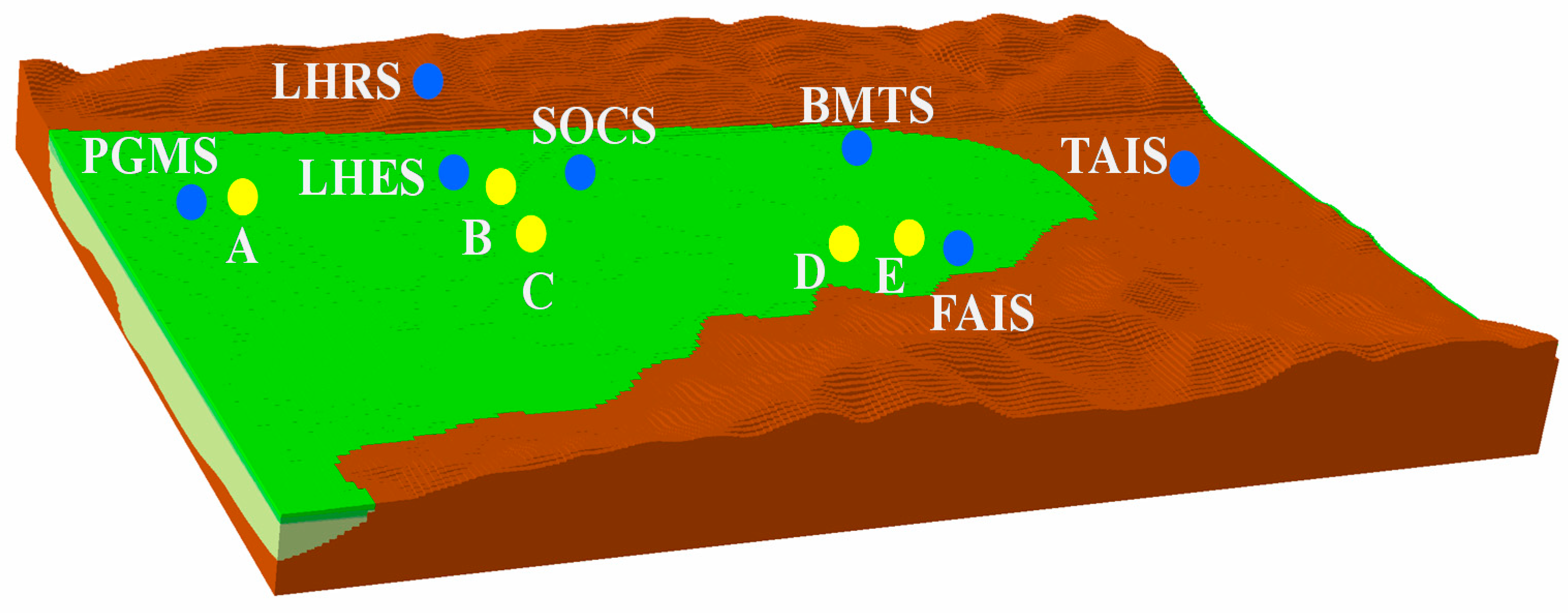

| Station | Latitude (S) | Longitude (E) | Thickness of Soil Layer (m) | V30 (m/s) |
|---|---|---|---|---|
| LHRS | 41°12′17″ | 174°53′35″ | 0.000 | 1500.000 |
| BMTS | 41°11′29″ | 174°55′34″ | 93.330 | 200.830 |
| LHES | 41°12′42″ | 174°54′12″ | 217.780 | 215.330 |
| FAIS | 41°12′27″ | 174°56′24″ | 62.220 | 206.000 |
| TAIS | 41°10′35″ | 174°58′12″ | 280.000 | 235.000 |
| PGMS | 41°13′28″ | 174°52′46″ | 130.670 | 236.000 |
| SOCS | 41°12′15″ | 174°54′57″ | 311.110 | 240.170 |
| Station Magnitude | LHRS | BMTS | LHES | FAIS | TAIS | PGMS | SOCS |
|---|---|---|---|---|---|---|---|
| M4.5 | 1.00 | 1.78 | 2.56 | 1.90 | 3.10 | 1.95 | 3.04 |
| M5.8 | 1.00 | 2.01 | 2.81 | 1.91 | 3.65 | 2.06 | 3.24 |
| M5.1 | 1.00 | 1.61 | 3.42 | 1.81 | 2.98 | 2.06 | 3.27 |
| M4.0 | 1.00 | 1.26 | 2.09 | 1.42 | 2.72 | 1.50 | 2.38 |
| M4.3 | 1.00 | — | 2.78 | 1.93 | 3.06 | 2.20 | 3.33 |
| M4.8 | 1.00 | 2.96 | 2.45 | — | 2.70 | 2.21 | 3.85 |
| M4.5 | 1.00 | 2.77 | 2.08 | — | 2.50 | 1.99 | 2.86 |
| M4.0 | 1.00 | 2.49 | 2.36 | — | 2.45 | 2.48 | 2.93 |
| M4.7 | 1.00 | 1.55 | 2.31 | 2.28 | 3.06 | 2.05 | 2.57 |
| M4.6 | 1.00 | 3.10 | 2.39 | 2.13 | 2.71 | 2.27 | 3.16 |
| M4.3 | 1.00 | 1.86 | 2.76 | 1.91 | 2.87 | 2.45 | 3.42 |
| M4.8 | 1.00 | 1.71 | 2.38 | 1.89 | — | 1.98 | — |
| CNN-FSPA | |
|---|---|
| Total | 44 earthquakes (274) |
| Training | 40 earthquakes (246) |
| Validation | 40 earthquakes (246) |
| Testing | 4 earthquakes (28) |
| CNN-PSPA | ||||||
|---|---|---|---|---|---|---|
| Total | All Stations (274) | All Stations (274) | All Stations (274) | All Stations (274) | All Stations (274) | All Stations (274) |
| Training | Non-SOCS (237) | Non-PGMS (233) | Non-TAIS (235) | Non-FAIS (242) | Non-LHES (235) | Non-BMTS (232) |
| Validation | (237) | (233) | (235) | (242) | (235) | (232) |
| Testing (PSPA) | SOCS (37) | PGMS (41) | TAIS (39) | FAIS (32) | LHES (39) | BMTS (42) |
| Models | CNN | BPNN | |
|---|---|---|---|
| Kernel Size | Kernel Number | Hidden Layer Size | |
| Test 1 | [2 1] [3 1] | 190 310 | 5 |
| Test 2 | [2 1] [3 1] | 190 320 | 6 |
| Test 3 | [2 1] [3 1] | 198 320 | 7 |
| Test 4 | [2 1] [3 1] [4 1] | 190 320 322 | 8 |
| Model | Magnitude | CNN-PSPA | BPNN-PSPA | ||||
|---|---|---|---|---|---|---|---|
| Observed (FAIS) | Predicted (FAIS) | Error | Observed (LHES) | Predicted (LHES) | Error | ||
| Best testing | M4.5 | 2.86 | 2.48 | 13.2% | 2.05 | 2.51 | 18.3% |
| M5.6 | 1.89 | 1.98 | 4.7% | 2.55 | 2.69 | 5.2% | |
| M5.1 | 1.90 | 1.93 | 1.7% | 2.80 | 3.04 | 8.3% | |
| M4.0 | 1.81 | 2.12 | 17.3% | 3.42 | 2.53 | 26.0% | |
| Model | Magnitude | Observed (BMTS) | Predicted (BMTS) | Error | Observed (TAIS) | Predicted (TAIS) | Error |
| Worst testing | M4.5 | 2.79 | 1.99 | 28.6% | 2.34 | 3.85 | 64.4% |
| M5.6 | 2.45 | 2.30 | 6.1% | 3.56 | 7.30 | 104.8% | |
| M5.1 | 1.78 | 1.77 | 0.7% | 3.10 | 4.61 | 48.6% | |
| M4.0 | 2.01 | 1.81 | 9.9% | 3.65 | 5.33 | 45.9% | |
| No Padding | Padding | ||||
|---|---|---|---|---|---|
| Kernel Size | Kernel Number | Error | Kernel Size | Kernel Number | Error |
| [2 1] | 192 | 18.3% | [2 1] | 192 | 19.7% |
| [2 1] [3 1] | 190 320 | 13.0% | [2 1] [3 1] | 190 320 | 12.6% |
| [2 1] [3 1] [4 1] | 190 320 330 | 13.3% | [2 1] [3 1] [4 1] | 190 320 330 | 12.8% |
| Layer | Type | Kernel No. | Kernel Size | Stride | Padding | Activation |
|---|---|---|---|---|---|---|
| 1 | Input | None | None | None | None | None |
| 2 | Convolution (C1) | 190 | 2 × 1 | 1 | 1 | Leaky ReLU |
| 3 | Convolution (C2) | 320 | 3 × 1 | 1 | 1 | Leaky ReLU |
| 4 | FC | None | None | None | None | None |
| 5 | Output | None | None | None | None | None |
| Station | Earthquakes | Observed | Predicted | Error | Average Error |
|---|---|---|---|---|---|
| LHRS | M4.5 | 1.00 | 1.02 | 2.0% | 8.5% |
| M5.6 | 1.00 | 0.99 | 1.0% | ||
| M5.1 | 1.00 | 1.02 | 2.0% | ||
| M4.0 | 1.00 | 1.03 | 2.9% | ||
| BMTS | M4.5 | 2.45 | 1.79 | 26.9% | |
| M5.6 | 1.78 | 1.89 | 5.8% | ||
| M5.1 | 2.01 | 1.76 | 12.4% | ||
| M4.0 | 1.61 | 1.55 | 3.7% | ||
| LHES | M4.5 | 2.05 | 2.23 | 8.1% | |
| M5.6 | 2.56 | 2.69 | 5.1% | ||
| M5.1 | 2.81 | 2.93 | 4.1% | ||
| M4.0 | 3.42 | 2.66 | 22.2% | ||
| FAIS | M4.5 | 2.86 | 2.30 | 19.6% | |
| M5.6 | 1.90 | 1.95 | 2.6% | ||
| M5.1 | 1.91 | 1.94 | 1.5% | ||
| M4.0 | 1.81 | 1.88 | 3.7% | ||
| TAIS | M4.5 | 3.56 | 3.08 | 13.5% | |
| M5.6 | 3.10 | 3.15 | 1.6% | ||
| M5.1 | 3.65 | 3.23 | 11.5% | ||
| M4.0 | 2.98 | 2.37 | 20.5% | ||
| PGMS | M4.5 | 1.83 | 2.10 | 12.9% | |
| M5.6 | 1.95 | 2.04 | 4.4% | ||
| M5.1 | 2.06 | 2.02 | 1.9% | ||
| M4.0 | 2.06 | 1.72 | 16.5% | ||
| SOCS | M4.5 | 2.50 | 2.61 | 4.2% | |
| M5.6 | 3.04 | 3.00 | 1.3% | ||
| M5.1 | 3.24 | 3.16 | 2.5% | ||
| M4.0 | 3.27 | 2.57 | 21.4% |
| Models | Predicted Station | Kernel Size | Kernel Number | Ave. Error | Error Fluctuation |
|---|---|---|---|---|---|
| non-SOCS | SOCS | [2 1] [3 1] | 190 310 | 16.5% | 8.7% |
| [2 1] [3 1] | 190 315 | 18.5% | |||
| [2 1] [3 1] | 190 318 | 14.2% | |||
| [2 1] [3 1] | 190 320 | 22.9% | |||
| non-PGMS | PGMS | [2 1] [3 1] | 190 320 | 23.1% | 9.1% |
| [2 1] [3 1] | 196 310 | 19.0% | |||
| [2 1] [3 1] | 196 320 | 24.5% | |||
| [2 1] [3 1] | 198 320 | 15.4% | |||
| non-TAIS | TAIS | [2 1] [3 1] [4 1] | 190 320 322 | 16.5% | 4.3% |
| [2 1] [3 1] [4 1] | 190 320 325 | 18.6% | |||
| [2 1] [3 1] [4 1] | 190 320 330 | 17.9% | |||
| [2 1] [3 1] [4 1] | 192 320 330 | 20.8% | |||
| non-FAIS | FAIS | [2 1] [3 1] | 190 315 | 22.4% | 9.8% |
| [2 1] [3 1] | 190 320 | 12.6% | |||
| [2 1] [3 1] | 196 320 | 13.2% | |||
| [2 1] [3 1] | 190 326 | 17.9% | |||
| non-LHES | LHES | [2 1] [3 1] | 188 320 | 22.1% | 9.9% |
| [2 1] [3 1] | 190 320 | 12.2% | |||
| [2 1] [3 1] | 192 320 | 16.0% | |||
| [2 1] [3 1] | 196 320 | 21.6% | |||
| non-BMTS | BMTS | [2 1] [3 1] | 190 320 | 21.1% | 3.9% |
| [2 1] [3 1] | 192 320 | 22.4% | |||
| [2 1] [3 1] | 192 330 | 25.0% | |||
| [2 1] [3 1] | 196 320 | 23.6% |
| Number | Earthquake | Epicentral Distance (km) | Depth (km) | CNN-PSPA | Average Error | |||
|---|---|---|---|---|---|---|---|---|
| Observed (LHES) | Predicted (LHES) | Error | ||||||
| 1 | M4.0 | 104 | 40 | 3.42 | 2.51 | 26.5% | 12.7% | 12.2% |
| 2 | M4.0 | 86 | 31 | 2.18 | 2.41 | 10.6% | ||
| 3 | M4.1 | 113 | 11 | 3.03 | 2.38 | 21.5% | ||
| 4 | M4.1 | 84 | 10 | 2.78 | 2.50 | 10.1% | ||
| 5 | M4.1 | 57 | 12 | 3.04 | 2.45 | 19.4% | ||
| 6 | M4.1 | 42 | 12 | 2.36 | 2.49 | 5.5% | ||
| 7 | M4.2 | 113 | 6 | 3.83 | 2.70 | 29.5% | ||
| 8 | M4.2 | 15 | 26 | 2.32 | 2.60 | 12.1% | ||
| 9 | M4.3 | 72 | 11 | 2.73 | 2.45 | 10.3% | ||
| 10 | M4.3 | 79 | 16 | 2.09 | 2.23 | 6.7% | ||
| 11 | M4.3 | 85 | 32 | 2.39 | 2.28 | 4.6% | ||
| 12 | M4.4 | 98 | 10 | 2.60 | 2.51 | 3.5% | ||
| 13 | M4.4 | 76 | 5 | 2.71 | 2.50 | 7.7% | ||
| 14 | M4.4 | 87 | 28 | 2.47 | 2.28 | 7.7% | ||
| 15 | M4.5 | 16 | 24 | 2.67 | 2.30 | 13.9% | ||
| 16 | M4.5 | 106 | 36 | 2.05 | 2.39 | 16.5% | ||
| 17 | M4.5 | 85 | 30 | 2.45 | 2.30 | 6.1% | ||
| 18 | M4.5 | 79 | 7 | 3.20 | 2.55 | 20.3% | ||
| 19 | M4.5 | 86 | 30 | 2.55 | 2.31 | 9.4% | ||
| 20 | M4.6 | 116 | 32 | 2.31 | 2.42 | 4.8% | 11.7% | |
| 21 | M4.6 | 82 | 12 | 3.31 | 2.63 | 20.5% | ||
| 22 | M4.7 | 81 | 33 | 2.36 | 2.21 | 6.4% | ||
| 23 | M4.7 | 57 | 13 | 3.23 | 2.59 | 19.8% | ||
| 24 | M4.8 | 72 | 11 | 2.59 | 2.39 | 7.7% | ||
| 25 | M4.8 | 74 | 12 | 2.78 | 2.39 | 14.0% | ||
| 26 | M4.8 | 84 | 54 | 2.76 | 2.59 | 6.2% | ||
| 27 | M4.8 | 74 | 9 | 2.91 | 2.42 | 16.8% | ||
| 28 | M5.0 | 86 | 36 | 2.63 | 2.34 | 11.0% | ||
| 29 | M5.0 | 50 | 13 | 2.73 | 2.28 | 16.5% | ||
| 30 | M5.0 | 76 | 8 | 2.99 | 2.43 | 18.7% | ||
| 31 | M5.1 | 78 | 5 | 2.81 | 2.52 | 10.4% | ||
| 32 | M5.2 | 121 | 8 | 2.90 | 2.66 | 8.3% | ||
| 33 | M5.4 | 82 | 34 | 2.14 | 2.24 | 4.7% | ||
| 34 | M5.5 | 74 | 17 | 2.38 | 2.15 | 9.7% | ||
| 35 | M5.5 | 91 | 15 | 3.65 | 2.97 | 18.6% | ||
| 36 | M5.6 | 85 | 7 | 2.56 | 2.42 | 5.5% | ||
| 37 | M5.6 | 82 | 13 | 2.58 | 2.38 | 7.8% | ||
| 38 | M5.8 | 85 | 37 | 2.11 | 2.48 | 17.5% | ||
| 39 | M6.2 | 104 | 34 | 2.57 | 2.81 | 9.3% | ||
| Magnitude | Predicted | CNN-PSPA | CNN-FSPA | |
|---|---|---|---|---|
| Models | Error | Error | ||
| M4.5 | SOCS | non-SOCS | 21.7% | 4.2% |
| PGMS | non-PGMS | 29.9% | 12.9% | |
| TAIS | non-TAIS | 37.9% | 13.5% | |
| FAIS | non-FAIS | 16.8% | 19.6% | |
| BMTS | non-BMTS | 12.1% | 26.9% | |
| LHES | non-LHES | 16.5% | 8.1% | |
| M5.6 | SOCS | non-SOCS | 16.6% | 1.3% |
| PGMS | non-PGMS | 21.7% | 4.4% | |
| TAIS | non-TAIS | 1.8% | 1.6% | |
| FAIS | non-FAIS | 4.7% | 2.6% | |
| BMTS | non-BMTS | 21.0% | 5.8% | |
| LHES | non-LHES | 5.5% | 5.1% | |
| M5.1 | SOCS | non-SOCS | 10.2% | 2.5% |
| PGMS | non-PGMS | 16.5% | 1.9% | |
| TAIS | non-TAIS | 13.5% | 11.5% | |
| FAIS | non-FAIS | 1.7% | 1.5% | |
| BMTS | non-BMTS | 20.8% | 12.4% | |
| LHES | non-LHES | 10.4% | 4.1% | |
| M4.0 | SOCS | non-SOCS | 10.0% | 21.4% |
| PGMS | non-PGMS | 21.3% | 16.5% | |
| TAIS | non-TAIS | 12.7% | 20.5% | |
| FAIS | non-FAIS | 17.3% | 3.7% | |
| BMTS | non-BMTS | 12.2% | 3.7% | |
| LHES | non-LHES | 26.5% | 22.2% | |
| Models | CNN-PSPA | ||||||
|---|---|---|---|---|---|---|---|
| Points | Non- SOCS | Non- PGMS | Non- TAIS | Non- FAIS | Non- LHES | Non- BMTS | |
| A | 26.8% | 8.6% | 10.5% | 24.9% | 24.9% | 20.6% | |
| B | 9.8% | 24.8% | 6.1% | 15.8% | 16.7% | 19.3% | |
| C | 13.0% | 18.5% | 4.9% | 16.7% | 26.6% | 14.5% | |
| D | 8.2% | 12.6% | 2.2% | 5.2% | 8.6% | 8.6% | |
| E | 5.0% | 3.9% | 12.7% | 14.4% | 0.9% | 6.2% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Chen, Y.; Teng, S.; Chen, G. A Novel Method for Predicting Local Site Amplification Factors Using 1-D Convolutional Neural Networks. Appl. Sci. 2021, 11, 11650. https://doi.org/10.3390/app112411650
Yang X, Chen Y, Teng S, Chen G. A Novel Method for Predicting Local Site Amplification Factors Using 1-D Convolutional Neural Networks. Applied Sciences. 2021; 11(24):11650. https://doi.org/10.3390/app112411650
Chicago/Turabian StyleYang, Xiaomei, Yongshan Chen, Shuai Teng, and Gongfa Chen. 2021. "A Novel Method for Predicting Local Site Amplification Factors Using 1-D Convolutional Neural Networks" Applied Sciences 11, no. 24: 11650. https://doi.org/10.3390/app112411650
APA StyleYang, X., Chen, Y., Teng, S., & Chen, G. (2021). A Novel Method for Predicting Local Site Amplification Factors Using 1-D Convolutional Neural Networks. Applied Sciences, 11(24), 11650. https://doi.org/10.3390/app112411650







