Trajectory Tracking Control of Intelligent Electric Vehicles Based on the Adaptive Spiral Sliding Mode

Abstract

Aiming at the multi-objective control problem of the tracking effect and vehicle stability in the process of intelligent vehicle trajectory tracking, a coordinated control strategy of the trajectory tracking and stability of intelligent electric vehicles is proposed based on the hierarchical control theory. The vehicle dynamics model and trajectory tracking model are established. In order to tackle the chattering problem in the traditional sliding mode controller, an Adaptive Spiral Sliding Mode controller is designed by taking the derivative of the controller as the upper controller, which is intended to reduce the heading deviation and lateral deviation in the trajectory tracking process whilst ensuring the stability of the vehicle itself. In the lower controller, a four-wheel tire force optimal distribution method is designed. According to the requirements of the upper controller, combined with the yaw stability of the vehicle, the directional control distribution of the four-wheel tire force is realized. A joint simulation model was built based on CarSim and Simulink, and simulation experiments were performed. The results show that the proposed control strategy can effectively control the heading deviation and lateral deviation in the vehicle trajectory tracking while ensuring the lateral stability of the vehicle.

1. Introduction

With the increasing maturity of control technology and the continuous improvement of drivers’ requirements for safety, maneuverability and ride comfort, the intelligent research of vehicles has received extensive attention [1]. Intelligent vehicles have better road utilization and higher safety, and their related research has been one of the research hotspots in recent years. Path-tracking control is a relatively common intelligent driving scheme in the intelligent driving process of intelligent vehicles. It aims to ensure that the heading error and lateral error in trajectory tracking approach zero. There have been many research results. Cai et al. [2] considered the longitudinal, lateral, yaw, and quasi-static roll motion of intelligent vehicles, designed a trajectory tracking control system based on model predictive control, and proposed a vehicle active and safe steering control method. In [3], a tracking-error learning control (TELC) algorithm was presented. In the TELC algorithm, the feedforward control actions are updated by using the tracking error dynamics, and the plant–model mismatch problem is thus discarded. Therefore, the feedforward controller gradually eliminates the feedback controller from the control of the system once the mobile robot has been put on-track. In addition to the proof of the stability, it was proven that the cost functions do not have local minima, such that the coefficients in the TELC algorithm guarantee that the global minimum is reached. The experimental results show that the TELC algorithm results in better path-tracking performance than the traditional tracking error-based control method. In [4], a path-tracking method based on model predictive control with a variable predictive horizon is proposed. Based on the designed model’s predictive controller for path tracking, the response analysis of the path-tracking control system under the different predictive horizons was carried out to clarify the influence of predictive horizon on path tracking accuracy, driving comfort and real-time of the control algorithm. In [5], researchers obtained the preview lateral position error according to the car motion parameters, road curvature and preview error model. They used this error to design a trajectory tracking control strategy to solve the front wheel angle that needs to be controlled when the car reaches the preview point in order to achieve the goal of tracking the desired trajectory. In [6], a potential field method to achieve the trajectory control of the autonomous electric vehicle with in-wheel motors is proposed. Instead of strictly following a desired trajectory, this method can form a steering corridor with a desired tracking error tolerance, and the vehicle can be steered smoothly with less control effort.

In the existing research, in order to realize the trajectory tracking of intelligent vehicles, many advanced control theories are applied to design trajectory tracking controllers, including model predictive control [7], robust control [8], and sliding mode control [9]. In addition, some researchers try to combine multiple control methods when designing vehicle trajectory following controllers, and integrate their advantages to improve the overall control performance. In order to ensure the stability of the autonomous vehicle during the trajectory-tracking process, Cui et al. [10] designed an unscented Kalman filter to estimate the vehicle operating state, and applied the multi-constraint model predictive control method to the ideal trajectory tracking. In the existing research on the trajectory tracking control of intelligent vehicles, most of the research focused on the improvement of the trajectory tracking control performance, ignoring the problem of the vehicle’s own stability during the trajectory tracking control process. In recent years, some researchers have also proposed some control methods that take into account the trajectory tracking effect and vehicle stability. However, no one has considered the problem of the coordinated control of trajectory tracking and vehicle stability under influencing factors such as parameter perturbation, uncertainty interference, time delay, and actuator saturation constraints in the vehicle dynamics model.

Indeed, the traditional first-order sliding mode (FOSM) control methods are able to improve the system performance issues of parameter perturbation, uncertainty interference and time delay. However, undesirable chattering always exists due to the fact that a sliding mode controller itself contains one or more discontinuous sign functions [11].The chattering phenomenon is harmful to control systems. As described in [12], it may induce fatigue in mechanical parts, and can destroy the system in a short time. In fact, as an alternative method, the second-order sliding mode (SOSM) can be used to reduce the chattering problem [13,14,15]. The spiral sliding mode (SSM) algorithm is a kind of SOSM algorithm, which has strong robustness to uncertain factors such as unmodeled dynamics, parameter perturbation, and external disturbance, etc. In this paper, the adaptive spiral sliding mode (ASSM) is proposed for the trajectory tracking control of intelligent electric vehicles.

This paper is organized as follows: In Section 2, the vehicle dynamics model and trajectory tracking model are established. The upper controller based on the ASSM is designed in Section 3, and the lower-level controller of the control system is also designed based on the optimal longitudinal force distribution algorithm in Section 3. In Section 4, co-simulation experiments based on CarSim and Simulink are shown. The paper ends with the conclusions.

2. Intelligent Vehicle Dynamics Model

2.1. Vehicle Dynamics Model

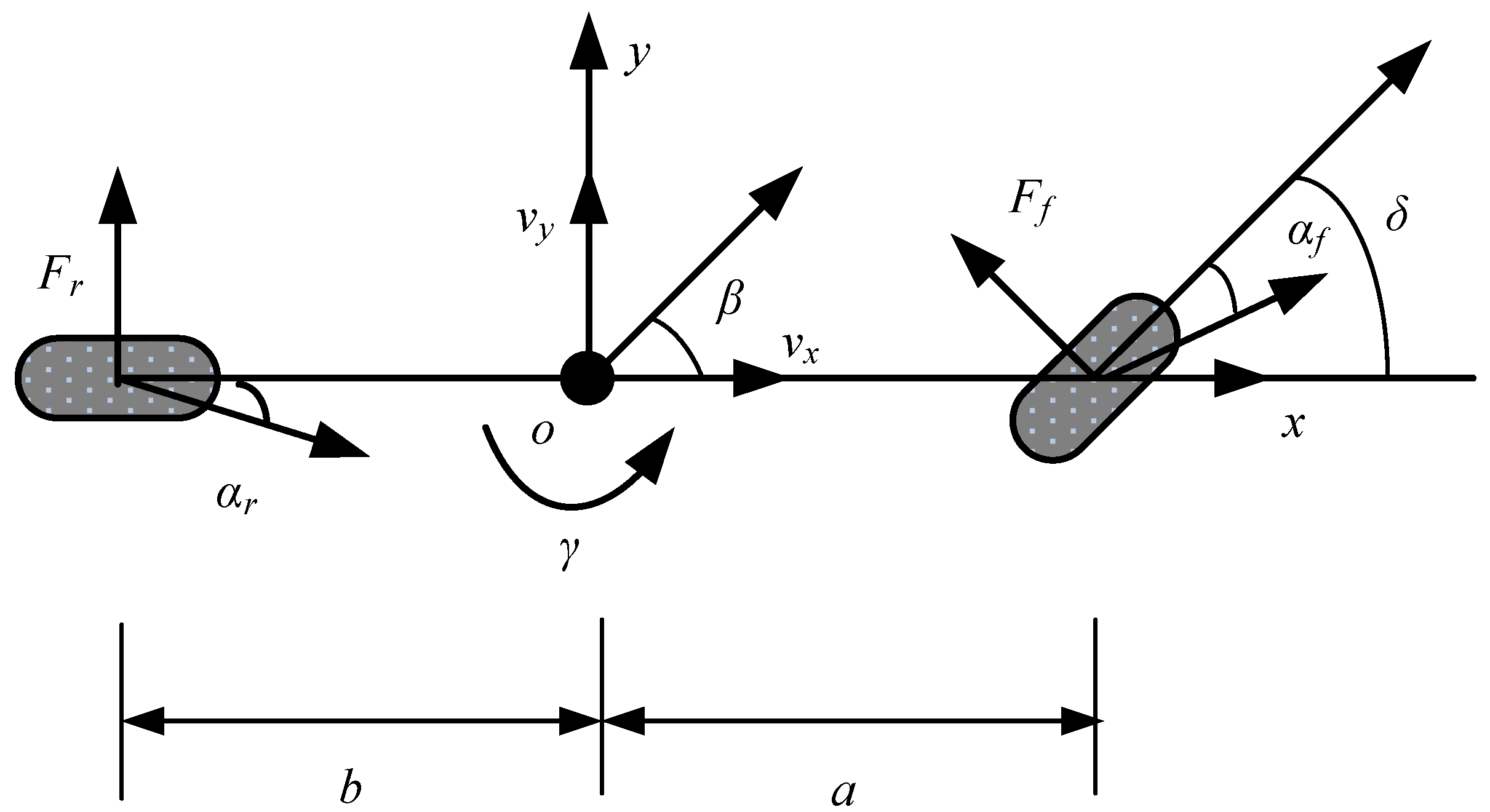
2.1.1. Three-Degrees-of-Freedom Vehicle Model

This article involves the design of observers for the driving state variables of smart electric vehicles: the yaw rate, the side slip angle of the center of mass, and the longitudinal vehicle speed. The design of the driving-state observer first needs to establish a nominal model. Therefore, this section establishes a three-degrees-of-freedom vehicle model as the nominal model of the smart electric vehicle driving-state observer, as shown in Figure 1. For modeling convenience, first make the following assumptions: (1) ignore the influence of air resistance, tire rolling resistance, etc. on the vehicle system; (2) the sideslip angles of the left and right tires of the front and rear axles are respectively equal; (3) the tire works in the linear region, that is, the tire force is proportional to the tire corner angle, and the dynamic characteristics of each tire are completely consistent; (4) ignore the role of the steering system, and the front wheel angle is an input to the vehicle system, ignore the role of the suspension system, ignore the wheel beating, and ignore the vertical movement of the vehicle body, etc.; the vehicle system moves parallel to the ground.

The vehicle dynamics coordinate axis stipulates that the center of mass of the vehicle coincides with the origin of the dynamic coordinate system fixed on the vehicle, the x-axis coincides with the axis of symmetry of the vehicle, and the forward direction is specified; the y-axis passes through the center of mass o of the vehicle, and the left direction is specified as positive. All of the angles and moments in the coordinate system shown are positive counterclockwise, and all of the vector components are positive with the positive direction of the coordinate axis.

In order to simplify the calculation, another assumption is made: the front wheel steering angle is small, so take it that the center of mass slip angle is small, $\beta =\frac{v_y}{v_x}$.

The three-degrees-of-freedom vehicle model includes the longitudinal, lateral and yaw motions of the vehicle. According to Newton’s second law, the dynamic equations of the respective degrees of motion can be obtained as follows:

Longitudinal movement:

$${\dot{v}}_x=v_y\gamma +a_x$$

(1)

Lateral movement:

$$m({\dot{v}}_y+v_x\gamma )=F_{yf}+F_{yr}$$

(2)

Yaw movement:

$$I_z\dot{\gamma }=a{F}_{yf}-b{F}_{yr}$$

(3)

Side slip angle of the front and rear axles:

$$\{\begin{array}{l}{\alpha }_f=\beta +\frac{a\gamma }{v_x}-\delta \\ {\alpha }_r=\beta -\frac{b\gamma }{v_x}\end{array}$$

(4)

Front and rear axle lateral tire force:

$$\{\begin{array}{c}{F}_{yf}=k_1{\alpha }_f\\ F_{yr}=k_2{\alpha }_r\end{array}$$

(5)

According to Formulas (1)–(5), the three-degrees-of-freedom vehicle model is obtained as follows:

$$\{\begin{array}{l}\dot{\gamma }=\frac{a^2{k}_1+b^2{k}_2}{I_z{v}_x}\gamma +\frac{a{k}_1-b{k}_2}{I_z}\beta -\frac{a{k}_1}{I_z}\delta \hfill \\ \dot{\beta }=(\frac{a{k}_1-b{k}_2}{m{v}_x^2}-1)\gamma +\frac{k_1+k_2}{m{v}_x}\beta -\frac{k_1}{m{v}_x}\delta \hfill \\ {\dot{v}}_x=\gamma \beta v_x+a_x\hfill \end{array}$$

(6)

$$a_y=\frac{a{k}_1-b{k}_2}{m{v}_x}\gamma +\frac{k_1+k_2}{m}\beta -\frac{k_1}{m}\delta$$

(7)

In Formulas (1)–(7), γ is the yaw rate, β is the side slip angle of the center of mass, v_x is the longitudinal vehicle speed, v_y is the lateral vehicle speed, δ is the front wheel angle (δ = δ_sw/i, δ_sw is the steering wheel angle), a_x is the longitudinal acceleration, a_y is the lateral acceleration, and the vehicle model parameters are shown in

Table 1. Vehicle parameters.

Symbol	Dimension	Value
m	kg	1296
Iz	kg·m2	1750
hg	m	0.54
a	m	1.25
b	m	1.32
B	m	1.405
r	m	0.286
Jw	kg·m2	0.8
k1	N/rad	100,000
k2	N/rad	100,000
i	-	20.4

.

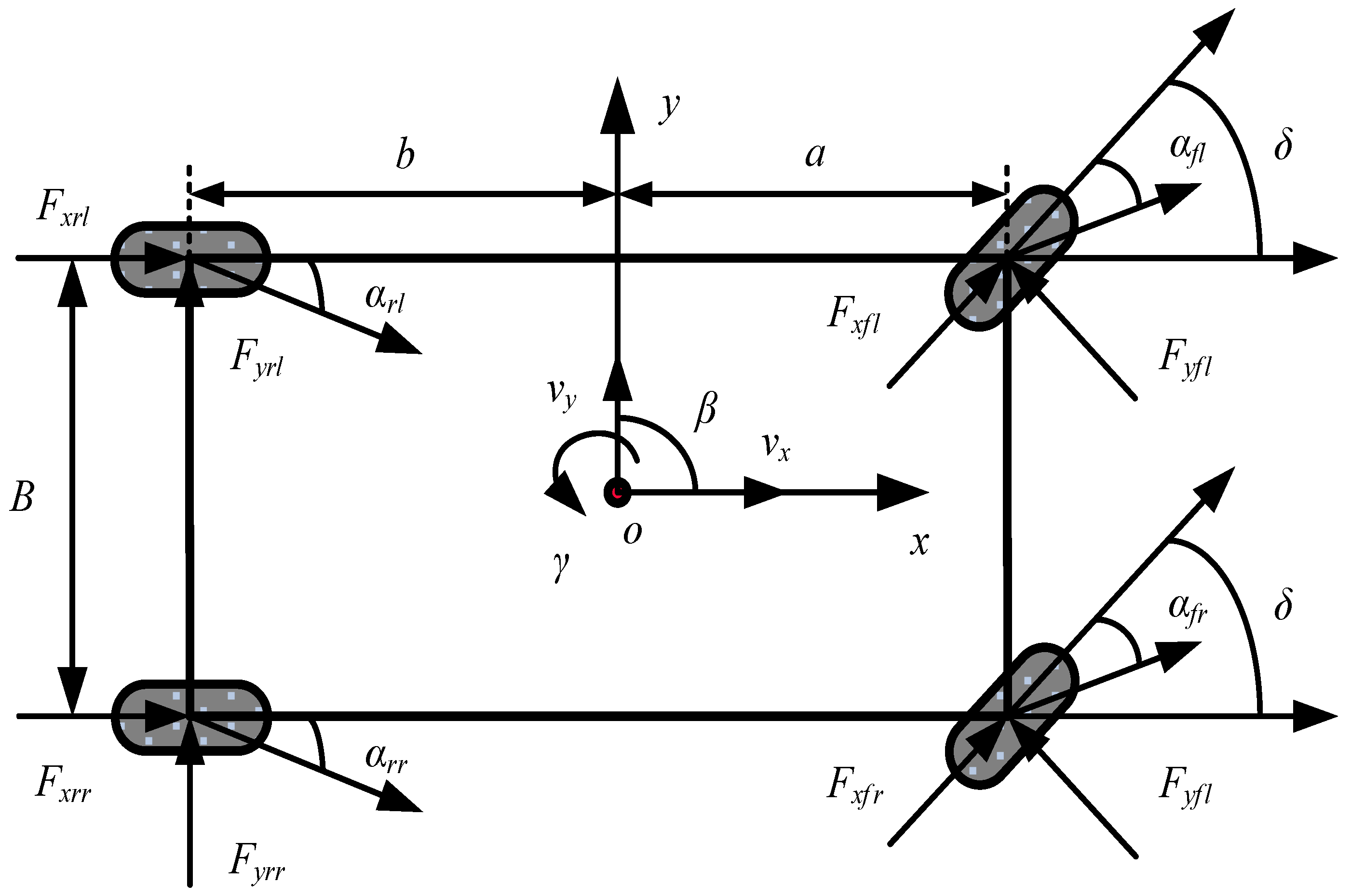
2.1.2. Seven-Degrees-of-Freedom Vehicle Model

This article relates to the design of the lateral stability control system of a distributed drive electric vehicle. The design of the model-based control system needs to be based on a vehicle model that is closer to reality and fully reflects the lateral, nonlinear, dynamic characteristics of the vehicle. Therefore, in this section, a seven-degrees-of-freedom vehicle model including the longitudinal, lateral, yaw, and four-wheel rotation of the vehicle is established, as shown in Figure 2.

In the same way, make the same assumptions as the three-degrees-of-freedom vehicle model, and the coordinate axis regulations are also the same.

Longitudinal movement:

$$m({\dot{v}}_x-v_y\gamma )=(F_{xfl}+F_{xfr})\cos \delta -(F_{yfl}+F_{yfr})\sin \delta +F_{xrl}+F_{xrr}$$

(8)

Lateral movement:

$$m({\dot{v}}_y+v_x\gamma )=(F_{xfl}+F_{xfr})\sin \delta +(F_{yfl}+F_{yfr})\cos \delta +F_{yrl}+F_{yrr}$$

(9)

Yaw movement:

$$I_z\dot{\gamma }=\frac{B}{2}(F_{yfl}-F_{yfr})\sin \delta +a(F_{yfl}+F_{yfr})\cos \delta -b(F_{yrl}+F_{yrr})+M_z$$

(10)

Among them, M_z is the direct yaw moment, which is produced by the combined action of the longitudinal forces of the four-wheel tires, as follows:

$$M_z=a(F_{xfl}+F_{xfr})\sin \delta -\frac{B}{2}(F_{xfl}-F_{xfr})\cos \delta -\frac{B}{2}(F_{xrl}-F_{xrr})$$

(11)

Rotation of the wheels:

$$J_w{\dot{w}}_{ij}=T_{ij}-F_{xij}r$$

(12)

In Formulas (8)–(12), r represents the tire radius. J_w represents the moment of inertia of the wheel assembly. T_ij is the output torque of the in-wheel motor; F_xij and F_yij are the tire longitudinal and lateral forces, respectively; i = f or i = r are the front or rear wheel respectively, j = f or j = r are the left or right wheel; w is the wheel rotation angular velocity. In the designed distributed-drive electric vehicle lateral stability control system, the optimal longitudinal force distribution algorithm in the lower controller decides the four-wheel longitudinal force distribution, which can be converted through the wheel model of the four-wheel torque distribution.

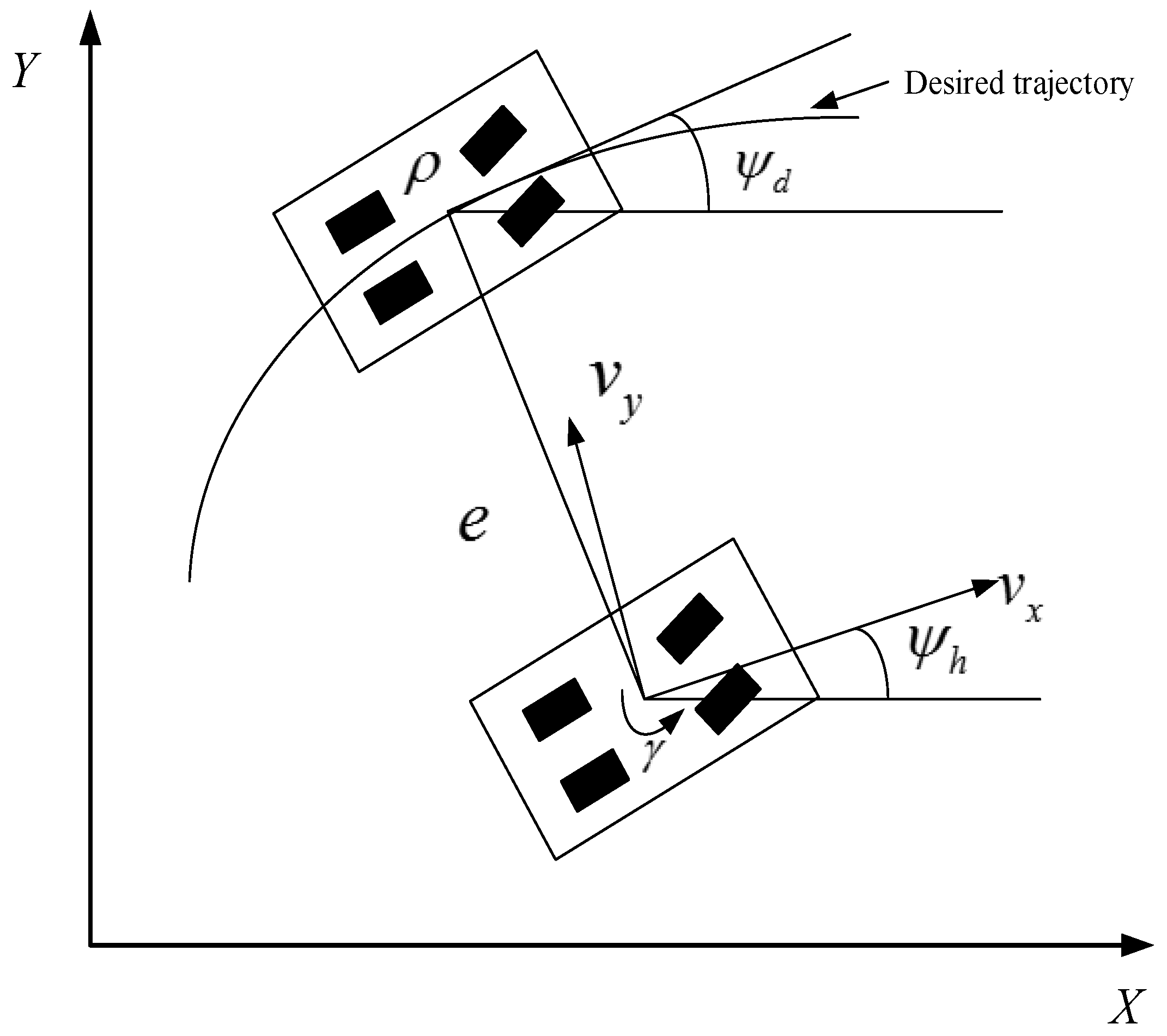
2.2. Trajectory Tracking Model

The vehicle trajectory tracking model uses the lateral deviation and heading deviation between the actual vehicle and the ideal trajectory to characterize the trajectory tracking effect. The established vehicle trajectory tracking model is shown in Figure 3, where X and Y are the coordinate axes of the geodetic coordinate system.

The heading deviation and its differential equation can be expressed as

$$\{\begin{array}{l}\psi ={\psi }_h-{\psi }_d\\ \dot{\psi }={\dot{\psi }}_h-{\dot{\psi }}_d\end{array}$$

(13)

In Formula (13), ψ is the heading deviation, ψ_h is the actual vehicle heading angle, and ψ_d is the desired heading angle of the vehicle.

ψ_h and ψ_d can be expressed as

$$\{\begin{array}{l}{\dot{\psi }}_h=\gamma \\ {\dot{\psi }}_d=\frac{v_x}{{\rho }_1}\end{array}$$

(14)

In Formula (14), ρ is the radius of the curvature of the desired trajectory.

Using the Serret–Frenet equation, the trajectory-tracking lateral deviation equation can be expressed as

$$\dot{e}=v_x\sin \psi +v_y\cos \psi$$

(15)

In Formula (15), e is the lateral deviation.

3. Control System Design

3.1. Problem Formulation

The method of hierarchical control was adopted to design the coordinated control strategy of the vehicle trajectory-tracking and stability, which is divided into the upper controller and lower controller. In the upper-level control, the control objective is to track the ideal vehicle driving state, and to make the lateral deviation and heading deviation in the trajectory tracking approach zero. The upper controller calculates the required vehicle front wheel steering angle and yaw moment according to the vehicle control target, and inputs it into the lower controller. For distributed-drive intelligent vehicles, four in-wheel motors are used for direct drive, which has a higher degree of freedom of maneuvering and torque-response capability, which is conducive to dynamic vehicle control in the process of trajectory tracking. The intelligent vehicle driven by four in-wheel motors is an overdrive system. Therefore, in the lower-level controller, an optimized distribution method of the four wheel and tire forces is designed to achieve the optimization of the power performance of the redundant drive system and meet the requirements of the upper-level controller. The control requirement of the controller realizes the coordinated control of trajectory tracking and vehicle stability. The overall hierarchical coordinated control strategy of unmanned vehicles is shown in Figure 4.

3.2. Upper Controller

3.2.1. Theoretical Basis of High-Order Sliding Mode Control

The sliding mode algorithm has a low sensitivity to internal and external disturbances in the system, and can be used for the high-precision control of dynamic systems under given constraints. Theoretically, it can realize control switching in an infinite frequency domain [16,17].

The biggest flaw of the sliding mode control algorithm is that high-frequency chattering effects may occur near the sliding mode surface. This chattering is characterized by an infinitely small amplitude near the sliding mode surface (in the state space) and near the first-order sliding mode surface. The amplitude is limited [18]. The core idea to solve the chattering problem is to change the dynamic characteristics of the small area of the discontinuous sliding mode surface in order to avoid discontinuities and ensure the main characteristics of the entire system [19].

3.2.2. Definition of the High-Order Sliding Mode Control Algorithm

For discontinuous differential equations:

$$\dot{x}=\upsilon (x)$$

(16)

In the formula, x∈Rⁿ, υ is a locally bounded and measurable (Lebesgue) vector function, such that Formula (16) can be expressed by an equivalent differential set:

$$\dot{x}\in V(x)$$

(17)

Assuming that the range of υ is continuous everywhere, when y→x, the function V(x) is the convex closed set of all of the possible limits of V(y) in the domain, and {y} is called the continuous point of υ. The solution set of this equation can be expressed as an absolutely continuous function x(t), which is differentiable everywhere.

Definition 1.

Let L be a sliding mode manifold, which is defined as a first-order sliding. The point set x∈L is defined as a second-order sliding, where V(x) is completely in the tangential space T_L at the point x relative to the manifold L.

Definition 2.

Suppose that there is a first-order (or second-order) sliding mode near the first-order (second-order) sliding point x on the manifold L if the first-order (second-order) sliding set near the point x is an integrable set composed of trajectories in the meaning of Filippov (that is, a combination of Filippov trajectories of discontinuous dynamic systems). Let L₁ = L, and let L₂ represent the second-order sliding point set of the relative manifold L. Assuming that L₂ is a sufficiently smooth manifold, similarly, L₃ represents a second-order sliding set relative to L₂, L₃ represents a third-order sliding set relative to L, and so on.

A constraint condition is represented by the equation σ(x) = 0, where σ: Rⁿ→R is a sufficiently smooth constraint function. Assuming that all of the trajectories $\sigma ,\dot{\sigma },\ddot{\sigma },\dots ,{\sigma }^{(r-1)}$ of the derivatives with respect to time exist and are univariate functions with respect to x, this means that discontinuities will not appear in the first r − 1 order derivative of the constraint function σ, and the r-th order sliding set is given by the following equation:

$$\sigma =\dot{\sigma }=\ddot{\sigma }=\cdots ={\sigma }^{(r-1)}=0$$

(18)

Definition 3.

Let the r-th order sliding set in Definition 1 be non-empty, and assume that it is a locally integrable set in the sense of Filippov; then, the corresponding motion satisfies Definition 1, which is called the r-th order sliding mode of the relative constraint function σ.

Set $\sigma ,\dot{\sigma },\ddot{\sigma },\dots ,{\sigma }^{(r-2)}$ as the derivative function with respect to x, and have

$$\mathrm{rank}\left\{\nabla \sigma ,\nabla \dot{\sigma },\dots ,\nabla {\sigma }^{(r-2)}\right\}=r-1$$

(19)

L_r can be obtained by Formula (19), and L_i, I = 1, ..., r − 1 are all smooth manifolds. If the differential manifold of L_r is required, then Equation (20) is extended to:

$$\mathrm{rank}\left\{\nabla \sigma ,\nabla \dot{\sigma },\dots ,\nabla {\sigma }^{(r-1)}\right\}=r$$

(20)

The condition under which the derivative of Formula (20) and its corresponding σ becomes the differentiable function of x is called the sliding regularity condition, and Formula (21) is called the weak sliding regularity condition. If Formula (20) holds, then a new local coordinate system can be established, and the system can be re-expressed as

$$y_1=\sigma ,{\dot{y}}_1=y_2,\cdots ,{\dot{y}}_{r-1}=y_r$$

(21)

$${\sigma }^{(r)}={\dot{y}}_r=\mathsf{\Phi }(y,\xi )$$

(22)

$$\dot{\xi }=\mathsf{\Psi }(y,\xi ),\xi \in R^{n-r}$$

(23)

Theorem 1.

If Equation (20) is full rank and Equation (18), the r-th order sliding manifold, is not empty, then if and only if the intersection of the Filippov vector set domain and the tangential space of the Equation (18) manifold for any r when the first-order sliding points are not empty, the r-th-order sliding mode of the constraint function σ exists.

Now suppose that σ is a smooth vector function, σ: Rⁿ→R^m, σ = (σ₁, …, σ_m), r = (r₁, …, r_m), where r_i is a natural number.

Definition 4.

Assuming that all of the derivatives of the first r_i continuous σ_i with respect to time are smooth functions, the set given by the following formula is a locally integrable set in the sense of Filippov:

$${\sigma }_i={\dot{\sigma }}_i={\ddot{\sigma }}_i=\cdots ={\sigma }_i^{r_i-1}=0,i=1,\dots ,m$$

(24)

Then, the motion mode existing in the set is called the sliding mode of the vector sliding order r with respect to the vector constraint function σ, and the corresponding sliding regularity condition is in the form:

$$\mathrm{rank}\left\{\nabla {\sigma }_i,\dots ,\nabla {\sigma }_i^{(r_i-1)}|i=1,\dots ,m\right\}=r_1+\cdots +r_m$$

(25)

$$\dot{x}=f(t,x,u),\sigma =\sigma (t,x)\in R,u=U(t,x)\in R$$

(26)

In the formula, t is the time, u is the control quantity, and f and σ are smooth functions. u is determined by the feedback u = U(t, x), where U is a discrete function. For the sake of simplicity, σ and u are considered scalars, but the following descriptions are all applicable to the vector sliding order.

The regular sliding mode satisfies the following conditions: the velocity V is not in the tangential space T_L, but intersects with the manifold σ = 0, and there is a trajectory in the manifold of the velocity vector at T_L. This mode is the main working mode of the variable structure system, and is called the first-order mode. When there is a switching error, the trajectory will leave the manifold at a certain angle. On the other hand, in the second-order sliding mode, even if there is a switching error, all of the possible velocities exist in the tangential space of the manifold, and the state trajectory is tangent to the manifold when it leaves.

Consider the following system:

$$\dot{x}=a(x)+b(x)u,\sigma =\sigma (x)\in R,u\in R$$

(27)

Among them, a, b, σ are smooth vector functions; let the system have a degree of freedom r relative to the output variable σ, which means that the derivative $L_b\sigma ,L_b{L}_a\sigma ,\dots ,L_b{L}_a^{r-2}\sigma$ near a given point is always equal to 0, and $L_b{L}_a^{r-1}\sigma$ is not equal to 0.

Consider the following dynamic system:

$$\dot{x}=a(t,x)+b(t,x)u,\sigma =\sigma (t,x),u=U(t,x)\in R$$

(28)

Theorem 2.

Assume that the degree of freedom of the relative output function σ of the system at a certain r-order sliding point (t₀, x₀) is r, and the range of the discontinuous function is [K, ∞), and (−∞, −K] is the upper point (for some non-zero sets on any region near any order sliding point near t₀, x₀), then as long as K is large enough, there must be an r-order sliding mode near the point (t₀, x₀).

3.2.3. Actual Slip and Finite Time Convergence

The quality of the control design is closely related to the sliding accuracy. When the switching characteristics disappear and the switching frequency tends to infinity, any ideal sliding mode can be considered as the limit of motion. Let ε denote the switching characteristics; then, the sliding accuracy of any sliding mode technology can be represented by asymptotically ε→0.

Definition 5.

Let (t, x(t, e)) denote a trajectory cluster, and search by ε∈R^μ; the initial condition is (t₀, x(t₀)), t ≥ t₀. Assuming that there is t₁ ≥ t₀ in each [t′, t″], where t′ ≥ t₁, the function σ(t, x(t, ε)) uniformly tends to 0, with ε→0. At this time, the trajectory cluster is called the real sliding cluster when the constraint σ = 0, the motion in the interval [t₀, t₁] is called a transient process, and the motion in the interval [t₀, ∞) is a steady-state process.

Definition 6.

The control algorithm that depends on the parameter ε∈R^μ is called the real sliding algorithm under the constraint σ = 0. If ε→0, it constitutes a real sliding cluster in any initial state.

Definition 7.

Let ϒ(ε) be a real function, and ϒ(ε)→0 when ε→0. For a real sliding algorithm of order r under the constraint σ = 0 with respect to ϒ(ε), if there is a constant C for any real set of initial conditions and any time interval [T₁, T₂], such a steady-state process satisfies at time $t\in [T_1,T_2]$:

|σ(t, x(t, ε))|≤ C|ϒ(ε)|^r

(29)

If ϒ(ε) is the minimum time interval to control the smoothness, it is called the r-order actual sliding algorithm under the constraint σ = 0.

3.2.4. Design of the Upper-Level Controller Based on the ASSM Algorithm

(1) Controller design based on SSM: Taking the three-degrees-of-freedom vehicle model as an ideal reference model, the upper-level controller of the control system is designed based on the SSM algorithm. The yaw dynamics Equation (10) of the electric vehicle driven by the distributed drive is as follows:

$$I_z\dot{\gamma }=M_z+\frac{B}{2}(F_{yfl}-F_{yfr})\sin \delta +a(F_{yfl}+F_{yfr})\cos \delta -b(F_{yrl}+F_{yrr})+d$$

(30)

In Formula (30), d is the aggregate disturbance caused by model uncertainty and interference.

Define the sliding mode variables as

$$s=\gamma -{\gamma }_d+\frac{1}{2}(\beta -{\beta }_d)$$

(31)

Find the first-order derivative and the second-order derivative of the sliding mode variables respectively, and substitute Equation (30) into

$$\begin{array}{c}\dot{s}=\frac{1}{I_z}\{M_z+\frac{B}{2}(F_{yfl}-F_{yfr})\sin \delta +a(F_{yfl}+F_{yfr})\cos \delta \\ -b(F_{yrl}+F_{yrr})+I_z[\frac{1}{2}(\dot{\beta }-{\dot{\beta }}_d)-{\dot{\gamma }}_d]+d\}\end{array}$$

(32)

$$\begin{array}{c}\ddot{s}=\frac{1}{I_z}\{{\dot{M}}_z+\frac{B}{2}({\dot{F}}_{yfl}-{\dot{F}}_{yfr})\sin \delta +\frac{B}{2}(F_{yfl}-F_{yfr})\cos \delta \cdot \dot{\delta }\\ +a({\dot{F}}_{yfl}+{\dot{F}}_{yfr})\cos \delta -a(F_{yfl}+F_{yfr})\sin \delta \cdot \dot{\delta }\\ -b({\dot{F}}_{yrl}+{\dot{F}}_{yrr})+I_z[\frac{1}{2}(\ddot{\beta }-{\ddot{\beta }}_d)-{\ddot{\gamma }}_d]+\dot{d}\}\end{array}$$

(33)

The output of the upper controller is

$$M_z=u=u_1+u_2$$

(34)

$$\{\begin{array}{cc}\hfill {\dot{u}}_1& =-I_z\cdot \alpha [\mathrm{sgn}(s)+\frac{1}{2}\mathrm{sgn}(\dot{s})]\hfill \\ \hfill u_2& =-\{\frac{B}{2}(F_{yfl}-F_{yfr})\sin \delta +a(F_{yfl}+F_{yfr})\cos \delta \hfill \\ & -b(F_{yrl}+F_{yrr})+I_z[\frac{1}{2}(\dot{\beta }-{\dot{\beta }}_d)-{\dot{\gamma }}_d]\}\hfill \end{array}$$

(35)

In Formula (35), γ and γ_d are the actual value of the lateral angular velocity and the ideal value based on the three-degrees-of-freedom vehicle reference model; β, β_d are the actual value of the center-of-mass slip angle and the ideal value based on the three-degrees-of-freedom vehicle reference model, respectively; α is the spiral sliding mode control gain; u₁ is the SSM control output, and u₂ is the modeling compensation feedforward output. From the structure of the SSM algorithm, it can be seen that the controller outputs the integral value of the sign function. If the controller is designed properly, it can effectively reduce or eliminate the system chattering caused by the sign function output.

(2) Design of the control gain adaptive law: In order to make the sliding mode variable and its derivative converge to 0 within a finite time, it is necessary to design a control gain adaptive law. To this end, the following control gain adaptive law is proposed:

$$\dot{\alpha }=\{\begin{array}{ll}\omega \sqrt{\frac{\theta }{2}}\mathrm{sgn}[E(s,\dot{s})-\rho ];\hfill & \alpha >{\alpha }_t\hfill \\ \lambda ;\hfill & \alpha \le {\alpha }_t\hfill \end{array}$$

(36)

Stability conditions:

$$\{\begin{array}{l}\alpha >2D\hfill \\ 0<\kappa <\min (\frac{2\sqrt{2\alpha }}{3}(\frac{\alpha }{2}-D),2{\alpha }^{\frac{3}{2}})\hfill \end{array}$$

(37)

In the Formulas (36) and (37), $E(s,\dot{s})=e^{k(s^2+\frac{1}{2}{\dot{s}}^2)}$, k, ω, θ, ρ, λ and α_t are all positive constants.

The design significance of the adaptive critical function $E(s,\dot{s})=e^{k(s^2+\frac{1}{2}{\dot{s}}^2)}$: It is designed in the form of an exponential function, such that when the deviation between the system state and the ideal state is small, there is a small compensation amount and compensation rate, which effectively reduces the chattering of the system when it is close to or reaches a steady state. When the deviation between the system state and the ideal state is large, the compensation amount and the compensation rate are large, such that the system quickly reaches the steady state or close to the steady state, and improves the robustness of the system.

3.2.5. Stability Analysis of the Upper Controller

The upper controller of the distributed drive electric vehicle lateral stability control system based on the ASSM algorithm needs to be effective under a certain stability condition. Therefore, this section constructs a Lyapunov function to analyze the stability of the upper controller, and finally obtains the stability conditions, which are as follows:

$$V(s,\dot{s},\alpha )=V_0(s,\dot{s})+\frac{1}{2\theta }{(\alpha -{\alpha }^{*})}^2$$

(38)

In Formula (38):

$$V_0(s,\dot{s})={\alpha }^2{s}^2+\kappa {\left|s\right|}^{\frac{3}{2}}\mathrm{sgn}(s)\dot{s}+\alpha \left|s\right|{\dot{s}}^2+\frac{1}{4}{\dot{s}}^4$$

(39)

In Formula (39), κ and α^* are both positive constants.

First, prove that it converges in a finite time:

$$V_0(s,\dot{s})=\left|s\right|S^{T}AS+\frac{1}{4}{\dot{s}}^4$$

(40)

In Formula (40): $S={\left[{\left|s\right|}^{\frac{1}{2}}\mathrm{sgn}(s)\dot{s}\right]}^T$, $A=\left[\begin{array}{cc}{\alpha }^2& \frac{\kappa }{2}\\ \frac{\kappa }{2}& \alpha \end{array}\right]$.

When 0 < $\kappa$ < 2α3/2 is satisfied, $V_0(s,\dot{s})\ge 0$ is established.

Derivation of $V_0(s,\dot{s})$:

$$\begin{array}{cc}\hfill {\dot{V}}_0(s,\dot{s})& =2{\alpha }^{2}s\dot{s}+\kappa {\left|s\right|}^{\frac{3}{2}}\mathrm{sgn}(s)\ddot{s}+\frac{3}{2}\kappa {\left|s\right|}^{\frac{1}{2}}{\dot{s}}^2+2\alpha \left|s\right|\dot{s}\ddot{s}+{\dot{s}}^3\ddot{s}\hfill \\ & =2{\alpha }^{2}s\dot{s}+\frac{3}{2}\kappa {\left|s\right|}^{\frac{1}{2}}{\dot{s}}^2+\kappa {\left|s\right|}^{\frac{3}{2}}\mathrm{sgn}(s)\{d^{*}-\alpha [\mathrm{sgn}(s)+\frac{1}{2}\mathrm{sgn}(\dot{s})]\}\hfill \\ & +2\alpha \left|s\right|\dot{s}\{d^{*}-\alpha [\mathrm{sgn}(s)+\frac{1}{2}\mathrm{sgn}(\dot{s})]\}+{\dot{s}}^3\{d^{*}-\alpha [\mathrm{sgn}(s)+\frac{1}{2}\mathrm{sgn}(\dot{s})]\}\hfill \end{array}$$

(41)

In Formula (41), $d^{*}=\frac{1}{I_z}\left|\dot{d}\right|<D$, D is a positive constant.

Simplify $V_0(s,\dot{s})$ to obtain the following:

$$\begin{array}{cc}\hfill {\dot{V}}_0(s,\dot{s})& =-{\alpha }^2\left|s\right|\left|\dot{s}\right|+\kappa {\left|s\right|}^{\frac{3}{2}}\mathrm{sgn}(s)\{d^{*}-\alpha [\mathrm{sgn}(s)+\frac{1}{2}\mathrm{sgn}(\dot{s})]\}\hfill \\ & +\frac{3}{2}\kappa {\left|s\right|}^{\frac{1}{2}}{\dot{s}}^2+2\alpha \left|s\right|\dot{s}{d}^{*}+{\dot{s}}^3\{d^{*}-\alpha [\mathrm{sgn}(s)+\frac{1}{2}\mathrm{sgn}(\dot{s})]\}\hfill \end{array}$$

(42)

Simplify the right side of Equation (42) and enlarge it appropriately to obtain the following:

$${\dot{V}}_0(s,\dot{s})\le -\kappa {\left|s\right|}^{\frac{3}{2}}(\frac{1}{2}\alpha -D)-{\alpha }^2\left|s\right|\left|\dot{s}\right|+\frac{3}{2}\kappa {\left|s\right|}^{\frac{1}{2}}{\dot{s}}^2+2\alpha \left|s\right|\left|\dot{s}\right|D+(D-\frac{1}{2}\alpha ){\dot{s}}^3$$

(43)

The right side of Formula (43) is written as:

$$-\kappa {\left|s\right|}^{\frac{3}{2}}(\frac{1}{2}\alpha -D)-\left|\dot{s}\right|S^{*}{}^{T}B{S}^{*}=-\kappa {\left|s\right|}^{\frac{3}{2}}(\frac{1}{2}\alpha -D)-\left|\dot{s}\right|V_0^{*}(\dot{s})$$

(44)

In Formula (44), $S^{*}={[\begin{array}{cc}{\left|\dot{s}\right|}^{\frac{1}{2}}& \left|\dot{s}\right|\end{array}]}^T$, $B=\left[\begin{array}{cc}\alpha (\alpha -2D)& -\frac{3}{4}\kappa \\ \frac{3}{4}\kappa & \frac{\alpha }{2}-D\end{array}\right]$.

If $\alpha >2D$ and $0<\kappa <\frac{2\sqrt{2\alpha }}{3}(\frac{\alpha }{2}-D)$ are satisfied, then

$${\dot{V}}_0(s,\dot{s})\le -\kappa {\left|s\right|}^{\frac{3}{2}}(\frac{1}{2}\alpha -D)-\left|\dot{s}\right|V_0^{*}(\dot{s})\le 0$$

(45)

Substituting Formula (45) into Formula (38), and we find the derivative:

$$\begin{array}{cc}\hfill \dot{V}(s,\dot{s},\alpha )& =V_0(s,\dot{s})+\frac{1}{\theta }(\alpha -{\alpha }^{*})\dot{\alpha }\hfill \\ & \le -\kappa {\left|s\right|}^{\frac{3}{2}}(\frac{1}{2}\alpha -D)-\left|\dot{s}\right|V_0^{*}(\dot{s})-\frac{\omega }{\sqrt{2\theta }}\left|\alpha -{\alpha }^{*}\right|\hfill \\ & +\frac{\omega }{\sqrt{2\theta }}\left|\alpha -{\alpha }^{*}\right|+\frac{1}{\theta }(\alpha -{\alpha }^{*})\dot{\alpha }\hfill \end{array}$$

(46)

Using inequality ${(x^2+y^2)}^{\frac{1}{2}}\le \left|x\right|+\left|y\right|$, the following formula is derivated:

$$\dot{V}(s,\dot{s},\alpha )\le -\kappa {\left|s\right|}^{\frac{3}{2}}(\frac{1}{2}\alpha -D)-\eta V_0^{*}(\dot{s})+\frac{\omega }{\sqrt{2\theta }}\left|\alpha -{\alpha }^{*}\right|+\frac{1}{\theta }(\alpha -{\alpha }^{*})\dot{\alpha }$$

(47)

In Formula (47), $\eta =\min (\left|\dot{s}\right|,\omega )$.

The control gain α of the adaptive law is bounded. This is because when $e^{k(s^2+\frac{1}{2}{\dot{s}}^2)}>\rho$ and 0 ≤ t ≤ t_c, there are

$$\alpha =\alpha (0)+\omega \sqrt{\frac{\theta }{2}}\cdot t_c$$

(48)

In Formula (48), t_c is the finite convergence time, so the control gain α is bounded; when $e^{k(s^2+\frac{1}{2}{\dot{s}}^2)}<\rho$, the gain α decreases until $e^{k(s^2+\frac{1}{2}{\dot{s}}^2)}>\rho$ is satisfied again.

From the above analysis of boundedness, we can see that there must be a positive number ${\alpha }^{*}$ that makes $\alpha -{\alpha }^{*}<0$ always hold. Therefore,

$$\begin{array}{cc}\hfill \dot{V}(s,\dot{s},\alpha )& \le -\kappa {\left|s\right|}^{\frac{3}{2}}(\frac{1}{2}\alpha -D)-\eta V_0^{*}(\dot{s})+(\frac{\omega }{\sqrt{2\theta }}-\frac{1}{\theta }\dot{\alpha })\left|\alpha -{\alpha }^{*}\right|\hfill \\ & =-\kappa {\left|s\right|}^{\frac{3}{2}}(\frac{1}{2}\alpha -D)-\eta V_0^{*}(\dot{s})\hfill \\ & \le 0\hfill \end{array}$$

(49)

Therefore, the objective function of the system can converge to near zero in a finite time. In summary, when satisfying

$$\{\begin{array}{l}\alpha >2D\hfill \\ 0<\kappa <\min (\frac{2\sqrt{2\alpha }}{3}(\frac{\alpha }{2}-D),2{\alpha }^{\frac{3}{2}})\hfill \end{array}$$

(50)

the designed controller is stable. The certificate is complete.

3.3. Design of Lower-Level Controller

The direct yaw moment calculated by the upper controller to maintain the lateral stability of the distributed drive electric vehicle needs to be converted into the four-wheel torque distribution by the lower controller in order to realize the lateral stability control. In this section, an optimal longitudinal force distribution algorithm is proposed, and the lower-level controller is designed. The optimal distribution function is designed as follows:

$$J=\{\begin{array}{cc}\max {\displaystyle \sum {(\frac{F_{xij}}{\mu F_{zij}})}^2}& \beta <{\beta }_t\\ \min {\displaystyle \sum {(\frac{F_{xij}}{\mu F_{zij}})}^2}& \beta \ge {\beta }_t\end{array}$$

(51)

In Formula (51), β_t is the center of mass slip angle threshold.

In order to make the tire work in the linear region as much as possible, and to consider the impact of road adhesion on the longitudinal tire force, combined with Formula (11), the optimal longitudinal force distribution is determined under the following constraints:

$$\{\begin{array}{l}\left|F_{xij}\right|\le \mu F_{zij}\hfill \\ M_z=a(F_{xfl}+F_{xfr})\sin \delta -\frac{B}{2}(F_{xfl}-F_{xfr})\cos \delta -\frac{B}{2}(F_{xrl}-F_{xrr})\hfill \end{array}$$

(52)

After deciding the optimal longitudinal force distribution, the wheel rotation dynamics model established in Section 2.1 can be converted to obtain the four-wheel torque distribution, which is the target torque distribution of the four-wheel hub motor. The design significance of the optimal longitudinal force distribution algorithm is that the center of mass slip angle threshold β_t is used to define whether the tire is working in a non-linear region. When β < β_t, it is considered that the tire is working in the linear region, and the tire can provide enough lateral tire force to ensure that the vehicle does not become unstable. Therefore, the objective function of the tire lateral force distribution should be small, such that the tire has enough surplus longitudinal direction, When β < β_t, it is considered that the tire is working in the non-linear region, and the tire’s lateral force is easily saturated. If the tire’s lateral force at saturation is still insufficient to ensure that the axle does not slip, the vehicle will be at risk of lateral instability. Therefore, the longitudinal force distribution objective function should be as small as possible, such that the tire can provide as much lateral force as possible to prevent the axle from sliding, and reduce the risk of lateral instability of the vehicle. The control system parameters are shown in

Table 2. Control system parameters.

Parameter	Value
k	1.3
ω	110
θ	180
ρ	6
λ	11
αt	18
βt	0.5

.

4. Simulation Results

In order to compare the effectiveness of the controller designed in the previous section, a joint simulation platform based on CarSim and Simulink was established, in which CarSim is used to provide the vehicle dynamics model, the designed controller and tire force distribution method are implemented in Simulink. A standard Carsim vehicle model is taken in the simulation. The key parameters of the vehicle model in Carsim are given in Table 1. In this section, a slalom test is used to verify the effectiveness of the designed controller.

The test settings of slalom simulation test are as follows: the maximum target speed of 65 km/h is carried out under the road adhesion coefficients μ = 0.85 and μ = 0.3. There are five cones in the slalom test scene, and the pile spacing L_s = 30 m. As shown in Figure 5, the simulation step is 0.001s.

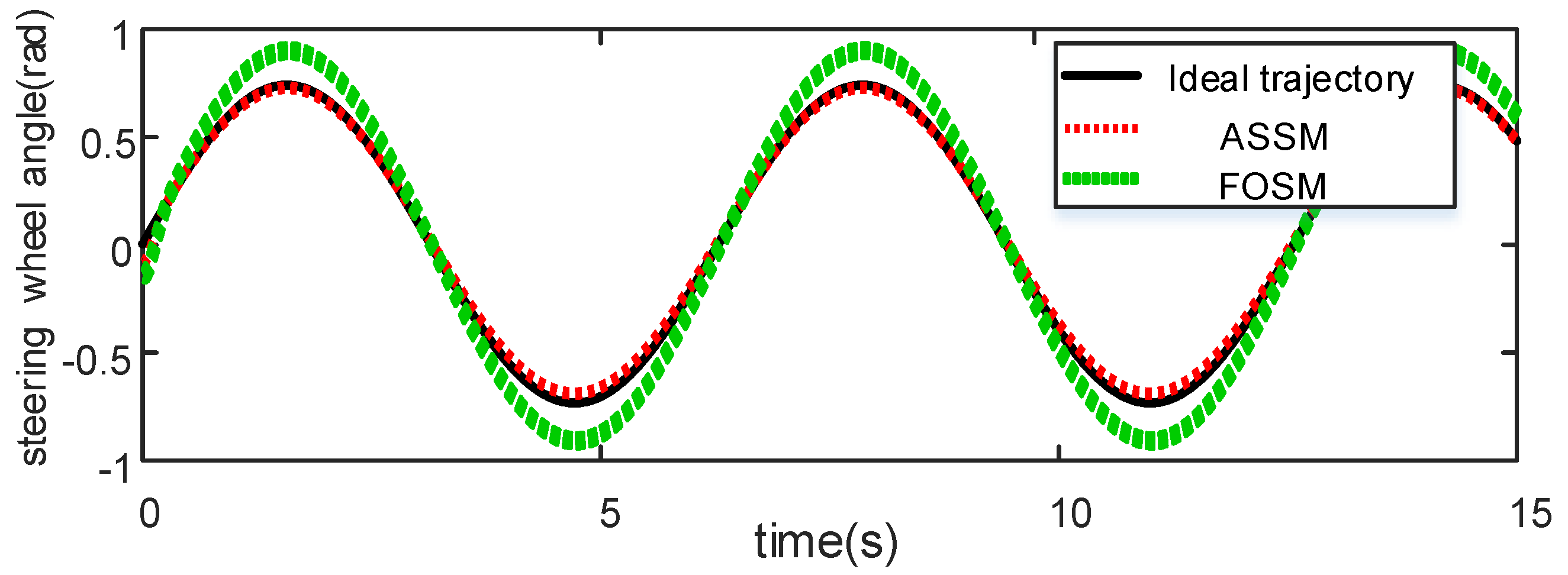
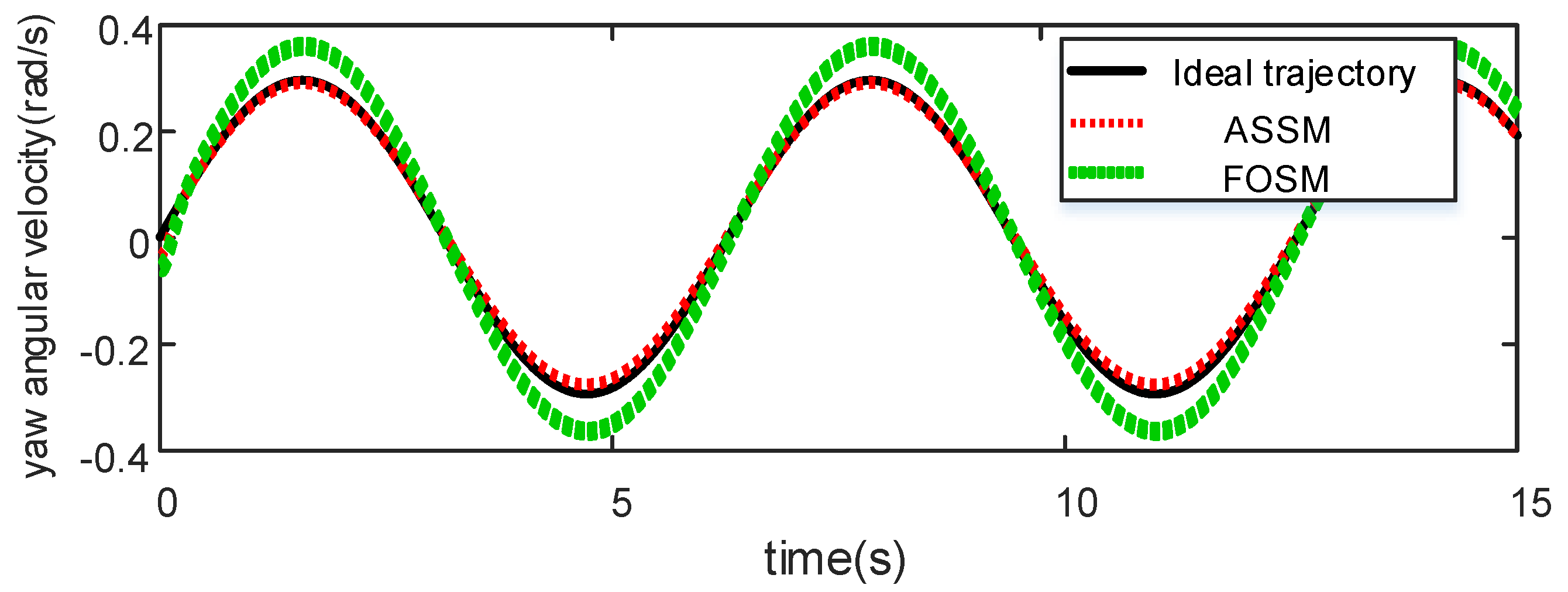
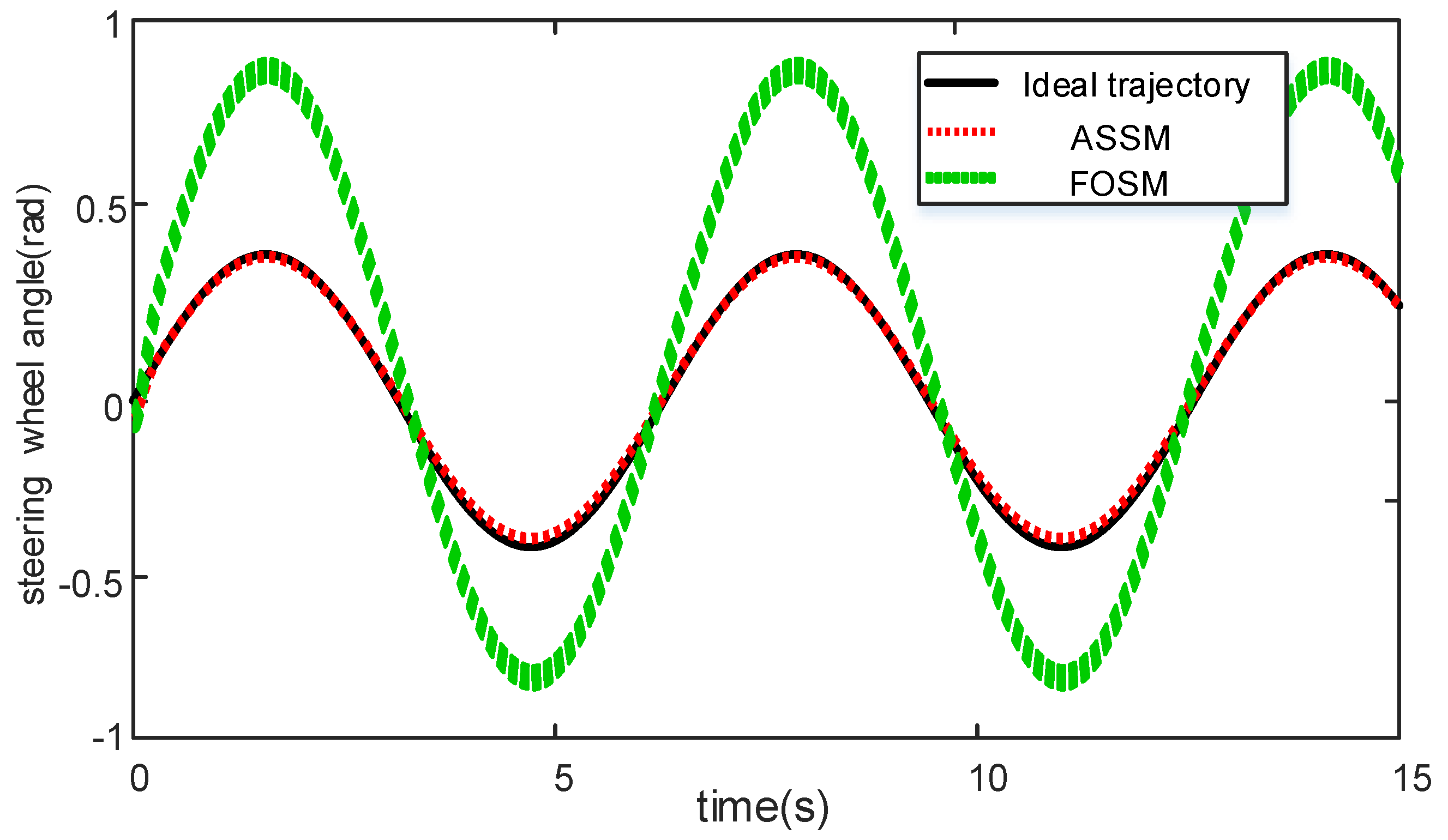
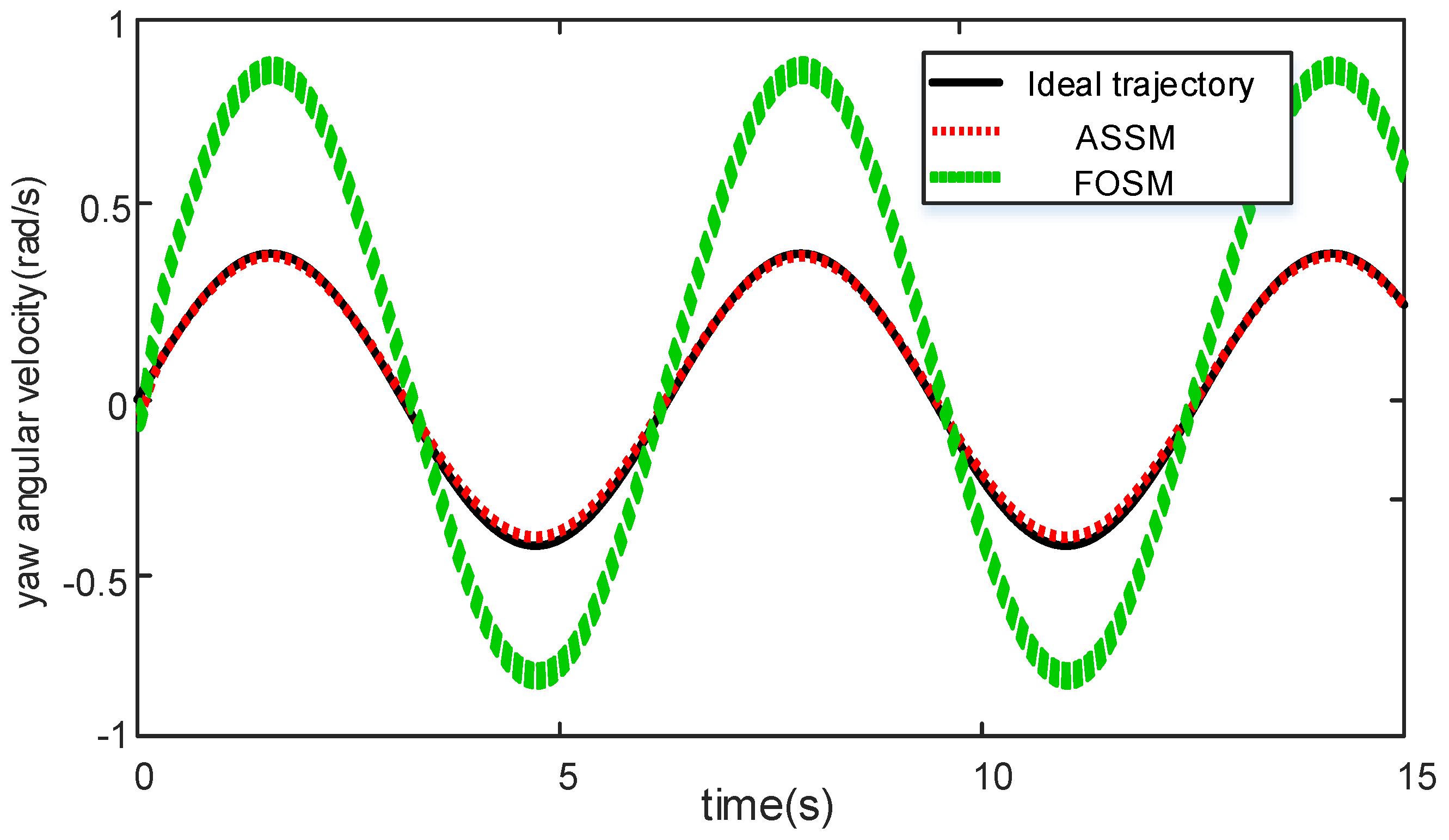
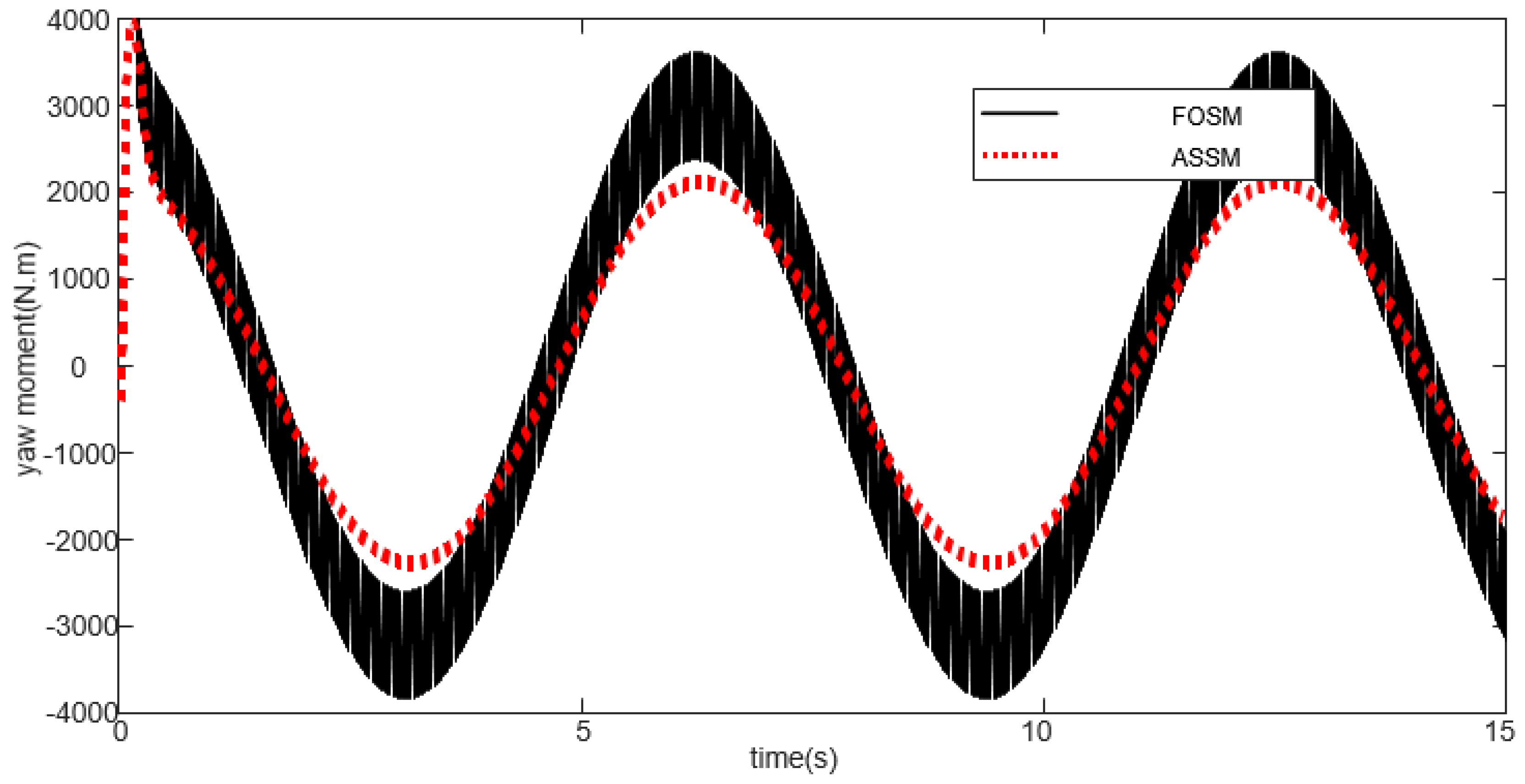
4.1. Slalom Condition 1: The Uniform Road Adhesion Coefficient μ = 0.85, and the Vehicle Speed Is 65 km/h

As can be seen from Figure 6 and Figure 7, the steering angle of the intelligent vehicle steering wheel can better track the steering wheel angle value of the vehicle’s ideal trajectory under slalom working conditions through the ASSM control. The high-precision automatic steering control is realized. Meanwhile, the yaw rate of the vehicle can be tracked for a long time in order to track the yaw angular velocity under the reference driving track, such that the driving stability of the intelligent vehicle can be guaranteed. However, under the FOSM control of the intelligent vehicle steering system, high control overshoot and control lag occur at both lower and higher vehicle speeds, which directly affects the steering control accuracy and driving stability of the vehicle. The control effect is significantly worse than the ASSM-based control effect proposed in this paper. Meanwhile, due to the discontinuous property of the first-order SMC, the FOSM controllers incur heavy chattering, while the ASSM controllers have almost no chattering, which can be verified by Figure 8.

4.2. Slalom Condition 1: The Uniform Road Adhesion Coefficient μ = 0.3, and the Vehicle Speed Is 65 km/h

As can be seen from Figure 9 and Figure 10, the steering angle of the intelligent vehicle steering wheel can better track the steering wheel angle value of the vehicle’s ideal trajectory under slalom working conditions (uniform road adhesion coefficient μ = 0.3) through the ASSM control. High-precision automatic steering control is realized. Meanwhile, the yaw rate of the vehicle can be tracked for a long time in order to track the yaw angular velocity under the reference driving track, such that the driving stability of the intelligent vehicle can be guaranteed. However, under the FOSM control of the intelligent vehicle steering system, high control overshoot and control lag occur at both lower and higher vehicle speeds, which directly affects the steering control accuracy and driving stability of the vehicle. The control effect is significantly worse than the ASSM-based control effect proposed in this paper. Meanwhile, due to the discontinuous property of the first-order SMC, the FOSM controllers incur heavy chattering, while the ASSM controllers have almost no chattering, which can be verified by Figure 11.

In summary, among the various working conditions, high-speed working conditions on low-adhesion roads are the most dangerous working conditions, but the designed control system can effectively control the heading deviation and lateral deviation in vehicle trajectory tracking while ensuring the lateral stability of the vehicle.

5. Conclusions

• The three-degrees-of-freedom and seven-degrees-of-freedom vehicle dynamics model and trajectory tracking model of the intelligent electric vehicle were established respectively, and were used as the basis for the design of vehicle path tracking and lateral stability controllers.
• A layered intelligent electric vehicle lateral stability controller was designed. The upper-level controller was designed based on the ASSM algorithm, and the stability of the upper-level controller was analyzed, and the stability conditions were obtained. The optimal longitudinal force distribution algorithm was proposed, based on which the lower-level controller was designed.
• A joint simulation model of CarSim and Simulink was built and a simulation experiment was carried out. The results show that the proposed vehicle coordinated control strategy can achieve accurate and rapid vehicle path tracking control effects, keep the lateral error in the path tracking process within a small range, and also ensure the lateral stability of the vehicle.
• It should be noted that the intelligent distributed drive electric vehicle model and road with a low adhesion coefficient in the slalom test are not real ones, but were simulated in experiments. Thus, the experimental platform does not completely match the real scenario at this stage. However, our control design and experimental validation are still valuable for industrial references. Our future work is to improve the experimental platform as a real intelligent distributed drive electric vehicle which can run on the road.