Positioning Errors Measurement of CNC Machine Tools Based on J-DBB Method
Abstract
:1. Introduction
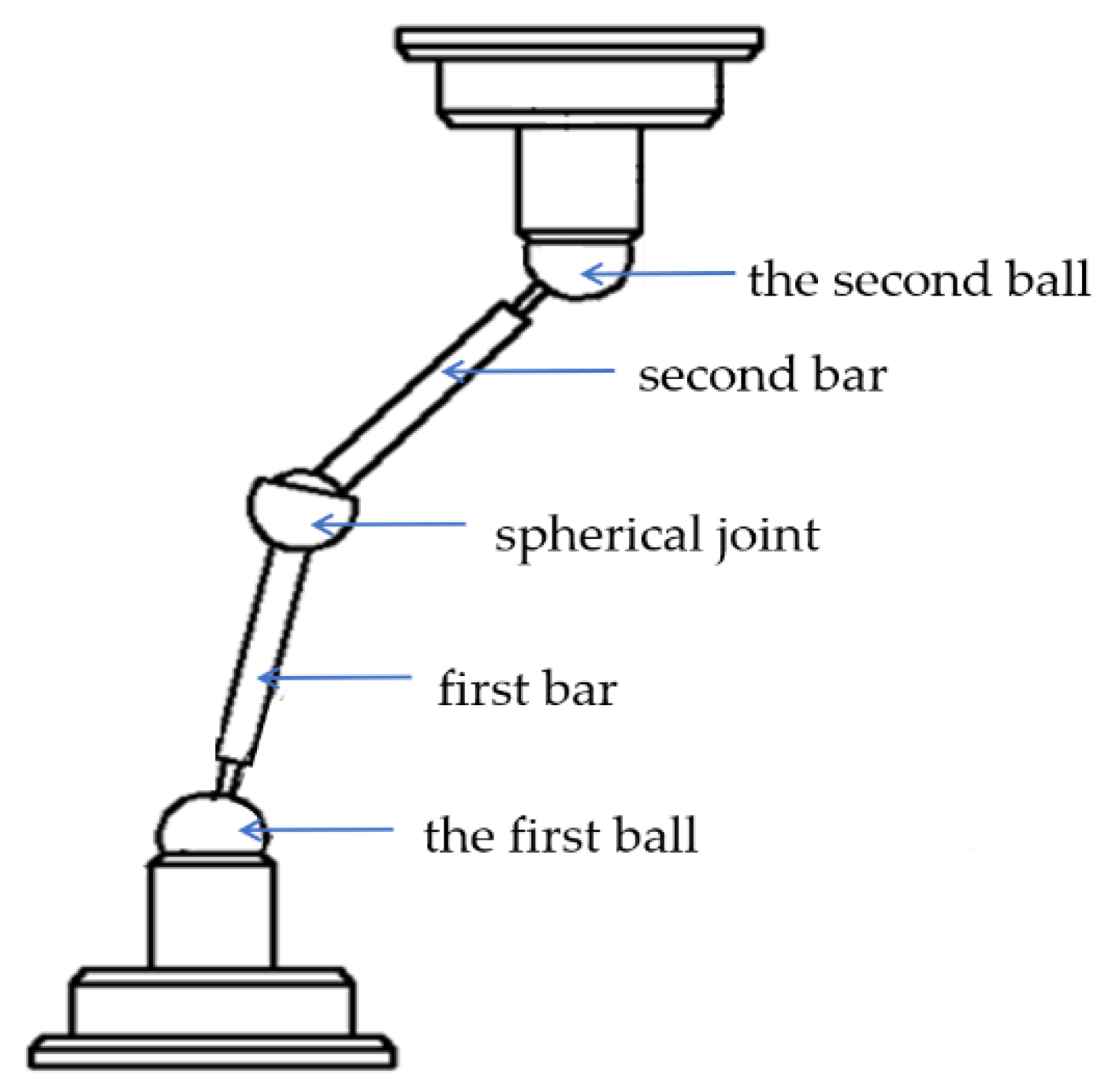
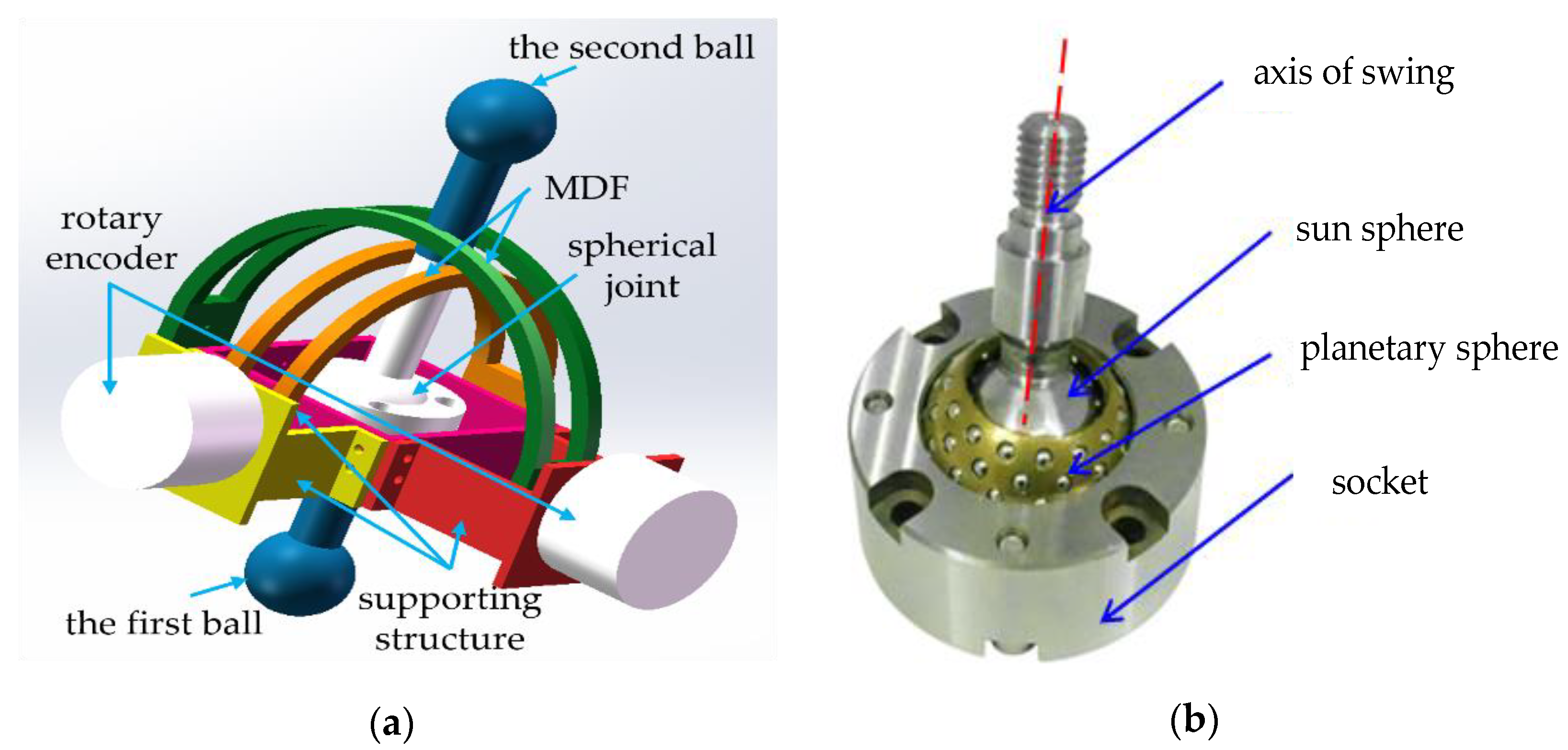
2. Principle of the J-DBB
2.1. Structure of the J-DBB
2.2. Error Equation Based on the J-DBB
3. Positioning Errors Analysis of Machine Tool
3.1. Uniform Contraction Error of Ball Screw and Linear Grating
3.2. Periodic Error of Ball Screw and Linear Grating
3.3. Interference of Detection Devices
3.4. Opposite Clearance
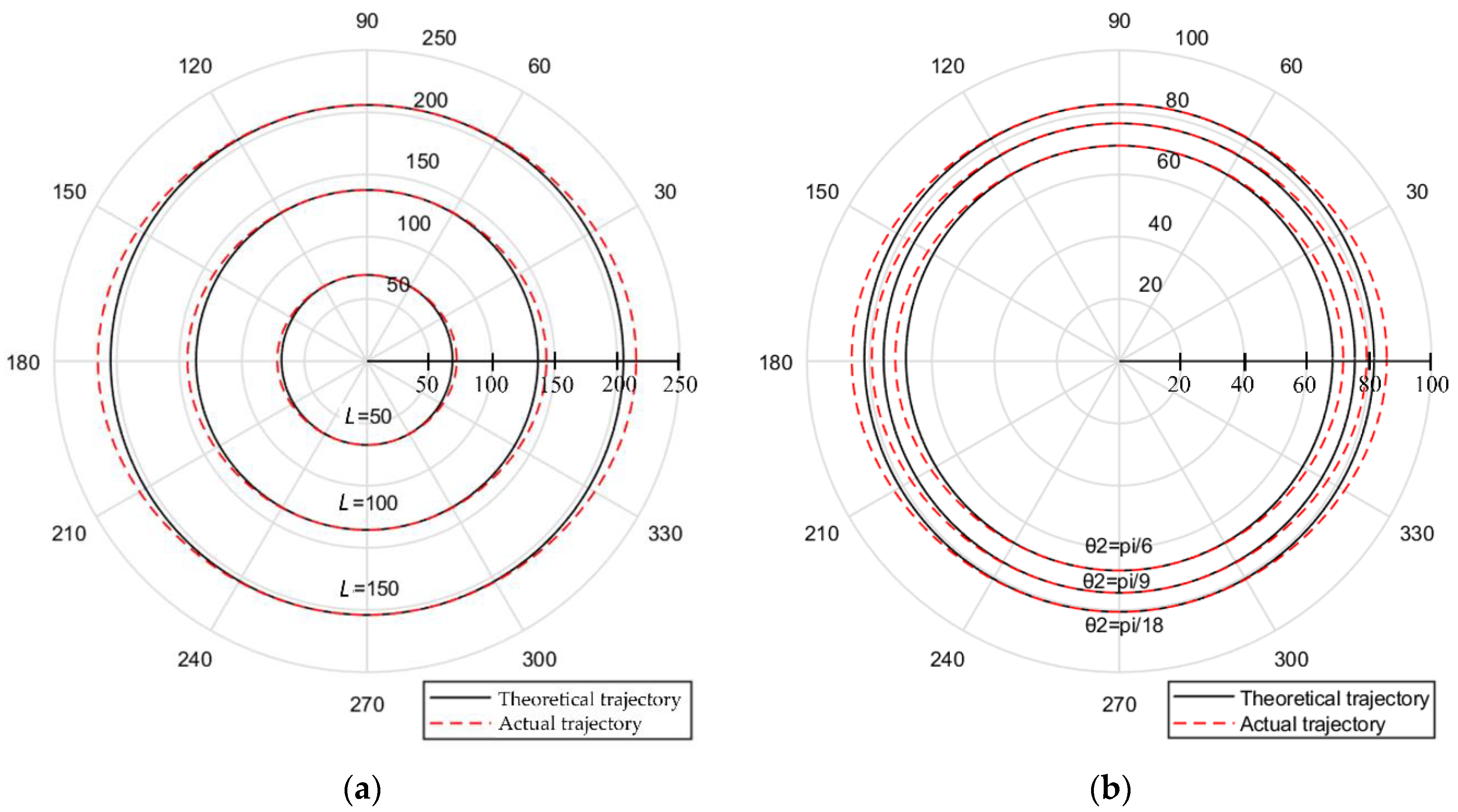
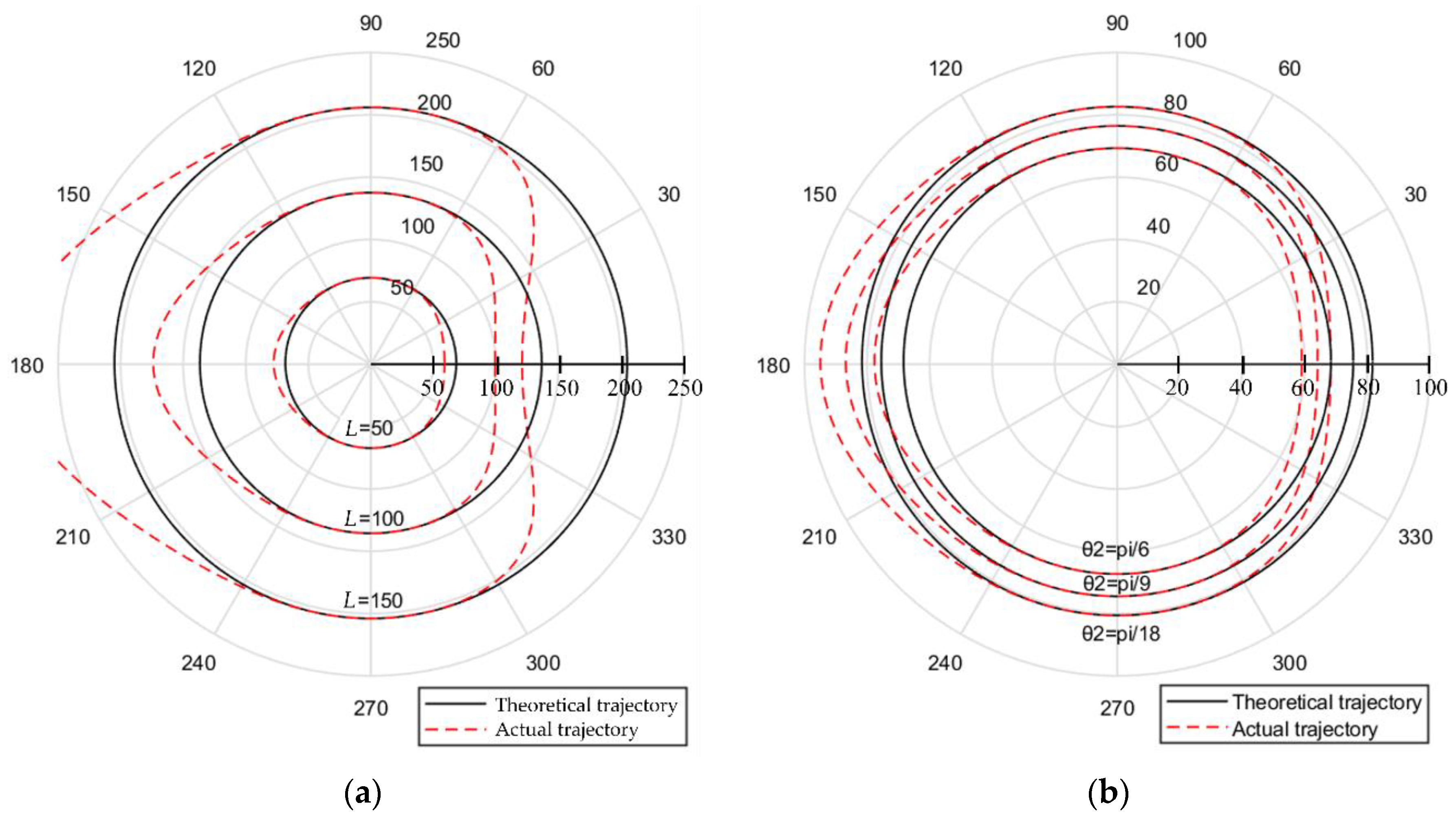
4. Simulation of the Positioning Errors
4.1. First-Order Contraction Error of the Ball Screw and Linear Grating
4.2. Second-Order Contraction Error of the Ball Screw and Linear Grating
4.3. Periodic Error of the Ball Screw and Linear Grating
4.4. Noise of Measurement Device
4.5. Opposite Clearance
5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| L | The distance between the spherical joint and each ball |
| θ1 | The angle between horizontal plane and bar 1 |
| θ2 | The acute angle between two connecting bars |
| θ3 = vRt | The angle of rotation of machine tool after running at speed v for t seconds |
| a | The contraction ratio of the ball screw and linear grating, μm/mm |
| ax | The contraction ratio of the ball screw and linear grating on x-axis, μm/mm |
| p | The screw pitch of the ball screw or the grating pitch of the linear grating |
| d | The amplitude |
| φ | The phase angle |
| bx | The ratio of amplitude to velocity along the x-axis direction |
| by | The ratio of amplitude to velocity along the y-axis direction |
| φx | The phase angle along the x-axis direction |
| φy | The phase angle along the y-axis direction |
| F | The velocity of machine tool spindle, m/s |
| f | The opposite clearance |
| r | The design trajectory of circular motion |
| r1 | The real trajectory of circular motion |
References
- Ibaraki, S.; Knapp, W. Indirect measurement of volumetric accuracy for three-axis and five-axis machine tools: A review. Int. J. Autom. Technol. 2012, 6, 110–124. [Google Scholar] [CrossRef] [Green Version]
- Mekid, S.; Ogedengbe, T. A review of machine tool accuracy enhancement through error compensation in serial and parallel kinematic machines. Int. J. Precis. Technol. 2010, 1, 251–286. [Google Scholar] [CrossRef]
- Huo, F.; Poo, A. Nonlinear autoregressive network with exogenous inputs based contour error reduction in CNC machines. Int. J. Mach. Tools Manuf. 2013, 67, 45–52. [Google Scholar] [CrossRef]
- Jiang, X.P.; Cripps, R. A method of testing position independent geometric errors in rotary axes of a five-axis machine tool using a double ball bar. Int. J. Mach. Tools Manuf. 2015, 89, 151–158. [Google Scholar] [CrossRef] [Green Version]
- Ramesh, R.; Mannan, M.A.; Poo, A.N. Error compensation in machine tools—Review: Part I: Geometric, cutting-force induced and fixture-dependent errors. Int. J. Mach. Tools Manuf. 2000, 40, 1235–1256. [Google Scholar] [CrossRef]
- Bryan, J.B. A simple method for testing measuring machines and machine tools, part 1: Principles and application. Precis. Eng. 1982, 4, 61–69. [Google Scholar] [CrossRef]
- Bryan, J.B. A simple method for testing measuring machines and machine tools, part 2: Construction. Precis. Eng. 1982, 4, 125–138. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Veldhuis, S.C. Modelling geometric and thermal errors in a five-axis CNC machine tool. Int. J. Mach. Tools Manuf. 1995, 35, 1321–1337. [Google Scholar] [CrossRef]
- Yang, S.H.; Kim, K.H.; Park, Y.K.; Lee, S.G. Error analysis and compensation for the volumetric errors of a vertical machining centre using a hemispherical helix ball bar test. Int. J. Adv. Manuf. Technol. 2004, 23, 495–500. [Google Scholar] [CrossRef]
- Lei, W.T.; Sung, M.P.; Liu, W.L.; Chuang, Y.C. Double-ball-bar test for the rotary axes of five-axis CNC machine tools. Int. J. Mach. Tools Manuf. 2007, 47, 273–285. [Google Scholar] [CrossRef]
- Lei, W.T.; Hsu, Y.Y. Error measurement of five-axis CNC machine with 3D probe-ball. J. Mater. Process. Technol. 2003, 139, 127–133. [Google Scholar] [CrossRef]
- Lee, K.I.; Yang, S.H. Accuracy evaluation of machine tools by modeling spherical deviation based on double ball-bar measurements. Int. J. Mach. Tools Manuf. 2013, 75, 46–54. [Google Scholar] [CrossRef]
- Lee, K.I.; Yang, S.H. Measurement and verification of position-independent geometric errors of a five-axis machine tool using a double ball-bar. Int. J. Mach. Tools Manuf. 2013, 70, 45–52. [Google Scholar] [CrossRef]
- Florussen, G.H.J.; Delbressine, F.L.M.; Schellekens, P.H.J. Assessing thermally induced errors of machine tools by 3D length measurements. Int. J. Mach. Tools Manuf. 2003, 27, 105–109. [Google Scholar] [CrossRef]
- Yukio, T.; Gang, S.; Hiroaki, F. A DBB-based kinematic calibration method for in-parallel actuated mechanisms using a fourier series. J. Mech. Des. 2004, 12, 846–857. [Google Scholar]
- Heui, J.P.; Young, S.K. A new technique for volumetric error assessment of CNC machine tools incorporating ball bar measurement and 3D volumetric error model. J. Mech. Des. 1997, 37, 1583–1596. [Google Scholar]
- Kakino, Y.; Ihara, Y.; Nakatsu, Y.; Okamura, K. The measurement of motion errors of NC machine tools and diagnosis of their origins by using telescoping magnetic ball bar method. CIRP Ann.-Manuf. Technol. 1987, 36, 377–380. [Google Scholar] [CrossRef]
- Iwai, H.; Mitsui, K. Development of a measuring method for motion accuracy of NC machine tools using links and rotary encoders. Int. J. Mach. Tools Manuf. 2009, 49, 99–108. [Google Scholar] [CrossRef]
- Furutani, R.; Kamahora, K. Development of a new artifact for the calibration of large scale instruments. Measurement 2001, 30, 139–143. [Google Scholar] [CrossRef]
- Qiu, H.; Li, Y.; Li, Y. A new method and device for motion accuracy measurement of NC machine tools. Part 1: Principle and equipment. Int. J. Mach. Tools Manuf. 2001, 41, 521–534. [Google Scholar] [CrossRef]
- Qiu, H.; Li, Y.; Li, Y. A new method and device for motion accuracy measurement of NC machine tools. Part 2: Device error identification and trajectory measurement of general planar motions. Int. J. Mach. Tools Manuf. 2001, 41, 535–554. [Google Scholar] [CrossRef]
- Kono, D.; Sakamoto, F.; Iwao, Y. Linked ball bar for flexible motion error measurement for machine tools. Int. J. Autom. Technol. 2017, 11, 188–196. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Z.F.; Zhu, Y.W.; He, Y.; Lu, K.; Shi, G.; Kui, X.; Ju, B. Full-scale measurement of CNC machine tools. Int. J. Adv. Manuf. Technol. 2020, 107, 2291–2301. [Google Scholar] [CrossRef]
- Shi, S.; Lin, J.; Wang, X.; Xu, X. Analysis of the transient backlash error in CNC machine tools with closed loops. Int. J. Mach. Tools Manuf. 2015, 93, 49–60. [Google Scholar] [CrossRef]
- Yadav, A.K.; Gaur, P. Modified IMC technique for nonlinear uncertain milling CNC machine tool system. Arab. J. Sci. Eng. 2020, 45, 2065–2080. [Google Scholar] [CrossRef]
- Yang, J.; Altintas, Y. A generalized on-line estimation and control of five-axis contouring errors of CNC machine tools. Int. J. Mach. Tools Manuf. 2015, 88, 9–23. [Google Scholar] [CrossRef]
- Du, Z.; Zhang, S.; Hong, M. Development of a multi-step measuring method for motion accuracy of NC machine tools based on cross grid encoder. Int. J. Mach. Tools Manuf. 2010, 50, 270–280. [Google Scholar] [CrossRef]
- Ibaraki, S.; Iritani, T.; Matsushita, T. Calibration of location errors of rotary axes on five-axis machine tools by on-the-machine measurement using a touch-trigger probe. Int. J. Mach. Tools Manuf. 2012, 58, 44–53. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.M.; Zhu, Z.; Lee, K.I.; Yang, S.H. Identification and measurement of geometric errors for a five-axis machine tool with a tilting head using a double ball-bar. Int. J. Precis. Eng. Manuf. 2011, 12, 337–343. [Google Scholar] [CrossRef]
- Xiang, S.; Yang, J.; Zhang, Y. Using a double ball bar to identify position-independent geometric errors on the rotary axes of five-axis machine tools. Int. J. Adv. Manuf. Technol. 2014, 70, 2071–2082. [Google Scholar] [CrossRef]

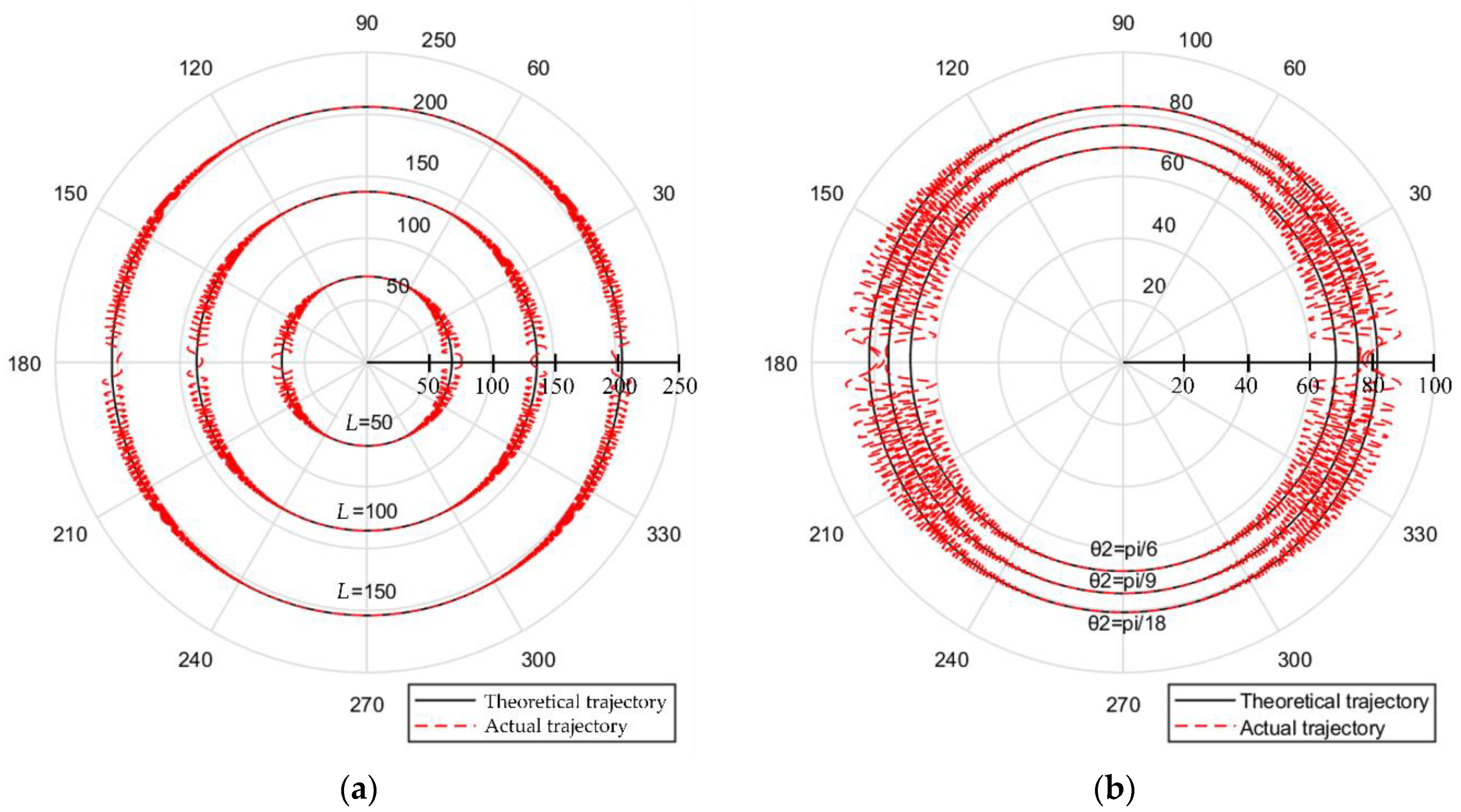
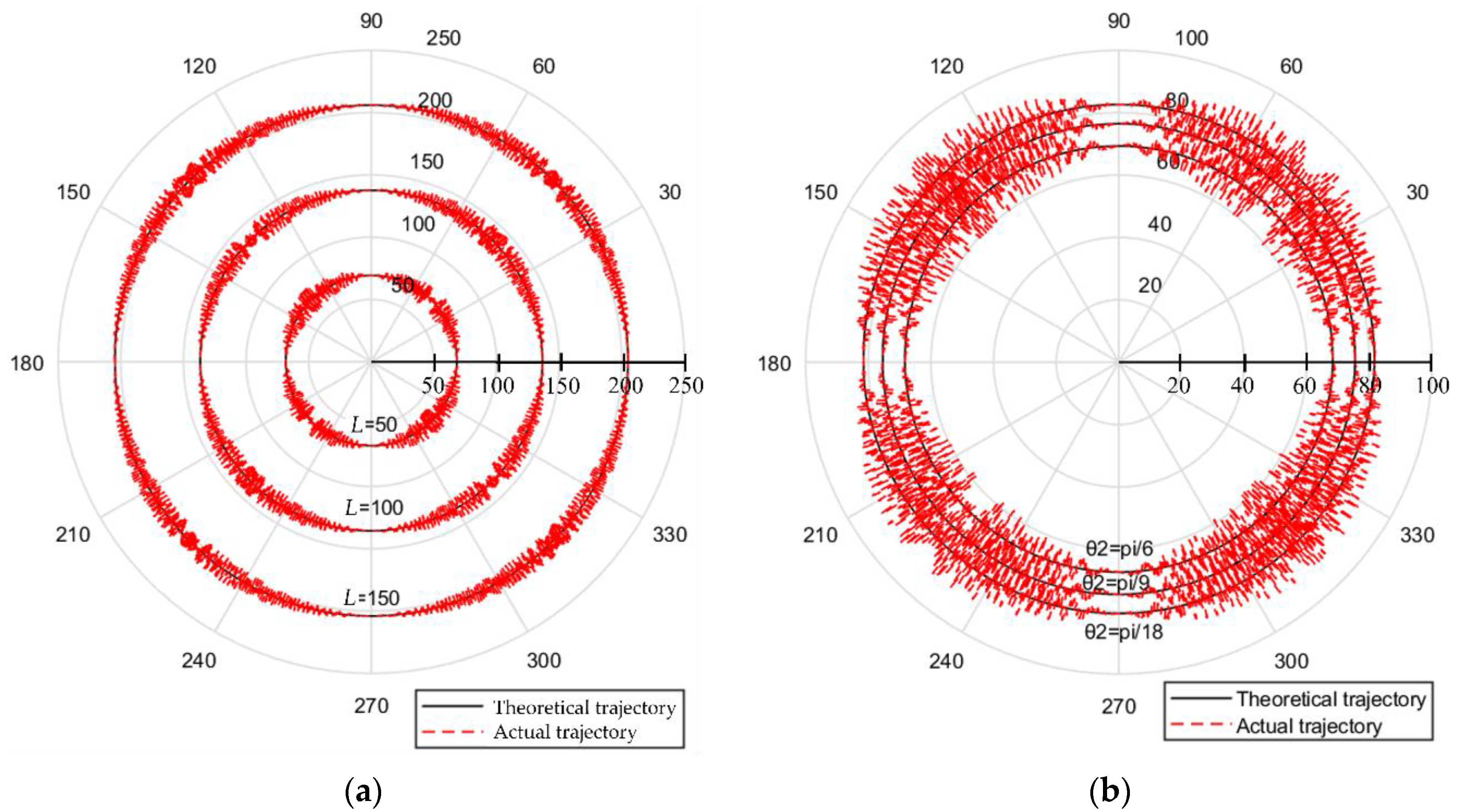
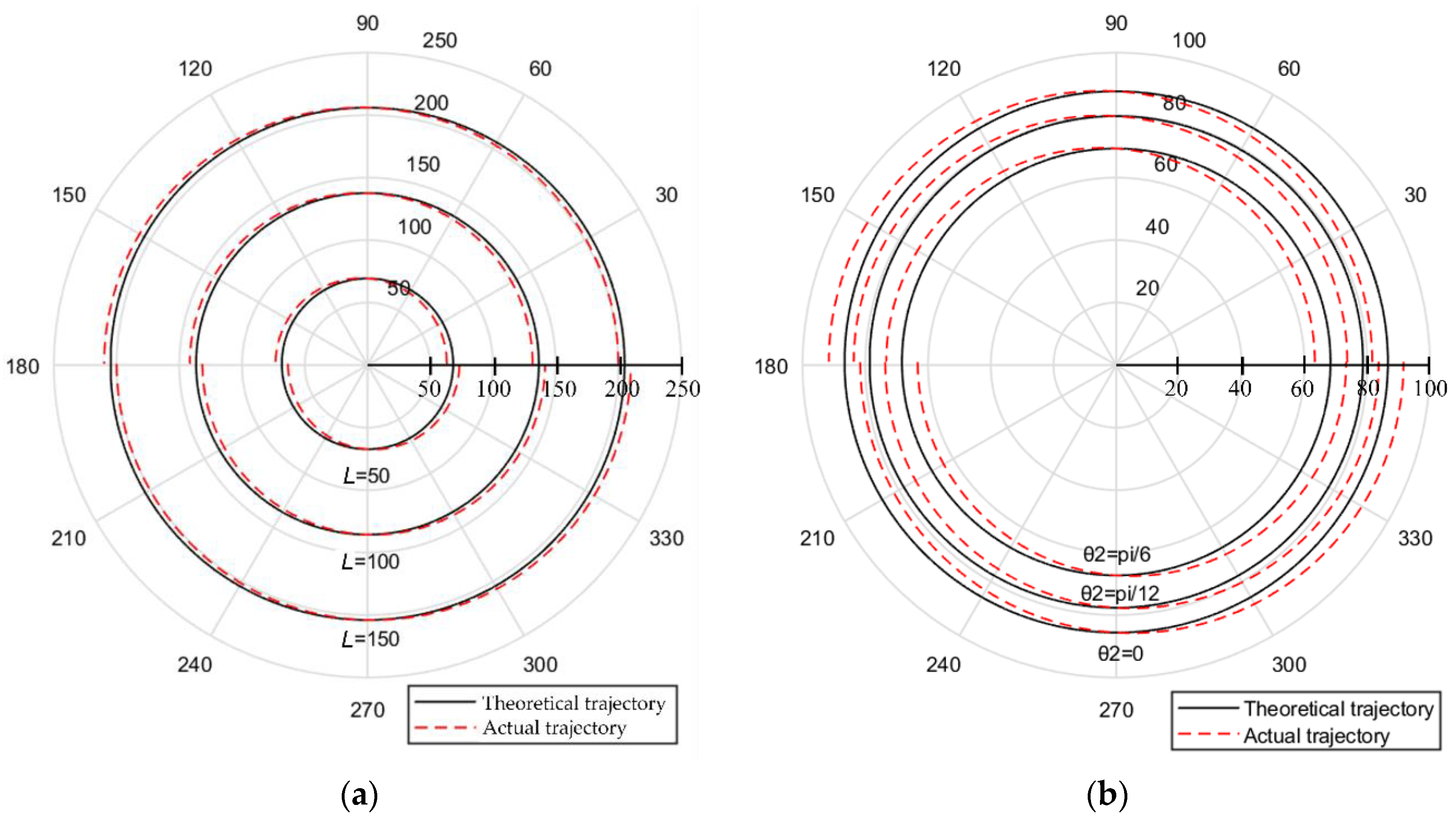
| Num. | Error Types |
|---|---|
| 1 | Uniform contraction error of ball screw and linear grating |
| 2 | Periodic error of the ball screw and linear grating |
| 3 | Interference of measurement devices |
| 4 | Opposite clearance |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Wang, W.; Chen, Z.; Zhu, Y.; Xu, K.; Wu, H.; Sang, Z.; Lu, K.; Yang, H. Positioning Errors Measurement of CNC Machine Tools Based on J-DBB Method. Appl. Sci. 2021, 11, 11770. https://doi.org/10.3390/app112411770
Sun T, Wang W, Chen Z, Zhu Y, Xu K, Wu H, Sang Z, Lu K, Yang H. Positioning Errors Measurement of CNC Machine Tools Based on J-DBB Method. Applied Sciences. 2021; 11(24):11770. https://doi.org/10.3390/app112411770
Chicago/Turabian StyleSun, Tao, Wen Wang, Zhanfeng Chen, Yewen Zhu, Kaifei Xu, Haimei Wu, Zhiqian Sang, Keqing Lu, and He Yang. 2021. "Positioning Errors Measurement of CNC Machine Tools Based on J-DBB Method" Applied Sciences 11, no. 24: 11770. https://doi.org/10.3390/app112411770
APA StyleSun, T., Wang, W., Chen, Z., Zhu, Y., Xu, K., Wu, H., Sang, Z., Lu, K., & Yang, H. (2021). Positioning Errors Measurement of CNC Machine Tools Based on J-DBB Method. Applied Sciences, 11(24), 11770. https://doi.org/10.3390/app112411770







