Experimental Measurement of Sharp THz Absorption Signatures from Nucleic Acid Solutions in Nanofluidic Channels
Abstract
:1. Introduction
2. Methods and Materials
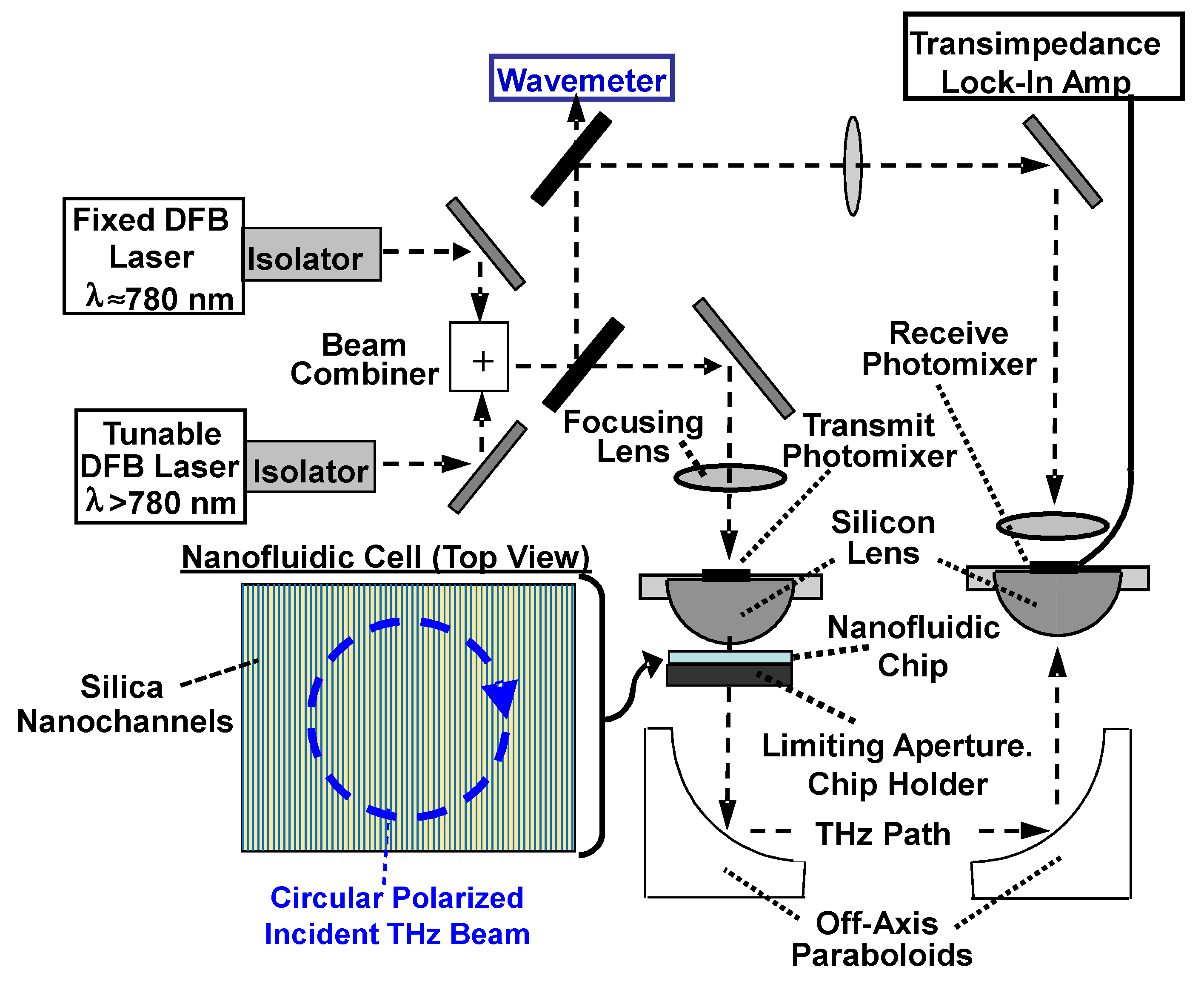
2.1. Wideband THz Transmittance Spectroscopy
2.2. Nanofluidic Chips
2.3. Nucleic Acid Samples
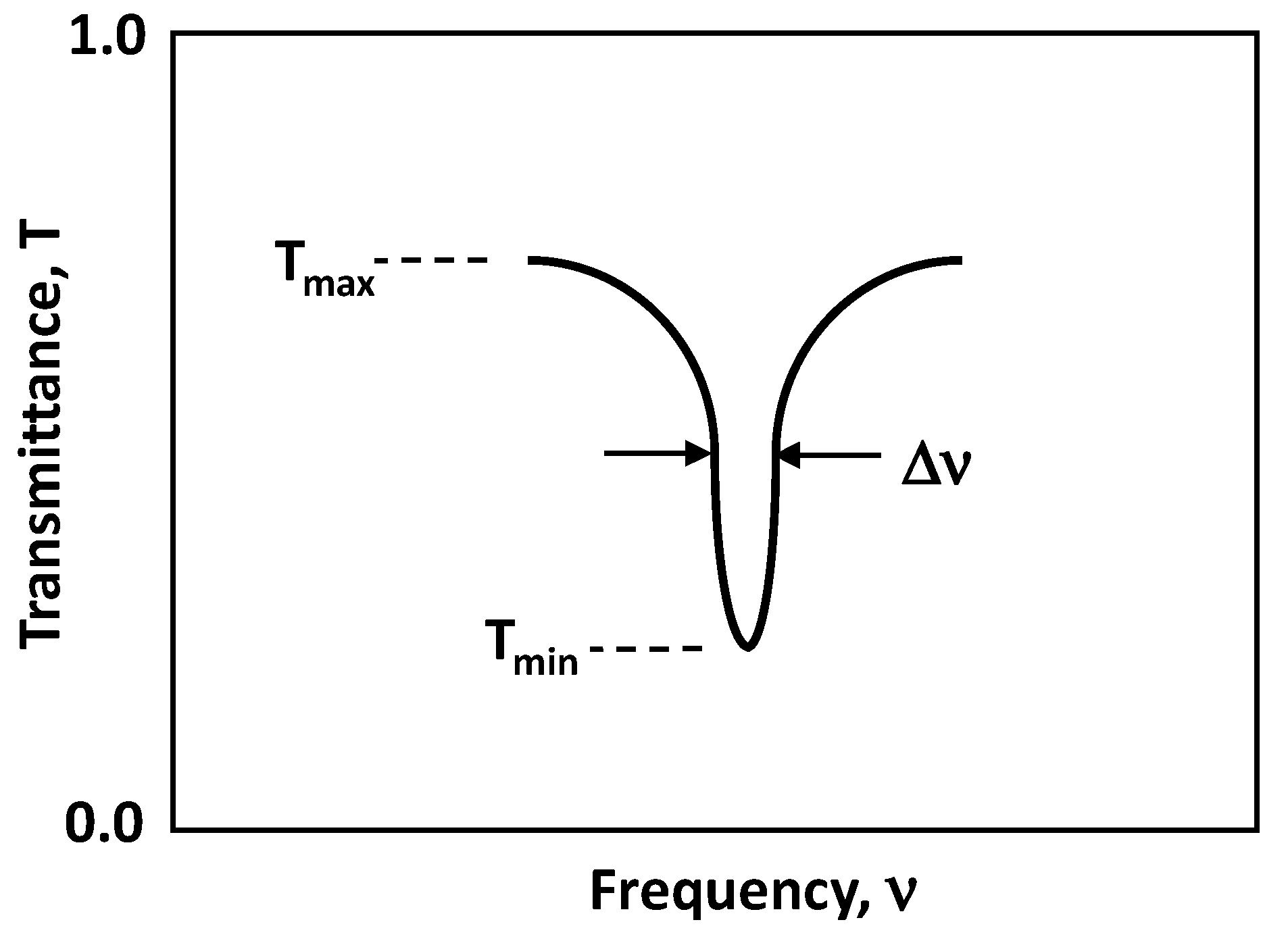
2.4. Optical Calculations
3. Experimental Results
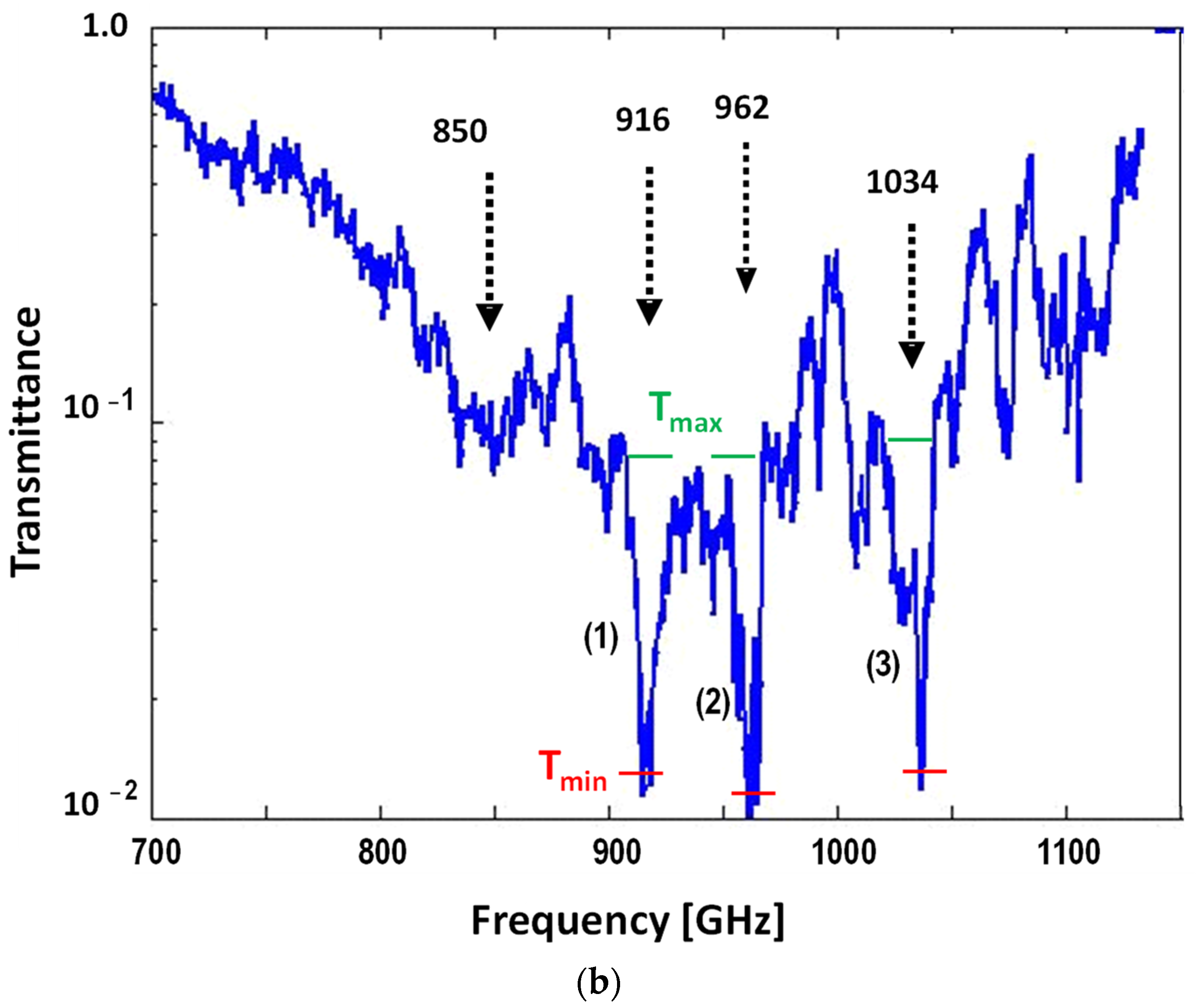
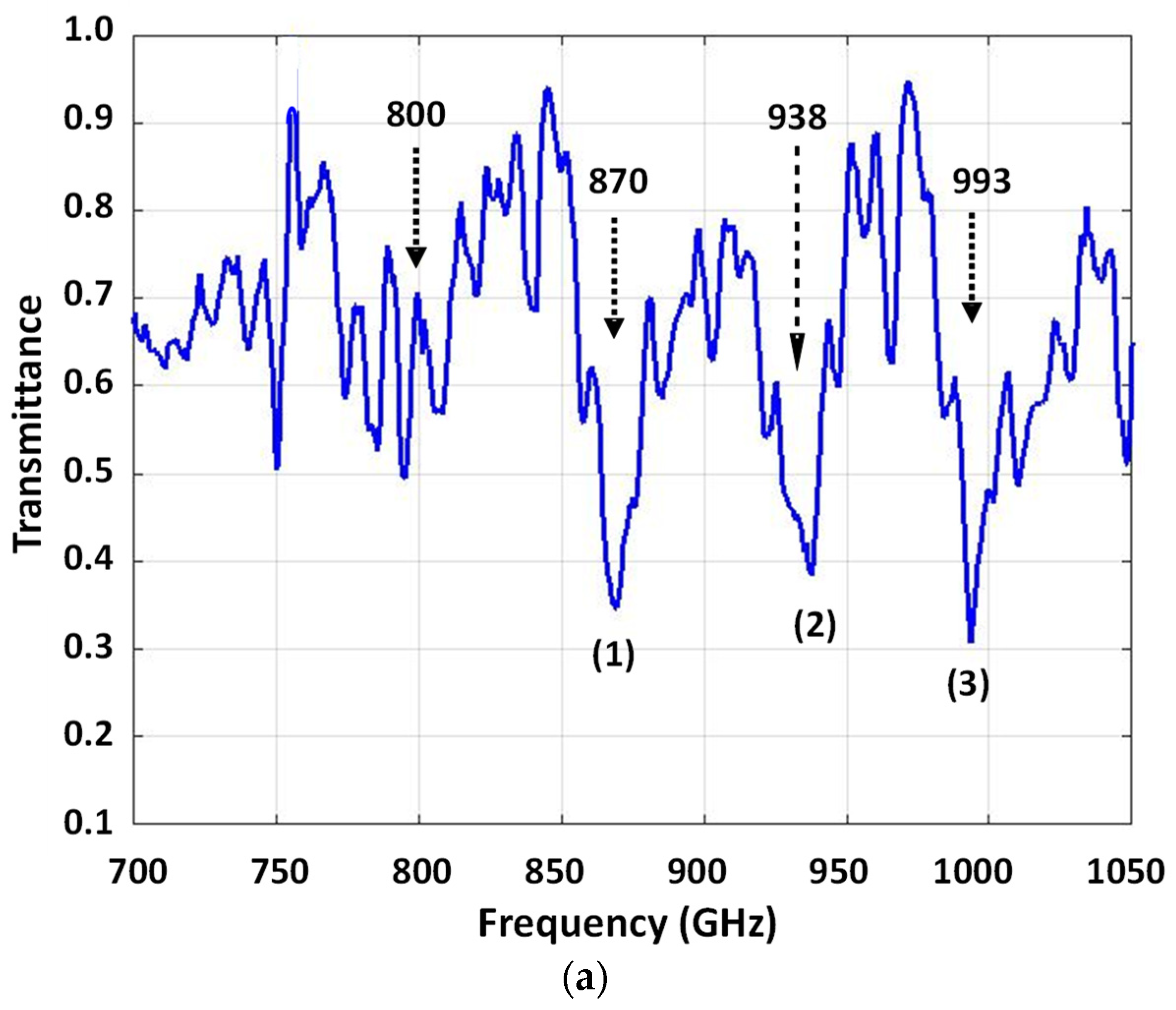
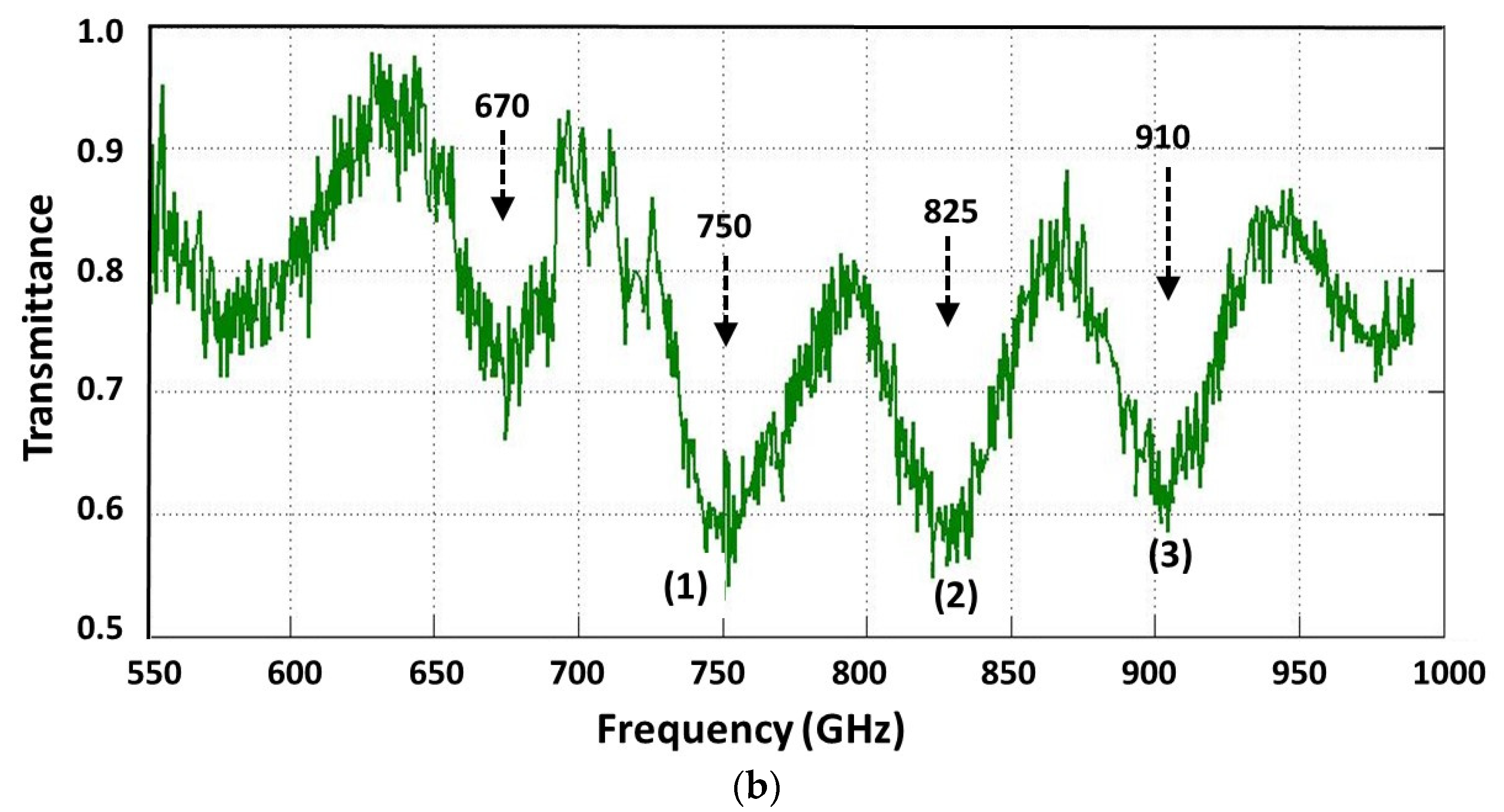
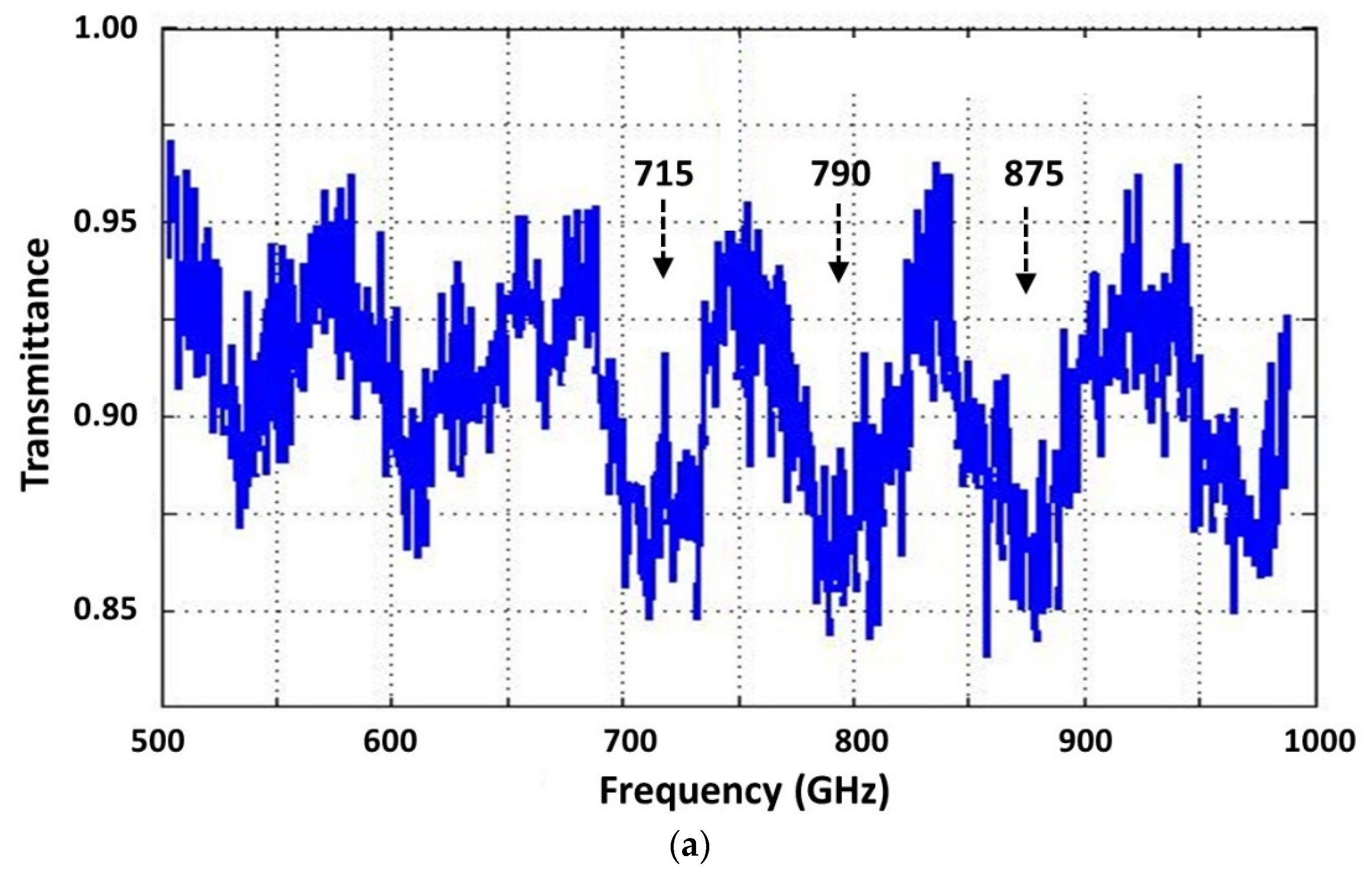
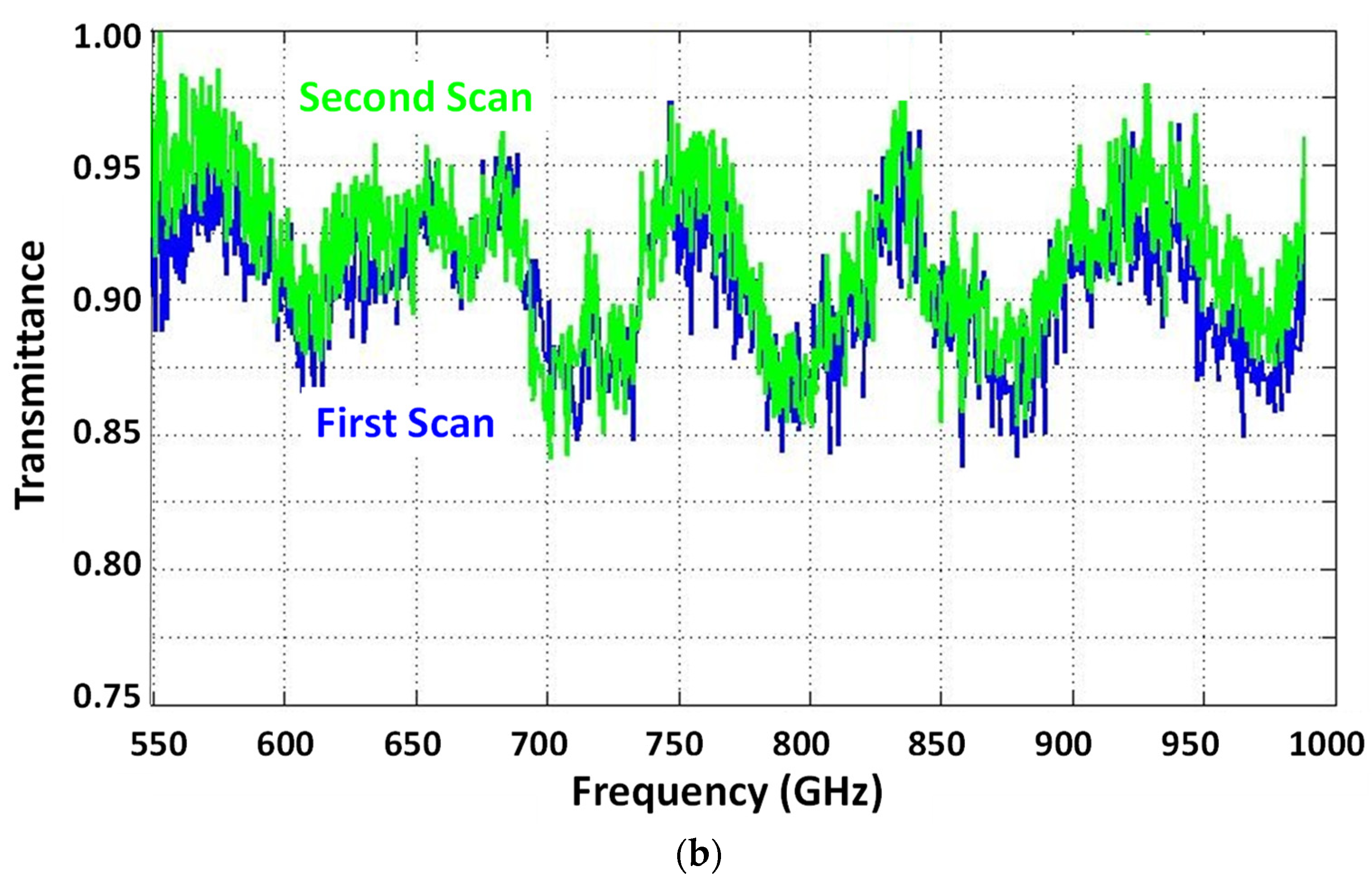
3.1. si-RNA and 50-bp Samples
3.2. 1-kbp and λ-DNA Samples
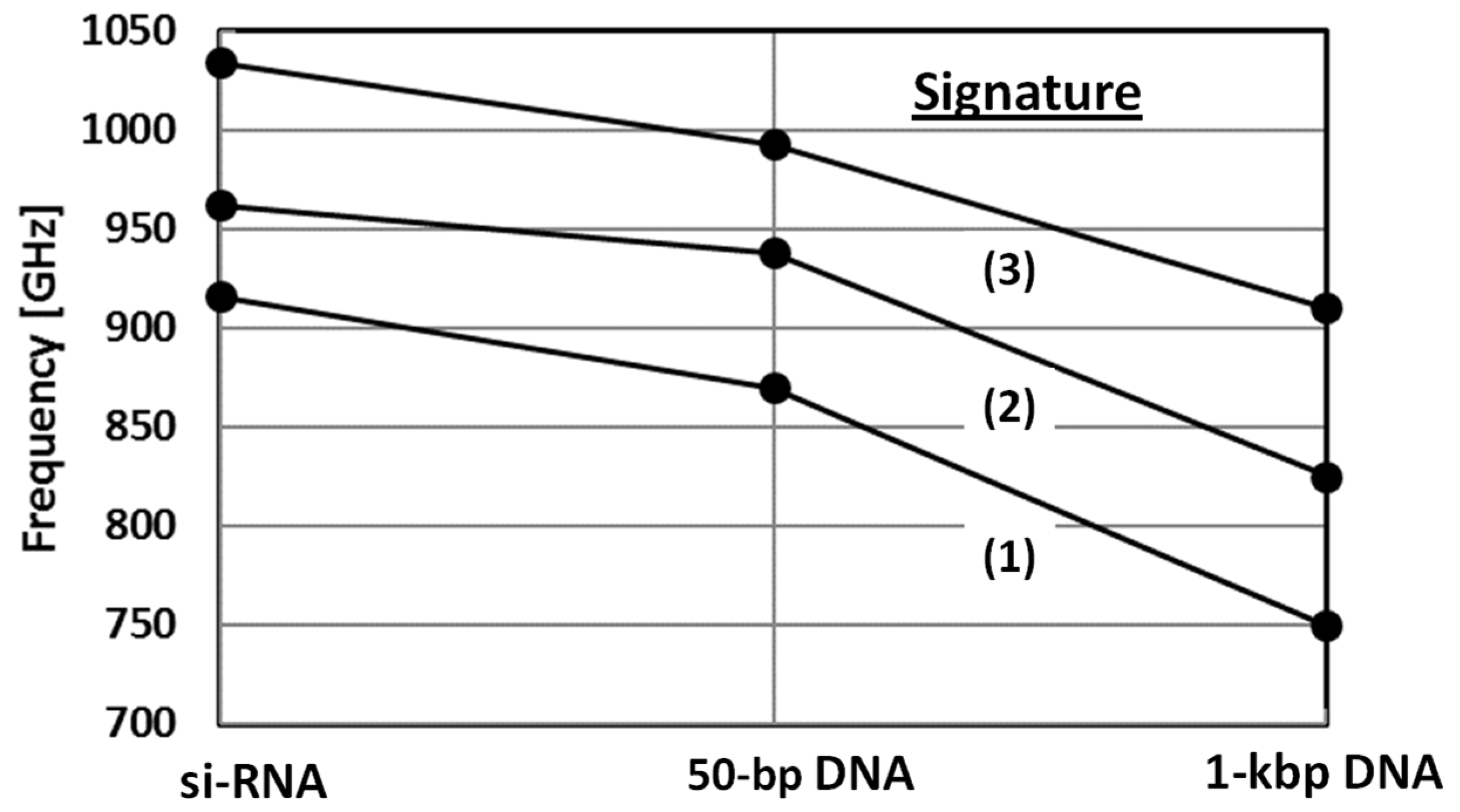
3.3. Optical Cross-Section and Red Shift
4. Discussion
4.1. Optical Effects
4.2. Instrumental Effects
4.3. Possible Biophysical Mechanism
4.4. Nanochannel Effect
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
Appendix A. Frequency-Domain Photomixing Spectrometer

Appendix B. Nanochannel Technology

Appendix C. Nucleic Acid Solutions
References
- Kohli, M.; Mei, W.N.; Van Zandt, L.L.; Prohofsky, E.W. Calculated Microwave Absorption by Double-Helical DNA. ACS Symp. Ser. 1981, 7, 101–106. [Google Scholar] [CrossRef]
- Urabe, H.; Tominaga, Y.; Kubota, K. Experimental evidence of collective vibrations in DNA double-helix (Raman spectroscopy). J. Chem. Phys. 1983, 78, 5937. [Google Scholar] [CrossRef]
- Lindsay, S.M.; Powell, J.W.; Rupprecht, A. Observation of Low-Lying Raman Bands in DNA by Tandem Interferometry. Phys. Rev. Lett. 1984, 53, 1853–1855. [Google Scholar] [CrossRef]
- Wittlin, A.; Genzel, L.; Kremer, F.; Häseler, S.; Poglitsch, A.; Rupprecht, A. Far-infrared spectroscopy on oriented films of dry and hydrated DNA. Phys. Rev. A 1986, 34, 493–500. [Google Scholar] [CrossRef]
- Van Zandt, L.L.; Saxena, V.K. Vibrational Local Modes in DNA Polymer. J. Biomol. Struct. Dyn. 1994, 11, 1149–1159. [Google Scholar] [CrossRef]
- Woolard, D.L.; Koscica, T.; Rhodes, D.L.; Cui, H.L.; Pastore, R.A.; Jensen, J.O.; Loerop, W.R.; Jacobsen, R.H.; Mittleman, D.; Nuss, M.C.; et al. Millimeter Wave-induced Vibrational Modes in DNA as a Possible Alternative to Animal Tests to Probe for Carcinogenic Mutations. J. Appl. Toxicol. 1997, 17, 243–246. [Google Scholar] [CrossRef]
- Globus, T.R.; Woolard, D.L.; Khromova, T.; Crowe, T.W.; Bykhovskaia, M.; Gelmont, B.L.; Hesler, J.; Samuels, A.C. THz Spectroscopy of Biological Molecules. J. Biol. Phys. 2003, 29, 89. [Google Scholar] [CrossRef]
- Markelz, A.G.; Roitberg, A.; Heilweil, E.J. Pulsed Terahertz Spectroscopy of DNA, Bovine Serum Albumin, and Collagen between 0.1 and 2.0 THz. Chem. Phys. Lett. 2000, 320, 42. [Google Scholar] [CrossRef]
- Brucherseifer, M.; Nagel, M.; Bolívar, P.H.; Kurz, H.; Bosserhoff, A.-K.; Büttner, R. Label-free probing of the binding state of DNA by time-domain terahertz sensing. Appl. Phys. Lett. 2000, 77, 4049–4051. [Google Scholar] [CrossRef] [Green Version]
- Fischer, B.M.; Hoffmann, M.; Helm, H.; Wilk, R.; Rutz, F.; Kleine-Ostmann, T.; Koch, M.; Jepsen, P.U. Terahertz time-domain spectroscopy and imaging of artificial RNA. Opt. Express 2005, 13, 5205–5215. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Globus, T.; Gelmont, B.; Salay, L.C.; Bykhovski, A. Terahertz Absorption of DNA Decamer Duplex. J. Phys. Chem. A 2008, 112, 12090–12096. [Google Scholar] [CrossRef]
- Jiménez, M.G.; Ramakrishnan, G.; Harwood, T.; Lapthorn, A.; Kelly, S.; Ellis, T.H.E.M.; Wynne, M.G.-J.G.R.A.J.L.K. Observation of coherent delocalized phonon-like modes in DNA under physiological conditions. Nat. Commun. 2016, 7, 11799. [Google Scholar] [CrossRef] [Green Version]
- Born, B.; Havenith, M. Terahertz dance of proteins and sugars with water. J. Infrared Millim. Terahertz Waves 2009, 30, 1245. [Google Scholar] [CrossRef]
- Gross, P.; Laurens, N.; Oddershede, L.B.; Bockelmann, U.; Peterman, E.; Wuite, G.J.L. Quantifying how DNA stretches, melts and changes twist under tension. Nat. Phys. 2011, 7, 731–736. [Google Scholar] [CrossRef]
- Brown, E.R.; Mendoza, E.A.; Xia, D.; Brueck, S.R.J. Narrow THz Spectral Signatures through DNA and RNA in Nanofluidic Channels. IEEE Sens. J. 2010, 10, 755. [Google Scholar] [CrossRef]
- Verghese, S.; McIntosh, K.A.; Calawa, S.; DiNatale, W.F.; Duerr, E.K.; Molvar, K.A. Generation and detection of coherent terahertz waves using two photomixers. Appl. Phys. Lett. 1998, 73, 3824–3826. [Google Scholar] [CrossRef] [Green Version]
- Bjarnason, J.E.; Brown, E.R. Sensitivity measurement and analysis of an ErAs:GaAs coherent photomixing transceiver. Appl. Phys. Lett. 2005, 87, 134105. [Google Scholar] [CrossRef]
- Demers, J.R.; Logan, J.R.T.; Bergeron, N.J.; Brown, E.R. A coherent frequency-domain THz spectrometer with a signal-to-noise ratio of 60 dB at 1 THz. In Proceedings of the SPIE Defense and Security Symposium 2008, Orlando, FL, USA, 16–20 March 2008; Volume 6949, p. 694909. [Google Scholar]
- Bolívar, P.H.; Brucherseifer, M.; Rivas, J.G.; Gonzalo, R.; Ederra, I.; Reynolds, A.L.; Holker, M.; De Maagt, P. Measurement of the dielectric constant and loss tangent of high dielectric-constant materials at terahertz frequencies. IEEE Trans. Microw. Theory Tech. 2003, 51, 1062–1066. [Google Scholar] [CrossRef] [Green Version]
- Naftaly, M.; Gregory, A. Terahertz and Microwave Optical Properties of single crystal and vitreious silica and the behavior of the boson peak. Appl. Sci. 2021, 11, 6733. [Google Scholar] [CrossRef]
- Purchased from New England Biolabs, Inc., Ipswich, MA, USA. Available online: www.neb.com/products/markers-and-ladders. (accessed on 18 October 2021).
- Liebe, H.J.; Hufford, G.A.; Manabe, T. A model for the complex permittivity of water at frequencies below 1 THz. Int. J. Infr. Millim. Waves 1991, 12, 659. [Google Scholar] [CrossRef]
- Xu, J.; Plaxco, K.; Allen, S.J.; Bjarnason, J.E.; Brown, E.R. 0.15–3.72 THz absorption of aqueous salts and saline solutions. Appl. Phys. Lett. 2007, 90, 31908. [Google Scholar] [CrossRef] [Green Version]
- Brown, E.R.; Bjarnason, J.E.; Fedor, A.M.; Korter, T.M. On the strong and narrow absorption signature in lactose at 0.53 THz. Appl. Phys. Lett. 2007, 90, 061908. [Google Scholar] [CrossRef]
- IUPAC. Compendium of Chemical Terminology, 2nd ed.; the “Gold Book”; McNaught, A.D., Wilkinson, A., Eds.; Blackwell Scientific Publications: Oxford, UK, 1997. [Google Scholar]
- Marion, J.B. Classical Dynamics of Particles and Systems; Academic: New York, NY, USA, 1965. [Google Scholar]
- Manning, G.S. The Persistence Length of DNA Is Reached from the Persistence Length of Its Null Isomer through an Internal Electrostatic Stretching Force. Biophys. J. 2006, 91, 3607–3616. [Google Scholar] [CrossRef] [Green Version]
- Abels, J.; Moreno-Herrero, F.; van der Heijden, T.; Dekker, C.; Dekker, N. Single-Molecule Measurements of the Persistence Length of Double-Stranded RNA. Biophys. J. 2005, 88, 2737–2744. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, K.; Chaya, H.; Fukushima, S.; Watanabe, S.; Takemoto, H.; Osada, K.; Nishiyama, N.; Miyata, K.; Kataoka, K. Influence of RNA Strand Rigidity on Polyion Complex Formation with Block Catiomers. Macromol. Rapid Commun. 2016, 37, 486–493. [Google Scholar] [CrossRef]
- Barkley, M.D.; Zimm, B.H. Theory of twisting and bending of chain macromolecules; analysis of the fluorescence depolarization of DNA. J. Chem. Phys. 1979, 70, 2991–3007. [Google Scholar] [CrossRef]
- Marko, J.F.; Siggia, E.D. Bending and twisting elasticity of DNA. Macromolecules 1994, 27, 981–988. [Google Scholar] [CrossRef]
- Smith, S.B.; Cui, Y.; Bustamante, C. Overstretching B-DNA: The elastic response of individual double-stranded and single-stranded DNA molecules. Science 1996, 271, 795–799. [Google Scholar] [CrossRef] [Green Version]
- Brown, E.R.; Bjarnason, J.; Chan, T.L.J.; Driscoll, D.C.; Hanson, M.; Gossard, A.C. Room temperature, THz photomixing sweep oscillator and its application to spectroscopic transmission through organic materials. Rev. Sci. Instrum. 2004, 75, 5333–5342. [Google Scholar] [CrossRef]
- Foquet, M.; Korlach, J.; Zipfel, W.; Webb, W.W.; Craighead, H.G. DNA Fragment Sizing by Single Molecule Detection in Submicrometer-Sized Closed Fluidic Channels. Anal. Chem. 2002, 74, 1415–1422. [Google Scholar] [CrossRef]
- Han, J.; Craighead, H.G. Separation of Long DNA Molecules in a Microfabricated Entropic Trap Array. Science 2000, 288, 1026–1029. [Google Scholar] [CrossRef] [PubMed]
- Reisner, W.; Morton, K.J.; Riehn, R.; Wang, Y.M.; Yu, Z.; Rosen, M.; Sturm, J.C.; Chou, S.Y.; Frey, E.; Austin, R.H. Statics and Dynamics of Single DNA Molecules Confined in Nanochannels. Phys. Rev. Lett. 2005, 94, 196101. [Google Scholar] [CrossRef] [Green Version]
- Xia, D.; Brueck, S.R.J. Fabrication of enclosed nanochannels using silica nanoparticles. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. 2005, 23, 2694. [Google Scholar] [CrossRef]
- Xia, D.; Gamble, T.C.; Mendoza, E.A.; Koch, S.J.; He, X.; Lopez, G.P.; Brueck, S.R.J. DNA Transport in Hierarchically-Structured Colloidal-Nanoparticle Porous-Wall Nanochannels. Nano Lett. 2008, 8, 1610–1618. [Google Scholar] [CrossRef]
- Elbashir, S.M.; Harborth, J.; Lendeckel, W.; Yalcin, A.; Weber, K.; Tuschl, T. Duplexes of 21-nucleotide RNAs mediate RNA interference in cultured mammalian cells. Nat. Cell Biol. 2001, 411, 494–498. [Google Scholar] [CrossRef]
- Alekseev, O.M.; Richardson, R.T.; O’Rand, M.G. Analysis of gene expression profiles in HeLa cells in response to over expression or siRNA-mediated depletion of NASP. Reprod. Biol. Endocrinol. 2009, 7, 194391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ge, Q.; Eisen, H.N.; Chen, J. Use of siRNAs to prevent and treat influenza virus infection. Virus Res. 2004, 102, 37–42. [Google Scholar] [CrossRef]
- Kumar, P.; Ban, H.-S.; Kim, S.-S.; Wu, H.; Pearson, T.; Greiner, D.L.; Laouar, A.; Yao, J.; Haridas, V.; Habiro, K.; et al. T Cell-Specific siRNA Delivery Suppresses HIV-1 Infection in Humanized Mice. Cell 2008, 134, 577–586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanger, F.; Coulson, A.R.; Hong, G.F.; Hill, D.F.; Petersen, G.B. Nucleotide sequence of bacteriophage λ DNA. J. Mol. Biol. 1982, 162, 729–773. [Google Scholar] [CrossRef]


| Sample | si RNA | 50-bp DNA | ||||
|---|---|---|---|---|---|---|
| Signature | (1) | (2) | (3) | (1) | (2) | (3) |
| Center Freq (GHz), ν0 | 916 | 962 | 1034 | 870 | 938 | 993 |
| FWHM (GHz), Δν | 10 | 10 | 12 | 15 | 16 | 20 |
| Quality Factor, QS | 92 | 96 | 86 | 58 | 59 | 50 |
| Tmin | 0.012 | 0.011 | 0.012 | 0.35 | 0.39 | 0.31 |
| Tmax | 0.080 | 0.080 | 0.090 | 0.75 | 0.75 | 0.75 |
| Signature Absorbance, As | 0.82 | 0.86 | 0.88 | 0.33 | 0.28 | 0.38 |
| Molecule/cm3 (diluted), ρm | 2.0 × 1014 | 2.0 × 1014 | 2.0 × 1014 | 9.6 × 1014 | 9.6 × 1014 | 9.6 × 1014 |
| Molecular Cross Sec (nm2) | 1.9 × 104 | 2.0 × 104 | 2.0 × 104 | 1.6 × 103 | 1.4 × 103 | 1.8 × 103 |
| Cross-Sec Diam, D (nm) | 154 | 158 | 159 | 45 | 42 | 48 |
| D/Molecular Length | 28.5 | 29.3 | 29.4 | 0.27 | 0.25 | 0.29 |
| Sample | 1-kbp DNA | ||
|---|---|---|---|
| Signature | (1) | (2) | (3) |
| Center Freq (GHz), ν0 | 750 | 825 | 910 |
| FWHM (GHz), Δν | 32 | 30 | 32 |
| Quality Factor, QS | 23 | 28 | 28 |
| Tmin | 0.59 | 0.6 | 0.62 |
| Tmax | 0.8 | 0.79 | 0.81 |
| Signature Absorbance, As | 0.13 | 0.12 | 0.12 |
| Molecule/cm3 (diluted), ρm | 6.2 × 1013 | 6.2 × 1013 | 6.2 × 1013 |
| Molecular Cross Sec (nm2) | 9.8 × 103 | 8.9 × 103 | 8.6 × 103 |
| Cross-Sec Diam, D (nm) | 112 | 106 | 105 |
| D/Molecular Length | 0.086 | 0.081 | 0.080 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, E.R.; Mendoza, E.A. Experimental Measurement of Sharp THz Absorption Signatures from Nucleic Acid Solutions in Nanofluidic Channels. Appl. Sci. 2021, 11, 11827. https://doi.org/10.3390/app112411827
Brown ER, Mendoza EA. Experimental Measurement of Sharp THz Absorption Signatures from Nucleic Acid Solutions in Nanofluidic Channels. Applied Sciences. 2021; 11(24):11827. https://doi.org/10.3390/app112411827
Chicago/Turabian StyleBrown, Elliott R., and Edgar A. Mendoza. 2021. "Experimental Measurement of Sharp THz Absorption Signatures from Nucleic Acid Solutions in Nanofluidic Channels" Applied Sciences 11, no. 24: 11827. https://doi.org/10.3390/app112411827
APA StyleBrown, E. R., & Mendoza, E. A. (2021). Experimental Measurement of Sharp THz Absorption Signatures from Nucleic Acid Solutions in Nanofluidic Channels. Applied Sciences, 11(24), 11827. https://doi.org/10.3390/app112411827





