Mechanical Properties of ASTM A572 Grades 50 and 60 Steels at High Temperatures
Abstract
:1. Introduction
2. Experimental Tests
2.1. Test Specimen Properties
2.2. Test Methods for Thermal Properties
3. Results and Discussion
3.1. Mechanical Properties
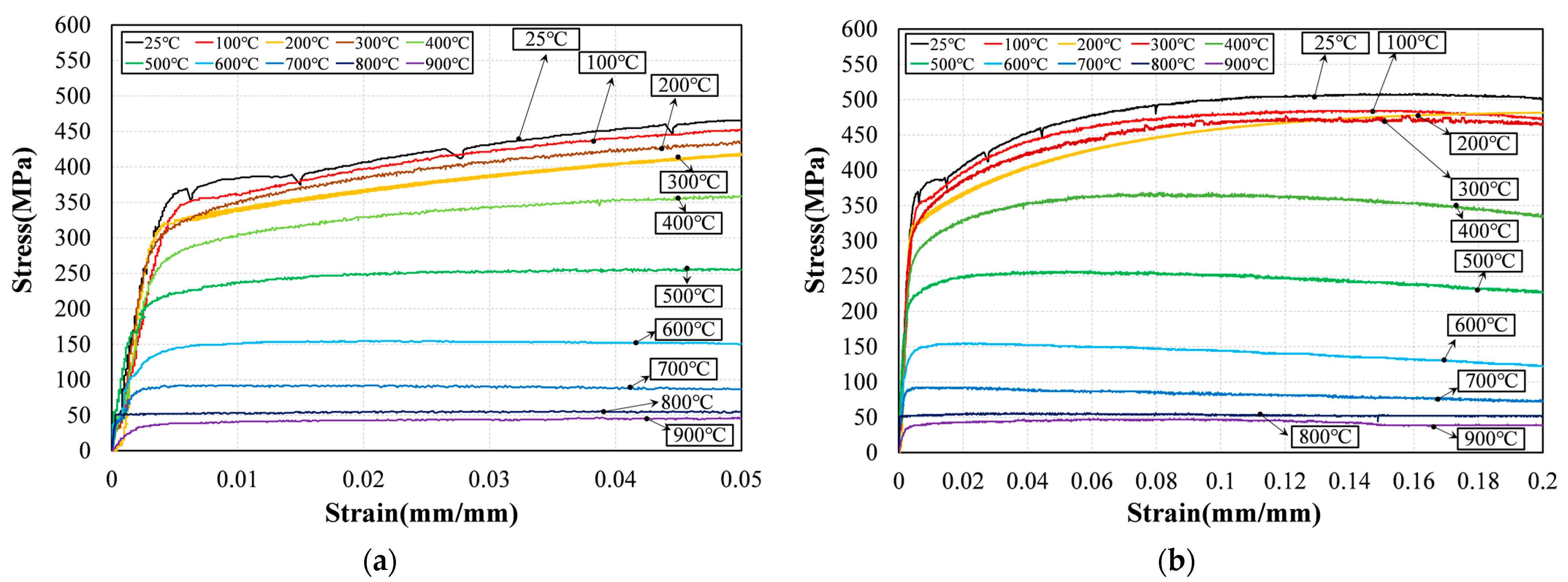
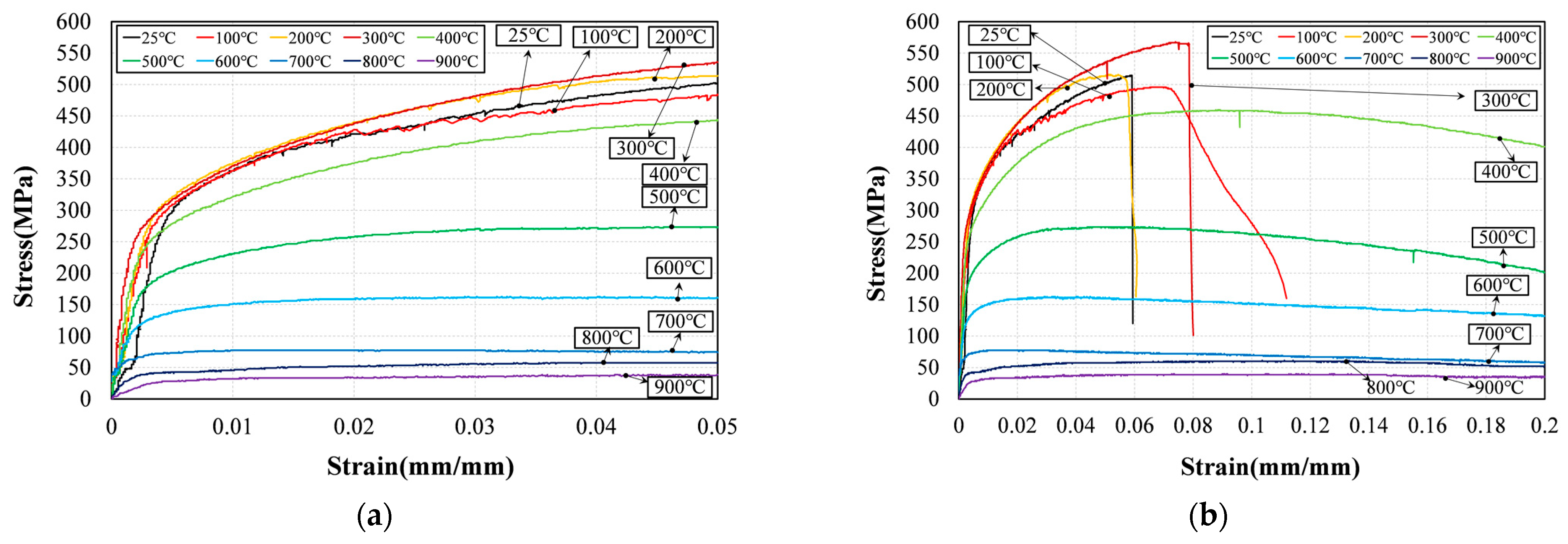
3.1.1. Stress–Strain Curve
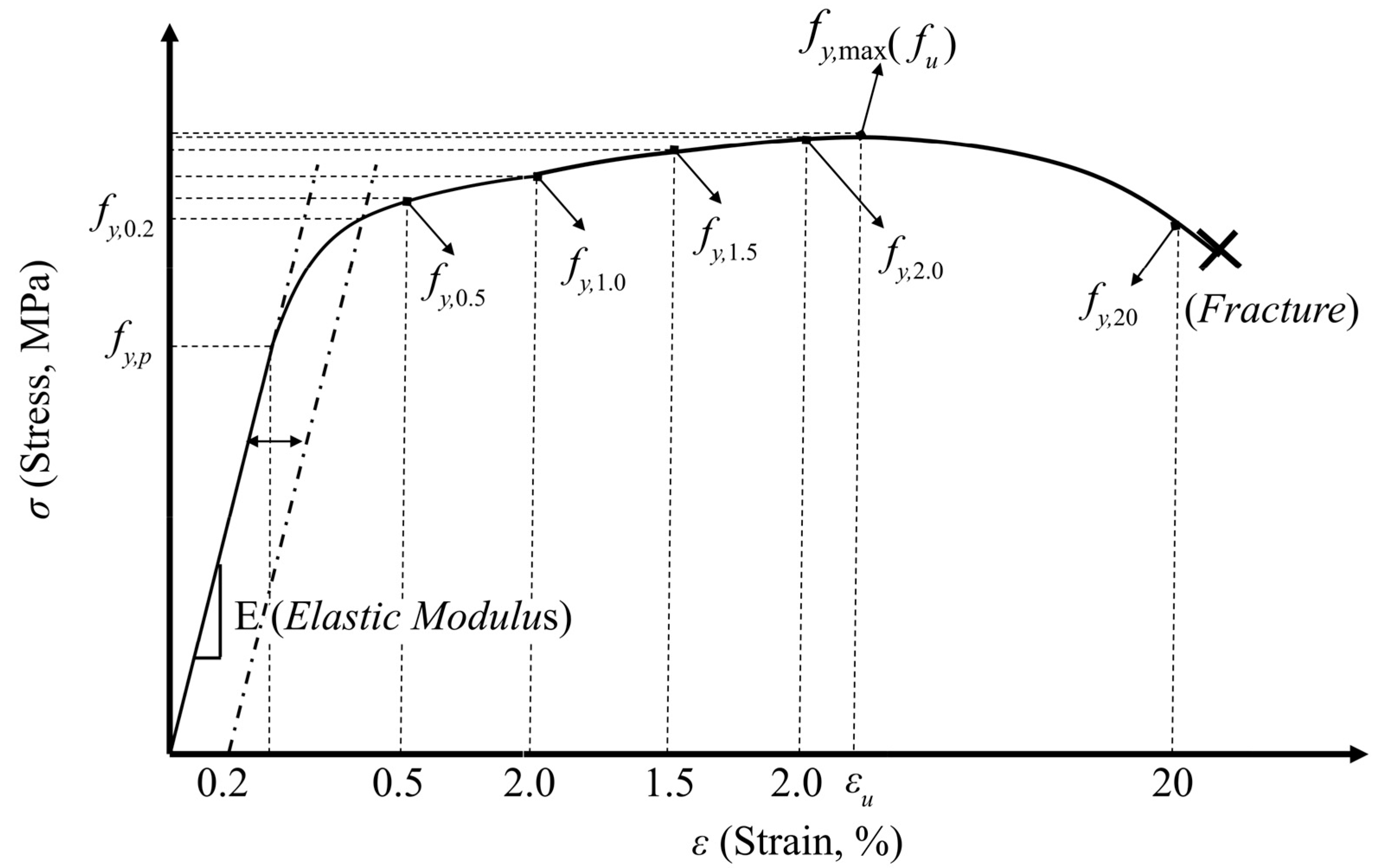
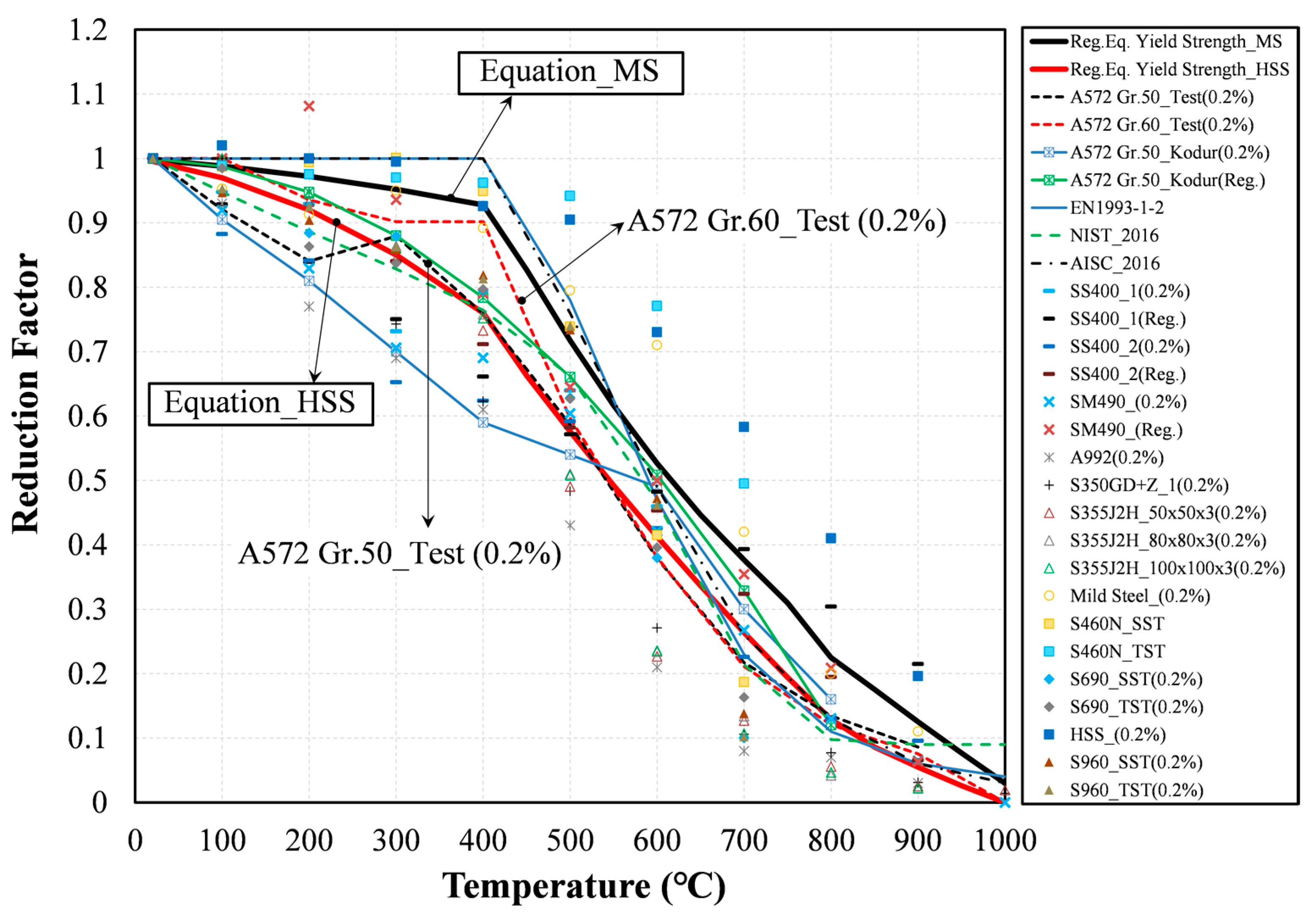
3.1.2. Yield Strength
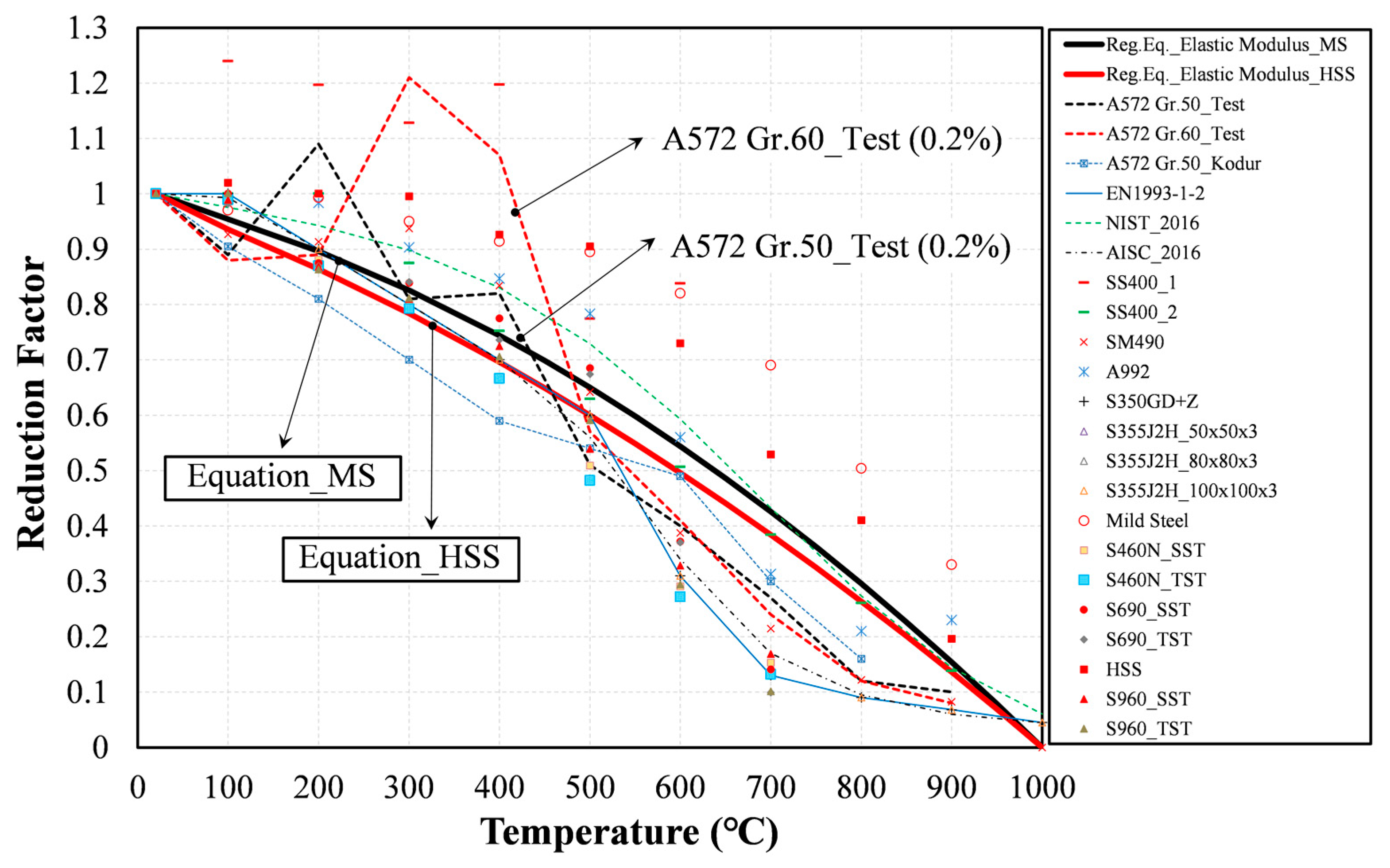
3.1.3. Elastic Modulus
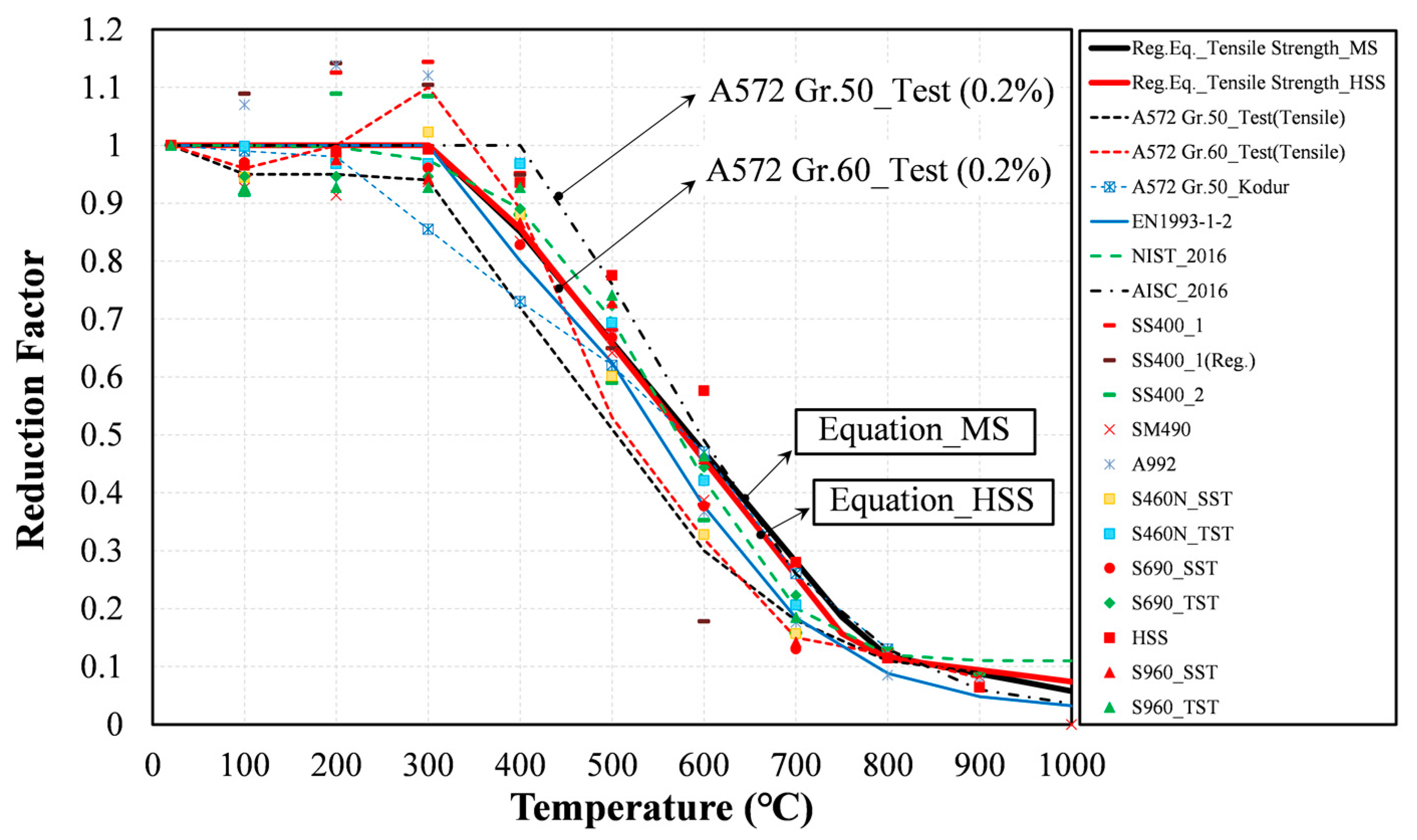
3.1.4. Tensile Strength
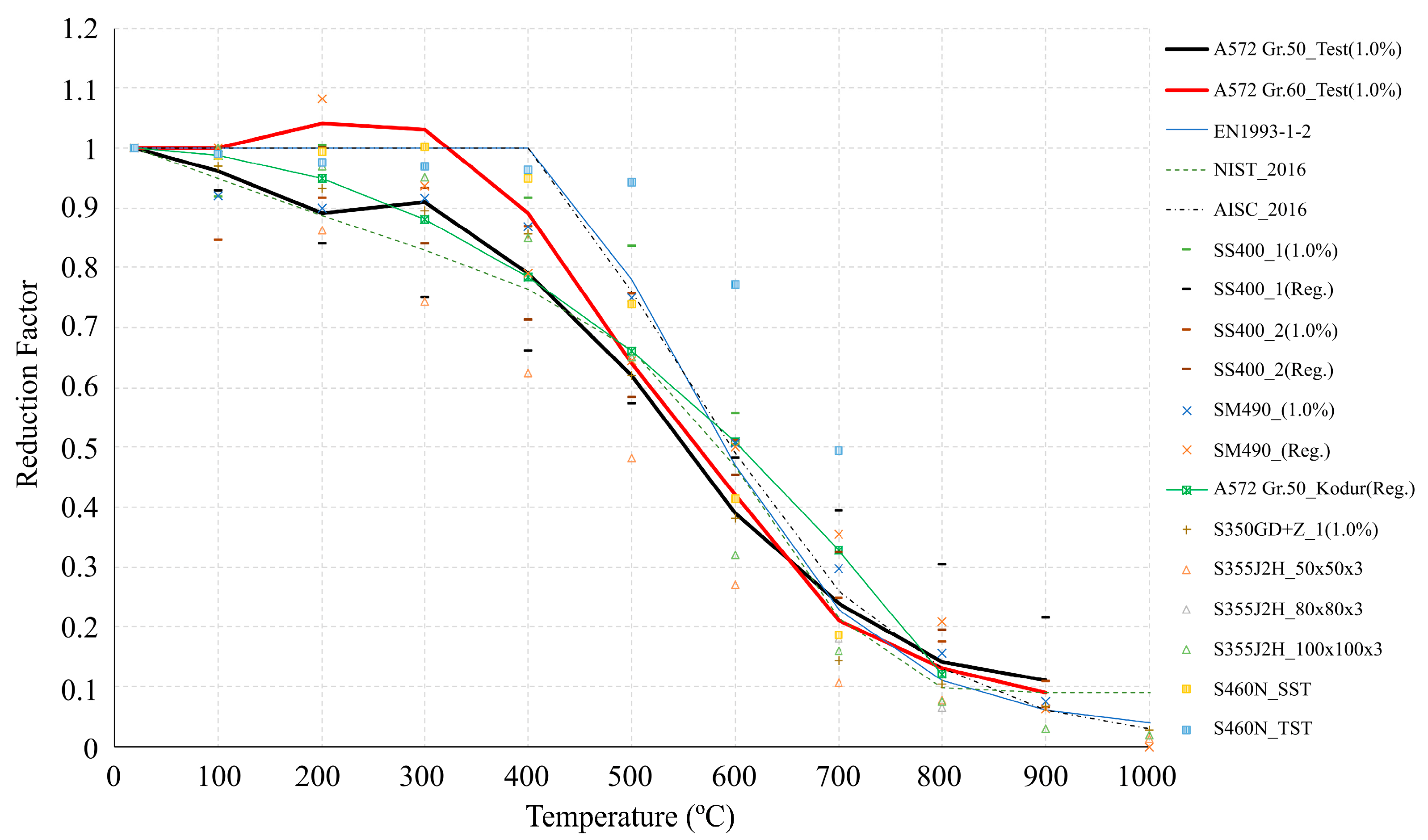
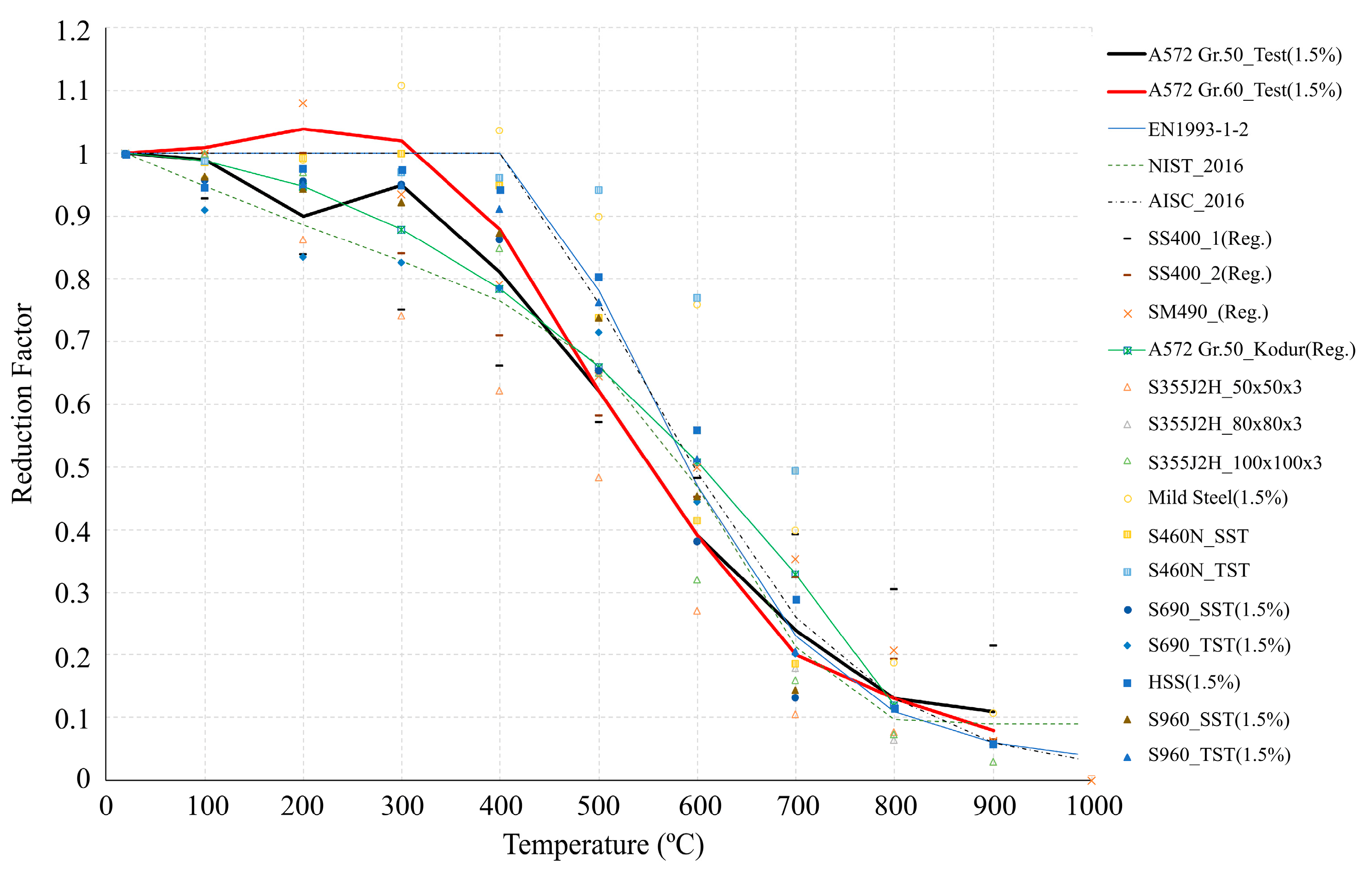
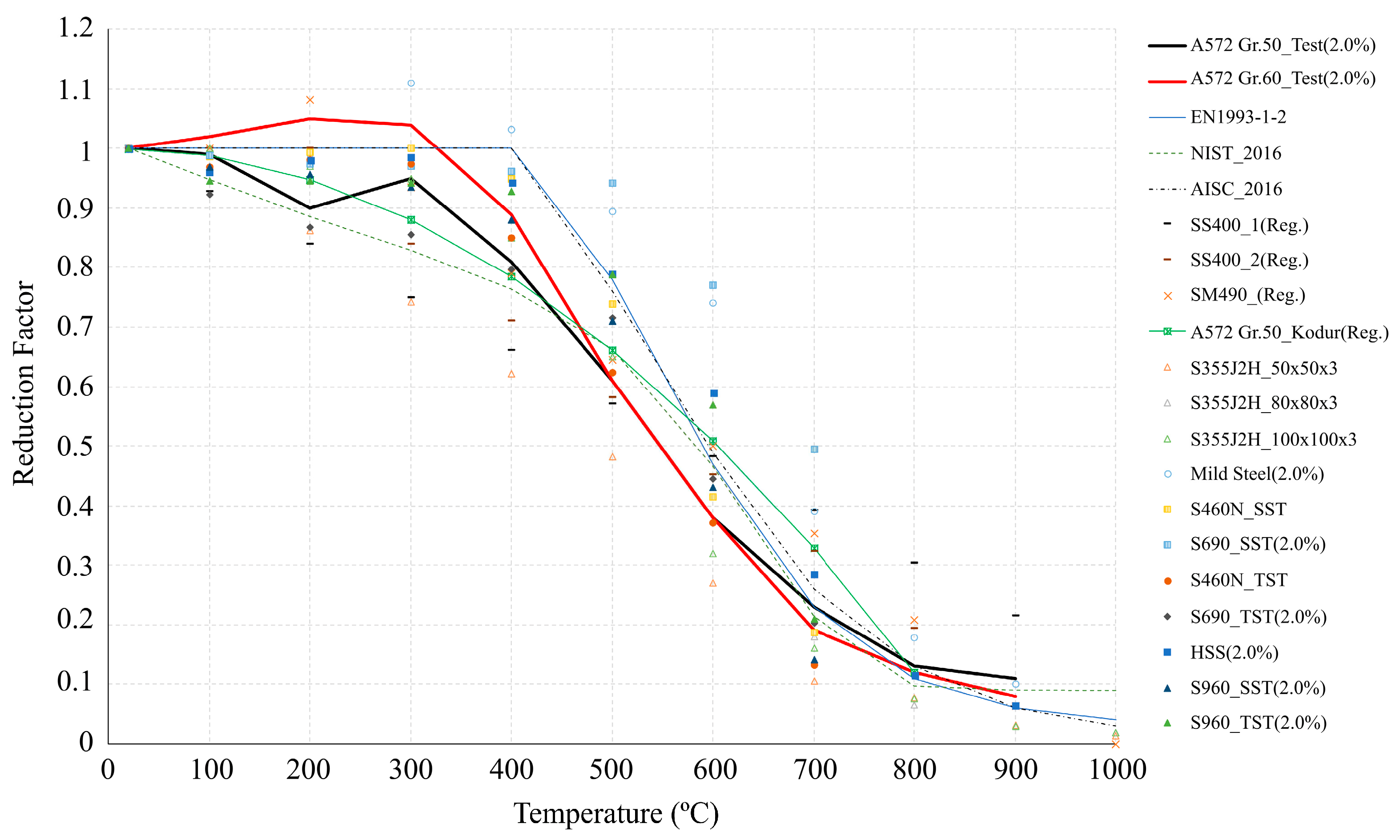
3.2. Proposed Reduction Factors for the Strength and Elastic Modulus
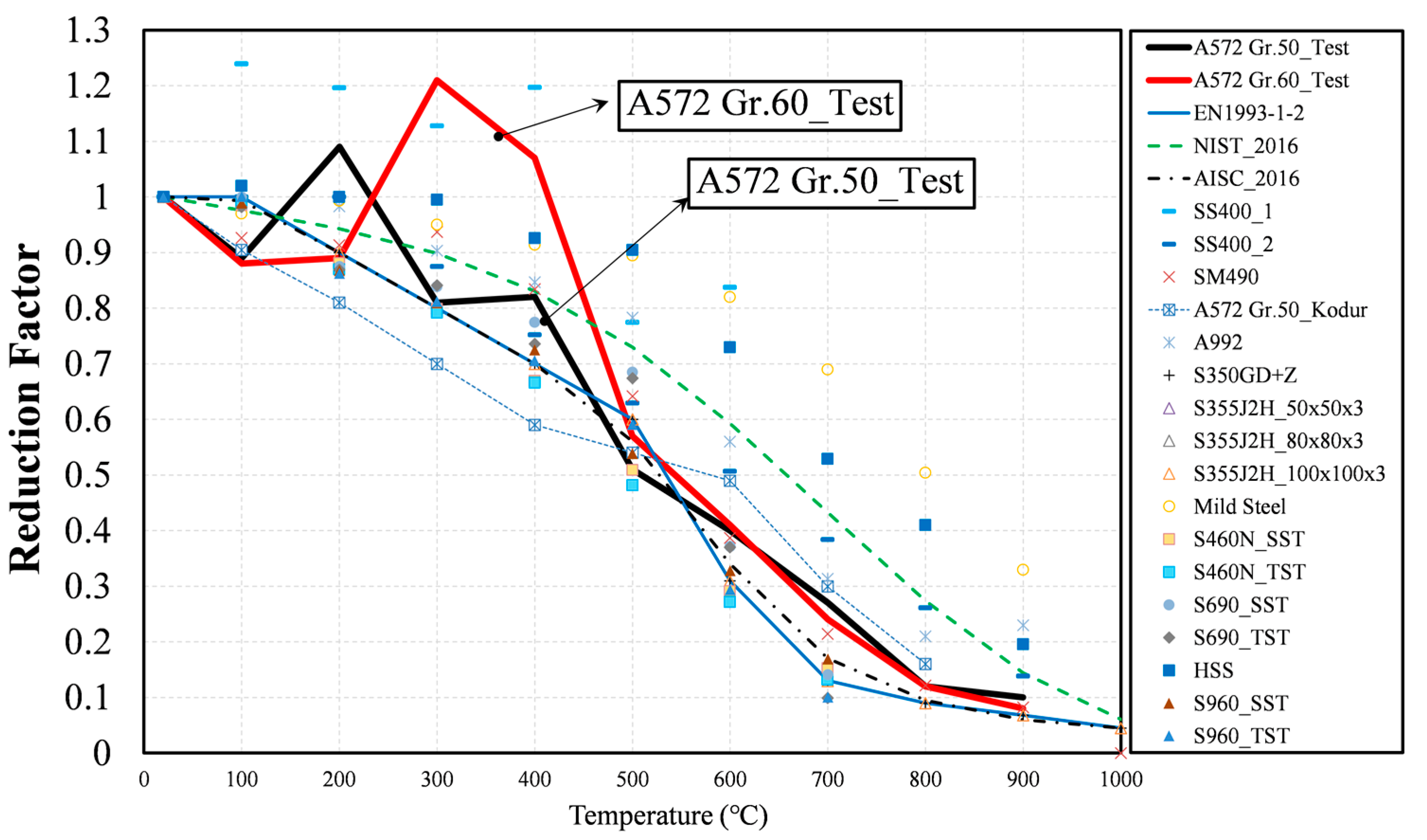
3.2.1. Yield Strength (0.2% Strain Level)
- MS (Mild Steel): Yield Strength Reduction Factor Equation
- HSS (High-Strength Steel): Yield Strength Reduction Factor Equation
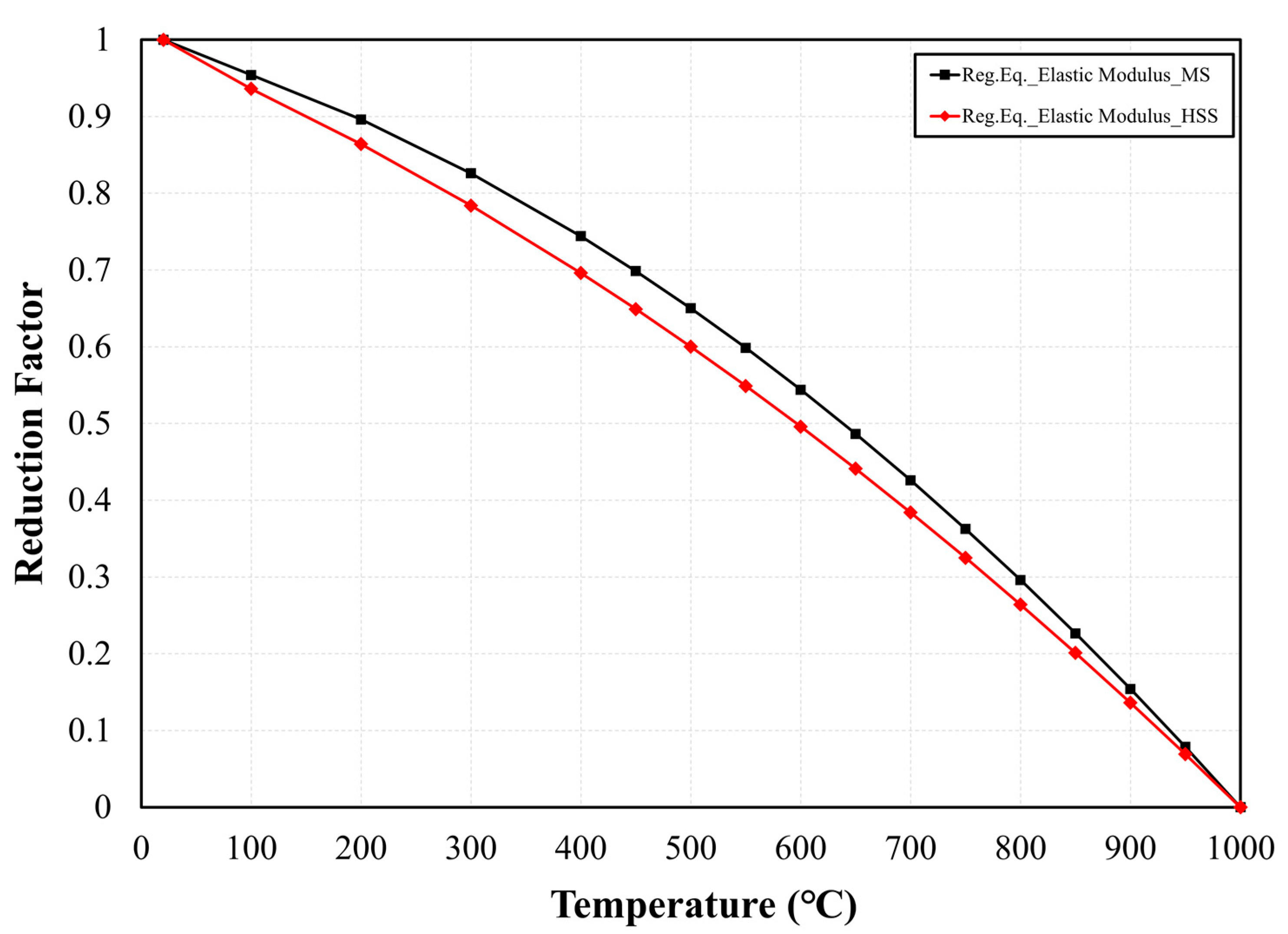
3.2.2. Elastic Modulus
- MS (Mild Steel): Elastic Modulus Reduction Factor Equation
- HSS (High-Strength Steel): Elastic Modulus Reduction Factor Equation
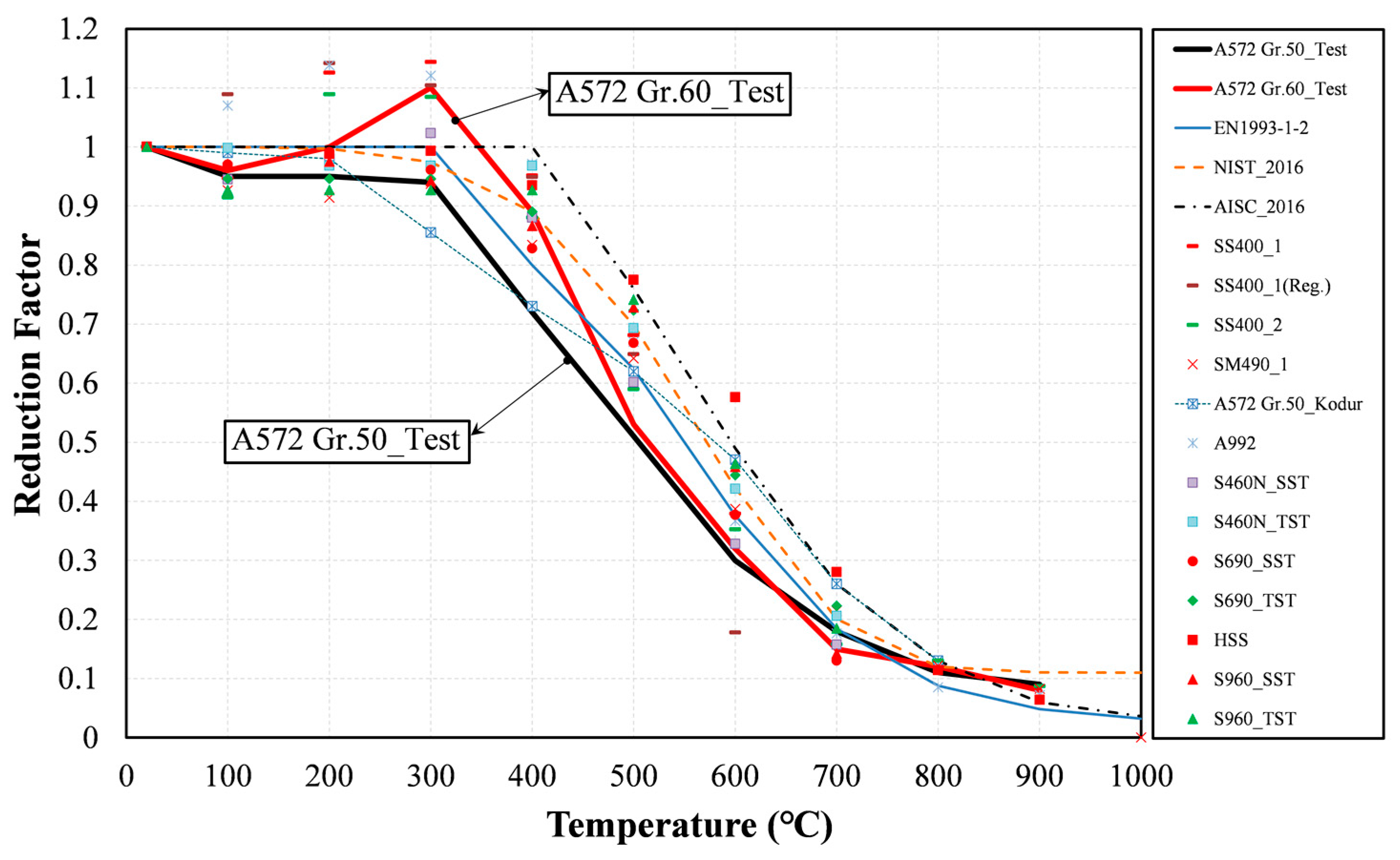
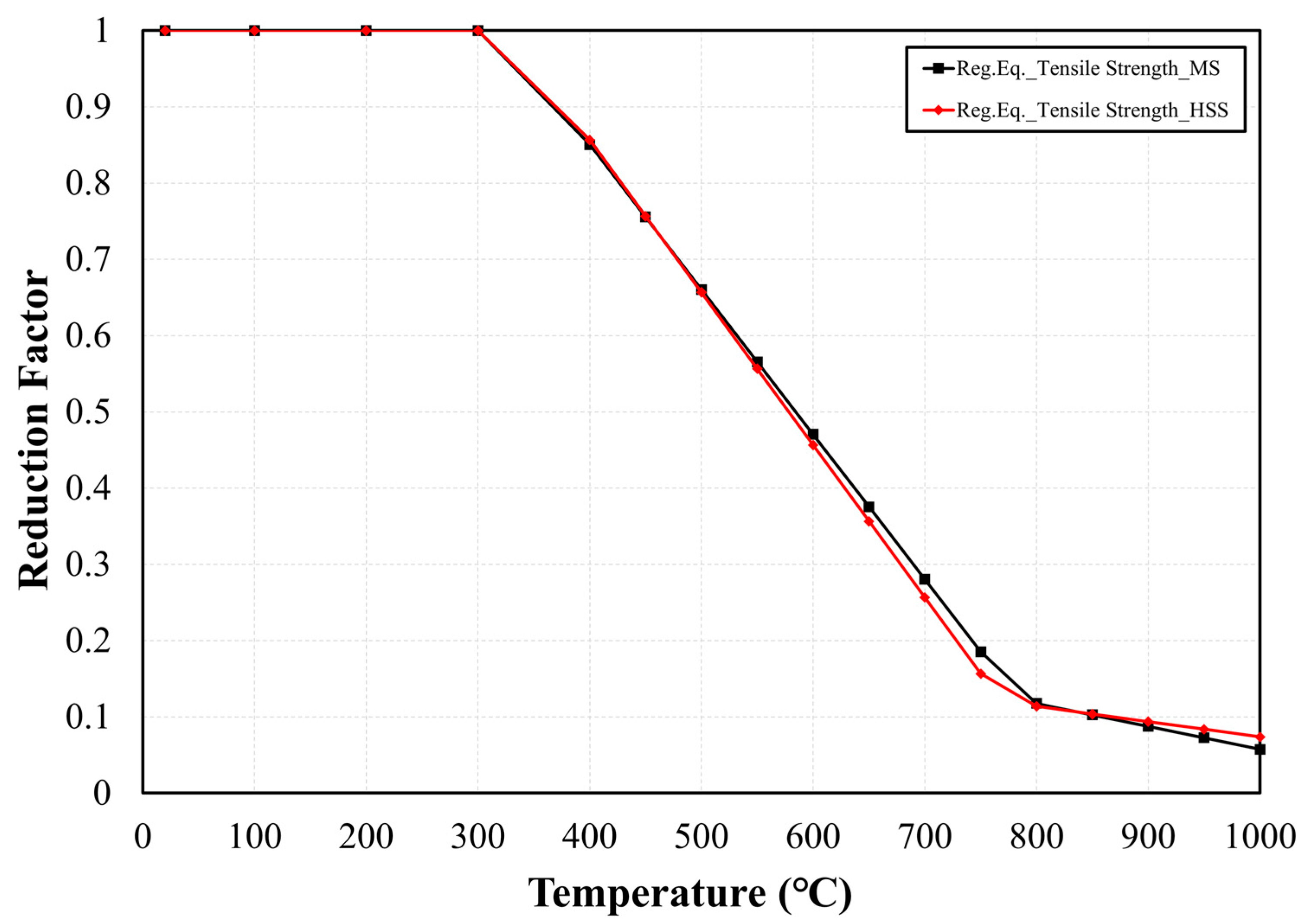
3.2.3. Tensile Strength
- MS (Mild Steel): Tensile Strength Reduction Factor Equation
- HSS (High-Strength Steel): Tensile Strength Reduction Factor Equation
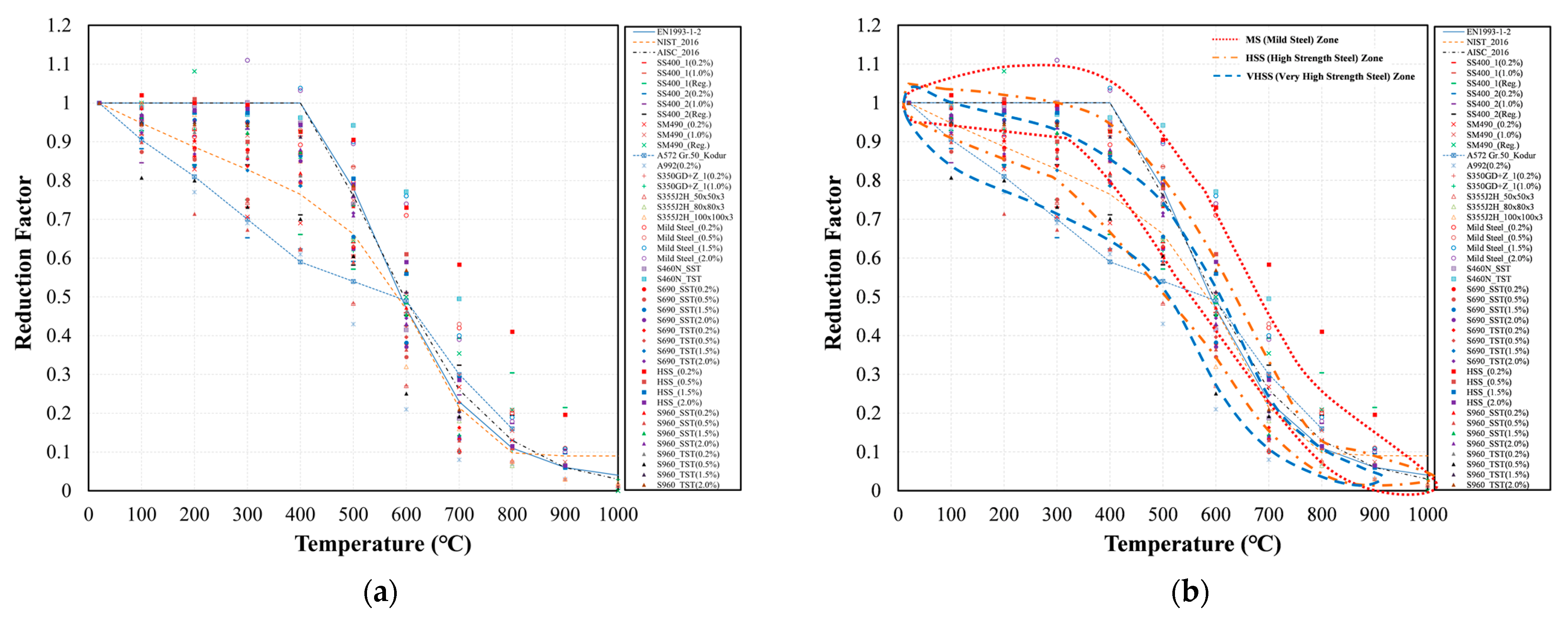
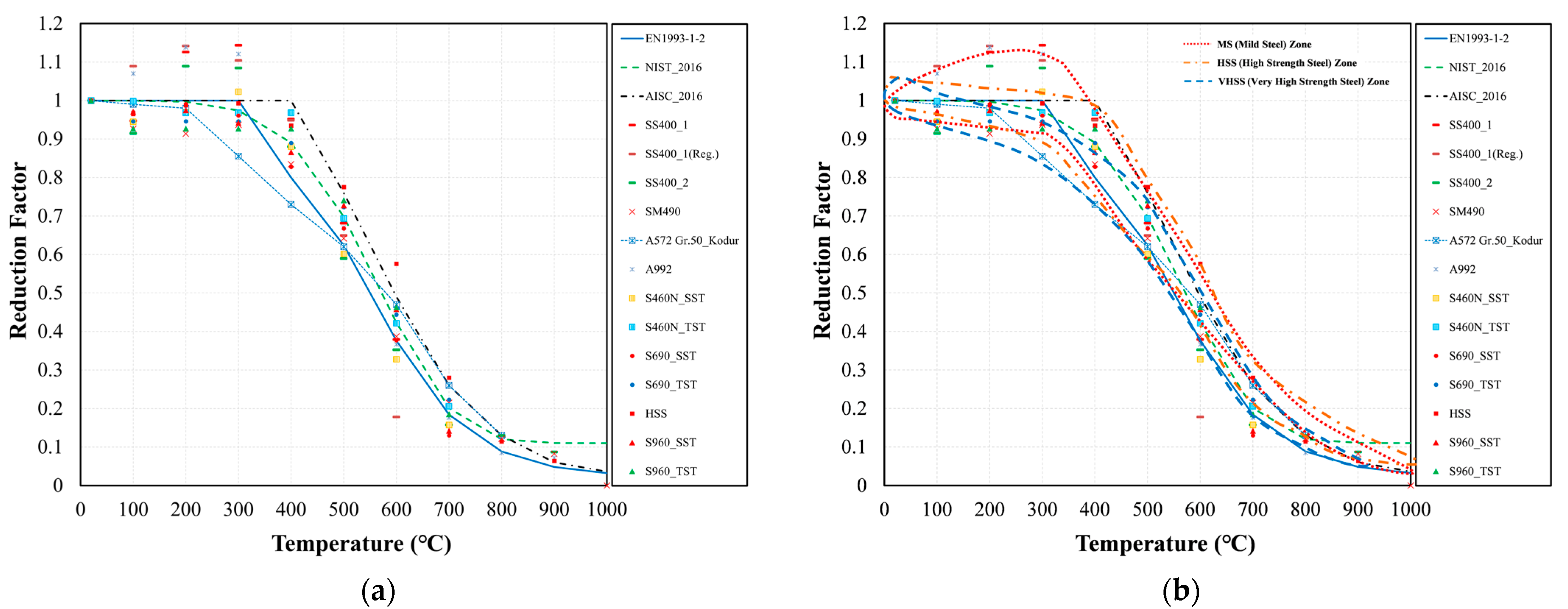
3.3. Comparisons of the Proposed Equations with the Literature
4. Conclusions
- When comparing the proposed MS Equations (1)–(3) of the yield strength reduction with the standard (EN 1993-1-2 and AISC 2016), the maximum difference of 24% occurred at 400 °C. On the other hand, the proposed MS Equations (1)–(3) did not differ from the ones of the NIST 1907 (0%). This indicates that the proposed MS Equations (1)–(3) and NIST equations differ from the ones of the standards (EN 1993-1-2 and AISC 2016) based on experimental data of various mild steels.
- Eurocode and AISC propose a yield strength reduction factor of 1.0 for mild steel at 400 °C, but the proposed MS Equations (1)–(3) and the NIST equations indicate a value of 0.76. Although the point at which the strength of steel material rapidly decreases is known to be 538 °C, this study suggests that the yield strength reduction starts from 400 °C for MS.
- The proposed Equations (4)–(6) of the yield strength reduction for the HSS at 400 °C are different from the ones of the standard (EN 1993-1-2, AISC 2016) by 7%, and differ by 16% from the NIST. The MS Equations (1)–(3) showed a difference of 5% from the ones of the NIST equation at 700 °C. The HSS Equations (4)–(6) were 16% different from the ones of the NIST at 700 °C.
- These results indicate that the HSS Equations (4)–(6) are closer to the yield strength reduction factor suggested by the standards (Eurocode and AISC) than the MS Equations (1)–(3) at 400 °C. However, it does not work at 700 °C such that the yield strength reduction factor of the HSS increases greatly compared with the standards (Eurocode and AISC).
- In the case of HSS, it is better to make the yield strength reduction factors lower than the ones of current design standards to ensure a safe design. Moreover, the strength reduction factors of the MS at both 400 °C and 700 °C agreed well with the NIST code rather than the standards, including the Eurocode and AISC.
- The differences in the elastic modulus reduction factor of the Eurocode and AISC to MS are 30% and 26%, respectively. However, the elastic modulus factors of the NIST are in good agreement under 5% based on the experimental works for both MS and HS. In the case of the elastic modulus reduction factor for the HSS, the decrement difference was approximately 25% from the one of Eurocode. As with the yield strength results, the proposed elastic modulus Equations (7) and (8) were close to the ones of the NIST compared to Eurocode or AISC.
- As a result of analyzing the tensile strength, there was a negligible difference in the reduction factor depending on the steel type compared to the yield strength and the elastic modulus. Because the minor difference occurred in the 300~700 °C range, it is necessary to perform careful investigation for much higher strength levels of steel.
- The reduction factor of the yield strength between MS and HSS showed consistently decaying patterns throughout all temperature ranges. The yield strength reduction of the HSS was smaller by 17% than the one of MS at 400 °C. Generally speaking, the yield strength, elastic modulus, and tensile strength equations of NIST 1907 (2016) are prepared based on experimental data for various mild steels, and the result is relatively similar to the equation proposed in this study.
- This paper covered various strength reduction factors, including the yield strength, tensile strength, and elastic modulus factors at elevated temperatures of up to 1000 °C. This paper only covers the comparisons of the strength reduction effects of the Grade 50 and 60 structural steels to some design codes, including EN, AISC and NIST. Further developments and comparisons on the strength reduction factors using various levels of high-strength structural steels are needed in the future. Moreover, the creep effects at elevated temperatures were not covered in this paper due to limitations. Future work needs to cover the creep effect at elevated temperatures with various stress levels in the fire-resistant design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Chemical Composition | Steel Type | |
| ASTM A572 Grade 50 (Gr. 50) | ASTM A572 Grade 60 (Gr. 60) | |
| Carbon, C (%) | 0.23 | 0.26 |
| Iron, Fe (%) | 98 | 98 |
| Manganese, Mn (%) | 1.35 | |
| Phosphorus, P (%) | 0.04 | |
| Silicon, Si (%) | 0.40 | |
| Sulfur, S (%) | 0.05 | |

References
- American Society of Civil Engineers. ASCE Manuals and Reports on Engineering Practice No. 138. Structural Fire Engineering; American Society of Civil Engineers: New York, NY, USA, 2018. [Google Scholar]
- Ye, J.; Chen, W. Elevated temperature material degradation of cold-formed steels under steady- and transient-state conditions. J. Mater. Civ. Eng. 2013, 25, 947–957. [Google Scholar] [CrossRef]
- Badaruddin, M.; Wardono, H.; Supriadi, H.; Salimor, M. Experimental investigation of mechanical properties of cold-drawn AISI 1018 steel at high-temperature steady-state conditions. J. Mater. Res. Technol. 2020, 9, 1893–1904. [Google Scholar] [CrossRef]
- Shakil, S.; Lu, W.; Puttonen, J. Experimental studies on mechanical properties of S700 MC steel at elevated temperatures. Fire Saf. J. 2020, 116, 103157. [Google Scholar] [CrossRef]
- Hanus, F.; Caillet, N. Strength reduction factors for S355 to S500 steel grades under steady-state and transient-state heating. J. Struct. Fire Eng. 2020, 11, 137–149. [Google Scholar] [CrossRef]
- Huang, L.; Li, G.Q.; Wang, X.X.; Zhang, C.; Choe, L.; Engelhardt, M. High temperature mechanical properties of high strength structural steels Q550, Q690 and Q890. Fire Technol. 2018, 54, 1609–1628. [Google Scholar] [CrossRef] [PubMed]
- Yuan, G.; Shu, Q.; Huang, Z.; Li, Q. An experimental investigation of properties of Q345 steel pipe at elevated temperatures. J. Constr. Steel Res. 2016, 118, 41–48. [Google Scholar] [CrossRef] [Green Version]
- Schneider, R.; Lange, J. Constitutive equations and empirical creep law of structural steel S460 at high temperatures. J. Struct. Fire Eng. 2011, 2, 217–229. [Google Scholar] [CrossRef]
- Comité Européen de Normalisation. EN 1993-1-2 Eurocode 3: Design of Steel Structures—Part 1–2: General Rules–Structural Fire Design; Comité Européen de Normalisation: Brussels, Belgium, 2005. [Google Scholar]
- Kodur, V.; Aziz, E. Effect of temperature on creep in ASTM A572 high-strength low-alloy steels. Mater. Struct. 2015, 48, 1669–1677. [Google Scholar] [CrossRef]
- Pijpers, R.J.M. Fatigue Strength of Welded Connections Made of Very High Strength Cast and Rolled Steels. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2011. [Google Scholar]
- Maraveas, C.; Fasoulakis, Z.C.; Tsavdaridis, K.D. Mechanical properties of high and very high steel at elevated temperatures and after cooling down. Fire Sci. Rev. 2017, 6, 1–13. [Google Scholar]
- Chen, J.; Young, B.; Uy, B. Behavior of high strength structural steel at elevated temperatures. J. Struct. Eng. 2006, 132, 1948–1954. [Google Scholar] [CrossRef] [Green Version]
- Qiang, X.; Bijlaard, F.S.K.; Kolstein, H. Dependence of mechanical properties of high strength steel S690 on elevated temperatures. Constr. Build. Mater. 2012, 30, 73–79. [Google Scholar] [CrossRef]
- Aziz, E.; Kodur, V. An approach for evaluating the residual strength of fire exposed bridge girders. J. Constr. Steel Res. 2013, 88, 34–42. [Google Scholar] [CrossRef]
- Qiang, X.; Bijlaard, F.S.K.; Kolstein, H. Post-fire mechanical properties of high strength structural steels S460 and S690. Eng. Struct. 2012, 35, 1–10. [Google Scholar] [CrossRef]
- Wang, W.Y.; Liu, B.; Kodur, V. Effect of temperature on strength and elastic modulus of high-strength steel. J. Mater. Civ. Eng. 2013, 25, 174–182. [Google Scholar] [CrossRef]
- Lee, J.W.; Engelhardt, M.D.; Choi, B.J. Constitutive model for ASTM A992 steel at elevated temperature. Int. J. Steel Struct. 2015, 15, 733–741. [Google Scholar] [CrossRef]
- Lee, J.W. Elevated Temperature Properties of Astm A992 Steel for Structural-Fire Engineering Analysis. Ph.D. Thesis, University of Texas, Austin, TX, USA, 2012. [Google Scholar]
- Azhari, F.; Heidarpour, A.; Zaho, X.L.; Hutchinson, C.R. Mechanical properties of ultra-high strength (grade 1200) steel tubes under cooling phase of a fire: An experimental investigation. Constr. Build. Mater. 2015, 93, 841–850. [Google Scholar] [CrossRef]
- Aziz, E.; Kodur, V. Effect of temperature and cooling regime on mechanical properties of high-strength low-allow steel. Fire Mater. 2015, 40, 926–939. [Google Scholar] [CrossRef]
- Qiang, X.; Bijlaard, F.S.K.; Kolstein, H. Elevated-temperature mechanical properties of high strength structural steel S460N: Experimental study and recommendations for fire-resistance design. Fire Saf. J. 2013, 55, 15–21. [Google Scholar] [CrossRef]
- Li, G.Q.; Lyu, H.B.; Zhang, C. Post-fire mechanical properties of high strength Q690 structural steel. J. Constr. Steel Res. 2017, 132, 108–116. [Google Scholar] [CrossRef]
- Outinen, J.; Mäkeläinen, P. Mechanical properties of structural steel at elevated temperatures and after cooling down. Fire Mater. 2004, 28, 237–251. [Google Scholar] [CrossRef]
- Kwon, I.K.; Jee, N.Y. Experimental study on the mechanical properties of structural steel SS400 at high temperature. J. Archit. Int. Korea Struct. Constr. 2001, 17, 89–96. [Google Scholar]
- National Institute of Standards and Technology (NIST). NIST-1907: Temperature Dependent Material Modeling for Structural Steels: Formulation and Application; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2016. [Google Scholar]
- American Institution of Steel Construction. AISC 2016: Specification for Structural Steel Buildings, 15th ed.; American Institution of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]
- American Society for Testing and Materials. Standard Test Method for Tension Testing of Metallic Materials; ASTM E8/E8M-09; American Society for Testing and Materials: West Conshohocken, PA, USA, 2009. [Google Scholar]
- American Society for Testing and Materials. Standard Test Method for Elevated Temperature Tension Test of Metallic Materials; ASTM E21-09; American Society for Testing and Materials: West Conshohocken, PA, USA, 2009. [Google Scholar]
- American Society for Testing and Materials. Standard Test Methods for Elevated Temperature Tension Tests of Metallic Materials; ASTM E21-92; American Society for Testing and Materials: West Conshohocken, PA, USA, 1992. [Google Scholar]
- Chen, J.; Young, B. Design of high strength steel columns at elevated temperatures. J. Constr. Steel Res. 2008, 64, 689–703. [Google Scholar] [CrossRef]
- Jang, K.H.; Lee, J.H.; Shin, Y.U. An experimental study on high temperature tensile property of high strength steel. Proc. KWS Conf. 2003, 53, 260–262. [Google Scholar]
- Cho, B.Y.; Jee, N.Y. A study on the mechanical properties of structural steels by welding at high temperature. In Proceedings of the Korean Institute of Building Construction Conference; The Korean Institute of Building Construction: Seoul, Korea, 2009; Volume 25, pp. 97–104. [Google Scholar]
- Kwon, I.K. Derivation of the mechanical properties of structural steels at high temperatures. J. Korean Inst. Fire Sci. Eng. 2007, 21, 47–55. [Google Scholar]
- Buchhanan, A.H. Structural Design for Fire Safety; CRC Press: New York, NY, USA, 2017. [Google Scholar]
- Qiang, X.; Jiang, X.; Bijlaard, F.S.K.; Kolstein, H. Mechanical properties and design recommendations of very high strength steel S960 in fire. Eng. Struct. 2016, 112, 60–70. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST). NIST-1714: High-Temperature Tensile Constitutive Data and Models for Structural Steels in Fire; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2011. [Google Scholar]




| Yield Strength (MPa) | Type | Description | Typical Example | Application |
|---|---|---|---|---|
| <400 | Mild steel (MS) | Regular structural steel | SS235 (SS400), SM355 (SM490), A572 (Gr. 50), S350, S355, A992 | Buildings |
| 400–690 | High-strength steel (HSS) | High-performance steel/high tensile steel | A572 (Gr. 60), S460 | Bridges, high-rise buildings |
| >690 | Very-high-strength steel (VHSS) | Ultra/super-high-strength steel | S690, S960 | Cranes, bridges, high-rise buildings, offshore structures |
| Group | Type | Grade | Yield Strength | Tensile Strength | Author |
|---|---|---|---|---|---|
| Index | EN1993-1-2 | Eurocode Standard (EN1993-1-2) [9] | |||
| NIST_2016 | NIST Regression Equation [26] | ||||
| AISC_2016 | AISC Standard [27] | ||||
| MS | SS400_1 | SS400 (SS235) | 235 | 400 | Kwon (2001) |
| SS400_2 | Kwon (2007) | ||||
| SM490 | SM490 (SM355) | 355 | 490 | Kwon (2007) | |
| A572 Gr. 50_Kodur | ASTM A572 Grade 50 | 345 | 450 | Kodur (2016) | |
| A572 Gr. 50_Test | This study | ||||
| A992 | ASTM A992 | 345 | 450 | Lee (2015) | |
| S350GD+Z | S350GD+Z | 350 | 420 | Outinen (2004) | |
| S355J2H_50503 | S355J2H | 355 | 470–630 | ||
| S355J2H_80803 | |||||
| S355J2H_1001003 | |||||
| Mild steel | Mild steel | 400–460 | 550 | Chen (2006) | |
| HSS | A572 Gr.60_Test | ASTM A572 Grade 60 | 415 (Min) | 520 | This study |
| S460N_SST | S460N | 460 | 540–720 | Qiang (2013) | |
| S460N_TST | |||||
| VHSS | S690_SST | S690 | 690 | 770–940 | Qiang (2013) |
| S690_TST | |||||
| HSS | High-strength steel | 780–820 | 850 | Chen (2006) | |
| S960_SST | S960 | 960 | 980–1150 | Qiang (2013) | |
| S960_TST | |||||
| Test | Steel Type | Plate Thickness (mm) | Target Temperature (°C) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 * | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | |||
| SST | ASTM A572 Grade 50 (Gr. 50) | 6 | 3 ** | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| ASTM A572 Grade 60 (Gr. 60) | 6 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |
| Mechanical Properties | Steel Type | |
|---|---|---|
| ASTM A572 Gr. 50 | ASTM A572 Gr. 60 | |
| Yield Strength (MPa) | 345 | 415 |
| Tensile Strength (MPa) | 450 | 520 |
| Elastic Modulus (MPa) | 200,000 | 200,000 |
| Elongation Break (%) | 18–21 | 16–18 |
| Bulk Modulus (GPa) | 160 | 160 |
| Shear Modulus (GPa) | 80 | 80 |
| Target Temperature (°C) | Strength Value (MPa) | Elastic Modulus (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.2% | 0.5% | 1.0% | 1.5% | 2.0% | 20% | Max | ||
| 25 | 369 ( | 366 ( | 385 ( | 390 ( | 406 ( | 501 ( | 508 ( | 206,666 ( |
| 100 | 353.33 | 356 | 368 | 386.7 | 402.7 | 460 | 484 | 184,000 |
| 200 | 321.5 | 322.17 | 341.24 | 351.05 | 366.7 | 481.5 | 481.71 | 225,000 |
| 300 | 314 | 314.6 | 352 | 372 | 384 | 464 | 477.3 | 166,667 |
| 400 | 278.7 | 276 | 305.3 | 317.3 | 329.3 | 334.7 | 368 | 170,000 |
| 500 | 217.3 | 221.3 | 237.3 | 242.7 | 248 | 228 | 257.3 | 105,000 |
| 600 | 136 | 144 | 150.7 | 153.3 | 154.7 | 122.7 | 154.7 | 81,666 |
| 700 | 89.4 | 92 | 90.7 | 92 | 92 | 74.7 | 92 | 55,000 |
| 800 | 50 | 52 | 52 | 52 | 54.6 | 50 | 56 | 25,000 |
| 900 | 36 | 38.7 | 41.3 | 42.7 | 42.7 | 38.7 | 48 | 21,667 |
| Target Temperature (°C) | Strength Reduction Factor (RF) | Elastic Modulus RF | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.2% | 0.5% | 1.0% | 1.5% | 2.0% | 20% | Max | ||
| 25 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 100 | 0.96 | 0.97 | 0.96 | 0.99 | 0.99 | 0.92 | 0.95 | 0.89 |
| 200 | 0.87 | 0.88 | 0.89 | 0.90 | 0.90 | 0.96 | 0.95 | 1.09 |
| 300 | 0.85 | 0.86 | 0.91 | 0.95 | 0.95 | 0.93 | 0.94 | 0.81 |
| 400 | 0.76 | 0.75 | 0.79 | 0.81 | 0.81 | 0.67 | 0.72 | 0.82 |
| 500 | 0.59 | 0.60 | 0.62 | 0.62 | 0.61 | 0.46 | 0.51 | 0.51 |
| 600 | 0.37 | 0.39 | 0.39 | 0.39 | 0.38 | 0.24 | 0.30 | 0.40 |
| 700 | 0.24 | 0.25 | 0.24 | 0.24 | 0.23 | 0.15 | 0.18 | 0.27 |
| 800 | 0.14 | 0.14 | 0.14 | 0.13 | 0.13 | 0.10 | 0.11 | 0.12 |
| 900 | 0.10 | 0.11 | 0.11 | 0.11 | 0.11 | 0.08 | 0.09 | 0.10 |
| Target Temperature (°C) | Strength Value (MPa) | Elastic Modulus (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.2% | 0.5% | 1.0% | 1.5% | 2.0% | 20% | Max | ||
| 25 | 332 | 292 | 358.7 | 397.3 | 418.7 | 466.7 | 514.7 | 205,000 |
| 100 | 310.7 | 306.7 | 360 | 400 | 425.3 | 476.85 | 496 | 180,000 |
| 200 | 321.3 | 318.7 | 373.3 | 412 | 437.7 | 502.65 | 516 | 182,000 |
| 300 | 298.6 | 316 | 369.3 | 406.7 | 437.3 | 502.65 | 568 | 248,000 |
| 400 | 268 | 276 | 320 | 350.7 | 374.7 | 405.3 | 460 | 220,000 |
| 500 | 196.7 | 201.3 | 229.3 | 246.7 | 257.3 | 205.3 | 273.3 | 116,667 |
| 600 | 128 | 138.7 | 152 | 156 | 160 | 133.3 | 162.7 | 85,000 |
| 700 | 60 | 72 | 76 | 77.7 | 77.7 | 58.7 | 77.7 | 50,000 |
| 800 | 41 | 42.7 | 45.3 | 50.7 | 52 | 52 | 61.3 | 25,000 |
| 900 | 28 | 28 | 32 | 33.3 | 33.3 | 34.7 | 40 | 16,667 |
| Target Temperature (°C) | Strength Reduction Factor (RF) | Elastic Modulus RF | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.2% | 0.5% | 1.0% | 1.5% | 2.0% | 20% | Max | ||
| 25 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 100 | 0.94 | 1.05 | 1.00 | 1.01 | 1.02 | 0.99 | 0.96 | 0.88 |
| 200 | 0.97 | 1.09 | 1.04 | 1.04 | 1.05 | 1.02 | 1.00 | 0.89 |
| 300 | 0.90 | 1.08 | 1.03 | 1.02 | 1.04 | 1.08 | 1.10 | 1.21 |
| 400 | 0.81 | 0.95 | 0.89 | 0.88 | 0.89 | 0.87 | 0.89 | 1.07 |
| 500 | 0.59 | 0.69 | 0.64 | 0.62 | 0.61 | 0.44 | 0.53 | 0.57 |
| 600 | 0.39 | 0.48 | 0.42 | 0.39 | 0.38 | 0.29 | 0.32 | 0.41 |
| 700 | 0.18 | 0.25 | 0.21 | 0.20 | 0.19 | 0.13 | 0.15 | 0.24 |
| 800 | 0.12 | 0.15 | 0.13 | 0.13 | 0.12 | 0.11 | 0.12 | 0.12 |
| 900 | 0.08 | 0.10 | 0.09 | 0.08 | 0.08 | 0.07 | 0.08 | 0.08 |
| Equation | Temp. | 400 °C | 700 °C | Row | ||||
| Standard | EC *, (E) | AISC, (A) | NIST, (N) | EC *, (E) | AISC, (A) | NIST, (N) | ||
| MS Equation (Equations (1)–(3), M) | Difference (%) | (M)–(A) | (M)–(N) | |||||
| 24 | 24 | 0 | 3 | 0 | 5 | (1) | ||
| HSS Equation (Equations (4)–(6), H) | Difference (%) | (H)–(A) | (H)–(N) | |||||
| 7 | 7 | 16 | 15 | 12 | 16 | (2) | ||
| Column | (a) | (b) | (c) | (d) | (e) | (f) | ||
| Equation | Temp. | 700 °C | Row | ||
| Standard | EC * (E) | AISC (A) | NIST (N) | ||
| MS Equation (Equation (7), M) | Difference (%) | ||||
| 30 | 26 | 0 | (1) | ||
| HSS Equation (Equation (8), H) | Difference (%) | ||||
| 25 | 21 | 5 | (2) | ||
| Column | (a) | (b) | (c) | ||
| Equation | Temp. | 400 °C | 700 °C | Row | ||||
| Standard | EC * (E) | AISC (A) | NIST (N) | EC * (E) | AISC (A) | NIST (N) | ||
| MS Equation (Equations (9)–(11), M) | Difference (%) | |||||||
| 5 | 15 | 4 | 10 | 2 | 8 | (1) | ||
| HSS Equation (Equations (12)–(14), H) | Difference (%) | |||||||
| 6 | 14 | 3 | 8 | 0 | 6 | (2) | ||
| Column | (a) | (b) | (c) | (d) | (e) | (f) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-H.; Choi, B.-J. Mechanical Properties of ASTM A572 Grades 50 and 60 Steels at High Temperatures. Appl. Sci. 2021, 11, 11833. https://doi.org/10.3390/app112411833
Lee S-H, Choi B-J. Mechanical Properties of ASTM A572 Grades 50 and 60 Steels at High Temperatures. Applied Sciences. 2021; 11(24):11833. https://doi.org/10.3390/app112411833
Chicago/Turabian StyleLee, Su-Hyeon, and Byong-Jeong Choi. 2021. "Mechanical Properties of ASTM A572 Grades 50 and 60 Steels at High Temperatures" Applied Sciences 11, no. 24: 11833. https://doi.org/10.3390/app112411833
APA StyleLee, S.-H., & Choi, B.-J. (2021). Mechanical Properties of ASTM A572 Grades 50 and 60 Steels at High Temperatures. Applied Sciences, 11(24), 11833. https://doi.org/10.3390/app112411833






