Development of Detection and Volumetric Methods for the Triceps of the Lower Leg Using Magnetic Resonance Images with Deep Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects
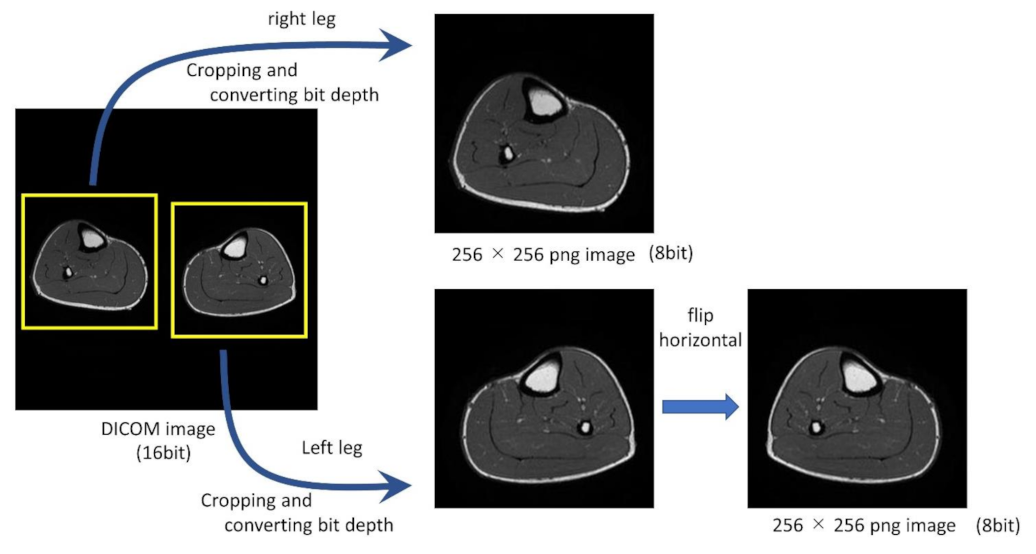
2.2. Preprocessing
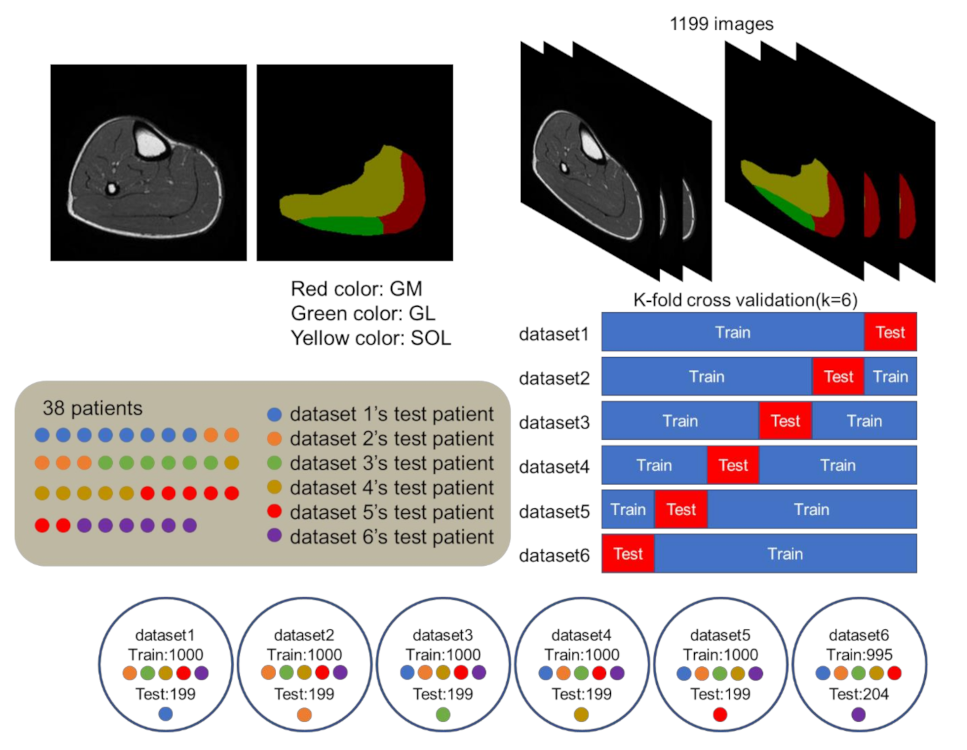
2.3. Dataset
2.4. Training for Creating Models
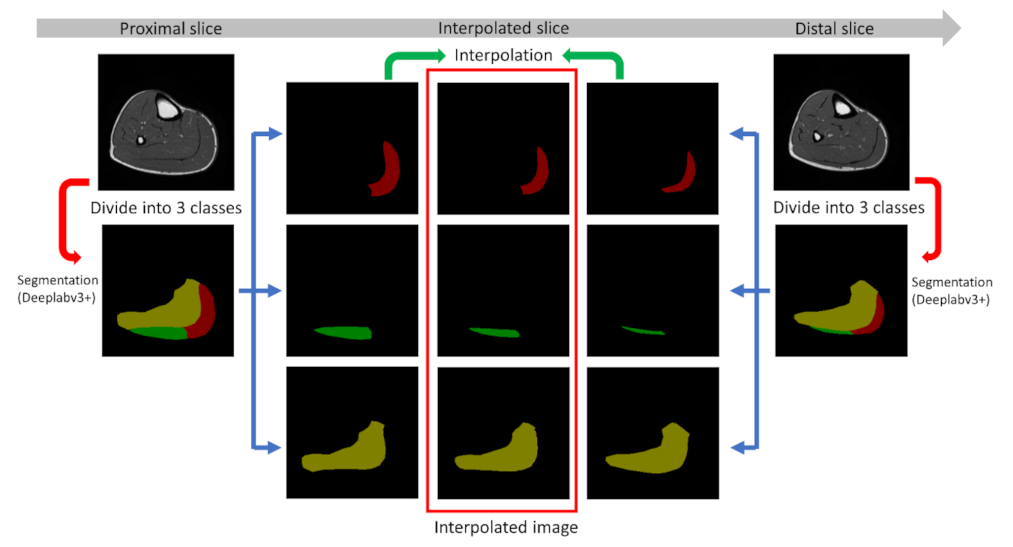
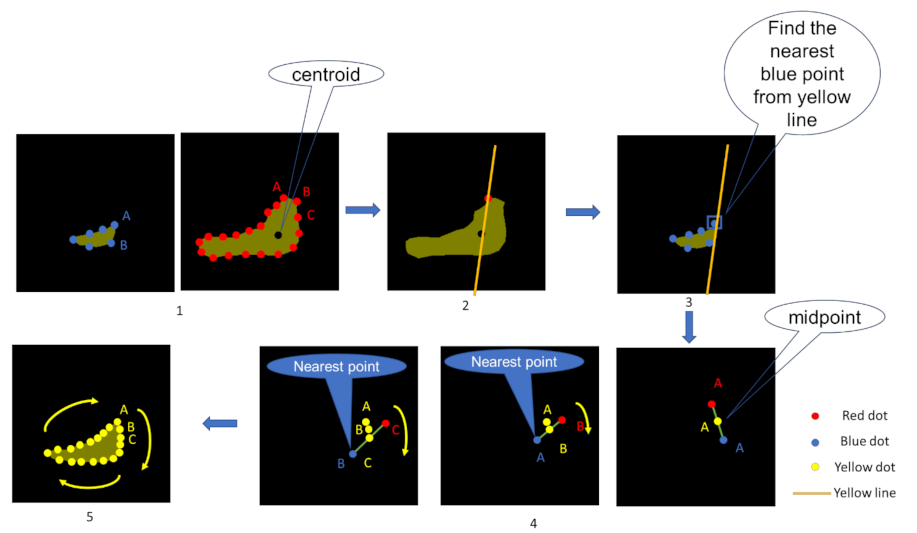
2.5. Interpolation
2.6. Indicators Used for Evaluation
2.6.1. DSC
2.6.2. Calculation of the Volume and Error Rate
2.7. Evaluation of the Created Models
2.8. Evaluation of the Interpolation Method
3. Results
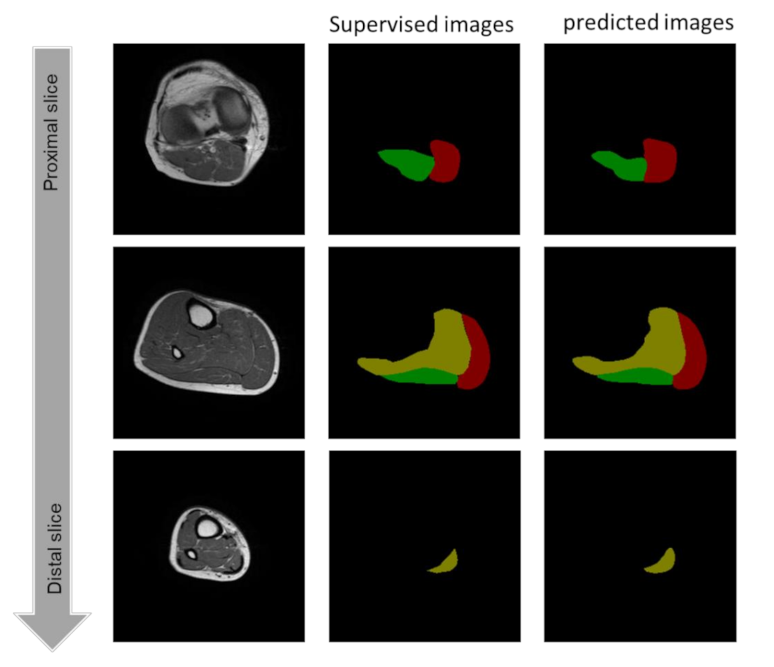
3.1. Evaluation of the Created Models
3.2. Evaluation of the Interpolation Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Son, S.; Jeong, Y.; Lee, B. An audification and visualization system (AVS) of an autonomous vehicle for blind and deaf people based on deep learning. Sensors 2019, 19, 5053. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Aggarwal, P.; Choi, J.; Jay, C.C. A deep learning approach to drone monitoring. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 686–691. [Google Scholar] [CrossRef] [Green Version]
- Ghaderi, A.; Sanandaji, B.M.; Ghaderi, F. Deep Forecast: Deep Learning-based Spatio-Temporal Forecasting. In Proceedings of the International Conference on Machine Learning, Time Series Workshop, Sydney, NSW, Australia, 6–11 August 2017. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Sugimori, H.; Hamaguchi, H.; Fujiwara, T.; Ishizaka, K. Classification of type of brain magnetic resonance images with deep learning technique. Magn. Reson. Imaging 2021, 77, 180–185. [Google Scholar] [CrossRef]
- Sugimori, H.; Kawakami, M. Automatic detection of a standard line for brain magnetic resonance imaging using deep learning. Appl. Sci. 2019, 9, 3849. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X. Automatic Segmentation of Multiple Organs on 3D CT Images by Using Deep Learning Approaches. Adv. Exp. Med. Biol. 2020, 1213, 135–147. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Kweon, J.; Roh, J.H.; Lee, J.H.; Kang, H.; Park, L.J.; Kim, D.J.; Yang, H.; Hur, J.; Kang, D.Y.; et al. Deep learning segmentation of major vessels in X-ray coronary angiography. Sci. Rep. 2019, 9, 16897. [Google Scholar] [CrossRef]
- Zhang, L.; Mohamed, A.A.; Chai, R.; Guo, Y.; Zheng, B.; Wu, S. Automated deep learning method for whole-breast segmentation in diffusion-weighted breast MRI. J. Magn. Reson. Imaging 2020, 51, 635–643. [Google Scholar] [CrossRef] [PubMed]
- Kessler, D.A.; MacKay, J.W.; Crowe, V.A.; Henson, F.M.D.; Graves, M.J.; Gilbert, F.J.; Kaggie, J.D. The optimisation of deep neural networks for segmenting multiple knee joint tissues from MRIs. Comput. Med. Imaging Graph. 2020, 86, 101793. [Google Scholar] [CrossRef] [PubMed]
- Cattagni, T.; Scaglioni, G.; Laroche, D.; Gremeaux, V.; Martin, A. The involvement of ankle muscles in maintaining balance in the upright posture is higher in elderly fallers. Exp. Gerontol. 2016, 77, 38–45. [Google Scholar] [CrossRef]
- Belavý, D.L.; Miokovic, T.; Rittweger, J.; Felsenberg, D. Estimation of changes in volume of individual lower-limb muscles using magnetic resonance imaging (during bed-rest). Physiol. Meas. 2011, 32, 35–50. [Google Scholar] [CrossRef]
- Tortorella, C.; Simone, O.; Piazzolla, G.; Stella, I.; Cappiello, V.; Antonaci, S. Role of phosphoinositide 3-kinase and extracellular signal-regulated kinase pathways in granulocyte macrophage-colony-stimulating factor failure to delay fas-induced neutrophil apoptosis in elderly humans. J. Gerontol. Ser. A 2006, 61, 1111–1118. [Google Scholar] [CrossRef]
- Karamanidis, K.; Epro, G.; König, M.; Mersmann, F.; Arampatzis, A. Simplified Triceps Surae Muscle Volume Assessment in Older Adults. Front. Physiol. 2019, 10, 1299. [Google Scholar] [CrossRef] [Green Version]
- Friedberger, A.; Figueiredo, C.; Bäuerle, T.; Schett, G.; Engelke, K. A new method for quantitative assessment of hand muscle volume and fat in magnetic resonance images. BMC Rheumatol. 2020, 4, 72. [Google Scholar] [CrossRef] [PubMed]
- Kemnitz, J.; Baumgartner, C.F.; Eckstein, F.; Chaudhari, A.; Ruhdorfer, A.; Wirth, W.; Eder, S.K.; Konukoglu, E. Clinical evaluation of fully automated thigh muscle and adipose tissue segmentation using a U-Net deep learning architecture in context of osteoarthritic knee pain. Magn. Reson. Mater. Phys. Biol. Med. 2020, 33, 483–493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, J.; Cao, P.; Chang, H.C.; Gao, Y.; Chan, S.H.S.; Vardhanabhuti, V. Deep learning-based thigh muscle segmentation for reproducible fat fraction quantification using fat–water decomposition MRI. Insights Imaging 2020, 11, 128. [Google Scholar] [CrossRef]
- Gadermayr, M.; Li, K.; Müller, M.; Truhn, D.; Krämer, N.; Merhof, D.; Gess, B. Domain-specific data augmentation for segmenting MR images of fatty infiltrated human thighs with neural networks. J. Magn. Reson. Imaging 2019, 49, 1676–1683. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Ray, N.; Boulanger, P. A Structured Deep-Learning Based Approach for the Automated Segmentation of Human Leg Muscle from 3D MRI. In Proceedings of the 2017 14th Conference on Computer and Robot Vision (CRV), Edmonton, AB, Canada, 16–19 May 2017; pp. 117–123. [Google Scholar] [CrossRef]
- Andrews, S.; Hamarneh, G. The Generalized Log-Ratio Transformation: Learning Shape and Adjacency Priors for Simultaneous Thigh Muscle Segmentation. IEEE Trans. Med. Imaging 2015, 34, 1773–1787. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baudin, P.-Y.; Azzabou, N.; Carlier, P.G.; Paragios, N. Automatic Skeletal Muscle Segmentation through Random Walks and Graph-Based Seed Placement. In Proceedings of the 2012 9th IEEE International Symposium on Biomedical Imaging (ISBI), Barcelona, Spain, 2–5 May 2012; pp. 1036–1039. [Google Scholar] [CrossRef] [Green Version]
- Essafi, S.; Langs, G.; Deux, J.F.; Rahmouni, A.; Bassez, G.; Paragios, N. Wavelet-driven knowledge-based MRI calf muscle segmentation. In Proceedings of the 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Boston, MA, USA, 28 June–1 July 2009; pp. 225–228. [Google Scholar] [CrossRef]
- Abdullah, J.Y.; Rajion, Z.A.; Martin, A.G.; Jaafar, A.; Ghani, A.R.I.; Abdullah, J.M. Shape-based interpolation method in measuring intracranial volume for pre- and post-operative decompressive craniectomy using open source software. Neurocirugia 2019, 30, 115–123. [Google Scholar] [CrossRef]
- Nordez, A.; Jolivet, E.; Südhoff, I.; Bonneau, D.; De Guise, J.A.; Skalli, W. Comparison of methods to assess quadriceps muscle volume using magnetic resonance imaging. J. Magn. Reson. Imaging 2009, 30, 1116–1123. [Google Scholar] [CrossRef]
- Ahmed, I.; Ahmad, M.; Khan, F.A.; Asif, M. Comparison of deep-learning-based segmentation models: Using top view person images. IEEE Access 2020, 8, 136361–136373. [Google Scholar] [CrossRef]
- Khan, Z.; Yahya, N.; Alsaih, K.; Ali, S.S.A.; Meriaudeau, F. Evaluation of deep neural networks for semantic segmentation of prostate in T2W MRI. Sensors 2020, 20, 3183. [Google Scholar] [CrossRef]
- Rundo, L.; Han, C.; Nagano, Y.; Zhang, J.; Hataya, R.; Militello, C.; Tangherloni, A.; Nobile, M.S.; Ferretti, C.; Besozzi, D.; et al. USE-Net: Incorporating Squeeze-and-Excitation blocks into U-Net for prostate zonal segmentation of multi-institutional MRI datasets. Neurocomputing 2019, 365, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Schlemper, J.; Oktay, O.; Schaap, M.; Heinrich, M.; Kainz, B.; Glocker, B.; Rueckert, D. Attention gated networks: Learning to leverage salient regions in medical images. Med. Image Anal. 2019, 53, 197–207. [Google Scholar] [CrossRef]
- Yeung, M.; Sala, E.; Schönlieb, C.-B.; Rundo, L. Focus U-Net: A novel dual attention-gated CNN for polyp segmentation during colonoscopy. Comput. Biol. Med. 2021, 137, 104815. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2018; pp. 833–851. [Google Scholar] [CrossRef] [Green Version]
- Do, D.T.; Le, T.Q.T.; Le, N.Q.K. Using deep neural networks and biological subwords to detect protein S-sulfenylation sites. Brief. Bioinform. 2021, 22, bbaa128. [Google Scholar] [CrossRef]
- Le, N.Q.K.; Huynh, T.T. Identifying SNAREs by Incorporating Deep Learning Architecture and Amino Acid Embedding Representation. Front. Physiol. 2019, 10, 1501. [Google Scholar] [CrossRef] [PubMed]
- Miyachi, R.; Yamazaki, T.; Ohno, N.; Miyati, T. Relationship between muscle cross-sectional area by mri and muscle thickness by ultrasonography of the triceps surae in the sitting position. Healthcare 2020, 8, 166. [Google Scholar] [CrossRef] [PubMed]
- Henninger, H.B.; Christensen, G.V.; Taylor, C.E.; Kawakami, J.; Hillyard, B.S.; Tashjian, R.Z.; Chalmers, P.N. The Muscle Cross-sectional Area on MRI of the Shoulder Can Predict Muscle Volume: An MRI Study in Cadavers. Clin. Orthop. Relat. Res. 2020, 478, 871–883. [Google Scholar] [CrossRef] [PubMed]
- Akagi, R.; Takai, Y.; Ohta, M.; Kanehisa, H.; Kawakami, Y.; Fukunaga, T. Muscle volume compared to cross-sectional area is more appropriate for evaluating muscle strength in young and elderly individuals. Age Ageing 2009, 38, 564–569. [Google Scholar] [CrossRef] [Green Version]


| Mean ± SD [Min–Max] | |
|---|---|
| Number of slices | 17.9 ± 4.9 [3–29] |
| Field of view [] | 342.1 × 295.0 [160 × 160–500 × 425] |
| Acquisition matrix size [pixel] | 446.0 × 402.4 [320 × 224–672 × 672] |
| Pixel size [] | 0.764 × 0.764 [0.559 × 0.559–0.928 × 0.928] |
| Slice thickness [] | 5.8 ± 0.5 [4–6] |
| Slice gap [] | 13.6 ± 4.7 [4.8–22.8] |
| Length of acquisition [] | 231.0 ± 76.2 [42–342] |
| Position | Dataset1 | Dataset2 | Dataset3 | Dataset4 | Dataset5 | Dataset6 | Mean ± SD |
|---|---|---|---|---|---|---|---|
| GM | 0.897 | 0.754 | 0.876 | 0.830 | 0.776 | 0.745 | 0.813 ± 0.064 |
| GL | 0.804 | 0.591 | 0.765 | 0.773 | 0.639 | 0.704 | 0.713 ± 0.084 |
| SOL | 0.889 | 0.820 | 0.791 | 0.823 | 0.840 | 0.844 | 0.835 ± 0.033 |
| Position | Dataset1 | Dataset2 | Dataset3 | Dataset4 | Dataset5 | Dataset6 | Mean ± SD |
|---|---|---|---|---|---|---|---|
| GM | 5.68 | 11.84 | 8.96 | 10.28 | 8.80 | 24.48 | 11.67 ± 6.60 |
| GL | 27.46 | 23.03 | 18.74 | 27.14 | 32.71 | 12.36 | 23.57 ± 7.22 |
| SOL | 11.71 | 17.22 | 14.60 | 6.87 | 5.92 | 9.24 | 10.93 ± 4.43 |
| total error | 11.07 | 13.38 | 11.87 | 7.27 | 7.84 | 12.43 | 10.64 ± 2.51 |
| Position | DSC |
|---|---|
| GM | 0.877 ± 0.134 |
| GL | 0.809 ± 0.170 |
| SOL | 0.867 ± 0.078 |
| Comparison Target | Position | Error Rate [%] | p Value |
|---|---|---|---|
| Supervised muscle and interpolated muscle | GM | 9.41 ± 7.65 | 0.5052 |
| GL | 17.89 ± 6.37 | 0.3098 | |
| SOL | 9.43 ± 5.07 | 0.7280 | |
| total error | 7.69 ± 3.49 | - | |
| Supervised muscle and non-interpolated muscle | GM | 20.28 ± 9.68 | 0.1499 |
| GL | 33.93 ± 7.54 | 0.2539 | |
| SOL | 12.70 ± 5.79 | 0.3442 | |
| total error | 14.97 ± 3.98 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asami, Y.; Yoshimura, T.; Manabe, K.; Yamada, T.; Sugimori, H. Development of Detection and Volumetric Methods for the Triceps of the Lower Leg Using Magnetic Resonance Images with Deep Learning. Appl. Sci. 2021, 11, 12006. https://doi.org/10.3390/app112412006
Asami Y, Yoshimura T, Manabe K, Yamada T, Sugimori H. Development of Detection and Volumetric Methods for the Triceps of the Lower Leg Using Magnetic Resonance Images with Deep Learning. Applied Sciences. 2021; 11(24):12006. https://doi.org/10.3390/app112412006
Chicago/Turabian StyleAsami, Yusuke, Takaaki Yoshimura, Keisuke Manabe, Tomonari Yamada, and Hiroyuki Sugimori. 2021. "Development of Detection and Volumetric Methods for the Triceps of the Lower Leg Using Magnetic Resonance Images with Deep Learning" Applied Sciences 11, no. 24: 12006. https://doi.org/10.3390/app112412006
APA StyleAsami, Y., Yoshimura, T., Manabe, K., Yamada, T., & Sugimori, H. (2021). Development of Detection and Volumetric Methods for the Triceps of the Lower Leg Using Magnetic Resonance Images with Deep Learning. Applied Sciences, 11(24), 12006. https://doi.org/10.3390/app112412006






