On the Development of a Surrogate Modelling Toolbox for Virtual Assembly
Abstract
:1. Introduction
1.1. Integration in the Context of Industry 4.0
1.2. Problem Setting
1.3. Scope and Aims
2. State of the Art
- Detection (of key points in order to reduce the number of points to register),
- Description (of the shape by local shape descriptors),
- Searching (of corresponding points) and
- Refinement (in an iterative optimization).
2.1. Methods for Relative Positioning
2.2. Prior Work for Surrogate Modelling for Joining Processes
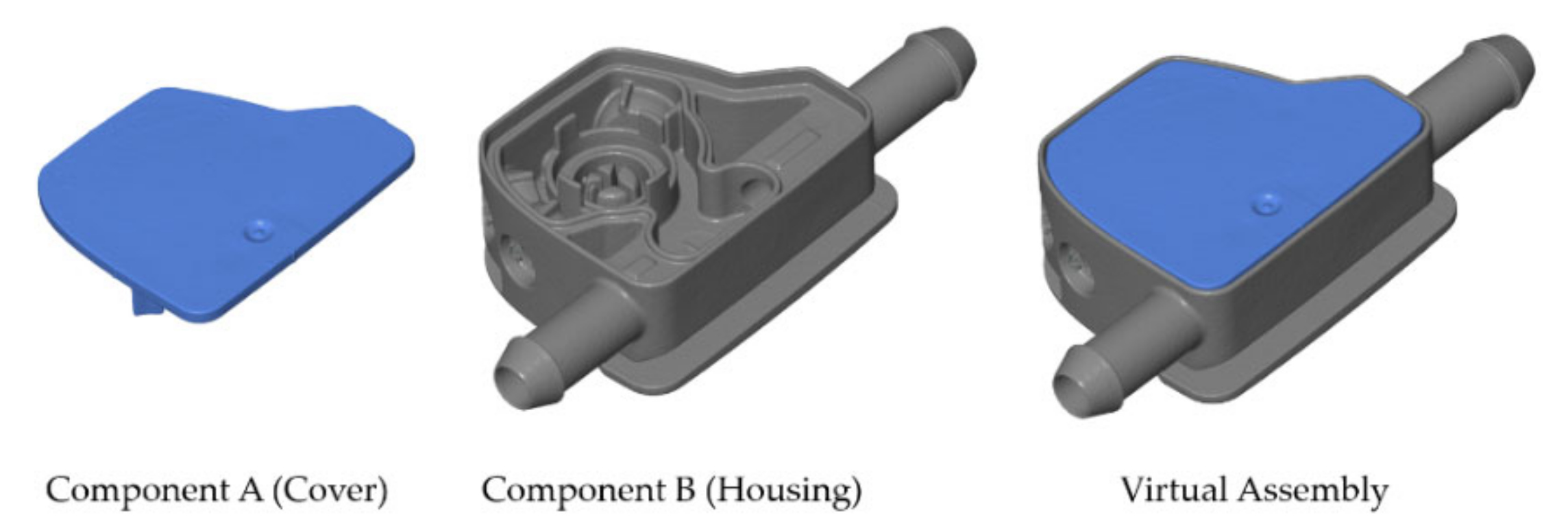
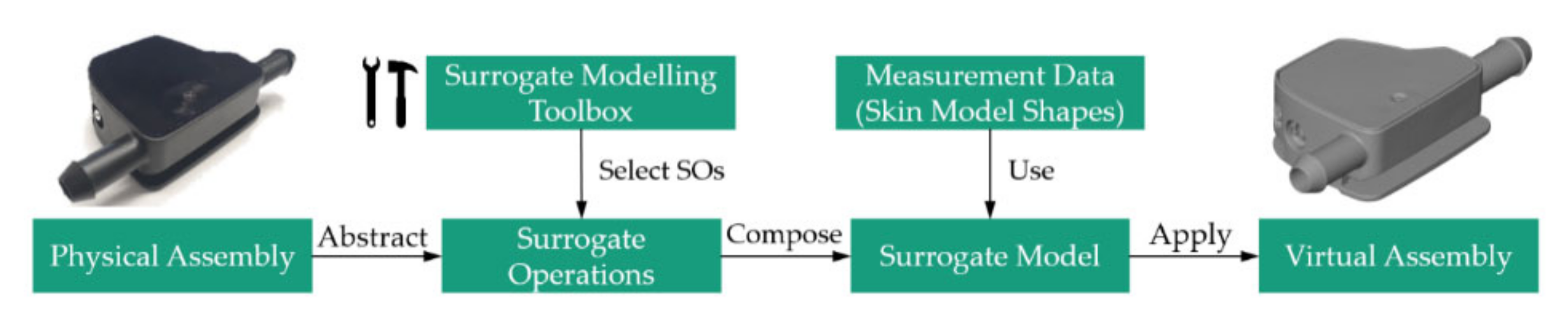
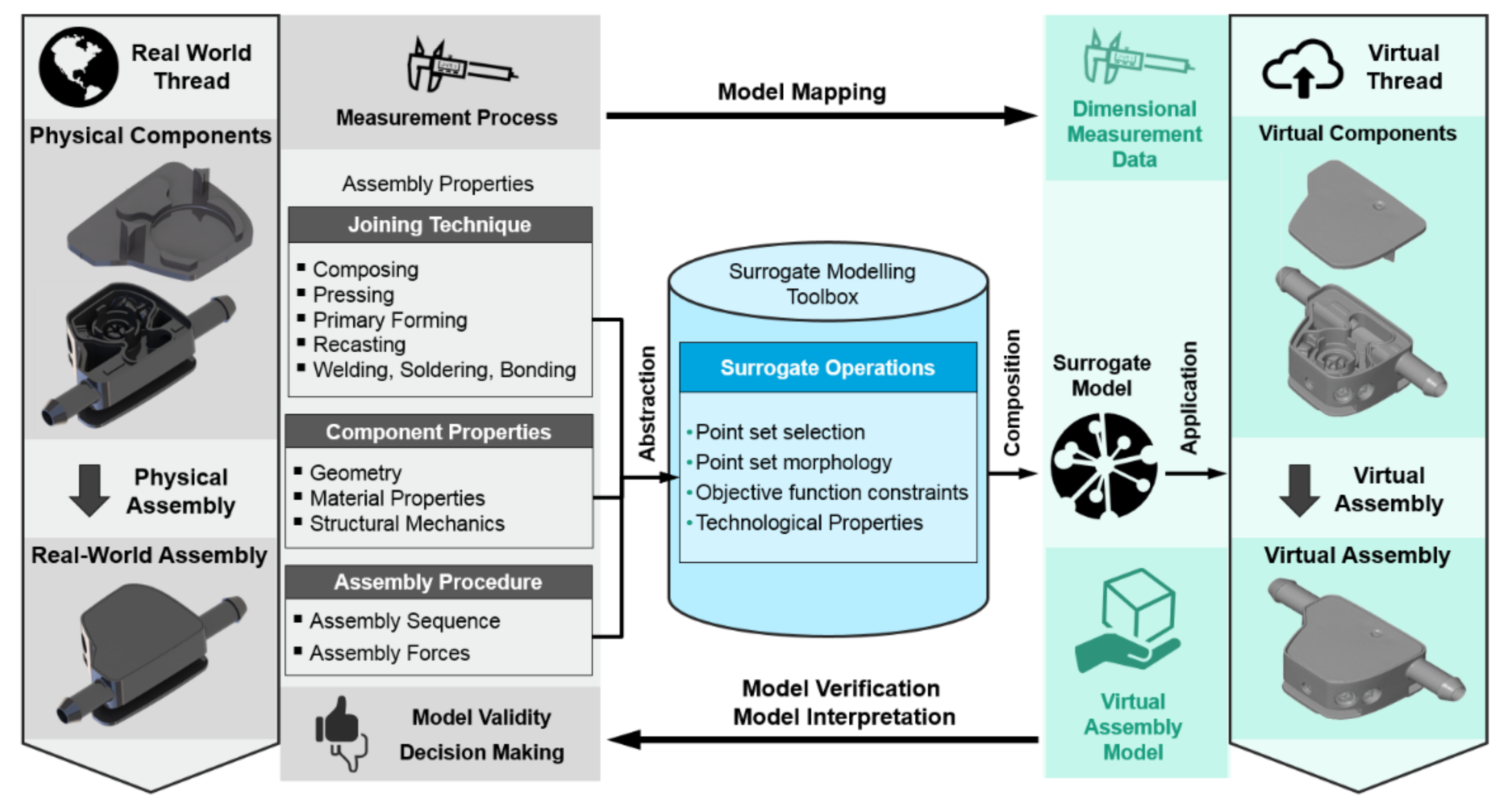
3. Development of a Surrogate Modelling Toolbox
- Operations for detecting relevant subsets of points (Point set selection),
- Operations for describing and manipulating the surface morphology (Point set morphology),
- Operations concerning point correspondence search and assembly position determination (Objective function constraints) and
- Technological properties such as point set refinement or simplification operations, which are not further discussed in this work.
4. Use Case Study for a Laser Welding Assembly
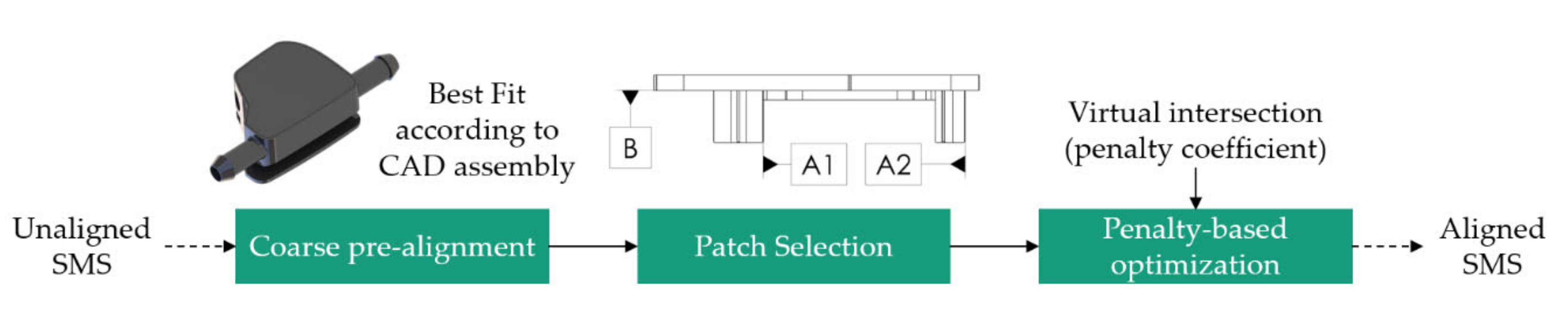
4.1. Surrogate Model Composition
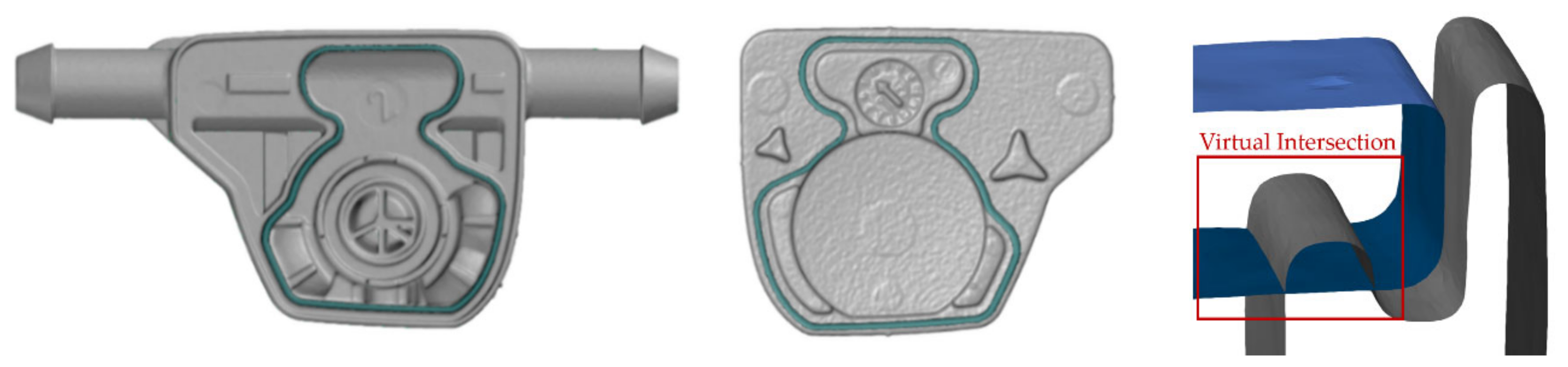
- Coarse Pre-Alignment according to the CAD assembly,
- Patch Selection of primary datum A (guiding pegs A1 and A2 at the cover and corresponding holes in the housing, see technical drawing in Figure 7) and secondary datum B (alignment of cover face in flush with the housing), and
- Virtual Intersection of the parts by using a penalty-based optimization approach as in [68].
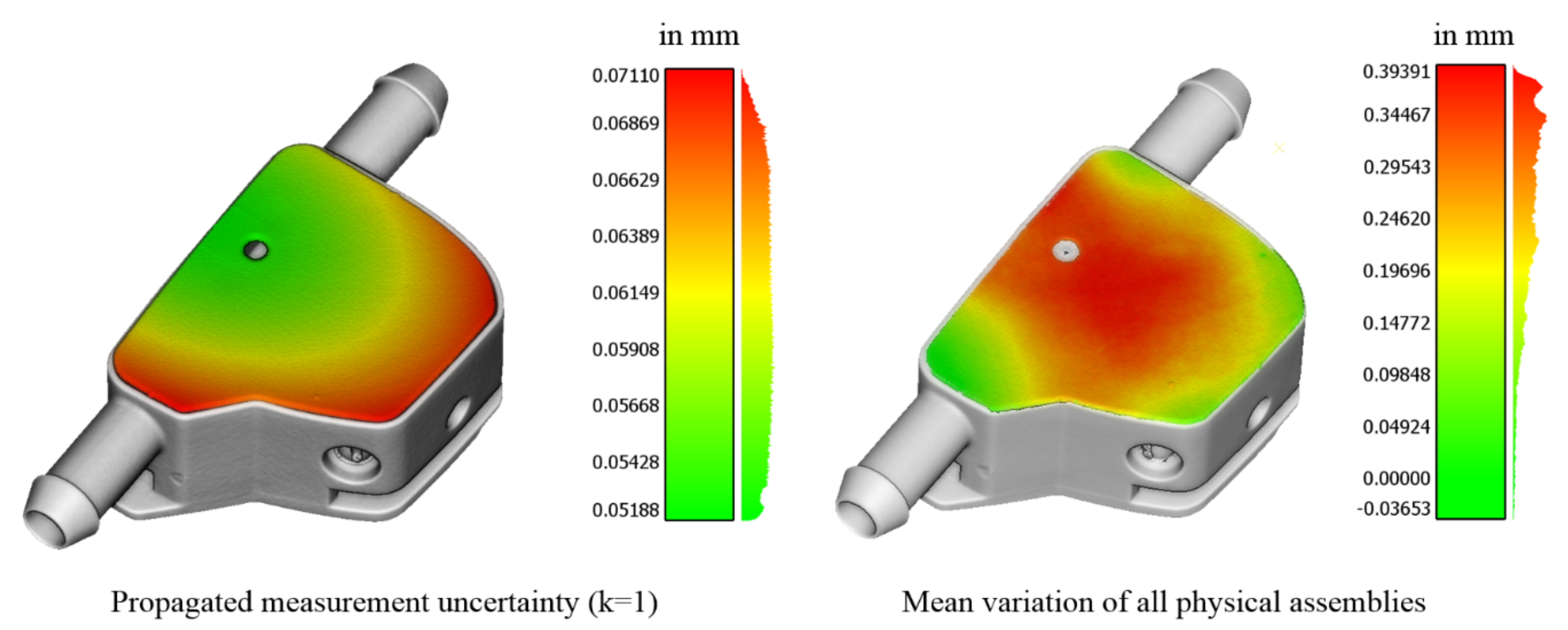
4.2. Validation against the Physical Assembly
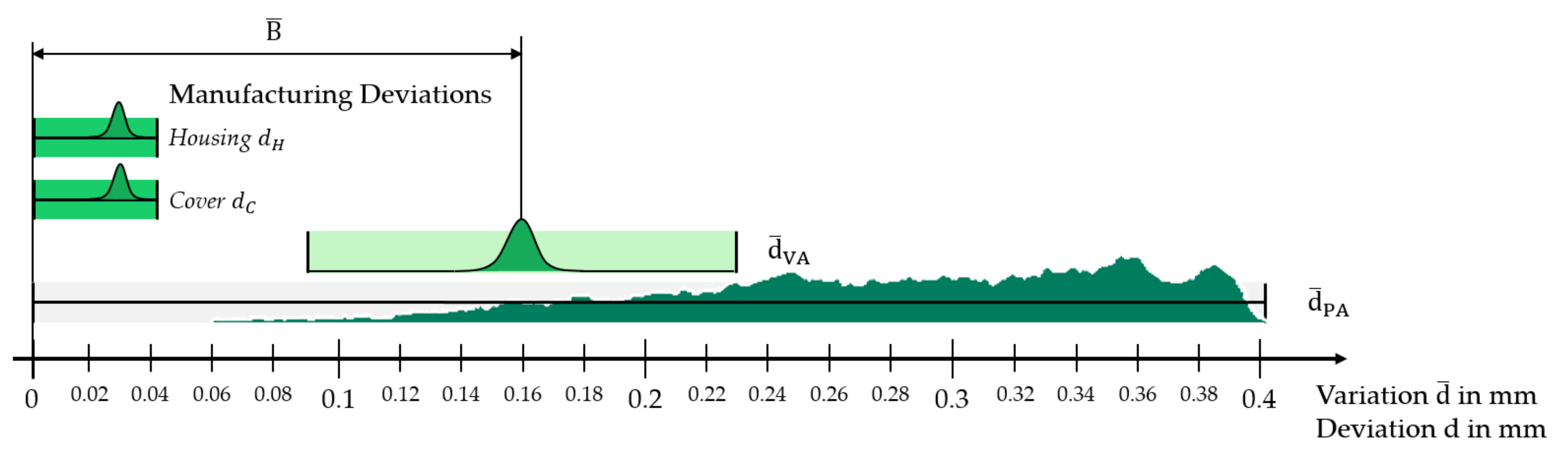
4.2.1. Comparison of Variation Distributions
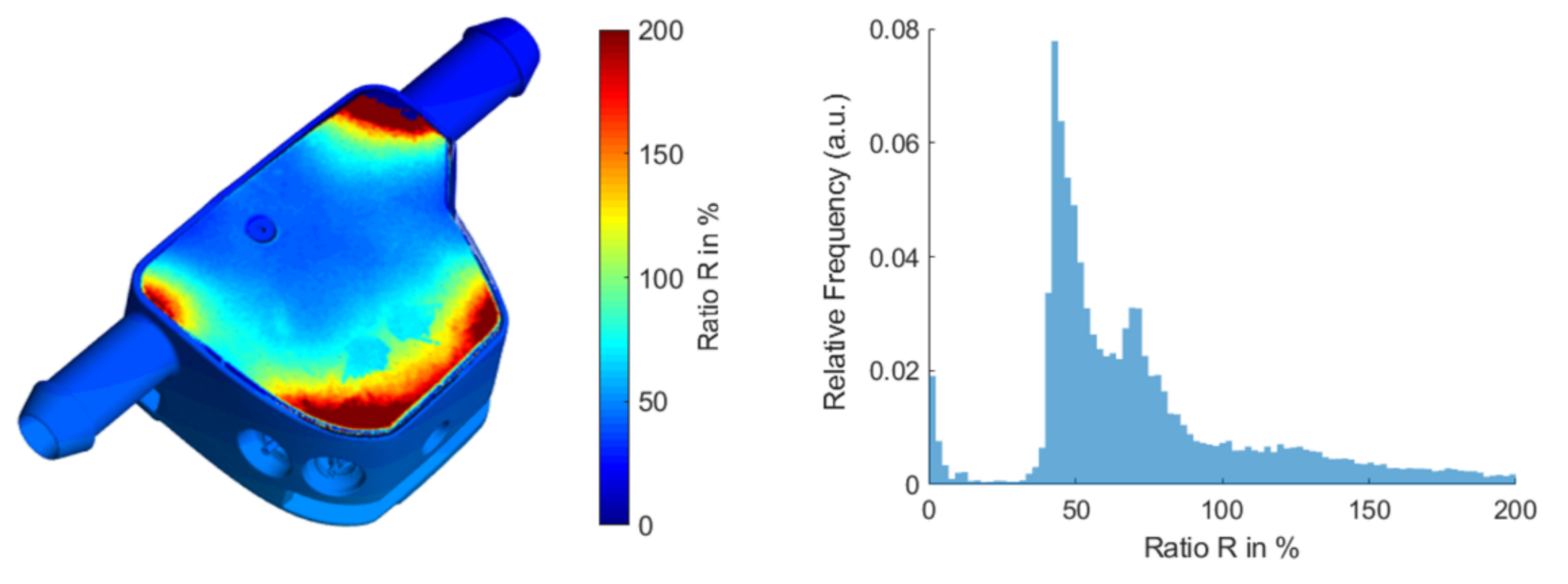
4.2.2. Comparison of Single Point Deviations
5. Conclusions
6. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CPS | Cyber-Physical Systems |
| CT | Computed Tomography |
| GD&T | Geometrical Dimensioning and Tolerancing |
| ICT | Information and Communication Technology |
| PA | Physical Assembly |
| SMS | Skin Model Shape |
| SMT | Surrogate Modelling Toolbox |
| SO | Surrogate Operation |
| VA | Virtual Assembly |
Appendix A
| Surrogate Operation | Description | Reference | Level of Detail |
|---|---|---|---|
| Point set selection | Detection of relevant subsets of points | ||
| Coarse Matching | Determine initial position before assembly closely to the final position [35] | ||
| Unconstrained Best Fit A | Alignment as provided by Iterative Closest Point-Algorithm (ICP) | [71] |  |
| Constrained Regular Geometries A | Alignment as provided by the ISO System for Geometrical Product Specification (GPS) datum definition in ISO 5459 [28] | [28] |  |
| Segmentation of contact faces A | Determination of subsets and that are by mechanical design provided as contact faces | ||
| Local shape descriptors A | Determination of hypothetically corresponding, salient key features in and , such as Principal Curvature or Harris Algorithm [72] | [35,72] |  |
| Semantic segmentation A | Determination of subsets corresponding to geometrical primitives | [73] |  |
| Patch Selection (CAD based) A | Determination of subsets corresponding to a maximal distance to a nominal geometry such as a CAD file | [74] |  |
| Point set morphology | Description and manipulation of the surface morphology | ||
| Definition of Offset and Intersection A | Definition of a certain offset between faces (e.g., to simulate adhesive gap) or of an intersection (virtual penetration) to simulate surface flattening or material loss (e.g., due to melting welding bead) | [41] |  |
| Morphological Filtering A | Manipulate surfaces locally to simulate surface flattening due to mechanical load | [51,52] |  |
| Hertzian Contact Formulation A | [41] |  | |
| Method of Influence Coefficients (MIC) A | Linearized computation of elastic deformation due to mechanical load | [50,57] |  |
| Linear Finite Element Analysis (FEA) A | Computation of elastic deformation due to mechanical load | [75,76] |  |
| Nonlinear FEA A | Computation of elastic and plastic deformation due to mechanical load | [65,66] |  |
| Objective Function | Searching of correspondences and the assembly position | ||
| Modalities for Distance Computation | Approaches to compute distances between and | ||
| Point to Point B | Distance computation discretized on single points | [71] |  |
| Point to Plane or Triangle B | Triangle-based algorithms for distance calculation that more precisely represent the physical distance | [77] |  |
| Point correspondence metric | Metric considered to determine corresponding points recreating the physical contact scenario [38] | ||
| Euclidean distance B | Only sufficient, when point clouds are relatively dense | [38] |  |
| Ray Casting in Normal Direction B | Improved correspondence for surfaces that are sufficiently coarse aligned | [38] |  |
| Ray Casting in Assembly Direction B | Most accurate representation of the physical assembly contact correspondence | [38] |  |
| Distance Metric | Metric considered to determine the discrepancy between and | ||
| Convex Hull of Gap Volume B | Minimization of the convex hull of the gap volume between and | [38] |  |
| Euclidean distance B | Minimization of local distances in corresponding points | [38] |  |
| Collision behavior | Collision behaviour stating an elastic or stiff contact | ||
| Penalize Intersection B | Allows a certain virtual intersection | [41] | n/a |
| Hard-Constrained Intersection B | Strict compliance to non-intersection | [41] | n/a |
| Collision detection | Determination and quantification of a collision between and | ||
| Sign of signed distances B | Negative signed distances represent a local intersection | [38] |  |
| Simplex-based B | Fast, approximative collision detection, only applicable for convex geometries, e.g., the GJK algorithm [78] | [78,79] |  |
| Bounding Volume Hierarchy B | More precise method applicable for closely positioned objects and initial collision | [79] |  |
| Datum Hierarchy | Representation of primary, secondary, tertiary datum hierarchy as per [28] | ||
| Datum Weighting B | Weighting factors applied to the objective values derived from primary, secondary and tertiary patches | [38] |  |
| Contact and Force Equilibrium B | Allow contact configurations only, where the contact triangle of the primary datum is maximized and intersected by the assembly force vector. The secondary datum constitutes a line contact and the tertiary datum a point contact. | [51] |  |
References
- International Standardization Organization. Quality Management Systems. Fundamentals and Vocabulary; Beuth Verlag GmbH: Berlin, Germany, 2015. [Google Scholar]
- Kayasa, M.J.; Herrmann, C. A Simulation-based evaluation of selective and adaptive production systems (SAPS) supported by quality strategy in production. Procedia CIRP 2012, 3, 14–19. [Google Scholar] [CrossRef] [Green Version]
- Kang, H.; Li, Z.-M. Assembly research of aero-engine casing involving bolted connection based on rigid-compliant coupling assembly deviation modeling. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 2803–2820. [Google Scholar] [CrossRef]
- Zmarzły, P. Technological Heredity of the Turning Process. Teh. Vjesn. Tech. Gaz. 2020, 27, 1194–1203. [Google Scholar] [CrossRef]
- Schleich, B.; Wärmefjord, K.; Söderberg, R.; Wartzack, S. Geometrical Variations management 4.0: Towards next Generation geometry assurance. Procedia CIRP 2018, 75, 3–10. [Google Scholar] [CrossRef]
- Söderberg, R.; Lindkvist, L.; Wärmefjord, K.; Carlson, J.S. Virtual geometry assurance process and toolbox. Procedia CIRP 2016, 43, 3–12. [Google Scholar] [CrossRef]
- Maropoulos, P.G.; Ceglarek, D. Design verification and validation in product lifecycle. CIRP Ann. 2010, 59, 740–759. [Google Scholar] [CrossRef]
- Kagermann, H.; Wahlster, W.; Helbig, J. Securing the Future of German Manufacturing Industry: Recommendations for Implementing the Strategic Initiative Industrie; National Academy of Science and Engineering: München, Germany, 2013. [Google Scholar]
- Hermann, M.; Pentek, T.; Otto, B. Design principles for industrie 4.0 scenarios. In Proceedings of the 2016 IEEE 49th Hawaii International Conference on System Sciences (HICSS), Koloa, HI, USA, 5–8 January 2016; pp. 3928–3937. [Google Scholar]
- Monostori, L.; Kádár, B.; Bauernhansl, T.; Kondoh, S.; Kumara, S.R.; Reinhart, G.; Sauer, O.; Schuh, G.; Sihn, W.; Ueda, K. Cyber-physical systems in manufacturing. CIRP Ann. 2016, 65, 621–641. [Google Scholar] [CrossRef]
- Dalenogare, L.S.; Benitez, G.B.; Ayala, N.F.; Frank, A.G. The expected contribution of industry 4.0 technologies for industrial performance. Int. J. Prod. Econ. 2018, 204, 383–394. [Google Scholar] [CrossRef]
- Bauernhansl, T.; Ten Hompel, M.; Vogel-Heuser, B. Industrie 4.0 in Produktion, Automatisierung und Logistik; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2014; ISBN 978-3-658-04681-1. (In German) [Google Scholar]
- Bauer, W.; Schlund, S.; Marrenbach, D.H.; Ganschar, O. Industrie 4.0—Volkswirtschaftliches Potential für Deutschland.; Bitkom: Berlin, Germany, 2014; Available online: https://www.bitkom.org/Bitkom/Publikationen/Industrie-40-Volkswirtschaftliches-Potenzial-fuer-Deutschland.html (accessed on 14 January 2021). (In German)
- Li, D.; Fast-Berglund, Å.; Paulin, D. Current and future industry 4.0 capabilities for information and knowledge sharing. Int. J. Adv. Manuf. Technol. 2019, 105, 3951–3963. [Google Scholar] [CrossRef] [Green Version]
- Rüßmann, M.; Lorenz, M.; Gerbert, P.; Waldner, M.; Justus, J.; Engel, P.; Harnisch, M. Industry 4.0: The Future of Productivity and Growth in Manufacturing; Boston Consulting Group: Boston, MA, USA, 2015. [Google Scholar]
- Bauernhansl, T.; Hartleif, S.; Felix, T. The Digital Shadow of production—A concept for the effective and efficient information supply in dynamic industrial environments. Procedia CIRP 2018, 72, 69–74. [Google Scholar] [CrossRef]
- Rosen, R.; Von Wichert, G.; Lo, G.; Bettenhausen, K.D. About the importance of autonomy and digital twins for the future of manufacturing. IFAC-Papersonline 2015, 48, 567–572. [Google Scholar] [CrossRef]
- Glaessgen, E.; Stargel, D. The digital twin paradigm for future NASA and U.S. air force vehicles. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012; American Institute of Aeronautics and Astronautics, Ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; p. 1818. [Google Scholar]
- Schleich, B.; Anwer, N.; Mathieu, L.; Wartzack, S. Shaping the digital twin for design and production engineering. CIRP Ann. 2017, 66, 141–144. [Google Scholar] [CrossRef] [Green Version]
- Dobrzański, L.A. Role of materials design in maintenance engineering in the context of industry 4.0 idea. J. Achiev. Mater. Manuf. Eng. 2019, 1, 12–49. [Google Scholar] [CrossRef]
- Dobrzański, L.A.; Dobrzański, L.B. Dentistry 4.0 concept in the design and manufacturing of prosthetic dental restorations. Process. 2020, 8, 525. [Google Scholar] [CrossRef]
- Dobrzański, L.A.; Dobrzański, L.B. Approach to the design and manufacturing of prosthetic dental restorations according to the rules of industry 4.0. Mater. Perform. Charact. 2020, 9, 394–476. [Google Scholar] [CrossRef]
- Wärmefjord, K.; Söderberg, R.; Lindkvist, L.; Lindau, B.; Carlson, J.S. Inspection data to support a digital twin for geometry assurance. In Advanced Manufacturing; Gupta, K., Ed.; ASME International: Tampla, FL, USA, 2017. [Google Scholar]
- Lanza, G.; Haefner, B.; Kraemer, A. Optimization of selective assembly and adaptive manufacturing by means of cyber-physical system based matching. CIRP Ann. 2015, 64, 399–402. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, H.S. New concepts in specifications, operators and uncertainties. In Proceedings of the 8th CIRP International Seminar on Computer Aided Tolerancing—Managing Geometric Uncertainty in the Product Lifecycle, Charlotte, NC, USA, 28–29 April 2003; Wilhelm, R.G., Ed.; The University of North Carolina at Charlotte, The Center for Precision Metrology: Charlotte, NC, USA, 2003; pp. 1–6. [Google Scholar]
- Gröger, S. Qualifizierung der 3D-Koordinatenmesstechnik zur standardisierten Bildung von Bezügen und Bezugssystemen (3D-BBS); Technische Universität Chemnitz: Chemnitz, Germany, 2015. (In German) [Google Scholar]
- Li, Y.; Zhao, Y.; Yu, H.; Lai, X. Compliant assembly variation analysis of sheet metal with shape errors based on primitive deformation patterns. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 2334–2351. [Google Scholar] [CrossRef]
- Deutsches Institut für Normung, E.V. Geometrische Produktspezifikation (GPS)—Geometrische Tolerierung. Bezüge und Bezugssysteme; Deutsche Fassung: Berlin, Germany, 2011. (In German) [Google Scholar]
- Shakarji, C.M.; Srinivasan, V. Toward a new mathematical definition of datums in standards to support advanced manufacturing. In Proceedings of the ASME 13th International Manufacturing Science and Engineering Conference—2018, College Station, TX, USA, 18–22 June 2018; ASME: New York, NY, USA, 2018. ISBN 978-0-7918-5137-1. [Google Scholar]
- Weißgerber, M.; Keller, F. Datum systems in coordinate measuring technique. In Proceedings of the XIth International Science Conference Coordinate Measuring Technique, Bielsko-Biala, Poland, 2–4 April 2014; Sładek, J., Jakubiec, W., Eds.; University of Bielsko-Biala, Laboratory of Metrology: Bielsko-Biała, Poland, 2015; pp. 77–81, ISBN 9788363713881. [Google Scholar]
- Weißgerber, M.; Ebermann, M.; Gröger, S.; Leidich, E. Requirements for datum systems in computer aided tolerancing and the verification process. Procedia CIRP 2016, 43, 238–243. [Google Scholar] [CrossRef] [Green Version]
- Deutsches Institut für Normung, E.V. Geometrische Produktspezifikation (GPS)—Grundlagen—Teil 1: Modell für die Geometrische Spezifikation und Prüfung; Beuth: Berlin, Germany, 2012. (In German) [Google Scholar]
- Schleich, B.; Anwer, N.; Mathieu, L.; Wartzack, S. Skin model shapes: A new paradigm shift for geometric variations modelling in mechanical engineering. Comput. Des. 2014, 50, 1–15. [Google Scholar] [CrossRef]
- Wärmefjord, K.; Söderberg, R.; Lindau, B.; Lindkvist, L.; Lorin, S. Joining in nonrigid variation simulation. In Computer-Aided Technologies—Applications in Engineering and Medicine; Udroiu, R., Ed.; IntechOpen: Rijeka, Croatia, 2016; p. 42. [Google Scholar]
- Garcia, F.R. Tools for 3D Point Cloud Registration. Master’s Thesis, University of Girona, Girona, Spain, 2017. [Google Scholar]
- Jiang, P.; Zhou, Q.; Shao, X. Surrogate Model-Based Engineering Design and Optimization; Springer Nature: Singapore, 2020. [Google Scholar]
- Liying, W.; Weidong, S. A review of range image registration methods with accuracy evaluation. In Proceedings of the 2009 Joint Urban Remote Sensing Event, Shanghai, China, 20–22 May 2009. [Google Scholar]
- Schleich, B.; Wartzack, S. Approaches for the assembly simulation of skin model shapes. Comput. Aided Des. 2015, 65, 18–33. [Google Scholar] [CrossRef]
- Floery, S. Constrained Matching of Point Clouds and Surfaces. Master’s Thesis, Technische Universität Wien, Wien, Austria, 2010. [Google Scholar]
- Pierce, R.S.; Rosen, D. Simulation of mating between non-analytic surfaces using a mathematical programming formulation. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Long Beach, CA, USA, 24–28 September 2005; ASME: New York, NY, USA, 2005; pp. 179–188. [Google Scholar]
- Banerjee, A.; Chanda, A.; Das, R. Historical origin and recent development on normal directional impact models for rigid body contact simulation: A critical review. Arch. Comput. Methods Eng. 2016, 24, 397–422. [Google Scholar] [CrossRef]
- Shakarji, C.M.; Srinivasan, V. Theory and Algorithms for L1 Fitting Used for Planar Datum Establishment in Support of Tolerancing Standards. In Proceedings of the 2012 ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Portland, OR, USA, 4–7 September 2013; ASME: New York, NY, USA, 2013. [Google Scholar]
- Deutsches Institut für Normung, E.V. Geometrische Produktspezifikation (GPS)—Geometrische Tolerierung—Bezüge und Bezugssysteme; Beuth: Berlin, Germany, 2017. (In German) [Google Scholar]
- Samper, S.; Adragna, P.-A.; Favreliere, H.; Pillet, M. Modeling of 2D and 3D assemblies taking into account form errors of plane surfaces. J. Comput. Inf. Sci. Eng. 2009, 9, 041005. [Google Scholar] [CrossRef]
- Formosa, F.; Samper, S. Modal Expression of Form Defects. In Models for Computer Aided Tolerancing in Design and Manufacturing; Davidson Joseph, K., Ed.; Springer: Dordrecht, The Netherlands, 2007; pp. 13–22. [Google Scholar]
- Grandjean, J.; Ledoux, Y.; Samper, S. Influence of form errors in plane surface assemblies. In Proceedings of the MProVE 2011—International Conference on Innovative Methods in Product Design, Venice, Italy, 15–17 June 2011; pp. 516–520. [Google Scholar]
- Stachowiak, H. Allgemeine Modelltheorie; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar]
- Kastens, U.; Kleine Büning, H. Modellierung. Grundlagen und formale Methoden, 4., erweiterte Auflage; Hanser: Munich, Germany, 2018; ISBN 9783446455399. [Google Scholar]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidyanathan, R.; Tucker, P.K. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Dahlström, S.; Lindkvist, L. variation simulation of sheet metal assemblies using the method of influence coefficients with contact modeling. J. Manuf. Sci. Eng. 2007, 129, 615–622. [Google Scholar] [CrossRef]
- Grandjean, J. Influence des Défauts de Forme sur les Performances D’assemblages: Application aux Prothèses Totales de Hanche. Master’s Thesis, Université de Grenoble, Grenoble, France, 2013. (In French). [Google Scholar]
- Grandjean, J.; LeDoux, Y.; Samper, S. On the role of form defects in assemblies subject to local deformations and mechanical loads. Int. J. Adv. Manuf. Technol. 2012, 65, 1769–1778. [Google Scholar] [CrossRef]
- Corrado, A.; Polini, W. FEA integration in the tolerance analysis using skin model shapes. Procedia CIRP 2018, 75, 285–290. [Google Scholar] [CrossRef]
- Polini, W.; Corrado, A. Digital twin of composite assembly manufacturing process. Int. J. Prod. Res. 2020, 58, 5238–5252. [Google Scholar] [CrossRef]
- Falgarone, H.; Thiébaut, F.; Coloos, J.; Mathieu, L. Variation simulation during assembly of non-rigid components. realistic assembly simulation with anatoleflex software. Procedia CIRP 2016, 43, 202–207. [Google Scholar] [CrossRef]
- Liu, S.C.; Hu, S.J. variation simulation for deformable sheet metal assemblies using finite element Methods. J. Manuf. Sci. Eng. 1997, 119, 368–374. [Google Scholar] [CrossRef]
- Polini, W.; Corrado, A. Methods of influence coefficients to evaluate stress and deviation distribution of flexible assemblies—A review. Int. J. Adv. Manuf. Technol. 2020, 107, 2901–2915. [Google Scholar] [CrossRef]
- Andolfatto, L.; Thiébaut, F.; Douilly, M.; Lartigue, C. On neural networks’ ability to approximate geometrical variation propagation in assembly. Procedia CIRP 2013, 10, 224–232. [Google Scholar] [CrossRef]
- Hallmann, M.; Schleich, B.; Wartzack, S. From tolerance allocation to tolerance-cost optimization: A comprehensive literature review. Int. J. Adv. Manuf. Technol. 2020, 107, 4859–4912. [Google Scholar] [CrossRef]
- Tabar, R.S.; Wärmefjord, K.; Söderberg, R. A new surrogate model–based method for individualized spot welding sequence optimization with respect to geometrical quality. Int. J. Adv. Manuf. Technol. 2019, 106, 2333–2346. [Google Scholar] [CrossRef] [Green Version]
- Haefner, B.; Biehler, M.; Wagner, R.; Lanza, G. Meta-Model based on artificial neural networks for tooth root stress analysis of micro-gears. Procedia CIRP 2018, 75, 155–160. [Google Scholar] [CrossRef]
- Deutsches Institut für Normung E.V. Fertigungsverfahren Fügen; Beuth Verlag GmbH: Berlin, Germany, 2003. [Google Scholar]
- Mori, K. Joining processes by plastic deformation. Adv. Mater. Res. 2014, 966, 29–47. [Google Scholar] [CrossRef]
- Bouwman, M.B.; Donderwinkel, T.; Krämer, E.; Wijskamp, S.; Costa, F. Overmolding—An integrated design approach for dimensional accuracy and strength of structural parts. In Proceedings of the 3rd Annual Composites and Advanced Materials Expo. CAMX 2016—Composites and Advanced Materials Expo, Anaheim, CA, USA, 26–29 August 2016. [Google Scholar]
- Neugebauer, R.; Rössinger, M.; Wahl, M.; Schulz, F.; Eckert, A.; Schützle, W. Predicting dimensional accuracy of mechanically joined car body assemblies. Key Eng. Mater. 2011, 473, 973–980. [Google Scholar] [CrossRef]
- Neugebauer, R.; Bernhardi, O.; Wahl, M.; Schulz, F.; Mauermann, R.; Schützle, W.; Werner, S. Predicting dimensional accuracy of laser welded aluminum add-on body parts. Key Eng. Mater. 2013, 549, 463–470. [Google Scholar] [CrossRef]
- Spur, G. Handbuch Fügen, Handhaben und Montieren, 1st ed; Carl Hanser Fachbuchverlag: Munich, Germany, 2013; ISBN 3446428275. (In German) [Google Scholar]
- Kaufmann, M.; Effenberger, I.; Huber, M. Selective assembly strategy for quality optimization in a laser welding Process. In Proceedings of the Stuttgart Conference on Automotive Production (SCAP 2020); Weißgraeber, P., Heieck, F., Ackermann, C., Eds.; Springer Vieweg: Berlin/Heidelberg, Germany, 2021; ISBN 978-3-662-62962-8. [Google Scholar]
- ISO/IEC. Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995); Beuth: Berlin, Germany, 2008. [Google Scholar]
- Stylidis, K.; Bursac, N.; Heitger, N.; Wickman, C.; Albers, A.; Söderberg, R. Perceived quality framework in product generation engineering: An automotive industry example. Des. Sci. 2019, 5. [Google Scholar] [CrossRef] [Green Version]
- Besl, P.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Li, Q.; Huang, X.; Li, S.; Deng, Z. Feature extraction from point clouds for rigid aircraft part inspection using an improved Harris algorithm. Meas. Sci. Technol. 2018, 29, 115202. [Google Scholar] [CrossRef]
- Ahn, S.J.; Effenberger, I.; Roth-Koch, S.; Westkämper, E. Geometric segmentation and object recognition in unordered and incomplete point cloud. In Proceedings of the Pattern Recognition, 25th DAGM Symposium, Magdeburg, Germany, 10–12 September 2003; Michaelis, B., Krell, G., Eds.; Springer: Berlin, Germany, 2003; pp. 450–457, ISBN 978-3-540-40861-1. [Google Scholar]
- Ip, C.Y.; Gupta, S.K. retrieving matching cad models by using partial 3d point clouds. Comput. Des. Appl. 2007, 4, 629–638. [Google Scholar] [CrossRef] [Green Version]
- Yue, X.; Wen, Y.; Hunt, J.H.; Shi, J.; Hunt, J. Surrogate model-based control considering uncertainties for composite fuselage assembly. J. Manuf. Sci. Eng. 2018, 140, 041017. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Li, Z.-M.; Jin, S.; Chen, W. Compliant assembly analysis including initial deviations and geometric nonlinearity—Part I: Beam structure. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 233, 4233–4246. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modeling by registration of multiple range images. In Proceedings of the IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 2002; pp. 2724–2729. [Google Scholar]
- Gilbert, E.; Johnson, D.W.; Keerthi, S.S. A fast procedure for computing the distance between complex objects in three-dimensional space. IEEE J. Robot. Autom. 1988, 4, 193–203. [Google Scholar] [CrossRef] [Green Version]
- Kockara, S.; Halic, T.; Iqbal, K.; Bayrak, C.; Rowe, R. Collision detection: A survey. In Proceedings of the 2007 IEEE International Conference on Systems, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007; pp. 4046–4051. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaufmann, M.; Effenberger, I.; Huber, M.F. On the Development of a Surrogate Modelling Toolbox for Virtual Assembly. Appl. Sci. 2021, 11, 1181. https://doi.org/10.3390/app11031181
Kaufmann M, Effenberger I, Huber MF. On the Development of a Surrogate Modelling Toolbox for Virtual Assembly. Applied Sciences. 2021; 11(3):1181. https://doi.org/10.3390/app11031181
Chicago/Turabian StyleKaufmann, Manuel, Ira Effenberger, and Marco F. Huber. 2021. "On the Development of a Surrogate Modelling Toolbox for Virtual Assembly" Applied Sciences 11, no. 3: 1181. https://doi.org/10.3390/app11031181
APA StyleKaufmann, M., Effenberger, I., & Huber, M. F. (2021). On the Development of a Surrogate Modelling Toolbox for Virtual Assembly. Applied Sciences, 11(3), 1181. https://doi.org/10.3390/app11031181






