Failure Analysis for Hydraulic System of Heavy-Duty Machine Tool with Incomplete Failure Data

Abstract

A hydraulic system is a key subsystem of heavy-duty machine tools with a high failure intensity, the failure of which often causes shutdown of production and economic loss in machining. Therefore, it is necessary to implement failure analysis to identify the weak links of system and improve the reliability. For hydraulic system, there is often an amount of failure data collected in field, which help to calculate the occurrence probability of basic events through fault tree analysis method. However, the data are incomplete and uncertain. To address this issue, this study presents a fault tree analysis methodology. Experts’ opinions are utilized, combined with field data based on the Dempster–Shafer theory and rough set theory to fill the incompleteness and eliminate the uncertainty. For application in a case study, a fault tree of the hydraulic system of heavy-duty machine tools is firstly constructed. Then, the importance analysis is performed to help identify the weak links of hydraulic system. The results show the critical basic events affecting the safety and reliability of a hydraulic system.

1. Introduction

Heavy-duty CNC machine tools (HCMTs) are responsible for the manufacturing of parts related to major pillar industries and national key projects [1,2,3] in fields of aerospace, marine, hydraulic engineering, metallurgy, energy, rail transit, etc. Among subsystems of HCMT, the hydraulic system plays a key role in the power transmission and control of HCMT [4], the failure frequency of which also accounts for the largest proportion [5]. The parts scrap or production accidents caused by hydraulic failure from seals [6], pipes, valves, and so on will lead to enormous waste, because HCMTs are mainly used to process large-scale and expensive parts [7]. Therefore, to avoid unnecessary waste and maintain the machine manufacturing sustainably, it is necessary to analyze the failure of hydraulic systems to find their weaknesses for reliability growth or for creating a maintenance strategy of HCMT.

Fault Tree Analysis (FTA) is a systematic approach that identifies weaknesses, evaluates possible upgrades, and monitors and predicts behavior and has been used in various areas [8,9,10,11], such as nuclear, electric power, aerospace, oil and gas transmission, etc. Thus far, researchers have applied the FTA method for reliability analyses of machine tool products [12,13,14,15,16]. They constructed fault trees of different kinds of machine tool products and minimal cut sets were obtained. Analyses of these fault trees are only performed on a qualitative level. The importance measure of a basic event (BE) cannot be mathematically calculated on a quantitative level [17], which helps to determine which components or parts of the system are more critical for risk management and decision making.

As a complex system with mechanisms, electronics and hydraulics, the BEs in the fault tree of hydraulic system are generally described as failure modes, regardless of the components, due to its complexity and the large number of components [18]. In addition, the hydraulic system of HCMT manifests a high failure rate. This means a certain amount of failure data can be collected on field. This corresponds well to the failure modes and also provide useful information for measuring the importance of BEs. Shen [19] constructed a fault tree for tool storage of machining center on a quantitative level and obtained an importance measure of BEs using failure data. In [20,21], the failure rate and importance measure of BEs were obtained through quantitative analysis of hydraulic system of excavator; the weakest components were identified. However, the result of quantitative analysis using field data only is questionable in the application of an HCMT hydraulic system because the data are always incomplete in practice, which is reflected in the following two cases: (a) The causes of some failures are uncertain. There may be several BEs jointly causing one failure, but the contribution weight of each BE cannot be determined. We call this a Type I problem for convenience. (b) The occurrence probabilities of some BEs are too low so that there is a lack of observed data in some cases, in which it is difficult to determine the occurrence probability in an objective manner. We call this a Type II problem. To handle imprecise and insufficient failure information of a system, researchers have applied fuzzy theory with expert judgement to define the events’ probabilities [22,23]. Mi [24] utilized fuzzy theory to qualify the uncertainty of basic events and applied it to a CNC hydraulic system. The application of fuzzy fault tree can also be found in the hydraulics of other machineries. Ren [25] obtained the importance degree of BEs for hydraulic system of A-frame launch and recovery system for the “Jiaolong” manned submersible from expert experiences by applying fuzzy theory, Li [26] proposed a fuzzy dynamic fault tree model to assess the probability of failure events in the absence of failure data. Li [27] used triangular fuzzy numbers to describe the probability of BEs in the fault tree of hydraulic system of Anchor Drilling Rigs. Zhang [28] performed quantitative analysis of hydraulic system based on a T-S fuzzy model. However, the selection of membership function in these researches is usually subjectively determined based on the engineers’ experience and intuition, which is a challenge for a hydraulic system of HCMT due to its complex composition [29,30]. Moreover, the information contained in failure data is precious and should not be ignored. The fusion of failure information and experts’ opinions is necessary.

This study aims at making the FTA results accurate for a hydraulic system of HCMT with incomplete failure data. Experts’ opinions are utilized in combination with field data to address the above issue. First, the collected failure data are used to preliminarily calculate the frequency of BEs. Next, in dealing with a Type I problem, the weight of each possible BE, which commonly leads to one failure, is evaluated using the Dempster–Shafer evidence theory to correct the probability obtained in the first step. In dealing with a Type II problem, the probability interval of BEs that lacks data is also estimated by experts using the rough set theory. The rest of this paper is organized as follows. Section 2 proposes the method based on the Dempster–Shafer theory and rough set theory to combine failure data and experts’ opinions. In Section 3, the proposed approach is applied in a case study to perform the final importance analysis of hydraulic system of HCMT. Finally, the results are summarized in Section 4.

2. Fault Tree Analysis Method Combining Incomplete Failure Data and Experts’ Opinions

The procedures of hydraulic system FTA can be given as follows:

• Model definition: System description, confirm the components of equipment, problem identification.
• Hazard analysis: Obtain the failure mode for components of the system.
• Fault tree construction: Identify the top event, Bes, and sub-events, then build up a fault tree according to the logical relationship.
• Qualitative analysis: Obtain the minimal cut sets.
• Quantitative analysis: Calculate the frequencies of BEs using failure data, then calculate the occurrence and importance measure of BEs.
• Risk assessment and control: Make decisions based on the results of the analysis and improve the reliability of the system.

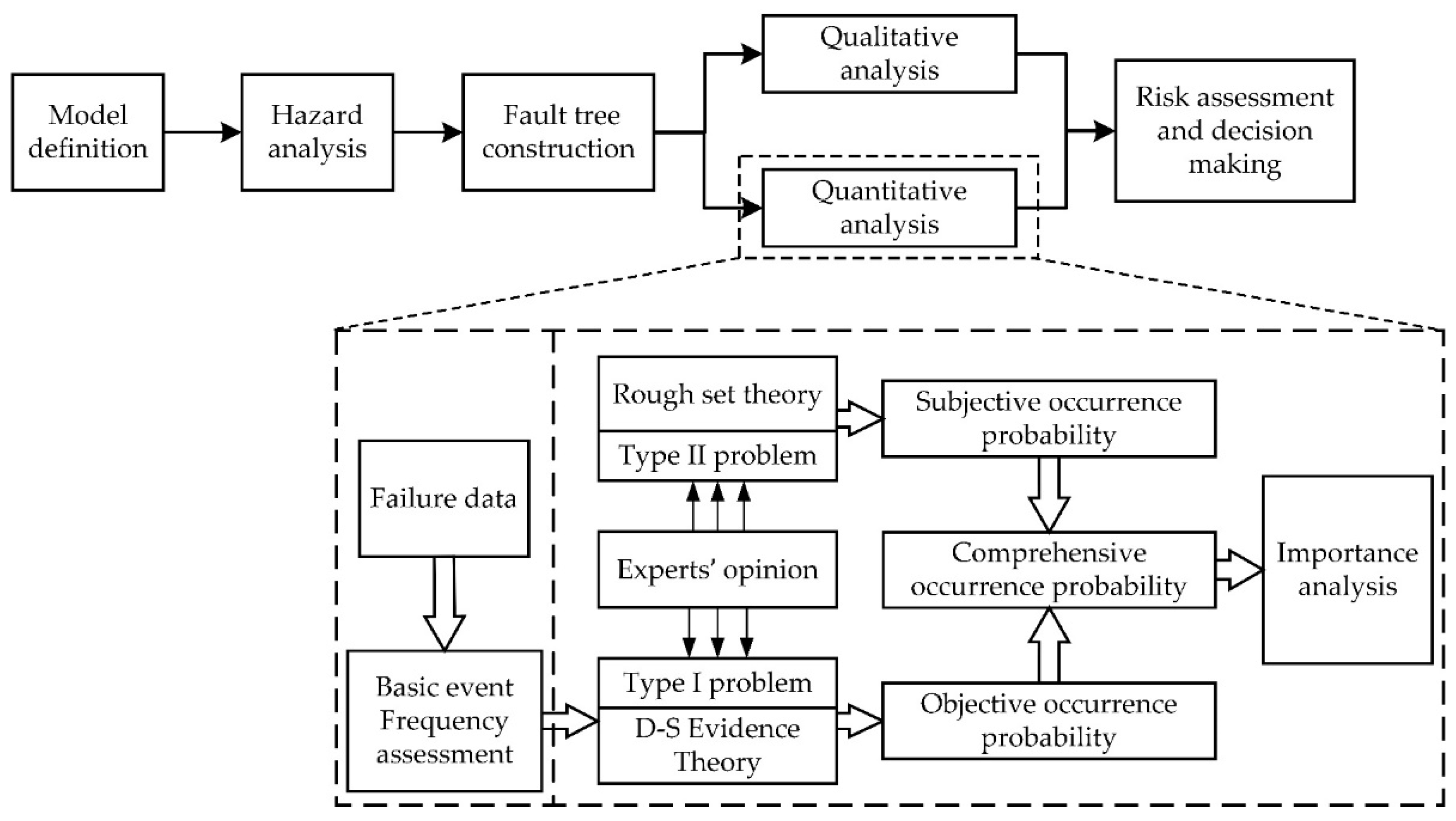
Due to Type I and Type II problems, the results of quantitative analysis just using field data are inaccurate using a conventional FTA method. Therefore, this study focuses on improving the quantitative analysis step; the framework of fault tree qualitative analysis is shown in Figure 1. The quantitative analysis, including the occurrence probability calculation of BEs and importance analysis, will be described in detail in the next body.

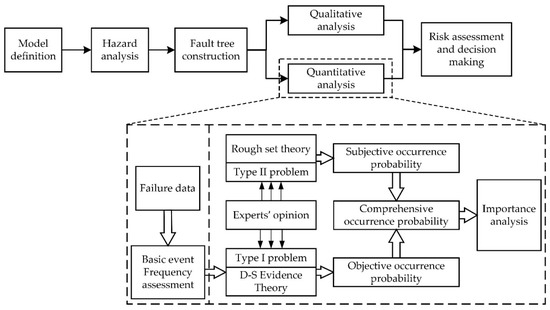
Figure 1. The framework of FTA for the hydraulic system of HCMT.

2.1. Occurrence Calculation

2.1.1. Objective Occurrence Calculation Based on the Dempster–Shafer Evidence Theory

Like conventional FTA, failure data are first preprocessed to calculated the frequencies of BEs. For data with Type I problem, experts’ opinions are needed to assign probability weights to all BEs that may cause the failure. The results might vary depending on measurement precision or the uncertainty in statements of experts. The Dempster–Shafer evidence theory (D-S theory) [31] is a mathematical theory of evidence developed to combine information supplied by different experts or from other sources. It performs well in dealing with uncertain information. Therefore, an approach of processing a Type I problem based on the D-S theory is given as the following steps:

Let X = {X₁, X₂, …, X_q} denote the BE set obtained through fault tree construction, where X_i (i = 1, …, q) is the ith BE. Step 1 is a frequency assessment based on failure data: analyze the failure data with clear causes. Trace the source and find all possible BEs causing the failure, then calculate the frequencies.

Step 2: From this step, failure data with a Type I problem is processed: for a single failure with an uncertain cause, a group of experts (E₁, …, E_m) determine all possible BEs that can cause the failure, which are expressed as (D₁, …, D_s), to establish the frame of discernment, symbolized by D = (D₁, …, D_s), with D_i ∈ X and D ⊆ X.

P(D) is denoted as the power set composed of 2^D elements of D; each element of 2^D represents a proposition. A mass assignment to each subset of P(D) is known as the basic probability assignment (BPA) M. If A₁, …, A_n are the sets of interest with A_j ∈ P(D), then a BPA is defined as:

$$M:P\left(D\right)\to \left[0,1\right], {\displaystyle \sum _{j=1}^{n}M\left(A_j\right)}=1, M(\varnothing )=0$$

(1)

Step 3: Experts determine all possible combinations of D₁, …, D_s, which are expressed as A₁, …, A_n, as focal elements of the frame of discernment. It shows that A_j ⊆ D (j = 1, …, n). Next, the assessment of each focal element is provided by each expert, as shown in Table 1, where M_k(A_j) (j = 1, …, n; k = 1, …, m) is the BPA provided by expert E_k on the assessment of A_j.

Table 1. The BPA value assigned by experts.

Focal Element	Expert E1	Expert E2	…	Expert Em
A1	M1(A1)	M2(A1)	…	Mm(A1)
A2	M1(A2)	M2(A2)	…	Mm(A2)
…	…	…	…
An	M1(An)	M2(An)	…	Mm(An)

Step 4: Evidence combination: if the evidence shows agreement, combine it with Dempster’s combination rule as follows:

$$\{\begin{array}{l}M\left(A\right)=\{\begin{array}{cc}\frac{{\displaystyle \sum _{\cap A_j^{}=A}^{}{\displaystyle \prod _{k=1}^m{M}_k}\left(A_j^{}\right)}}{1-K},& A\ne \varnothing ,A\subseteq D\hfill \\ 0,\hfill & A=\varnothing ,A\subseteq D\hfill \end{array}\\ K={\displaystyle \sum _{\cap A_j^{}=\varnothing }^{}{\displaystyle \prod _{k=1}^m{M}_k}\left(A_j^{}\right)}\end{array}$$

(2)

When evidence highly conflicts with each other, the above combination rule is not efficient; thus, a new combination rule [32] for conflict evidence is introduced as Equation (3):

$$\{\begin{array}{l}M\left(A\right)=\{\begin{array}{cc}\frac{{\displaystyle \sum _{A_i^{}\cap A_j^{}=A}^{}\left({\displaystyle \sum _{k=1}^m{M}_k\left(A_i^{}\right)}\right)\left({\displaystyle \sum _{l=1}^m{M}_l\left(A_j^{}\right)}\right)}}{m^2-K},& A\ne \varnothing ,A\subseteq D\hfill \\ 0,\hfill & A=\varnothing ,A\subseteq D\hfill \end{array}\\ K={\displaystyle \sum _{A_i^{}\cap A_j^{}=\varnothing }^{}\left({\displaystyle \sum _{k=1}^m{M}_k\left(A_i^{}\right)}\right)\left({\displaystyle \sum _{l=1}^m{M}_l\left(A_j^{}\right)}\right)}\end{array}$$

(3)

where K is the conflict coefficient and m is the amount of evidence in the frame of discernment D. Then, the aggregated assessment of focal elements with respect to each BPA can be calculated by the combination rule, a group assessment matrix M is constructed as M = [M(A₁), M(A₂), …, M(A_t)].

Step 5: Calculate the belief and plausibility function of D_i, which are defined as follows:

$$\{\begin{array}{l}Bel\left(D_i\right)={\displaystyle \sum _{A_j\subseteq D_i}M\left(A_j\right)}\\ Pl\left(D_i\right)={\displaystyle \sum _{A_j\cap D_i\ne \varnothing }M\left(A_j\right)}& , D_i\subseteq D\hfill \end{array}$$

(4)

The results of the belief and plausibility function of D_i compose the frequency interval, as shown in Table 2.

Table 2. Frequency interval of D_i.

Combination	D1	D2	…	Ds
Frequency interval	[Bel(D1), Pl(D1)]	[Bel(D2), Pl(D2)]	…	[Bel(Ds), Pl(Ds)]

Step 6: Merge the results in Table 2 with the frequency of corresponding BEs obtained in Step 1.

Repeat Step 2 to Step 6 until all data with Type I problem are processed. Additionally, the mass has to be normalized, because experts tend to ignore the restriction in Equation (1). The final result, $P_{{\mathrm{X}}_i}^1$, is normalized by Equation (5) and defined as the objective occurrence probability of BE X_i, which represents the occurrence probability calculated by solving a Type I problem:

$$P_{{\mathrm{X}}_i}^1=\frac{\left[N_{{\mathrm{X}}_i}^{-},N_{{\mathrm{X}}_i}^{+}\right]}{N}$$

(5)

where N denotes the number of failures and $\left[N_{{\mathrm{X}}_i}^{-},N_{{\mathrm{X}}_i}^{+}\right]$ is the merged frequency interval of X_i.

2.1.2. Subjective Occurrence Estimation Based on Rough Set Theory

For BEs with a Type II problem, human judgments become an essential requirement. Hence, experts’ opinions are also introduced to estimate the occurrence probability. Unlike fuzzy set theory, which defines a set by a partial membership without a clear boundary, the rough set theory utilizes the boundary region of a set to express vagueness. Additionally, there is no need for it to require additional subjective information to analyze data [33], which remains objective. The steps of subjective occurrence estimation based on rough set theory are proposed as follows [34]:

Step 1: Define the problem. Find all possible BEs with insufficient failure data to form a set T as T = {T₁, T₂,...., T_p}, where T_i is the ith BE with Type II problem, T_i ∈ X, I = 1, …, p.

Assume there are three experts, including designers F₁, maintainers F₂, and users F₃, which give an estimation of the occurrence of each BE, which is expressed by the interval rough number, as shown in Table 3, where ${\xi }_{ij}=\left(\left[a_{ij},b_{ij}\right],\left[c_{ij},d_{ij}\right]\right)$, c_ij < a_ij < b_ij < d_ij, indicating the occurrence of T_i given by expert F_j, j = 1, 2, 3.

Table 3. Estimation of occurrence given by experts.

BE	Designers F1	Maintainers F2	Users F3
T1	ξ11	ξ12	ξ13
T2	ξ21	ξ22	ξ23
…	…	…	…
Tp	ξp1	ξp2	ξp3

Step 2: Determine the expert weight.

When determining the weight of each expert, the influence of expert risk preferences is considered and reflected by the distance between the expert estimation and its positive and negative ideal point.

(1) Determine the positive and negative ideal point: For expert F_j, the positive ideal point is defined as the maximum estimation of the occurrence of all T_i by Equation (6), while the negative ideal point is defined as the minimum estimation of the occurrence of all T_i by Equation (7):

$${\xi }_j^{+}=\left(\left[\underset{i}{\max }{a}_{ij},\underset{i}{\max }{b}_{ij}\right],\left[\underset{i}{\max }{c}_{ij},\underset{i}{\max }{d}_{ij}\right]\right)$$

(6)

$${\xi }_j^{-}=\left(\left[\underset{i}{\min }{a}_{ij},\underset{i}{\min }{b}_{ij}\right],\left[\underset{i}{\min }{c}_{ij},\underset{i}{\min }{d}_{ij}\right]\right)$$

(7)

(2) Calculate the distance between the occurrence estimation and its positive and negative ideal point by Equations (8) and (9), respectively:

$$d_{ij}^{+}=d\left({\xi }_{ij},{\xi }_j^{+}\right)$$

(8)

$$d_{ij}^{-}=d\left({\xi }_{ij},{\xi }_j^{-}\right)$$

(9)

where for interval rough number ${\xi }_1=\left(\left[a_1,b_1\right],\left[c_1,d_1\right]\right)$ and ${\xi }_2=\left(\left[a_2,b_2\right],\left[c_2,d_2\right]\right)$, the operator d(•) is defined as follows:

$$d\left({\xi }_1,{\xi }_2\right)=\sqrt{\frac{{\left(a_1-a_2\right)}^2+{\left(b_1-b_2\right)}^2+{\left(c_1-c_2\right)}^2+{\left(d_1-d_2\right)}^2}{4}}$$

(10)

(3) The risk preference coefficient is fused into the above distances to produce a new distance, called the preference distance, which represents the difference in the subjective assessment of different types of experts. The preference distance is defined as follows:

$$d_{ij}^{}=\tau d_{ij}^{+}+(1-\tau )d_{ij}^{-}$$

(11)

where τ is the risk preference coefficient. If the expert is a risk liker, then τ > 0.5; if the expert is neutral, then τ = 0.5; if the expert is a risk evader, then τ < 0.5.

(4) The entropy weight method is adopted in determination of the expert weight by Equation (12):

$$\{\begin{array}{l}{e}_j^{}=-\frac{1}{\ln p}{\displaystyle \sum _{i=1}^p\frac{d_{ij}}{{\displaystyle \sum _{i=1}^p{d}_{ij}}}}\cdot \ln \frac{d_{ij}}{{\displaystyle \sum _{i=1}^p{d}_{ij}}}\\ w_j^{}=\frac{1-e_j^{}}{{\displaystyle \sum _{j=1}^3\left(1-e_j^{}\right)}}\end{array}$$

(12)

where e_j is the distance entropy for expert F_j, w_j is the weight of expert F_j, with j = 1, 2, 3, 0≤ w_j ≤1, and ${\displaystyle \sum _{j=1}^3{w}_j}=1$.

Step 3: Calculate the utility value of each interval rough number and its expectation:

$$u_i^{}={\displaystyle \sum _{j=1}^3{\xi }_{ij}}{w}_j,i=1,2,\cdots ,p$$

(13)

$$P_{T_i}^2=E\left[u_i\right]$$

(14)

where the expectation is calculated as $E\left[\xi \right]=\frac{1}{4}\left(a+b+c+d\right)$ for $\xi =\left(\left[a,b\right],\left[c,d\right]\right)$.

The final result, $P_{T_i}^2$, is defined as the subjective occurrence of T_i, which represents the occurrence probability estimated by solving a Type II problem.

2.1.3. Fusion of the Objective Occurrence and Subjective Occurrence

After calculating the objective and subjective occurrence, the results need to be combined. Denote the objective occurrence vector as $P_{{\mathrm{X}}_i}^1=\left[P_{{\mathrm{X}}_1}^1,P_{{\mathrm{X}}_2}^1,\cdots ,P_{{\mathrm{X}}_q}^1\right]$ and the subjective occurrence vector as $P_{{\mathrm{X}}_i}^2=\left[P_{{\mathrm{X}}_1}^2,P_{{\mathrm{X}}_2}^2,\cdots ,P_{{\mathrm{X}}_q}^2\right]$, where $P_{{\mathrm{X}}_i}^1=0$ for X_i that is not involved in a Type I problem, and $P_{{\mathrm{X}}_i}^2=0$ for X_i that is not involved in a Type II problem.

Combine and normalize the two occurrences by Equation (15):

$$P_{{\mathrm{X}}_i}^{}=\frac{P_{{\mathrm{X}}_i}^1+P_{{\mathrm{X}}_i}^2}{{\displaystyle \sum _{i=1}^q\left(P_{{\mathrm{X}}_i}^1+P_{{\mathrm{X}}_i}^2\right)}}$$

(15)

The final result, $P_{{\mathrm{X}}_i}^{}$, is defined as the comprehensive occurrence. Since the objective occurrence is in the form of an interval, the result after its fusion with subjective occurrence is still an interval, i.e., $P_{{\mathrm{X}}_i}^{}=\left[P_{{\mathrm{X}}_i}^{-},P_{{\mathrm{X}}_i}^{+}\right]$, where:

$$P_{{\mathrm{X}}_i}^{-}=\frac{P_{{\mathrm{X}}_i}^{1-}+P_{{\mathrm{X}}_i}^2}{{\displaystyle \sum _{i=1}^q\left(P_{{\mathrm{X}}_i}^{1+}+P_{{\mathrm{X}}_i}^2\right)}},P_{{\mathrm{X}}_i}^{+}=\frac{P_{{\mathrm{X}}_i}^{1+}+P_{{\mathrm{X}}_i}^2}{{\displaystyle \sum _{i=1}^q\left(P_{{\mathrm{X}}_i}^{1-}+P_{{\mathrm{X}}_i}^2\right)}}$$

(16)

2.2. Importance Analysis

An important analysis can help identify which BEs are critical and need to be improved; it is useful for decision making. In this study, the probability importance is employed to evaluate the contribution of each BE to the occurrence probability of top event, which is expressed as follow:

$$I_{{\mathrm{X}}_i}^g={\displaystyle \prod _{j=1,i\ne j}^n\left(1-P_{{\mathrm{X}}_j}\right)}$$

(17)

where $I_{{\mathrm{X}}_i}^g$ is the probability importance of X_i.

For the comprehensive occurrence probability in the form of an interval, the corresponding probability importance is still an interval, which is $I_{{\mathrm{X}}_i}^g=\left[I_{{\mathrm{X}}_i}^{g-},I_{{\mathrm{X}}_i}^{g+}\right]$, where:

$$I_{{\mathrm{X}}_i}^{g-}={\displaystyle \prod _{j=1,i\ne j}^q\left(1-P_{{\mathrm{X}}_j}^{+}\right)},I_{{\mathrm{X}}_i}^{g+}={\displaystyle \prod _{j=1,i\ne j}^q\left(1-P_{{\mathrm{X}}_j}^{-}\right)}$$

(18)

Therefore, the ranking of importance is essentially the ranking of interval numbers. A ranking rule based on possibility degree matrix for interval numbers is introduced [35]; the steps are as follows:

Step 1: Establish the possibility matrix $P={\left(p_{ij}\right)}_{q\times q}$ (i, j=1, …, q), using the possibility formula as follows:

$$I_{{\mathrm{X}}_i}^g={\displaystyle \prod _{j=1,i\ne j}^n\left(1-P_{{\mathrm{X}}_j}\right)}$$

(19)

Step 2: Construct a Boolean matrix $Q={\left(q_{ij}\right)}_{q\times q}$, where:

$$q_{ij}=\{\begin{array}{cc}1,& p_{ij}\ge 0.5\hfill \\ 0,& p_{ij}<0.5\hfill \end{array}$$

(20)

Step 3: Sum the Boolean matrix in rows; the results are as follows:

$$R_i={\displaystyle \sum _{j=1}^q{q}_{ij}}i=1,2,\cdots ,q$$

(21)

Step 4: Order the probability importance according to the size of R_i.

After the above steps are completed, the probability importance ranking of each BE is obtained and used for subsequent safety assessment and decision making.

3. A Case Study

The proposed method is applied to fault tree analysis for the hydraulic system of heavy horizontal lathe and heavy gantry boring and milling machine in a factory, which are two typical HCMTs. After more than 12 months of field tracking (over 2000 h in total), a total of 143 hydraulic related failure data of heavy-duty horizontal lathe and 88 hydraulic related failure of heavy gantry boring and milling machines were collected, which were recorded according to the Chinese national standard GB/T 23567.1. Failure data contain information including failure time, failure position, failure symptoms, maintenance time, and maintenance mode. For the sake of convenience, the failure data were combined for analysis, because the hydraulic systems of the two types of HCMT are similar in structure and configuration.

3.1. Fault Tree Construction

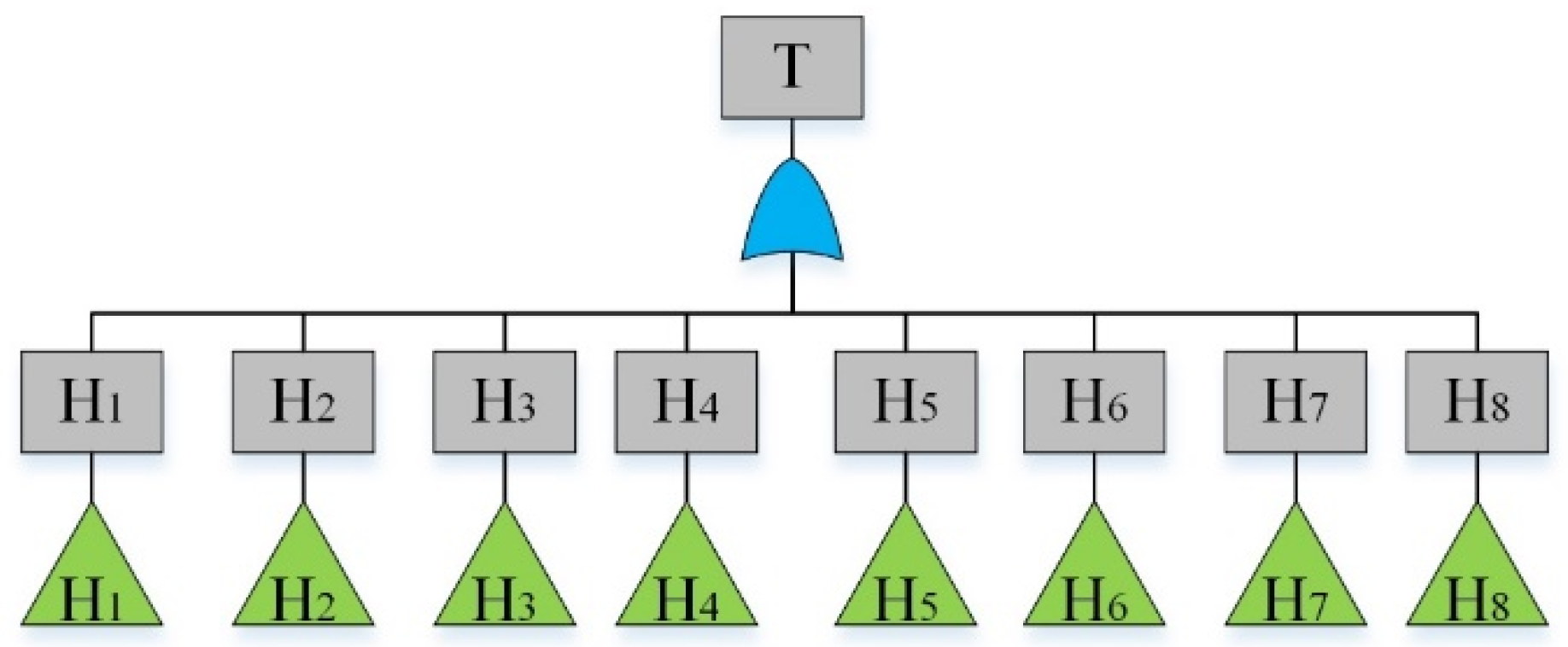
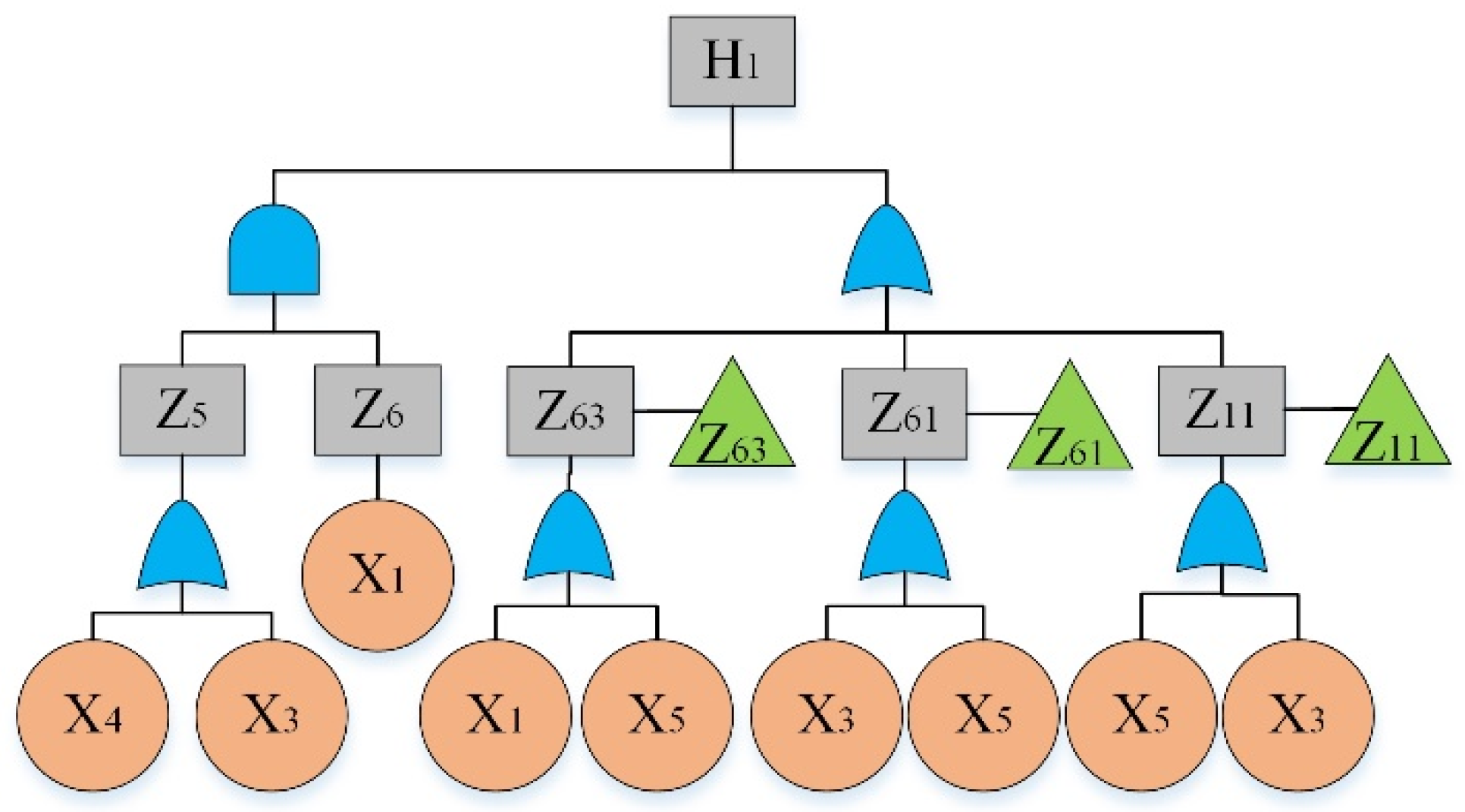
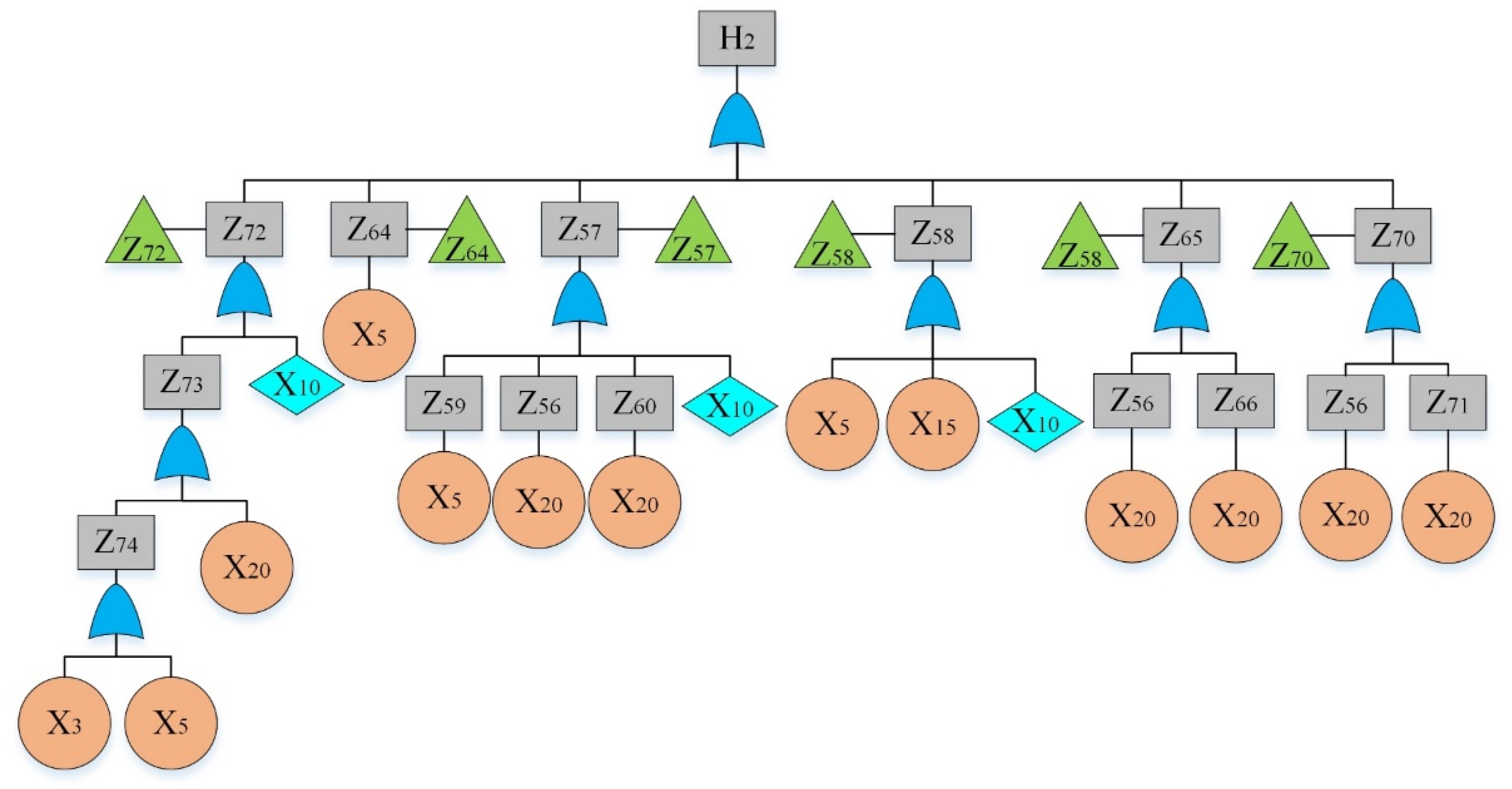
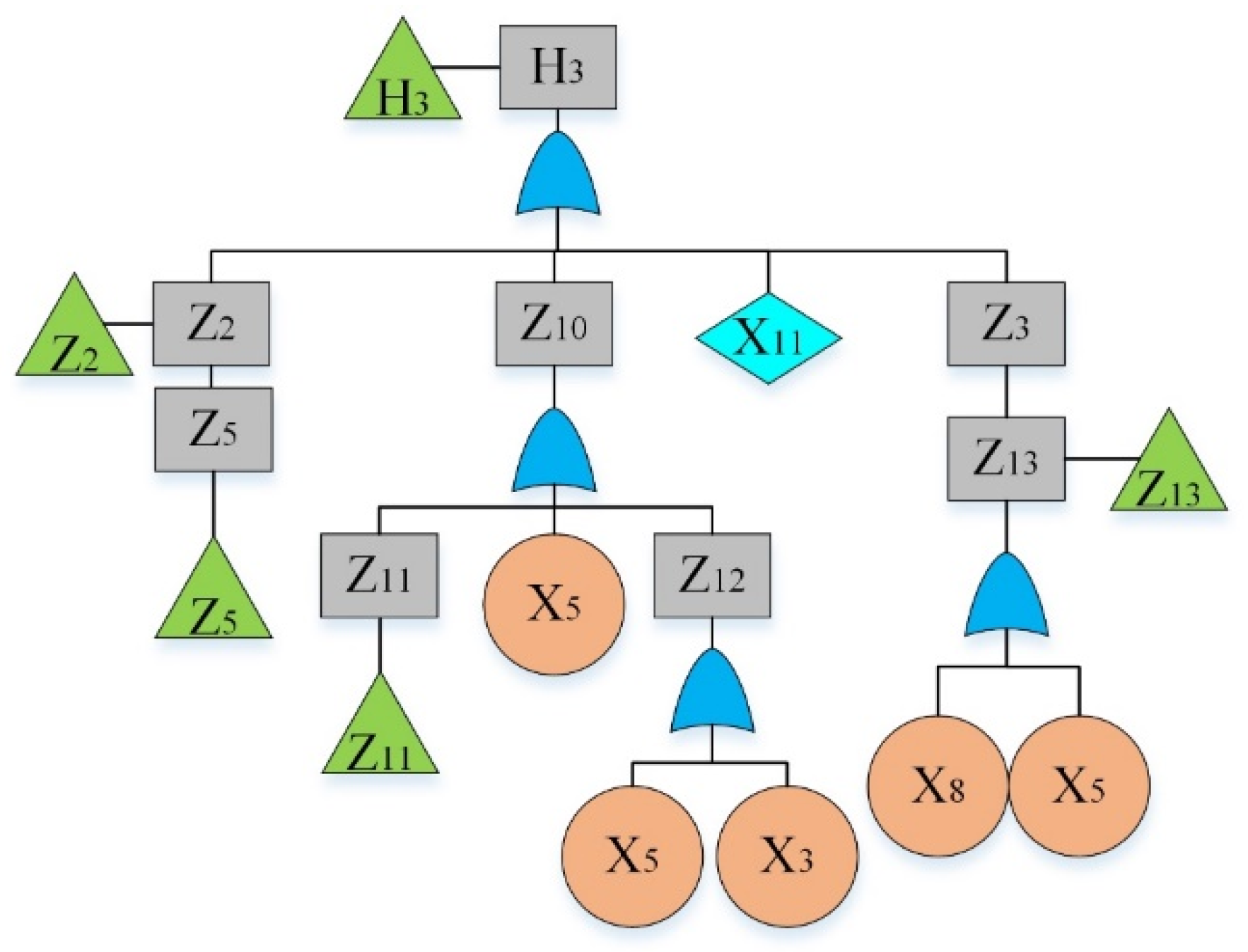
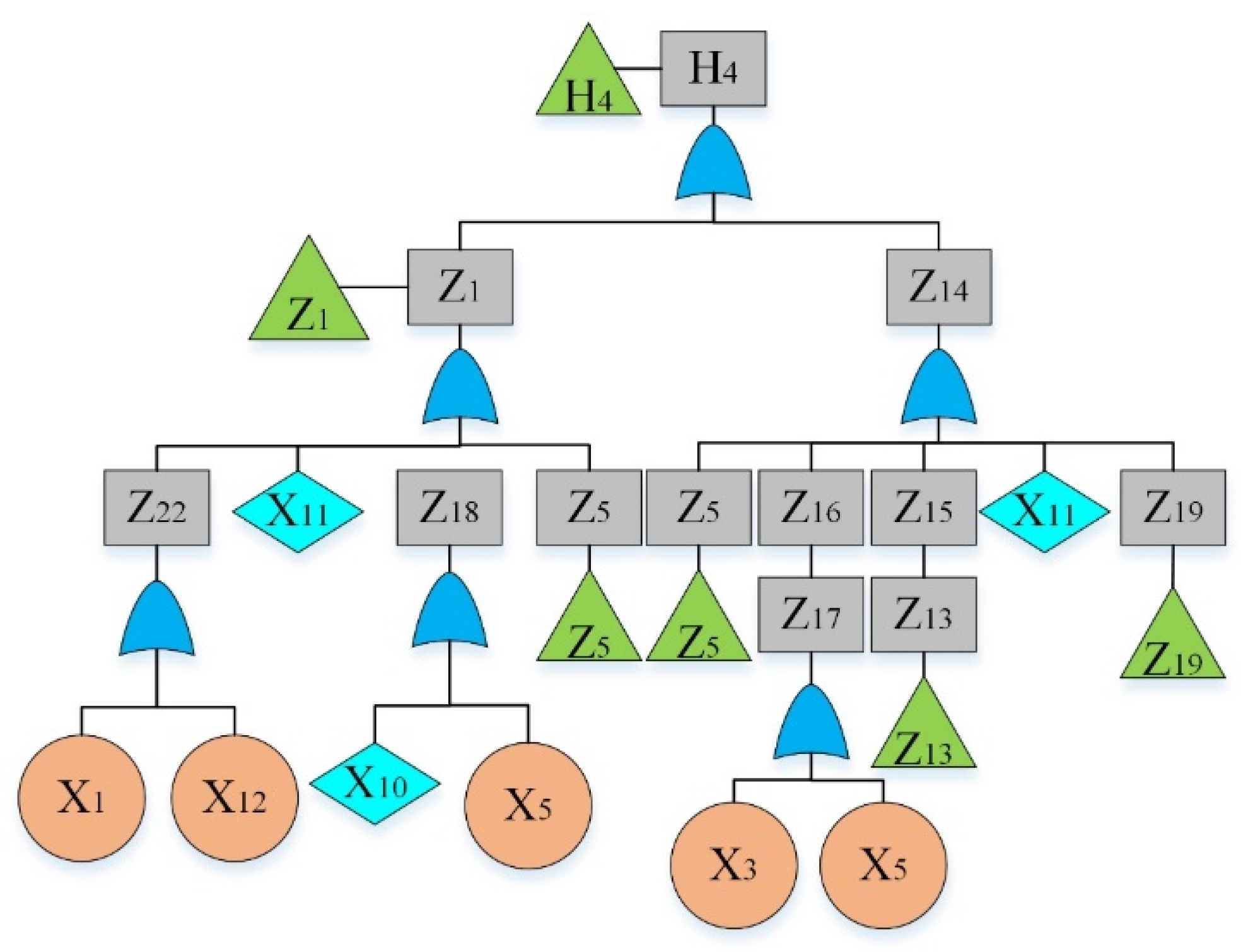
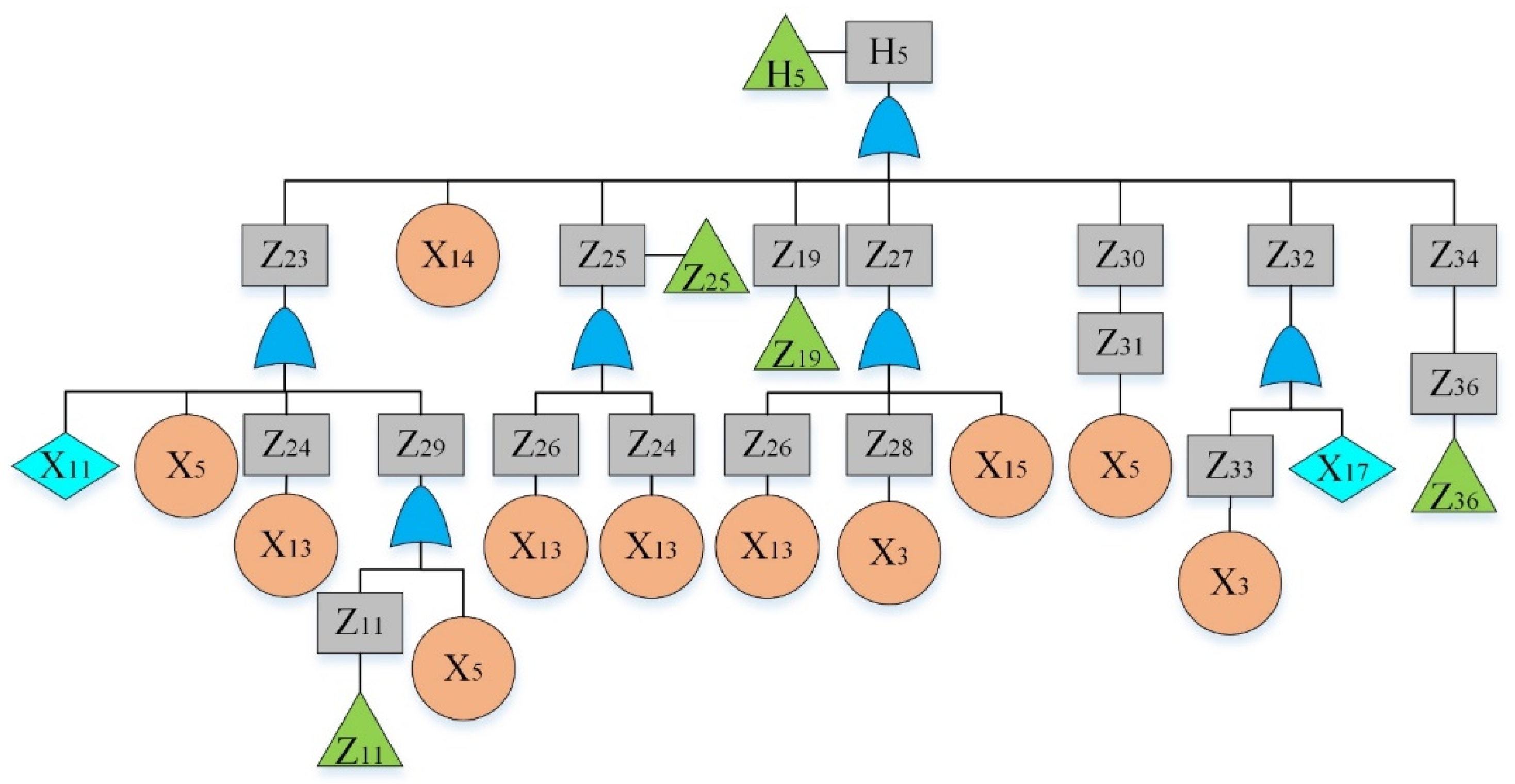
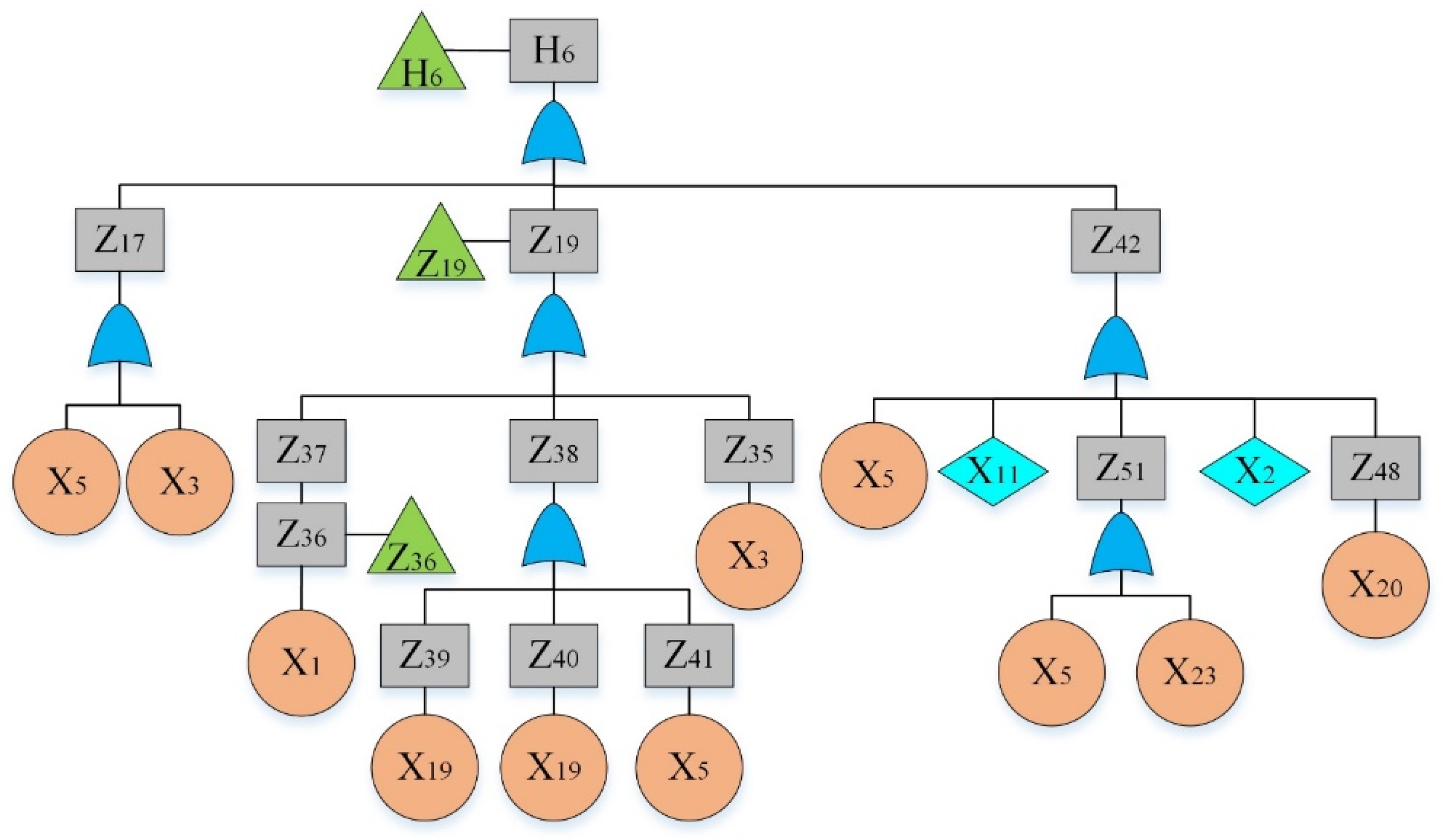
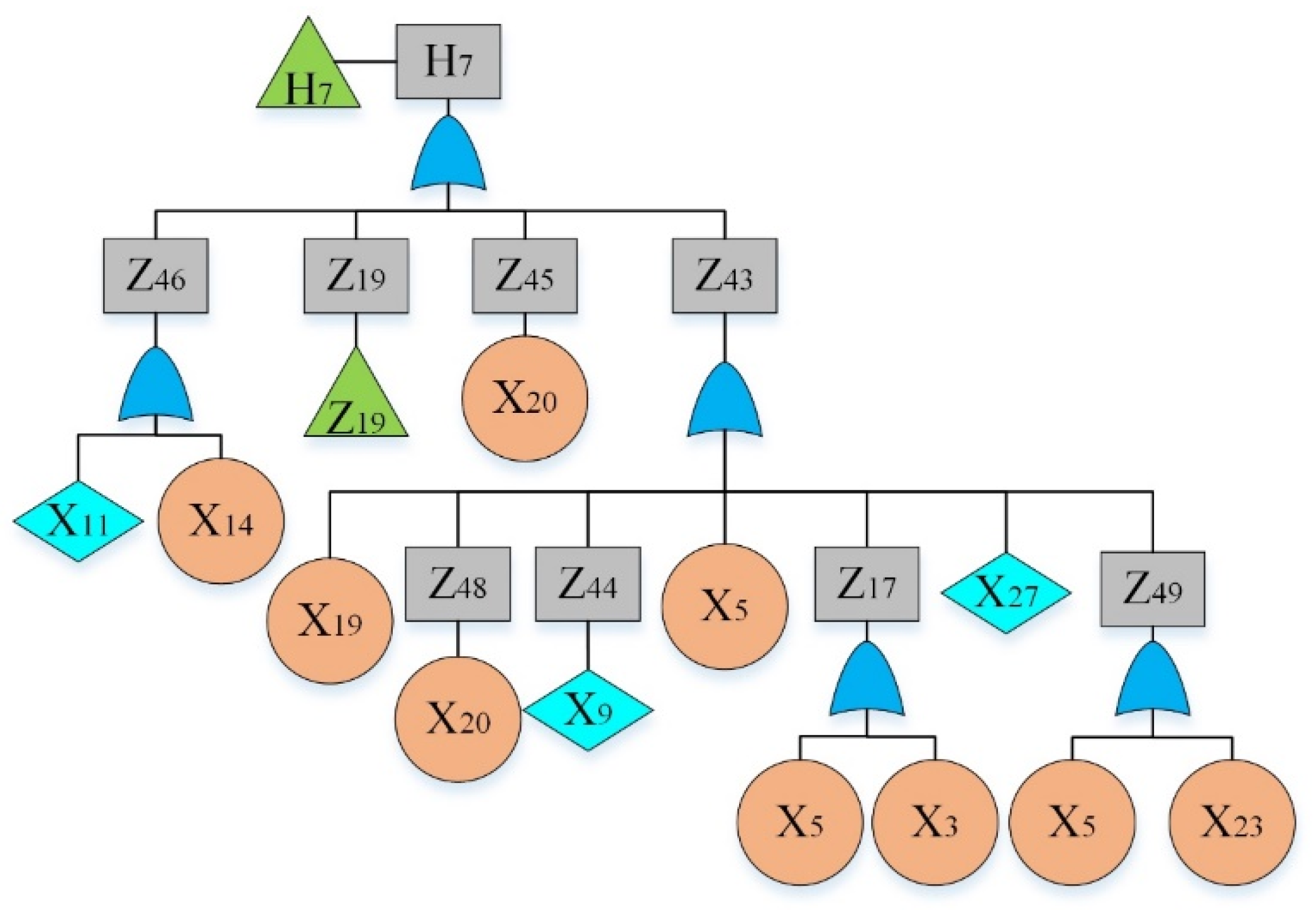
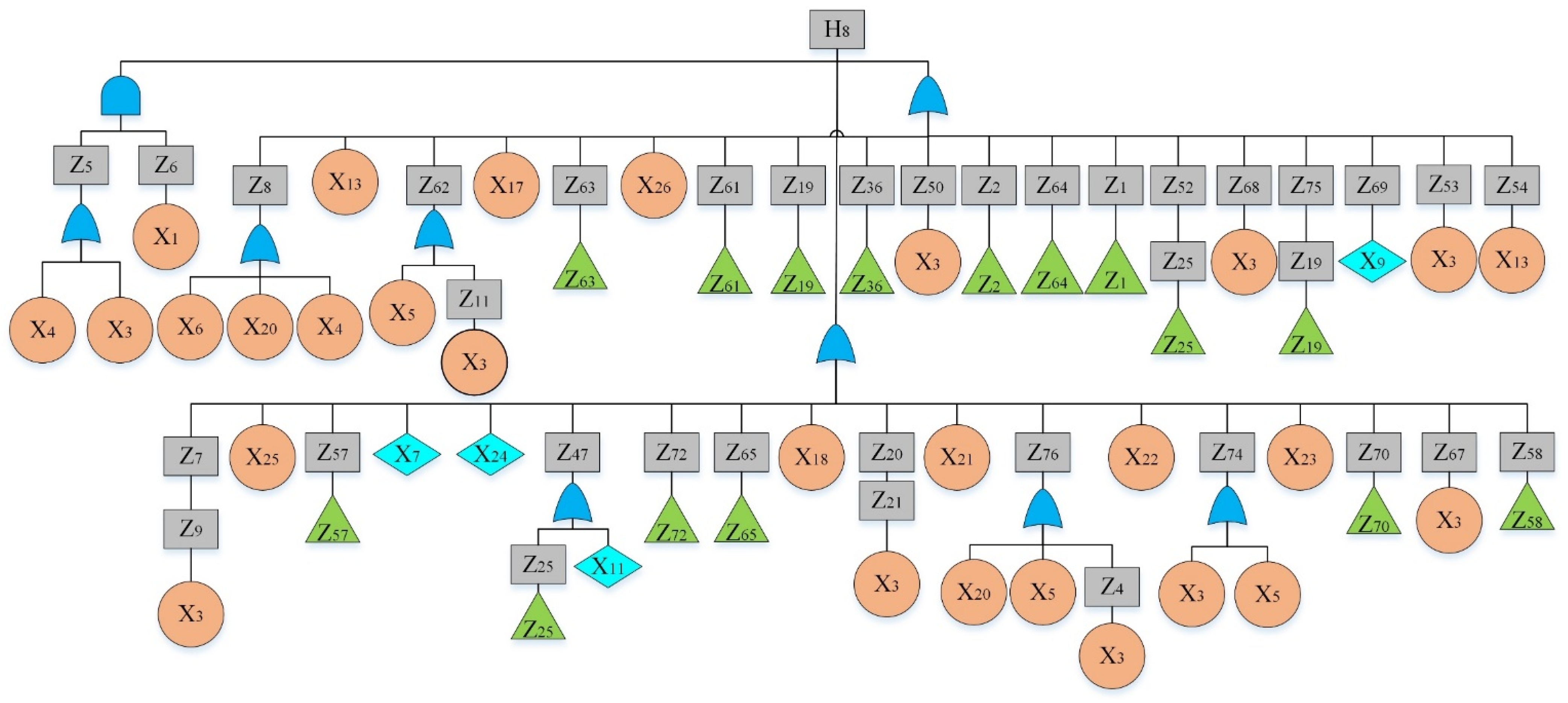
By analyzing the failure data, “The hydraulic system of HCMT cannot work” was considered as the top event. By reviewing previous hazard records [36] and using the experts’ opinions, main sub-event failures were determined and given in Table 4. The fault tree is constructed and shown in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, where Figure 2 is the main tree and Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 are the sub-trees. Table 5 shows the symbols used in fault trees and Table 6 lists all the sub-events and BEs in the tree; the basic event set is X = {X₁, X₂, …, X₂₇}. Through qualitative analysis, the minimal cut sets are obtained as: {X₁}, {X₂}, {X₃}, {X₄}, {X₅}, {X₆}, {X₇}, {X₈}, {X₉}, {X₁₀}, {X₁₁}, {X₁₂}, {X₁₃}, {X₁₄}, {X₁₅}, {X₁₆}, {X₁₇}, {X₁₈}, {X₁₉}, {X₂₀}, {X₂₁}, {X₂₂}, {X₂₃}, {X₂₄}, {X₂₅}, {X₂₆}, and {X₂₇}.

Table 4. Main sub-event failures of a hydraulic system.

Code	Failure Mode	Code	Failure Mode
H1	Oil passage blocked	H5	Oil temperature too high
H2	Leakage	H6	Too much noise
H3	Insufficient or fluctuating flow	H7	Heavy vibration
H4	Insufficient or fluctuating pressure	H8	Hydraulic elements fault

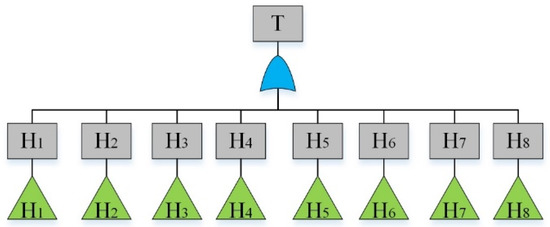
Figure 2. Fault tree of a hydraulic system: main tree.

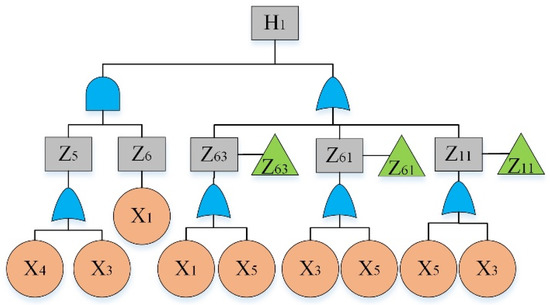
Figure 3. Fault tree of a hydraulic system: sub-tree I.

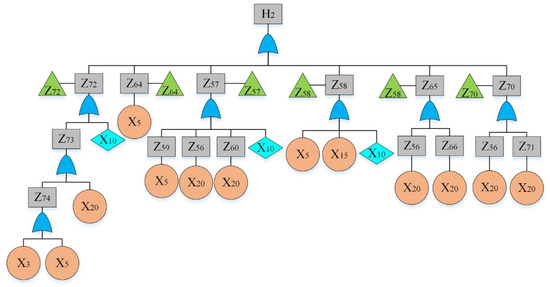
Figure 4. Fault tree of a hydraulic system: sub-tree II.

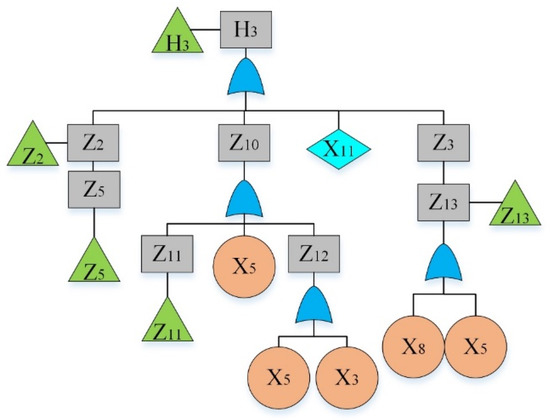
Figure 5. Fault tree of a hydraulic system: sub-tree III.

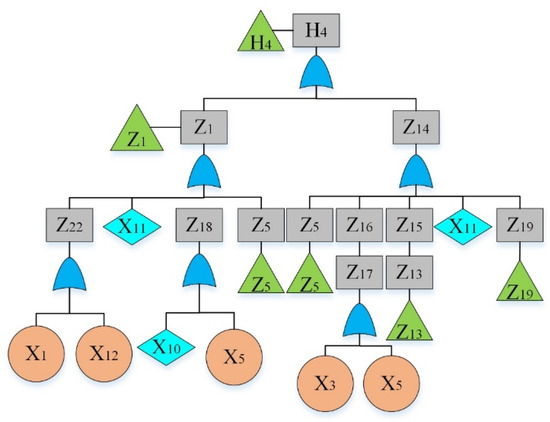
Figure 6. Fault tree of a hydraulic system: sub-tree IV.

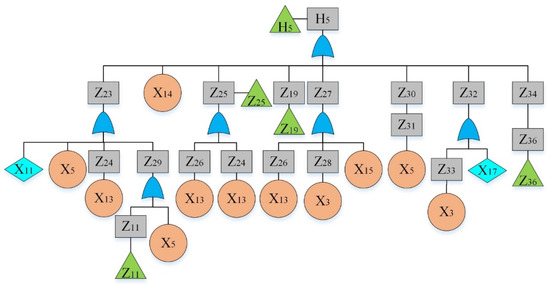
Figure 7. Fault tree of a hydraulic system: sub-tree V.

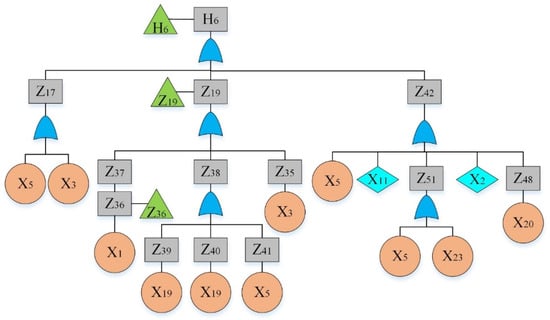
Figure 8. Fault tree of a hydraulic system: sub-tree VI.

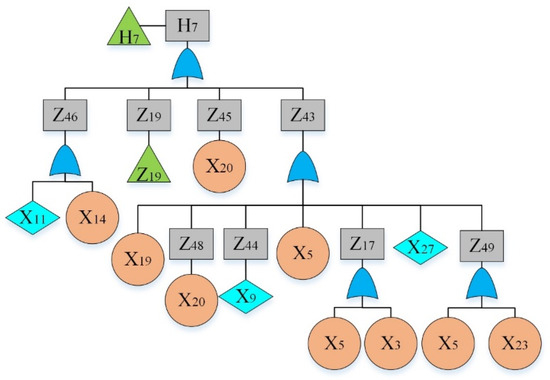
Figure 9. Fault tree of a hydraulic system: sub-tree VII.

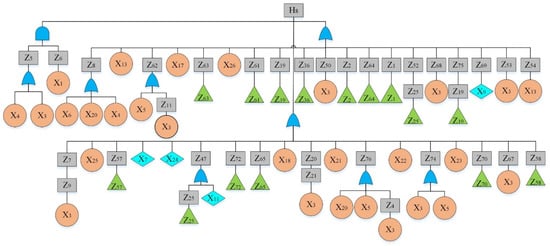
Figure 10. Fault tree of a hydraulic system: sub-tree VIII.

Table 5. Symbols used in the fault trees.

Symbol	Meaning	Symbol	Meaning
	Top event		AND gate
	Intermediate event		OR gate
	Basic event		Transfer-in
	Undeveloped event		Transfer-out

Table 6. Events in the fault tree.

Event	Content	Event	Content
Z1	Lack of pressure	Z53	Impurity interference
Z2	Lack or fluctuation of oil flow in filter	Z54	Improper set value of sensor
Z3	Pump Flow unstable	Z55	Seal wear
Z4	Impurity entry the execute component	Z56	Poor sealing
Z5	Deposition of contaminants in filter	Z57	Pipe joint leakage
Z6	Filter not replaced or cleaned	Z58	Pipe leakage
Z7	Filter element damage	Z59	Poor pipe joint quality
Z8	Bypass leakage of filter too much	Z60	Pipe joints loose
Z9	Impact of oil contamination	Z61	Pipe wear
Z10	Lack or fluctuation of oil flow in the valve	Z62	Oversize gap between the throttle valve body and spool
Z11	Valve wear	Z63	Pipes bending deformation
Z12	Valve rust	Z64	Valve Leakage
Z13	Pump unstable	Z65	Junction between the valve and pipe leakage
Z14	Fluctuation of oil flow	Z66	Junction between the valve and pipe loose
Z15	Oil pressure of the pump unstable	Z67	Impurity entry to the throttle valve
Z16	The pump–outlet pressure unstable	Z68	Flow area of the throttle too small
Z17	Internal pump wear	Z69	Throttle position change
Z18	Insufficient pump oil pressure	Z70	Hydraulic actuator junction leakage
Z19	Air gets into the pump	Z71	Junction of actuator loose
Z20	The movement of the valve core of the overflow valve not sensitive	Z72	Actuator leakage
Z21	Impurity entry to the overflow valve	Z73	Internal clearance in actuator too large
Z22	Oil starvation in tank	Z74	Internal wear in actuator
Z23	Inside leakage	Z75	Air into the actuator
Z24	Pressure set of the relief valve too large	Z76	Actuator gets stuck
Z25	Improper pressure setting	X1	Improper maintenance
Z26	Pressure setting of the back pressure valve too large	X2	Rotors of motor loose
Z27	Oil return resistance too large	X3	Oil pollution
Z28	Oil discharge filter plug	X4	Wrong choice of filter
Z29	Valve gap too large	X5	Outsourced parts fault
Z30	Excessive friction between hydraulic elements	X6	Poor processing quality of parts
Z31	Valve gap too narrow	X7	Other mechanical faults
Z32	Poor heat dissipation	X8	Motor supply voltage not stable
Z33	Deposition of contaminants in heatsink	X9	Vibration of mechanical system too heavy
Z34	Insufficient circulating oil	X10	Product damage
Z35	Plugged oil inlet	X11	Excessive oil viscosity
Z36	Low oil level	X12	Tank leakage
Z37	Filter above oil level	X13	Parameter setting error
Z38	Suction line leakage	X14	Wrong choice of oil
Z39	Suction line loose	X15	Piping delaminating
Z40	Suction line damaged	X16	Oil viscosity too low
Z41	Suction line seal damaged	X17	Radiator failure
Z42	Hydraulic station too loud	X18	Material aging
Z43	Vibration of hydraulic station too heavy	X19	Pipeline is not fixed
Z44	Fixing bolt of motor is loose	X20	Improper assembly
Z45	Coupling loose between the motor and pump	X21	Motor power fault
Z46	Bubbles generate in the oil	X22	Motor supply voltage too low
Z47	Pump load too heavy	X23	Motor bearings not sufficiently lubricated
Z48	Misalignment of coupling	X24	Motor rotor stuck
Z49	Excessive motor bearing clearance	X25	Motor overheating
Z50	The suction line plugs	X26	Motor supply voltage too high
Z51	Motor bearing wear	X27	Motor rotor unbalanced
Z52	The pressure gauge over range

3.2. Quantitative Analysis

The results of frequency assessment based on failure data are shown in Table 7. As one can see, there are 21 failures evaluated as “uncertain,” i.e., Type I data.

Table 7. The result of the frequency assessment.

BE	Frequency	BE	Frequency	BE	Frequency
X1	29	X10	15	X19	4
X2	2	X11	12	X20	2
X3	95	X12	1	X23	1
X4	4	X13	1	X25	1
X5	23	X15	3	X26	1
X6	3	X16	1	Uncertain	21
X7	4	X17	3
X9	4	X18	1

For the purpose of illustration, one of the Type I data, which is the “check valve leakage,” was taken as an example for analysis. Two maintenance personnel gave three possible reasons for the failure: “Internal leakage caused by wear,” “Quality problems of check valve,” and “Connection looseness caused by mechanical vibration,” which constituted the frame of discernment D = {D₁ = X₃, D₂ = X₅, D₃ = X₉}. Four possible combinations are determined as focal elements, the BPA of each focal element was assigned, and the aggregated BPA was obtained by combining evidence, as shown in Table 8. Then, the frequency interval of D₁, D₂, and D₃ was calculated, as shown in Table 9. The results were consequently merged into corresponding BEs in Table 6. After the remaining Type I data were processed, the objective occurrence was obtained.

Table 8. The BPA of each combination.

Combination	M1	M2	M
{D1}	0.6	0.7	0.859
{D2}	0.15	0.15	0.043
{D3}	0.15	0.15	0.082
{D1, D2, D3}	0.1	0.1	0.016

Table 9. The confidence interval of D₁, D₂, and D_3.

BE	D1	D2	D3
Confidence interval	[0.859,0.875]	[0.043,0.059]	[0.082,0.098]

There are six BEs with a Type II problem, which are expressed as a set T = {T₁ = X₈, T₂ = X₁₄, T₃ = X₂₁, T₄ = X₂₂, T₅ = X₂₄, T₆ = X₂₇}. The occurrence estimation was given by the designers, maintainers, and users, respectively, in the form of an interval rough number, as shown in Table 10.

Table 10. The occurrence estimation given by experts.

BE	Designers F1	Maintainers F2	Users F3
X8	([0.003, 0.005], [0.002, 0.008])	([0.002, 0.004], [0.002, 0.005])	([0.003, 0.004], [0.003, 0.007])
X14	([0.008, 0.012], [0.005, 0.015])	([0.007, 0.011], [0.004, 0.012])	([0.007, 0.012], [0.005, 0.014])
X21	([0.002, 0.004], [0.001, 0.005])	([0.002, 0.004], [0.002, 0.005])	([0.003, 0.004], [0.002, 0.006])
X22	([0.003, 0.005], [0.002, 0.008])	([0.001, 0.004], [0.001, 0.005])	([0.002, 0.003], [0.001, 0.004])
X24	([0.004, 0.006], [0.003, 0.008])	([0.005, 0.006], [0.004, 0.007])	([0.003, 0.005], [0.003, 0.008])
X27	([0.007, 0.009], [0.005, 0.013])	([0.006, 0.008], [0.005, 0.011])	([0.008, 0.009], [0.006, 0.011])

The positive and negative ideal point of F_j is given as: ${\xi }_1^{+}$ = ([0.008, 0.012], [0.005, 0.015]), ${\xi }_1^{-}$ = ([0.002, 0.004], [0.001, 0.005]), ${\xi }_2^{+}$ = ([0.007, 0.011], [0.005, 0.012]), ${\xi }_2^{-}$ = ([0.001, 0.004], [0.001, 0.005]), ${\xi }_3^{+}$ = ([0.008, 0.012], [0.006, 0.014]), and ${\xi }_3^{-}$ = ([0.002, 0.003], [0.001, 0.004]).

All the three experts prefer to avoid risks; thus, risk preference coefficient τ was determined as τ = 0.3 to calculate the preference distance, of which the result is shown in Table 11. Then, the weight of expert was calculated, as shown in Table 12. By substituting w_j, we calculated the utility value and its expectation. Thus, the subjective occurrence was obtained, as shown in Table 13.

Table 11. The preference distance.

BE	Designers F1			Maintainers F2			Users F3
	${\mathit{d}}_{\mathit{i}\mathit{j}}^{+}$	${\mathit{d}}_{\mathit{i}\mathit{j}}^{-}$	Preference Distance	${\mathit{d}}_{\mathit{i}\mathit{j}}^{+}$	${\mathit{d}}_{\mathit{i}\mathit{j}}^{-}$	Preference Distance	${\mathit{d}}_{\mathit{i}\mathit{j}}^{+}$	${\mathit{d}}_{\mathit{i}\mathit{j}}^{-}$	Preference Distance
X8	0.006	0.002	0.003	0.006	0.001	0.002	0.006	0.002	0.003
X14	0	0.007	0.005	0.001	0.006	0.004	0.001	0.007	0.005
X21	0.007	0	0.002	0.006	0.001	0.002	0.007	0.001	0.003
X22	0.006	0.002	0.003	0.006	0	0.002	0.008	0	0.002
X24	0.005	0.002	0.003	0.004	0.003	0.003	0.005	0.003	0.003
X27	0.002	0.006	0.005	0.002	0.005	0.004	0.002	0.006	0.005

Table 12. The expert weight.

Index	F1	F2	F3
ej	0.977	0.973	0.975
wj	0.311	0.364	0.325

Table 13. The subjective occurrence.

BE	Utility Value	Expectation
X8	([0.003, 0.004], [0.002, 0.007])	0.004
X14	([0.007, 0.012], [0.005, 0.014])	0.009
X21	([0.002, 0.004], [0.002, 0.005])	0.003
X22	([0.002, 0.004], [0.001, 0.006])	0.003
X24	([0.004, 0.006], [0.003, 0.008])	0.005
X27	([0.007, 0.009], [0.005, 0.012])	0.008

3.3. Importance Analysis and Decision Making

Next, the objective and subjective occurrence were combined to derive the comprehensive occurrence. Table 14 summarizes the results of quantitative analysis.

Table 14. Results of quantitative analysis.

Basic Event	Frequency	Objective Occurrence	Subjective Occurrence	Comprehensive Occurrence	Expectation
X1	[32.752, 33.128]	[0.142, 0.143]	0	[0.137, 0.139]	0.138
X2	[2, 2]	[0.009, 0.009]	0	[0.008, 0.008]	0.008
X3	[103.951, 104.541]	[0.450, 0.453]	0	[0.434, 0.440]	0.437
X4	[5.127, 5.225]	[0.022, 0.023]	0	[0.021, 0.022]	0.022
X5	[24.896, 25.058]	[0.108, 0.108]	0	[0.104, 0.105]	0.105
X6	[3, 3]	[0.013, 0.013]	0	[0.013, 0.013]	0.013
X7	[4.657, 4.802]	[0.020, 0.021]	0	[0.019, 0.020]	0.020
X8	0	0	0.004	[0.004, 0.004]	0.004
X9	[4, 4]	[0.017, 0.017]	0	[0.017, 0.017]	0.017
X10	[17.112, 17.308]	[0.074, 0.075]	0	[0.071, 0.073]	0.072
X11	[12.989, 13]	[0.056, 0.056]	0	[0.054, 0.055]	0.054
X12	[1, 1]	[0.004, 0.004]	0	[0.004, 0.004]	0.004
X13	[1, 1]	[0.004, 0.004]	0	[0.004, 0.004]	0.004
X14	0	0	0.009	[0.009, 0.009]	0.009
X15	[3, 3]	[0.013, 0.013]	0	[0.013, 0.013]	0.013
X16	[1, 1]	[0.004, 0.004]	0	[0.004, 0.004]	0.004
X17	[3, 3]	[0.013, 0.013]	0	[0.013, 0.013]	0.013
X18	[1, 1]	[0.004, 0.004]		[0.004, 0.004]	0.004
X19	[4.866, 4.991]	[0.021, 0.022]	0	[0.020, 0.021]	0.021
X20	[2, 2]	[0.009, 0.009]	0	[0.008, 0.008]	0.008
X21	0	0	0.003	[0.003, 0.003]	0.003
X22	0	0	0.003	[0.003, 0.003]	0.003
X23	[1, 1]	[0.004, 0.004]	0	[0.004, 0.004]	0.004
X24	0	0	0.005	[0.005, 0.005]	0.005
X25	[1, 1]	[0.004, 0.004]	0	[0.004, 0.004]	0.004
X26	[1, 1]	[0.004, 0.004]	0	[0.004, 0.004]	0.004
X27	0	0	0.008	[0.008, 0.008]	0.008

Finally, the probability importance of each BE was calculated and shown in Table 15.

Table 15. Probability importance of each BE.

BE	Index	BE	Index	BE	Index
X1	[0.3609, 0.3669]	X10	[0.3350, 0.3411]	X19	[0.3173, 0.3233]
X2	[0.3133, 0.3194]	X11	[0.3286, 0.3349]	X20	[0.3133, 0.3194]
X3	[0.5545, 0.5597]	X12	[0.3120, 0.3181]	X21	[0.3116, 0.3176]
X4	[0.3176, 0.3237]	X13	[0.3120, 0.3181]	X22	[0.3116, 0.3176]
X5	[0.3473, 0.3535]	X14	[0.3134, 0.3195]	X23	[0.3120, 0.3181]
X6	[0.3146, 0.3207]	X15	[0.3146, 0.3207]	X24	[0.3122, 0.3183]
X7	[0.3171, 0.3230]	X16	[0.3120, 0.3181]	X25	[0.3120, 0.3181]
X8	[0.3119, 0.3180]	X17	[0.3146, 0.3207]	X26	[0.3120, 0.3181]
X9	[0.3160, 0.3221]	X18	[0.3120, 0.3181]	X27	[0.3131, 0.3192]

According to the ranking rule of interval number, the probability importance of all BEs is listed in Table 16 and ranked as follows (largest to smallest):

$$\begin{array}{l}{\mathrm{X}}_3{>\mathrm{X}}_1{>\mathrm{X}}_5{>\mathrm{X}}_{10}{>\mathrm{X}}_{11}{>\mathrm{X}}_4\succ {\mathrm{X}}_{19}\succ {\mathrm{X}}_7\succ {\mathrm{X}}_9\succ {\mathrm{X}}_6\succ {\mathrm{X}}_{15}\succ {\mathrm{X}}_{17}\succ {\mathrm{X}}_{14}\succ {\mathrm{X}}_2{=\mathrm{X}}_{20}\succ \\ {\mathrm{X}}_{27}\succ {\mathrm{X}}_{24}\succ {\mathrm{X}}_{12}{=\mathrm{X}}_{13}{=\mathrm{X}}_{16}{=\mathrm{X}}_{18}{=\mathrm{X}}_{23}{=\mathrm{X}}_{25}{=\mathrm{X}}_{26}\succ {\mathrm{X}}_8\succ {\mathrm{X}}_{21}{=\mathrm{X}}_{22}\end{array}$$

Table 16. Importance ranking of each BE.

BE	Index	BE	Index	BE	Index
X1	0.363929987	X10	0.338072619	X19	0.320304036
X2	0.316339954	X11	0.331756299	X20	0.316339954
X3	0.557089359	X12	0.315008549	X21	0.314602054
X4	0.320643759	X13	0.315008549	X22	0.314602054
X5	0.350364665	X14	0.316445615	X23	0.315008549
X6	0.317682661	X15	0.317682661	X24	0.315214182
X7	0.320031414	X16	0.315008549	X25	0.315008549
X8	0.314907821	X17	0.317682661	X26	0.315008549
X9	0.319036815	X18	0.315008549	X27	0.316136855

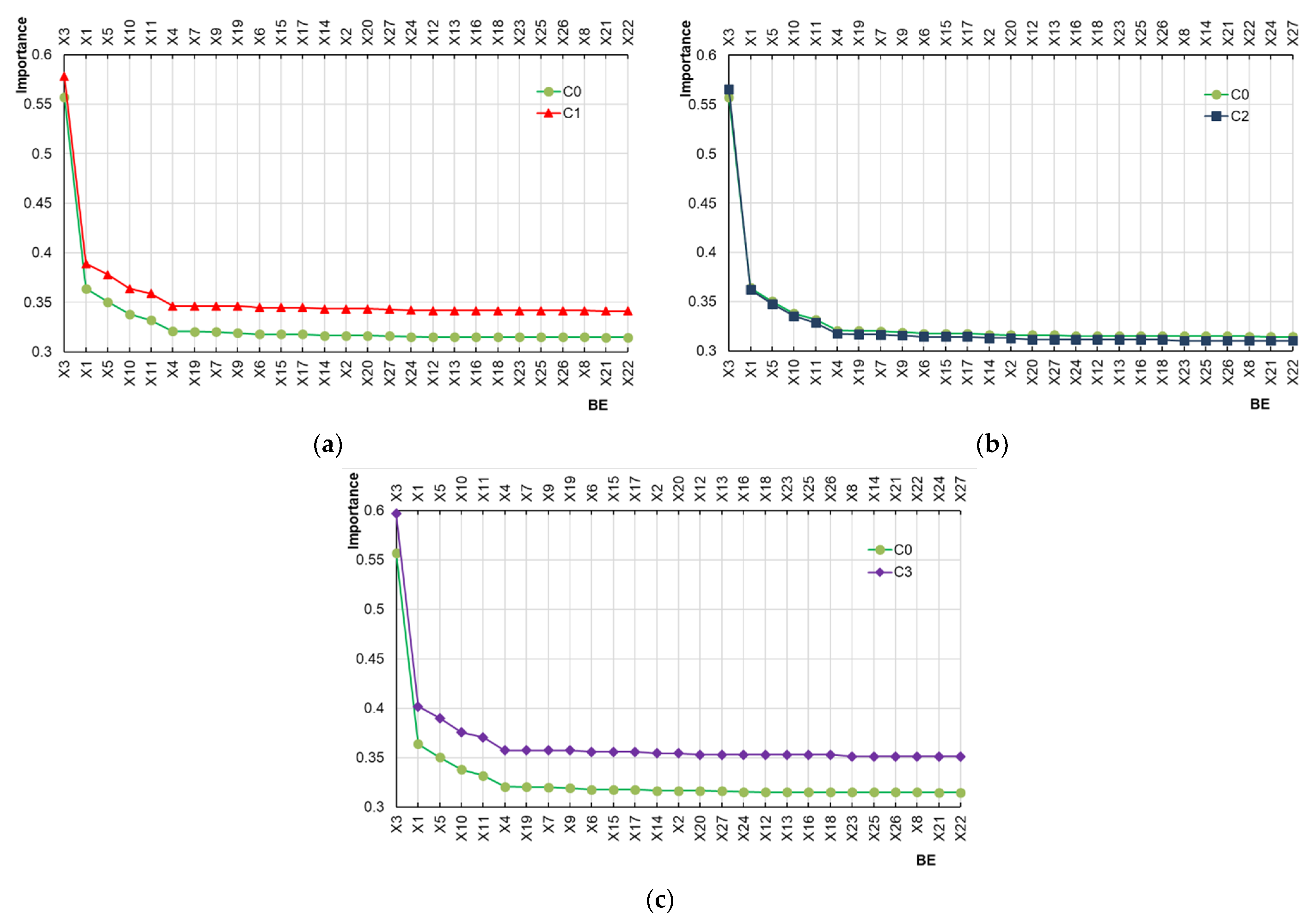
For comparison purposes, the importance was measured and ranked in another three cases: In case 1 (C₁), Type I problem was ignored, that is, the failure data of which the reason was identified as “Uncertain” were not used for analysis; in case 2 (C₂), the Type II problem was ignored; in case 3 (C₃), both Type I and Type II problems were ignored, which amounts to a conventional FTA approach. The importance ranking in three cases was compared to the result by the proposed approach, which is marked as C₀, as shown in Figure 11. The results show that:

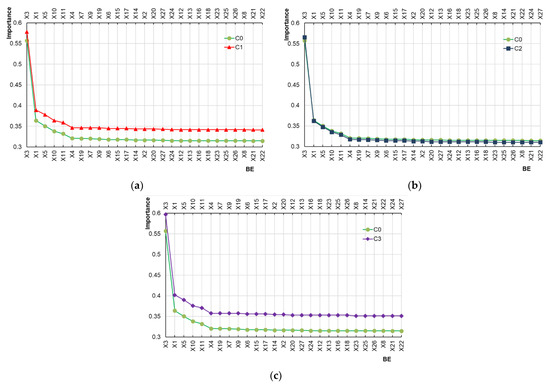
Figure 11. Comparison results of importance analysis in different cases: (a) Comparison between C₀ and C₁; (b) Comparison between C₀ and C₂; (c) Comparison between C₀ and C₃.

Compared to C₀, the ranking of X₁₉ becomes lower in C₁, which means that ignoring type I problems will change the ranking of BEs to some extent.

The rankings of X₁₄, X₂₄, and X₂₇ become lower in C₂ compared to C₀. It should be noted that the three BEs are all Type II problem-related. This indicates that the importance of some BEs will be underestimated due to the lack of data support if a Type II problem is ignored.

The ranking of X₁₉, X₁₄, X₂₄, and X₂₇ changes in C₃, which is the aggregate result of C₁ and C₂. The main reason for the differences is that the failure data incompleteness and uncertainty are not considered in C₃ as compared to C₀.

Finally, as one can see from the result, the top three critical BEs are “X₃: Oil pollution,” “X₁: Improper maintenance,” and “X₅: Poor outsourced parts quality” in this case study, which make up more than 50% of the failure. Oil pollution is the most critical BE of a hydraulic system, which is the same as the result in [37]. This shows that the proposed approach ensures the veracity of analysis. Meanwhile, the result also gives advice about the reliability growth of the hydraulic system of HCMT: control the source of oil pollution and improve the filtering capacity. The service time threshold of key components should be clear, along with a proper maintenance plan, so that necessary repairs or replacements can be made in an appropriate time. In addition, the quality of outsourced parts should be strictly checked and the screen process should be carried out if necessary.

4. Conclusions

The hydraulic system of HCMT is a complex system with a high failure rate. For its fault tree quantitative analysis, failure data contains a lot of information about reliability and is useful for measuring the probability of BEs. However, conventional FTA approaches just using failure data have some limitations in quantitative analysis.

In this study, the proposed approach, which incorporates the experts’ opinions and the conventional FTA technique, is demonstrated as a viable method for the estimation of the occurrence probability when encountered with data uncertainty and incompleteness. Through a case study, the fault tree of a hydraulic system of HCMT is constructed, and the result shows that there are 27 basic events that cause hydraulic failure in an HCMT, where oil pollution is the most critical basic event.

The function of experts’ opinions is embodied from two aspects: (1) Experts’ opinions are utilized for correcting failure data with uncertainty, so that the data can be used for quantitative analysis; (2) Experts’ opinions are used as supplementary information for BEs with no observed data. The purpose is to integrate the subjective information with the objective information to improve the accuracy of quantitative analysis results. Therefore, based on the above idea, the proposed approach is also applicable to the fault tree quantitative analysis of other products with incomplete failure data.

Finally, although expert opinion was introduced for uncertainty and incompleteness of failure data, it more or less brought subjectivity. One solution is to detect the fault accurately through analyzing condition signals of hydraulic such as vibration, flow, leakage, oil pollution, and so on, without relying on the experience of experts. Due to the complexity and ambiguity of hydraulic failure mechanism, an intelligent diagnosis approach may be needed to learn fault features from fault data. In addition, considering there is no single intelligent diagnosis approach that can be suitable for all fault diagnosis tasks, ensemble methods, such as bagging, boosting, and other rules, are also needed to combine multiple base intelligent fault diagnosis approaches to become a strong learning mode. This put forward demands on the condition monitoring technique of a hydraulic system and related algorithms, which cannot be implemented in this article, because only fault event data were obtained. Nonetheless, it provides a direction for future FTA works.