Local Sensitivity Analysis of Steady-State Response of Rotors with Rub-Impact to Parameters of Rubbing Interfaces
Abstract
:1. Introduction
2. Methods
2.1. Harmonic Balnace Method
2.2. Pseudo Arc-Length Continuation Method
2.3. Sensitivity Analysis
3. Numerical Results and Discussion
3.1. Models for Verification
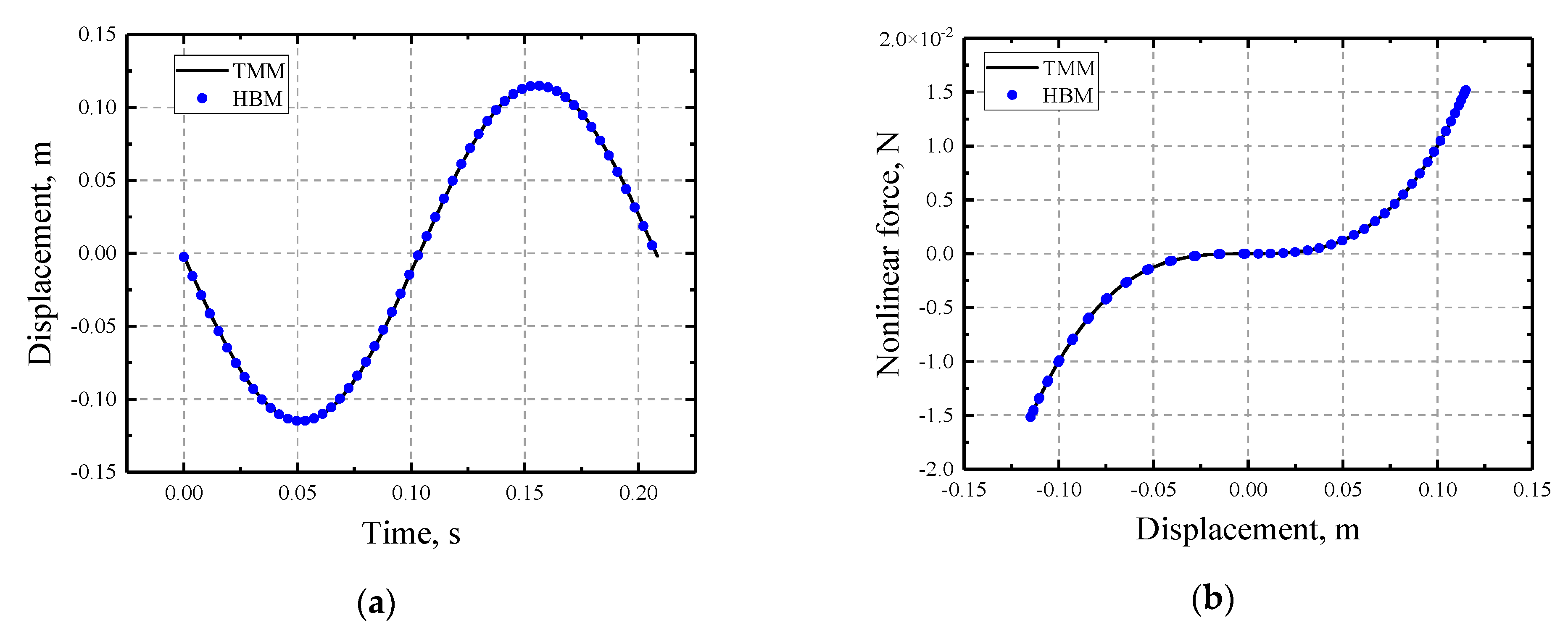
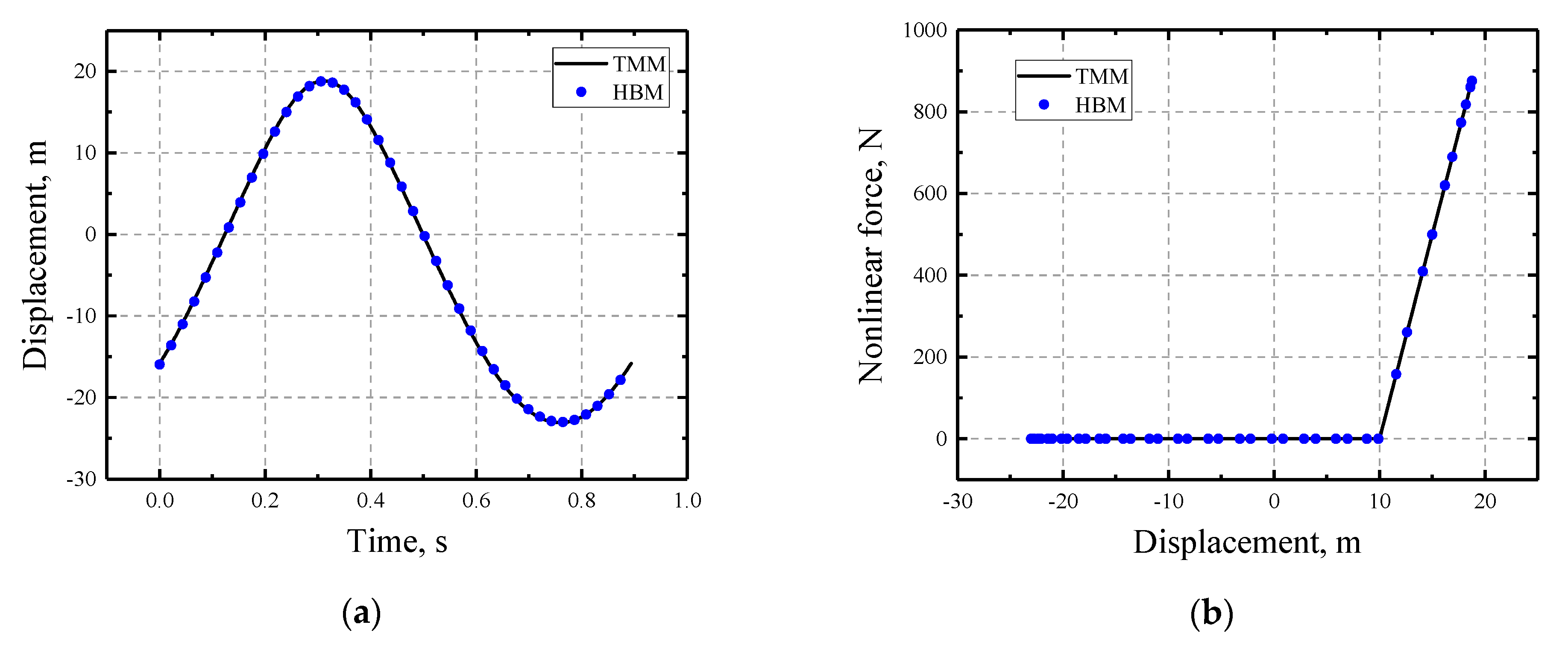
3.1.1. The Duffing Oscillator
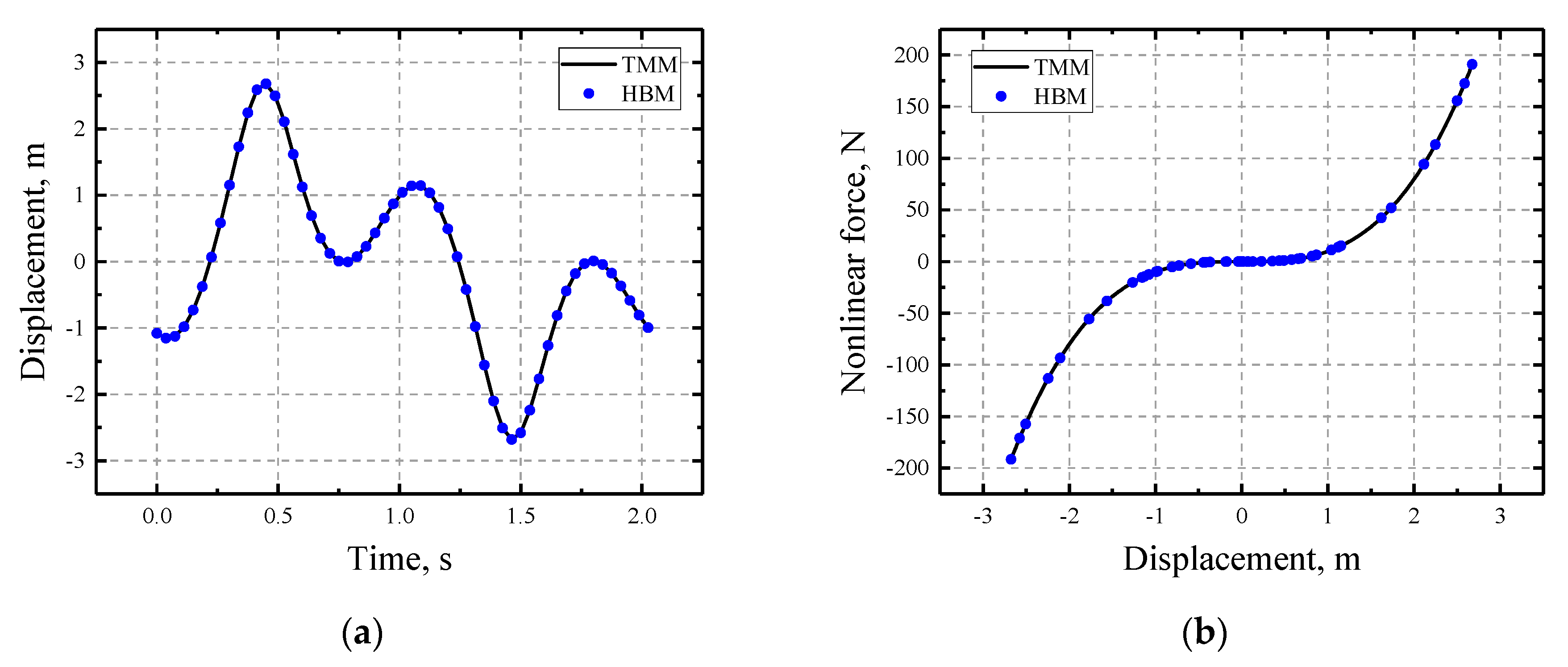
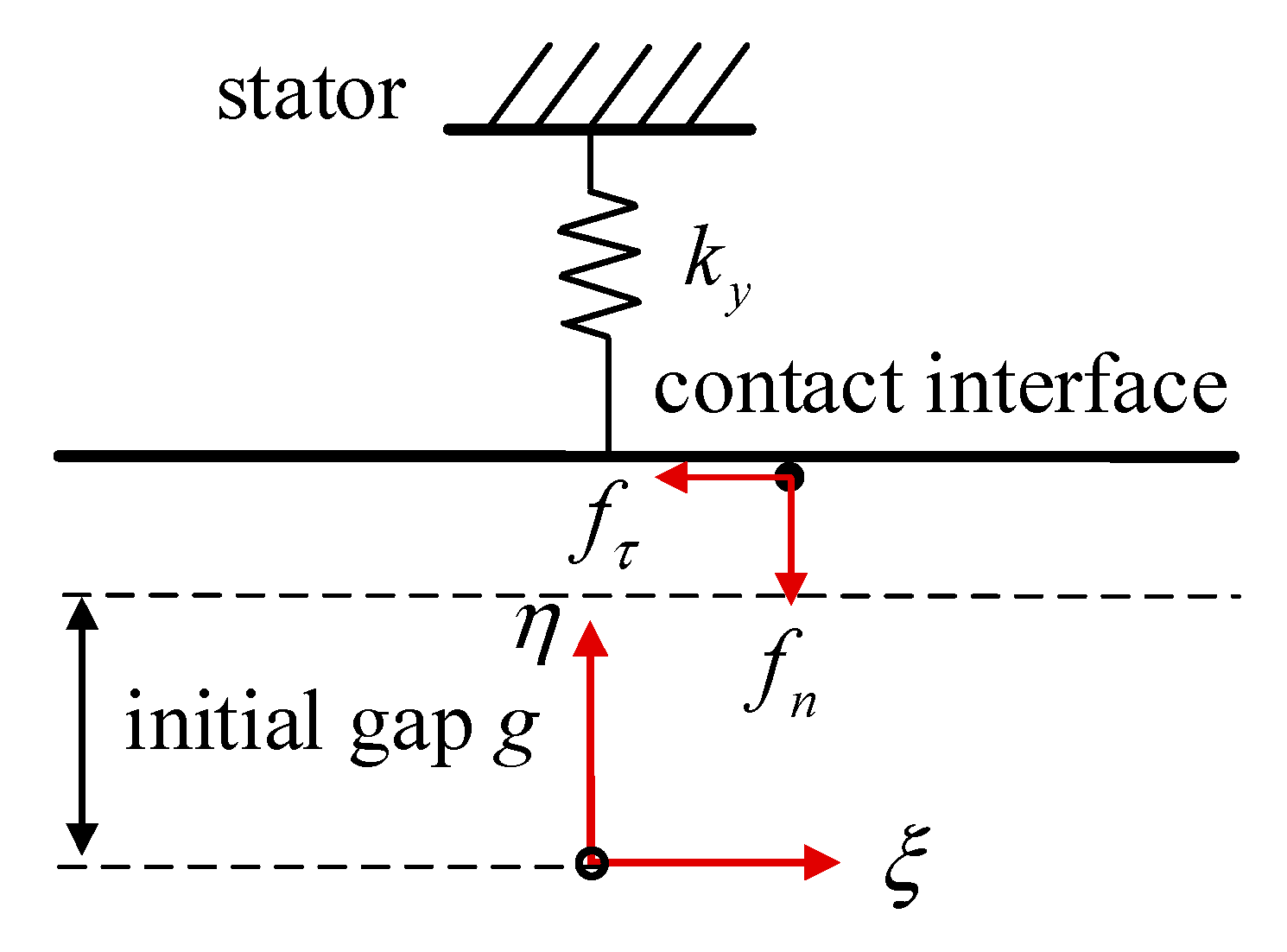
3.1.2. The Gap Model
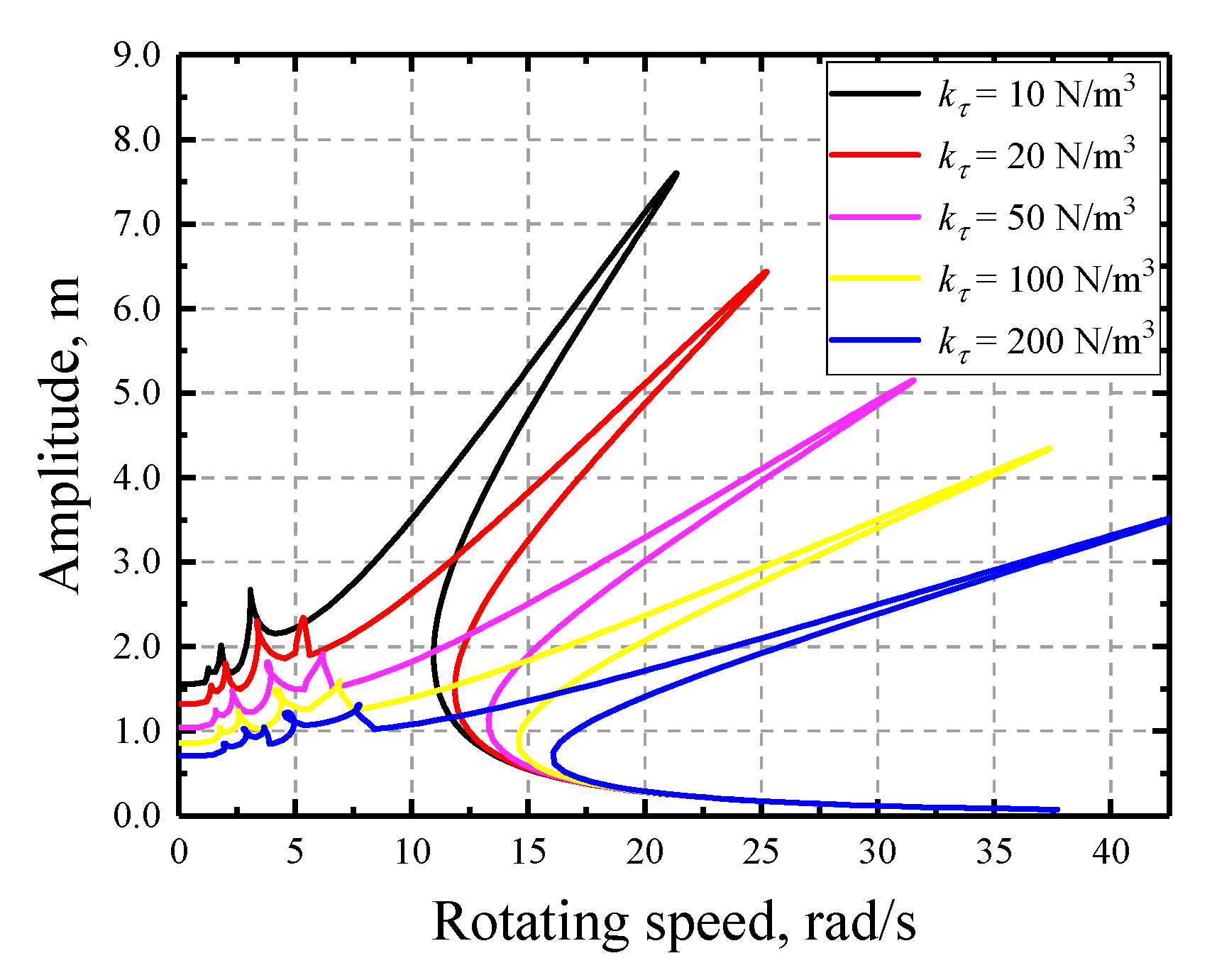
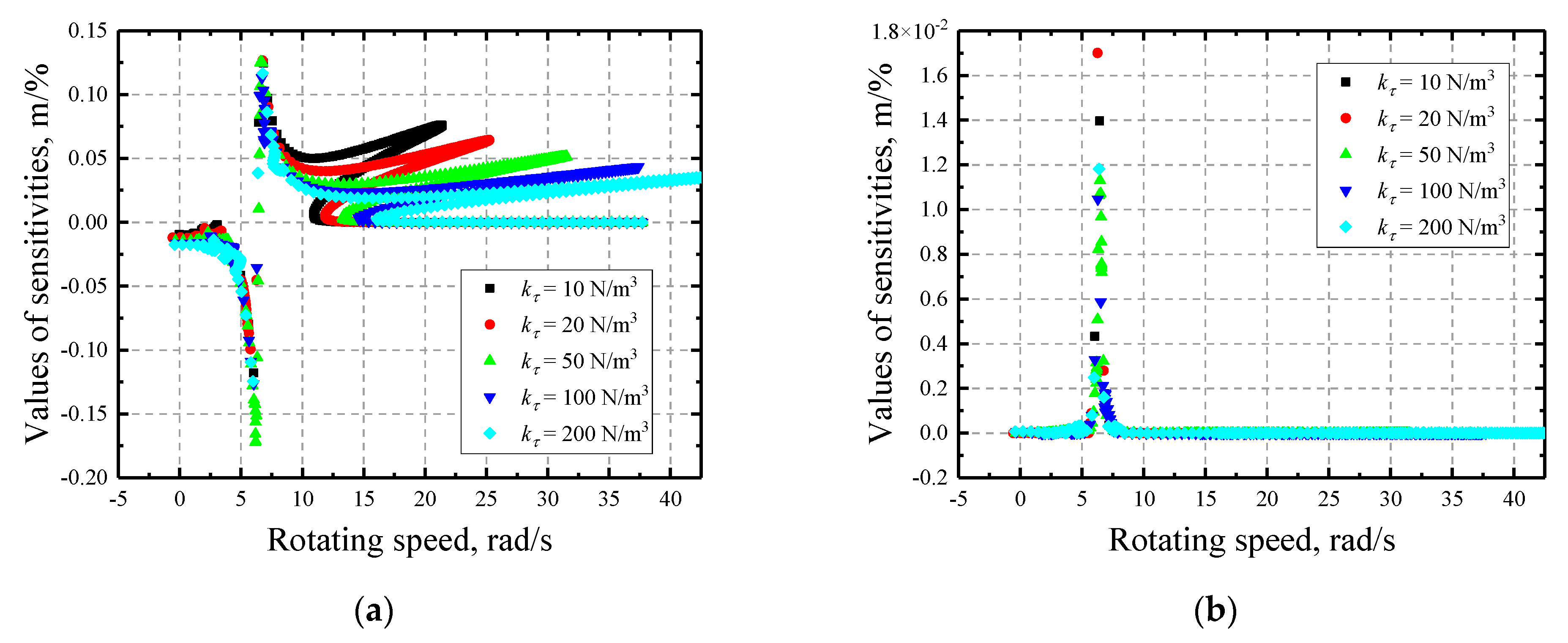
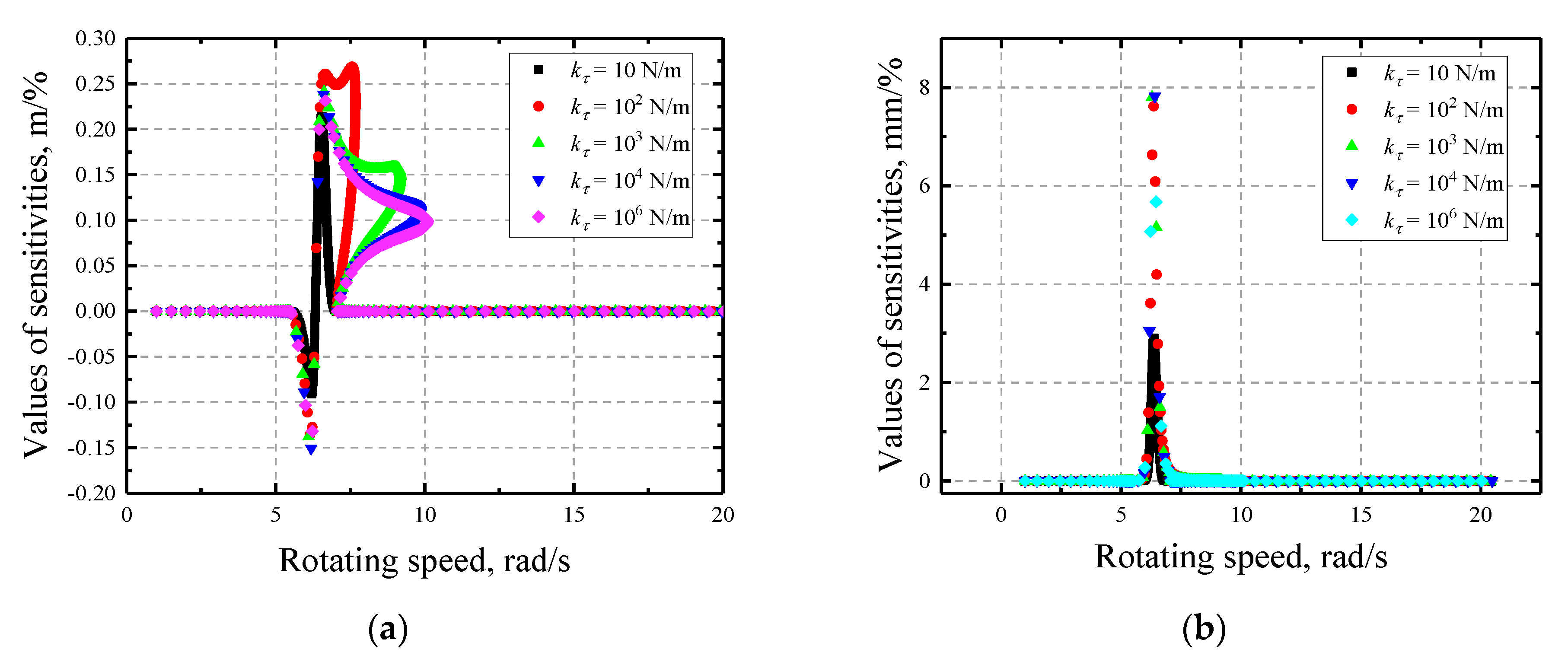
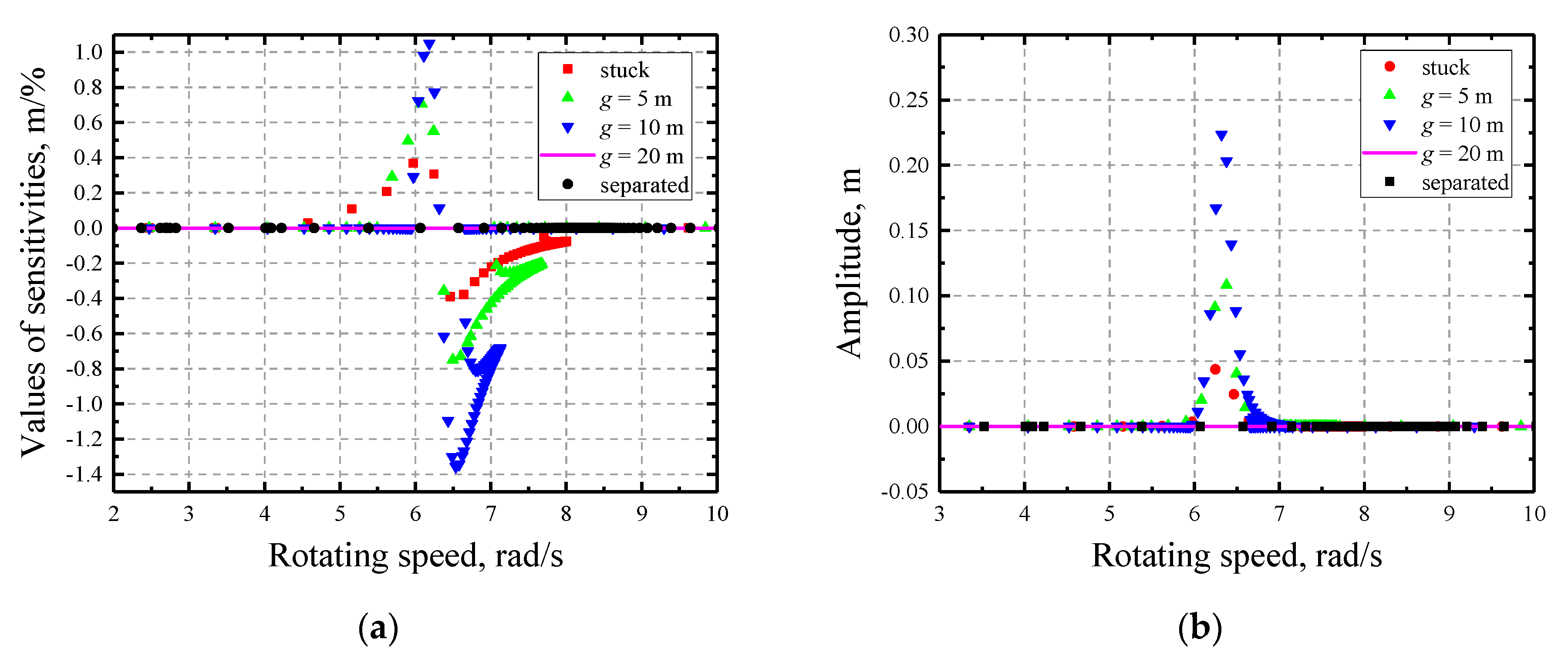
3.2. Sensitivity Analysisof a Jeffcott Rotor
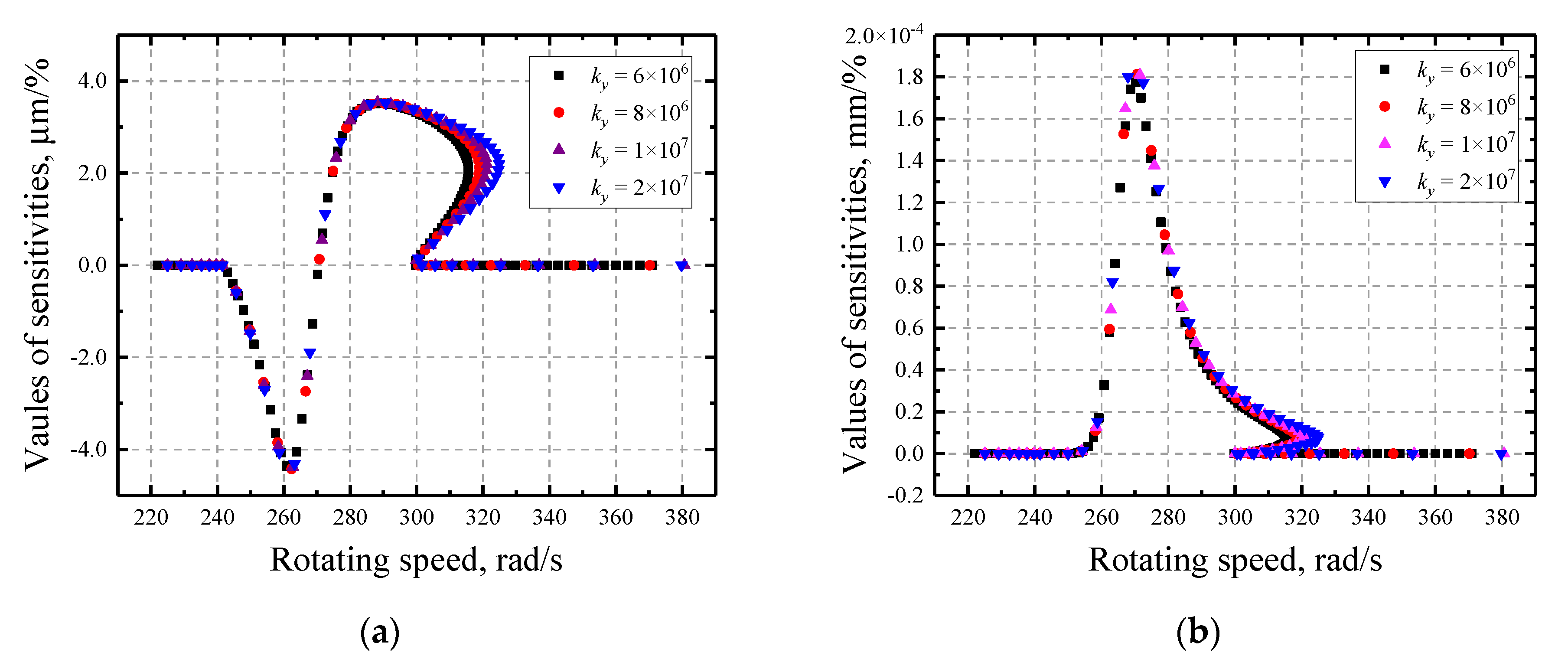
3.3. Sensitivity Analysis Based on Finite Element Model
4. Conclusions
- (1)
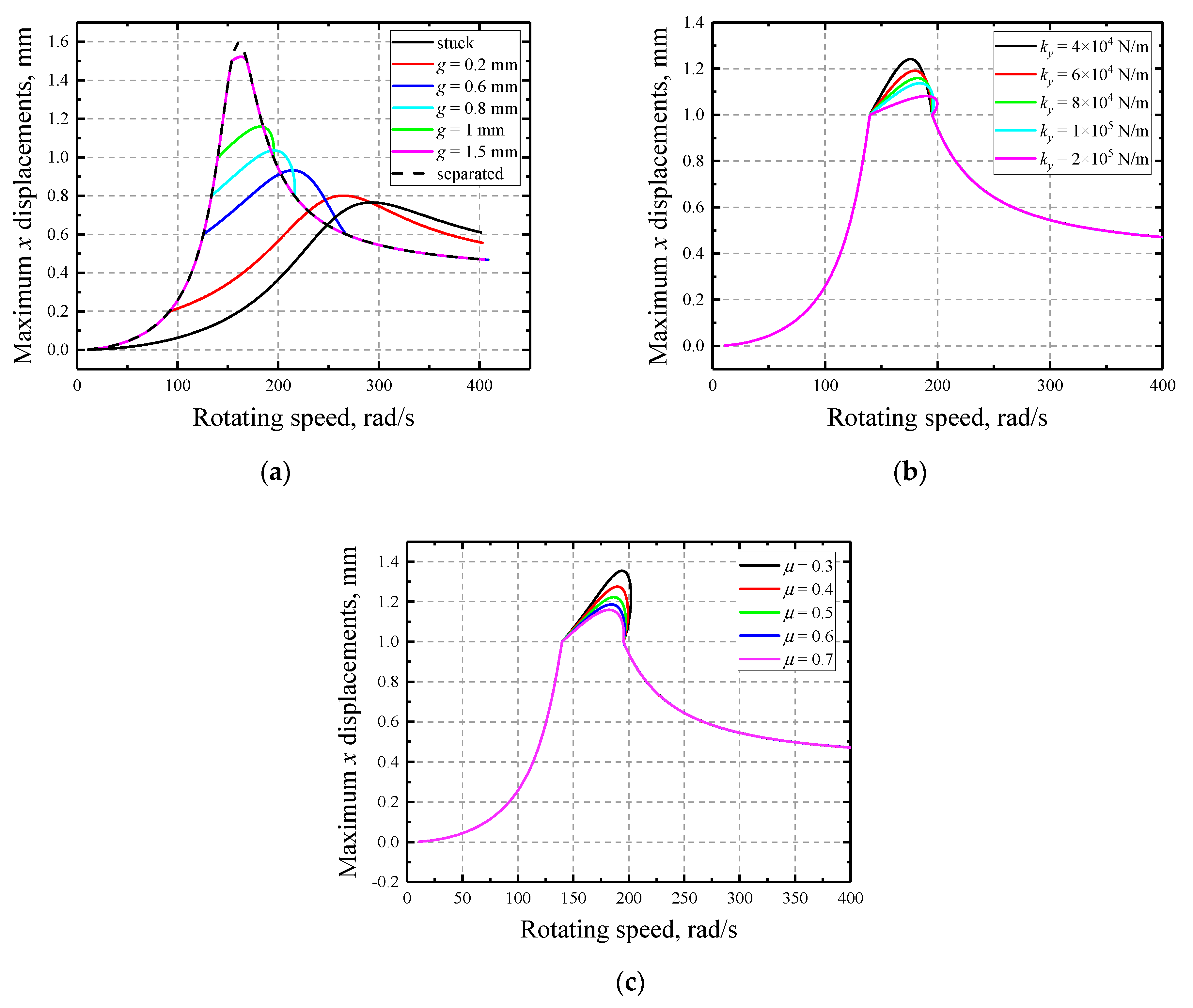
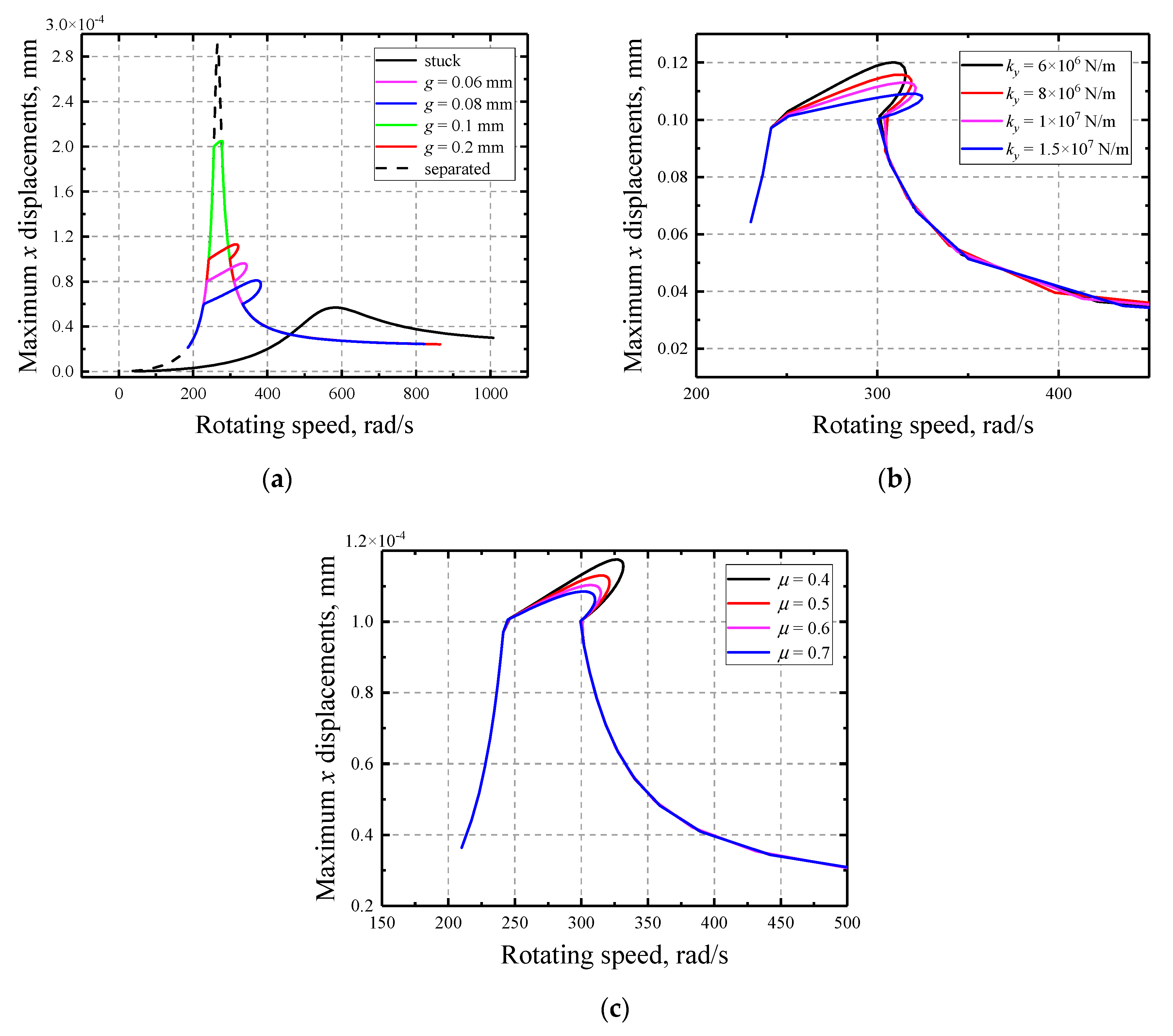
- The response of rotors subjected to rub-impact is sensitive to the parameters of rub interfaces only when the amplitudes are large enough to reach or exceed the prescribed initial clearance. If that is not the case, the whole system is equal to a linear system under a periodical excitation force.
- (2)
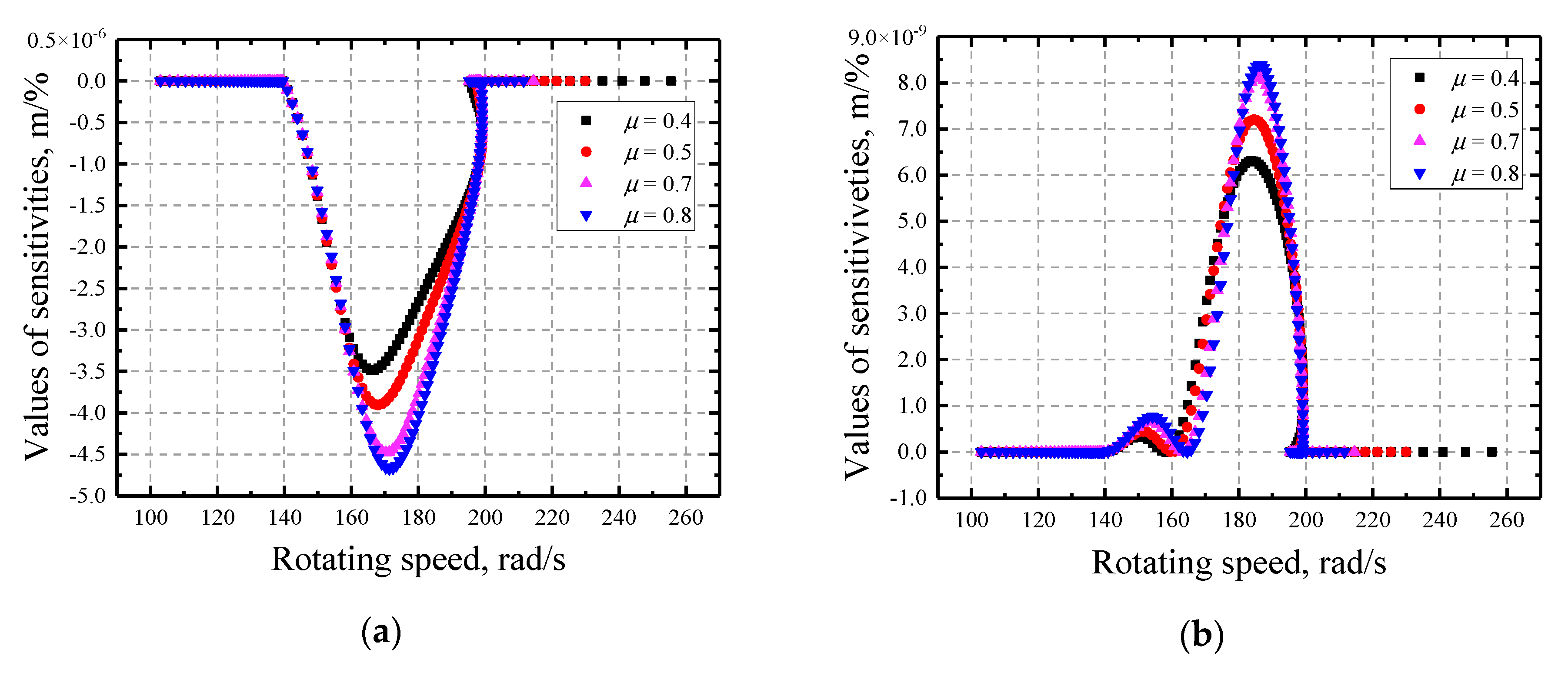
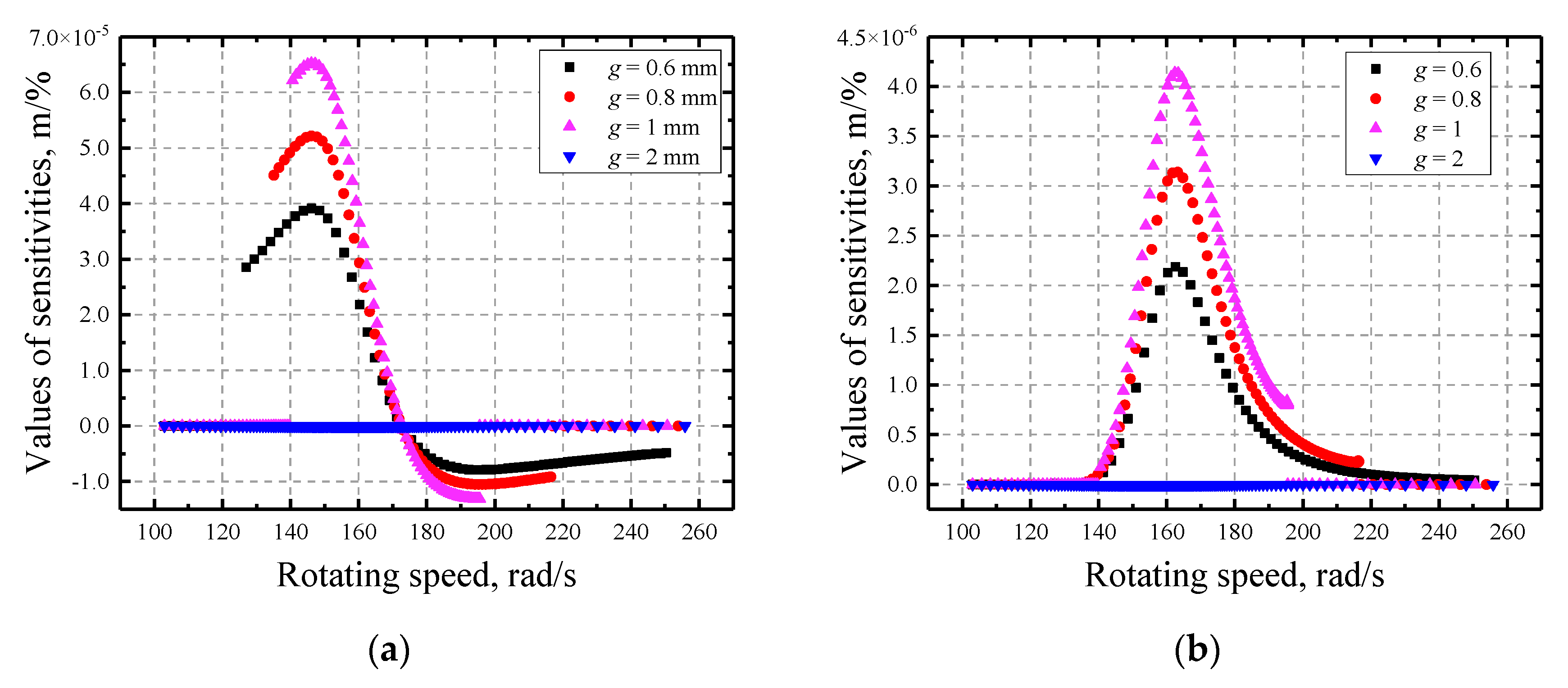
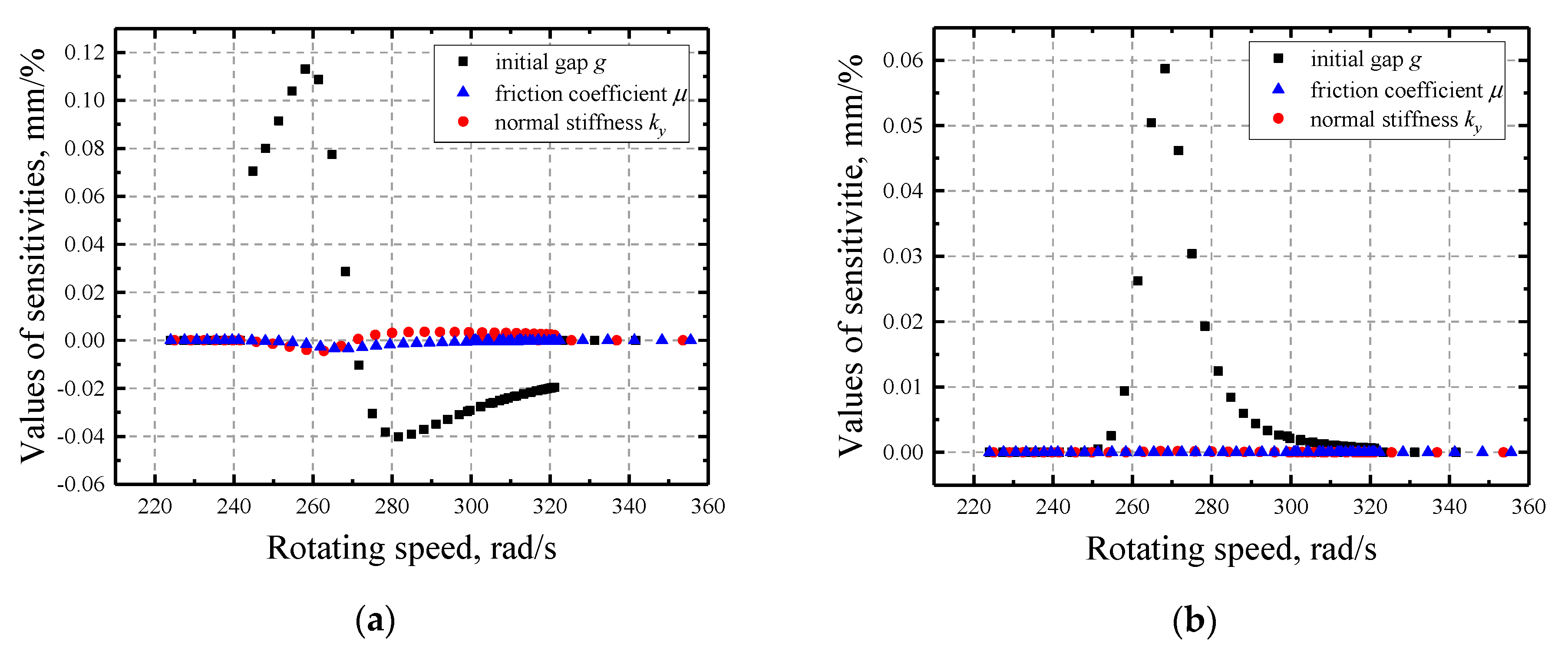
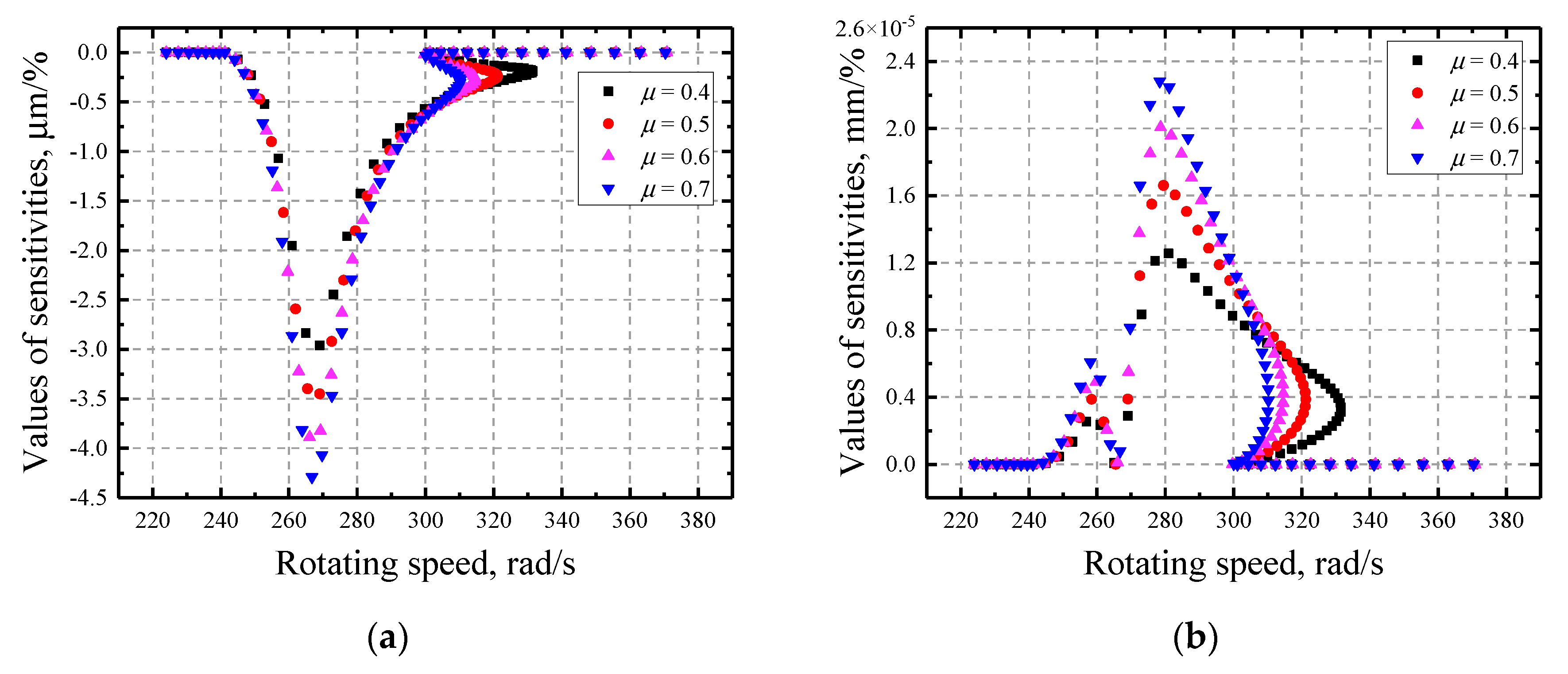
- The response of the rotor is much more sensitive to the initial gap with the two other factors being relatively insignificant. The sensitivities to the initial gap g are not contiguous at rotating speeds where a separation/contact status transformation happens since it determines the existence of rub-impact.
- (3)
- With the increase of initial gap, the rotors become more sensitive. In contrast, the friction coefficient has negative impact on the sensitivities and the multi-solution region grows larger with its decrease. Moreover, the variation of normal stiffness has relatively little influence on the sensitivities but it does influence the characteristics of the multi-solution region, i.e., the region expands as it increases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, Y.; Wang, S.; Yang, Z. Stability Margin Sensitivity Analysis of a Multi-Rotor System Geared by Spiral Bevel Gear pairs. Manuf. Sci. Eng. 2010, 97, 3215–3218. [Google Scholar] [CrossRef]
- Kim, J.; Sim, W.; Chung, J. Modal characteristics and dynamic stability of a whirling rotor with flexible blades. Appl. Math. Model. 2021, 89, 1–18. [Google Scholar] [CrossRef]
- Zhang, Y.-M.; Liu, Q.-L.; Li, H.; Wen, B.-C. Reliability sensitivity investigation of impact-rub for rotor-stator systems. J. Mol. Endocrinol. 2006, 21, 848–853. [Google Scholar] [CrossRef] [Green Version]
- Ritto, T.G.; Lopez, R.H.; Sampaio, R.; de Cursi, J.E.S. Robust optimization of a flexible rotor-bearing system using the Campbell diagram. Eng. Optimiz. 2011, 43, 77–96. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; TerMaath, S.; Shields, M.D. Imprecise global sensitivity analysis using bayesian multimodel inference and importance sampling. Mech. Syst. Signal Process. 2021, 148, 107162. [Google Scholar] [CrossRef]
- Changqing, S.U.; Yimin, Z.; Chunmei, L.V.; Hui, M.A. Natural frequency reliability sensitivity analysis of a rotor system. J. Vib. Shock. 2009, 28, 56–59. [Google Scholar] [CrossRef]
- Melchers, R.E.; Ahammed, M. A fast approximate method for parameter sensitivity estimation in Monte Carlo structural reliability. Comput. Struct. 2004, 82, 55–61. [Google Scholar] [CrossRef]
- Lataillade, A.D.; Blanco, S.; Clergent, Y.; Dufresne, J.L.; Hafi, M.E.; Fournier, R. Monte Carlo method and sensitivity estimations. J. Quant. Spectrosc. Radiat. Transf. 2018, 75, 529–538. [Google Scholar] [CrossRef] [Green Version]
- Petrov, E.P. Sensitivity analysis of nonlinear forced response for bladed discs with friction contact interfaces. In Proceedings of the Asme Turbo Expo 2005, Reno, NV, USA, 6–9 June 2005; Volume 4, pp. 483–494. [Google Scholar] [CrossRef]
- Petrov, E.P. Analysis of sensitivity and robustness of forced response for nonlinear dynamic structures. Mech. Syst. Signal Process. 2009, 23, 68–86. [Google Scholar] [CrossRef]
- Leister, T.; Baum, C.; Seemann, W. Sensitivity of computational rotor dynamics towards the empirically estimated lubrication gap clearance of foil air journal bearings. Proc. Appl. Math. Mech. 2016, 16, 285–286. [Google Scholar] [CrossRef]
- Yan, S.; Sievert, R. Vibration Sensitivity of Large Turbine Generator Shaft Trains to Unbalance. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics, Cham, Switzerland, 22–25 September 2015; pp. 3–14. [Google Scholar]
- Pan, H.; Yuan, H.; Zhao, T.; Yang, W. Sensitivity Analysis of Wheel Quality and Location on Rotor Critical Speed. J. Vib. Meas. Diagn. 2017, 37, 532–538. [Google Scholar] [CrossRef]
- Papini, L.; Gerada, C. Sensitivity Analysis of Rotor Parameters in Solid Rotor Induction Machine. In Proceedings of the IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 21–24 May 2017. [Google Scholar]
- Ying, G.; Wu, W.; Liu, S.; Zheng, S. Research on Bearing Load Sensitivity for Multi-support Rotor System. Zhejiang Electr. Power 2017, 36, 39–42. [Google Scholar] [CrossRef]
- Anusonti-Inthra, P.; Corle, E.; Smith, B.; Nieto, Z. Sensitivity Analysis and Uncertainty Quantification of a Coaxial Rotor System. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 15. [Google Scholar]
- Choy, F.K.; Padovan, J. Non-linear transient analysis of rotor-casing rub events. J. Sound Vib. 1987, 113, 529–545. [Google Scholar] [CrossRef]
- Dai, X.; Zhang, X.; Jin, X. The partial and full rubbing of a flywheel rotor-bearing-stop system. Int. J. Mech. Sci. 2001, 43, 505–519. [Google Scholar] [CrossRef]
- Feng, Z.C.; Zhang, X.Z. Rubbing phenomena in rotor-stator contact. Chaos Solitons Fractals 2002, 14, 257–267. [Google Scholar] [CrossRef]
- Patel, T.H.; Darpe, A.K. Vibration response of a cracked rotor in presence of rotor-stator rub. J. Sound Vib. 2008, 317, 841–865. [Google Scholar] [CrossRef]
- Popprath, S.; Ecker, H. Nonlinear dynamics of a rotor contacting an elastically suspended stator. J. Sound Vib. 2007, 308, 767–784. [Google Scholar] [CrossRef]
- Liu, G.-Z.; Chen, Y.-Z.; Liu, Y.; Wen, B.-C. Experimental investigation of rotor rubbing faults. Adv. Mater. Res. 2012, 490, 1048–1052. [Google Scholar] [CrossRef]
- Ma, H.; Tai, X.; Zhang, Z.; Wen, B. Dynamic Characteristic Analysis of a Rotor System with Rub-impact Fault Considering Rotor-stator Misalignment. Prz. Elektrotechniczny 2012, 88, 145–149. [Google Scholar]
- Shen, X.; Jia, J.; Zhao, M. Effect of parameters on the rubbing condition of an unbalanced rotor system with initial permanent deflection. Arch. Appl. Mech. 2007, 77, 883–892. [Google Scholar] [CrossRef]
- Yao, H.; Han, Q.; Li, L.; Wen, B. Method for Detecting Rubbing Fault in Rotor System Based on Harmonic Components. J. Mech. Eng. 2012, 48, 43–48. [Google Scholar] [CrossRef]
- Behzad, M.; Alvandi, M. Friction-induced backward rub of rotors in non-annular clearances: Experimental observations and numerical analysis. Tribol. Int. 2020, 152. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.T.; Feng, K.P.; Zhao, Y.L.; Yan, X.X.; Ma, H. A novel fault diagnosis method for rotor rub-impact based on nonlinear output frequency response functions and stochastic resonance. J. Sound Vib. 2020, 481, 17. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, B.; Liu, Q. Sensitivity Analysis for Rotor Systems with Impact-rub. Mach. Des. Res. 2002, 18, 28–29. [Google Scholar] [CrossRef]
- Yin, Y.; Di, Y.; Yao, Z. Arc-length Continuation Algorithm for Nonlinear Finite Element Equations. Acta Sci. Nat. Univ. Pekin. 2017, 53, 793–800. [Google Scholar] [CrossRef]
- Petrov, E.P.; Ewins, D.J. Analytical formulation of friction interface elements for analysis of nonlinear multi-harmonic vibrations of bladed disks. J. Turbomach. Trans. ASME 2003, 125, 364–371. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2015, 248, 869–887. [Google Scholar] [CrossRef]



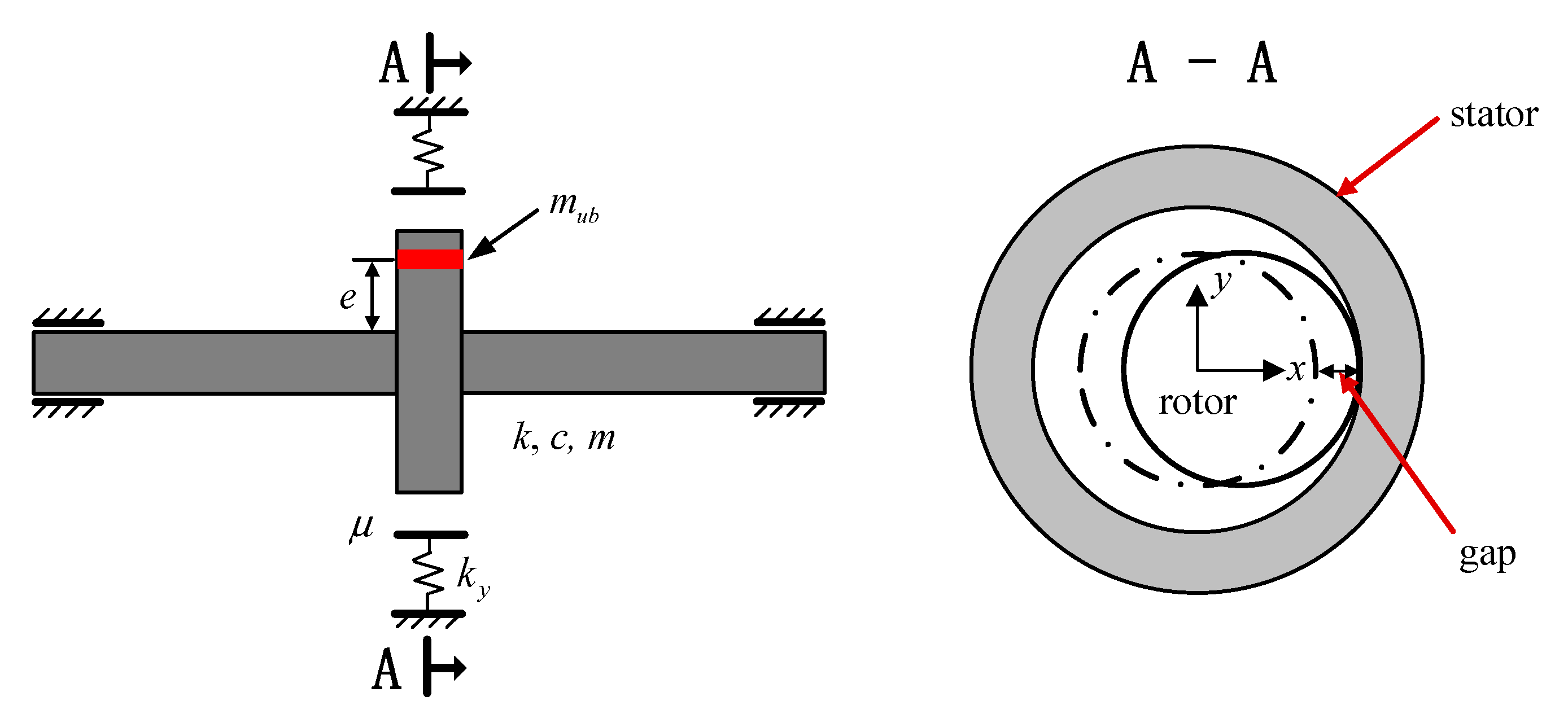


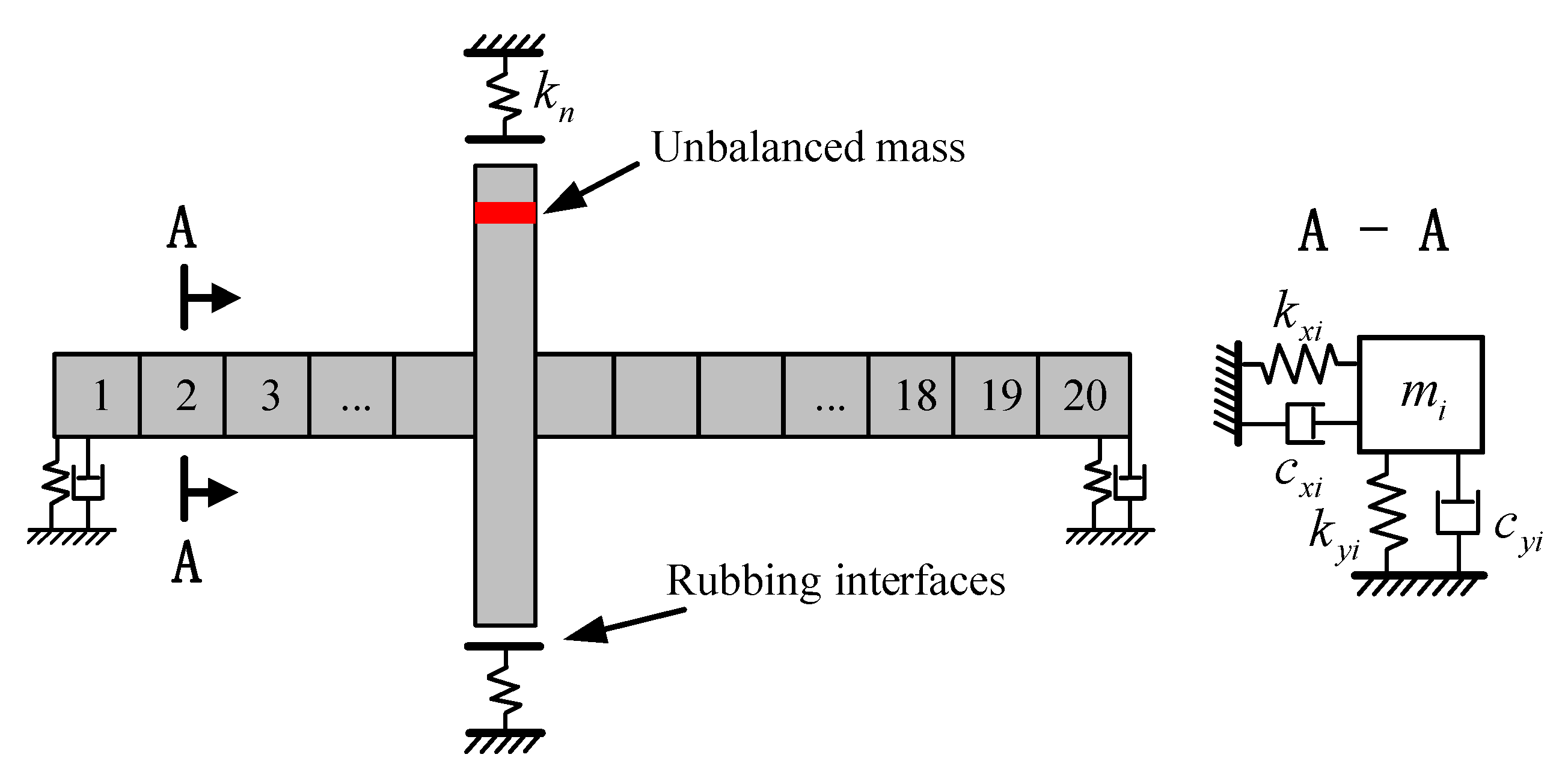

| Parameter Name | Unit | Value |
|---|---|---|
| Eccentric distance e | mm | 0.4 |
| Stiffness k | N/m | 5 × 104 |
| Mass m | kg | 2 |
| Damping coefficient c | (N·s)/m | 80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, M.; Zheng, Z.; Xie, Y.; Zhang, D. Local Sensitivity Analysis of Steady-State Response of Rotors with Rub-Impact to Parameters of Rubbing Interfaces. Appl. Sci. 2021, 11, 1307. https://doi.org/10.3390/app11031307
Jiang M, Zheng Z, Xie Y, Zhang D. Local Sensitivity Analysis of Steady-State Response of Rotors with Rub-Impact to Parameters of Rubbing Interfaces. Applied Sciences. 2021; 11(3):1307. https://doi.org/10.3390/app11031307
Chicago/Turabian StyleJiang, Minghong, Zhaoli Zheng, Yonghui Xie, and Di Zhang. 2021. "Local Sensitivity Analysis of Steady-State Response of Rotors with Rub-Impact to Parameters of Rubbing Interfaces" Applied Sciences 11, no. 3: 1307. https://doi.org/10.3390/app11031307






