Numerical Study on Track–Bridge Interaction of Integral Railway Rigid-Frame Bridge
Abstract
:1. Introduction
2. Track–Bridge Interaction of Integral Rigid-Frame Bridge
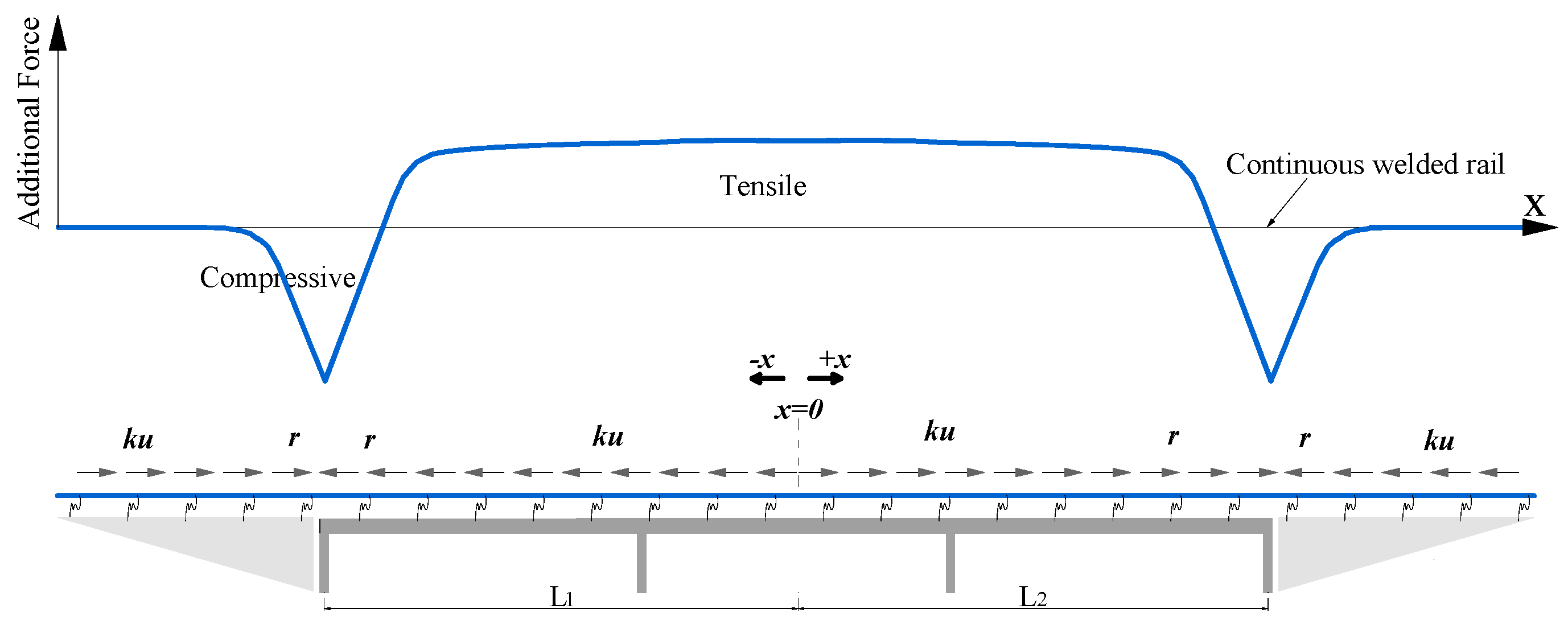
2.1. Basic Principle
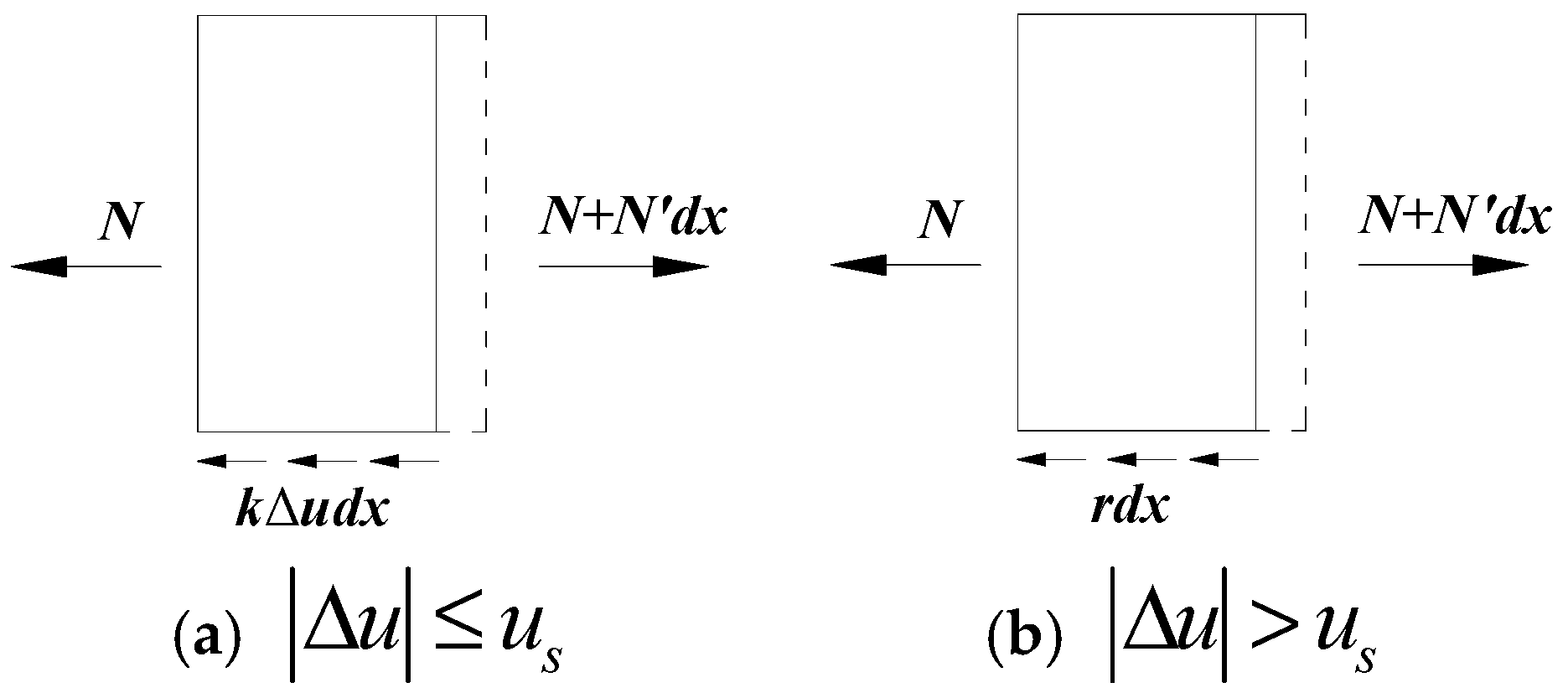
2.2. Differential Equation
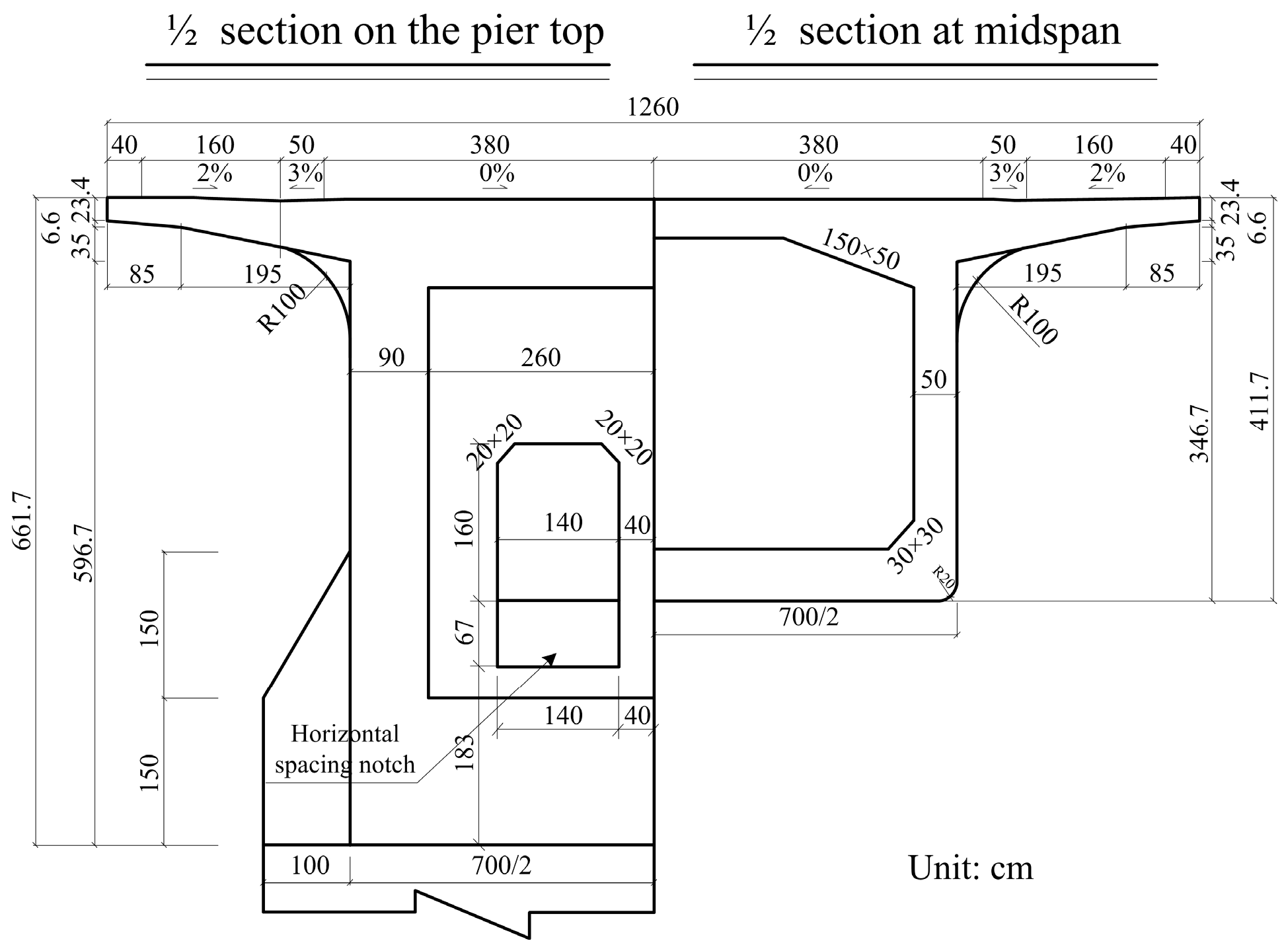
3. Project Introduction and Fine Element Model
4. Analysis of Additional Longitudinal Forces
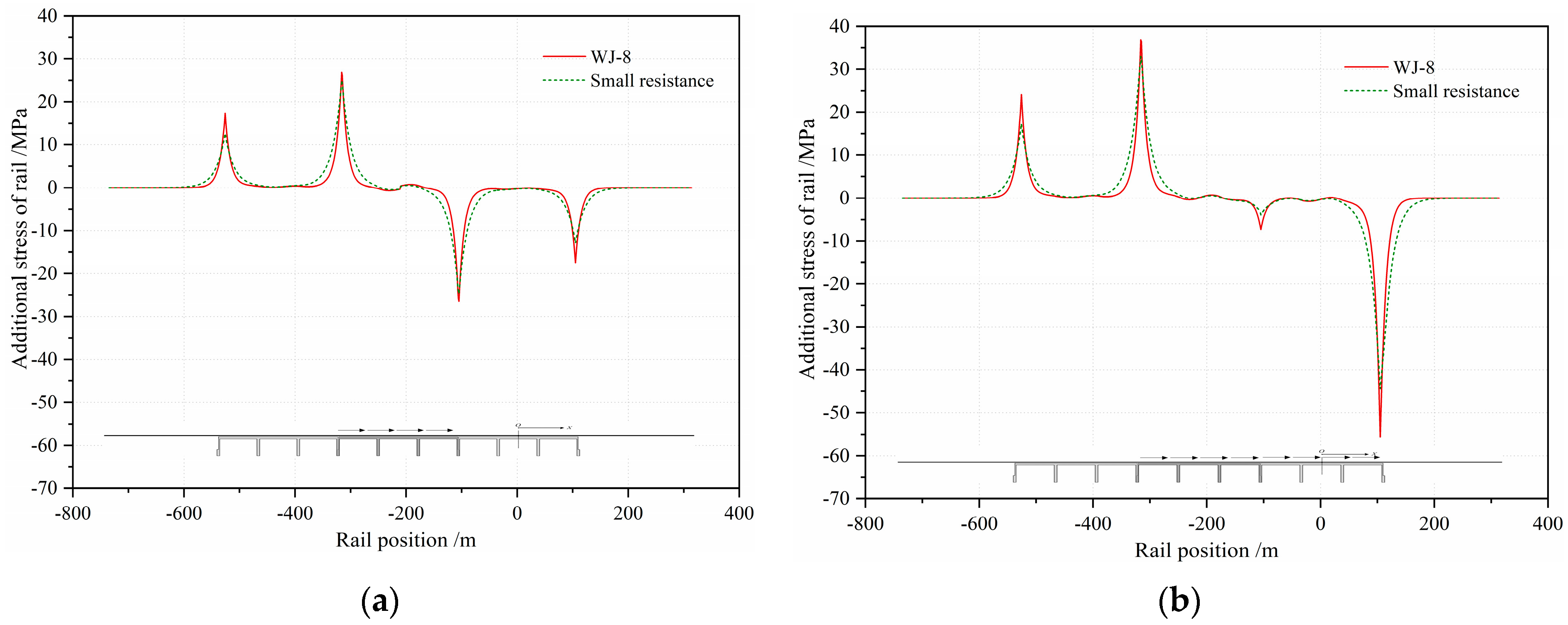
4.1. Additional Expansion Force
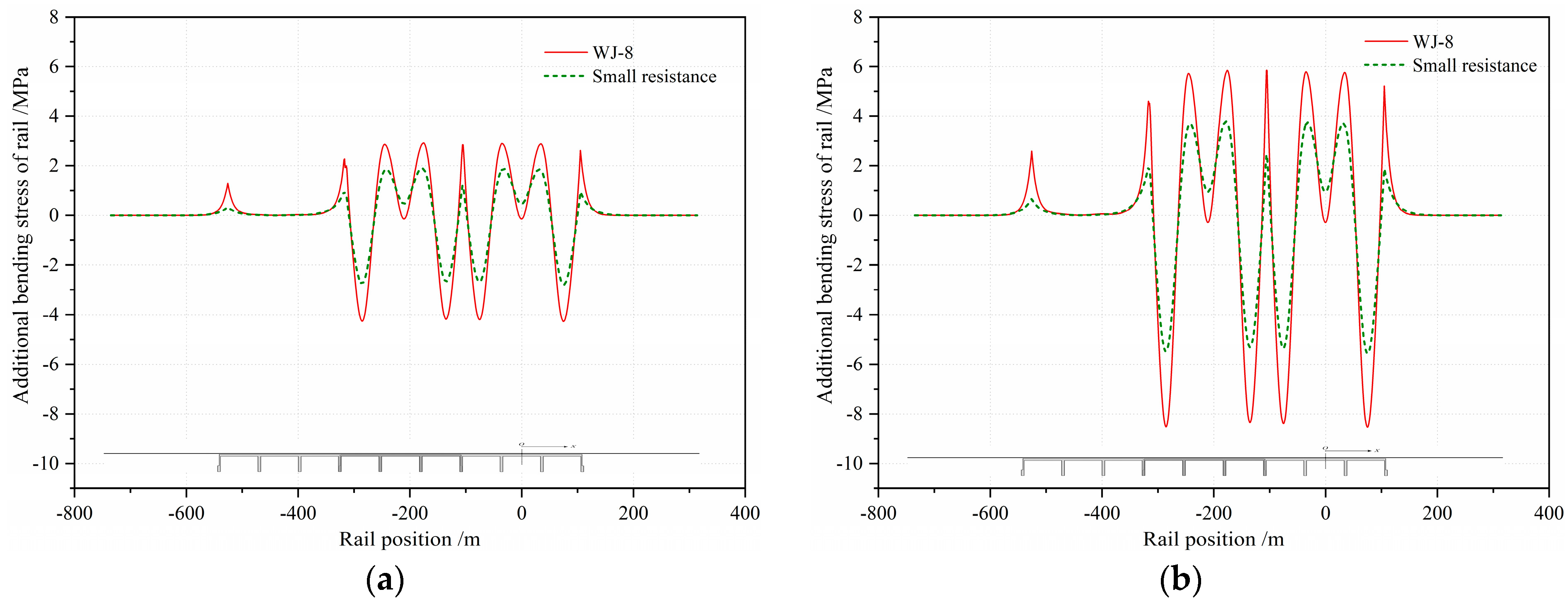
4.2. Additional Bending Force
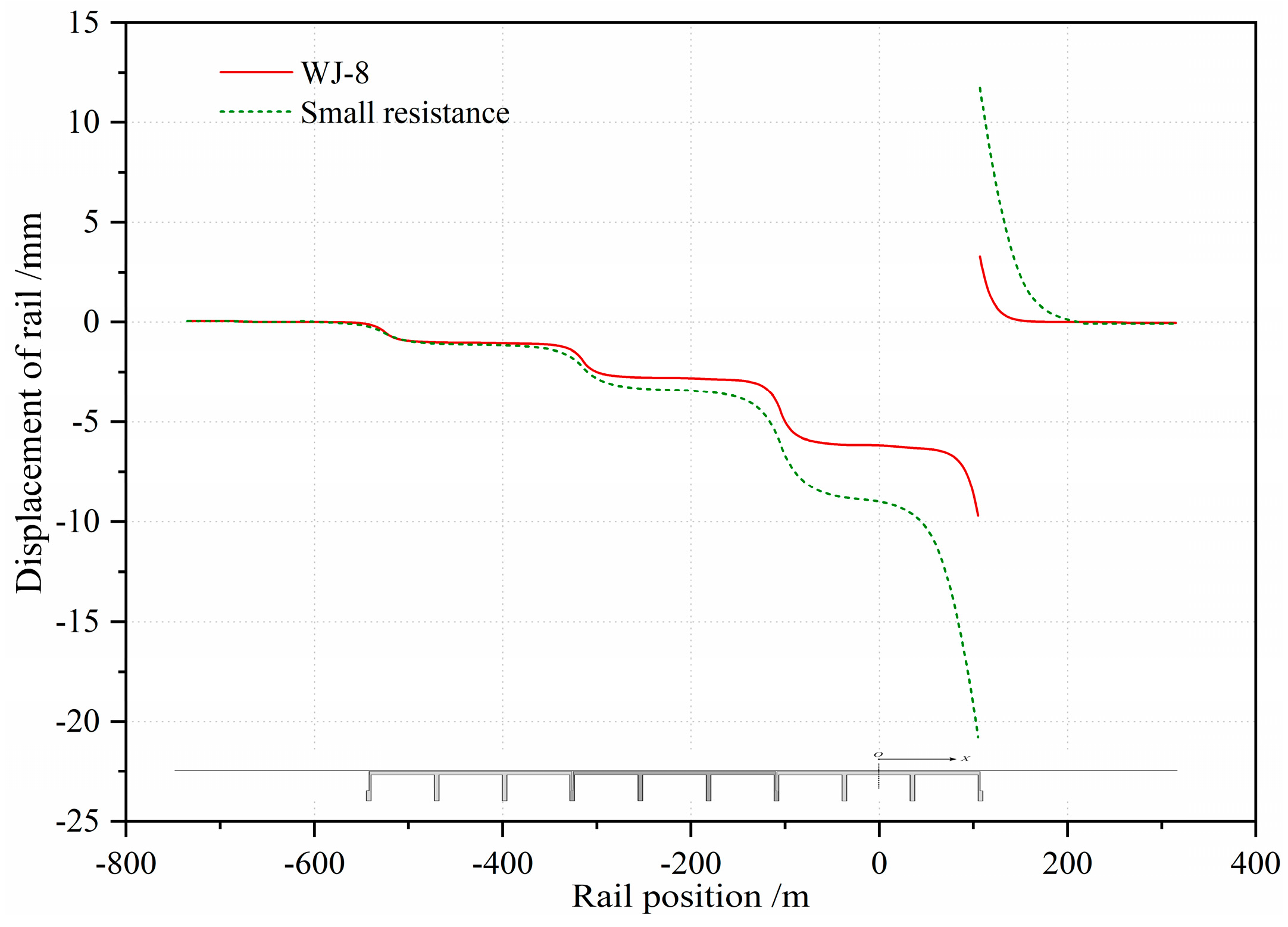
4.3. Additional Braking Force
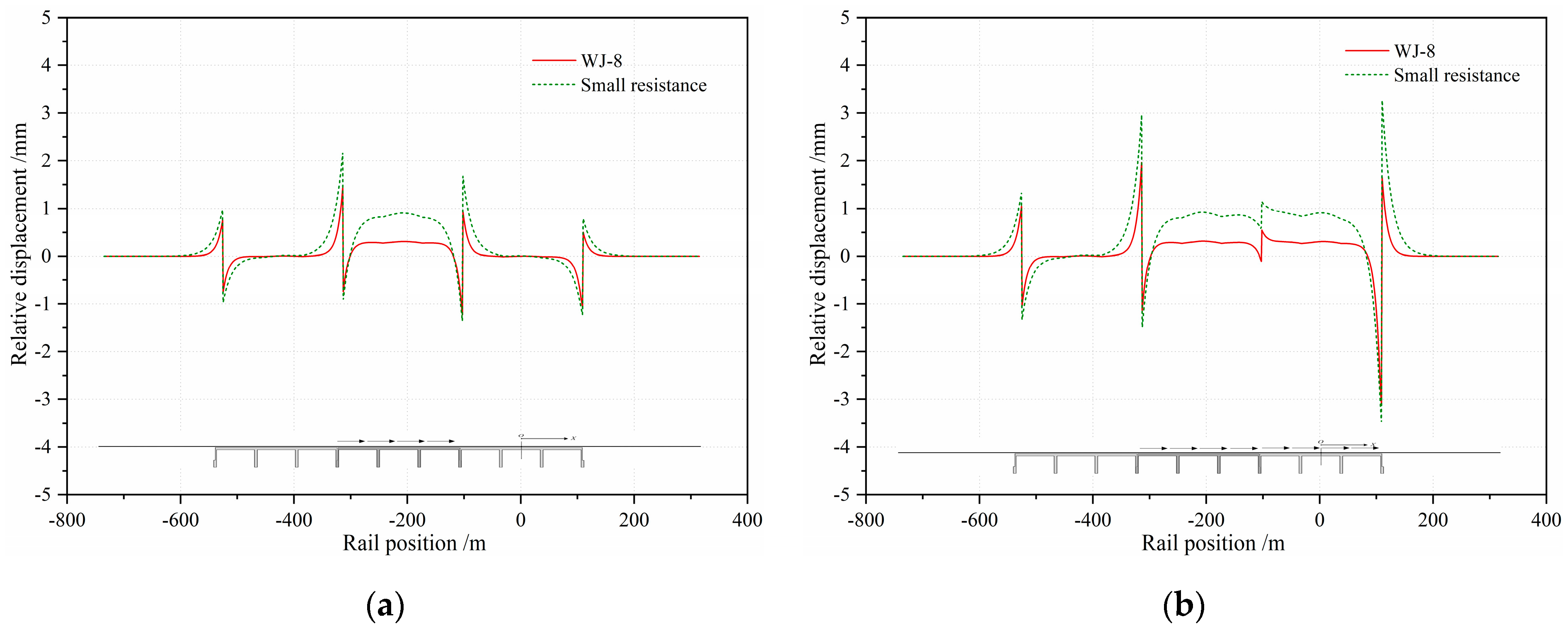
4.4. Rail-Broken Gap
5. Parameters Study
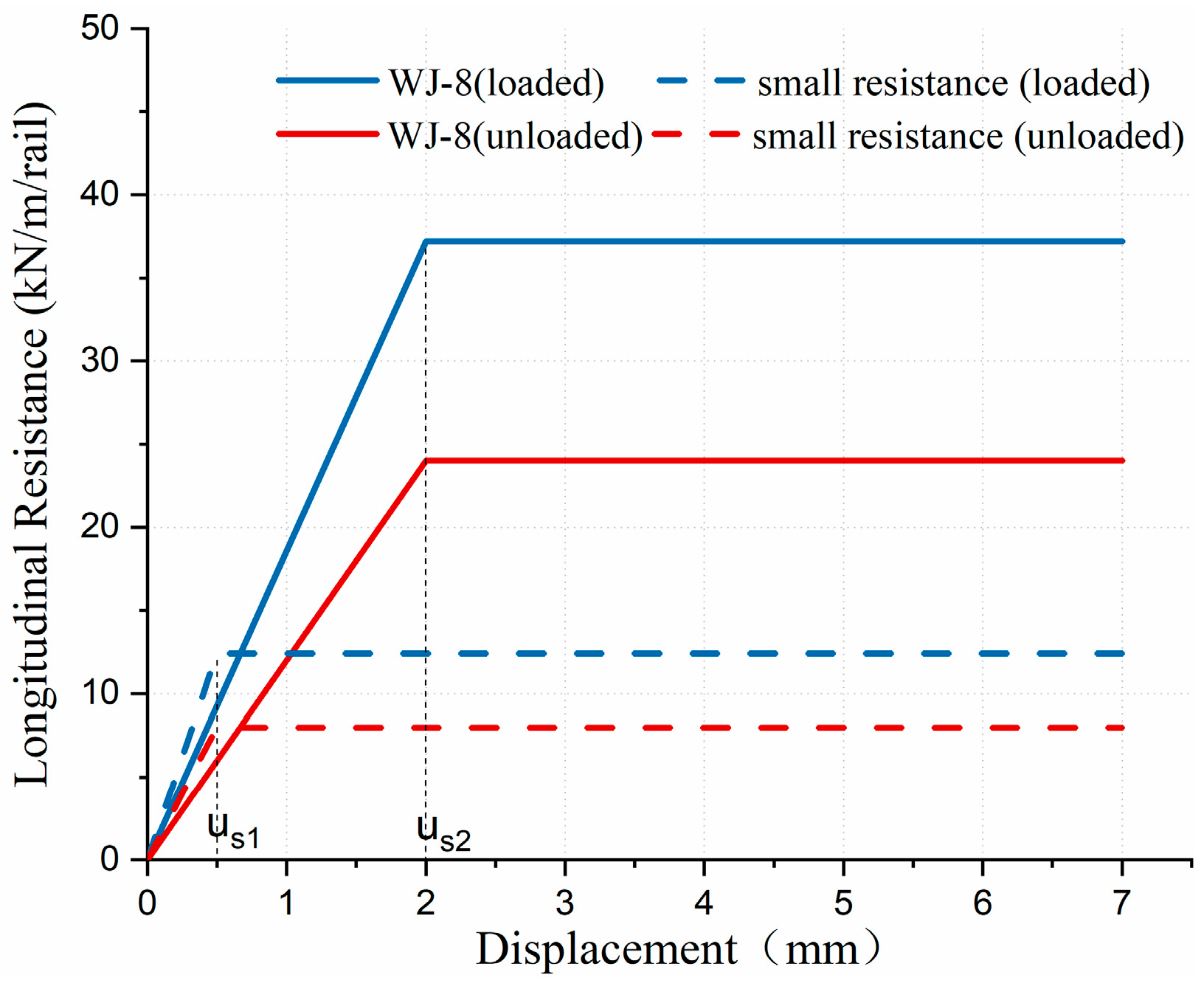
5.1. Longitudinal Resistance
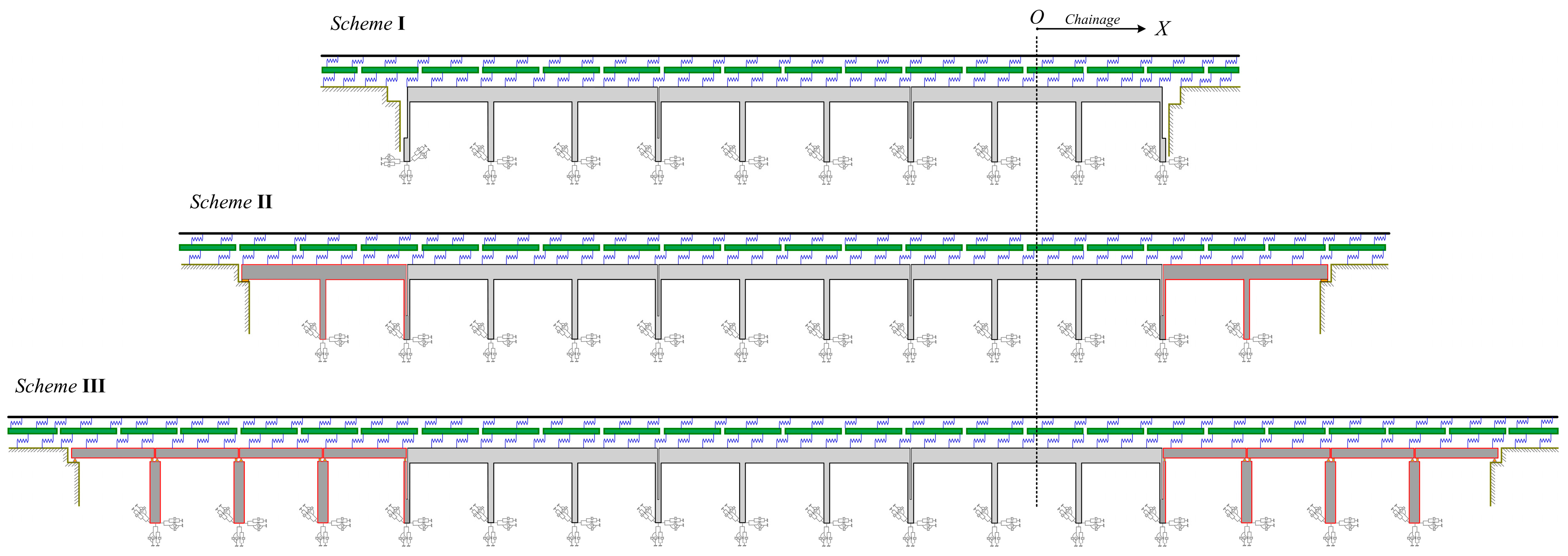
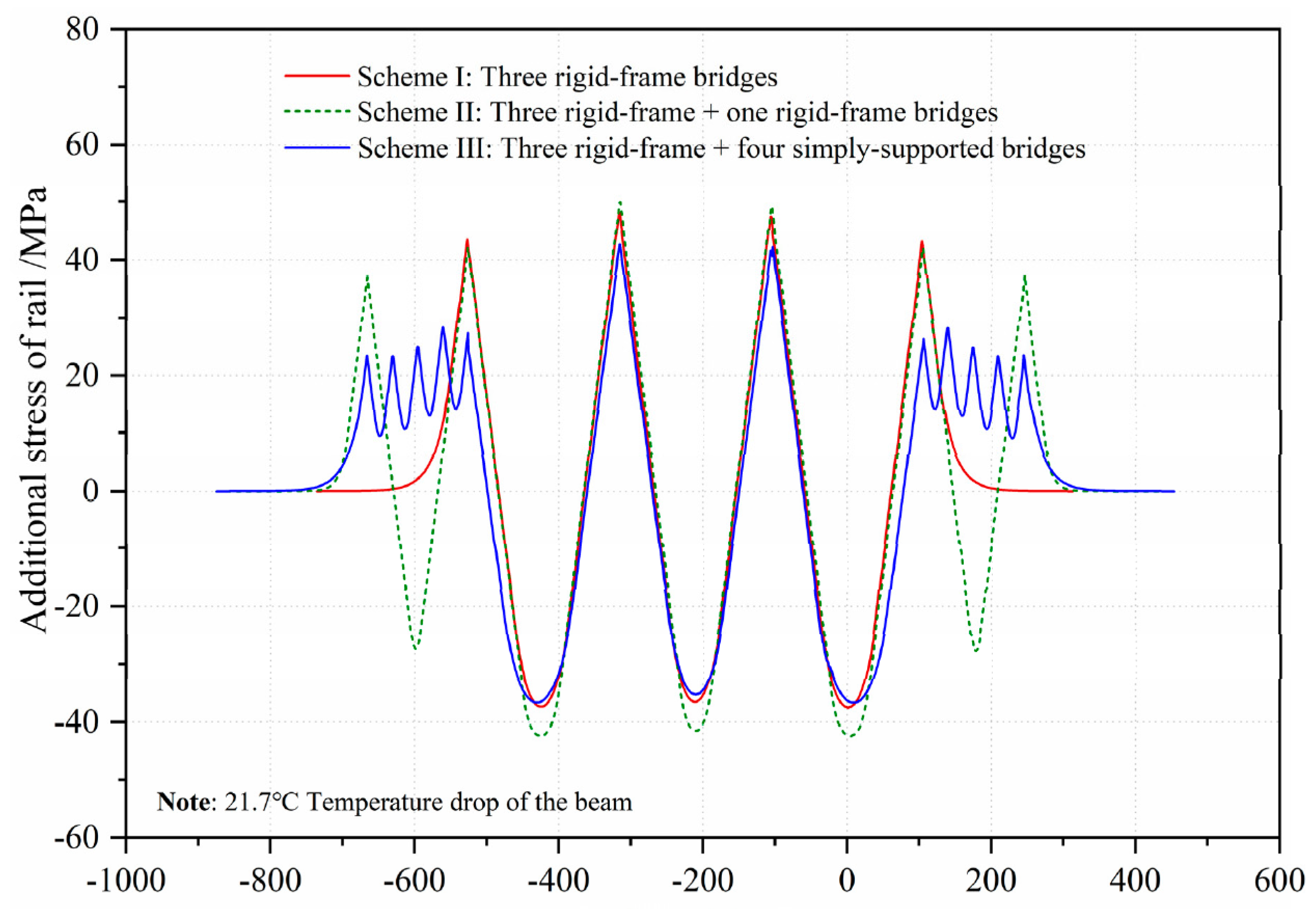
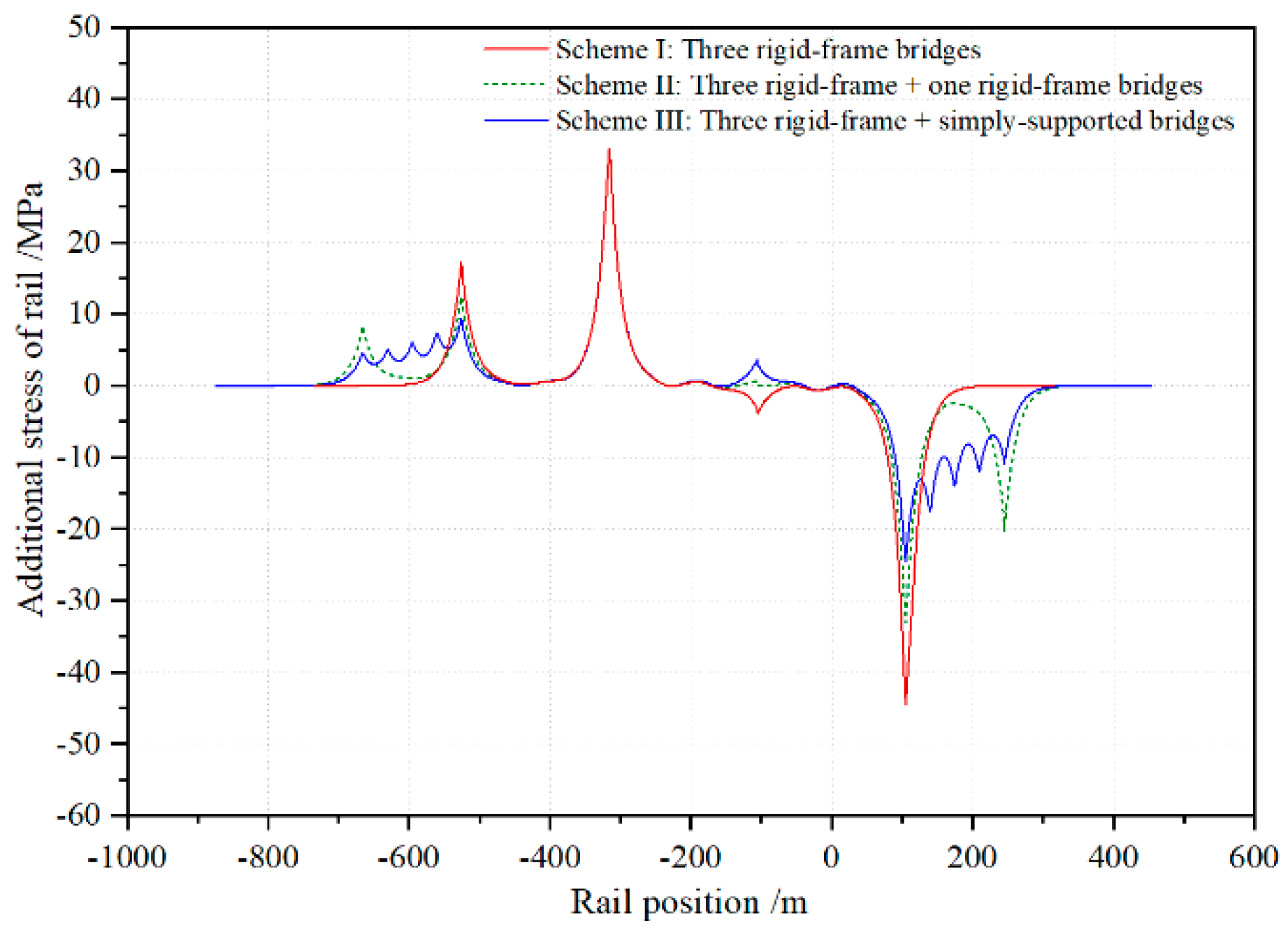
5.2. Influence of the Arrangement Schemes of Adjacent Bridges
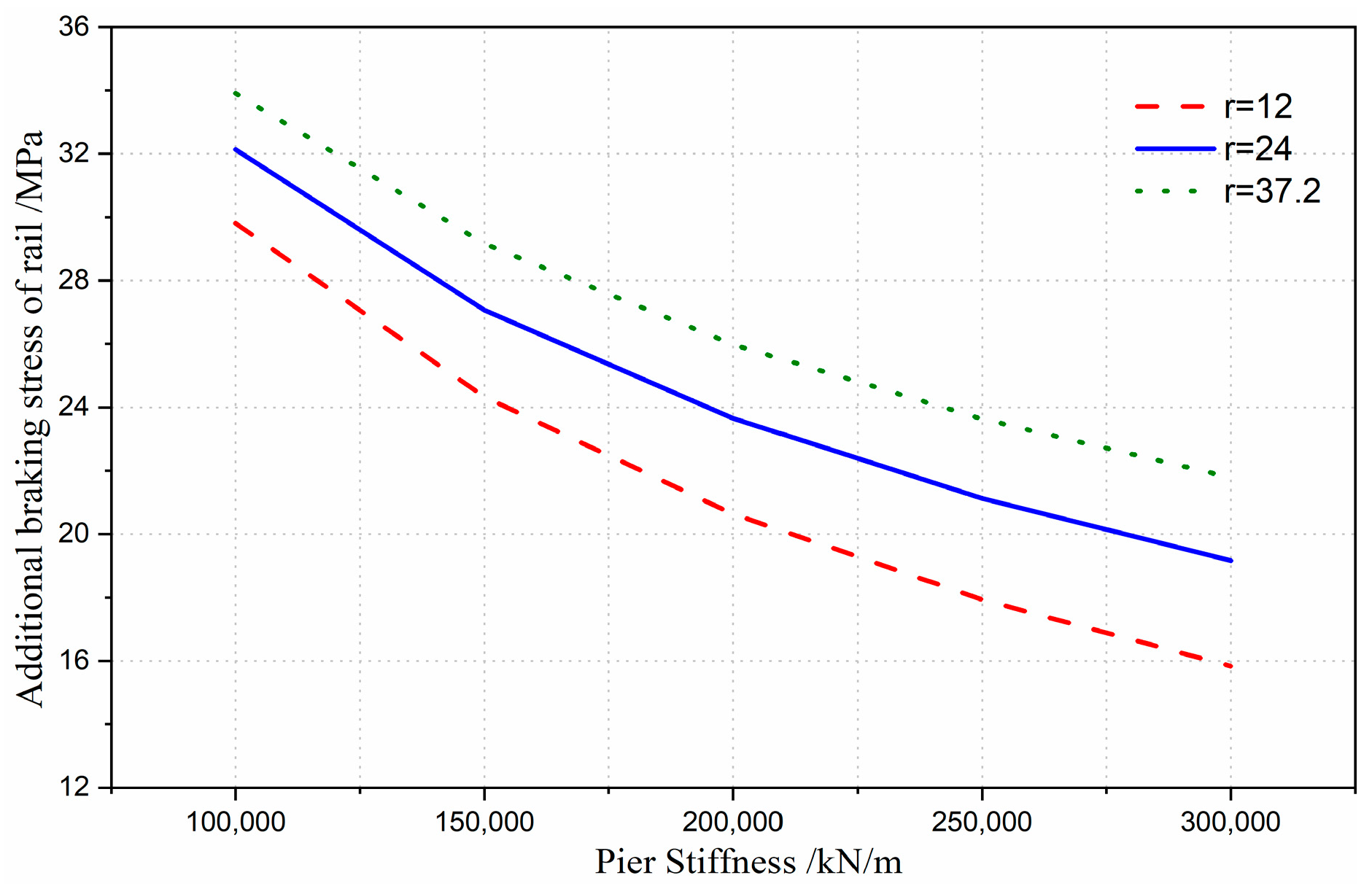
5.3. Influence of the Pier Stiffness
6. Conclusions
- (1)
- The additional expansion force accounts for the largest proportion of the additional force of integral rigid-frame bridges, followed by the additional braking force. Due to the large vertical stiffness of this kind of bridge, the additional bending force is small and can be ignored.
- (2)
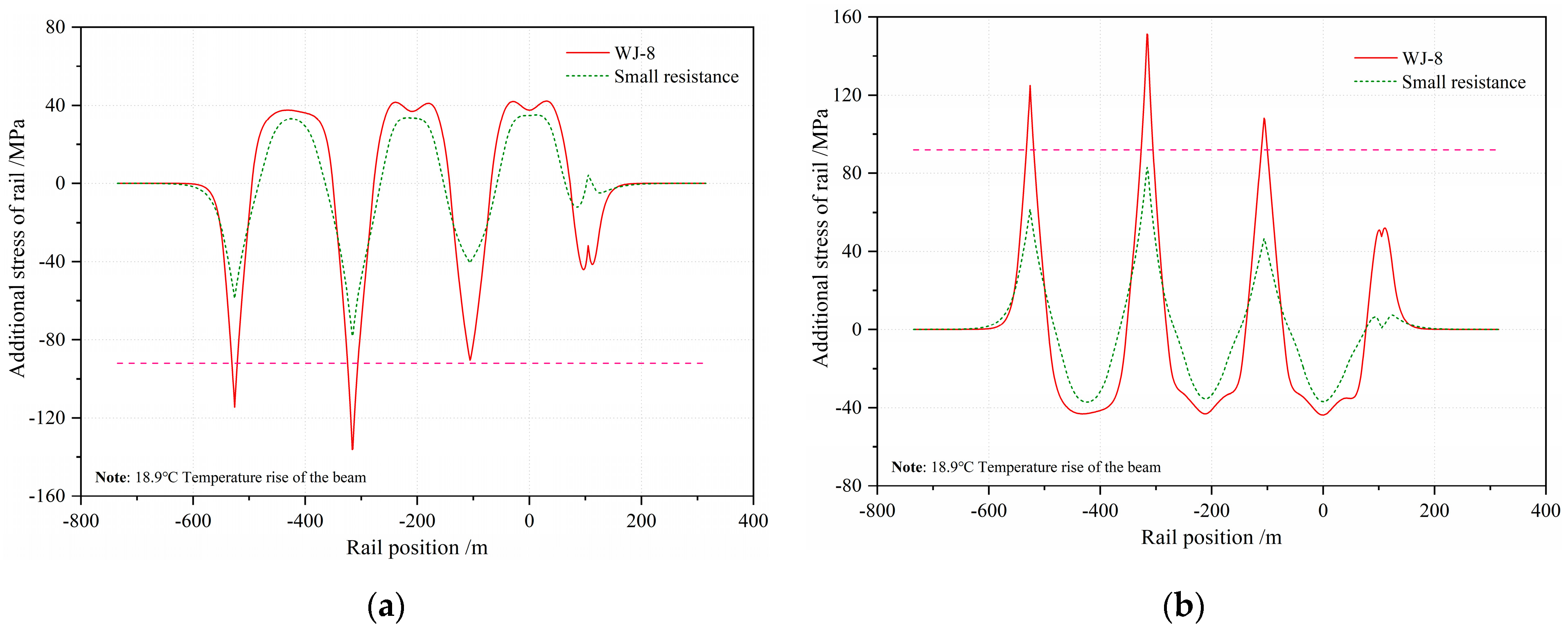
- Through comparative studies of two types of fasteners with different longitudinal resistances, this study verified that a decrease of resistance weakens the various additional forces caused by the interaction between track and bridge; notably, the additional expansion stress of the rail decreased by 55%. However, the rail broken gap increases greatly.
- (3)
- For this 3 × 70 m integral rigid-frame bridge, adopting the widely-used WJ-8 fasteners, the total additional stresses reached −143.1 MPa and 151.7 MPa, which both exceed the standard limit in the UIC code. If no rail expansion joints are arranged, small resistance fasteners are suggested to be adopted for this new HSR line to reduce the additional stress of the CWR.
- (4)
- By adopting 4 × 32 m simply supported beams as the adjacent span arrangement scheme, the additional expansion stress and the additional braking stress of the rails in the integral rigid-frame bridge were less than the corresponding stresses in other schemes.
- (5)
- The minimum threshold value of the pier stiffness for integral rigid-frame bridges is closely related to the longitudinal resistance of HSR lines. With an increase of the longitudinal resistance between the CWR and the bridge, the minimum threshold value of the pier stiffness increases accordingly.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Esveld, L.C. Modern Railway Track, 2nd ed.; MRT Production: Kâğıthane/İstanbul, Turkey, 2001. [Google Scholar]
- Guang, Z.Y. Railway Continuous Welded Rail, 4th ed.; China Railway Publishing House: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Frýba, L. Dynamics of Railway Bridges; Thomas Telford Ltd.: London, UK, 1996. [Google Scholar]
- Gao, L. Research and Application of Key Technologies of Continuous Welded Rails on High-Speed Railway; China Railway Publishing House: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Yang, G.T.; Bradford, M.A. Thermal-induced buckling and postbuckling analysis of continuous railway tracks. Int. J. Solids Struct. 2016, 97, 637–649. [Google Scholar] [CrossRef]
- Frýba, L. Quasi-static distribution of braking and starting forces in rail and bridges. Rail Int. 1974, 22, 698–716. [Google Scholar]
- German Standard DS899/59. Special Procedures on Railway Shinkansen Bridge; Bridge Institute of Railway Bridge Authority: Berlin, Germany, 1985. (In German) [Google Scholar]
- International Union of Railways. 774-3R. In Track-Bridge Interaction Recommendations for Calculations, 2nd ed.; UIC International Union of Railways: Paris, France, 2001. [Google Scholar]
- Ruge, P.; Birk, C. Longitudinal forces in continuously welded rails on bridge decks due to nonlinear track-bridge interaction. Comput. Struct. 2007, 85, 458–475. [Google Scholar] [CrossRef]
- Ruge, P.; Widarda, D.R.; Schmälzlin, G.; Bagayoko, L. Longitudinal track-bridge interaction due to sudden change of coupling interface. Comput. Struct. 2009, 87, 47–58. [Google Scholar] [CrossRef]
- Calçada, R.; Delgado, R.; e Matos, A.C.; Goicolea, J.M.; Gabaldon, F. Track-Bridge Interaction on High-Speed Railways: Selected and Revised Papers from the Workshop on Track-Bridge Interaction on High-Speed Railways; CRC Press: Porto, Portugal, 2008. [Google Scholar]
- Zhang, J.; Wu, D.J.; Li, Q. Loading-history-based track-bridge interaction analysis with experimental fastener resistance. Eng. Struct. 2015, 83, 62–73. [Google Scholar] [CrossRef]
- Yang, S.C.; Jang, S.Y. Track-bridge interaction analysis using interface elements adaptive to various loading case. J. Bridge Eng. 2016, 21, 04016056. [Google Scholar] [CrossRef]
- Dai, G.L.; Ge, H.; Liu, W.S.; Chen, Y.F. Interaction analysis of continuous slab track (CST) on long-span continuous high-speed rail bridges. Struct. Eng. Mech. 2017, 63, 713–723. [Google Scholar]
- Choi, H.S.; Lee, K.C.; Lee, S.C.; Lee, J. Interaction analysis of sliding slab track on railway bridge considering behavior of end-supporting anchors. Int. J. Steel Struct. 2019, 19, 1939–1950. [Google Scholar] [CrossRef]
- Cho, S.; Lee, K.C.; Jang, S.Y.; Lee, I.; Chung, W. Sequential track-bridge interaction analysis of quick-hardening track on bridge considering interlayer friction. Appl. Sci. 2020, 10, 5066. [Google Scholar] [CrossRef]
- Chen, R.; Wang, P.; Wei, X.K. Track-bridge longitudinal interaction of continuous welded rails on arch bridge. Math. Probl. Eng. 2013, 2013, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.S.; Dai, G.L.; Yu, Z.W.; Chen, Y.F.; He, X.H. Interaction between continuous welded rail and long-span steel truss arch bridge of a high-speed railway under seismic action. Struct. Infrastruct. Eng. 2018, 14, 1051–1064. [Google Scholar] [CrossRef]
- Cai, X.P.; Liu, W.L.; Xie, K.Z.; Zhu, W.J.; Tan, X.Y.; Gao, Y.J. Layout optimization of rail expansion joint on long-span cable-stayed bridge for high-speed railway. Adv. Civ. Eng. 2020, 2020. [Google Scholar]
- Yan, B.; Zhang, G.X.; Han, Z.S.; Lou, P. Longitudinal force of continuously welded rail on suspension bridge with length exceeding 1000 m. Struct. Eng. Int. 2019, 29, 390–395. [Google Scholar] [CrossRef]
- Marx, S.; Seidl, G. Integral railway bridges in Germany. Struct. Eng. Int. 2011, 21, 332–340. [Google Scholar] [CrossRef]
- Kang, C.J.; Schneider, S.; Wenner, M.; Marx, S. Development of design and construction of high-speed railway bridges in Germany. Eng. Struct. 2018, 163, 184–196. [Google Scholar] [CrossRef]
- Zhu, L.B. Application of no support continuous rigid-framed system in Line 6. Superv. Test Cost Constr. 2017, 10, 38–41. (In Chinese) [Google Scholar]
- Wen, W.Q.; Wang, D.Z.; Wu, B.; Ling, Y.F.; Kou, Y.C. Design of integral rigid-frame bridge without bearings on high-speed railway. Bridge Constr. 2020, 50, 86–91. (In Chinese) [Google Scholar]
- Xiong, Z.W.; Xie, K.Z.; Liu, H.; Wang, P. Influence of train braking on relative displacement between girder and rail of continuous welded rail upon rigid-frame bridge. Railw. Stand. Des. 2013, 57, 10–14. (In Chinese) [Google Scholar]
- Liu, H.; Ren, J.J.; Liu, Y.; Liu, X.Y. Study on dynamic characteristics of continuously welded rail track on rigid bridge with long steep grade. Railw. Stand. Des. 2015, 59, 5–8. (In Chinese) [Google Scholar]
- Dai, G.L.; Liu, W.S. Applicability of small resistance fastener on long-span continuous bridges of high-speed railway. J. Cent. South Univ. 2013, 20, 1426–1433. [Google Scholar] [CrossRef]
- Liu, W.S.; Dai, G.L.; He, X.H. Sensitive factors research for track-bridge interaction of a long-span X-style steel-box arch bridge on high-speed railway. J. Cent. South Univ. 2013, 20, 3314–3323. [Google Scholar] [CrossRef]
- Qing-yuan, X. Static and Dynamic 3D Finite Element Analysis of Additional Longitudinal Forces Transmission between CWR and High-Speed Railway Bridges [D]; Central South University: Changsha, China, 2005. (In Chinese) [Google Scholar]
- Chinese National Standard, TB10015-2012. Code for Design of Railway Continuous Welded Rail; China Railway Publishing House: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Chinese National Standard, TB-10621-2014. Code for Design of High Speed Railway; China Railway Publishing House: Beijing, China, 2016. (In Chinese) [Google Scholar]

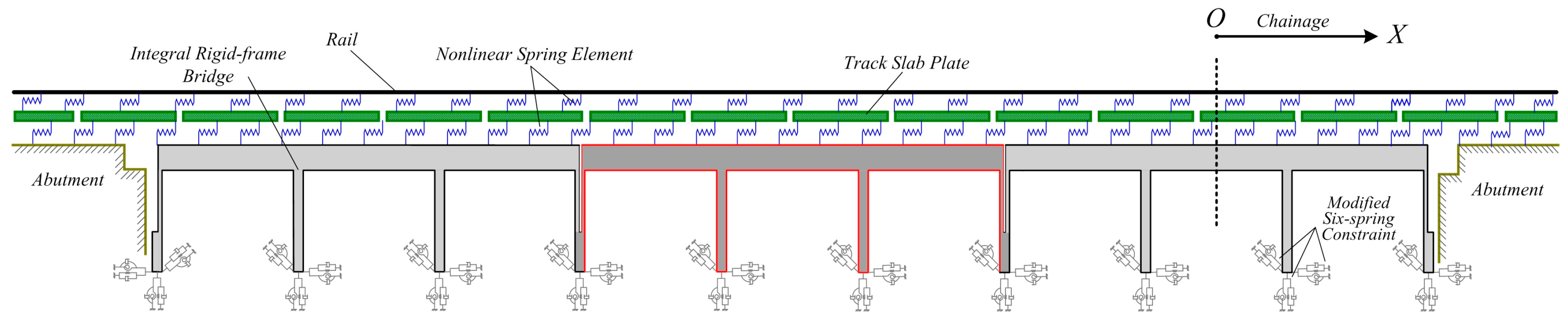
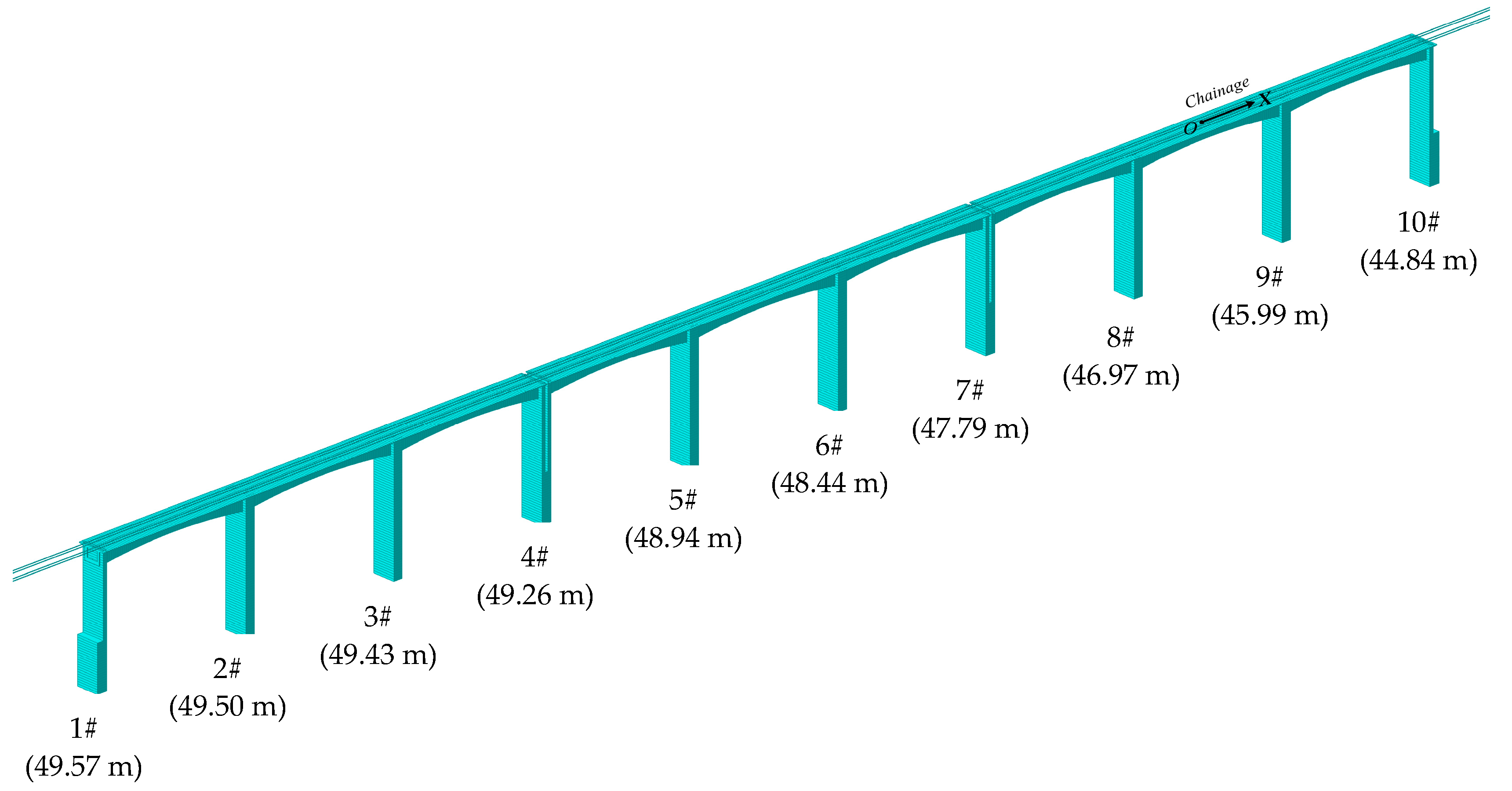
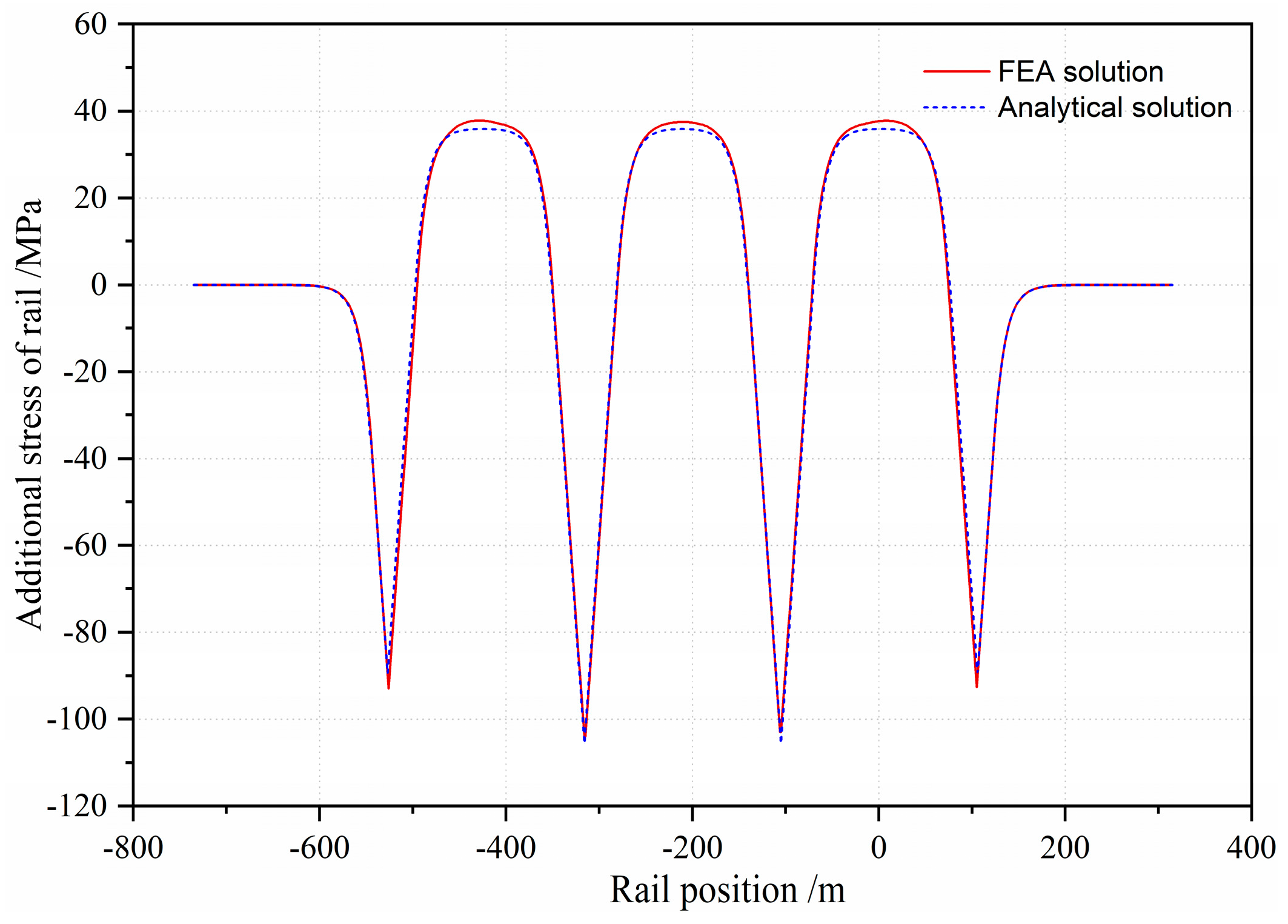
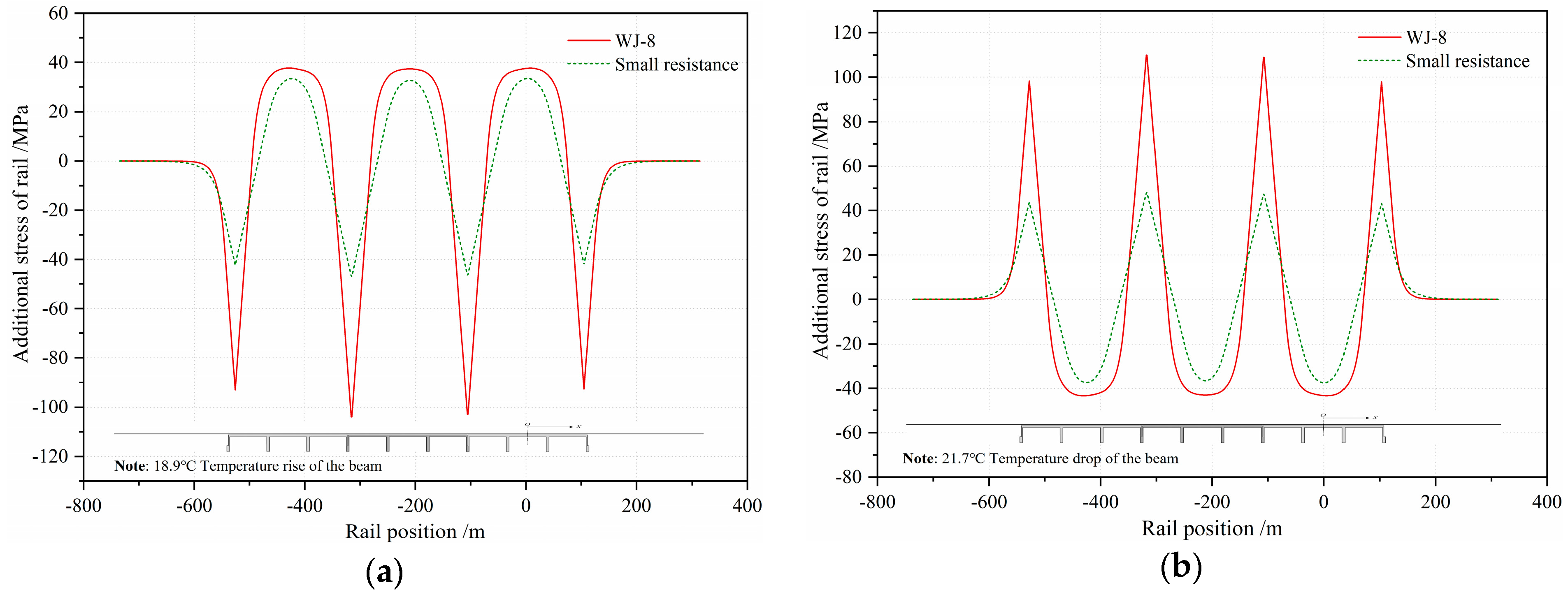



| Structure Layer | Material | Young’s Modulus | Thermal Expansion Coefficient | Poisson’s Ratio | Volume Weight |
|---|---|---|---|---|---|
| Rail | U71 | 2.06 × 105 MPa | 1.18 × 10−5 | 0.3 | 78.5 kN/m3 |
| Slab plate | C40 | 3.40 × 104 MPa | 1.0 × 10−5 | 0.2 | 25 kN/m3 |
| Base plate | C40 | 3.40 × 104 MPa | 1.0 × 10−5 | 0.2 | 25 kN/m3 |
| Bridge beam | C50 | 3.55 × 104 MPa | 1.0 × 10−5 | 0.2 | 25 kN/m3 |
| Pier | C50 | 3.55 × 104 MPa | 1.0 × 10−5 | 0.2 | 25 kN/m3 |
| Connection Constraint | Spring Direction | Spring Type | Spring Stiffness |
|---|---|---|---|
| Rail and track slab | Vertical | Linear spring | 25–35 kN/mm |
| Longitudinal | Nonlinear spring | WJ-8(load) WJ-8(unload) Small(load) Small(unload) | |
| Lateral | Linear spring | 10 kN/mm | |
| Track slab and bed slab (geotextile cushion and groove) | Vertical | Linear spring | −1.0 × 106 kN/mm |
| Longitudinal and lateral | Linear spring | 1.0 × 108 kN/mm |
| Area | Highest Air Temperature/°C | Lowest Air Temperature/°C | Highest Rail Temperature/°C | Lowest Rail Temperature/°C | Note |
|---|---|---|---|---|---|
| Fuzhou | 41.7 | −1.7 | 61.7 | −1.7 | Code for Design of Railway CWR (TB10015-2012) |
| Quanzhou | 38.9 | −1.7 | 61.7 | −2.3 | Field survey(bridge location) |
| Fasteners | Design Stress-Free Rail Temperature/°C | Maximum Temperature Drop of the Rail/°C | Broken Gap /mm | Allowable Gap /mm |
|---|---|---|---|---|
| WJ-8 fastener | 30 ± 5 | 37.3 | 12.9 | 70 |
| Small resistance fastener | 30 ± 5 | 37.3 | 38.6 | 70 |
| Schemes | Additional Expansion Stress of Rail /MPa | Additional Bending Stress of Rail /MPa | Additional Braking Stress of Rail /MPa | Total Additional Stress of Rail /MPa | Gap /mm | ||
|---|---|---|---|---|---|---|---|
| Min/Max | Min/Max | Min/Max | Min/Max | Min/Max | Min/Max | Max | |
| WJ-8 fastener | −103/109 | −4.3/2.9 | −8.5/5.9 | −26.5/26.9 | −55.6/36.8 | −143.1/151.7 | 12.9 |
| Small resistance fastener | −46.9/48.1 | −2.8/1.9 | −5.6/3.8 | −24.7/25.0 | −44.5/33.0 | −84.6/84.9 | 38.6 |
| Limit | / | / | / | / | / | −92/92 | 70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Lai, H.; Dai, G.; Rao, S.; Wang, D.; Wu, B. Numerical Study on Track–Bridge Interaction of Integral Railway Rigid-Frame Bridge. Appl. Sci. 2021, 11, 922. https://doi.org/10.3390/app11030922
Liu W, Lai H, Dai G, Rao S, Wang D, Wu B. Numerical Study on Track–Bridge Interaction of Integral Railway Rigid-Frame Bridge. Applied Sciences. 2021; 11(3):922. https://doi.org/10.3390/app11030922
Chicago/Turabian StyleLiu, Wenshuo, Hao Lai, Gonglian Dai, Shiwei Rao, Dezhi Wang, and Bing Wu. 2021. "Numerical Study on Track–Bridge Interaction of Integral Railway Rigid-Frame Bridge" Applied Sciences 11, no. 3: 922. https://doi.org/10.3390/app11030922
APA StyleLiu, W., Lai, H., Dai, G., Rao, S., Wang, D., & Wu, B. (2021). Numerical Study on Track–Bridge Interaction of Integral Railway Rigid-Frame Bridge. Applied Sciences, 11(3), 922. https://doi.org/10.3390/app11030922





