Vertical Vibrations of Footbridges Due to Group Loading: Effect of Pedestrian–Structure Interaction
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
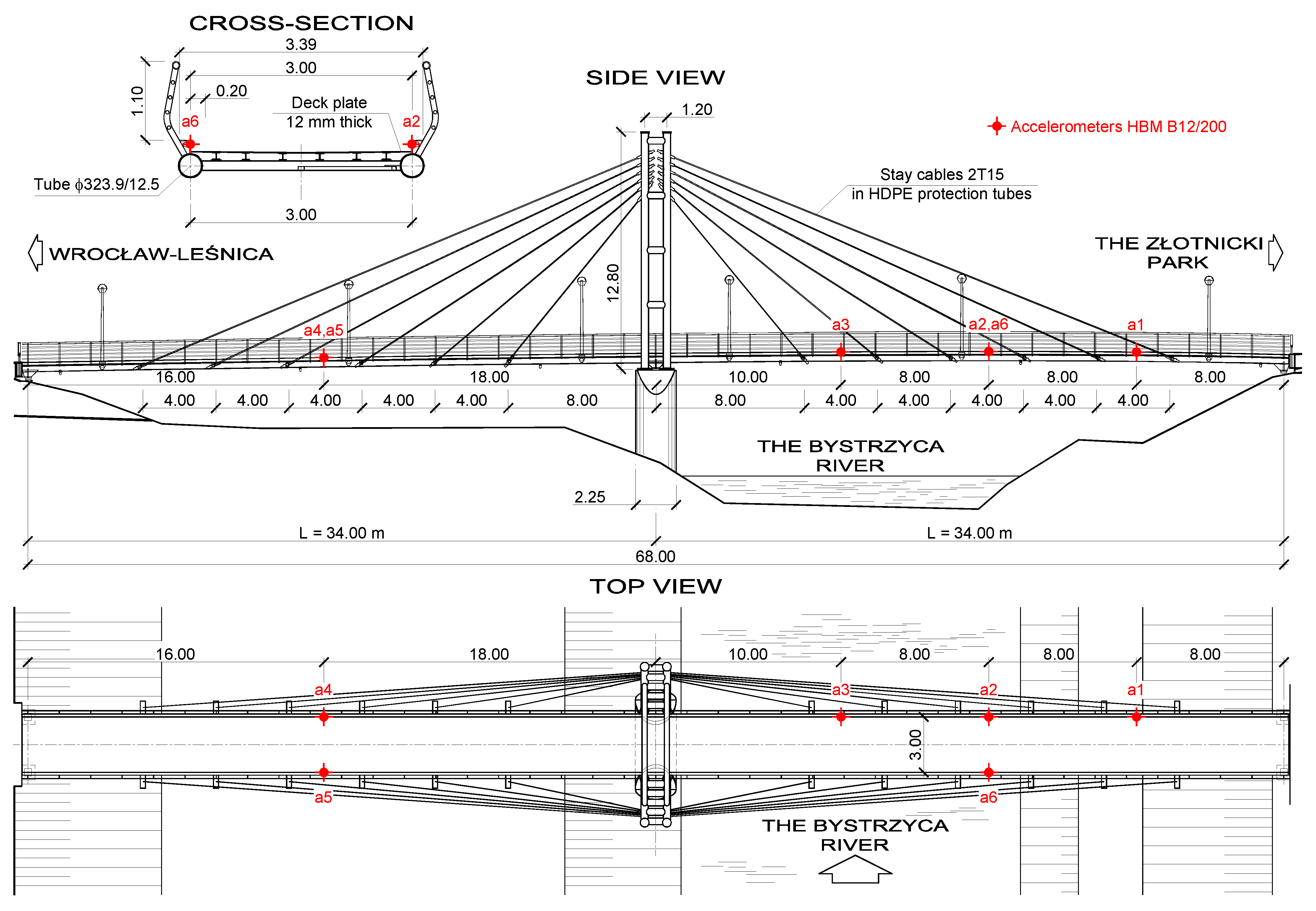
2.1. Test Structure and Pedestrian Tests
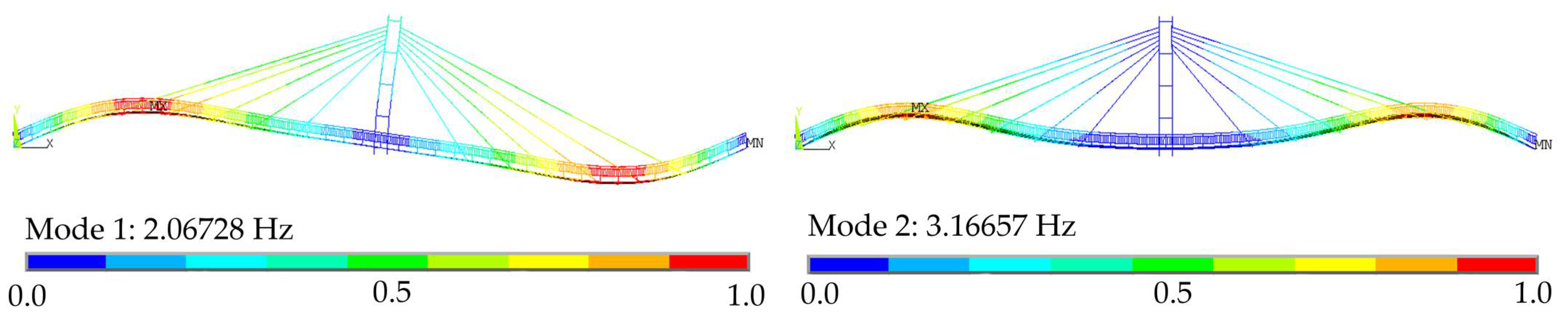
2.2. Procedure for Numerical Simulations
3. Results and Discussions
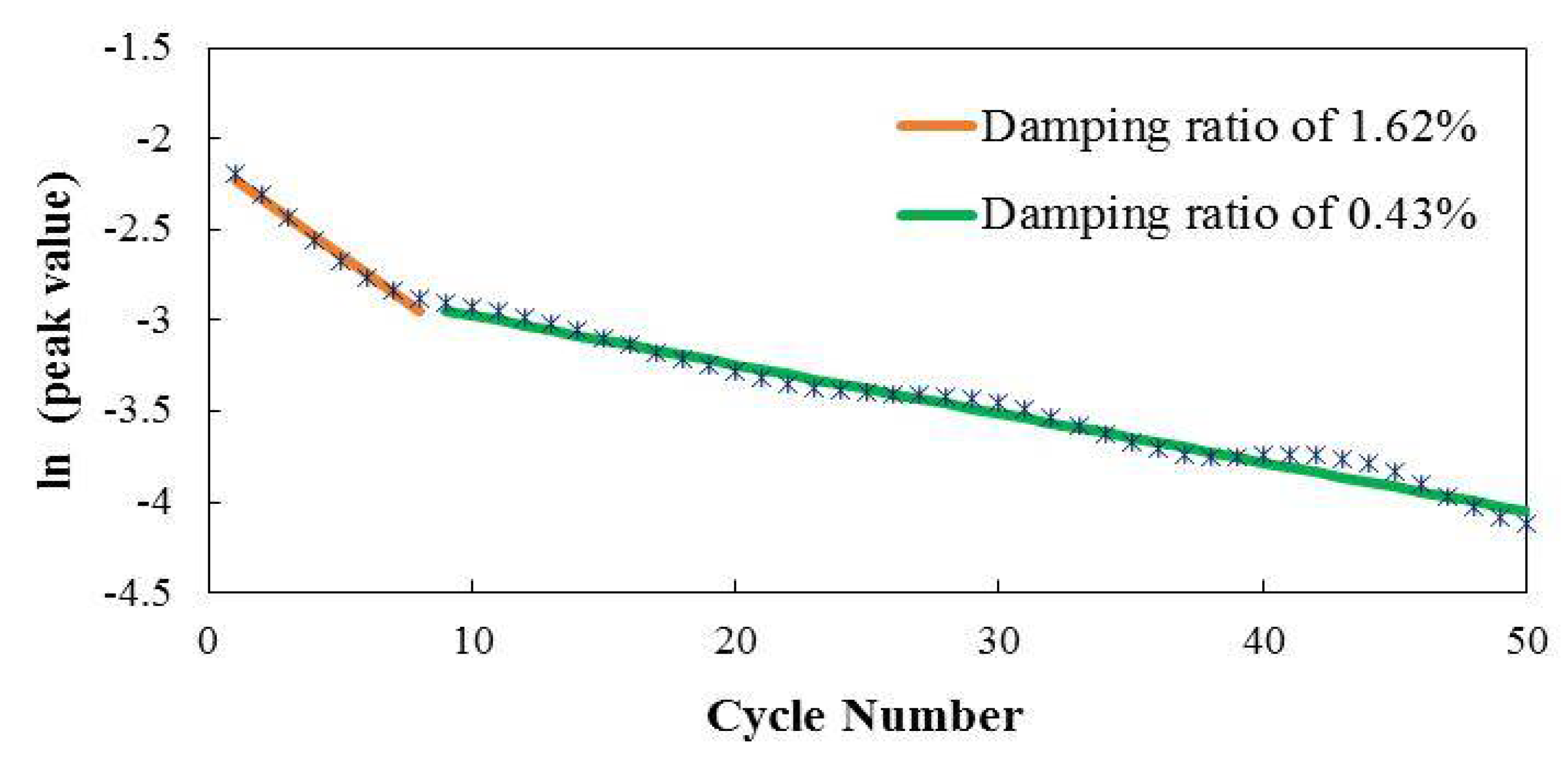
3.1. Obtaining Structural Damping and the DLF of Each Pedestrian
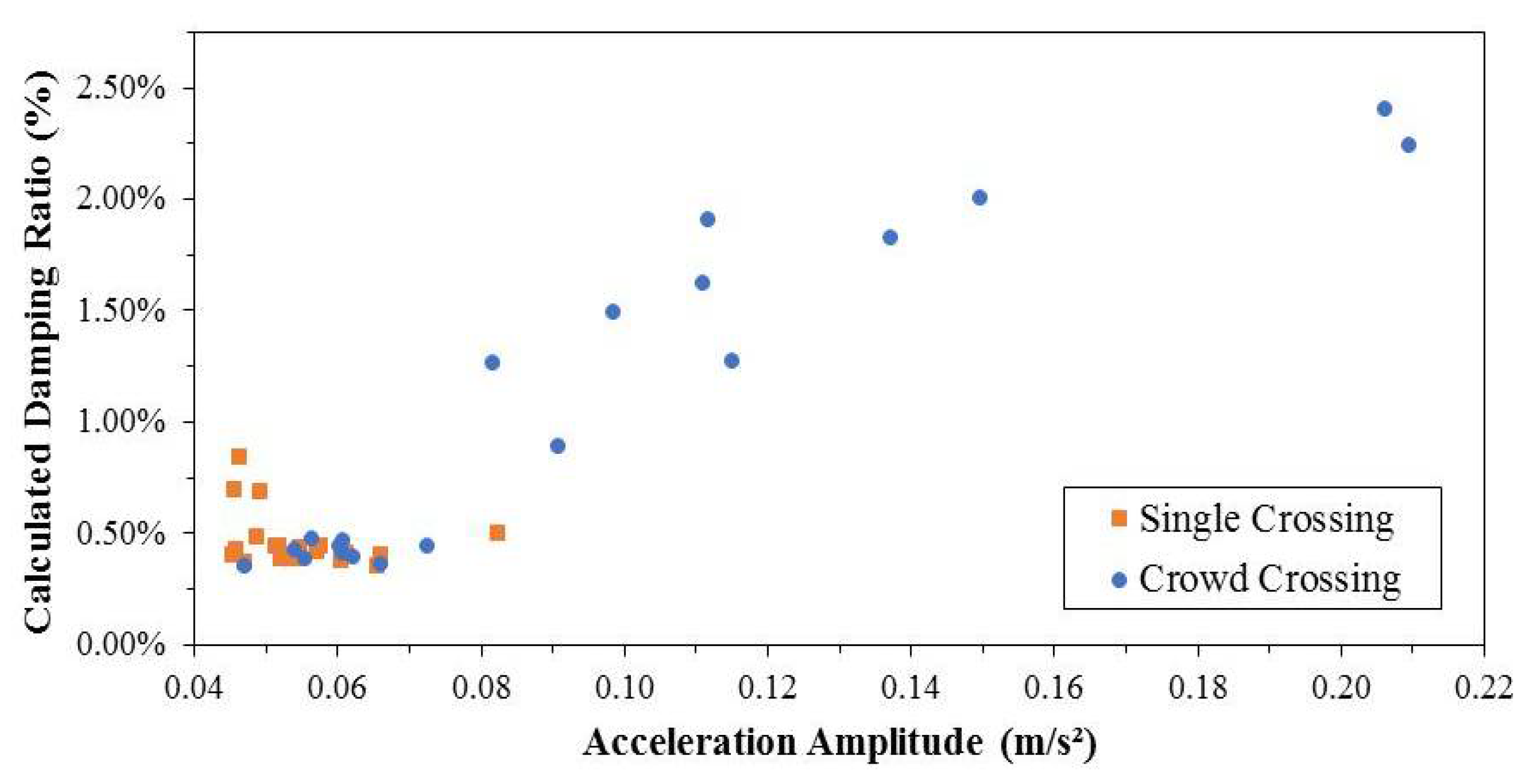
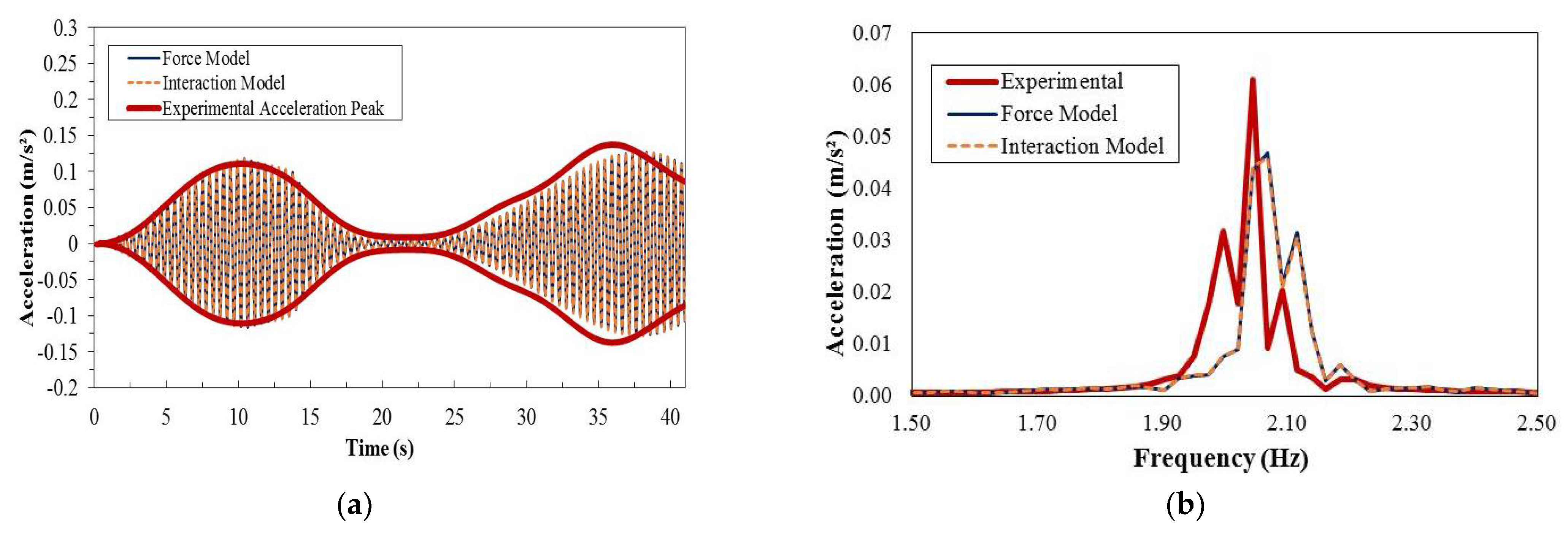
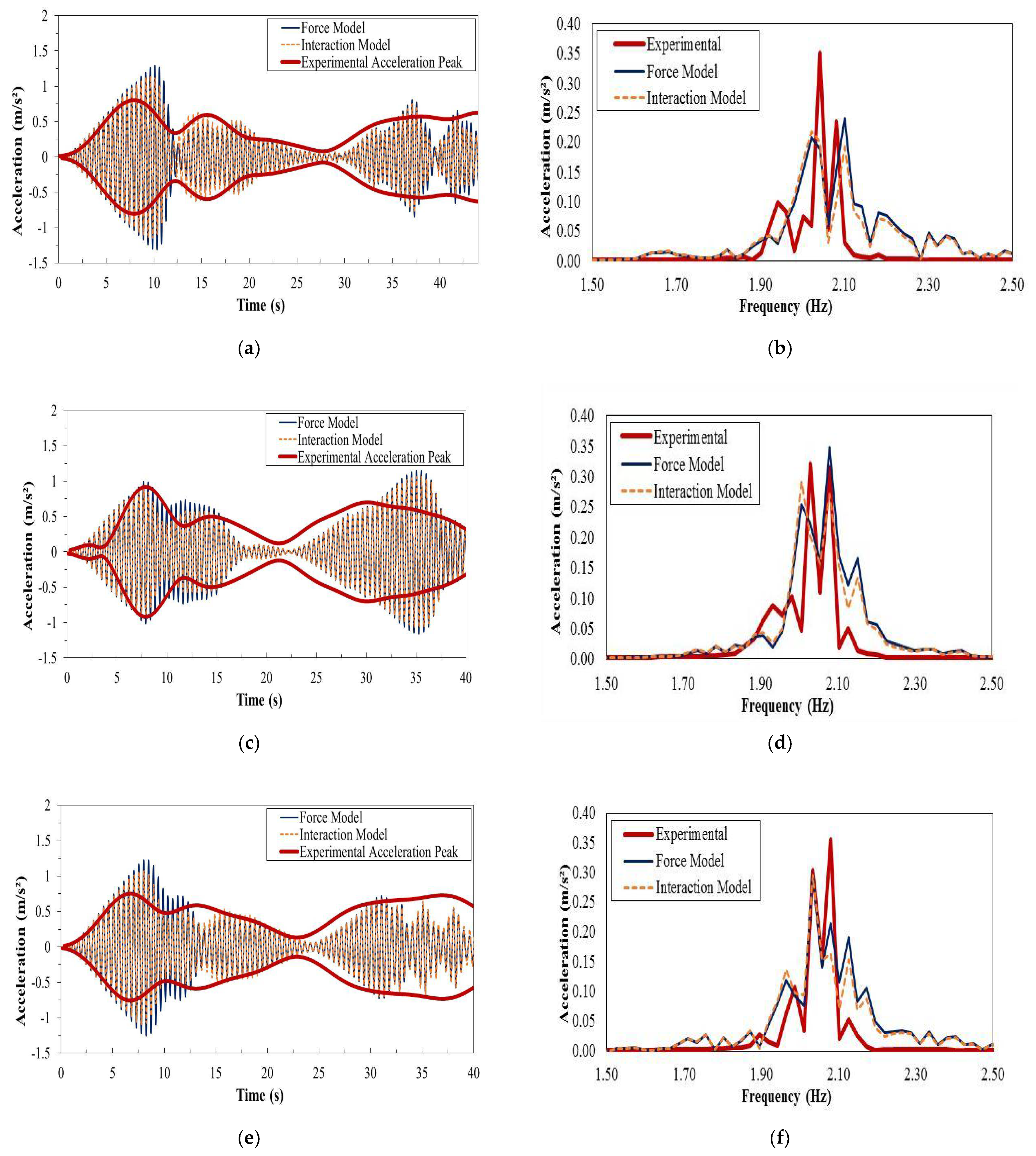
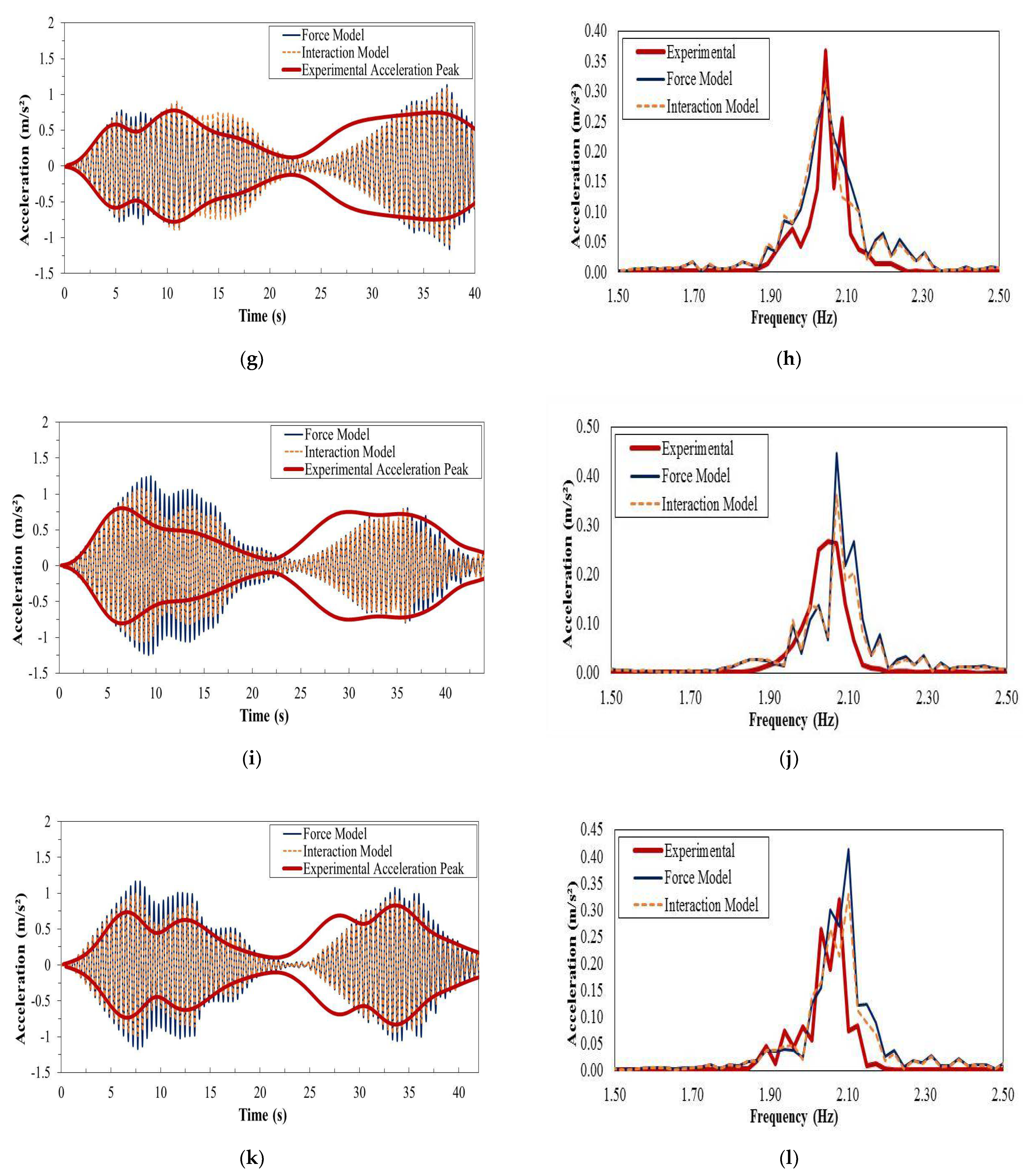
3.2. Investigation of Group Loading
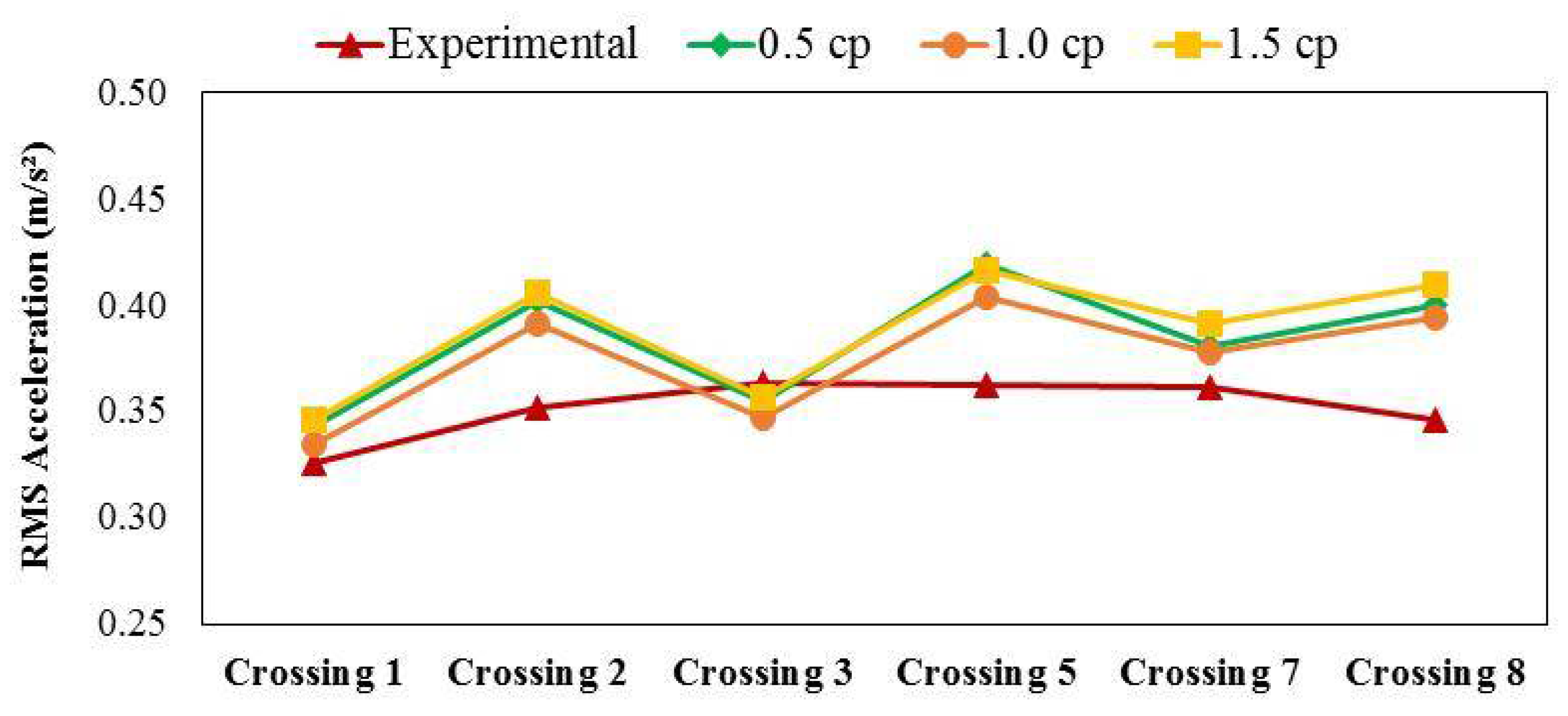
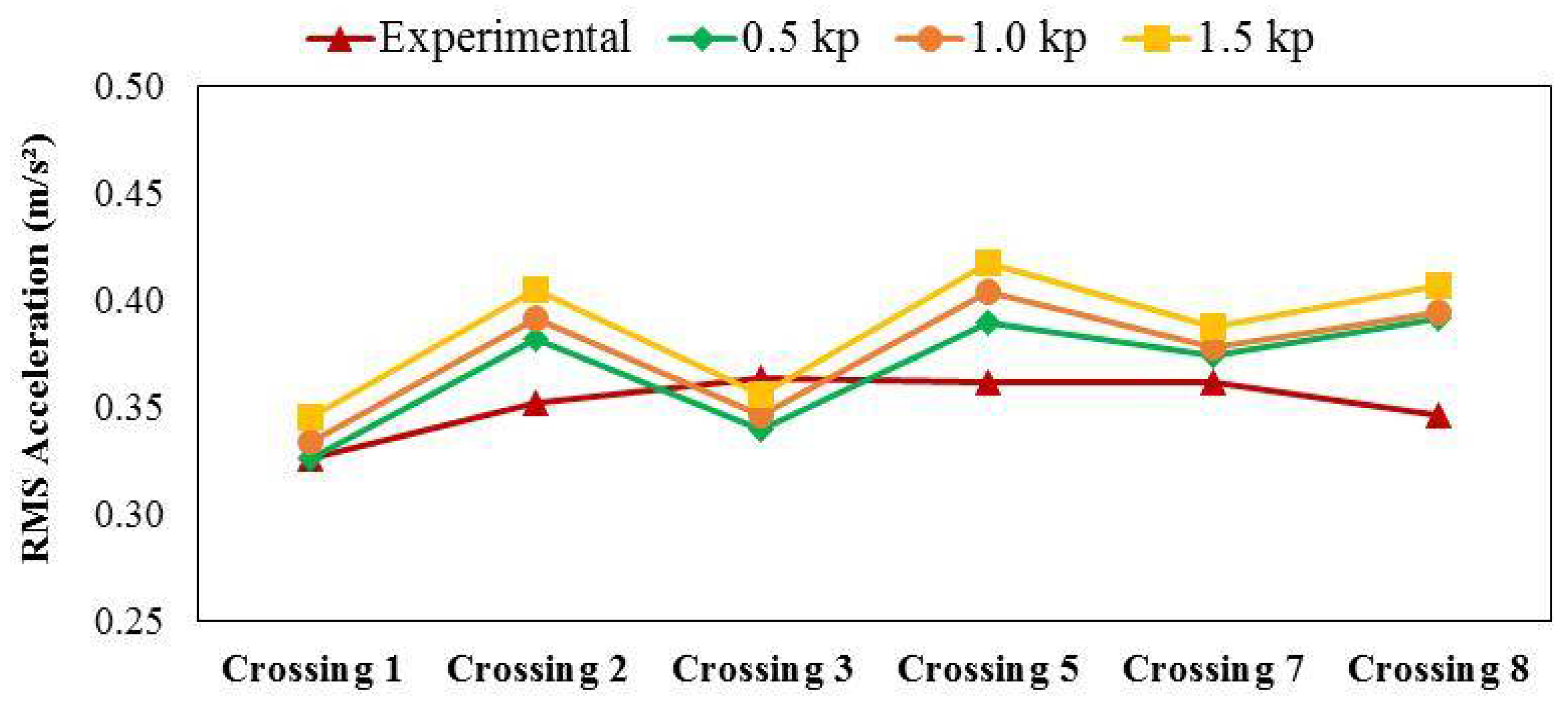
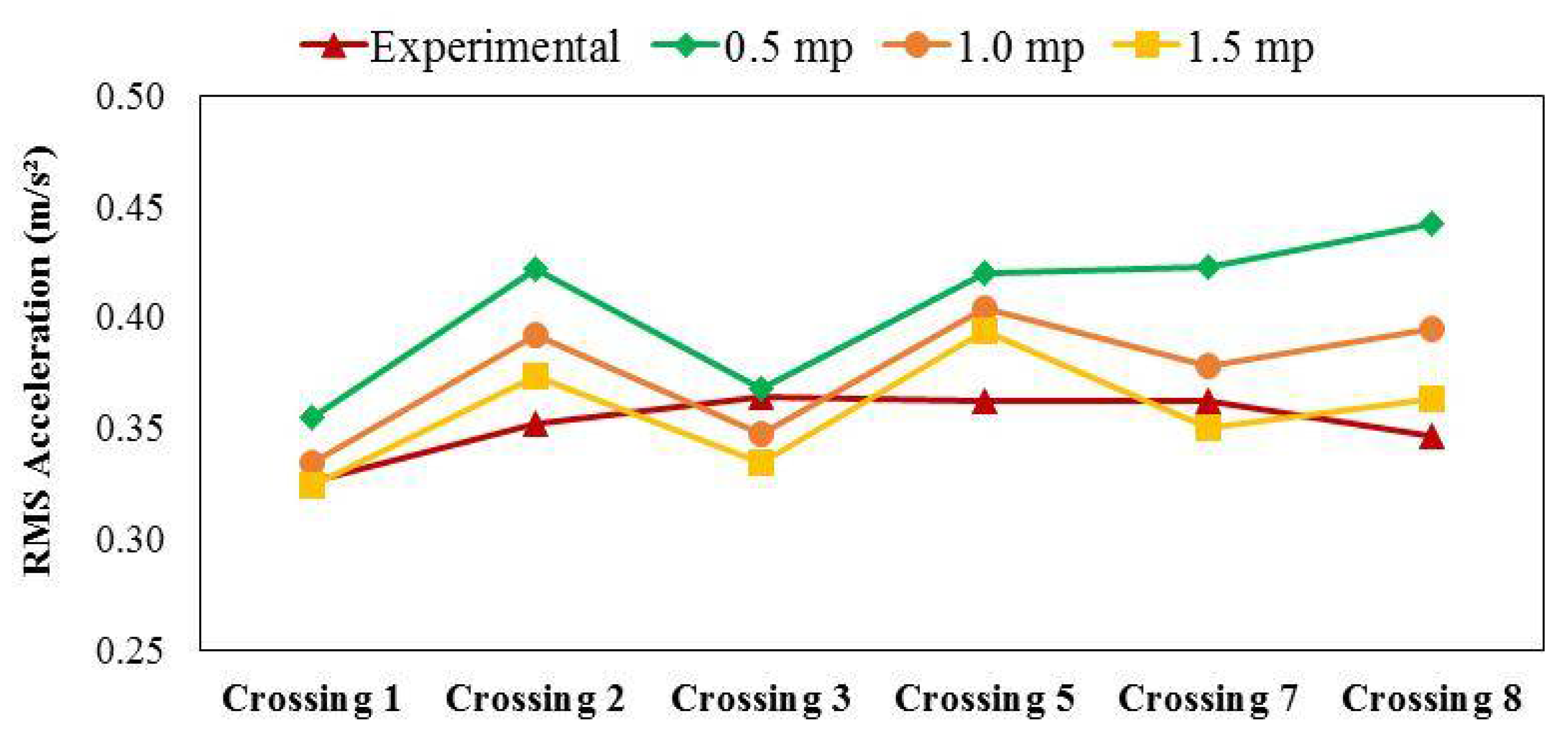
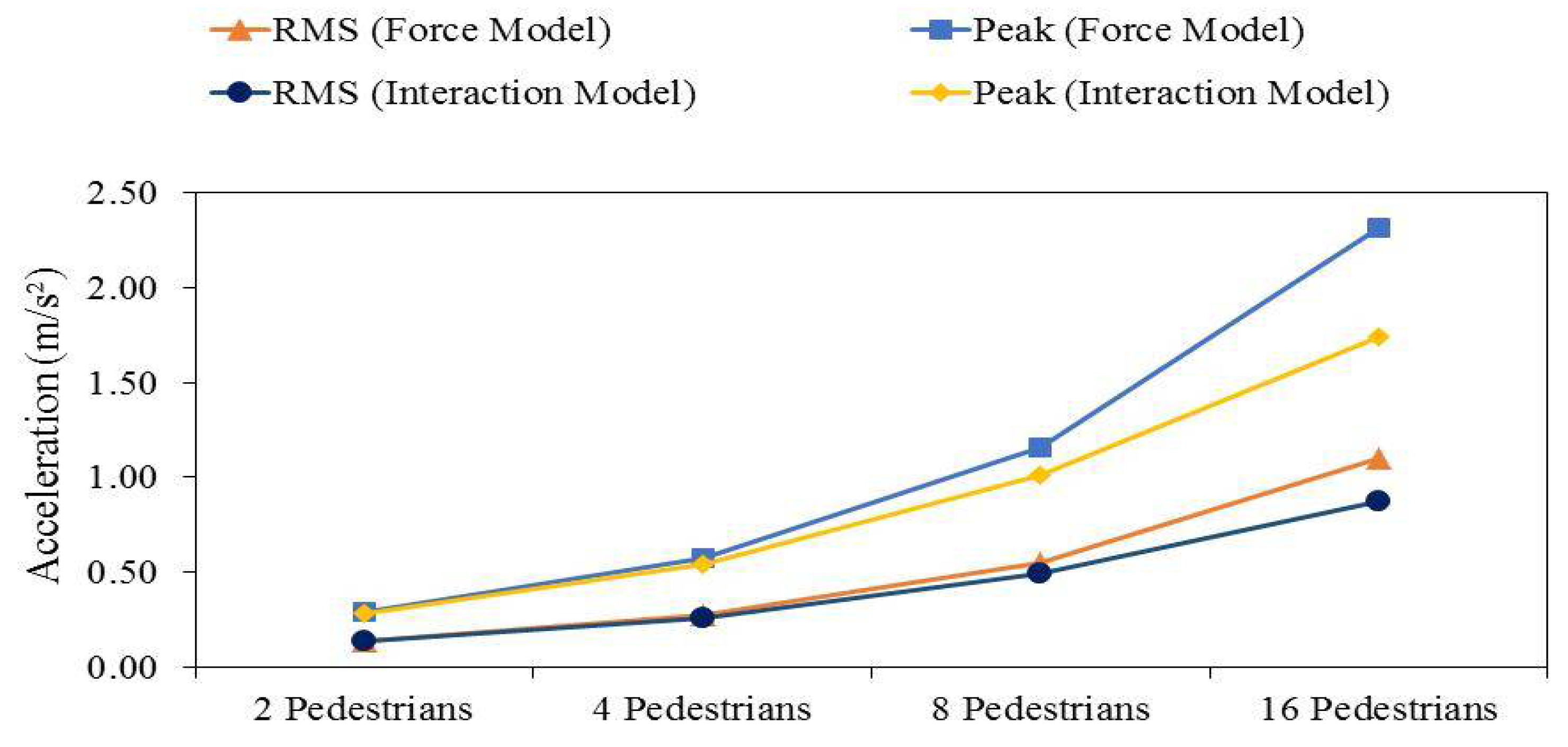
3.3. Effect of the Number of Pedestrians in the Group
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pimentel, R.L.; Pavic, A.; Waldron, P. Evaluation of design requirements for footbridges excited by vertical forces from walking. Can. J. Civil Eng. 2001, 28, 769–777. [Google Scholar] [CrossRef]
- Dallard, P.; Fitzpatrick, T.; Flint, A.; Low, A.; Smith, R.R.; Willford, M.; Roche, M. London Millennium Bridge: Pedestrian-induced lateral vibration. J. Bridge Eng. 2001, 6, 412–417. [Google Scholar] [CrossRef]
- Danbon, F.; Grillaud, G. Dynamic behavior of a steel footbridge—Characterisation and modeling of the dynamic loading induced by a moving crowd on the Solferino footbridge in Paris. In Proceedings of the Footbridge 2005 Second International Congress, Venezia, Italy, 6–8 December 2005. [Google Scholar]
- Nakamura, S.; Kawasaki, T. Lateral vibration of footbridges by synchronous walking. J. Constr. Steel Res. 2006, 62, 1148–1160. [Google Scholar] [CrossRef]
- Zivanovic, S.; Pavic, A.; Reynolds, P. Finite element modelling and updating of a lively footbridge: The complete process. J. Sound Vib. 2007, 301, 126–145. [Google Scholar] [CrossRef] [Green Version]
- Pospíšil, S.; Hračov, S.; Urushadze, S.; Jermoljev, D. Analysis and Mitigation of Vibration of Steel Footbridge with Excessive Amplitudes. In Topics in Dynamics of Bridges Volume 3, Conference Proceedings of the Society for Experimental Mechanics Series; Cunha, A., Ed.; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Tubino, F.; Carassale, L.; Piccardo, G. Human-Induced Vibrations on Two Lively Footbridges in Milan. J. Bridge Eng. 2016, 21, C4015002. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, A.; Moutinho, C.; Hu, W.-H. Continuous Dynamic Monitoring of Lively Footbridges. Int. J. Online Eng. 2016, 12, 49–51. [Google Scholar] [CrossRef] [Green Version]
- Drygała, I.J.; Polak, M.A.; Dulińska, J.M. Vibration serviceability assessment of GFRP pedestrian bridges. Eng. Struct. 2019, 184, 176–185. [Google Scholar] [CrossRef]
- Banaś, A.; Jankowski, R. Experimental and Numerical Study on Dynamics of Two Footbridges with Different Shapes of Girders. Appl. Sci. 2020, 10, 4505. [Google Scholar] [CrossRef]
- Bocian, M.; Brownjohn, J.M.W.; Racic, V.; Hester, D.; Quattrone, A.; Monnickendam, R. A framework for experimental determination of localised vertical pedestrian forces on full-scale structures using wireless attitude and heading reference systems. J. Sound Vib. 2016, 376, 217–243. [Google Scholar] [CrossRef] [Green Version]
- Pańtak, M. Ground Reaction Forces Generated by Runners—Harmonic Analyses and Modeling. Appl. Sci. 2020, 10, 1575. [Google Scholar] [CrossRef] [Green Version]
- British Standards Institute. BS5400 British Standards—Steel, Concrete and Composite Bridges: Specification for Loads; Part 2, Appendix C; BSI: London, UK, 1978. [Google Scholar]
- British Standards Institute. UK National Annex to Eurocode 1: Actions on Structures—Part 2: Traffic Loads on Bridges; NA to BS EN 1991-2:2003; BSI: London, UK, 2008. [Google Scholar]
- SÉTRA—Service d’Études Techniques des Routes et Autoroutes. Technical Guide Footbridges—Assessment of Vibrational Behaviour of Footbridges under Pedestrian Loading; Association Française de Génie Civil: Paris, France, 2006. [Google Scholar]
- Hivoss—Human Induced Vibrations of Steel Structures. Design of Footbridges Guideline; Research Fund for Coal & Steel, European Commission: Luxembourg, 2008. [Google Scholar]
- Shahabpoor, E.; Pavic, A.; Racic, V. Interaction between Walking Humans and Structures in Vertical Direction: A Literature Review. Shock Vib. 2016, 2016, 3430285. [Google Scholar] [CrossRef] [Green Version]
- Archbold, P.J. Interactive Load Models for Pedestrian Footbridges. Ph.D. Thesis, National University of Ireland University College, Dublin, Ireland, 2004. [Google Scholar]
- Caprani, C.C.; Keogh, J.; Archbold, P.; Fanning, P. Characteristic vertical response of a footbridge due to crowd loading. In Proceedings of the VIII International Conference on Structural Dynamics Eurodyn 2011, Leuven, Belgium, 4–6 July 2011. [Google Scholar]
- Pfeil, M.; Amador, N.; Pimentel, R.; Vasconcelos, R. Analytic-numerical model for walking person—Footbridge structure interaction. In Proceedings of the IX International Conference on Structural Dynamics Eurodyn 2014, Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- Jiménez-Alonso, J.F.; Sáez, A. A direct pedestrian structure interaction model to characterize the human induced vibrations on slender footbridges. Inf. Constr. 2014, 66, m007. [Google Scholar] [CrossRef] [Green Version]
- Venuti, F.; Racic, V.; Corbetta, A. Modelling framework for dynamic interaction between multiple pedestrians and vertical vibrations of footbridge. J. Sound Vib. 2016, 379, 245–263. [Google Scholar] [CrossRef] [Green Version]
- Shahabpoor, E.; Pavic, A.; Racic, V. Identification of mass–spring–damper model of walking humans. Structures 2016, 5, 233–246. [Google Scholar] [CrossRef] [Green Version]
- Gomez, D.; Dyke, S.J.; Rietdyk, S. Experimental Verification of a Substructure-Based Model to Describe Pedestrian–Bridge Interaction. J. Bridge Eng. 2018, 23, 04018013. [Google Scholar] [CrossRef] [Green Version]
- Silva, R.L.; Pimentel, R.L.; Pavic, A. Performance of biodynamic models to represent the action of a pedestrian in the vertical direction. In Proceedings of the XI International Conference on Structural Dynamics Eurodyn 2020, Athens, Greece, 23–26 November 2020. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Lombaert, G.; De Roeck, G.; Van den Broeck, P. The impact of vertical human-structure interaction on the response of footbridges to pedestrian excitation. J. Sound Vib. 2017, 402, 104–121. [Google Scholar] [CrossRef] [Green Version]
- Hawryszków, P.; Pimentel, R.; Silva, F. Vibration effects of loads due to groups crossing a lively footbridge. Procedia Eng. 2017, 199, 2808–2813. [Google Scholar] [CrossRef]
- Silva, F.T.; Pimentel, R.L. Biodynamic walking model for vibration serviceability of footbridges in vertical direction. In Proceedings of the VIII International Conference on Structural Dynamics Eurodyn 2011, Leuven, Belgium, 4–6 July 2011. [Google Scholar]
- Bachmann, H.; Ammann, H. Vibration in Structures Induced by Man and Machines; Structural Engineering Document No. 3; International Association for bridge and Structure Engineering: Zurich, Switzerland, 1987. [Google Scholar]




| Pedestrian Number | Mass (kg) | Pedestrian Number | Mass (kg) |
|---|---|---|---|
| 1 | 69 | 6 | 67 |
| 2 | 48 | 7 | 81 |
| 3 | 85 | 8 | 87 |
| 4 | 90 | 9 | 70 |
| 5 | 82 | 10 | 44 |
| Pedestrian Number | Modal Mass mp (kg) | Modal Stiffness kp (N/m) | Modal Damping cp (Ns/m) |
|---|---|---|---|
| 1 | 38.43 | 12,311.32 | 728.21 |
| 2 | 32.65 | 12,574.66 | 630.68 |
| 3 | 42.83 | 12,550.82 | 801.36 |
| 4 | 44.20 | 12,701.11 | 824.04 |
| 5 | 42.00 | 12,477.72 | 787.72 |
| 6 | 37.88 | 12,307.72 | 719.00 |
| 7 | 41.73 | 12,456.22 | 783.16 |
| 8 | 43.38 | 12,606.68 | 810.44 |
| 9 | 38.70 | 12,315.35 | 732.81 |
| 10 | 31.55 | 12,701.95 | 611.88 |
| Pedestrian | DLF | SD | Pedestrian | DLF | SD |
|---|---|---|---|---|---|
| 1 | 0.25 | 0.00 | 6 | 0.30 | 0.01 |
| 2 | 0.26 | 0.00 | 7 | 0.28 | 0.01 |
| 3 | 0.30 | 0.01 | 8 | 0.25 | 0.03 |
| 4 | 0.26 | 0.01 | 9 | 0.25 | 0.01 |
| 5 | 0.23 | 0.02 | 10 | 0.35 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hawryszków, P.; Pimentel, R.; Silva, R.; Silva, F. Vertical Vibrations of Footbridges Due to Group Loading: Effect of Pedestrian–Structure Interaction. Appl. Sci. 2021, 11, 1355. https://doi.org/10.3390/app11041355
Hawryszków P, Pimentel R, Silva R, Silva F. Vertical Vibrations of Footbridges Due to Group Loading: Effect of Pedestrian–Structure Interaction. Applied Sciences. 2021; 11(4):1355. https://doi.org/10.3390/app11041355
Chicago/Turabian StyleHawryszków, Paweł, Roberto Pimentel, Rafaela Silva, and Felipe Silva. 2021. "Vertical Vibrations of Footbridges Due to Group Loading: Effect of Pedestrian–Structure Interaction" Applied Sciences 11, no. 4: 1355. https://doi.org/10.3390/app11041355
APA StyleHawryszków, P., Pimentel, R., Silva, R., & Silva, F. (2021). Vertical Vibrations of Footbridges Due to Group Loading: Effect of Pedestrian–Structure Interaction. Applied Sciences, 11(4), 1355. https://doi.org/10.3390/app11041355








