A Scheme for Controlled Cyclic Asymmetric Remote State Preparation in Noisy Environment
Abstract
:1. Introduction
2. Four-Party Controlled Cyclic Asymmetrical RSP Protocol of Sequentially Increasing Qubits States
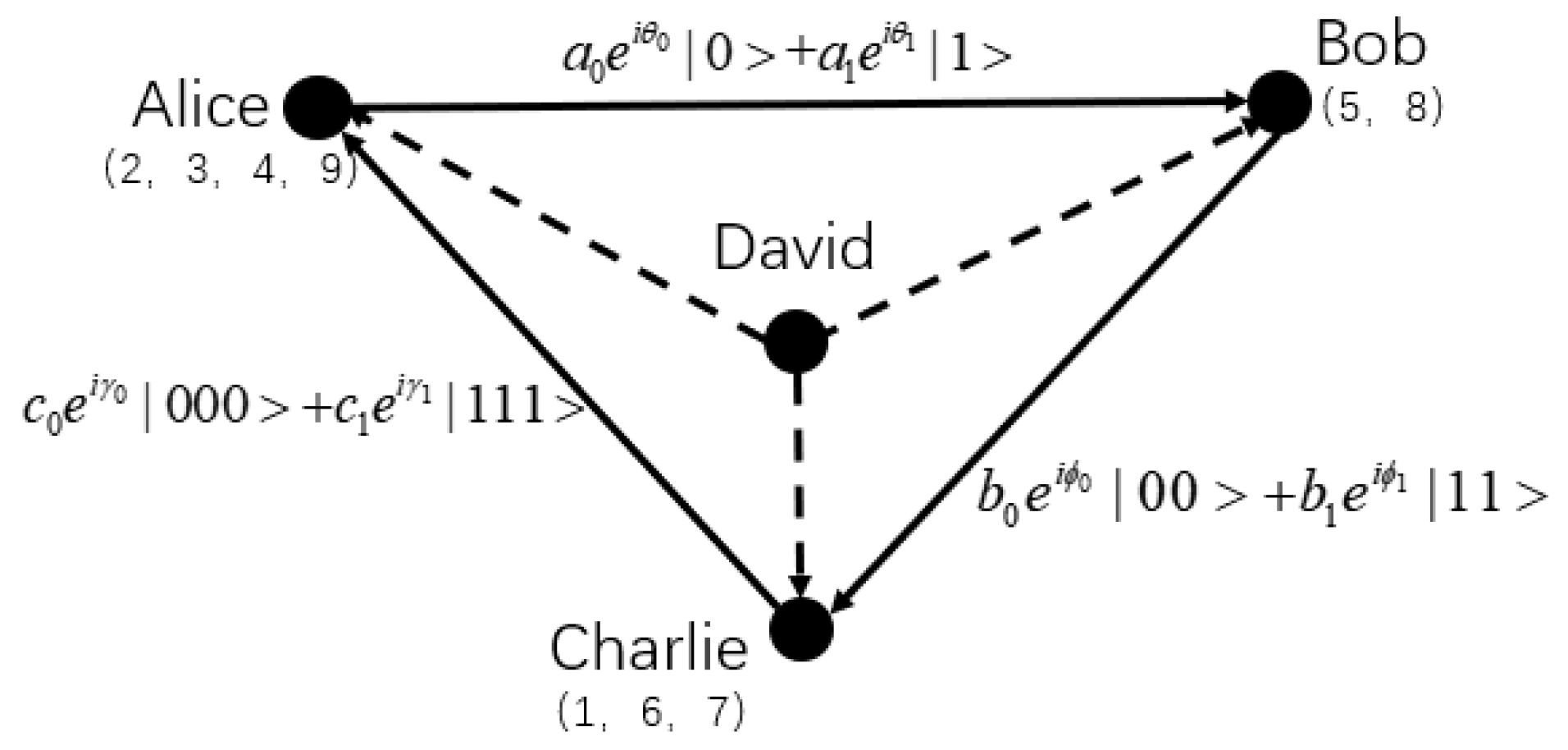
2.1. Preparation of Quantum Channel
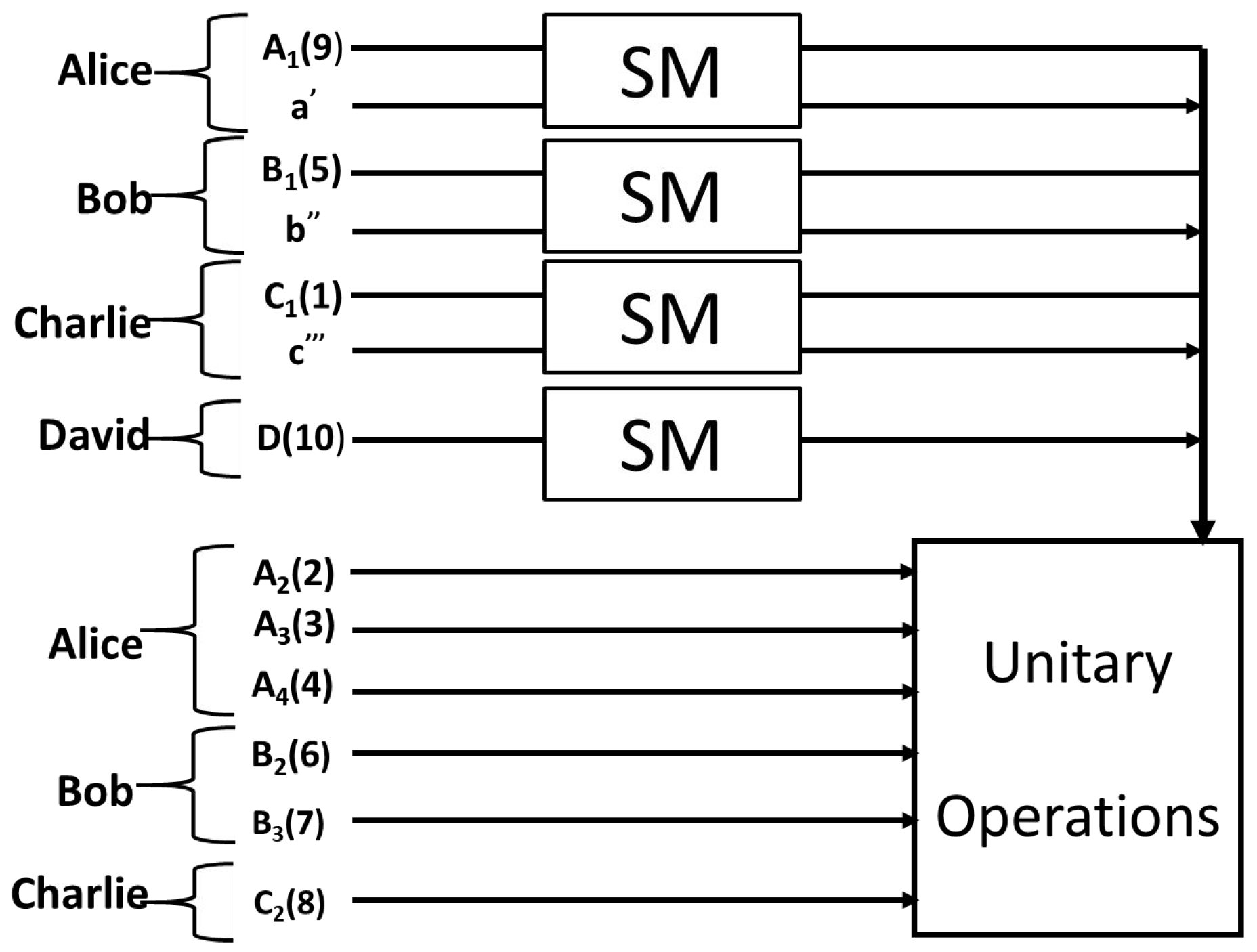
2.2. Description of Four-Party Controlled Cyclic Asymmetrical RSP Protocol
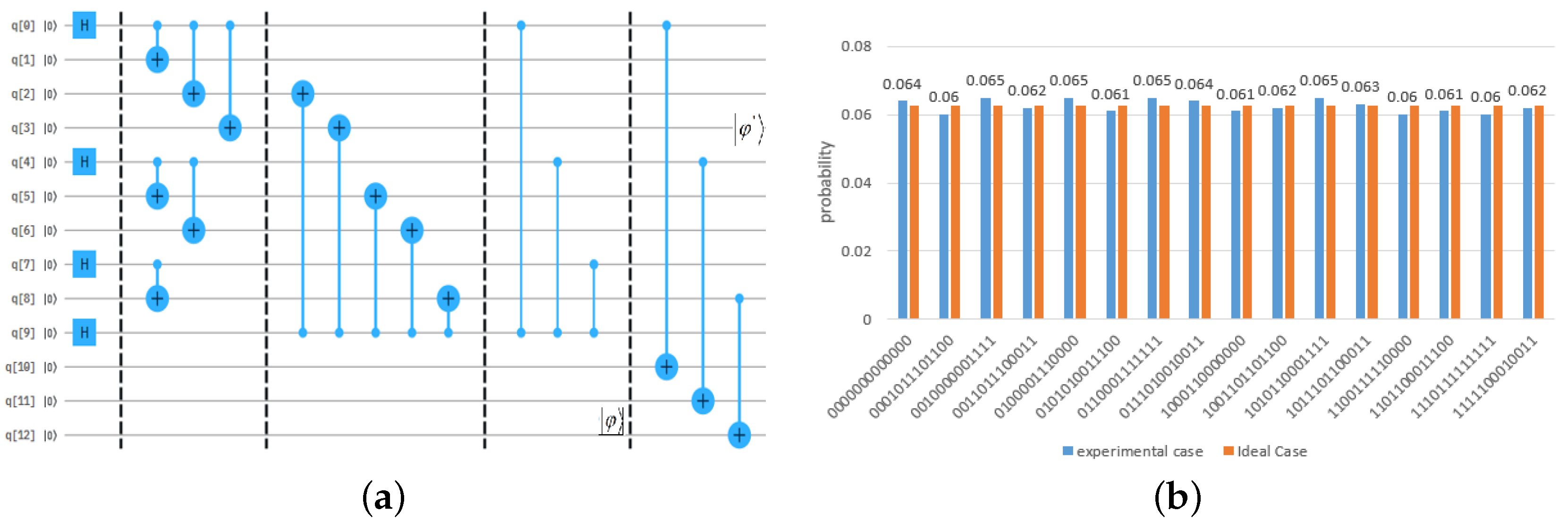
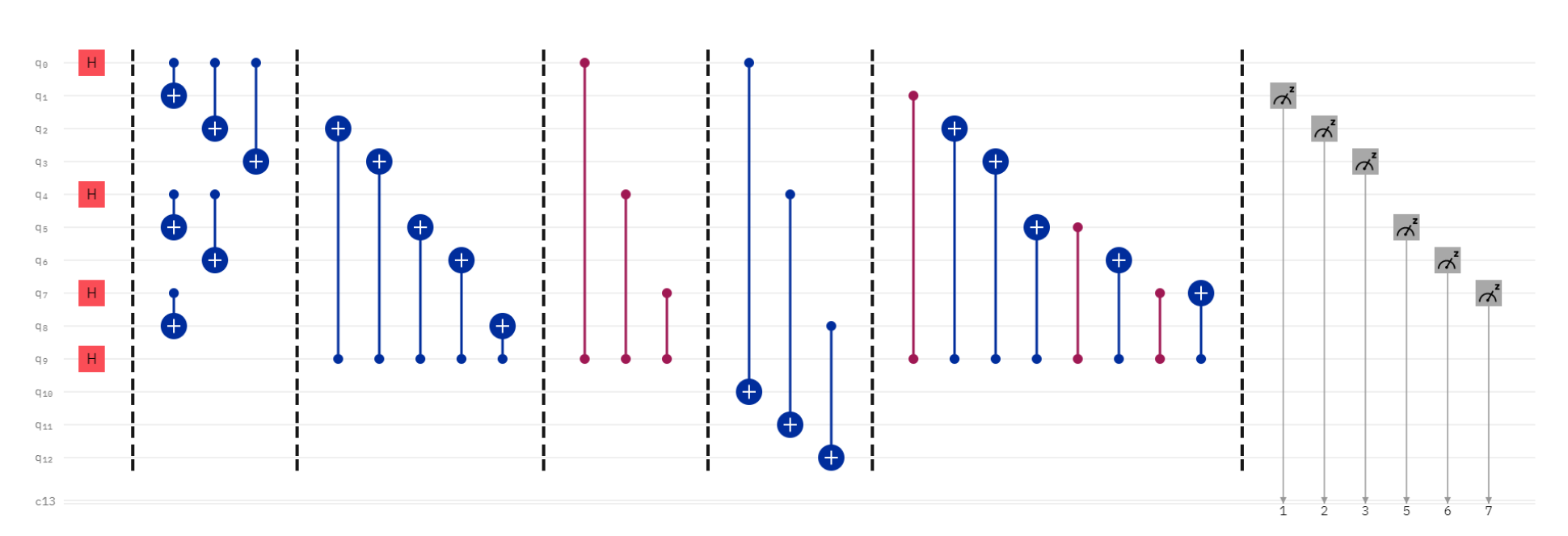
2.3. Experimental Realization in IBM QE
3. Multi-Party Controlled Cyclic Asymmetrical RSP Protocol of Sequentially Increasing Qubits States
4. Four-Party Controlled Cyclic Asymmetrical RSP Protocol in Noisy Environments
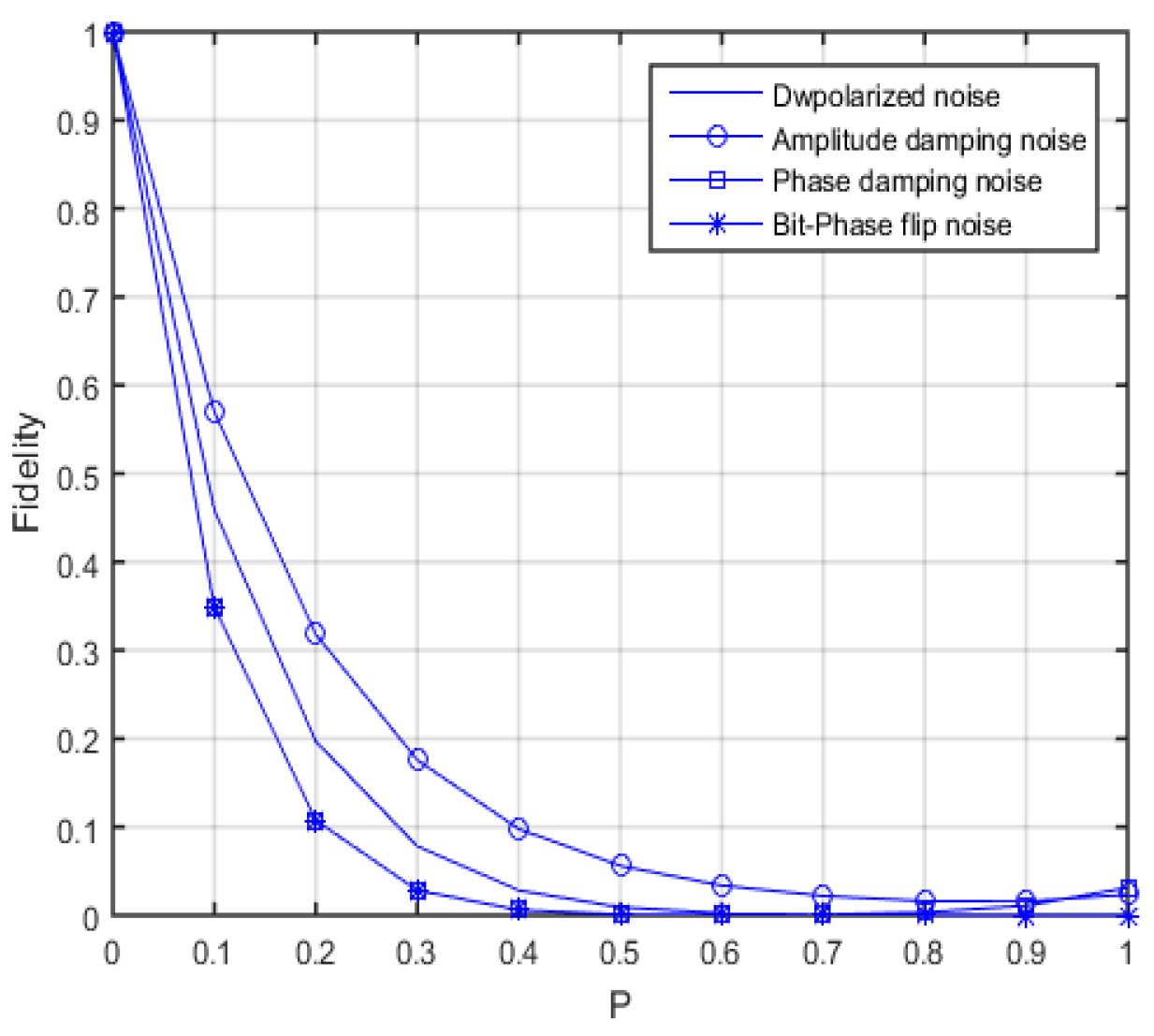
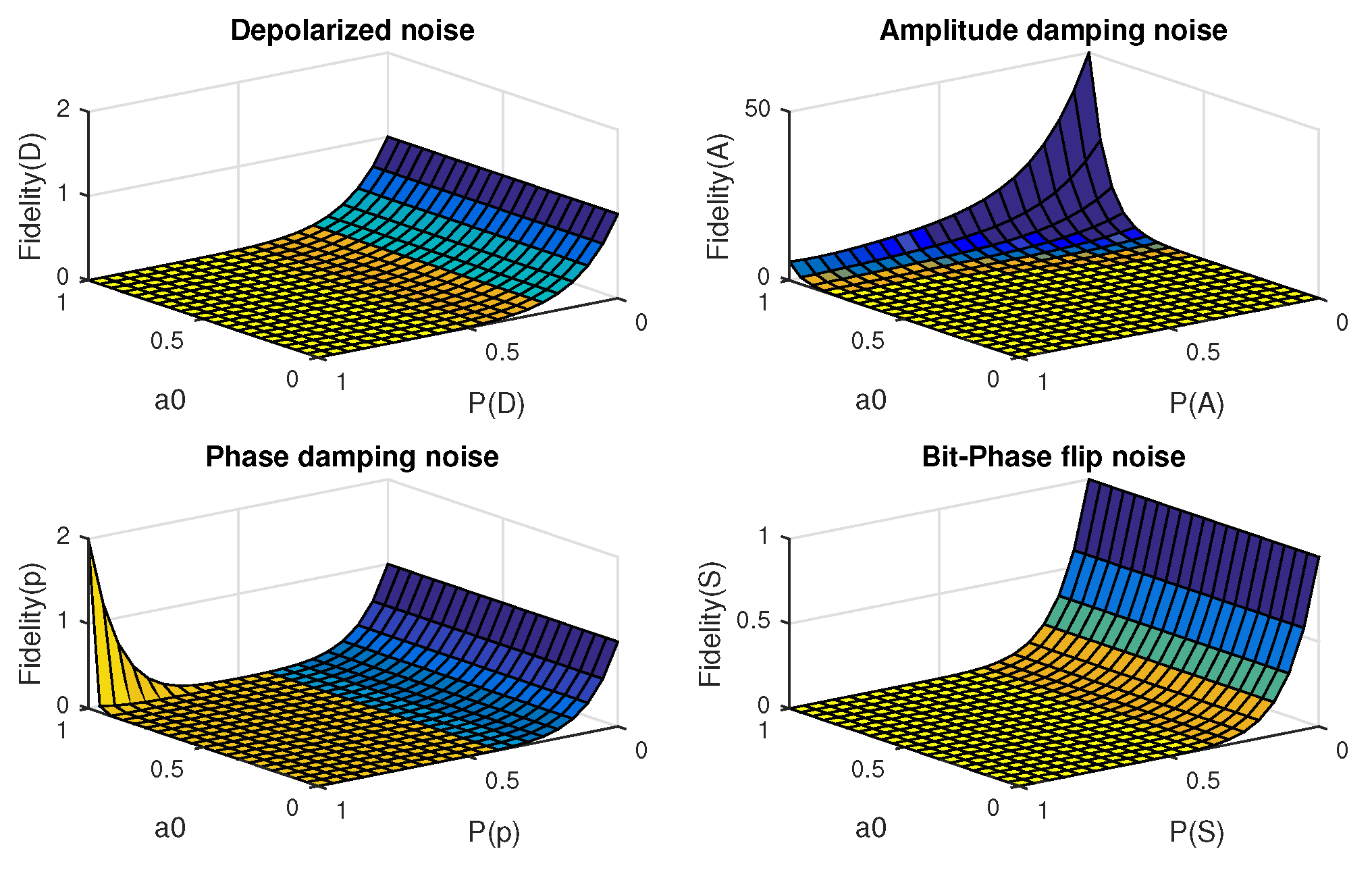
4.1. Depolarized Noise
4.2. Amplitude Damping Noise
4.3. Phase Damping Noise
4.4. Bit-Phase Flip Noise
4.5. Analysis of the Effect of the Scheme in Four Noisy Environments
5. Comparison and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aspect, A.; Dalibard, J.; Roger, G. Experimental realization of einstein-podolsky-rosen-bohm gedankenexperiment: A new violation of bell’s inequalities. Phys. Rev. Lett. 1982, 49, 91–94. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels. Phys. Rev. Lett. 1993, 70, 13–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lo, H.-K. Classical-communication cost in distributed quantum-information processing: A generalization of quantum-communication complexity. Phys. Rev. A 2000, 62, 012313. [Google Scholar] [CrossRef] [Green Version]
- Pati, K.A. Minimum classical bit for remote preparation and measurement of a qubit. Phys. Rev. A 2000, 63, 94–98. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.H.; Divincenzo, D.P.; Shor, P.W.; Smolin, J.A.; Terhal, B.M.; Wootters, W.K. Remote state preparation. Phys. Rev. Lett. 2001, 87, 077902. [Google Scholar] [CrossRef] [Green Version]
- Moreno, M.G.M.; Cunha, M.M.; Parisio, F. Remote preparation of w states from imperfect bipartite sources. Quantum Inf. Process. 2016, 15, 3869–3879. [Google Scholar] [CrossRef] [Green Version]
- Devetak, I.; Berger, T. Low-entanglement remote state preparation. Phys. Rev. Lett. 2001, 87, 197901. [Google Scholar] [CrossRef] [Green Version]
- Ma, S.; Gao, C.; Zhang, P.; Qu, Z.G. Deterministic remote preparation via the Brown state. Quantum Inf. Process. 2017, 16, 1–22. [Google Scholar] [CrossRef]
- Leung, D.W.; Shor, P.W. Oblivious remote state preparation. Phys. Rev. Lett. 2003, 90, 127905. [Google Scholar] [CrossRef] [Green Version]
- Xiang, G.; Li, J.; Guo, G.C. Remote State Preparation and Operation for Photons. Photonics Asia 2004 Inf. Process. Data Storage 2004, 5631, 13. [Google Scholar]
- Zhan, Y.-B. Remote State Preparation of a Greenberger-Horne-Zeilinger Class State. Commun. Theor. Phys. 2005, 43, 637–640. [Google Scholar]
- Wang, Z.-Y.; Liu, Y.-M.; Zuo, X.-Q.; Zhang, Z.-J. Controlled Remote State Preparation. Commun. Theor. Phys. 2009, 52, 235–240. [Google Scholar]
- Wang, C.; Zeng, Z.; Li, X.-H. Controlled remote state preparation via partially entangled quantum channel. Quantum Inf. Process. 2015, 14, 1077–1089. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.-Y.; Bai, M.-Q.; Mo, Z.-W. Bidirectional controlled joint remote state preparation. Quantum Inf. Process. 2015, 14, 4263–4278. [Google Scholar] [CrossRef]
- Choudhury, B.S.; Samanta, S. An optional remote state preparation protocol for a four-qubit entangled state. Quantum Inf. Process. 2019, 18, 118. [Google Scholar] [CrossRef]
- Chen, H.B.; Fu, H.; Li, X.W.; Ma, P.C.; Zhan, Y.B. Economic scheme for remote preparation of an arbitrary five-qubit brown-type state. Pramana 2016, 86, 783–788. [Google Scholar] [CrossRef]
- Ding, M.X.; Jiang, M.; Liu, Y.H. Deterministic joint remote preparation of an arbitrary six-qubit cluster-type state. Opt. Int. J. Light Electron Opt. 2016, 127, 10681–10686. [Google Scholar] [CrossRef]
- Choudhury, B.S.; Samanta, S. Perfect joint remote state preparation of arbitrary six-qubit cluster-type states. Quantum Inf. Process. 2018, 17, 1–12. [Google Scholar] [CrossRef]
- Fang, S.; Jiang, M. A Novel Scheme for Bidirectional and Hybrid Quantum Information Transmission via a Seven-Qubit State. Int. J. Theor. Phys. 2018, 57, 523–532. [Google Scholar] [CrossRef]
- Wu, H.; Zha, X.-W.; Yang, Y.-Q. Controlled Bidirectional Hybrid of Remote State Preparation and Quantum Teleportation via Seven-Qubit Entangled State. Int. J. Theor. Phys. 2018, 57, 28–35. [Google Scholar] [CrossRef]
- Cao, L.Y.; Jiang, M.; Chen, C. Joint remote state preparation of an arbitrary eight-qubit cluster-type state. Pramana 2020, 94, 41. [Google Scholar] [CrossRef]
- Jiang, S.-X.; Zhou, R.-G.; Xu, R.; Luo, G. Cyclic Hybrid Double-channel Quantum Communication Via Bell-state and Ghz-state In Noisy Environments. IEEE Access 2019, 7, 80530–80541. [Google Scholar] [CrossRef]
- Wang, M.; Yang, C.; Mousoli, R. Controlled cyclic remote state preparation of arbitrary qubit states. Comput. Mater. Contin. 2018, 55, 321–329. [Google Scholar] [CrossRef]
- Li, Y.; Qiao, Y.; Sang, M.; Nie, Y. Bidirectional Controlled Remote State Preparation of an Arbitrary Two-Qubit State. Int. J. Theor. Phys. 2019, 58, 2228–2234. [Google Scholar] [CrossRef]
- Sang, Z. Cyclic Controlled Joint Remote State Preparation by Using a Ten-Qubit Entangled State. Int. J. Theor. Phys. 2019, 58, 255–260. [Google Scholar] [CrossRef]
- Sun, L.; Wu, S.; Qu, Z.; Wang, M.; Wang, X. The effect of quantum noise on two different deterministic remote state preparation of an arbitrary three-particle state protocols. Quantum Inf. Process. 2018, 17, 1–18. [Google Scholar] [CrossRef]
- Espoukeh, P.; Pedram, P. Quantum teleportation through noisy channels with multi-qubit GHZ states. Quantum Inf. Process. 2014, 13, 1789–1811. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Shukla, C.; Banerjee, S.; Pathak, A. Controlled bidirectional remote state preparation in noisy environment: A generalized view. Quantum Inf. Process. 2015, 14, 3441–3464. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Huang, L. Effects of Noise on Joint Remote State Preparation of an Arbitrary Equatorial Two-Qubit State. Int. J. Theor. Phys. 2017, 56, 720–728. [Google Scholar] [CrossRef]
- Sun, Y.-R.; Xu, G.; Chen, X.-B.; Yang, Y.; Yang, Y.-X. Asymmetric Controlled Bidirectional Remote Preparation of Single- and Three-Qubit Equatorial State in Noisy Environment. IEEE Access 2019, 7, 2811–2822. [Google Scholar] [CrossRef]
- Dash, T.; Sk, R.; Panigrahi, P.K. Deterministic joint remote state preparation of arbitrary two-qubit state through noisy cluster-GHZ channel. Opt. Commun. 2020, 464. [Google Scholar] [CrossRef]
- Wei, S.J.; Xin, T.; Long, G.L. Efficient universal quantum channel simulation in IBM’s cloud quantum computer. Sci. China (Phys. Mech. Astron.) 2018, 7, 48–57. [Google Scholar]
- Sisodia, M.; Shukla, A.; Pathak, A. Experimental realization of nondestructive discrimination of Bell states using a five-qubit quantum computer. Phys. Lett. A 2017, 381, 3860–3874. [Google Scholar] [CrossRef] [Green Version]
- Rajiuddin, S.; Baishya, A.; Behera, B.K.; Panigrahi, P.K. Experimental realization of quantum teleportation of an arbitrary two-qubit state using a four-qubit cluster state. Quantum Inf. Process. 2020, 19, 87. [Google Scholar] [CrossRef]
- Kalra, A.R.; Gupta, N.; Behera, B.K.; Prakash, S.; Panigrahi, P.K. Demonstration of the no-hiding theorem on the 5-Qubit IBM quantum computer in a category-theoretic framework. Quantum Inf. Process. 2019, 18, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Joschka, R.; David, H.; Nicholas, C.; Dominic, H.; Viv, K. Protecting quantum memories using coherent parity check codes. Quantum Sci. Technol. 2018, 3, 035010. [Google Scholar]
- Alvarez-Rodriguez, U.; Sanz, M.; Lamata, L.; Solano, E. Quantum artificial life in an ibm quantum computer. Sci. Rep. 2018, 8, 14793. [Google Scholar] [CrossRef]
- Zhang, C.; Bai, M.; Zhou, S. Cyclic joint remote state preparation in noisy environment. Quantum Inf. Process. 2018, 17, 1–20. [Google Scholar] [CrossRef]
- Banerjee, A.; Pathak, A. Maximally efficient protocols for direct secure quantum communication. Phys. Lett. A 2012, 376, 2944–2950. [Google Scholar] [CrossRef]
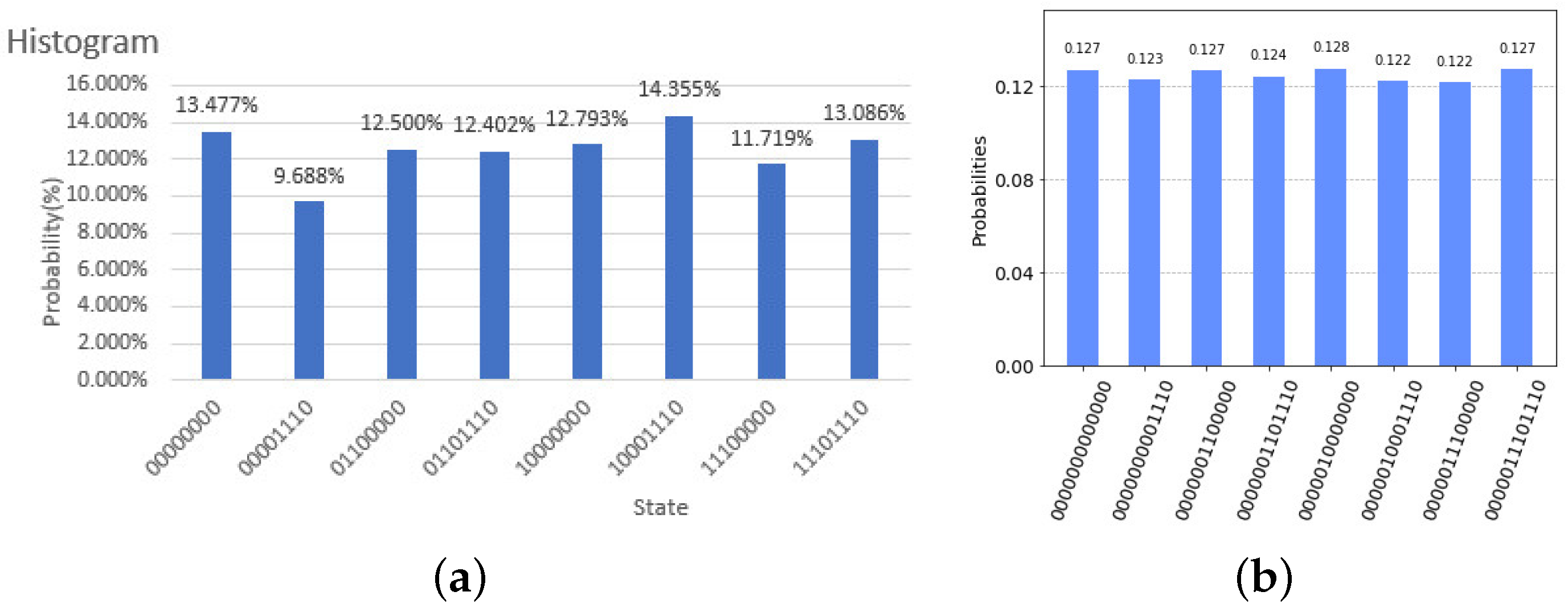
| SPM1(A) | SPM1(B) | SPM1(C) | SPM2(A) | SPM2(B) | SPM2(C) | SPM(D) | Transformations | ||
|---|---|---|---|---|---|---|---|---|---|
| Alice | Bob | Charlie | |||||||
| . |
| Runs | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.125 | 0.117 | 0.126 | 0.118 | 0.118 | 0.138 | 0.130 | 0.128 |
| 2 | 0.132 | 0.125 | 0.122 | 0.121 | 0.129 | 0.131 | 0.119 | 0.121 |
| 3 | 0.120 | 0.128 | 0.124 | 0.127 | 0.129 | 0.118 | 0.126 | 0.127 |
| 4 | 0.125 | 0.123 | 0.130 | 0.127 | 0.123 | 0.127 | 0.120 | 0,125 |
| 5 | 0.132 | 0.123 | 0.129 | 0.122 | 0.124 | 0.118 | 0.125 | 0.127 |
| 6 | 0.128 | 0.129 | 0.122 | 0.125 | 0.124 | 0.122 | 0.129 | 0.121 |
| 7 | 0.124 | 0.126 | 0.124 | 0.129 | 0.122 | 0.119 | 0.132 | 0.123 |
| 8 | 0.121 | 0.121 | 0.123 | 0.130 | 0.127 | 0.126 | 0.124 | 0.127 |
| 9 | 0.120 | 0.131 | 0.122 | 0.129 | 0.121 | 0.125 | 0.120 | 0.132 |
| 10 | 0.123 | 0.130 | 0.126 | 0.125 | 0.125 | 0.124 | 0.124 | 0.124 |
| A | 0.125 | 0.1253 | 0.1248 | 0.1253 | 0.1242 | 0.1248 | 0.1249 | 0.1255 |
| S | 0.0044 | 0.0044 | 0.0029 | 0.0039 | 0.0035 | 0.0063 | 0.0045 | 0.0039 |
| Scheme | Type | Operation | Efficiency | |||
|---|---|---|---|---|---|---|
| [25] | CCJRSP | 3 (three arbitrary single-qubit) | 10 | 6 | 7 SM | 19% |
| [32] | CJRSP | 3 (three arbitrary single-qubit) | 9 | 9 | 6 SM | 17% |
| [30] | CCJRSP | 2 (An arbitrary two-qubit state) | 7 | 5 | 5 SM | 17% |
| [24] | CBRSP | 4(Two arbitrary two-qubit ) | 9 | 8 | 9 SM | 24% |
| [16] | CBRSP and QT | 2 (two arbitrary single-qubit) | 7 | 4 | 1 BSM,3 SM | 18% |
| [23] | CCRSP | 3 (three arbitrary single-qubit) | 7 | 6 | 6 SM | 23% |
| Ours | CCARSP | 6(A single-qubit, a two-qubit, a three-qubit) | 13 | 6 | 7 SM | 32% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, N.; Wu, T.; Yu, Y.; Pei, C. A Scheme for Controlled Cyclic Asymmetric Remote State Preparation in Noisy Environment. Appl. Sci. 2021, 11, 1405. https://doi.org/10.3390/app11041405
Zhao N, Wu T, Yu Y, Pei C. A Scheme for Controlled Cyclic Asymmetric Remote State Preparation in Noisy Environment. Applied Sciences. 2021; 11(4):1405. https://doi.org/10.3390/app11041405
Chicago/Turabian StyleZhao, Nan, Tingting Wu, Yan Yu, and Changxing Pei. 2021. "A Scheme for Controlled Cyclic Asymmetric Remote State Preparation in Noisy Environment" Applied Sciences 11, no. 4: 1405. https://doi.org/10.3390/app11041405
APA StyleZhao, N., Wu, T., Yu, Y., & Pei, C. (2021). A Scheme for Controlled Cyclic Asymmetric Remote State Preparation in Noisy Environment. Applied Sciences, 11(4), 1405. https://doi.org/10.3390/app11041405









