The Reproduction and Evaluation of Star Fields with the Milky Way in a Planetarium
Abstract
:1. Introduction
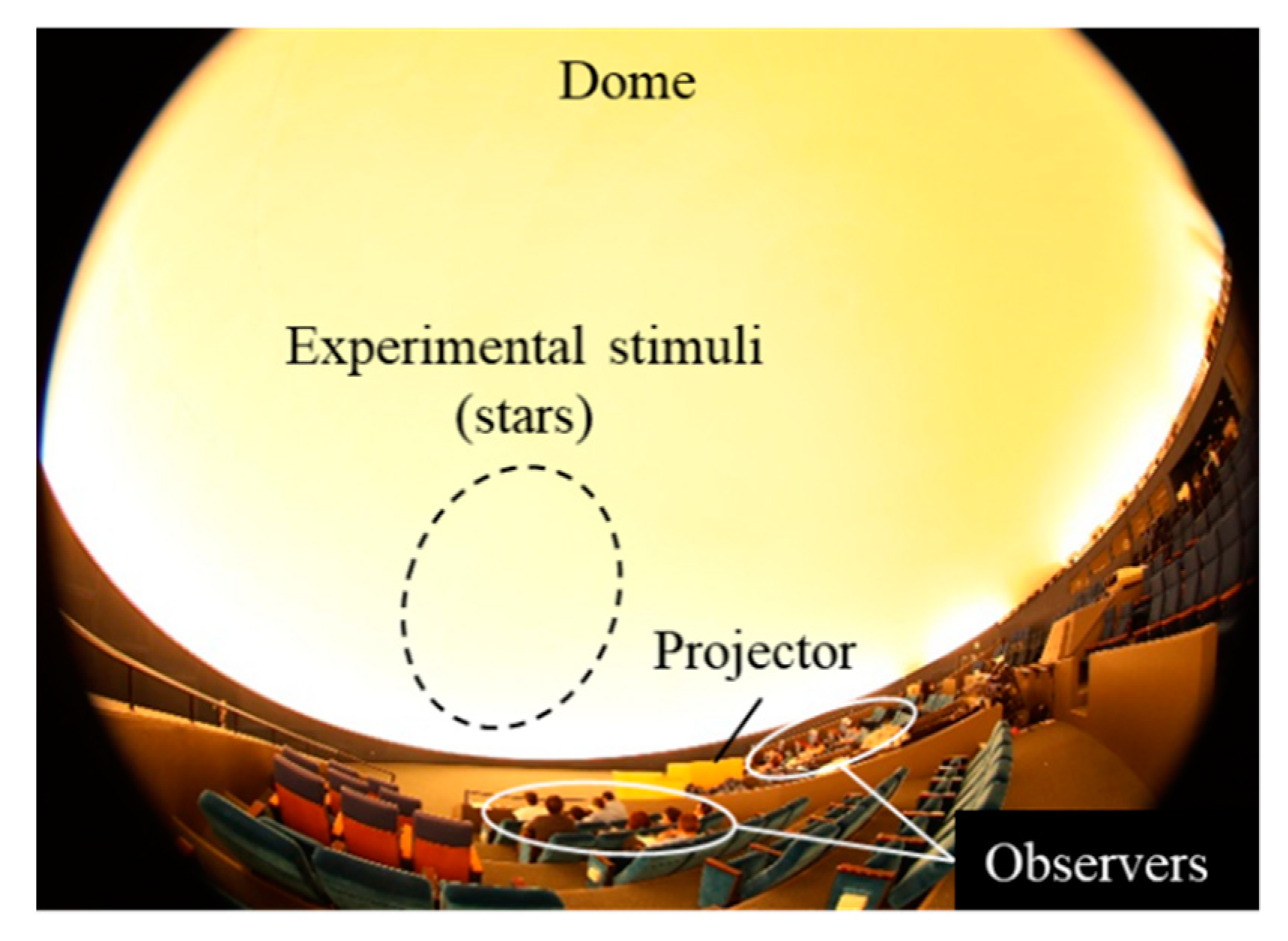
2. Experiment
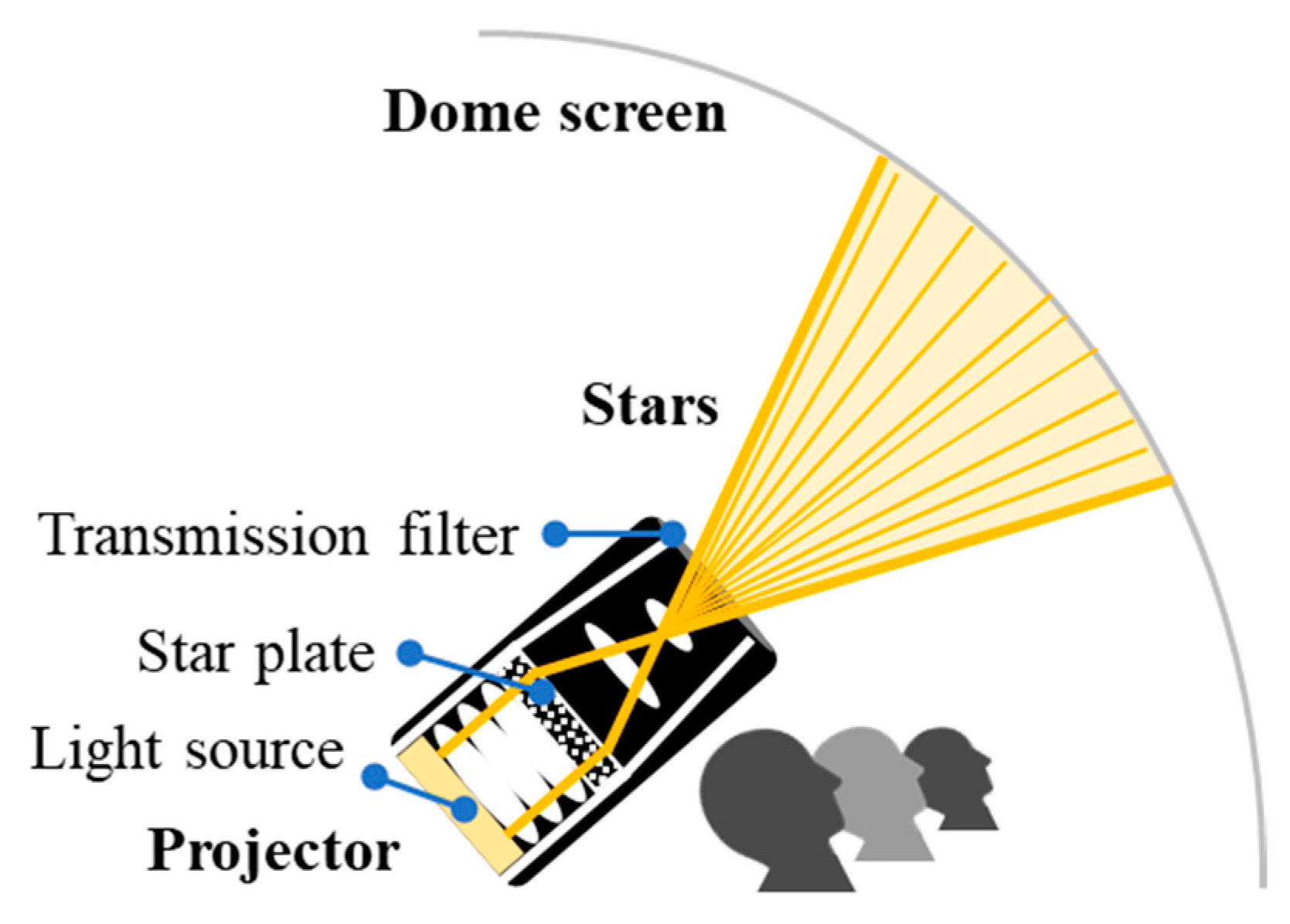
2.1. Reproduction Apparatus
2.2. Experimental Stimulus
2.2.1. Standard Pattern
2.2.2. Additional Pattern
2.3. Experimental Index
- Faithfulness: whether the observation target is faithful to one’s impression of the actual Milky Way.
- Preference: whether the observation target can meet one’s impression of an expected Milky Way in a planetarium.
- Depth feeling: whether the observation target conveys the depth of the universe.
2.4. Experimental Procedure
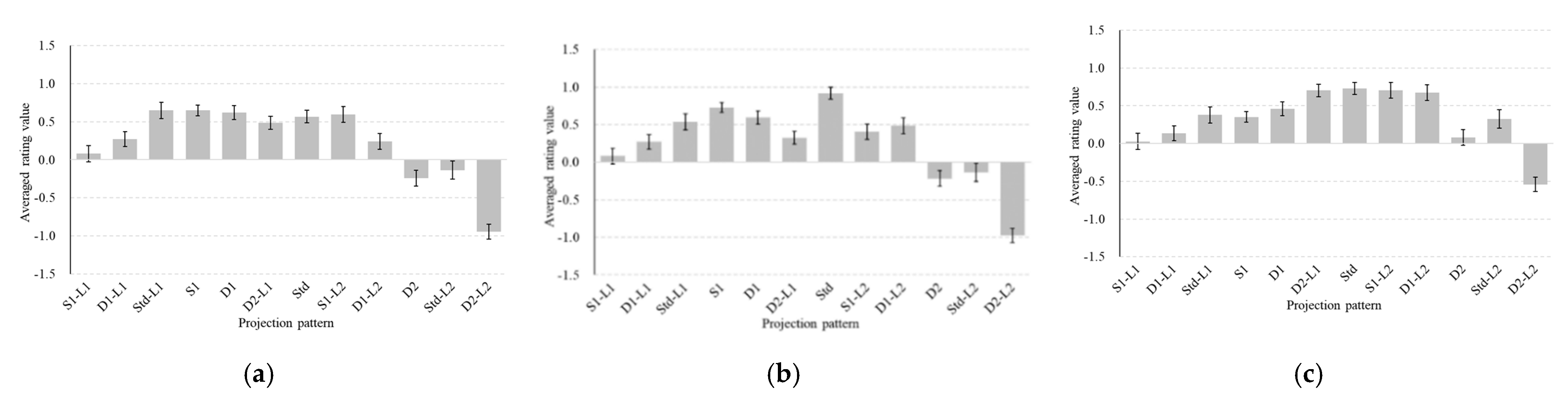
2.5. Experimental Results
3. Modeling
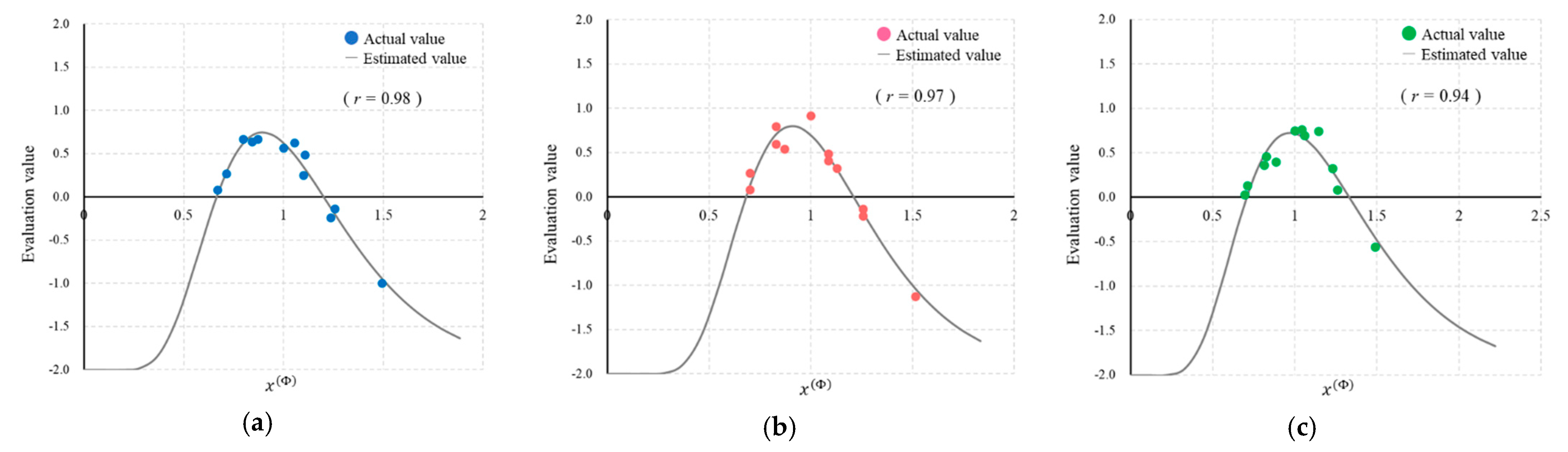
3.1. Estimation Model for Physical Factors
- Psychometric evaluations can be described using a logarithmic scale that conforms to the Weber–Fechner law.
- Each psychometric evaluation follows a normal distribution in the logarithmic domain because the average rating value for each evaluation is unimodal, as depicted in Figure 5.
- Humans evaluate faithfulness, preference, and depth feeling using all physical factors comprehensively, and this process can be described as addition in a numerical formula.
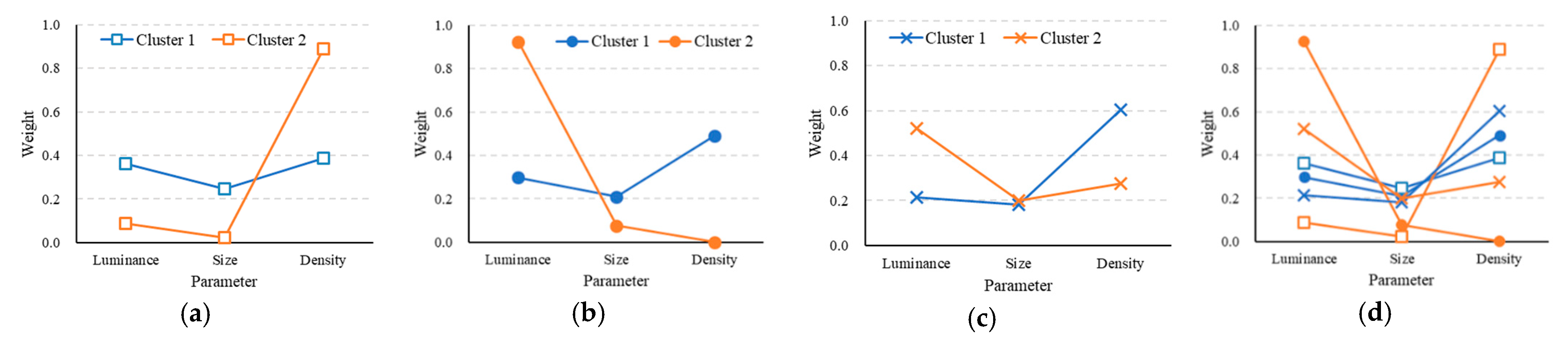
3.2. Evaluation Trends of Observers
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Astronomical Union. Available online: http://www.iau.org (accessed on 4 February 2021).
- International Dark-Sky Association. Available online: http://www.darksky.org/light-pollution/ (accessed on 4 February 2021).
- International Planetarium Society. Available online: http://www.ips-planetarium.org (accessed on 4 February 2021).
- Good, G.A. Observing Variable Stars; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Jensen, H.W.; Durand, F.; Dorsey, J.; Stark, M.M.; Shirley, P.; Premože, S. A physically-based night sky model. In Proceedings of the 28th Annual Conference ACM, Los Angeles, CA, USA, 12–17 August 2001; pp. 399–408. [Google Scholar]
- Jensen, H.W.; Premože, S.; Shirley, P.; Thompson, W.B.; Ferwerda, J.A.; Stark, M.M. Night Rendering; Technical Report UUCS-00-016; Department of Computer Science, University of Utah: Salt Lake City, UT, USA, 2000. [Google Scholar]
- Tanaka, M.; Horiuchi, T.; Otani, K.; Hung, P.-C. Evaluation for Faithful Reproduction of Star Fields in a Planetarium. Electron. Imaging 2018, 2018, 060401-1. [Google Scholar] [CrossRef]
- Tanaka, M.; Horiuchi, T.; Otani, K. Relationship between Faithfulness and Preference of Stars in a Planetarium. J. Percept. Imaging 2019, 2, 10402-1–10402-11. [Google Scholar] [CrossRef]
- Peli, E.; Arend, L.; Labianca, A.T. Contrast perception across changes in luminance and spatial frequency. J. Opt. Soc. Am. A 1996, 13, 1953–1959. [Google Scholar] [CrossRef] [PubMed]
- Durgin, F.H.; Hammer, J.T. Visual aftereffects of sequential perception: Dynamic adaptation to changes in texture density and contrast. Vis. Res. 2001, 41, 2607–2617. [Google Scholar] [CrossRef] [Green Version]
- Leinert, C.; Bowyer, S.; Haikala, L.K.; Hanner, M.S.; Hauser, M.G.; Levasseur-Regourd, A.-C.; Mann, I.; Mattila, K.; Reach, W.T.; Schlosser, W.; et al. The 1997 reference of diffuse night sky brightness. Astron. Astrophys. Suppl. Ser. 1998, 127, 1–99. [Google Scholar] [CrossRef] [Green Version]
- Schaefer, B.E. Telescopic limiting magnitudes. Publ. Astron. Soc. Pac. 1990, 102, 212. [Google Scholar] [CrossRef]
- Jones, D. Norman Pogson and the Definition of Stellar Magnitude; Astronomical Society of the Pacific Leaflets: San Francisco, CA, USA, 1967; Volume 10, pp. 145–152. [Google Scholar]
- Perryman, M.A.C.; Lindergren, L.; Kovalevsky, L.; Hoeg, E.; Bastian, U.; Bernacca, P.L.; Crézé, M.; Donati, F.; Grenon, M.; Grewing, M.; et al. The Hipparcos Catalogue. Astron. Astrophys. 1997, 323, 49–52. [Google Scholar]
- Williamson, S.J.; Cummins, H.Z. Light and Color in Nature and Art; John Wiley and Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Carifio, J.; Perla, R. Resolving the 50-year debate around using and misusing Likert scales. Med. Educ. 2008, 42, 1150–1152. [Google Scholar] [CrossRef] [PubMed]
- Norman, G. Likert scales, levels of measurement and the “laws” of statistics. Adv. Health Sci. Educ. 2010, 15, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Mansfield, R.J.W. Measurement, Invariance, and Psychophysics; Springer: Dordrecht, The Netherlands, 1974; pp. 113–128. [Google Scholar]
- Shao, Z.; Wu, J.; Ouyang, Q.; He, C.; Cao, Z. Multi-Layered Perceptual Model for Haptic Perception of Compliance. Electronics 2019, 8, 1497. [Google Scholar] [CrossRef] [Green Version]
- Hennig, C. Clustering Strategy and Method Selection. arXiv 2015, arXiv:1503.02059. [Google Scholar]


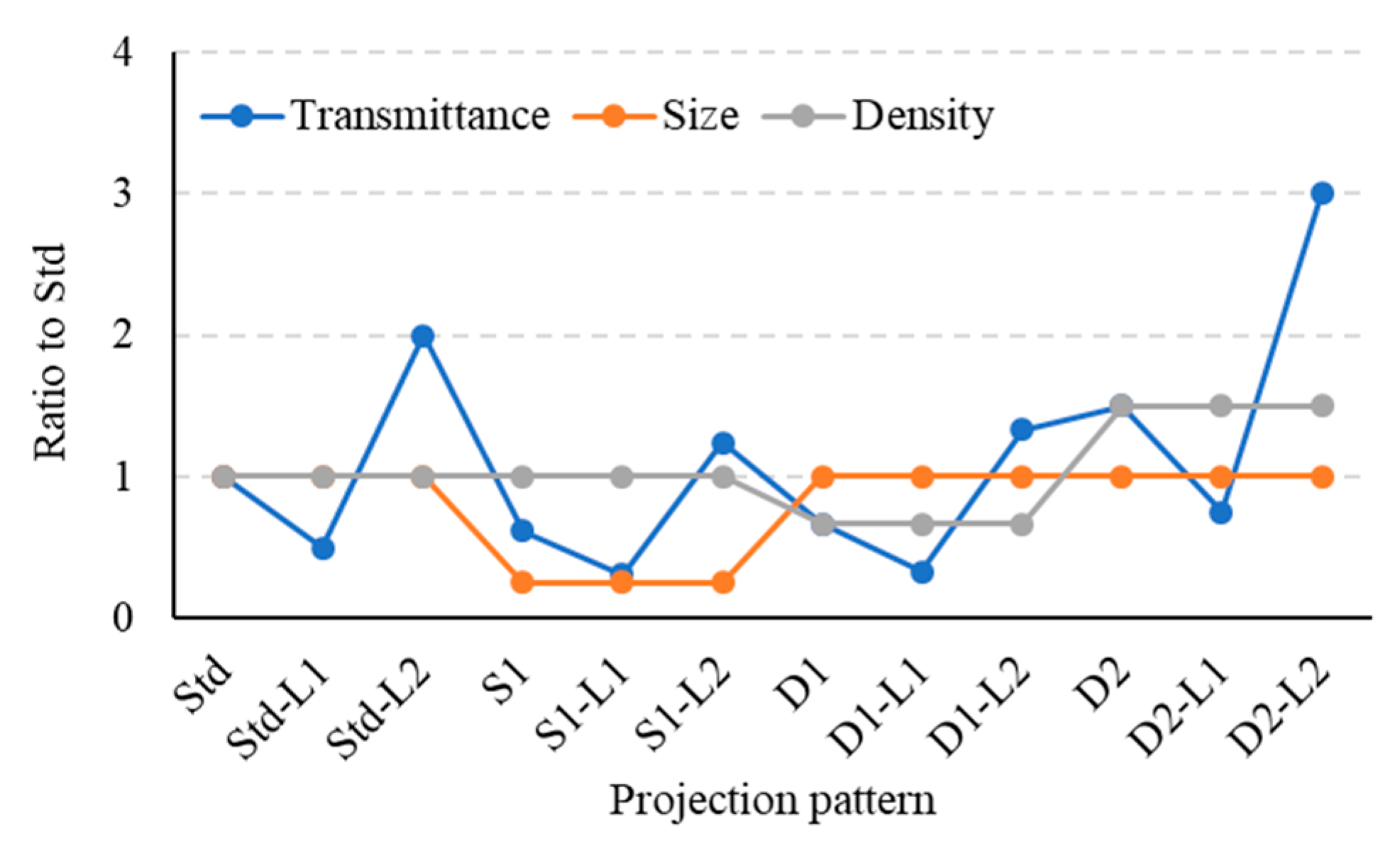

| Pattern | Changed Parameters, with Std as the Benchmark | Remarks |
|---|---|---|
| Std | N/A | |
| Std-L1 | Transmittance | Pattern Std but half transmittance |
| Std-L2 | Transmittance | Pattern Std but double transmittance |
| S1 | Size | Pattern Std but half diameter |
| S1-L1 | Size and Transmittance | Pattern S but half transmittance |
| S1-L2 | Size and Transmittance | Pattern S but double transmittance |
| D1 | Density | Pattern Std but 2/3 times density |
| D1-L1 | Density and Transmittance | Pattern D1 but half transmittance |
| D1-L2 | Density and Transmittance | Pattern D1 but double transmittance |
| D2 | Density | Pattern Std but 3/2 times density |
| D2-L1 | Density and Transmittance | Pattern D2 but half transmittance |
| D2-L2 | Density and Transmittance | Pattern D2 but double transmittance |
| Age Bracket | Male | Female | Total |
|---|---|---|---|
| 20s | 4 | 5 | 9 |
| 30s | 5 | 5 | 10 |
| 40s | 6 | 5 | 11 |
| Over 50 | 7 | 0 | 7 |
| Total | 22 | 15 | 37 |
| Index Φ | Mean μ | Standard Deviation σ |
|---|---|---|
| Faithfulness | 4.00 | 0.37 |
| Preference | 4.03 | 0.35 |
| Depth feeling | 3.94 | 0.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanaka, M.; Otani, K.; Setoguchi, S.; Horiuchi, T. The Reproduction and Evaluation of Star Fields with the Milky Way in a Planetarium. Appl. Sci. 2021, 11, 1413. https://doi.org/10.3390/app11041413
Tanaka M, Otani K, Setoguchi S, Horiuchi T. The Reproduction and Evaluation of Star Fields with the Milky Way in a Planetarium. Applied Sciences. 2021; 11(4):1413. https://doi.org/10.3390/app11041413
Chicago/Turabian StyleTanaka, Midori, Ken’ichi Otani, Saori Setoguchi, and Takahiko Horiuchi. 2021. "The Reproduction and Evaluation of Star Fields with the Milky Way in a Planetarium" Applied Sciences 11, no. 4: 1413. https://doi.org/10.3390/app11041413
APA StyleTanaka, M., Otani, K., Setoguchi, S., & Horiuchi, T. (2021). The Reproduction and Evaluation of Star Fields with the Milky Way in a Planetarium. Applied Sciences, 11(4), 1413. https://doi.org/10.3390/app11041413







