Rockfall Modelling in Forested Areas: The Role of Digital Terrain Model Grid Cell Size
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Rockfall Modelling
2.3. Used Datasets
2.3.1. Simulation Settings and Block Definition
2.3.2. Surface Roughness Parameters and Soil Types
2.3.3. Simulation with Forest
2.4. Calibration of Surface Roughness Parameters
2.5. Evaluation of Calibration and Validation
2.6. Comparison of Additional Output Data
2.7. Model Sensitivity to Initial Fall Height and Variation of the Rock Volume
3. Results
3.1. Model Calibration for DTM2
3.2. Validation of the Modelled Rockfall Runout Zones with and without Forest
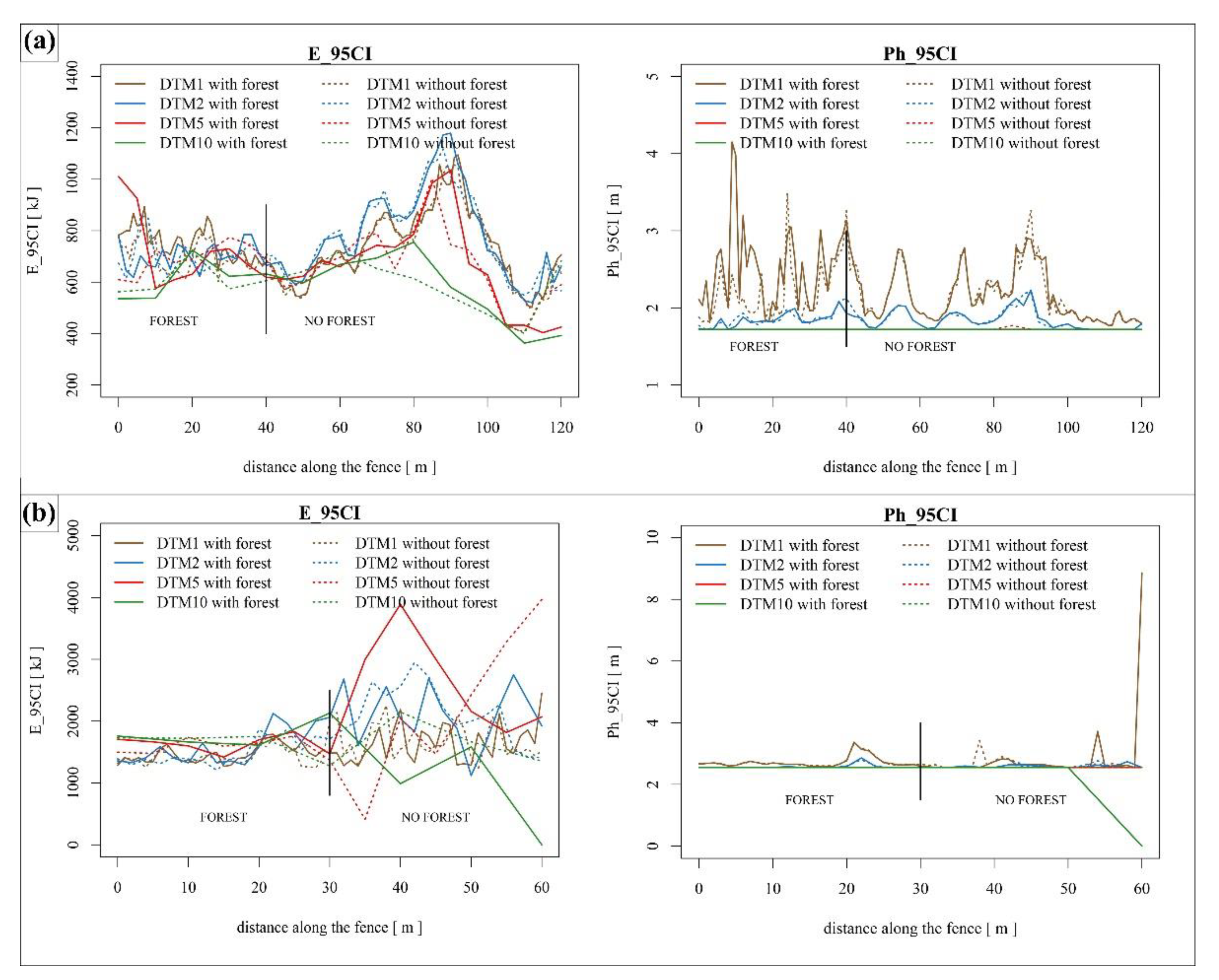
3.3. Comparison of the Maximum Kinetic Energy and Maximum Passing Heights between DTMs and Modelling Scenarios
3.4. Results of Model Sensitivity Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Frattini, P.; Crosta, G.B.; Agliardi, F. Rockfall characterization and modelling. In Landslides: Types, Mechanisms and Modeling; Clague, J., Stead, D., Eds.; Cambridge University Press: Cambridge, UK, 2012; pp. 267–281. [Google Scholar]
- Varnes, D.J. Slope movement types and processes. In Landslide Analysis and Control; Special Report 176; Schuster, R.L., Krizek, R.J., Eds.; National Academy of Sciences: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- Cruden, D.M.; Varnes, D.J. Landslide types and processes. In Landslides: Investigation and Mitigation, Transportation Research Board; Special Report 247; Turner, A.K., Schuster, R.L., Eds.; National Research Council: Washington, DC, USA, 1996; pp. 36–75. [Google Scholar]
- Abbruzzese, J.M.; Sauthier, C.; Labiouse, V. Considerations on Swiss methodologies for rock hazard mapping based on trajectory modelling. Nat. Hazards Earth Syst. Sci. 2009, 9, 1095–1109. [Google Scholar] [CrossRef] [Green Version]
- Dorren, L.K.A. A review of rockfall mechanics and modelling approaches. Prog. Phys. Geog. 2003, 27, 69–87. [Google Scholar] [CrossRef]
- Dorren, L.K.A.; Domaas, U.; Kronholm, K.; Labiouse, V. Method for predicting rockfall trajectories and run–out zones. In Rockfall Engineering; Lambert, S., Nicot, F., Eds.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2011; pp. 143–173. [Google Scholar]
- Volkwein, A.; Schellenberg, K.; Labiouse, V.; Agliardi, F.; Berger, F.; Bourrier, F.; Dorren, L.K.A.; Jaboyedoff, M. Rockfall characterization and structural protection—A review. Nat. Hazards Earth Syst. Sci. 2011, 11, 2617–2651. [Google Scholar] [CrossRef] [Green Version]
- Dorren, L.K.A.; Berger, F.; Le Hir, C.; Mermin, E.; Tardif, P. Mechanisms, effects and management implications of rockfall in forests. Forest Ecol. Manag. 2005, 215, 183–195. [Google Scholar] [CrossRef]
- Wyllie, D.C. Rock Fall Engineering, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017; p. 243. [Google Scholar]
- Howlad, E.P.; Abbruzzese, J.M.; Grisanti, C. An approach for evaluating the role of protection measures in rockfall hazard zoning based on the Swiss experience. Nat. Hazards Earth Syst. Sci. 2017, 17, 1127–1144. [Google Scholar]
- Berger, F.; Dorren, L.; Kleemayr, K.; Maier, B.; Planinsek, S.; Bigot, C.; Bourrier, F.; Jancke, O.; Toe, D.; Cerbu, G. Eco-engineering and protection forest against rockfalls and snow avalanches. In Management Strategies to Adapt Alpine Space Forests to Climate Change Risks; Cerbu, G.A., Hanewinkel, M., Gerosa, G., Jandl, R., Eds.; Intech Open: London, UK, 2013; pp. 191–210. [Google Scholar]
- Toe, D.; Berger, F. Regional mapping of forest with a protection function against rockfall. In Engineering Geology for Society and Territory; Lollino, G., Giordan, D., Crosta, G.B., Corominas, J., Azzam, R., Wasowski, J., Sciarra, N., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 2, pp. 1957–1959. [Google Scholar]
- Dorren, L.K.A.; Berger, F. Steam breakage of trees and energy dissipation during rockfall impacts. Tree Physiol. 2006, 26, 63–71. [Google Scholar] [CrossRef]
- Lundström, T.; Jonsson, M.J.; Volkwein, A.; Stoffel, M. Reactions and energy absorption of trees subject to rockfall: A detailed assessment using a new experimental method. Tree Physiol. 2009, 29, 345–359. [Google Scholar] [CrossRef] [Green Version]
- Bertrand, D.; Bourrier, F.; Olmedo, I.; Brun, M.; Berger, F.; Liamam, A. Experimental and numerical dynamic analysis of a live tree steam impacted by a Charpy pendulum. Int. J. Solids Struct. 2013, 50, 1689–1698. [Google Scholar] [CrossRef]
- Guzzeti, F.; Crosta, G.; Detti, R.; Agliardi, F. STONE: A computer program for the three-dimensional simulation of rock-falls. Comput. Geosci. 2002, 28, 1079–1093. [Google Scholar] [CrossRef]
- Crosta, G.B.; Agliardi, F.; Frattini, P.; Imposimato, S. A three-dimensional hybrid numerical model for rockfall simulation. Geophys. Res. Abstr. 2004, 6, 4502. [Google Scholar]
- Jaboyedoff, M.; Labiouse, V. Technical note: Preliminary estimation of rockfall runout zones. Nat. Hazards Earth Syst. Sci. 2011, 11, 819–828. [Google Scholar] [CrossRef] [Green Version]
- Christen, M.; Bühler, Y.; Bartelt, P.; Leine, R.; Glover, J.; Schweizer, A.; McArdell, B.W.; Gerber, W.; Deubelbeiss, Y.; Feistl, T.; et al. Integral hazard management using a unified software environment. Numerical simulation tool “RAMMS” for gravitational natural hazards. In Proceedings of the 12th Interpraevent, Grenoble, France, 23–26 April 2012; pp. 77–86. [Google Scholar]
- Horton, P.; Jaboyedoff, M.; Rudaz, B.; Zimmermann, M. Flow-R, a model for susceptibility mapping of debris flows and other gravitational hazards at a regional scale. Nat. Hazards Earth Syst. Sci. 2013, 13, 869–885. [Google Scholar] [CrossRef] [Green Version]
- Dorren, L.K.A. Rockyfor3D (v5.2) Revealed. Transparent Description of the Complete 3D Rockfall Model; International Association for Natural Hazard Risk Management EcorisQ: Geneva, Switzerland, 2016; p. 32. [Google Scholar]
- Berger, F.; Quetel, C.; Dorren, L.K.A. Forest: A natural protection mean against rockfalls, but with which efficiency. In Proceedings of the International Congress Interpraevent, 24–27 May 2004; pp. 815–826. [Google Scholar]
- Dorren, L.; Berger, F.; Jonsson, M.; Krautblatter, M.; Mölk, M.; Stoffel, M.; Wehrli, A. State of the art in rockfall—Forest interactions. Schweiz Z Forstwes. 2007, 6, 128–141. [Google Scholar] [CrossRef] [Green Version]
- Dupire, S.; Bourrier, F.; Monnet, J.-M.; Bigot, S.; Borgniet, L.; Berger, F.; Curt, T. Novel quantitative indicators to characterize the protective effect of mountain forest against rockfall. Ecol. Indic. 2016, 67, 98–107. [Google Scholar] [CrossRef] [Green Version]
- Michoud, C.; Derron, M.-H.; Horton, P.; Jaboyedoff, M.; Baillifard, F.-J.; Loye, A.; Nicolet, P.; Pedrazzini, A.; Queyrel, A. Rockfall hazard and risk assessment along roads at regional scale: Example in Swiss Alps. Nat. Hazards Earth Syst. Sci. 2012, 12, 615–629. [Google Scholar] [CrossRef] [Green Version]
- Crosta, G.B.; Agliardi, F.; Frattini, P.; Lari, S. Key issues in rock fall modelling, hazard and risk assessment for rockfall protection. In Engineering Geology for Society and Territory; Lollino, G., Giordan, D., Crosta, G.B., Corominas, J., Azzam, R., Wasowski, J., Sciarra, N., Eds.; Springer: Cham, Switzerland, 2015; Volume 2, pp. 43–58. [Google Scholar]
- Frattini, P.; Crosta, G.B.; Agliardi, F.; Imposimato, S. Challenging calibration in 3D modelling. In Landslide Science and Practices; Margottini, C., Canuti, P., Sassa, K., Eds.; Springer: Berlin, Germany, 2013; Volume 3, pp. 169–175. [Google Scholar]
- Moos, C.; Fehlmann, M.; Trappmann, D.; Stoffel, M.; Dorren, L. Integrating the mitigating effect of forests into quantitative rockfall risk analysis—Two case studies in Switzerland. Int. J. Disast. Risk. 2018, 32, 55–74. [Google Scholar] [CrossRef]
- Lan, H.; Martin, C.D.; Zhou, C.; Ho Lim, C. Rockfall hazard analysis using LIDAR and spatial modelling. Geomorphology 2010, 118, 213–223. [Google Scholar] [CrossRef]
- Bühler, Y.; Christen, M.; Glover, J.; Christen, M.; Bartelt, P. Significance of digital elevation model resolution for numerical rockfall simulations. In Proceedings of the 3rd RSS Rock Slope Stability Conference, Lyon, France, 15–17 November 2016; pp. 1–2. [Google Scholar]
- Dorren, L.K.A.; Heuvelink, G.B.N. Effect of support size on the accuracy of a distributed rockfall model. Int. J. Geog. Inf. Sci. 2004, 18, 595–609. [Google Scholar] [CrossRef]
- Zieher, T.; Formanek, T.; Bremer, M.; Meissl, G.; Rutzinger, M. Digital terrain model resolution and its influence on estimating the extent of rockfall areas. Trans. GIS 2012, 16, 691–699. [Google Scholar] [CrossRef]
- Loye, A.; Jaboyedoff, M.; Pedrazzini, A. Identification of potential rockfall source areas at a regional scale using a DTM-based geomorphometric analysis. Nat. Hazards Earth Syst. Sci. 2009, 9, 1643–1653. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Choffet, M.; Derron, M.-H.; Horton, P.; Loye, A.; Longshamp, C.; Mazzotti, B.; Michoud, C.; Pedrazzini, A. Preliminary Slope Mass Movement Susceptibility Mapping Using DEM and LiDAR DEM. In Terrigenous Mass Movements; Pradhan, B., Buchroithner, M., Eds.; Springer: Berlin, Germany, 2012; pp. 109–170. [Google Scholar]
- Žabota, B.; Repe, B.; Kobal, M. Influence of digital elevation model resolution on rockfall modelling. Geomorphology 2019, 328, 183–195. [Google Scholar] [CrossRef]
- Abbruzzese, J.M.; Labiouse, V. New Cadanav Methodology for Rock Fall Hazard Zoning Based on 3D Trajectory Modelling. Geosciences 2020, 10, 434. [Google Scholar] [CrossRef]
- Jurkovšek, B. Tolmač listov Beljak in Ponteba: Osnovna Geološka Karta SFRJ 1:100 000; Zvezni Geološki Zavod: Belgrade, Serbia, 1987; p. 55. [Google Scholar]
- Placer, L. Osnovne tektonske razčlenitve Slovenije. Geologija 2008, 51, 205–217. [Google Scholar] [CrossRef]
- Zupan Hajna, N.; Petrič, M.; Zdešar, A. Trenta—Triglavski narodni park. In Proceedings of the 3. Slovenski Geološki Kongres, Bovec, Slovenia, 16–18 September 2010; pp. 69–80. [Google Scholar]
- Čarni, A.; Marinček, L.; Seliškar, A.; Zupančič, M. Vegetacijska Karta Gozdnih Združb Slovenije, Merilo 1:400,000; Biološki Inštitut Jovana Hadžija: Ljubljana, Slovenia, 2002. [Google Scholar]
- Zorn, M. Rockfalls in Slovene Alps. Acta Geogr. 2002, 42, 124–160. [Google Scholar]
- Zorn, M.; Komac, B. Recent mass movements in Slovenia. In Slovenia: A Geographical Overview; Orožen Adamič, M., Ed.; Association of the Geographical Societies of Slovenia: Ljubljana, Slovenia, 2004; pp. 73–80. [Google Scholar]
- Rekanje, B.; Kobal, M. Vpliv vremenskih razmer na pogostost padanja kamenja v Baški grapi. Gozdarski Vestn. 2020, 78, 402–403. [Google Scholar]
- Mikoš, M.; Fazarinc, R.; Ribičič, M. Sediment production and delivery from recent large landslides and earthquake-induced rock falls in the Upper Soča River Valley, Slovenia. Eng. Geol. 2006, 86, 198–210. [Google Scholar] [CrossRef]
- Mikoš, M.; Jemec Auflič, M.; Ribičič, M.; Čarman, M.; Komac, M. Earthquake-induced Landslides in Slovenia: Historical Evidence and Present Analyses. In Proceedings of the International Symposium on Earthquake-Induced Landslides, Kiryu, Japan, 7–9 November 2012; pp. 225–233. [Google Scholar]
- Žabota, B.; Trappmann, D.; Levanič, T.; Kobal, M. Reconstruction of rockfall activity through dendrogeomorphology and a scar-counting approach: A study in a beech forest stand in the Trenta valley. Acta Silvae Ligni 2020, 121, 19–32. [Google Scholar] [CrossRef]
- Berger, F.; Dorren, L.K.A. Principles of the tool Rockfor.net for quantifying the rockfall hazard below a protection forest. Schweiz. Z. Forstwes. 2007, 158, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Blair, T.C.; McPherson, J.G. Grain-size and textural classification of coarse sedimentary particles. J. Sediment. Res. 1999, 69, 6–19. [Google Scholar] [CrossRef]
- Blott, S.J.; Pye, K. Particle size scales and classification of sediment types based on particle size distributions: Review and recommended procedures. Sedimentology 2012, 59, 2071–2096. [Google Scholar] [CrossRef]
- Terry, J.P.; Goff, J. Megaclasts: Proposed revised nomenclature at the coarse end of the Udden-Wentworth gain-size scale for sedimentary particles. J. Sediment. Res. 2014, 84, 192–197. [Google Scholar] [CrossRef]
- Bruno, D.E.; Ruban, D.A. Something more than boulders: A geological comment on the nomenclature of megaclasts on extraterrestrial bodies. Planet. Space Sci. 2017, 135, 37–42. [Google Scholar] [CrossRef]
- Ruban, D.A.; Sallam, E.S.; Ermolaev, V.A.; Yashalova, N.N. Aesthetic Value of Colluvial Blocks in Geosite-Based Tourist Destinations: Evidence from SW Russia. Geosciences 2020, 10, 51. [Google Scholar] [CrossRef] [Green Version]
- SMARS: LiDAR Data in D96TM Projection; The Surveying and Mapping Authority of the Republic Slovenia: Ljubljana, Slovenia, 2014.
- ArcGIS Pro 2.5.1, Esri. Available online: https://www.esri.com/en-us/arcgis/products/arcgis-pro/resources (accessed on 15 May 2020).
- Dorren, L.K.A. FINT—Find Individual Trees. User Manual; EcorisQ: Geneva, Switzerland, 2017; p. 5. [Google Scholar]
- Slovenian Forest Service. Forest Stand Data. Available online: http://prostor.zgs.gov.si/pregledovalnik/?locale=en (accessed on 15 May 2020).
- Bourrier, F.; Hungr, O. Rockfall dynamics: A critical review of collision and rebound models. In Rockfall Engineering; Lambert, S., Nicot, F., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 175–209. [Google Scholar]
- Gischig, V.S.; Hung, O.; Mitchell, A.; Bourrier, F. Pierre3D: A 3D stochastic rockfall simulator based on random ground roughness and hyperbolic restitution factors. Can. Geotech. J. 2015, 52, 1–14. [Google Scholar] [CrossRef]
- RStudio Team. RStudio: Integrated Development for R; RStudio, Inc.: Boston, MA, USA, 2016. [Google Scholar]
- Formetta, G.; Capparelli, G.; Versace, P. Evaluating performance of simplified physically based models for shallow landslide susceptibility. Hydrol. Earth Syst. Sci. 2016, 20, 4585–4603. [Google Scholar] [CrossRef] [Green Version]
- Goodenough, D.J.; Rossmann, K.; Lusted, L.B. Radiographic applications of receiver operating characteristic (ROC) analysis. Radiology 1974, 110, 89–95. [Google Scholar] [CrossRef]
- Žabota, B.; Kobal, M. A new methodology for mapping past rockfall events: From mobile crowdsourcing to rockfall simulation validation. Int. J. Geo Inf. 2020, 9, 1–21. [Google Scholar] [CrossRef]
- Corona, C.; Lopez-Saez, J.; Favillier, A.; Mainieri, R.; Eckert, N.; Trappmann, D.; Stoffel, M.; Bourrier, F.; Berger, F. Modelling rockfall frequency and bounce height from three-dimensional simulation process models and growth disturbances in submontane broadleaved trees. Geomorphology 2017, 281, 66–77. [Google Scholar] [CrossRef]
- Lanfranconi, C.; Sala, G.; Frattini, P.; Crosta, G.B.; Valagussa, A. Assessing the rockfall protection efficiency of forests at the regional scale. Landslides 2020, 17, 2703–2721. [Google Scholar] [CrossRef]
- Rammer, W.; Brauner, M.; Ruprecht, H.; Lexer, M.J. Evaluating the effect of forest management on rockfall protection and timber production at slope scale. Scand. J. Forest Res. 2015, 30, 719–731. [Google Scholar] [CrossRef]
- Lopez-Saez, J.; Corona, C.; Eckert, N.; Stoffel, M.; Bourrier, F.; Berger, F. Impacts of land-use and land-cover changes on rockfall propagation: Insights from the Grenoble conurbation. Sci. Total Environ. 2016, 547, 345–355. [Google Scholar] [CrossRef]
- Moos, C.; Dorren, L.; Stoffel, M. Quantifying the effect of forests on frequency and intensity of rockfalls. Nat. Hazards Earth Syst. Sci. 2017, 17, 291–304. [Google Scholar] [CrossRef] [Green Version]
- Crosta, G.B.; Agliardi, F. Parametric evaluation of 3D dispersion of rockfall trajectories. Nat. Hazards Earth Syst. Sci. 2004, 4, 583–598. [Google Scholar] [CrossRef] [Green Version]
- Clouet, N.; Berger, F.; Liévois, J. Rockfall modelling and risk zoning: A case study in the French Alps using geomatics, airborne laser scanning, 2D & 3D runout models. In Proceedings of the 12th Congress INTERPRAEVENT 2012, Grenoble, France, 23–26 April 2012; pp. 479–486. [Google Scholar]
- Radtke, A.; Toe, D.; Berger, F.; Zerbe, S.; Bourrier, F. Managing coppice forests for rockfall protection: Lessons from modelling. Ann. For. Sci. 2014, 71, 485–494. [Google Scholar] [CrossRef] [Green Version]
- Fuhr, M.; Bourrier, F.; Cordonnier, T. Protection against rockfall along a maturity gradient in mountain forests. For. Ecol. Manag. 2015, 354, 224–231. [Google Scholar] [CrossRef]




| ROCKFALL SITE 1 | ||||||
|---|---|---|---|---|---|---|
| Intervals Used for Creation of 30 Random Calibration Runs | Optimal rg Values Obtained in Calibration Run 17 | |||||
| sub area | rg70 | rg20 | rg10 | rg70 | rg20 | rg10 |
| area 1 | 0.31 (0–0.71) | 0.6 (0.20–0.80) | 0.7 (0.3–1) | 0.14 | 0.36 | 0.65 |
| area 2 | 0.31 (0–0.71) | 0.31 (0–0.71) | 0.4 0–0.80 | 0.44 | 0.37 | 0.54 |
| area 3 | 0.31 (0–0.71) | 0.35 (0–0.75) | 0.4 (0–0.80) | 0.13 | 0.44 | 0.53 |
| ROCKFALL SITE 2 | ||||||
| Intervals Used for Creation of 30 Random Calibration Runs | Optimal rg Values Obtained in Calibration Run 4 | |||||
| sub area | rg70 | rg20 | rg10 | rg70 | rg20 | rg10 |
| area 1 | 0.21 (0–0.51) | 0.4 (0.10–0.70) | 0.5 (0.20–0.80) | 0.26 | 0.21 | 0.31 |
| area 2 | 0.35 (0.05–0.65) | 0.4 (0.10–0.70) | 0.45 (0.15–0.75) | 0.5 | 0.53 | 0.26 |
| area 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| area 4 | 0.3 (0–0.60) | 0.3 (0–0.60) | 0.35 (0.05–0.65) | 0.17 | 0.32 | 0.53 |
| Name | Definition | Range | Optimal Value |
|---|---|---|---|
| Success index (SI) | SI = ½ × ((TP/(TP + FN)) + (TN/(FP + TN)) | [0, 1] | 1.0 |
| Distance to the perfect classification (D2PC) | D2PC = √((1 − TPR)2 + (FPR)2) | [0, 1] | 0.0 |
| Average index (AI) | AI = 1/4 × ((TP/(TP + FN)) + (TP/(TP + FP)) + (TN/(FP + TN)) + (TN/(FN + TN))) | [0, 1] | 1.0 |
| True skill statistics (TSS) | TSS = ((TP × TN) − (FP × FN))/((TP + FN) × (FP + TN)) | [−1, 1] | 1.0 |
| ROCKFALL SITE 1 | ROCKFALL SITE 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Calibration Run | AI | SI | D2PC | TSS | Calibration Run | AI | SI | D2PC | TSS |
| 17 | 0.855 | 0.837 | 0.285 | 0.673 | 4 | 0.892 | 0.892 | 0.153 | 0.785 |
| 27 | 0.820 | 0.824 | 0.250 | 0.647 | 25 | 0.886 | 0.886 | 0.162 | 0.772 |
| 23 | 0.820 | 0.822 | 0.253 | 0.644 | 3 | 0.885 | 0.886 | 0.167 | 0.771 |
| ROCKFALL SITE 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| scenario without forest | scenario with forest | |||||||
| DTM grid cell size | AI | SI | D2PC | TSS | AI | SI | D2PC | TSS |
| DTM1 | 0.927 | 0.957 | 0.076 | 0.914 | 0.893 | 0.934 | 0.126 | 0.868 |
| DTM2 | 0.927 | 0.947 | 0.076 | 0.894 | 0.897 | 0.931 | 0.110 | 0.862 |
| DTM5 | 0.927 | 0.930 | 0.110 | 0.859 | 0.922 | 0.931 | 0.103 | 0.862 |
| DTM10 | 0.922 | 0.932 | 0.100 | 0.864 | 0.928 | 0.939 | 0.090 | 0.877 |
| ROCKFALL SITE 2 | ||||||||
| scenario without forest | scenario with forest | |||||||
| DTM grid cell size | AI | SI | D2PC | TSS | AI | SI | D2PC | TSS |
| DTM1 | 0.920 | 0.940 | 0.089 | 0.879 | 0.918 | 0.940 | 0.092 | 0.880 |
| DTM2 | 0.924 | 0.929 | 0.106 | 0.857 | 0.914 | 0.924 | 0.109 | 0.848 |
| DTM5 | 0.908 | 0.927 | 0.104 | 0.853 | 0.903 | 0.923 | 0.110 | 0.846 |
| DTM10 | 0.908 | 0.933 | 0.107 | 0.867 | 0.902 | 0.926 | 0.114 | 0.853 |
| ROCKFALL SITE 1 | SCENARIO WITHOUT FOREST | SCENARIO WITH FOREST | |||||||
|---|---|---|---|---|---|---|---|---|---|
| AI | SI | D2PC | TSS | AI | SI | D2PC | TSS | ||
| initial fall height (m) | 50 | 0.925 | 0.982 | 0.032 | 0.963 | 0.945 | 0.976 | 0.046 | 0.951 |
| 20 | 0.936 | 0.925 | 0.149 | 0.849 | 0.937 | 0.914 | 0.172 | 0.828 | |
| 10 | 0.928 | 0.889 | 0.221 | 0.778 | 0.924 | 0.878 | 0.244 | 0.755 | |
| variation of rock volume (%) | 0 | 0.925 | 0.982 | 0.032 | 0.963 | 0.945 | 0.976 | 0.046 | 0.951 |
| 5 | 0.925 | 0.982 | 0.032 | 0.964 | 0.945 | 0.977 | 0.044 | 0.953 | |
| 10 | 0.925 | 0.982 | 0.031 | 0.964 | 0.946 | 0.978 | 0.041 | 0.956 | |
| 20 | 0.924 | 0.982 | 0.032 | 0.964 | 0.944 | 0.977 | 0.043 | 0.954 | |
| 50 | 0.924 | 0.983 | 0.030 | 0.966 | 0.945 | 0.979 | 0.039 | 0.959 | |
| ROCKFALL SITE 2 | SCENARIO WITHOUT FOREST | SCENARIO WITH FOREST | |||||||
| AI | SI | D2PC | TSS | AI | SI | D2PC | TSS | ||
| initial fall height (m) | 50 | 0.936 | 0.953 | 0.088 | 0.906 | 0.943 | 0.951 | 0.093 | 0.902 |
| 20 | 0.921 | 0.877 | 0.245 | 0.753 | 0.917 | 0.872 | 0.254 | 0.744 | |
| 10 | 0.909 | 0.846 | 0.308 | 0.691 | 0.905 | 0.838 | 0.323 | 0.676 | |
| variation of rock volume (%) | 0 | 0.936 | 0.953 | 0.088 | 0.906 | 0.943 | 0.951 | 0.093 | 0.902 |
| 5 | 0.940 | 0.955 | 0.086 | 0.909 | 0.939 | 0.949 | 0.098 | 0.897 | |
| 10 | 0.937 | 0.956 | 0.083 | 0.912 | 0.940 | 0.948 | 0.099 | 0.896 | |
| 20 | 0.942 | 0.958 | 0.079 | 0.916 | 0.936 | 0.942 | 0.112 | 0.884 | |
| 50 | 0.941 | 0.961 | 0.073 | 0.922 | 0.941 | 0.951 | 0.093 | 0.903 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Žabota, B.; Mikoš, M.; Kobal, M. Rockfall Modelling in Forested Areas: The Role of Digital Terrain Model Grid Cell Size. Appl. Sci. 2021, 11, 1461. https://doi.org/10.3390/app11041461
Žabota B, Mikoš M, Kobal M. Rockfall Modelling in Forested Areas: The Role of Digital Terrain Model Grid Cell Size. Applied Sciences. 2021; 11(4):1461. https://doi.org/10.3390/app11041461
Chicago/Turabian StyleŽabota, Barbara, Matjaž Mikoš, and Milan Kobal. 2021. "Rockfall Modelling in Forested Areas: The Role of Digital Terrain Model Grid Cell Size" Applied Sciences 11, no. 4: 1461. https://doi.org/10.3390/app11041461







