Comparison of Extragraft Bone Formation after Anterior Cervical Discectomy and Fusion Using Simultaneous and Sequential Algorithms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Finite Element Model of the Operated C5–C6 Motion Segment
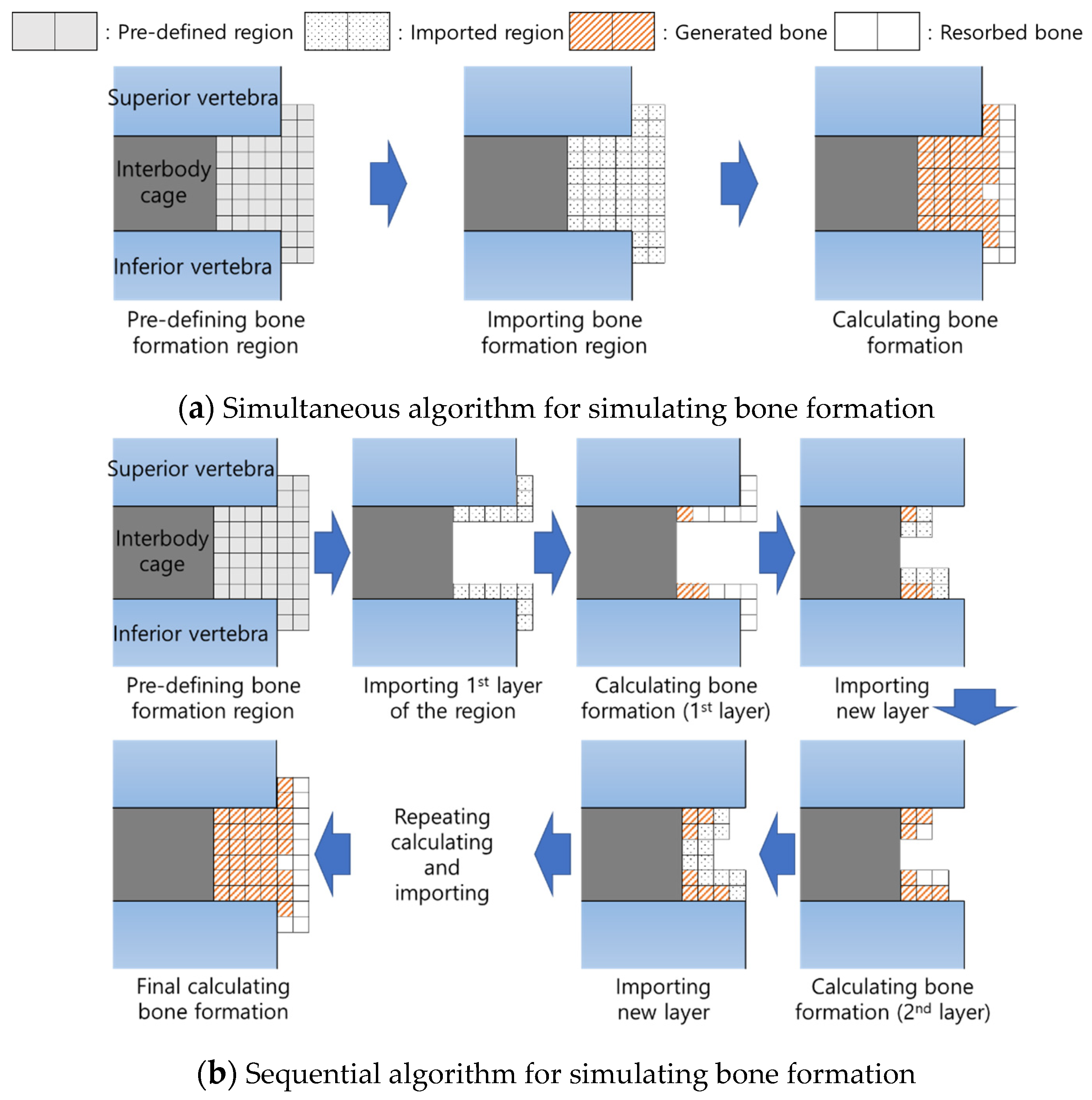
2.2. Modelling of the Predefined Region for Bone Formation around the Interbody Cage
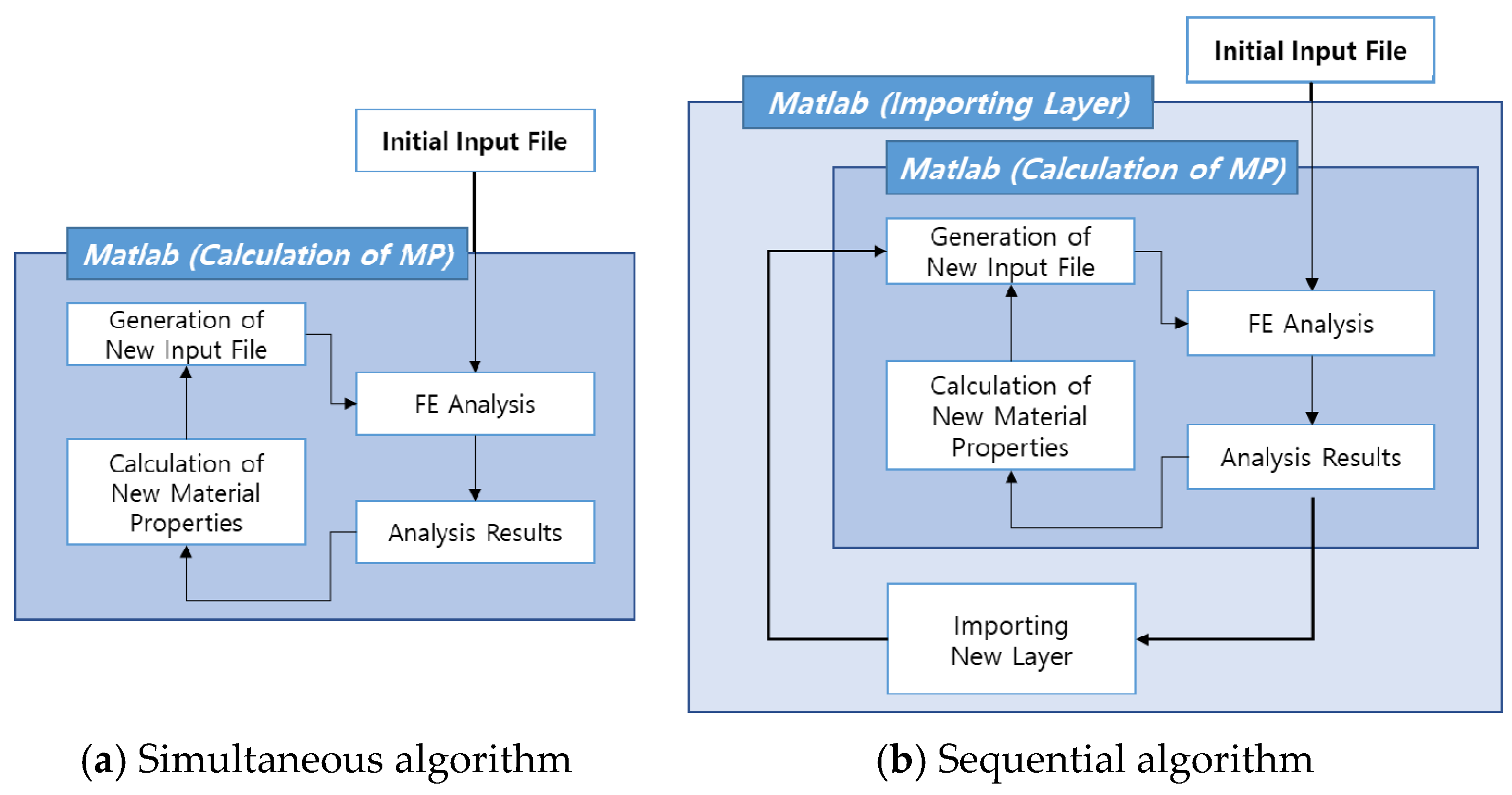
2.3. Simulation of Bone Formation around the Embedded Interbody Cage
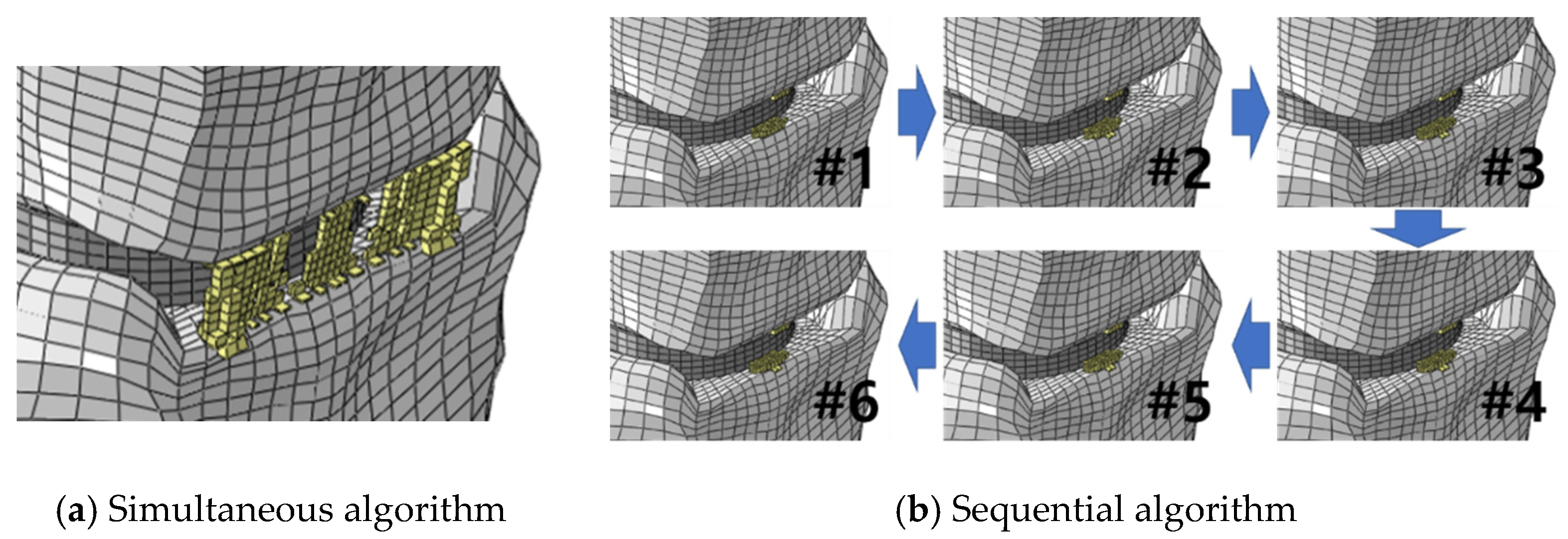
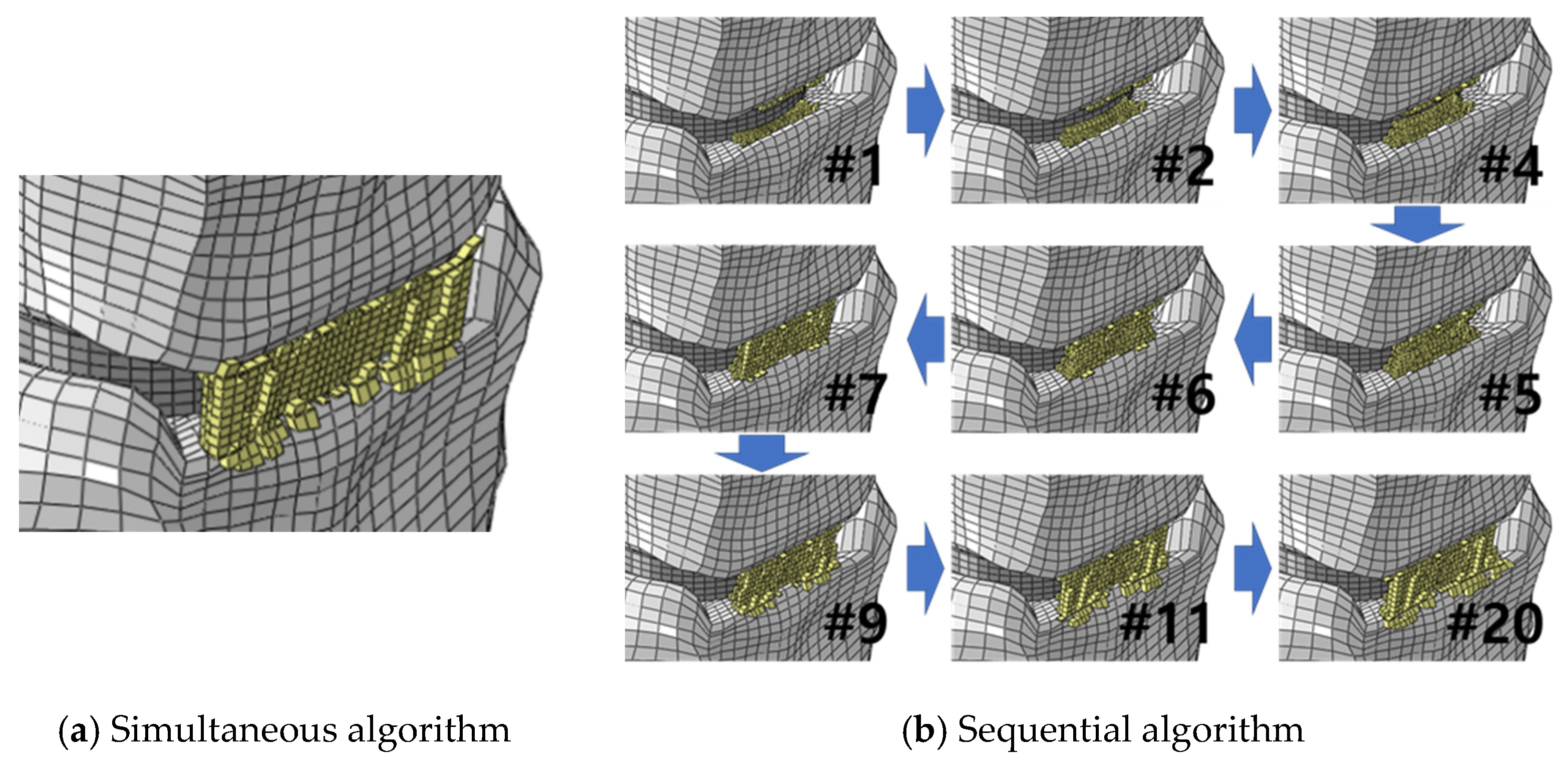
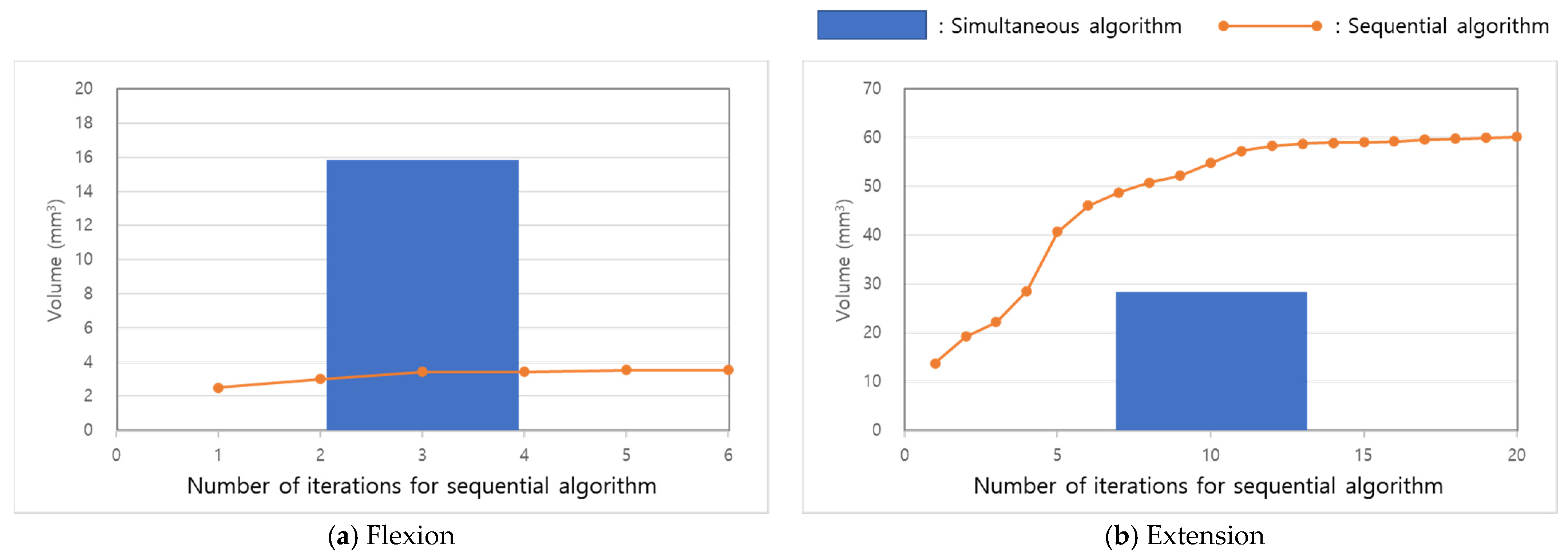
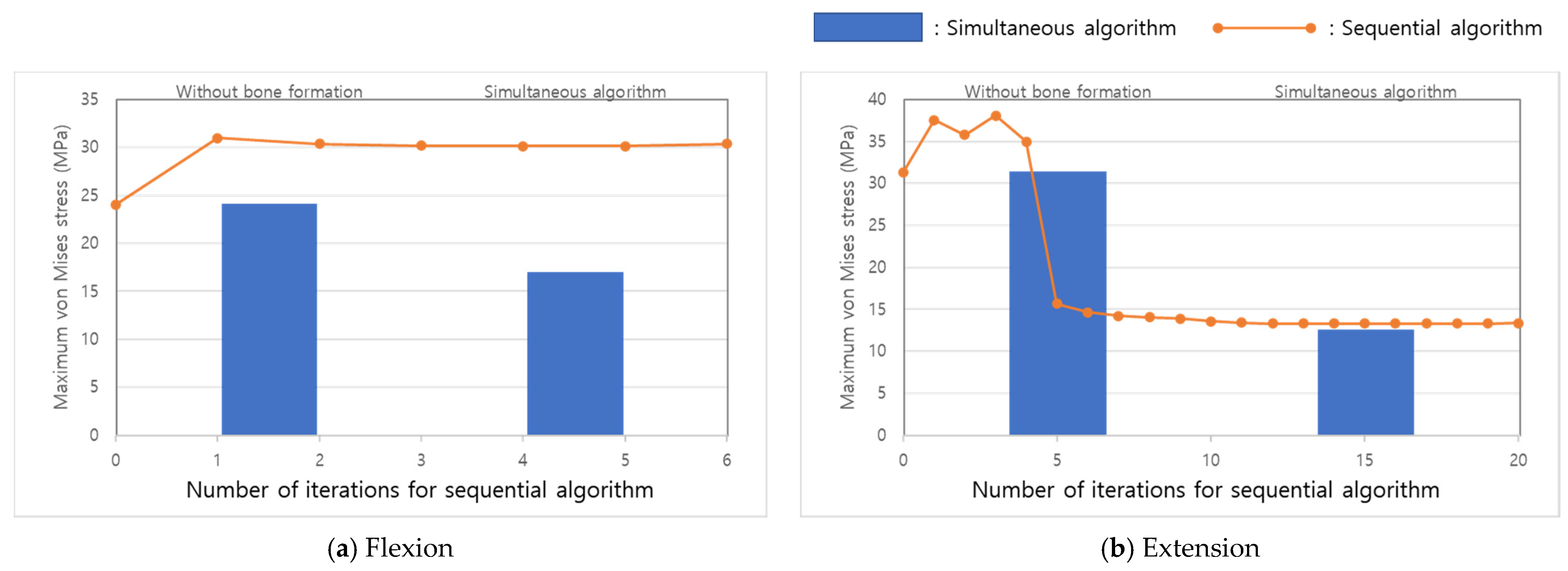
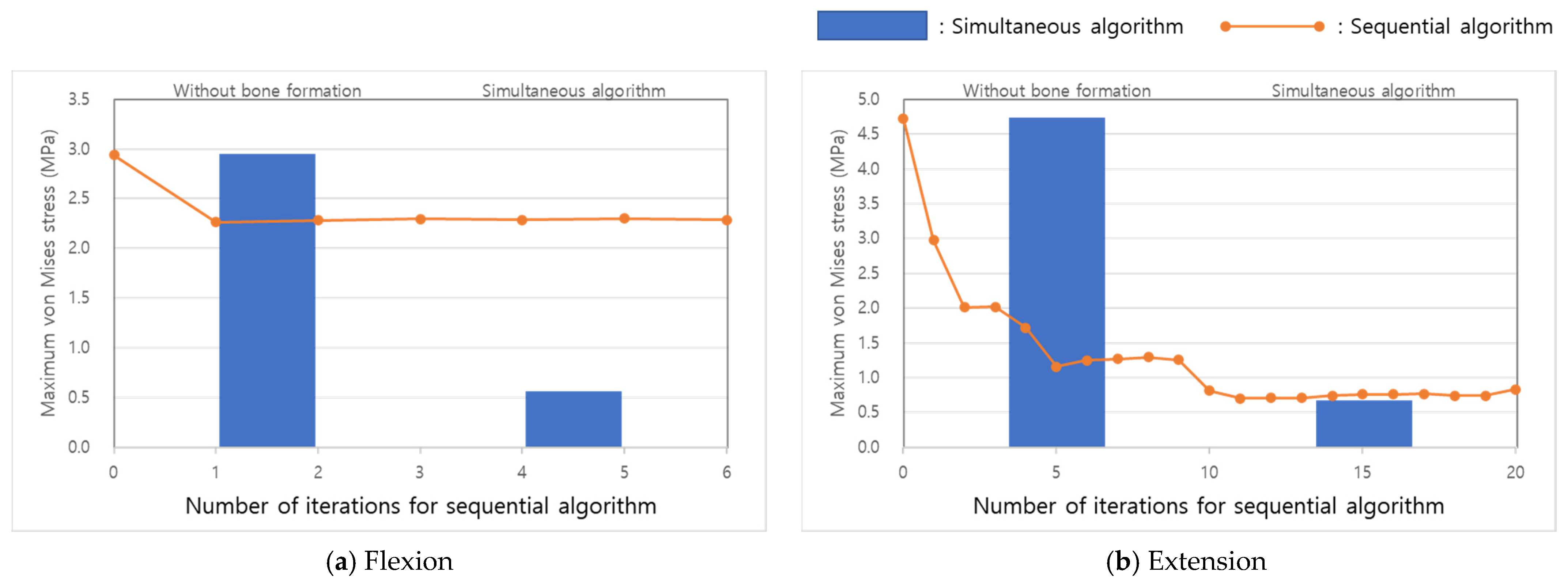
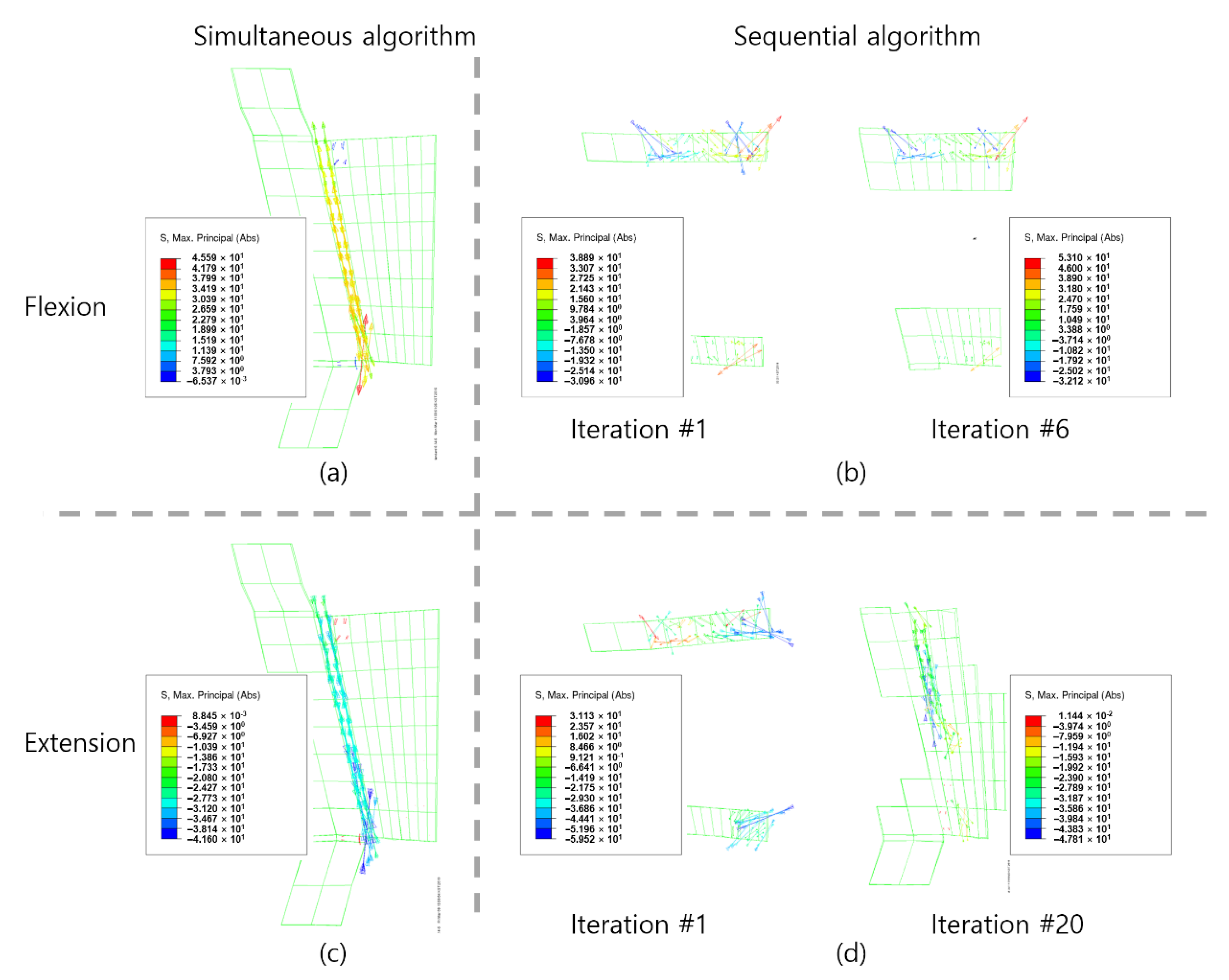
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wolff, J. Das Gesetz von der Transformation der Knochen; Pro Business: Berlin, Germany, 1892; ISBN 9783868056488. [Google Scholar]
- Jang, I.G.; Kim, I.Y. Application of design space optimization to bone remodeling simulation of trabecular architecture in human proximal femur for higher computational efficiency. Finite Elem. Anal. Des. 2010, 46, 311–319. [Google Scholar] [CrossRef]
- Jang, I.G.; Kim, I.Y.; Kwak, B.B. Analogy of strain energy density based bone-remodeling algorithm and structural topology optimization. J. Biomech. Eng. 2009, 131, 011012. [Google Scholar] [CrossRef]
- Boyle, C.; Kim, I.Y. Three-dimensional micro-level computational study of Wolff’s law via trabecular bone remodeling in the human proximal femur using design space topology optimization. J. Biomech. 2011, 44, 935–942. [Google Scholar] [CrossRef]
- Tsubota, K.I.; Suzuki, Y.; Yamada, T.; Hojo, M.; Makinouchi, A.; Adachi, T. Computer simulation of trabecular remodeling in human proximal femur using large-scale voxel FE models: Approach to understanding Wolff’s law. J. Biomech. 2009, 42, 1088–1094. [Google Scholar] [CrossRef]
- Song, K.S.; Chaiwat, P.; Kim, H.J.; Mesfin, A.; Park, S.M.; Riew, K.D. Anterior cervical fusion assessment using reconstructed computed tomographic scans: Surgical confirmation of 254 segments. Spine 2013, 38, 2171–2177. [Google Scholar] [CrossRef]
- Lee, S.E.; Chung, C.K.; Kim, C.H. Difference in canal encroachment by the fusion mass between anterior cervical discectomy and fusion with bone autograft and anterior plating, and stand-alone cage. J. Clin. Neurosci. 2016, 29, 121–127. [Google Scholar] [CrossRef]
- Perrini, P.; Gambacciani, C.; Martini, C.; Montemurro, N.; Lepori, P. Anterior cervical corpectomy for cervical spondylotic myelopathy: Reconstruction with expandable cylindrical cage versus iliac crest autograft. A retrospective study. Clin. Neurol. Neurosurg. 2015, 139, 258–263. [Google Scholar] [CrossRef]
- Maida, G.; Marcati, E.; Sarubbo, S. Heterotopic Ossification in Vertebral Interlaminar/Interspinous Instrumentation: Report of a Case. Case Rep. Surg. 2012, 2012, 970642. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.J.; Park, S.B.; Kim, M.J.; Kim, K.J.; Kim, H.J. An analysis of heterotopic ossification in cervical disc arthroplasty: A novel morphologic classification of an ossified mass. Spine J. 2013, 13, 408–420. [Google Scholar] [CrossRef]
- Lee, J.-H.; Jung, T.-G.; Kim, H.-S.; Jang, J.-S.; Lee, S.-H. Analysis of the incidence and clinical effect of the heterotopic ossification in a single-level cervical artificial disc replacement. Spine J. 2010, 10, 676–682. [Google Scholar] [CrossRef]
- Yi, S.; Kim, K.N.; Yang, M.S.; Yang, J.W.; Kim, H.; Ha, Y.; Yoon, D.H.; Shin, H.C. Difference in occurrence of heterotopic ossification according to prosthesis type in the cervical artificial disc replacement. Spine 2010, 35, 1556–1561. [Google Scholar] [CrossRef]
- Montemurro, N.; Perrini, P.; Mangini, V.; Galli, M.; Papini, A. The Y-shaped trabecular bone structure in the odontoid process of the axis: A CT scan study in 54 healthy subjects and biomechanical considerations. J. Neurosurg. Spine 2019, 1, 1–8. [Google Scholar] [CrossRef]
- Teo, E.C.; Ng, H.W. First cervical vertebra (atlas) fracture mechanism studies using finite element method. J. Biomech. 2001, 34, 13–21. [Google Scholar] [CrossRef]
- Ganbat, D.; Kim, K.; Jin, Y.J.; Kim, Y.H. Heterotopic ossification in cervical total disk replacement: A finite element analysis. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2014, 228, 200–205. [Google Scholar] [CrossRef]
- Ganbat, D.; Kim, Y.H.; Kim, K.; Jin, Y.J.; Park, W.M. Effect of mechanical loading on heterotopic ossification in cervical total disc replacement: A three-dimensional finite element analysis. Biomech. Model. Mechanobiol. 2016, 15, 1191–1199. [Google Scholar] [CrossRef]
- Malcolm, G.P. Surgical disorders of the cervical spine: Presentation and management of common disorders. Neurol. Pract. 2002, 73, i34–i41. [Google Scholar] [CrossRef]
- Quraishi, N.A.; Elsayed, S. A traumatic, high-energy and unstable fracture of the C5 vertebra managed with kyphoplasty: A previously unreported case. Eur. Spine J. 2011, 20, 1589–1592. [Google Scholar] [CrossRef] [Green Version]
- Park, W.M.; Jin, Y.J. Biomechanical investigation of extragraft bone formation influences on the operated motion segment after anterior cervical spinal discectomy and fusion. Sci. Rep. 2019. [Google Scholar] [CrossRef]
- Weinans, H.; Huiskes, R.; Grootenboer, H.J. The behavior of adaptive bone-remodeling simulation models. J. Biomech. 1992, 25, 1425–1441. [Google Scholar] [CrossRef] [Green Version]
- Carter, D.R.; Hayes, W.C. The Compressive Behavior Porous of Bone Structure as a Two-Phase. J. bone Jt. Surg. 1977, 59, 954–962. [Google Scholar] [CrossRef]
- Espinha, L.C.; Fernandes, P.R.; Folgado, J. Computational analysis of bone remodeling during an anterior cervical fusion. J. Biomech. 2010, 43, 2875–2880. [Google Scholar] [CrossRef]
- Huiskes, R.; Weinans, H.; Grootenboer, H.J.; Dalstra, M.; Fudala, B.; Slooff, T.J. Adaptive bone-remodeling theory applied to prosthetic-design analysis. J. Biomech. 1987, 20, 1135–1150. [Google Scholar] [CrossRef] [Green Version]
- Kim, I.Y.; Kwak, B.M. Design space optimization using a numerical design continuation method. Int. J. Numer. Methods Eng. 2002, 53, 1979–2002. [Google Scholar] [CrossRef]
- Schulte, F.A.; Zwahlen, A.; Lambers, F.M.; Kuhn, G.; Ruffoni, D.; Betts, D.; Webster, D.J.; Müller, R. Strain-adaptive in silico modeling of bone adaptation—A computer simulation validated by in vivo micro-computed tomography data. Bone 2013, 52, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Park, S.B.; Yang, H.J.; Kim, C.H.; Chung, C.K. Difference in spinal fusion process in osteopenic and nonosteopenic living rat models using serial microcomputed tomography. J. Korean Neurosurg. Soc. 2017, 60, 348–354. [Google Scholar] [CrossRef]
- Puzas, J.E.; Miller, M.D.; Rosier, R.N. Pathologic bone formation. Clin. Orthop. Relat. Res. 1989, 245, 269–281. [Google Scholar] [CrossRef]
- Leung, C.; Casey, A.T.; Goffin, J.; Kehr, P.; Liebig, K.; Lind, B.; Logroscino, C.; Pointillart, V. Clinical significance of heterotopic ossification in cervical disc replacement: A prospective multicenter clinical trial. Neurosurgery 2005, 57, 759–763. [Google Scholar] [CrossRef]
- Jang, I.G.; Kim, I.Y. Computational study of Wolff’s law with trabecular architecture in the human proximal femur using topology optimization. J. Biomech. 2008, 41, 2353–2361. [Google Scholar] [CrossRef]
- Mauck, J.; Wieding, J.; Kluess, D.; Bader, R. Numerical simulation of mechanically stimulated bone remodelling. Curr. Dir. Biomed. Eng. 2016, 2, 643–647. [Google Scholar] [CrossRef]
- Perrini, P.; Montemurro, N. Congenital absence of a cervical spine pedicle. Neurol. India 2016, 64, 189–190. [Google Scholar] [CrossRef]
- Dimitrov, D.F.; Bronec, P.R.; Friedman, A.H. Congenitally absent C-7 pedicle presenting as a jumped locked facet. Case illustration. J. Neurosurg. 2003, 99, 239. [Google Scholar] [CrossRef]
- Wiener, M.D.; Martinez, S.; Forsberg, D.A. Congenital absence of a cervical spine pedicle: Clinical and radiologic findings. Am. J. Roentgenol. 1990, 155, 1037–1041. [Google Scholar] [CrossRef] [PubMed]
- Oh, Y.M.; Eun, J.P. Congenital absence of a cervical spine pedicle: Report of two cases and review of the literature. J. Korean Neurosurg. Soc. 2008, 44, 389–391. [Google Scholar] [CrossRef] [PubMed]


| Loading Condition | Number of Iterations | Computing Time (Days) | ||
|---|---|---|---|---|
| Inner | Outer | |||
| Simultaneous algorithm | Flexion | 124 | 1 | 1.6 |
| Extension | 240 | 1 | 3.0 | |
| Sequential algorithm | Flexion | 24 | 6 | 1.8 |
| Extension | 64 | 20 | 15.9 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.J.; Park, W.M. Comparison of Extragraft Bone Formation after Anterior Cervical Discectomy and Fusion Using Simultaneous and Sequential Algorithms. Appl. Sci. 2021, 11, 1487. https://doi.org/10.3390/app11041487
Jin YJ, Park WM. Comparison of Extragraft Bone Formation after Anterior Cervical Discectomy and Fusion Using Simultaneous and Sequential Algorithms. Applied Sciences. 2021; 11(4):1487. https://doi.org/10.3390/app11041487
Chicago/Turabian StyleJin, Yong Jun, and Won Man Park. 2021. "Comparison of Extragraft Bone Formation after Anterior Cervical Discectomy and Fusion Using Simultaneous and Sequential Algorithms" Applied Sciences 11, no. 4: 1487. https://doi.org/10.3390/app11041487
APA StyleJin, Y. J., & Park, W. M. (2021). Comparison of Extragraft Bone Formation after Anterior Cervical Discectomy and Fusion Using Simultaneous and Sequential Algorithms. Applied Sciences, 11(4), 1487. https://doi.org/10.3390/app11041487






