Featured Application
Human–computer interface.
Abstract
In this paper, a real-time dynamic hand gesture recognition system with gesture spotting function is proposed. In the proposed system, input video frames are converted to feature vectors, and they are used to form a posture sequence vector that represents the input gesture. Then, gesture identification and gesture spotting are carried out in the self-organizing map (SOM)-Hebb classifier. The gesture spotting function detects the end of the gesture by using the vector distance between the posture sequence vector and the winner neuron’s weight vector. The proposed gesture recognition method was tested by simulation and real-time gesture recognition experiment. Results revealed that the system could recognize nine types of gesture with an accuracy of 96.6%, and it successfully outputted the recognition result at the end of gesture using the spotting result.
1. Introduction
Hand gestures are one of the most important communication tools frequently used in our daily lives, and they can be used as an attractive means of human–computer interaction (HCI). Hand gestures are generally either static hand signs or dynamic hand gesture. Hand signs are static hand poses without any movements, and the hand gesture is defined as dynamic movement, which is a sequence of hand poses. Thus, a hand sign recognition system identifies the meaning of a hand pose. Meanwhile, in the dynamic gesture recognition, each gesture is defined as the trajectory of the hand movement or a sequence of hand poses.
A number of video-based hand gesture recognition algorithm and systems have been proposed [1]. This approach can use a conventional camera that most laptop PCs are equipped with. Thus, the video-based gesture recognition system can easily be implemented on widely available platforms. Another approach is based on three-dimensional hand image, which has attracted researchers in gesture recognition because the use of 3D image can improve performance [2]. However, the 3D gesture recognition requires a special device such as a Microsoft Kinect and a Leap Motion.
The gesture recognition system should work in real-time for practical use. One of the important function required for the real-time dynamic gesture recognition system is gesture spotting. The gesture spotting segments a meaningful portion from a continuous data stream, and it finds the start and end of gesture. The simplest way to provide the gesture spotting is to define key posture that indicates the start and end of gesture. However, this approach disturbs the natural flow of the intended sequence of gesture. Thus, a new approach that can detect the start and end of gesture naturally in continuous sequence of hand motion, is desired.
In our previous work, a hardware hand sign recognition system was proposed, which was video based system and recognized static hand signs [3]. Its recognition algorithm of the system consisted of feature vector generation and a vector classifier, and the whole system was implemented as a custom hardware on a field programmable gate array (FPGA). Self-organizing map (SOM) and Hebbian learning network were combined to form a SOM-Hebb classifier, which was used as the vector classifier. The SOM [4] is an unsupervised neural network that has been used in pattern recognition, data analysis, and visualization by using its clustering or vector quantization capabilities. The feature vector was computed from video frames and the hand sign recognition was carried out in real time by taking advantage of its high speed computation power of the dedicated hardware.
This paper proposes a new video-based dynamic hand gesture recognition system with the gesture spotting. The SOM-Hebb classifier is enhanced to SOM-SOM-Hebb classifier for the dynamic gesture classification. The proposed system consists of feature vector computation and two SOMs and a Hebbian learning network. The feature vectors computed from video frames are quantized by the first SOM, and a posture sequence vector that represents the current gesture is generated. Then, the SOM-Hebb classifier that contains the second SOM, recognizes the input gesture. During the gesture classification, the end of gesture is detected by the SOM-Hebb classifier, and a recognized gesture class is outputted when the gesture’s end is detected. As a result, natural gesture spotting without any key pose is implemented. This paper examines detailed performance of the proposed recognition system by simulation and experiment by using nine types of dynamic gesture.
2. Related Work
In the gesture recognition, a hand segmentation is carried out first, which detects the hand position or hand shape. A popular segmentation method in the vision based system is skin color detection that extracts hand portion from cluttered background [5,6]. Yun et al. [7] proposed a multi-feature fusion method that improved recognition results by extracting angle count, skin color angle, and non-skin color angle in combination with Hu invariant moments features. Some gesture recognition systems simplified hand extraction from the background with the help of inexpensive color-coded gloves for hand segmentation. A glove providing color-coding with six unique colors were used in [8,9]. Wang and Popovi [10] employed an ordinary cloth glove being printed with a custom pattern that was designed to estimate the poses. Our previous work [3] also employed a two-colored glove for hand segmentation. Another option for gesture segmentation is the use of the 3D image that is taken through depth sensors, such as the Microsoft Kinect depth camera and the Leap Motion. The 3D camera views the subject in the front plane and generates a depth image of the subject, and the depth image is used for background removal, followed by the generation of the depth profile of the subject. Gesture recognition systems with the Kinect are found in [11,12,13,14,15]. Molina et al. [16] used another depth camera called Time-Of-Flight range camera that supplied real-time depth information per pixel. In terms of applicability, the vision-based gesture segmentation is desirable since it requires only a conventional camera available on most laptop PCs, and no special depth sensor is needed.
Unlike the Kinect sensor and other depth sensors, the output of the Leap Motion is the depth data which consists of palm direction, fingertips positions, palm center position, and other relevant points. Therefore, no extra computational work is needed to get these information. Due to its unique features, the Leap Motion has been applied to dynamic hand gesture recognition by by researchers. Lu et al. [17] proposed a dynamic gesture recognition system, in which the Leap Motion was used to compute feature vector of the gesture, and a hidden conditional neural field (HCNF) classifier was used to recognize dynamic hand gesture. Another example is the work done by H. Li et al. [18]. Their hand gesture recognition system was based on the Leap Motion and a spatial fuzzy matching (SFM). Hand–eye coordination means the ability to combine seeing and hand movement. Ujbanyi et al. [19,20] examined the correlations between eye motion and the motion of the mouse cursor regarding hand–eye coordination, and they used an hand–eye tracking system which was made of the Leap Motion and Eye Tribe tracker.
Challenge of real-time dynamic gesture recognition is the gesture spotting or temporal segmentation that detects when the gesture starts and ends. In the system proposed by Varshini et al. [13], each dynamic gesture was defined as a sequence of trigger-poses, and the start and end of the gesture were detected by finding the start and end triggers. Chai et al. [21] used hand positions to perform the temporal segmentation by assuming that a user put hands-up pose at the start of gesture and put hands-down pose at end of the gesture. A real-time dynamic hand gesture recognition system proposed by Chen et al. [15] used two hand configurations (open-hand, closed-hand) to achieve gesture spotting and its 3D motion trajectory of the dynamic gesture was captured by the Kinect sensor. These approaches disturb the natural flow of gesture, and thus a new approach that can detect the start and end of gesture naturally, is desirable.
A static hand gesture recognition can be achieved by applying standard pattern recognition techniques such as template matching, whereas dynamic gesture recognition requires time-series pattern recognition algorithm such as a hidden Markov model (HMM) or dynamic time warping (DTW) algorithm. The HMM is a statistical Markov model in which the system being modeled is assumed to be a Markov process. The HMM is a doubly stochastic process with an underlying stochastic process that is not observable, but can be observed through another set of stochastic processes that produce a sequence of observed symbols, and the model is known for their applications to various fields including the gesture recognition such as [22]. Problem of the gesture recognition with the HMM is that its recognition accuracy decreases if the behavior during the gesture transition has not been precisely trained. The DTW is one of the algorithms for measuring similarity between two temporal sequences which may vary in speed. Plouffe et al. [14] and Molina et al. [16] employed the DTW algorithm for their dynamic gesture recognition systems.
Another popular recognition algorithm is a neural network and its derivatives, especially deep learning methodologies [23]. Most modern deep learning models are based on convolutional neural networks (CNNs). The CNNs have been well studied and applied to fields of image recognition. The most crucial challenge in deep learning based gesture recognition is the handling of the temporal dimension. One approach uses 3D filters in the convolutional layer of the CNN. The 3D-CNN captures features of both spatial and temporal dimensions while maintaining a certain temporal structure. Another approach combines a temporal sequence modeling with a 2D (or 3D) CNN. One of the most used networks for the temporal modeling is a recurrent neural network (RNN), which can take into account the temporal data using recurrent connections in hidden layers. The drawback of this network is its short-term memory, and long short-term memory (LSTM) was proposed to solve the problem.
Molchanov et al. [24] proposed a recurrent 3D-CNN that performed simultaneous detection and classification of dynamic hand gesture from multi-modal data. Wu et al. [25] employed a novel method called deep dynamic neural networks (DDNN) for multimodal gesture recognition. The multimodal gesture recognition method based on 3D convolutional LSTM network was proposed by Zhu et al. [26]. Naguri [27] proposed a gesture recognition system based on the LSTM and a convolutional neural network (CNN) that were trained to process input sequences of 3D hand positions and velocity. Chai et al. [21] proposed a continuous gesture recognition method with a two-stream RNN (2S-RNN) for the RGB-depth image recognition. John et al. [28] proposed a vision-based gesture recognition system for automotive user interface, and they employed a long-term recurrent convolution network to classify the video sequence of the dynamic hand gesture.
A recognition system proposed by Chen et al. [15] employed a Support Vector Machine (SVM) as the recognition algorithm. Kim et al. [29] proposed a novel method to measure the video-to-video volume similarity by extending a canonical correlation analysis (CCA). Then, the proposed matching method was demonstrated for action classification by a simple nearest neighbor classifier. Jordan recurrent neural network (JRNN) is a class of recurrent neural networks, which is a three-layer network with addition of a set of context units [30]. The context units are fed from the output layer, and they have a recurrent connection to themselves. This allows the JRNN to exhibit temporal dynamic behavior and can be applied for the gesture recognition. Araga et al. [31] employed the JRNN to implement their dynamic gesture recognition system.
3. Gesture Recognition System
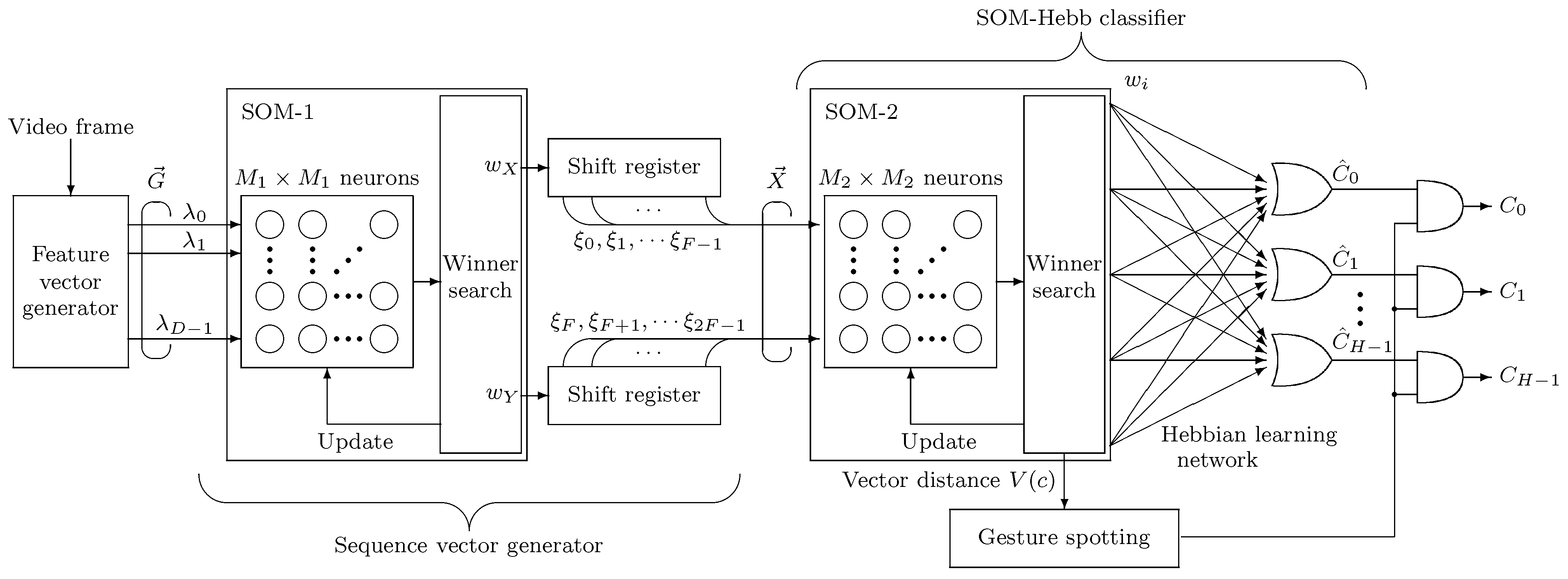
Figure 1 outlines the flow for the gesture recognition algorithm. The proposed system consists of a feature vector generator, a sequence vector generator, and the SOM-Hebb classifier. Input to the system is video frames, and a dynamic hand gestures are assumed to be made of a sequence of F video frames. Since each frame contains different types of posture, the dynamic gesture can be classified by examining change of the posture in the F consecutive video frames.
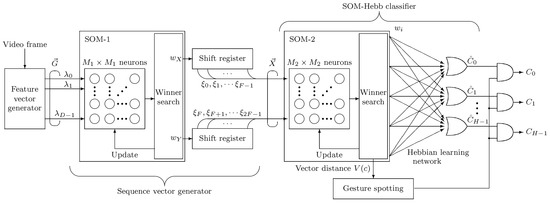
Figure 1.
Dynamic gesture recognition system.
3.1. Feature Vector Generation
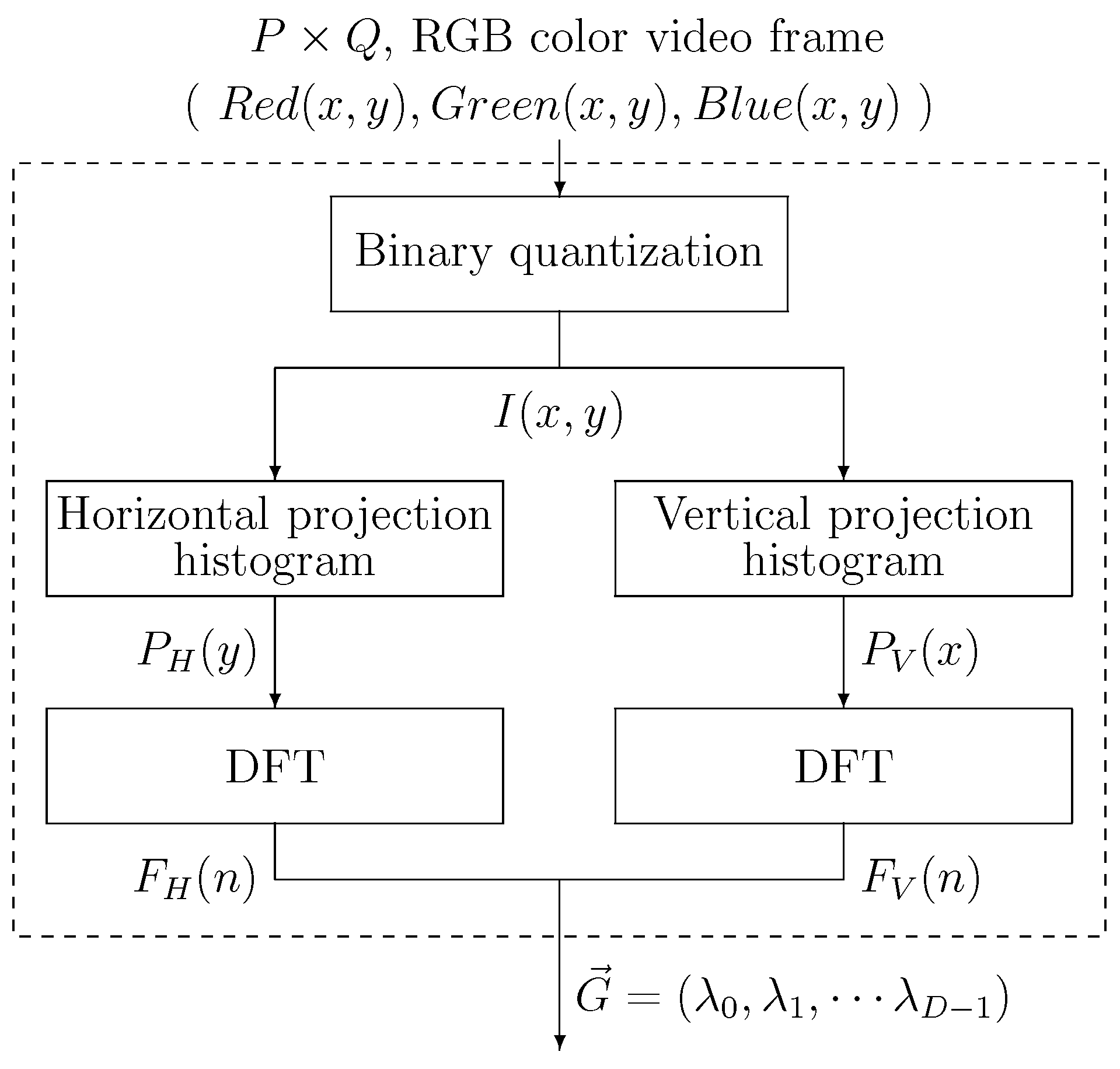
In the feature vector generator, the image frame that is pixels in RGB color format is converted to the feature vector . The feature vector proposed in [3] is employed. Computation to obtain the feature vector is shown in Figure 2, which consists of a binary quantization, horizontal and vertical projection histogram calculations, and two discrete Fourier transforms (DFTs). Output is the D dimensional feature vector .
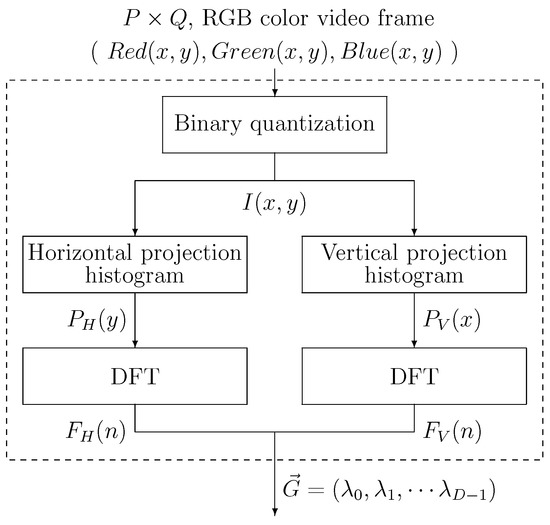
Figure 2.
Feature vector generation.
Firstly, the input color frame image is converted to a binary image . For the system to remove the background image including the arm as well as to extract the finger segments, the user is required to wear a glove, finger portion of which is colored in red. If color of pixel is red the pixel is treated as 1, otherwise 0. Then horizontal and vertical histograms and of are calculated as follows:
After the histogram calculations, DFTs are carried out on the histograms.
Here, , and , are real and imaginary parts of the frequency components of the histograms. Then, and , i.e., the magnitude spectra of and are computed as
The and of the same hand posture images placed in different positions are identical because they are the magnitude spectra lacking the phase information related to the hand posture position. Since most of the image’s feature information is concentrated in the lower frequency components, they are used as the feature vector. The D-dimensional feature vector, is formed from and as;
This feature vector is fed to the sequence vector generator.
3.2. Sequence Vector Generator
The SOM-1 in the sequence vector generator quantizes the input vectors, and the quantization results are sequentially stored in the shift registers. The contents of the shift registers form the sequence vector, which represents temporal change of the input posture, and is fed to the next SOM-Hebb classifier. The SOM-1 includes neurons, and D-dimensional vector that is called a weight vector is included in each neuron.
where, j is the neuron number.
Operation of the SOM is divided into learning and recall phases. The weight vectors of the neurons are trained with a set of input vectors in the learning phase. The learning phase is made of a winner search and weight update. During the recall phase, only the winner search is carried out by using the map of the trained weight vectors.
The winner neuron has the weight vector that is the nearest to the input vector. Euclidean distance between the input vector and weight vector of neuron-j, is calculated for the winner search.
The winner neuron-c is then determined.
In the weight update, weight vectors of the winner and its neighborhood neurons are updated to be closer to the input vector as;
where t is time index, and is a function called neighborhood function, which is defined as;
where is a learning coefficient, (). The and are the coordinate vectors of the winner neuron-c, and a neuron-j, respectively. The represents the neighborhood radius, and the weight vectors within the radius from the winner neuron are updated.
After the learning phase, all weight vectors are kept unchanged and the weight map is used in the recall phase. The winner neuron represents the cluster to which the input vector belongs, and the coordinates of the winner neuron for the input vector are treated as the quantization result. These coordinates are stored sequentially in the shift registers, so their contents represent the sequence of the input video frames. In this paper, this vector is called the sequence vector, , which is a -dimensional vector. Its vector element is defined as:
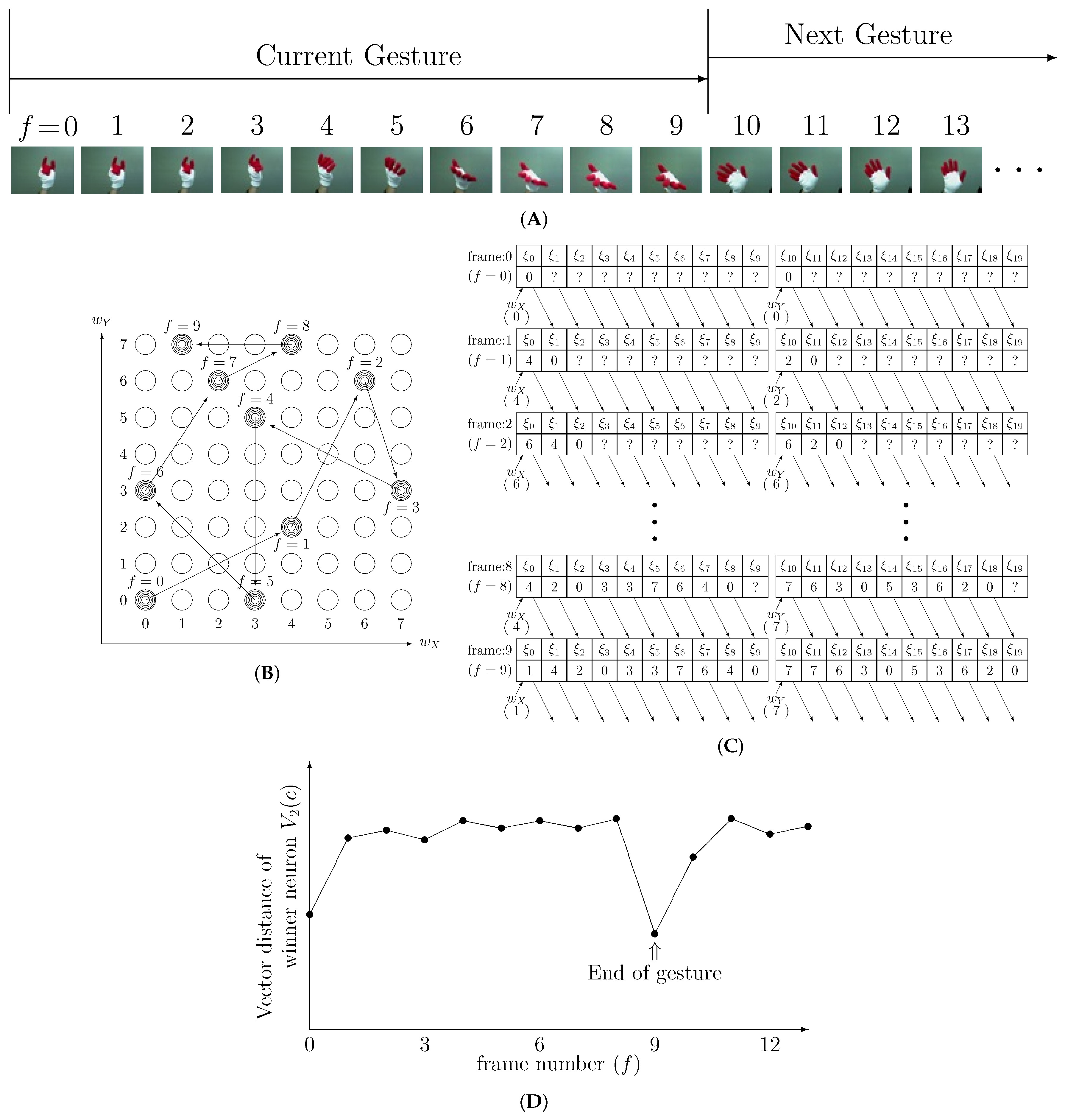
Figure 3 shows examples explaining operation of the system. As shown in Figure 3A, a gesture is made of 10 posture images in different video frames. In the example, SOM-1 is composed of neurons and Figure 3B shows the transition of the winner neuron with respect to the input video frames. Posture in the first video frame () makes a neuron at the winner. Then the coordinates of the winner neuron are stored in the registers in the sequence vector generator as shown in Figure 3C. Question marks in Figure 3C are the coordinates of the winner neurons of the previous gesture, which are not related to the current gesture. The winner for the second posture () is a neuron at . The registers are shifted to the right and the new winner coordinates is stored into the registers’ most left position. For the third posture at , and are loaded into the registers. In this way, the information of the previous gesture in the registers are gradually replaced with that of the current gesture. Therefore, the sequence vector representing the current gesture approaches completion as the video frame progresses, and is completed at the 10th frame . The vector is fed to the SOM-Hebb classifier that is described in the next subsection.
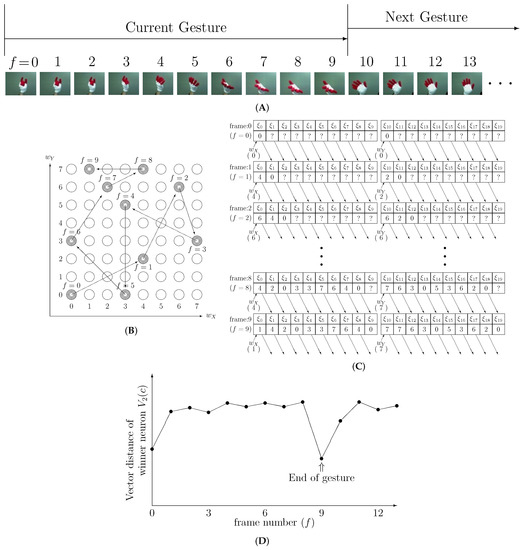
Figure 3.
Example of operation of the proposed system, (A) Input gesture frames, (B) Winner neurons in the SOM-1, (C) Development of the shift registers, (D) Vector distance of winner neurons in the SOM-2.
3.3. SOM-Hebb Classifier for Sequence Vector Classification
The SOM-Hebb classifier classifies the sequence vector and identifies the input gesture. This classifier is the same one that was proposed in our previous work [3]. The SOM-2 in this classifier consists of neurons and -dimensional weight vectors are included in the neurons. The SOM-2 is trained in the same way as was explained in the previous section. Note that is the vector distance of the winner neuron’s weight vector to the input vector that is the sequence vector , and is used to implement the gesture spotting function.
During the recall phase, the class to which the input vector belongs can be identified from the winner neuron of the SOM-2. Here, H represents the number of classes. The Hebb network generates its output from the winner neuron. Each neuron represents a single cluster in the input vector space. Since a single gesture class may consist of combination of multiple clusters, multiple neurons must be associated to the single class in that case. Selection of the neurons belonging to the same class is done by a single layer feedforward network. This network is trained by the Hebbian training algorithm, which is a supervised training. During the Hebb training, training vectors with their class data are sequentially fed to the network. Every training vector makes one of the neurons the winner. If strong correlation is found between training vectors in class h and neuron j, then the neuron j is assigned to the class h. In practice, the class of the input vectors with which the neuron j won the most, is associated to the neuron.
The SOM-2 must have appropriate number of neurons for the SOM-Hebb network to work properly. It happens that some neurons may have no connection to any gesture class. Obviously, the selection of such neuron as the winner in the recognition phase causes false recognition. To avoid this situation, neurons without connections to class ID are culled. The culling replaces the weight vectors of these neurons with huge vectors so that they never win.
3.4. Gesture Spotting
An important function required for the dynamic gesture recognition system is the gesture spotting which detects when gesture ends so that a meaningful gesture is segmented from the sequence of hand motions. The gesture spotting is implemented in the SOM-Hebb classifier by using that is the vector distance of the winner neuron’s weight vector in the SOM-2 to the input vector. The SOM-Hebb classifier performs the recognition for every input frame and generates its recognition results . However most of the are not correct because the contents of the shift registers are not complete vector sequence for the current input gesture until the last gesture frame is input. The recognition result is outputted only when the spotting module detects the end of gesture.
The end of gesture is detected by observing the transition of the vector distance . Figure 3C shows the transitions in the shift registers, which is development process of the posture sequence vector, . Each gesture consisted of 10 frames in this example, therefore the shift register is filled with appropriate vector’s elements at 10th frame () and posture sequence vector is completed as shown in Figure 3C. The completed vector matches with one of the weight vectors in SOM-2, which decreases the vector distance remarkably as shown in Figure 3D. After that, the distance increases because the next gesture vector elements are loaded into the register. Therefore, the end of gesture can be detected by searching a dip in the transition of the vector distance . However, the actual distance transition is not as smooth as that plotted in Figure 3C. The transition in the actual input fluctuates, which makes it difficult to find the dip. In order to solve the problem, a moving average of the vector distance is employed. The moving average is computed as;
where is the at video frame f, and L is the number of samples to be averaged.
4. Simulation and Experiment
Performance of the proposed system was examined by computer simulation and experiment.
4.1. Simulation
The system was configured as follows.
- Frame size:.
- Feature vector dimension:.
- Sequence vector dimension:.
- The numbers of neurons in the SOMs:.
- Moving average: in Equation (17).
- The number of gesture classes:.
Data set for the simulation was vector sequence taken from video frames of recorded gesture video. Nine types of gesture shown in Figure 4 were used for the test. We defined the gesture by using the Cambridge Hand Gesture Data set [29] for reference. As Figure 4 shows, the data set consisted of nine classes. Each class gesture was defined with 10 frames, therefore the dimension of the sequence vector was 20. Class labels 1 to 9 are assigned to every types of gesture. Note that the labels are used to distinguish class of the gesture types, and the number does not represent numerical character. Gesture motions are combinations of three basic poses (Flat, Spread, V-shape) and three movements (Leftward, Rightward, Contract). Thus, the gesture classes are made of three groups, i.e., 1-2-3, 4-5-6, and 7-8-9. Note that the last posture of gesture 1 is also the first posture of gesture 2, and the last posture of class 2 is the first posture of gesture class 3. The other gesture groups were designed in the same way so that the gesture classes in the same group could be performed seamlessly. The number of training vectors per class was 50, and 100 test vectors were used.

Figure 4.
Nine types of gesture.
For comparison purpose, recognition performance of the JRNN [30] was examined using the same feature vectors . Table 1 summarizes the recognition accuracies of the two methods.

Table 1.
Gesture recognition accuracies of various classifiers.
4.2. Real-Time Gesture Recognition
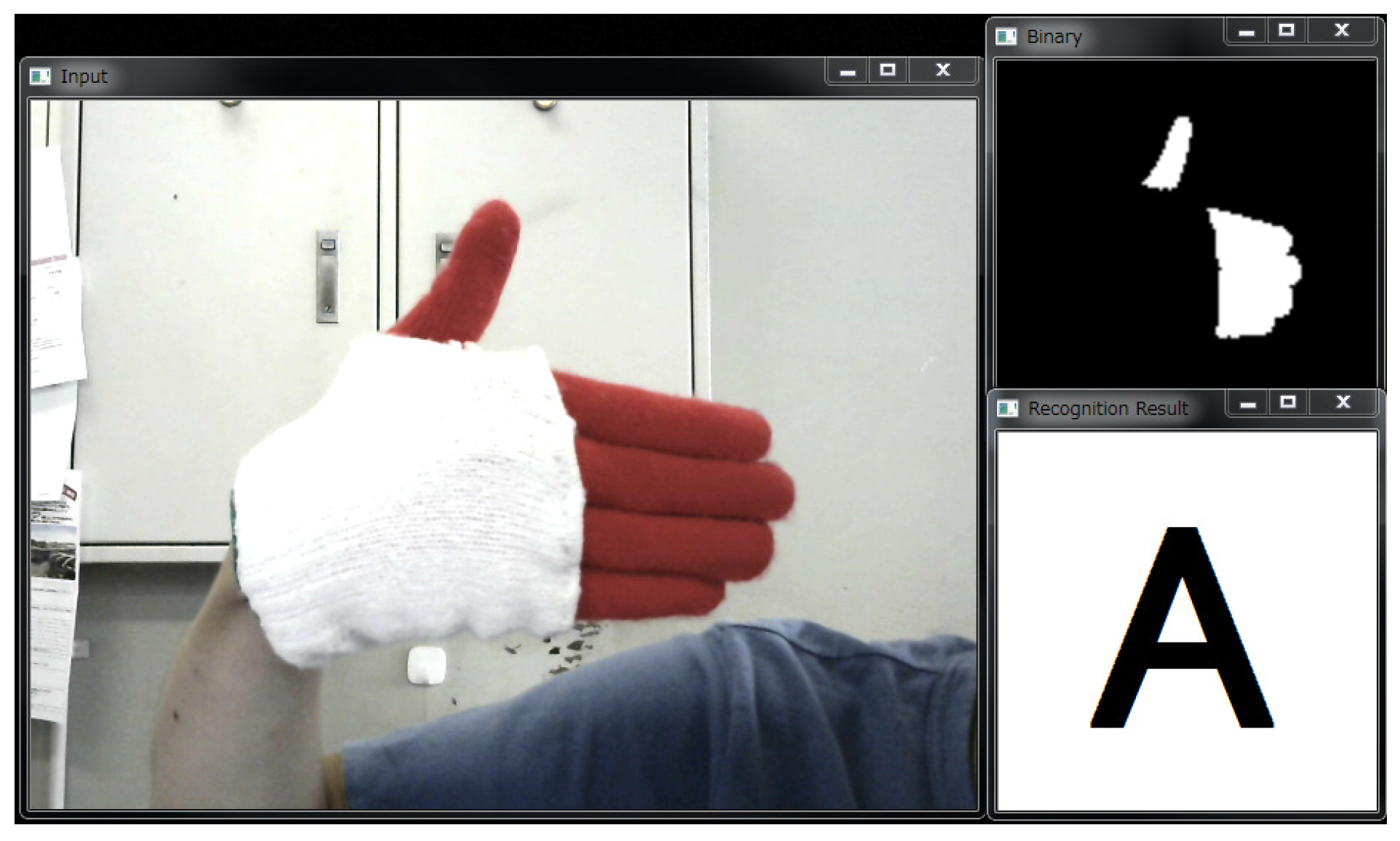
To conduct the experiment, real-time gesture recognition system was developed in software that ran on a PC. The input gesture was taken by the USB camera, and fed to the system. The recognition result was outputted only when the spotting function detected the end of the gesture. Figure 5 is a screen shot of the implemented real-time gesture recognition system.
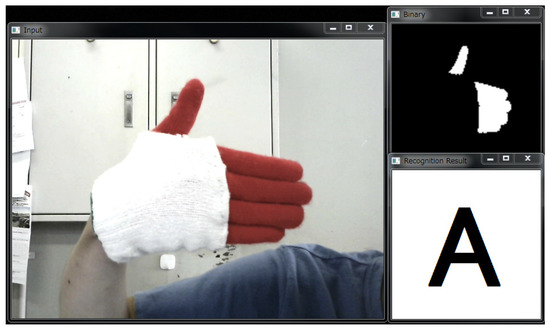
Figure 5.
Real-time gesture recognition system.
The system was tested with the same gesture that was used in the simulation. The system was trained off-line by using pre-captured gesture data set. The number of training data for the off-line training was 50 samples for each gesture class. Each training sample was acquired by simply capturing 10 consecutive frames. Neither setting up the key posture that represented the gesture, nor manual selection of key frame was done in the acquisition of the training data set. The recognition system then classified the dynamic gesture presented in real-time using the weight vectors obtained from the off-line training. In the experiment, recognition test was carried out 100 times for each gesture by the same person who had provided the training data set. Most of the gesture ends were correctly detected even though the gesture groups 1-2-3, 4-5-6, and 7-8-9 were performed in succession (video of the experiment (10 fps) is available on http://www2.kansai-u.ac.jp/hikawa/ichikawa.mp4, 19 February 2021). Since the gesture in our method is defined by the fixed number of posture types, the input gesture must be made of the same number of posture types. Therefore, the speed of gesture to be recognized depends on the speed of gesture that has been captured as the training data. The recognition tests were carried out with two speeds, i.e., 5 frames per second (fps) and 10 fps. Since (10 frames for one gesture), the gesture speeds were 2 second/gesture in case of 5 fps, and 1 second/gesture in case of 10 fps.
Table 2 shows the experimental results of 5 fps frame rate. The average accuracy of the recognition was 96.6%. NS in the table is the number of cases where no spotting was detected, and MS is the number of cases where multiple spotting occurred. Both cases were counted as errors. Table 3 summarizes the experimental results of 10 fps frame rate. The average accuracy of the recognition rate was 97.0%, and no significant difference is found due to the speed difference.

Table 2.
Confusion table (5 fps).

Table 3.
Confusion table (10 fps).
5. Discussion
The simulation results show that the proposed method outperformed the JRNN. Difficulty of this gesture data set is that class pairs 1–2, 4–5, 7–8 are reverse gestures. Appearance of poses in the gesture is reverse order and those pairs include the same hand poses. For classes 1 and 2, the proposed system is inferior to the JRNN, but the proposed method recognized class 5 better. Another noticeable point is that the recognition accuracies of the JRNN for classes 6 and 9 are significantly worse than those of the proposed system. This is caused by the another difficulty of the data set. As shown in Figure 4, the class pairs 4–6 and 7–9 have the same poses in their beginning, which confuse the classifiers.
The experimental results shown in Table 2 and Table 3 disclose that the recognition and spotting performances of the proposed system are very high. Regarding the spotting, the spotting may be easily implemented by counting the frames because the number of frames of gestures are fixed. To do so, the start of gesture must be detected correctly, and a possible method is the use of key poses to indicate the start of gestures, which was used in [15,21]. However, these approaches disturb the natural flow of gesture. Meanwhile the proposed spotting finds the end of gesture automatically when the sequence of frames matches one of the pre-trained ones, therefore the user can start gesture at any time without the key poses.
The tables also indicate that the most of the recognition errors were caused by the spotting errors. In case of NS, no spotting was detected, and the recognition result was not available. During the experiment, we observed that the proposed spotting detected the end of gesture twice in all MS cases, and two recognition results were outputted. In most of such cases, recognition results at the first spotting were incorrect and the second ones were correct. Therefore, if the detection accuracy of the spotting function is more precise, recognition results would be improved.
Table 4 compares the recognition accuracies of the proposed system with the state-of-the-art in the literature. Since experimental conditions are not the same, the accuracies in the table should not be directly compared. Six of them are real-time recognition systems, and the others were tested with various gesture data sets. Four of them are vision based systems, and the others used 3D gesture images taken from the special sensors. Vision based system is more challenging than the 3D gesture recognition since it uses limited 2D information, but it can be realized with the simple readily available cameras. Additional burdens of the real-time recognition system are high speed computation and the gesture spotting. Note that the proposed system provides the natural spotting function with no special key posture that indicates the start or end of gesture. Considering features of vision-based, real-time accurate gesture recognition and spotting function, the overall contribution of the proposed system in dynamic gesture recognition application is very high. However, even though the proposed system does not require the special sensors, it still requires users to wear the color glove, which may prevent it being used in everyday life. To solve the problem, use of the skin color detection [5,6] is one of the choice for the hand segmentation without the colored glove.

Table 4.
Comparison of accuracies.
6. Conclusions
This paper proposed a vision-based real-time dynamic hand gesture recognition system with a gesture spotting function. In order to recognize the dynamic gesture, the SOM-SOM-Hebb classifier was newly devised. To provide the spotting function, end of gesture was detected from transitions of the vector distance between input and winner neuron’s weight vectors. This gesture spotting capability made the system much more practical.
The proposed recognition algorithm was examined by simulation and real-time experiment. The results revealed that the system could recognize the nine types of gesture with an accuracy of , which was better than that of other recognition sysems. Other advantages of our system over the compared methods are its real-time operability and the gesture spotting function.
Major drawback of the proposed system is the use of the color glove, and implementation of the hand segmentation without the glove is left for our future work. Another future research objective is to develop a hardware gesture recognition system with faster recognition speed, higher portability, and lower power consumption than those of PC implementation.
Author Contributions
Conceptualization, H.H. and Y.M.; methodology, H.H.; software, Y.I.; validation, Y.I. and H.H.; formal analysis, H.I. and H.H.; writing—original draft preparation, H.H. and Y.I.; writing—review and editing, H.I.; supervision, Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by JSPS KAKENHI Grant Number JP18K11483, JP20K11999, and the Kansai University Fund for the Promotion and Enhancement of Education and Research, “Development of System Analysis and Design Methods Integrating Model and Data Premised on IOT Technology.”
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
http://www2.kansai-u.ac.jp/hikawa/ichikawa.mp4, accessed on 19 February 2021.
References
- Pavlovic, V.I.; Sharma, R.; Huang, T.S. Visual Interpretation of Hand Gestures for Human-Computer Interaction: A Review. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 677–695. [Google Scholar] [CrossRef]
- Cheng, H.; Yang, L.; Liu, Z. Survey on 3D Hand Gesture Recognition. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 1659–1673. [Google Scholar] [CrossRef]
- Hikawa, H.; Kaida, K. Novel FPGA Implementation of Hand Sign Recognition System with SOM-Hebb Classifier. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 153–166. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps, 3rd ed.; Springer Series in Information Sciences 30; Springer: New York, NY, USA, 2001. [Google Scholar]
- Alon, J.; Athitsos, V.; Yuan, Q.; Sclaroff, S. A Unified Framework for Gesture Recognition and Spatiotemporal Gesture Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 685–1699. [Google Scholar] [CrossRef] [PubMed]
- Dardas, N.H.; Georganas, N.D. Real-Time Hand Gesture Detection and Recognition Using Bag-of-Features and Support Vector Machine Techniques. IEEE Trans. Instrum. Meas. 2011, 60, 3592–3607. [Google Scholar] [CrossRef]
- Yun, L.; Lifeng, Z.; Shujun, Z. A hand gesture recognition method based on multi-feature fusion and template matching. Procedia Eng. 2012, 29, 1678–1684. [Google Scholar] [CrossRef]
- Lamar, M.V.; Bhuiyan, M.S.; Iwata, A. Hand Gesture Recognition Using T-CombNet: A New Neural Network Model. IEICE Trans. Inf. Syst. 2000, E-38-D, 1986–1995. [Google Scholar]
- Bragatto, T.A.C.; Ruas, G.S.I.; Lamar, M.V. Real-Time Hand Postures Recognition using Low Computational Complexity Artificial Neural Networks and Support Vector Machines. In Proceedings of the ISCCSP 2008, Saint Julian’s, Malta, 12–14 March 2008; pp. 1530–1535. [Google Scholar] [CrossRef]
- Wang, R.Y.; Popovi, J. Real-time handtracking with a color glove. In Proceedings of the ACM Transactions on Graphics (SIGGRAPH 2009), New Orleans, LA, USA, 3–7 Augst 2009; Volume 28, pp. 1–8. [Google Scholar] [CrossRef]
- Biswas, K.K.; Basu, S.K. Gesture recognition using Microsoft Kinect R. In Proceedings of the 5th International Conference on Automation, Robotics and Applications, Wellington, New Zealand, 6–8 December 2011; pp. 100–103. [Google Scholar] [CrossRef]
- Li, Y. Hand gesture recognition using Kinect. In Proceedings of the 2012 IEEE International Conference on Computer Science and Automation Engineering, Beijing, China, 22–24 June 2012; pp. 196–199. [Google Scholar] [CrossRef]
- Varshini, M.R.L.; Vidhyapathi, C.M. Dynamic fingure gesture recognition using KINECT. In Proceedings of the 2016 International Conference on Advanced Communication Control and Computing Technologies (ICACCCT), Ramanathapuram, India, 25–27 May 2016. [Google Scholar] [CrossRef]
- Plouffe, G.; Cretu, A.-M. Static and dynamic hand gesture recognition in depth data using dynamic time warping. IEEE Trans. Instrum. Meas. 2015, 65, 305–316. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, B.; Chen, Y.-L.; Liang, G.; Wu, X. A real-time dynamic hand gesture recognition system using kinect sensor. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2015; pp. 2026–2030. [Google Scholar] [CrossRef]
- Molina, J.; Pajuelo, J.A.; Martinez, J.M. Real-time motion-based hand gestures recognition from time-of-flight video. J. Signal Process. Syst. 2017, 86, 17–25. [Google Scholar] [CrossRef][Green Version]
- Lu, W.; Tong, Z.; Chu, J. Dynamic Hand Gesture Recognition with Leap Motion Controller. IEEE Signal Process. Lett. 2016, 23, 1188–1192. [Google Scholar] [CrossRef]
- Li, H.; Wu, L.; Wang, H.; Han, C.; Quan, W.; Zhao, J. Hand Gesture Recognition Enhancement Based on Spatial Fuzzy Matching in Leap Motion. IEEE Trans. Ind. Inform. 2020, 16, 1885–1894. [Google Scholar] [CrossRef]
- Ujbanyi, T. Examination of eye-hand coordination using computer mouse and hand tracking cursor control. In Proceedings of the 2018 9th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Budapest, Hungary, 22–24 August 2018; pp. 000353–000354. [Google Scholar] [CrossRef]
- Ujbanyi, T.; Kovari, A.; Sziladi, G.; Katona, J. Examination of the eye-hand coordination related to computer mouse movement. Infocommun. J. 2020, XII. [Google Scholar] [CrossRef]
- Chai, X.; Liu, Z.; Yin, F.; Liu, Z.; Chen, X. Two streams recurrent neural networks for large-scale continuous gesture recognition. In Proceedings of the IEEE 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 31–36. [Google Scholar] [CrossRef]
- Deng, J.W.; Tsui, H.T. An HMM-based approach for gesture segmentation and recognition. In Proceedings of the 15th International Conference on Pattern Recognition. ICPR-2000, Barcelona, Spain, 3–7 September 2000; Volume 3, pp. 679–682. [Google Scholar] [CrossRef]
- Asadi-Aghbolaghi, M.; Clapes, A.; Bellantonio, M.; Jair Escalante, H.; Ponce-Lopez, V.; Baro, X.; Guyon, I.; Kasaei, S.; Escalera, S. A Survey on Deep Learning Based Approaches for Action and Gesture Recognition in Image Sequences. In Proceedings of the 2017 12th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2017), Washington, DC, USA, 30 May–3 June 2017; pp. 476–483. [Google Scholar] [CrossRef]
- Molchanov, P.; Yang, X.; Gupta, S.; Kim, K.; Tyree, S.; Kautz, J. Online Detection and Classification of Dynamic Hand Gestures with Recurrent 3D Convolutional Neural Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4207–4215. [Google Scholar] [CrossRef]
- Wu, D.; Pigou, L.; Kindermans, P.; Le, N.D.; Shao, L.; Dambre, J.; Odobez, J. Deep Dynamic Neural Networks for Multimodal Gesture Segmentation and Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1583–1597. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Zhang, L.; Shen, P.; Song, J. Multimodal Gesture Recognition Using 3-D Convolution and Convolutional LSTM. IEEE Access 2017, 5, 4517–4524. [Google Scholar] [CrossRef]
- Naguri, C.R.; Bunescu, R.C. Recognition of Dynamic Hand Gestures from 3D Motion Data Using LSTM and CNN Architectures. In Proceedings of the 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), Cancun, Mexico, 18–21 December 2017; pp. 1130–1133. [Google Scholar] [CrossRef]
- John, V.; Boyali, A.; Mita, S.; Imanishi, M.; Sanma, N. Deep learning-based fast hand gesture recognition using representative frames. In Proceedings of the 2016 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Gold Coast, QLD, Australia, 30 November–2 Decembere 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Kim, T.K.; Cipolla, R. Canonical correlation analysis of video volume tensors for action categorization and detection. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 1415–1428. [Google Scholar] [CrossRef]
- Jordan, M. Serial order: A parallel distributed processing approach. Adv. Psychol. 1997, 211, 471–495. [Google Scholar]
- Araga, Y.; Shirabayashi, M.; Kaida, K.; Hikawa, H. Real time gesture recognition system using posture classifier and Jordan recurrent neural network. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).