Effective Safety Assessment of Aged Concrete Gravity Dam based on the Reliability Index in a Seismically Induced Site
Abstract
1. Introduction
Background and Scope
2. Theoretical Background
2.1. Classical Reliability Assessment
2.2. Seismic Performance Assessment
2.2.1. Intensity and Damage Measure
2.2.2. Fragility Formulation
2.2.3. Seismic Hazard Analysis
2.2.4. Reliability Index
3. Numerical Example
3.1. Dam Specification
3.2. FEM Configuration
3.3. Aged-CGD Modeling
4. Optimization of FEM
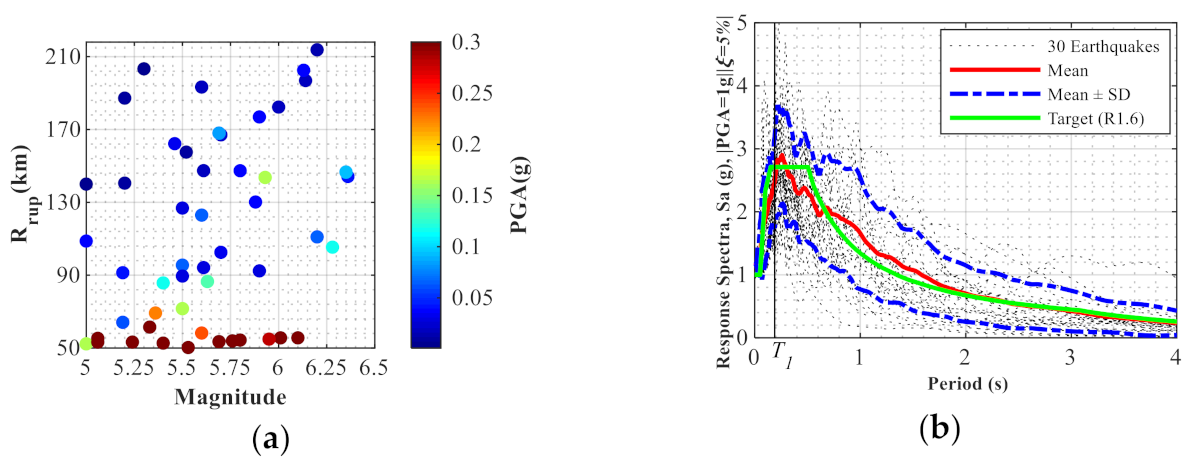
5. Ground Motion Selection
6. Result and Discussion
6.1. Seismic Failure Assessment
6.2. Site Seismic Hazard Analysis
6.3. Safety Assessment of Aged-CGD
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohammadi, R.; Massumi, A.; Meshkat-Dini, A. Structural reliability index versus behavior factor in RC frames with equal lateral resistance. Earthq. Struct. 2015, 8, 996–1016. [Google Scholar] [CrossRef]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef]
- Mohajeri, S.; Aziz, H.A.; Isa, M.H.; Zahed, M.A.; Bashir, M.J.; Adlan, M.N. Application of the central composite design for condition optimization for semi-aerobic landfill leachate treatment using electrochemical oxidation. Water Sci. Technol. 2010, 61, 1257–1266. [Google Scholar] [CrossRef] [PubMed]
- Abu-Odeh, A.Y.; Jones, H.L. Optimum design of composite plates using response surface method. Compos. Struct. 1998, 43, 233–242. [Google Scholar] [CrossRef]
- Chávez-Valencia, L.; Manzano-Ramírez, A.; Alonso-Guzmán, E.; Contreras-García, M. Modelling of the performance of asphalt pavement using response surface methodology—the kinetics of the aging. Build. Environ. 2007, 42, 933–939. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Lin, C.-C. Regression of the response surface of laminated composite structures. Compos. Struct. 2003, 62, 91–105. [Google Scholar] [CrossRef]
- Ghanaat, Y.; Patev, R.; Chudgar, A. Seismic fragility for risk assessment of concrete gravity dams. In Proceedings of the 35th United States Society on Dams Annual Meeting and Conference, Louisville, KY, USA, 13–17 April 2015; pp. 645–660. [Google Scholar]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Adamo, N.; Al-Ansari, N.; Laue, J.; Knutsson, S.; Sissakian, V. Risk management concepts in dam safety evaluation: Mosul dam as a case study. J. Civ. Eng. Archit. 2017, 11, 635–652. [Google Scholar] [CrossRef]
- Choi, I.-K.; Nakajima, M.; Choun, Y.-S.; Ohtori, Y. Development of the site-specific uniform hazard spectra for Korean nuclear power plant sites. Nucl. Eng. Des. 2009, 239, 790–799. [Google Scholar] [CrossRef]
- Sørensen, J.D. Notes in Structural Reliability Theory and Risk Analysis; Building Technology and Structural Engineering: Aalborg, Denmark, 2004; p. 231. [Google Scholar]
- Melchers, R.E.; Beck, A.T. Structural Reliability Analysis and Prediction, 3rd ed.; John Wiley & Sons Ltd: Hoboken, NJ, USA, 2018; p. 514. [Google Scholar]
- Marelli, S.; Schöbi, R.; Sudret, B. UQLab User Manual–Structural Reliability (Rare Event Estimation); UQLab-V1.1-107; Chair of Risk, Safety & Uncertainty Quantification: Zürich, Switzerland, 2018; p. 64. [Google Scholar]
- Jeppsson, J. Reliability-Based Assessment Procedures for Existing Concrete Structures. Ph.D. Thesis, Lund University, Lund, Sweden, 2003. [Google Scholar]
- Li, Q.; Wang, C.; Ellingwood, B.R. Time-dependent reliability of aging structures in the presence of non-stationary loads and degradation. Struct. Saf. 2015, 52, 132–141. [Google Scholar] [CrossRef]
- Ditlevsen, O.; Madsen, H.O. Structural Reliability Methods, 1st ed.; John Wiley & Sons Ltd.: Chichester, UK, 1996; Volume 178, p. 384. [Google Scholar]
- Thoft-Cristensen, P.; Baker, M.J. Structural Reliability Theory and its Applications, 1st ed.; Springer Science & Business Media: Berlin, Germany, 1982; p. 268. [Google Scholar]
- Tichý, M. Applied Methods of Structural Reliability, 1st ed.; Springer Netherlands: Dordrecht, The Netherlands, 2012; Volume 2, p. 415. [Google Scholar]
- Harbitz, A. An efficient sampling method for probability of failure calculation. Struct. Saf. 1986, 3, 109–115. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Au, S.-K.; Beck, J.L. Estimation of small failure probabilities in high dimensions by subset simulation. Probabilistic Eng. Mech. 2001, 16, 263–277. [Google Scholar] [CrossRef]
- Pejovic, J.; Jankovic, S. Selection of ground motion intensity measure for reinforced concrete structure. Procedia Eng. 2015, 117, 588–595. [Google Scholar] [CrossRef]
- Nahar, T.T.; Cao, A.-T.; Kim, D. Risk assessment of aged concrete gravity dam subjected to material deterioration under seismic excitation. Earthq. Eng Struct. Dyn. 2020, 14, 1–17. [Google Scholar] [CrossRef]
- Sen, U. Risk Assessment of Concrete Gravity Dams under Earthquake Loads. Master’s Thesis, Louisiana State University, Louisiana, LA, USA, 2018. [Google Scholar]
- Tekie, P.B.; Ellingwood, B.R. Seismic fragility assessment of concrete gravity dams. Earthq. Eng. Struct. Dyn. 2003, 32, 2221–2240. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Vamvatsikos, D. Seismic performance uncertainty estimation via IDA with progressive accelerogram-wise latin hypercube sampling. J. Struct. Eng. 2014, 140, A4014015. [Google Scholar] [CrossRef]
- Kennedy, R.; Ravindra, M. Seismic fragilities for nuclear power plant risk studies. Nucl. Eng. Des. 1984, 79, 47–68. [Google Scholar] [CrossRef]
- Mandal, T.K.; Ghosh, S.; Pujari, N.N. Seismic fragility analysis of a typical Indian PHWR containment: Comparison of fragility models. Struct. Saf. 2016, 58, 11–19. [Google Scholar] [CrossRef]
- Sfahani, M.; Guan, H.; Loo, Y.-C. Seismic reliability and risk assessment of structures based on fragility analysis–A review. Adv. Struct. Eng. 2015, 18, 1653–1669. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Nuss, L.K. Seismic risk prioritization of a large portfolio of dams: Revisited. Adv. Mech. Eng. 2018, 10, 1–20. [Google Scholar] [CrossRef]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: New Jersey, NJ, USA, 1996; p. 673. [Google Scholar]
- Baker, J.W. An Introduction to Probabilistic Seismic Hazard Analysis (PSHA); White Paper, Version 1.3; Stanford University: Stanford, CA, USA, 2008; p. 72. [Google Scholar]
- Pailoplee, S.; Palasri, C. CU-PSHA: A Matlab software for probabilistic seismic hazard analysis. J. Earthq. Tsunami 2014, 8, 1450008. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Nahar, T.T.; Rahman, M.M.; Kim, D. PSHRisk-Tool: A python-based computational tool for developing site seismic hazard analysis and failure risk assessment of infrastructure. Appl. Sci. 2020, 10, 7487. [Google Scholar] [CrossRef]
- Bensoussan, A. Reliability index. In Optimal Control and Dynamic Games; Springer: Dordrecht, The Netherlands, 2005; pp. 311–317. [Google Scholar]
- ICOLD; CIGB. Risk Assessment in Dam Safety Management: A Reconnaissance of Benefits, Methods and Current Applications; International Comission of Large Dams: Paris, France, 2005; Volume 130, p. 276. [Google Scholar]
- Cao, A.-T.; Nahar, T.T.; Kim, D.; Choi, B. Earthquake risk assessment of concrete gravity dam by cumulative absolute velocity and response surface methodology. Earthq. Struct. 2019, 17, 511–519. [Google Scholar] [CrossRef]
- Rahman, M.M.; Nahar, T.T.; Kim, D. Seismic reliability assessment of calibrated concrete gravity dam using high-dimensional model representation and cornell’s approach: A case study. In Proceedings of the 2nd International Conference on Earthquake Engineering and Post Disaster Reconstruction Planning, Bhaktapur, Nepal, 25–27 April 2019; pp. 230–239. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 4th ed.; Prentice Hall: New Jersey, NJ, USA, 2011. [Google Scholar]
- Løkke, A. Earthquake Analysis of Concrete Gravity Dams: Review and Modernization of Two Analysis Procedures. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2013. [Google Scholar]
- Wahalathantri, B.L.; Thambiratnam, D.; Chan, T.; Fawzia, S. A material model for flexural crack simulation in reinforced concrete elements using ABAQUS. In Proceedings of the 1st International Conference on Engineering, Designing and Developing the Built Environment for Sustainable Wellbeing, Jogjakarta, Indonesia, 27–29 May 2011; pp. 260–264. [Google Scholar]
- Birtel, V.; Mark, P. Parameterised finite element modelling of RC beam shear failure. In Proceedings of the ABAQUS Users’ Conference, Boston, MA, USA, 23–25 May 2006; pp. 95–108. [Google Scholar]
- Pavlović, M.; Marković, Z.; Veljković, M.; Buđevac, D. Bolted shear connectors vs. headed studs behaviour in push-out tests. J. Constr. Steel Res. 2013, 88, 134–149. [Google Scholar] [CrossRef]
- Cornelissen, H.; Hordijk, D.; Reinhardt, H. Experimental determination of crack softening characteristics of normalweight and lightweight. Heron 1986, 31, 45–46. [Google Scholar]
- Mirza, S.A.; MacGregor, J.G.; Hatzinikolas, M. Statistical descriptions of strength of concrete. J. Struct. Div. 1979, 105, 1021–1037. [Google Scholar] [CrossRef]
- Kuhl, D.; Bangert, F.; Meschke, G. Coupled chemo-mechanical deterioration of cementitious materials Part II: Numerical methods and simulations. Int. J. Solids Struct. 2004, 41, 41–67. [Google Scholar] [CrossRef]
- Gogoi, I.; Maity, D. Influence of sediment layers on dynamic behavior of aged concrete dams. J. Eng. Mech. 2007, 133, 400–413. [Google Scholar] [CrossRef]
- Gogoi, I.; Maity, D. Vulnerability of aged concrete gravity dams. In Proceedings of the World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; p. 1839. [Google Scholar]
- Box, G.E.; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. Series B (Methodological) 1951, 13, 1–38. [Google Scholar] [CrossRef]
- Habib, S. Optimization of machining parameters and wire vibration in wire electrical discharge machining process. Mech. Adv. Mater. Mod. Process. 2017, 3, 3. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization using Designed Experiments, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; p. 856. [Google Scholar]
- Cao, A.-T.; Tran, T.-T.; Nahar, T.T.; Kim, D. A Proposed Method for Inspecting and Predicting the Seismic Vulnerability of Dam Structures in Korea. In ICSCEA 2019; Springer: Gateway East, Singapore, 2020; pp. 1027–1035. [Google Scholar]
- Grigoli, F.; Cesca, S.; Rinaldi, A.P.; Manconi, A.; Lopez-Comino, J.A.; Clinton, J.; Westaway, R.; Cauzzi, C.; Dahm, T.; Wiemer, S. The november 2017 Mw 5.5 Pohang earthquake: A possible case of induced seismicity in South Korea. Science 2018, 360, 1003–1006. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification from ambient responses using frequency domain decomposition. In Proceedings of the 18th International Modal Analysis Conference (IMAC), San Antoni, TX, USA, 7–10 February 2000; pp. 625–630. [Google Scholar]
- Ko, S.; Cho, S.G.; Kim, D.; Cui, J. Modal identification of cabinets of nuclear power plant based on experimental study. In Proceedings of the 35th Regular Academic Conference and Civil Expo, Gangwon, Korea, 21–23 October 2009; pp. 826–829. [Google Scholar]
- Shah, C. Mesh discretization error and criteria for accuracy of finite element solutions. In Proceedings of the 4th ASEAN ANSYS User Conference, Central Region, Singapore, 5–6 November 2002; p. 12. [Google Scholar]
- Mashayekhi, M.; Estekanchi, H.E.; Vafai, H.; Mirfarhadi, S.A. Development of hysteretic energy compatible endurance time excitations and its application. Eng. Struct. 2018, 177, 753–769. [Google Scholar] [CrossRef]
- Lapajne, J.K.; Fajfar, P. Seismic hazard reassessment of an existing NPP in Slovenia. Nucl. Eng. Des. 1997, 175, 215–226. [Google Scholar] [CrossRef][Green Version]
- Jayaram, N.; Lin, T.; Baker, J.W. A computationally efficient ground-motion selection algorithm for matching a target response spectrum mean and variance. Earthq. Spectra 2011, 27, 797–815. [Google Scholar] [CrossRef]
- Choun, Y.S.; Choi, I.K.; Ohtori, Y.; Shiba, Y.; Nakajima, M. Korea-Japan Joint Research on Development of Seismic Capacity Evaluation and Enhancement Technology Considering Near-Fault Effects; KAERI/RR-2688/2006; Korea Atomic Energy Research Institute: Daejeon, Korea, 2003; p. 164. [Google Scholar]
- Commission, U.N.R. A Performance-Based Approach to Define the Site-Specific Earthquake Ground Motion; Regulatory guide 1.208; U.S. Nuclear Regulatory Commission: North Bethesda, MD, USA, 2007; p. 24.
- Heo, Y.; Kunnath, S.K. Damage-based seismic performance evaluation of reinforced concrete frames. Earthq. Eng Struct. Dyn. 2013, 7, 175–182. [Google Scholar] [CrossRef]
- Jalayer, F.; Cornell, C.A. A Technical Framework for Probability-Based Demand and Capacity Factor (DCFD) Seismic Formats; PEER-2003/08; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2003; p. 106. [Google Scholar]
- Seo, J.M.; Choun, Y.S.; Choi, I.K. Reduction of Uncertainties in Probabilistic Seismic Hazard Analysis; KAERI/CR-65/99; Korea Atomic Energy Research Institute: Daejeon, Korea, 1999; p. 552. [Google Scholar]
- Cornell, C.A.; Banon, H.; Shakal, A.F. Seismic motion and response prediction alternatives. Earthq. Eng. Struct. Dyn. 1979, 7, 295–315. [Google Scholar] [CrossRef]
- FEMA. Prestandard and Commentary for the Seismic Rehabilitation of Buildings; FEMA 356; Federal Emergency Management Agency: Washington, DC, USA, 2000; p. 518.




















| Physical Feature of CGD | Inside Material | Outside Material |
|---|---|---|
| Compressive strength (MPa) | 12 | 18 |
| Modulus of elasticity (MPa) | 13,767 | 16,861 |
| The tensile strength (MPa) | 1.3 | 1.6 |
| Poisson ratio | 0.18 | 0.18 |
| Density (ton/m3) | 2.3 | 2.3 |
| Aging-Effect (year) | Mean | 16% Fractile | 84% Fractile | |||
|---|---|---|---|---|---|---|
| Serviceability | Safety | Serviceability | Safety | Serviceability | Safety | |
| 0 years | 0.259 | 0.425 | 0.269 | 0.422 | 0.227 | 0.405 |
| 25 years | 0.250 | 0.438 | 0.220 | 0.338 | 0.200 | 0.390 |
| 50 years | 0.210 | 0.400 | 0.159 | 0.382 | 0.170 | 0.375 |
| 75 years | 0.159 | 0.375 | 0.175 | 0.351 | 0.180 | 0.350 |
| Aging-Effect (year) | HCLPF Point | |
|---|---|---|
| Serviceability | Safety | |
| 0 years | 0.176 | 0.284 |
| 25 years | 0.127 | 0.256 |
| 50 years | 0.100 | 0.237 |
| 75 years | 0.093 | 0.229 |
| Age of CGD | Limit States | Target β | EQs Level | Safety Check | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 16% fractile | Mean(50% fractile) | 84% fractile | 16% Fractile | Mean (50% fractile) | S/US | 84% Fractile | |||||
| β value | S/US | β value | S/US | ||||||||
| 0 | Serviceability | 5.12 | 4.46 | 3.89 | OP | 8.35 | S | 7.47 | S | 6.6 | S |
| Safety | 5.36 | 4.72 | 3.46 | LS | 6.24 | S | 5.49 | S | 3.72 | S | |
| 25 | Serviceability | 4.92 | 4.22 | 3.61 | OP | 6.21 | S | 5.39 | S | 4.62 | S |
| Safety | 5.3 | 4.65 | 3.21 | LS | 5.76 | S | 5.05 | S | 3.29 | S | |
| 50 | Serviceability | 4.81 | 4.12 | 3.52 | OP | 5.61 | S | 4.74 | S | 3.13 | S |
| Safety | 5.27 | 4.62 | 2.99 | LS | 5.5 | S | 4.84 | S | 2.96 | US | |
| 75 | Serviceability | 4.74 | 4.02 | 3.39 | OP | 5.18 | S | 4.41 | S | 3.71 | S |
| Safety | 5.27 | 4.62 | 2.98 | LS | 5.4 | S | 4.82 | S | 2.93 | US | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nahar, T.T.; Rahman, M.M.; Kim, D. Effective Safety Assessment of Aged Concrete Gravity Dam based on the Reliability Index in a Seismically Induced Site. Appl. Sci. 2021, 11, 1987. https://doi.org/10.3390/app11051987
Nahar TT, Rahman MM, Kim D. Effective Safety Assessment of Aged Concrete Gravity Dam based on the Reliability Index in a Seismically Induced Site. Applied Sciences. 2021; 11(5):1987. https://doi.org/10.3390/app11051987
Chicago/Turabian StyleNahar, Tahmina Tasnim, Md Motiur Rahman, and Dookie Kim. 2021. "Effective Safety Assessment of Aged Concrete Gravity Dam based on the Reliability Index in a Seismically Induced Site" Applied Sciences 11, no. 5: 1987. https://doi.org/10.3390/app11051987
APA StyleNahar, T. T., Rahman, M. M., & Kim, D. (2021). Effective Safety Assessment of Aged Concrete Gravity Dam based on the Reliability Index in a Seismically Induced Site. Applied Sciences, 11(5), 1987. https://doi.org/10.3390/app11051987






