Comparison of Hysteresis Based PWM Schemes ΔΣ-PWM and Direct Torque Control
Abstract
1. Introduction
2. Model of a PMSM
2.1. Coordinate Transformations
2.2. Equations of a PMSM
3. Hysteresis Based Pulse Width Modulation Schemes
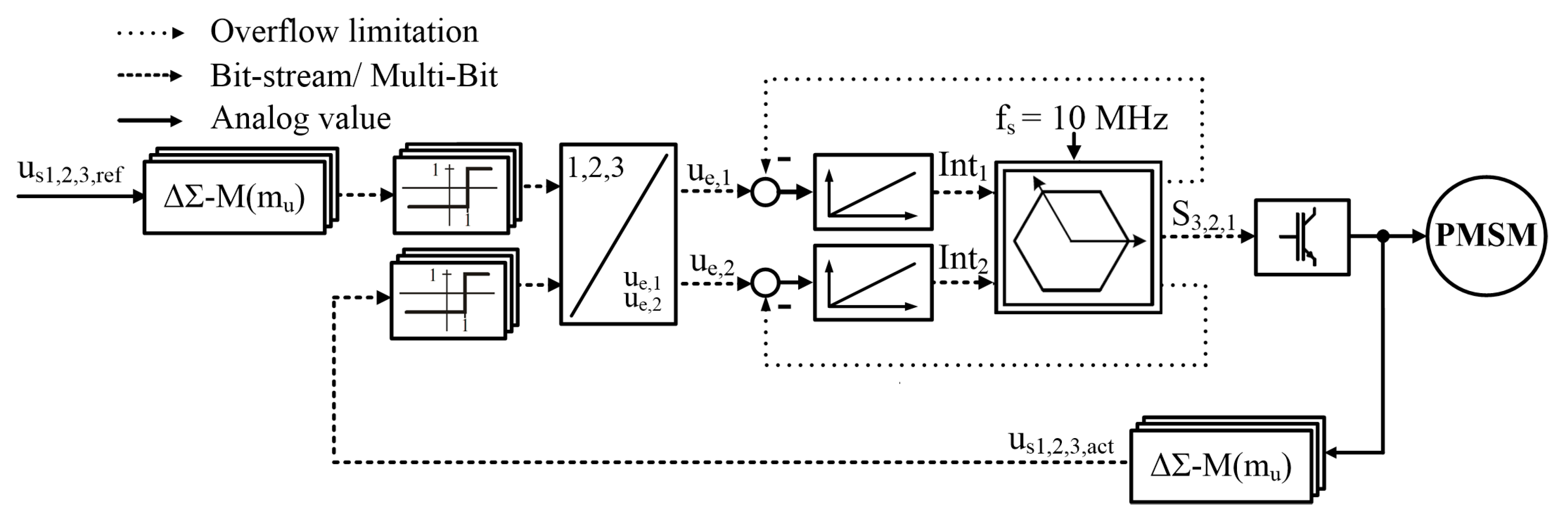
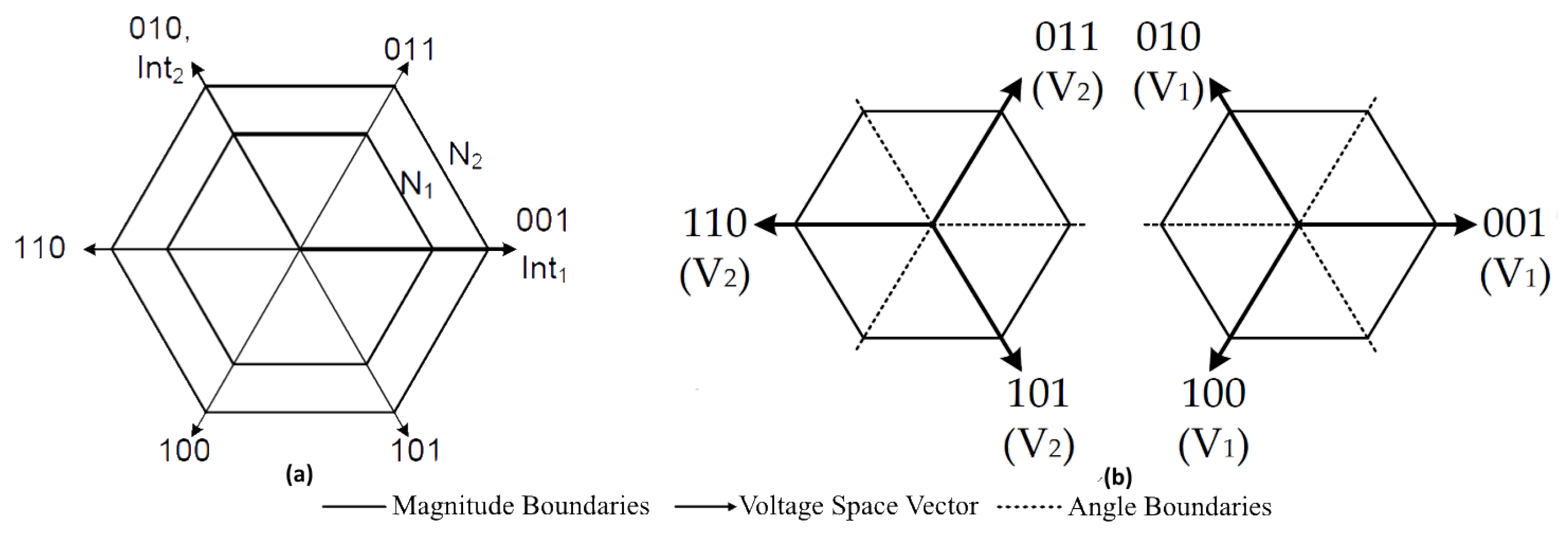
3.1. -PWM
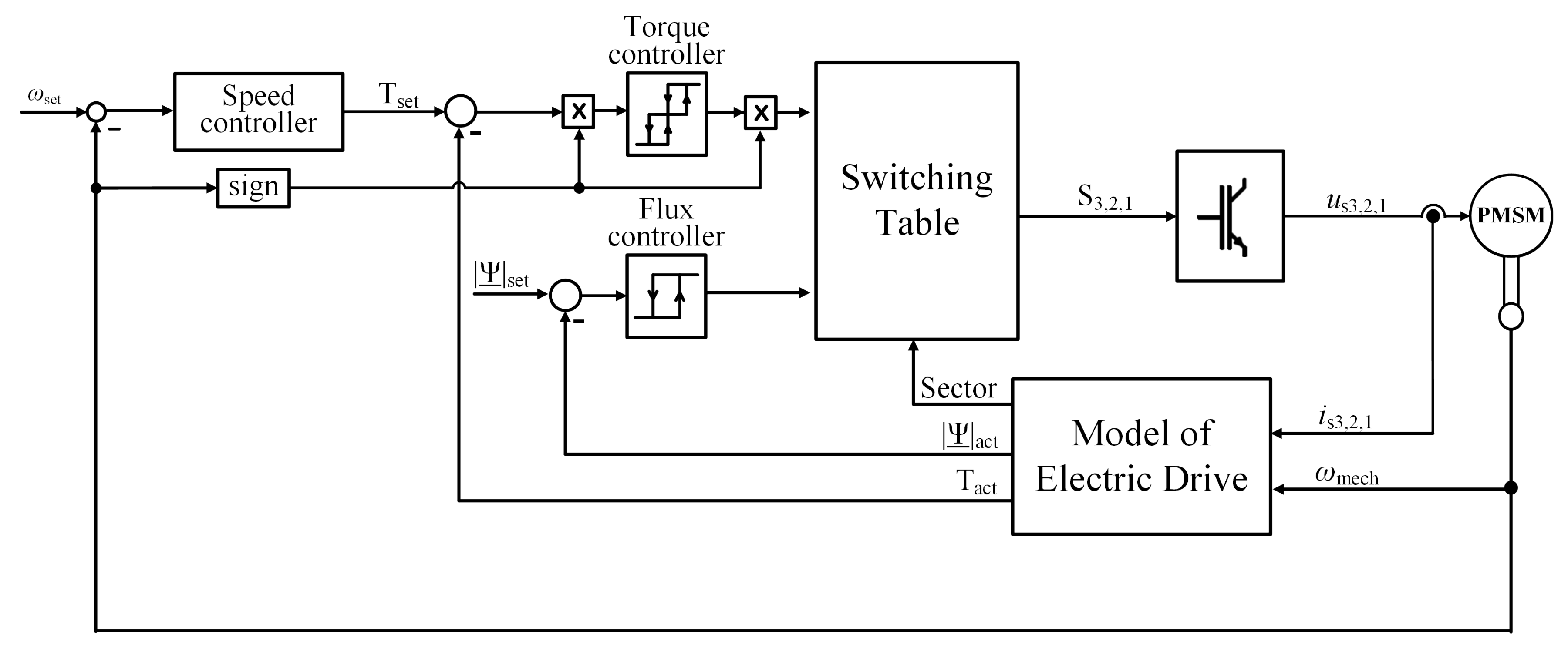
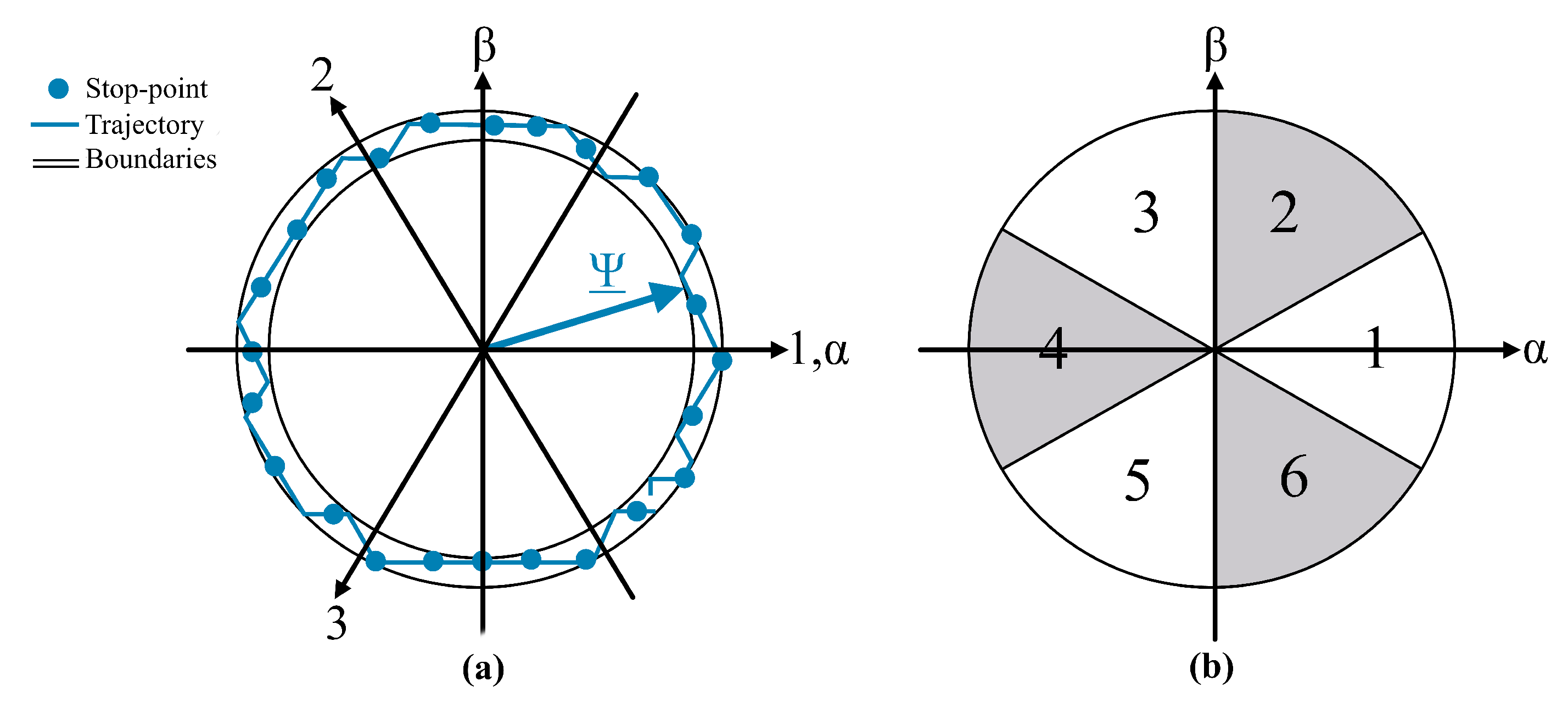
3.2. Direct Torque Control
3.3. Design of Control Parameters
4. Simulation Results
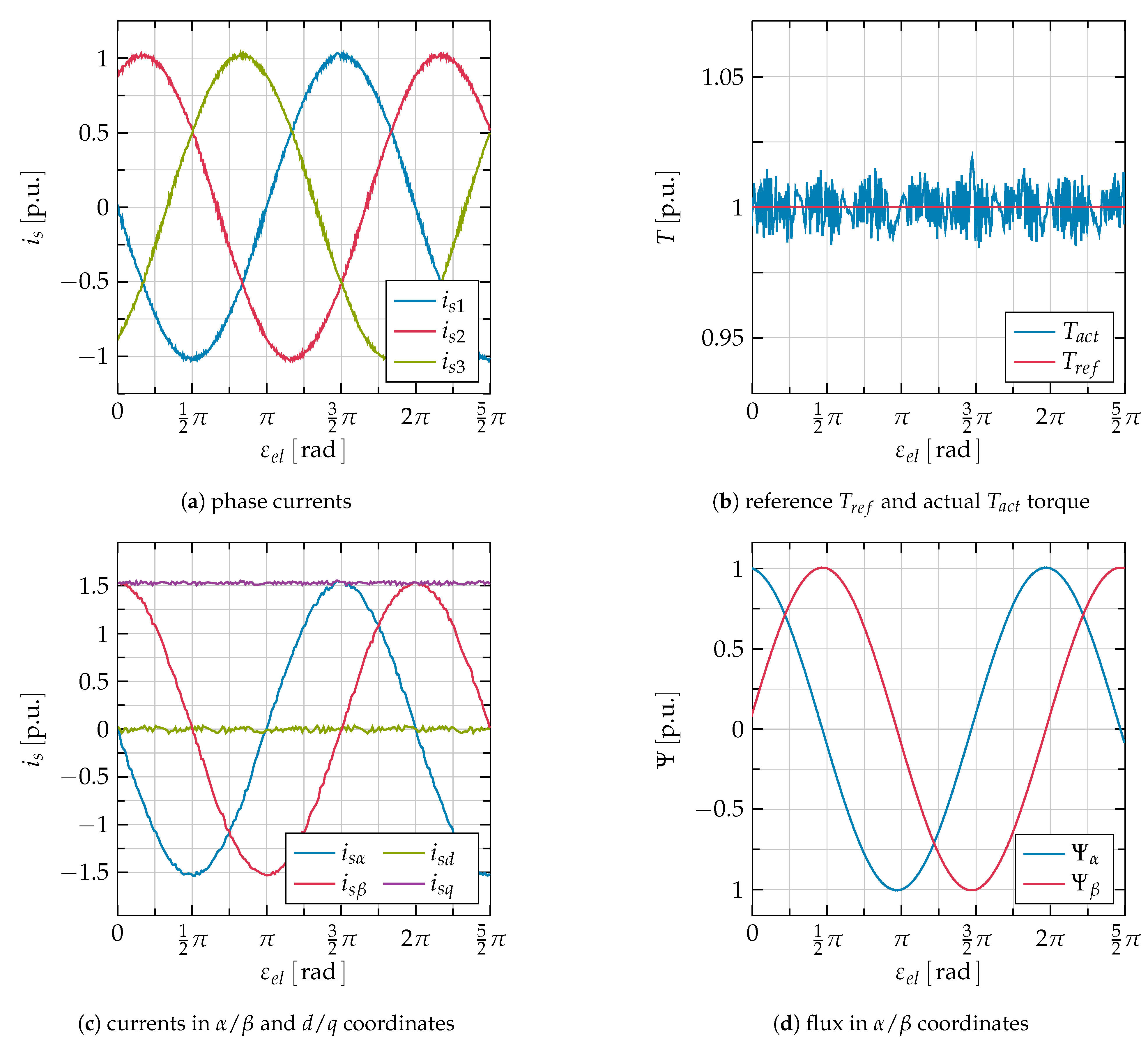
4.1. Stationary Behavior of Both PWM Schemes
4.2. Comparison of Voltage Space Vector Trajectory
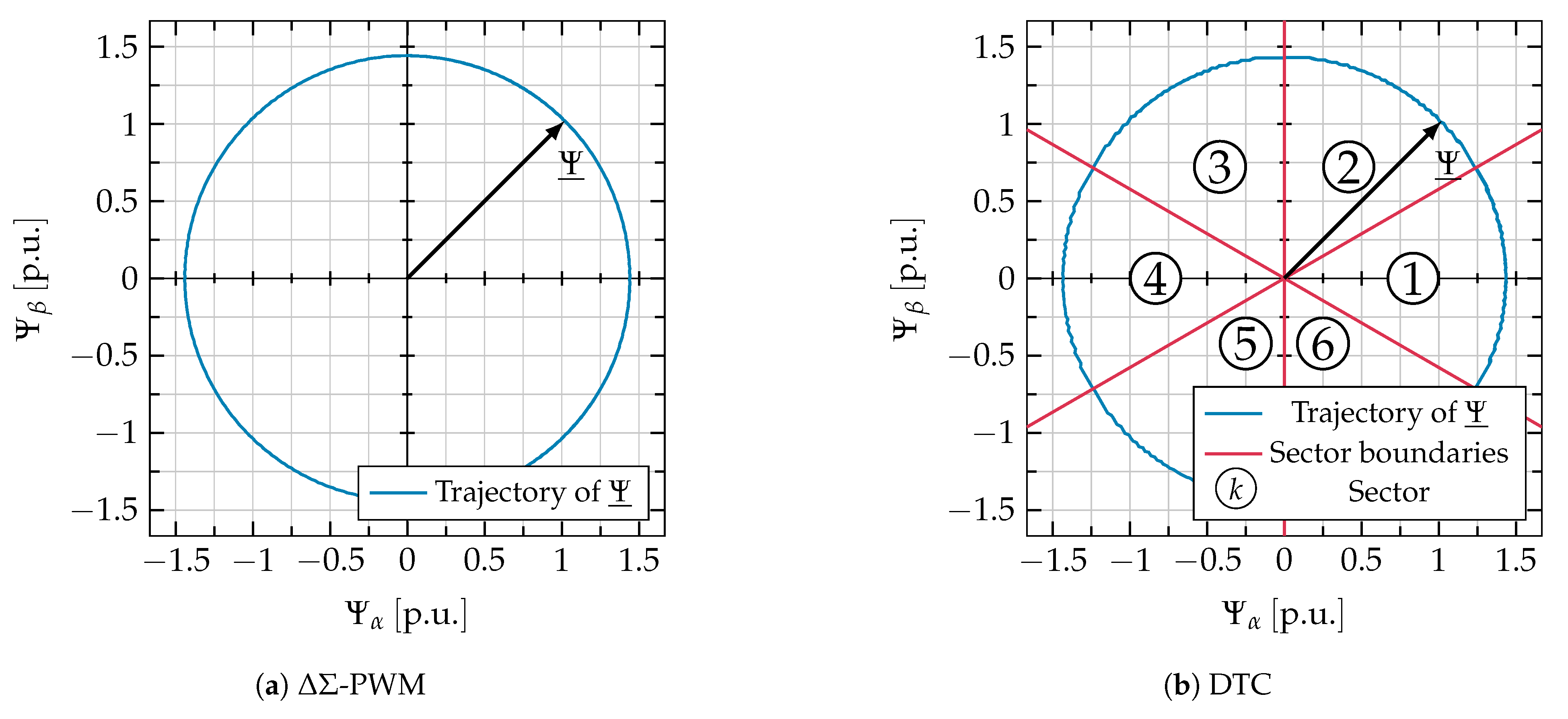
4.3. Comparison of Flux Space Vector Trajectory
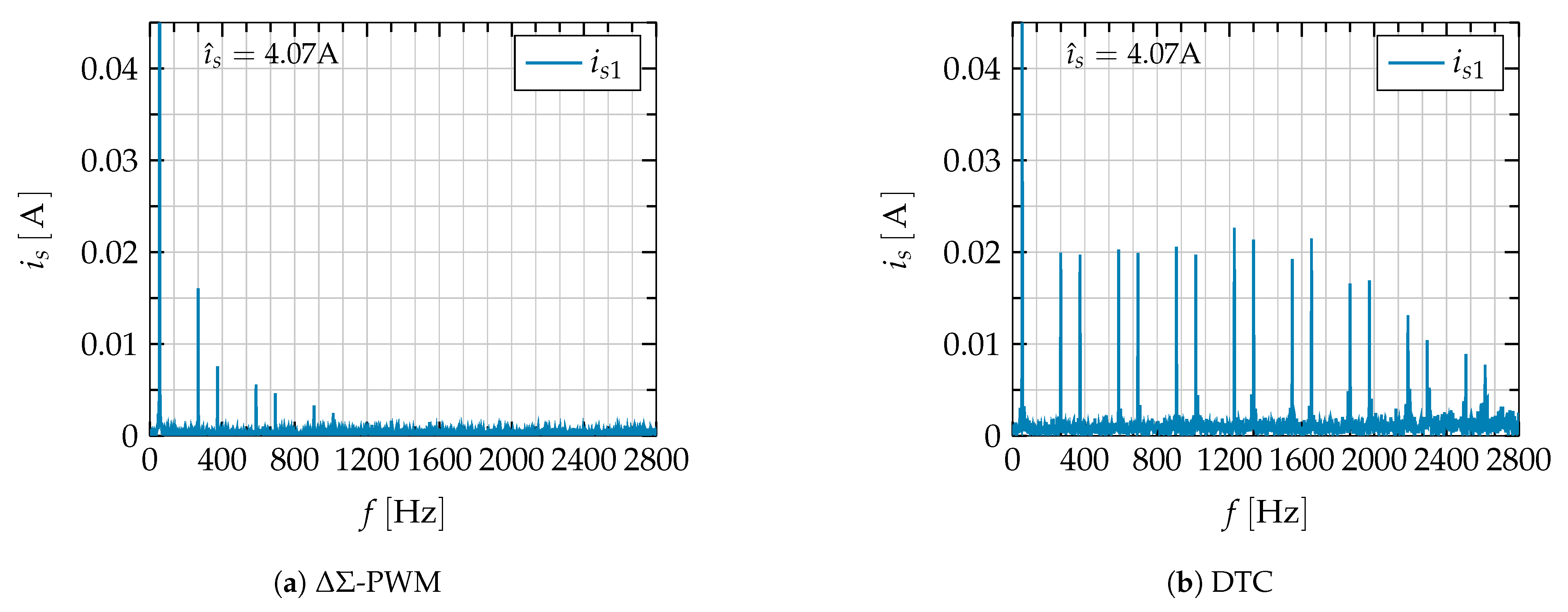
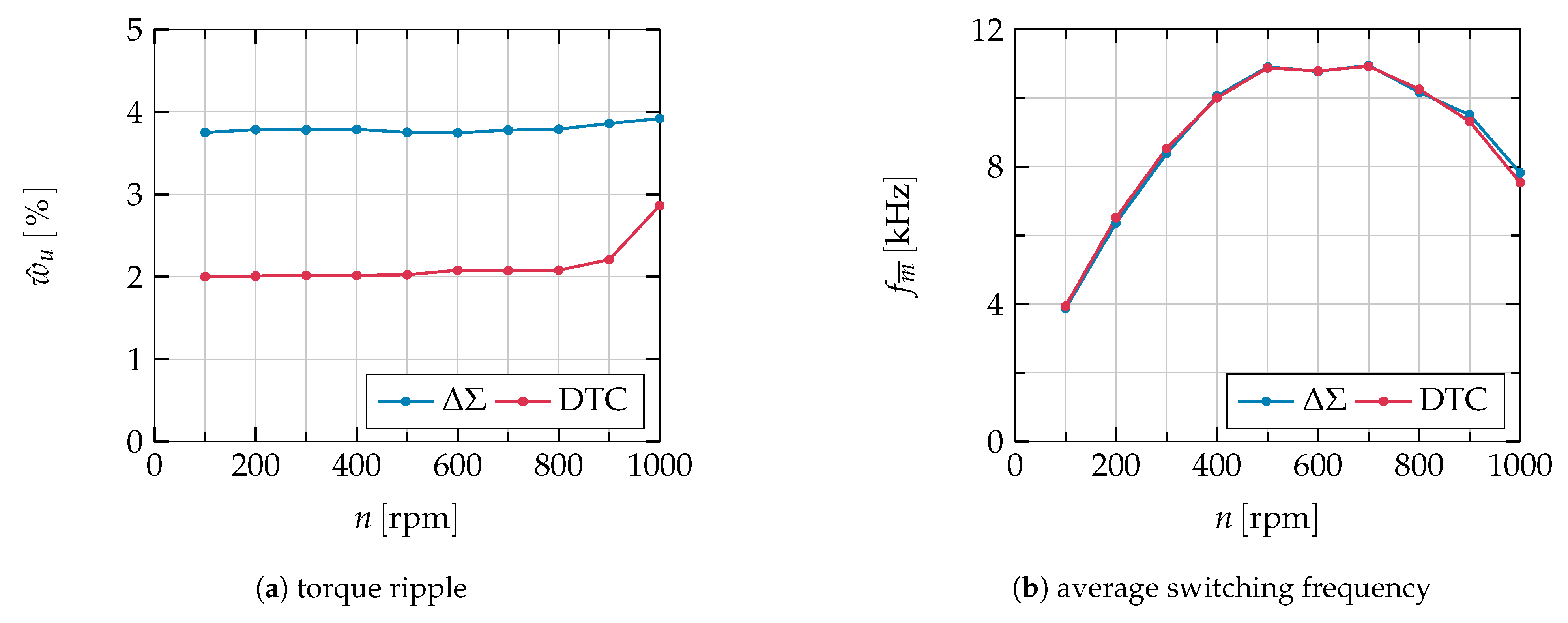
4.4. Comparison of Instantaneous Switching Frequencies
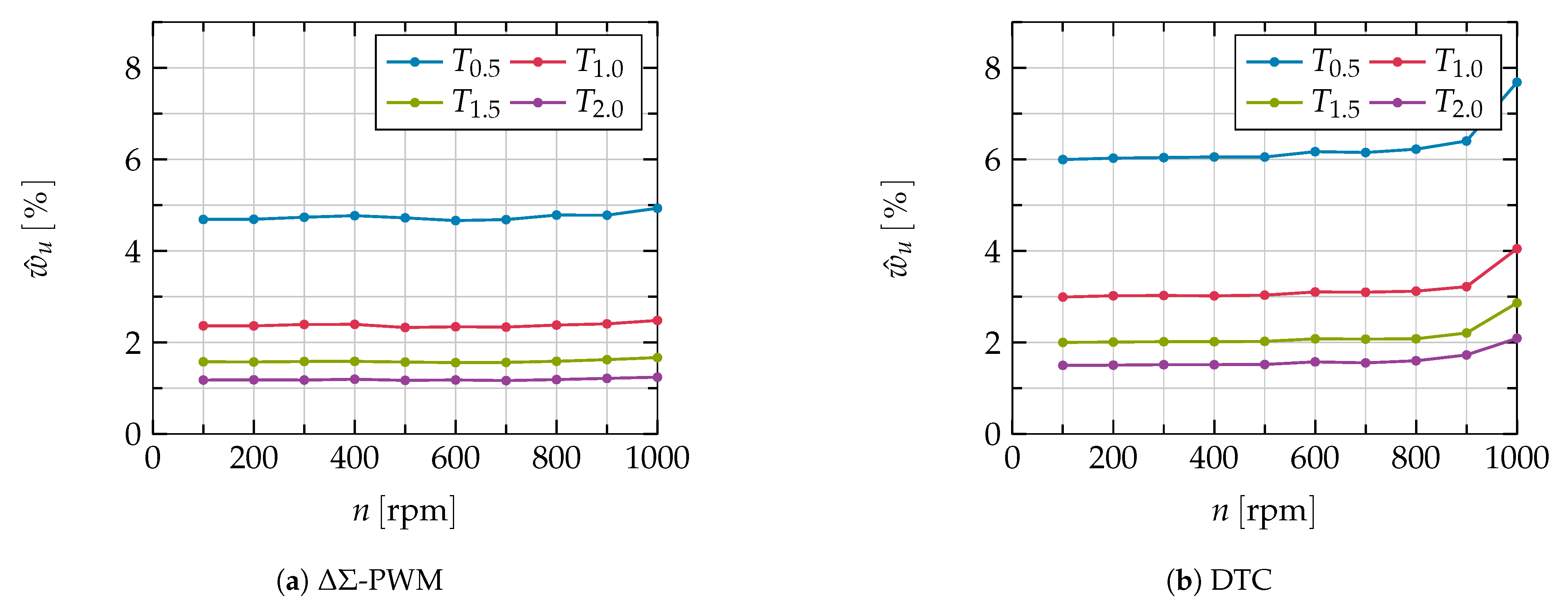
4.5. Comparison of Torque Ripple
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PMSM | permanent magnetic synchronous machine |
| PWM | puls width modulation |
| DTC | Direct Torque Control |
| -PWM | pulse width modulation |
References
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E. A Comprehensive Study of Key Electric Vehicle (EV) Components, Technologies, Challenges, Impacts, and Future Direction of Development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- IEA. Global EV Outlook 2020; IEA: Paris, France, 2020; Available online: https://www.iea.org/reports/global-ev-outlook-2020 (accessed on 20 January 2021).
- Mi, C.; Abul Masrur, M. Hybrid Electric Vehicles—Principles ans Applications with Practical Perspectives; Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Shao, L.; Karci, A.E.H.; Tavernini, D.; Sorniotti, A.; Cheng, M. Design Approaches and Control Strategies for Energy-Efficient Electric Machines for Electric Vehicles—A Review. IEEE Access 2020, 8, 116900–116913. [Google Scholar] [CrossRef]
- Homann, M.; Klein, A.; Schumacher, W. Direct Delta Sigma Signal Processing for Control of Power Electronics. In PCIM Europe 2016; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy Management; VDE: Nürnberg, Germany, 2016. [Google Scholar]
- Homann, M. Hochdynamische Strom- und Spannungsregelung von Permanenterrregten Synchronmaschinen auf Basis von Delta-Sigma Bitströmen. Ph.D. Thesis, Technische Universität Braunschweig, Braunschweig, Germany, 2016. [Google Scholar]
- Bradshaw, J.; Madawala, U.; Patel, N.; Vilathgamuwa, M. A Bit- Stream based Space Vector Modulator. In Proceedings of the International Power Electronics Conference (IPEC), Sapporo, Japan, 21–24 June 2010; pp. 855–861. [Google Scholar]
- Bradshaw, J.B. Bit-Stream Control of Doubly Fed Induction Generators. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 2012. [Google Scholar]
- Thielmann, M.; Klein, A.; Homann, M.; Schumacher, W. Analysis of instantaneous switching frequency of a hysteresis based PWM for control of power electronics. In PCIM Europe 2017; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy Management; VDE: Nürnberg, Germany, 2017. [Google Scholar]
- Klein, A.; Thielmann, M.; Homann, M.; Schumacher, W. Operation Modes of a High Bandwidth Three Phase Hysteresis Modulator based on Delta Sigma Bitstreams. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. 1–10. [Google Scholar]
- Haun, A. Vergleich von Steuerverfahren für Spannungseinprägende Umrichter zur Speisung von Käfigläufermotoren. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 1992. [Google Scholar]
- Takahashi, I.; Noguchi, T. A New Quick-Response and High-Efficiency Control Strategy of an Induction Motor. IEEE Trans. Ind. Appl. 1986, 5, 820–827. [Google Scholar] [CrossRef]
- Ammar, A.; Kheldoun, A.; Metidji, B.; Talbi, B.; Ameid, T.; Azzog, Y. Comparative analysis of different control approaches of direct torque control induction motor drive. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; pp. 831–835. [Google Scholar]
- Koratkar, P.J.; Sabnis, A. Comparative analysis of different control approaches of direct torque control induction motor drive. In Proceedings of the 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kannur, India, 6–7 July 2017; pp. 831–835. [Google Scholar]
- Harikrishnan, R.; George, A.E. Direct Torque Control of PMSM using hysteresis modulation, PWM and DTC PWM based on PI Control for EV—A comparative analysis between the three strategies. In Proceedings of the 2019 2nd International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kannur, India, 5–6 July 2019; pp. 566–571. [Google Scholar]
- Zhang, X.H.; Chen, P.F. Efficiency Optimization of Direct Torque Controlled Interior Permanent Magnet Synchronous Motor Considering Iron Losses. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Tokyo, Japan, 13–16 November 2016; pp. 1–5. [Google Scholar]
- Dankadai, N.K.; Mcdonald, S.P.; Elgendy, M.A.; Atkinson, D.J.; Ullah, S.; Atkinson, G. Direct Instantaneous Torque Control of Switched Reluctance Motor for Aerospace Applications. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, Scotland, 4–7 September 2018; pp. 1–6. [Google Scholar]
- Sung, S.; Lin, W.; Yu, C. Predictive Direct Torque Control ASIC with Speed Feedback Controller in Motor Drive. In Proceedings of the 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Diego, CA, USA, 5–8 October 2014; pp. 2284–2288. [Google Scholar]
- Homann, M.; Schumacher, W. High Bandwidth Phase Voltage and Phase Current Control Loop of Permanent Magnet Synchronous Motor based on Delta Sigma Bitstreams. In Proceedings of the 18th European Conference on Power Electronics and Applications (EPE), Karlsruhe, Germany, 5–8 September 2008. [Google Scholar]
- Klein, A. Delta-Sigma Signalverarbeitung in der Regelungstechnik; Technische Universität Braunschweig: Braunschweig, Germany, 2019. [Google Scholar]
- Matthes, C.; Thielmann, M.; Klein, A. Ressourceneffiziente Regelungen im FPGA. ATP Mag. 2018, 60, 56–65. [Google Scholar] [CrossRef]
- Ammar, A.; Kheldoun, A.; Metidji, B.; Talbi, B.; Ameid, T.; Azzoug, Y. An Experimental Assessment of Direct Torque Control and Model Predictive Control Methods for Induction machine drive. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; pp. 1–6. [Google Scholar]
- Wang, S.; Li, C.; Che, C.; Xu, D. Direct torque control for 2L-VSI PMSM using switching instant table. IEEE Trans. Ind. Electron. 2018, 65, 9410–9420. [Google Scholar] [CrossRef]
- Xia, C.; Wang, S.; Gu, X.; Yan, Y.; Shi, T. Direct torque control for VSI-PMSM using vector evaluation factor table. IEEE Trans. Ind. Electron. 2016, 63, 4571–4583. [Google Scholar] [CrossRef]
- Hans, F.; Oeltze, M.; Schumacher, W. A Modified ZOH Model for Representing the Small-Signal PWM Behavior in Digital DC-AC Converter Systems. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 1514–1520. [Google Scholar]
- Monmasson, E. Power Electronic Converters. PWM Strategies and Current Control Techniques. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 2006. [Google Scholar]
- Leonhard, W. Control of Electrical Drives; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Schröder, D. Elektrische Antriebe—Regelung von Antriebssystemen; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Lehmann, O. Geberfreie Regelung perManentmagneterregter Synchronmaschinen im Elektrischen Antriebsstrang von Straßenfahrzeugen. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2017. [Google Scholar]
- Sadek, S.M. Direct Torque Control of Permanent Magnet Synchronous Motors; University of Kairo: Kairo, Egypt, 2016. [Google Scholar]
- Klein, A.; Schumacher, W. Algebraic Operation on Delta-Sigma bit streams. Math. Comput. Appl. 2018, 23, 49. [Google Scholar] [CrossRef]
- Zrilic, D.G. Circuits and Systems Based on Delta Modulation; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Schreier, R.; Temes, G.C. Understanding Delta-Sigma Data Converters; IEEE Press: Piscataway, NJ, USA, 2005. [Google Scholar]
- Wang, L.; Gao, Y. A Novel Strategy of Direct Torque Control for PMSM drive Reducing Ripple in Torque and Flux. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; Vo1ume 1, pp. 403–406. [Google Scholar]
- Jänecke, M.; Kremer, R.; Steuerwald, G. Direct self-control (DSC), a novel method of controlling asynchronous machines in traction applications. Elektrische Bahnen eb 1990, 88, 81–87. [Google Scholar]
- Knop, A. Entwicklung Eines Schnelltakenden Stromrichters für Netzimpedanzanalyse im Frequenzbereich bis 10 kHz; Christian-Albrechts-Universität zu Kiel: Kiel, Germany, 2013. [Google Scholar]
- Klein, A.; Thielmann, M.; Schumacher, W. Switching Frequency Control for a ΔΣ-PWM. In PCIM Europe 2018; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management; VDE: Nürnberg, Germany, 2018. [Google Scholar]


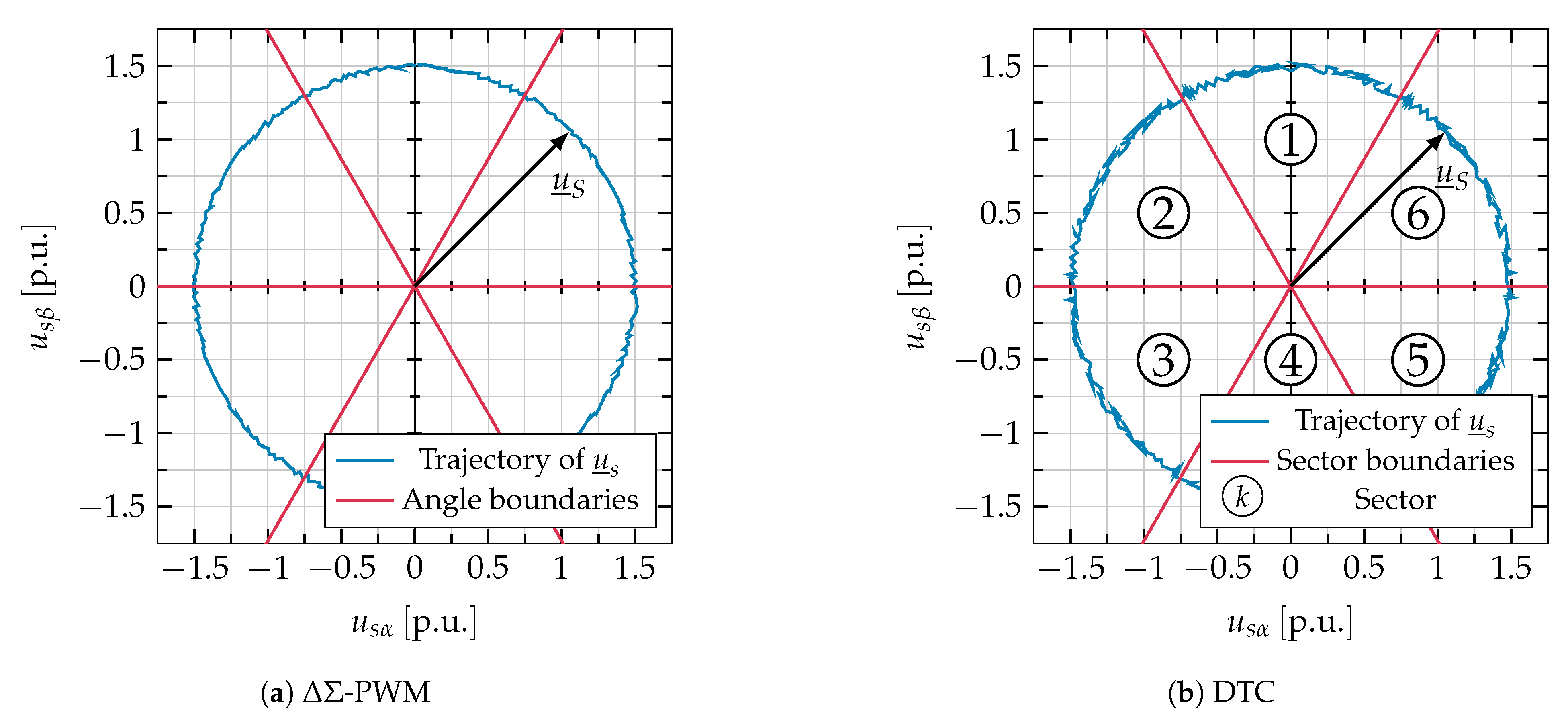


| Change in Flux | Change in Torque | S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|---|---|
| Increase (1) | 011 | 010 | 110 | 100 | 101 | 001 | |
| Increase (1) | Slow Decrease (0) | 111 | 000 | 111 | 000 | 111 | 000 |
| Decrease (−1) | 101 | 001 | 011 | 010 | 110 | 100 | |
| Increase (1) | 010 | 110 | 100 | 101 | 001 | 011 | |
| Decrease (−1) | Slow Decrease (0) | 000 | 111 | 000 | 111 | 000 | 111 |
| Decrease (−1) | 100 | 101 | 001 | 011 | 010 | 110 |
| Variable | Value | Variable | Value |
|---|---|---|---|
| Rated speed () | 800 rpm | Rated torque () | Nm |
| Rated phase voltage () | 20 V | Rated phase current () | 4 A |
| Number of pole pairs (p) | 4 | Stator winding resistance () | m |
| d axis inductance () | mH | q axis inductance () | mH |
| Flux linkage () | 86 mWb | Nominal inertia (J) | 3.96 × 10 |
| Control parameters of -PWM | ||||||||||||
| Hysterisis element | = 58 | = 78 | ||||||||||
| Current controller | = 2 V/A | = s | = 2 V/A | = s | ||||||||
| Speed controller | = 2 As | = s | ||||||||||
| Control parameters of DTC | ||||||||||||
| Flux controller | = mWb | = mWb | ||||||||||
| Torque controller | = Nm | = Nm | = Nm | |||||||||
| Speed controller | = As | = s | ||||||||||
| Ripple | Switching Frequency | |||||
|---|---|---|---|---|---|---|
| Scheme | Torque | Voltage | Flux | Max | Min | Average |
| -PWM | % | 3% | % | kHz | kHz | kHz |
| DTC | 2% | % | 1% | kHz | 660 Hz | kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klarmann, K.; Thielmann, M.; Schumacher, W. Comparison of Hysteresis Based PWM Schemes ΔΣ-PWM and Direct Torque Control. Appl. Sci. 2021, 11, 2293. https://doi.org/10.3390/app11052293
Klarmann K, Thielmann M, Schumacher W. Comparison of Hysteresis Based PWM Schemes ΔΣ-PWM and Direct Torque Control. Applied Sciences. 2021; 11(5):2293. https://doi.org/10.3390/app11052293
Chicago/Turabian StyleKlarmann, Kevin, Malte Thielmann, and Walter Schumacher. 2021. "Comparison of Hysteresis Based PWM Schemes ΔΣ-PWM and Direct Torque Control" Applied Sciences 11, no. 5: 2293. https://doi.org/10.3390/app11052293
APA StyleKlarmann, K., Thielmann, M., & Schumacher, W. (2021). Comparison of Hysteresis Based PWM Schemes ΔΣ-PWM and Direct Torque Control. Applied Sciences, 11(5), 2293. https://doi.org/10.3390/app11052293






