Effects of Flexural Stiffness on Deformation Behaviour of Steel and FRP Stress-Ribbon Bridges
Abstract
:Featured Application
Abstract
1. Introduction
2. Design Procedure of the Bridge with Flexural-Stiff Ribbons
3. Experimental Program
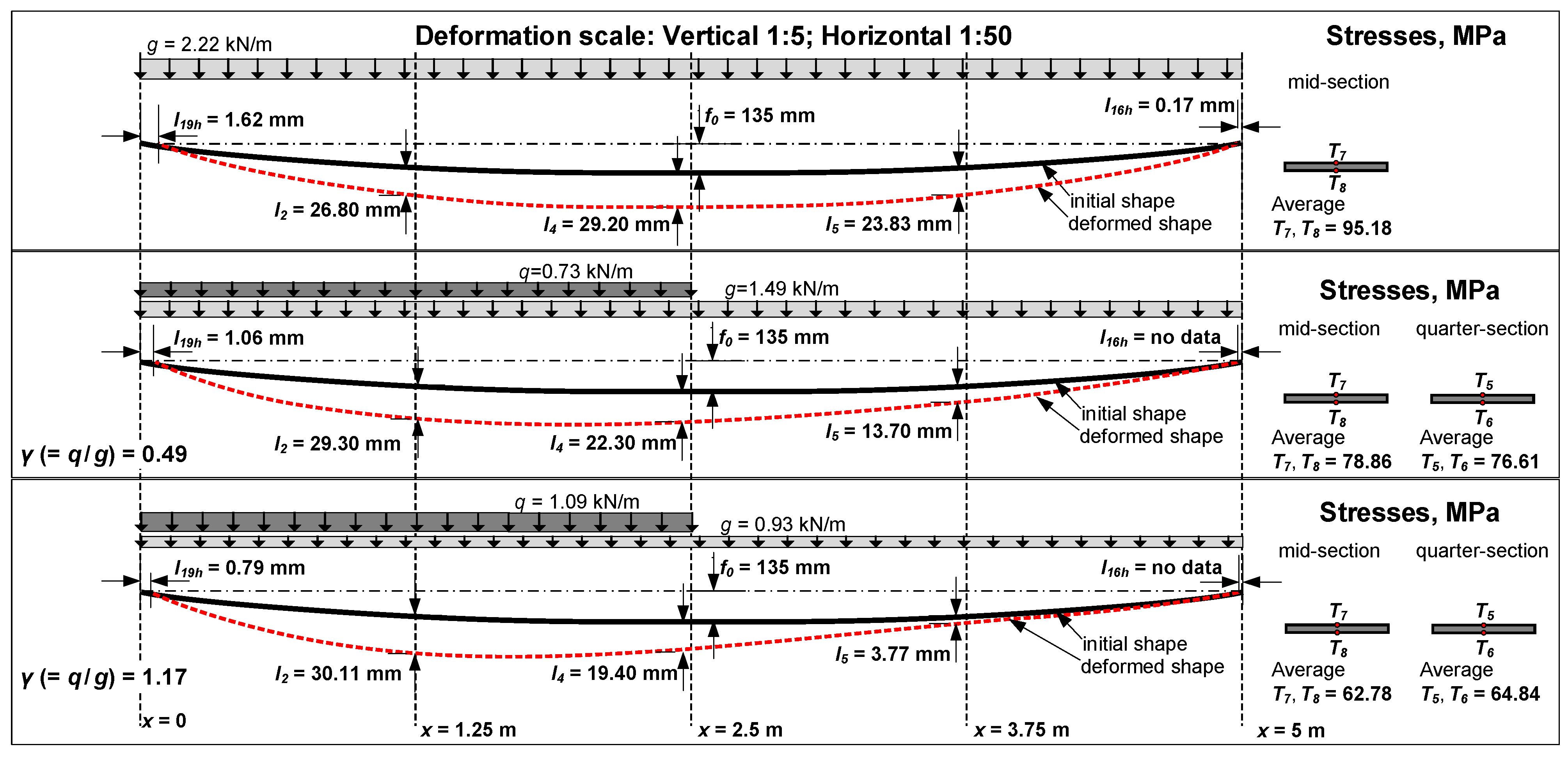
3.1. Loading Procedure
3.2. Test Results
4. Numerical Modelling
4.1. The Numerical Models’ Verification
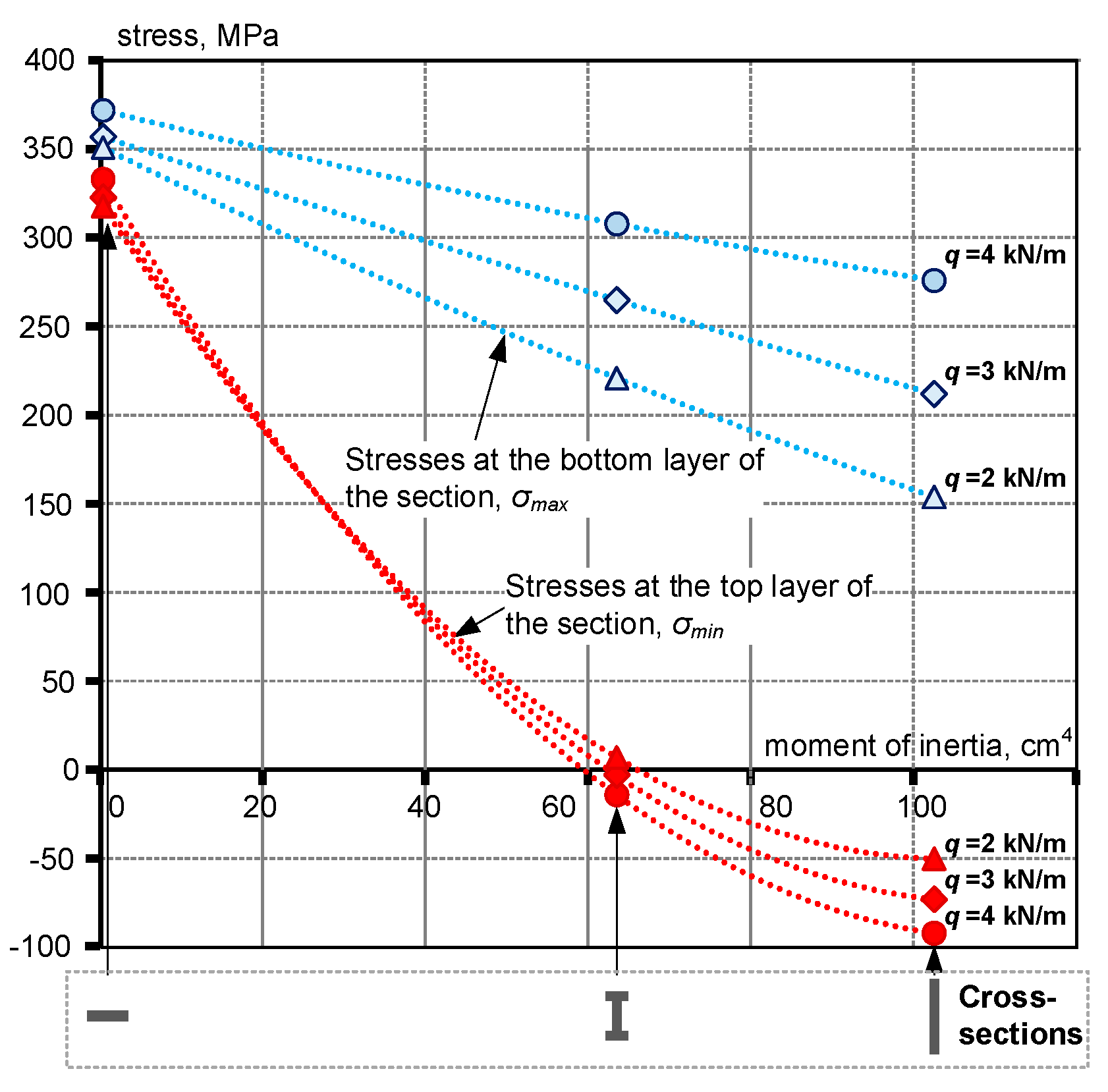
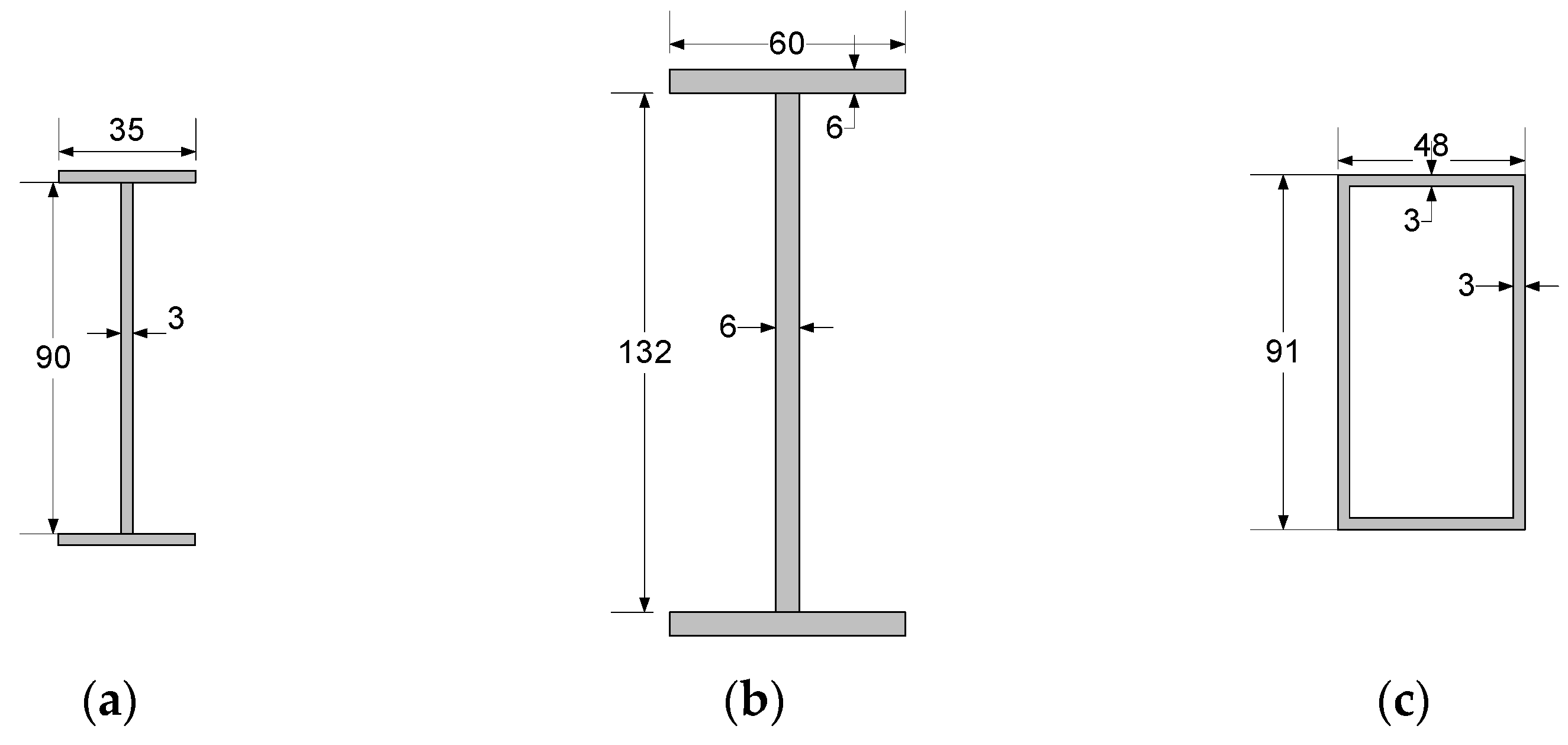
4.2. Parametric Analysis
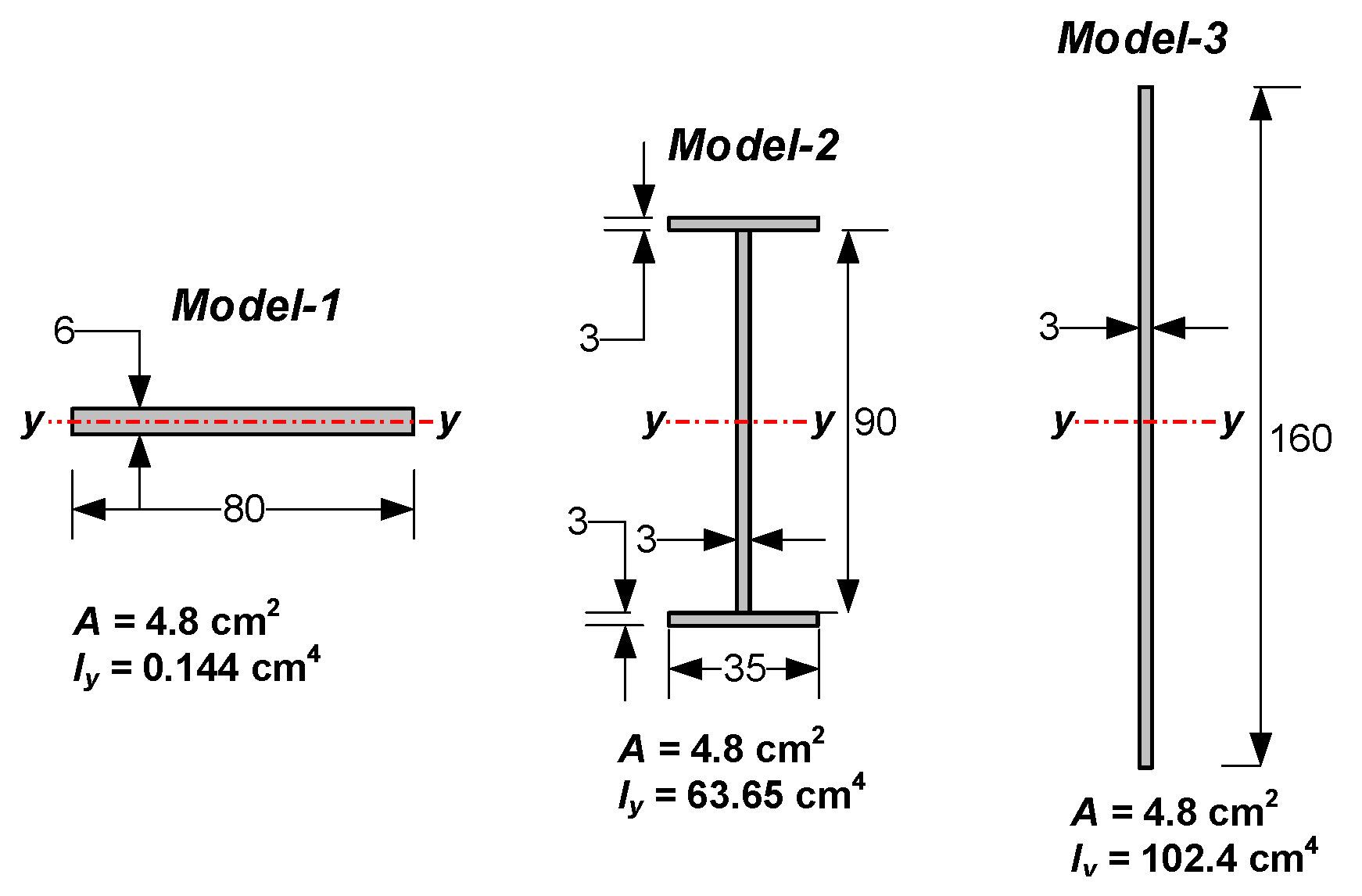
- The existing assortment of GFRP profiles, based on the similarity of cross-section dimensions of the polymer and steel profiles, does not ensure achieving adequate efficiency as steel counterparts in situations when equivalent axial and flexural stiffness are required in conjunction.
- CFRP profiles are applicable as flexural-stiff stress-ribbons. The development of such structural systems is the object of further research.
5. Conclusions
- A more sustainable deformation behaviour is characteristic of the bridge prototype with the innovative flexural-stiff ribbons regarding the model with flexible bands of the same axial stiffness. Even under asymmetrical load distribution (unfavourable for the typical bridge systems), the proposed ribbon-profiles did not experience undesirable camber of the unloaded part of the span. At the same time, the proposed design procedure can limit unacceptable compressive stresses in the ribbons.
- An engineering methodology and design equations are proposed to choose the cross-section geometry of the flexural-stiff ribbon-profiles. It allows composing the ribbons of any materials, increasing the versatility of the stress-ribbon structural systems.
- The existing dimensioning system of GFRP profiles, based on the cross-section similarity to the steel profiles, is inefficient in situations that require the satisfaction of both the axial stiffness and the flexural stiffness limitations. The application of CFRP profiles is a promising alternative to steel in flexural-stiff stress-ribbon structural systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Strasky, J. Stress Ribbon and Cable-Supported Pedestrian Bridges; Thomas Telford: London, UK, 2005. [Google Scholar]
- Goldack, A.; Schlaich, M.; Meiselbach, M. Stress ribbon bridges: Mechanics of the stress ribbon on the saddle. ASCE J. Bridge Eng. 2016, 21, 04015089. [Google Scholar] [CrossRef]
- Tubino, F.; Pagnini, L.; Piccardo, G. Uncertainty propagation in the serviceability assessment of footbridges. Struct. Infrastruct. Eng. 2020, 16, 123–137. [Google Scholar] [CrossRef]
- Romera, L.; Hernández, S.; Baldomir, A.; Nieto, F. Study of pedestrian comfort in a three span stress ribbon footbridge with carbon fibre cables. WIT Trans. Built Environ. 2020, 196, 139–152. [Google Scholar]
- Xiao, X.; Xue, H.; Chen, B. Nonlinear model for the dynamic analysis of a time-dependent vehicle-cableway bridge system. Appl. Math. Model. 2021, 90, 1049–1068. [Google Scholar] [CrossRef]
- Liu, Y.; Zwingmann, B.; Schlaich, M. Carbon fiber reinforced polymer for cable structures—A review. Polymers 2015, 7, 2078–2099. [Google Scholar] [CrossRef] [Green Version]
- fib (The International Federation for Structural Concrete). Guidelines for the Design of Footbridges; fib: Lausanne, Switzerland, 2005. [Google Scholar]
- Han, K.J.; Lim, N.H.; Ko, M.G.; Kim, K.D. Efficient assumption of design variables for stress ribbon footbridges. KSCE J. Civ. Eng. 2016, 20, 250–260. [Google Scholar] [CrossRef]
- del Arco, C.D.; Aparicio, A.C.; Mari, A.R. Preliminary design of pre-stressed concrete stress ribbon bridges. ASCE J. Bridge Eng. 2001, 6, 234–241. [Google Scholar] [CrossRef]
- Juozapaitis, A.; Norkus, A. Shape determining of loaded cable via total displacements. Technol. Econ. Dev. Econ. 2005, 11, 248–259. [Google Scholar] [CrossRef]
- Scheer, J. Failed Bridges: Case Studies, Causes and Consequences; Ernst&Sohn Verlag: Berlin, Germany, 2010. [Google Scholar]
- Radnić, J.; Matešan, D.; Buklijaš-Kobojević, D. Numerical model for analysis of stress-ribbon bridges. Građevinar 2015, 67, 959–973. [Google Scholar]
- Juozapaitis, A.; Vainiunas, P.; Kaklauskas, G. A new steel structural system of a suspension pedestrian bridge. J. Constr. Steel Res. 2006, 62, 1257–1263. [Google Scholar] [CrossRef]
- Gholami, M.; Sam, A.R.M.; Yatim, J.M.; Tahir, M.M. A review on steel/CFRP strengthening systems focusing environmental performance. Constr. Build. Mater. 2013, 47, 301–310. [Google Scholar] [CrossRef]
- Gholami, M.; Mohd Sam, A.R.; Marsono, A.K.; Tahir, M.M.; Faridmehr, I. Performance of steel beams strengthened with pultruded CFRP plate under various exposures. Steel Compos. Struct. 2016, 20, 999–1022. [Google Scholar] [CrossRef]
- Arnautov, A.K.; Kulakov, V.; Andersons, J.; Gribniak, V.; Juozapaitis, A. Experimental investigation on stiffness and strength of single-lap z-pinned joints in a laminated CFRP stress-ribbon strip. Balt. J. Road Bridge Eng. 2016, 11, 120–126. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.Q.; Luo, B.; Wang, Q.; Feng, B. Experimental and numerical investigation of the anti-debonding performance for novel CFRP-steel tube composite member under tension. J. Build. Eng. 2021, 35, 102004. [Google Scholar] [CrossRef]
- Segal, E.M.; Rhode-Barbarigos, L.; Adriaenssens, S.; Coelho, R.D.F. Multi-objective optimization of polyester-rope and steel-rope suspended footbridges. Eng. Struct. 2015, 99, 559–567. [Google Scholar] [CrossRef]
- Quaranta, G.; Demartino, C.; Xiao, Y. Experimental dynamic characterization of a new composite glubam-steel truss structure. J. Build. Eng. 2019, 25, 100773. [Google Scholar] [CrossRef]
- Alaedini, S.; Kabir, M.Z.; Al-Mahaidi, R. Stability performance of thin-walled pultruded beams with geometric web-flange junction imperfections. J. Build. Eng. 2021, 33, 101549. [Google Scholar] [CrossRef]
- Wadi, A.; Pettersson, L.; Karoumi, R. FEM simulation of a full-scale loading-to-failure test of a corrugated steel culvert. Steel Compos. Struct. 2018, 27, 217–227. [Google Scholar]
- Votsis, R.A.; Stratford, T.J.; Chryssanthopoulos, M.K.; Tantele, E.A. Dynamic assessment of a FRP suspension footbridge through field testing and finite element modelling. Steel Compos. Struct. 2017, 23, 205–215. [Google Scholar] [CrossRef] [Green Version]
- Bleicher, A.; Schlaich, M.; Fujino, Y.; Schauer, T. Model-based design and experimental validation of active vibration control for a stress ribbon bridge using pneumatic muscle actuators. Eng. Struct. 2011, 33, 2237–2247. [Google Scholar] [CrossRef]
- Juozapaitis, A.; Merkevičius, T.; Daniūnas, A.; Kliukas, R.; Sandovič, G.; Lukoševičienė, O. Analysis of innovative two-span suspension bridges. Balt. J. Road Bridge Eng. 2015, 10, 269–275. [Google Scholar] [CrossRef] [Green Version]
- Sandovic, G.; Juozapaitis, A.; Gribniak, V. Experimental and analytical investigation of deformations and stress distribution in steel bands of a two-span stress-ribbon pedestrian bridge. Math. Probl. Eng. 2017, 2017, 9324520. [Google Scholar] [CrossRef]
- Juozapaitis, A.; Norkus, A. Determination of rational parameters for the advanced structure of a pedestrian suspension steel bridge. Balt. J. Road Bridge Eng. 2007, 2, 173–181. [Google Scholar]
- Tong, Z.; Song, X.; Huang, Q. Deflection calculation method on GFRP-concrete-steel composite beam. Steel Compos. Struct. 2018, 26, 595–606. [Google Scholar]
- Jakubovskis, R.; Kupliauskas, R.; Rimkus, A.; Gribniak, V. Application of FE approach to deformation analysis of RC elements under direct tension. Struct. Eng. Mech. 2018, 68, 345–358. [Google Scholar]
- Cervenka, V.; Jendele, L.; Cervenka, J. ATENA Program. Documentation, Part. 1: Theory; Cervenka Consulting: Prague, Czechia, 2007. [Google Scholar]
- Fiberline. The Fiberline Design Manual, 2nd ed.; Fiberline Composites: Middelfart, Denmark, 2003. [Google Scholar]
- Röchling. Durostone® Composite Profiles: Fibre Reinforced Plastics; Röchling Industrial: Laupheim, Germany, 2017. [Google Scholar]










| Cross-Section Type (EN 10365) | Height, mm | Estimated Coefficient |
|---|---|---|
| IPE-beam | 160–600 | 0.410–0.405 |
| HE-beam | 200–900 | 0.430–0.405 |
| Square hollow section | 80–400 | 0.381–0.393 |
| Round hollow section | 88.9–1219 | 0.337–0.348 |
| Source | Model-1 | Model-2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Symmetrical Load | Asymmetrical Load (q/g = 0.49) | Symmetrical Load | Asymmetrical Load (q/g = 0.49) | |||||
| umax, mm | H, kN | umax, mm | H, kN | umax, mm | H, kN | umax, mm | H, kN | |
| Test | 29.2 | 36.0 | 29.3 | 29.5 | 49.9 | 41.3 | 44.8 | 30.2 |
| Finite element simulations | 30.5 | 37.9 | 29.5 | 31.7 | 48.8 | 43.2 | 42.0 | 30.6 |
| Difference | –4.5% | –5.0% | –0.7% | –6.9% | 2.2% | –4.4% | 6.2% | –1.3% |
| Bridge Model | q = 2 kN/m | q = 3 kN/m | q = 4 kN/m | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| g, kN/m | utot, mm | uq, mm | σmin, MPa | σmax, MPa | H, kN | g, kN/m | utot, mm | uq, mm | σmin, MPa | σmax, MPa | H, kN | g, kN/m | utot, mm | uq, mm | σmin, MPa | σmax, MPa | H, kN | |
| Model-1 | 8.9 | 62.0 | 8.4 | 318 | 351 | 155.3 | 8.6 | 63.6 | 12.2 | 323 | 357 | 157.9 | 8.6 | 66.4 | 15.6 | 333 | 372 | 164.5 |
| Model-2 | 2.0 | 22.6 | 8.4 | 7 | 221 | 54.2 | 2.0 | 26.3 | 12.2 | –3 | 265 | 62.3 | 2.0 | 29.4 | 15.6 | –14 | 308 | 70.3 |
| Model-3 | 0.4 | 11.3 | 8.4 | –50 | 154 | 12.6 | 0.4 | 15.1 | 12.2 | –73 | 212 | 16.8 | 0.6 | 19.5 | 15.6 | –92 | 276 | 22.2 |
| Model-4 | 2.0 | 39.6 | 12.3 | –4 | 64 | 44.2 | 2.0 | 45.0 | 18.2 | –7 | 73 | 46.3 | 2.0 | 50.2 | 23.6 | –10 | 84 | 52 |
| Model-5 | 2.0 | 18.6 | 7.3 | 5 | 137 | 57 | 2.0 | 22.1 | 10.9 | –6 | 165 | 65.3 | 2.0 | 24.8 | 13.8 | –9 | 194 | 74.1 |
| Parameter | Steel (Model-2) | GFRP (Model-4) | CFRP (Model-5) |
|---|---|---|---|
| Iy, cm4 | 63.7 | 458 | 86.5 |
| A, cm2 | 4.8 | 15.1 | 8.0 |
| E, GPa | 208 | 28 | 148 |
| ν | 0.30 | 0.23 | 0.28 |
| EIy, kNm2 | 127.3 | 128.2 | 128.0 |
| EA, MN | 96.0 | 42.3 | 118.1 |
| m, kg/m | 3.77 | 2.72 | 1.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juozapaitis, A.; Sandovič, G.; Jakubovskis, R.; Gribniak, V. Effects of Flexural Stiffness on Deformation Behaviour of Steel and FRP Stress-Ribbon Bridges. Appl. Sci. 2021, 11, 2585. https://doi.org/10.3390/app11062585
Juozapaitis A, Sandovič G, Jakubovskis R, Gribniak V. Effects of Flexural Stiffness on Deformation Behaviour of Steel and FRP Stress-Ribbon Bridges. Applied Sciences. 2021; 11(6):2585. https://doi.org/10.3390/app11062585
Chicago/Turabian StyleJuozapaitis, Algirdas, Giedrė Sandovič, Ronaldas Jakubovskis, and Viktor Gribniak. 2021. "Effects of Flexural Stiffness on Deformation Behaviour of Steel and FRP Stress-Ribbon Bridges" Applied Sciences 11, no. 6: 2585. https://doi.org/10.3390/app11062585
APA StyleJuozapaitis, A., Sandovič, G., Jakubovskis, R., & Gribniak, V. (2021). Effects of Flexural Stiffness on Deformation Behaviour of Steel and FRP Stress-Ribbon Bridges. Applied Sciences, 11(6), 2585. https://doi.org/10.3390/app11062585







