Design of a Fuzzy Optimization Control Structure for Nonlinear Systems: A Disturbance-Rejection Method

Abstract

This paper tackles the control problem of nonlinear disturbed polynomial systems using the formalism of output feedback linearization and a subsequent sliding mode control design. This aims to ensure the asymptotic stability of an unstable equilibrium point. The class of systems under investigation has an equivalent Byrnes–Isidori normal form, which reveals stable zero dynamics. For the case of modeling uncertainties and/or process dynamic disturbances, conventional feedback linearizing control strategies may fail to be efficient. To design a robust control strategy, meta-heuristic techniques are synthesized with feedback linearization and sliding mode control. The resulting control design guarantees the decoupling of the system output from disturbances and achieves the desired output trajectory tracking with asymptotically stable dynamic behavior. The effectiveness and efficiency of the designed technique were assessed based on a benchmark model of a continuous stirred tank reactor (CSTR) through numerical simulation analysis.

1. Introduction

Stabilization and tracking are two important issues in the field of nonlinear control with the former being more intricate than the latter. In this respect, several methodologies have been proposed. These include sliding mode control (SMC), feedback linearization (FBL), regulation control, adaptive backstepping control, H∞ adaptive fuzzy control and internal model principle.

Lately, variable structure control has been presented for tackling nonlinear systems [1,2,3]. Backstepping is a powerful technique for creating controllers for several nonlinear systems. Nevertheless, it is characterized by the complexity explosion, which is a consequence of recurrent complex differentiation of specific nonlinear functions [4,5]. Output regulation is used by the output tracking system [6], assuming that an exosystem leads to output excitation. Nonlinear functions are characterized by complex solutions of partial differential equations. Furthermore, the states of the exosystem need switching to provide the necessary difference at the output leading to transient tracking issues [7].

The tracking problem is transformed into a nonlinear one using the fundamentals of the internal model. It has been addressed using ordinary differential equations resulting in asymptotic solutions for specific nonlinear scenarios and required paths [8,9]. However, for several industrial controlled systems, it is difficult to obtain precise analytical models. Uncertainties, such as un-modeled or unknown dynamics, process parameter variations and external disturbances appear in the built models [10] and influence the performance. Consequently, the design of control systems is significantly affected when the disturbance is attenuated [11,12,13,14]. As a result, control algorithms created based on disturbance observers have been formulated to neutralize such uncertainties [15,16,17,18]. The almost disturbance decoupling problem, which reduces the disturbance at the output to a random level of accuracy in nonlinear and linear systems, has been considered in [19,20,21,22,23], and interesting results were obtained for these systems.

Several chemical processes, such as pH neutralization, exhibit nonlinear dynamic behavior and linear-based controllers are utilized to ensure stable steady-state performance. However, optimal performance is not attained because of the inherent nonlinearities of the process, and in some cases, the control fails if the process drifts. In such cases, nonlinear compensators, characterized by nontrivial designs, are employed.

Control techniques using feedback linearization established for linear control have been adapted to control nonlinear systems [24,25,26,27,28,29,30].

The authors in [31] discussed a nonlinear control technique, called “linearization of the dynamics”, where the system dynamics are changed in a way that the pole assignment technique is used. It begins by identifying a process that states variable coordinate transformation that leads to an equivalent linear input-state dynamic. “Linearization of the input/output (I/O) behavior” is a second approach that aims to linearize some dynamics in the I/O perspective.

If the emphasis is on the behavior of the measured outputs then, I/O FBL is used since it enables the straightforward association of the design variables with performance requirements. However, there may be instances where it may not be feasible to completely linearize a nonlinear system [30]. In this case, a portion of the linearized model stays nonlinear. “Zero dynamics” (ZD) refers to the dynamic aspects of that part, and has a critical role in the design of the controller, and can precede an appropriate output [6]. This technique may not be flexible enough when disturbances or potential uncertainties specific to the parameters are present. Consequently, the control strategy requires a change in the feedback-manipulated variable such that the desired output conforms to the specifications [6].

Among the many techniques, SMC was proposed in [32] as an “outer loop” feedback so that the control mechanism can be made more flexible [33]. Nevertheless, it has been established that in certain states and disturbances go unmeasured; the disturbance-rejection may not happen even though a bounded output might exist.

It is clear from the above discussion that there is a need for the design of a robust controller that can handle a system operating under uncertainties. In this context, this work presents the analysis and design of a systematic nonlinear control technique. Its goal is to ensure the global asymptotical stability of an uncertain system operating on feedback. It is characterized by output monitoring and disturbance decoupling for a set of nonlinear control plants having parameters and model uncertainties.

To address this challenge, an advanced SMC method is proposed for a nonlinear forecast system [34,35,36]. It was recognized that the projected regulator is flexible and handles undetermined disturbances. In addition, it does not have the typical SMC chattering problem.

Moreover, an analytical form of the I/O FBL control is developed. The controller integrates PSO optimization with conventional FBL and fuzzy logic. This work comprises the development of a fundamental control technique for FBL using SMC. Next, a fuzzy-PSO technique is integrated to ensure that the sliding mode state is reached even during external disturbance or uncertainties in the control parameters. For sliding mode, this fuzzy-logic-based PSO technique is used to enhance control ability and decrease chattering.

Generally, the feedback linearization technique (FBL) has satisfactory performance, provided that disturbances, modeling errors and parameter uncertainties are ignored. This is acceptable in an ideal scenario. However, in practice, external disturbances and/or inherent parameter variations do occur, resulting in the degradation of the performance of the FBL. Moreover, the FBL is mainly based on the complicated differential geometry theory, which creates major difficulties for engineers when implementing it in practical situations. By employing the Taylor series to represent the nonlinear systems by a polynomial model, computing the decoupling control input becomes generic. We believe that the proposed polynomial solution of the FBL problem is one of the major contributions of this paper.

It is worth mentioning that the performance of the FBL control will hardly be affected by injecting disturbances (whether internal or external) into the model. That is to say; the model does not correct for the disturbances. The SMC approach is, therefore, used to minimize the effects of these disturbances leading to the enhancement of the dynamic behavior of the control and state variables. Indeed, the system’s closed-loop will be stabilized in the neighborhood of the focused equilibrium point while employing the feedback control design. However, the system dynamics become affected by chattering, which is unacceptable in terms of physical process constraints. In addition, because of the uncertainties in the model, complete elimination of the disturbances cannot be achieved using only conventional SMC. Consequently, the computed values of the state variables, which also influence the SMC through the reaching law, remain incorrect.

In this respect and in order to attain the optimal controller gains associated with the above problems, one must reduce the long gap of the sliding surface, which is a delicate control task. To solve this problem, a fuzzy technique along with a PSO method will be implemented to allow accurate tuning of the controller gains. The robustness and steady-state accuracy will be established in an efficient way, even in the case of a hard desired output trajectory. This latter objective will construct the key contribution of this work.

This paper explicitly emphasizes controlling a CSTR by taking temperature measurements against concentration measurements. It is required that the controller regulate the temperature to keep it below a maximum threshold. During such control, disturbance-rejection is expected, while the inlet stream acts as a source of unmeasured and measured disturbances.

The remaining part of this paper is organized as follows: In Section 2, characteristics of SMC and I/O FBL are presented. An advanced tracking control strategy to strengthen the nonlinear polynomial controller is shown in Section 3, where the design combines FBL formalism with SMC. In Section 4, fundamentals of the PSO algorithm and fuzzy logic control synthesis are provided. Section 5 also shows the application of the above approaches to the CSTR. Finally, concluding remarks and perspectives are given in Section 5.

2. Study of a Robust Nonlinear Control Strategy

2.1. Preliminaries

There is a short description of the primary factors comprising the I/O FBL technique in order to touch upon the fundamental topics. If the reader wishes to have more information concerning the background and comprehensive aspects of the framework, reading the works of [31,37] is suggested.

The following expression concerns the general form of a nonlinear affine system

$$\left\{\begin{array}{l}\dot{X}=F(X)+G(X)U+\lambda (X)D\\ y=H(X)\end{array}\right.$$

(1)

where $X\in {\mathfrak{R}}^n$, $U\in \mathfrak{R}$, $y\in \mathfrak{R}$, $D\in {\mathfrak{R}}^m$; $F\left(.\right):{\mathfrak{R}}^n\to {\mathfrak{R}}^n$; $G\left(.\right):{\mathfrak{R}}^n\to {\mathfrak{R}}^{}$ and $\lambda \left(.\right):{\mathfrak{R}}^n\to {\mathfrak{R}}^m$ are $C^{\infty }$ vector fields, and $H\left(.\right):{\mathfrak{R}}^n\to \mathfrak{R}$ is a $C^{\infty }$ function.

It is straightforward to transform the model into the Kronecker product and Taylor expansions so that it can be converted to a polynomial expression specified below:

$$\left\{\begin{array}{l}\dot{X}={\displaystyle \sum _{i=1}^q\left(F_i{X}^{\left[i\right]}\right)+{\displaystyle \sum _{j=0}^q\left(G_j{X}^{\left[j\right]}\right)U+{\displaystyle \sum _{k=0}^q{\lambda }_k{X}^{\left[k\right]}D}}}\\ y={\displaystyle \sum _{s=1}^q\left(H_s{X}^{\left[s\right]}\right)}\end{array}\right.,$$

(2)

Lemma 1

[37].Let the real function$H\left(X\right)$expressed under the polynomial form by:$H\left(X\right)={\displaystyle \sum _{i\ge 1}{H}_i}{X}^{\left[i\right]}$and the vector field:

$$F(X)={\displaystyle \sum _{i\ge 0}{F}_i{X}^{\left[i\right]}},$$

(3)

The Lie derivative of$H\left(X\right)$with respect to$F\left(X\right)$denoted by$L_{F}H\left(X\right)$is given by:

$$L_{F}H\left(X\right)={\displaystyle \sum _{k\ge 0}{\mathsf{\Lambda }}_k{X}^{\left[k\right]}},$$

(4)

where

$${\mathsf{\Lambda }}_k={\displaystyle \sum _{j=1}^k{\mathsf{\Lambda }}_{k-j+1}}{V}^{\left(k-j+1\right)}\left(F_i\otimes I_{n^{\left(k-j\right)}}\right),$$

(5)

By exploiting this lemma, the quantities$L_F^{i}H\left(X\right)$are then written:

$$L_F^{i}H\left(X\right)={\displaystyle \sum _{l\ge 1}{\mathsf{\Lambda }}_l^i}{X}^{\left[l\right]}\mathrm{for}1\le i\le n,$$

(6)

where

$$\left\{\begin{array}{l}{\mathsf{\Lambda }}_l^0=H_l\\ {\mathsf{\Lambda }}_l^i={\displaystyle \sum _{j=1}^l{\mathsf{\Lambda }}_{l-j+1}^{i-1}{V}^{\left(l-j+1\right)}\left(F_j\otimes I_{n^{\left(l-j\right)}}\right)}\end{array}\right.$$

where$V^{\left[k\right]}={\displaystyle \sum _{j=0}^{i-1}\left(U_{n^j\times n}\otimes I_{n^{\left(i-j-1\right)}}\right)}$and$U_{p\times q}$denotes the Kronecker permutation matrix. Moreover, we express in a similar way the quantities

$$L_G{L}_F^{q-1}H\left(X\right)={\displaystyle \sum _{k\ge 0}{J}_k^j{X}^{\left[k\right]}},$$

(7)

where

$$J_k^j={\displaystyle \sum _{l=0}^k{\mathsf{\Lambda }}_{k-l+1}^{q-1}}{V}^{\left(k-l+1\right)}\left(G_{j^l}\otimes I_{n^{\left(k-l\right)}}\right)$$

Definition 1

[38].System (1) is characterized by a local relative degree $q$ at an operating point $X_0$ if

• $L_G{L}_F^{k}H\left(X\right)={\displaystyle \sum _{j\ge 0}{N}_j^i}{X}^{\left[j\right]}=0$for all X close to$X_0$and for all$k<q-1$;

where $N_j^i={\displaystyle \sum _{l=0}^j{\mathsf{\Lambda }}_{j-l+1}^k}{V}^{\left(j-l+1\right)}\left(G_{i^l}\otimes I_{n^{\left(j-l\right)}}\right)$

• $L_G{L}_F^{q-1}H\left(X\right)={\displaystyle \sum _{k\ge 0}{J}_k^j}{X}^{\left[k\right]}\ne 0$;

Considering that the system has a measurable relative degree, it is feasible to determine a coordinate function$Z=\mathsf{\Gamma }\left(X\right)$that is obtained by repeatedly differentiating the output. This system is now specified as a function of the new coordinates having the normal form. Considering the situation where there is a lack of disturbance, the output of the normal form is the canonical controllability form:

$$\left\{\begin{array}{c}{\dot{Z}}_1=Z_2=L_{F}H\left(X\right)={\displaystyle \sum _{l\ge 1}{\mathsf{\Lambda }}_l^1{X}^{\left[l\right]}}\\ {\dot{Z}}_2=Z_3=L_F^{2}H\left(X\right)={\displaystyle \sum _{l\ge 1}{\mathsf{\Lambda }}_l^2{X}^{\left[l\right]}}\\ ⋮\\ {\dot{Z}}_{q-1}=Z_q=L_F^{q-1}H\left(X\right)={\displaystyle \sum _{l\ge 1}{\mathsf{\Lambda }}_l^{q-1}{X}^{\left[l\right]}}\\ {\dot{Z}}_q=v\\ {\dot{Z}}_i=\vartheta \left(Z\right),q+1\le i\le n\\ y=Z_1=H\left(X\right)\end{array}\right.$$

(8)

$Z={\left[\begin{array}{cc}{\mathsf{{\rm Y}}}_1& {\mathsf{{\rm Y}}}_2\end{array}\right]}^T$with${\mathsf{{\rm Y}}}_1=\left[\begin{array}{ccccc}H\left(X\right)& L_{F}H\left(X\right)& L_F^{2}H\left(X\right)& \dots & L_F^{q-1}H\left(X\right)\end{array}\right]$and${\mathsf{{\rm Y}}}_2=\left[\begin{array}{ccc}{\phi }_1\left(X\right)& \dots & {\phi }_{n-q}H\left(X\right)\end{array}\right]$is the compensator.

It is straight obvious that if$q<n$the original nonlinear model will come into a nonlinear${\mathfrak{R}}^{n-q}$subsystem whose behavior does not assign the desired system output and a linear${\mathfrak{R}}^q$one, which evolves with linear dynamics. Such a nonlinear subsystem is designated as the ZD.

A nonlinear model where$q<n$is I/O linearizable only in case of minimum phase characteristic, which signifies that the ZD is locally asymptotically stable [39]. In order to overcome the output decoupling problem from process disturbances, [39] have addressed measurable disturbances as external inputs. In this respect, they have defined the new concept of disturbances relative degree.

Definition 2

[38].Let the disturbance$D\in {\mathfrak{R}}^m$affects the dynamics of the nonlinear affine system (1). The system output$y\left(t\right)$is said to have a relative degree related to the disturbance$D_i(0\le i\le m)$if there exists an integer$C_i$satisfying:

$$L_{{\lambda }_i}{L}_F^{C_i-1}H(X)={\displaystyle \sum _{k=0}^{C_i-1}{P}_k^i}{X}^{\left[k\right]}\ne 0,$$

(9)

where$P_k^i={\displaystyle \sum _{l=0}^k{\mathsf{\Lambda }}_{k-l+1}^{C_i-1}{V}^{\left(k-l+1\right)}\left({\lambda }_{i^l}\otimes I_{n^{\left(k-l\right)}}\right)}$.

The following lemma is stated based on the concept of disturbance relative degree stated on Definition 2.

Lemma 2.

If$C_i>q$then the output of the system$y\left(t\right)$is decoupled from the disturbance$D_i$and the control input can be obtained by [38]:

$$U=a\left(X\right)+b\left(X\right)v$$

(10)

where$\left\{\begin{array}{ll}a\left(X\right)={\displaystyle \sum _{i=1}{a}_i{X}^{\left[i\right]}},& a_i={\mathsf{\Pi }}_0^{-1}\left[{\mathsf{\Lambda }}_i-{\displaystyle \sum _{p=1}^{i-1}{\mathsf{\Pi }}_{i-p}\otimes a_p}\right]\\ b\left(X\right)={\displaystyle \sum _{j=1}{b}_j{X}^{\left[j\right]}},& b_j=-{\mathsf{\Pi }}_0^{-1}{\displaystyle \sum _{p=1}^{i-1}{\mathsf{\Pi }}_{i-p}\otimes b_p}\end{array}\right.$and$v$is the control input of the normal controllability canonical form.

Proof. 

The disturbance affects to a lesser degree compared to the control input in case $C_i>q$. The information corresponding to disturbance $D_i$ can be obtained using the system states; therefore, decoupling $y\left(t\right)$ and $D_i$ needs no additional effort.

Here, it can be easily confirmed that for $i=0,1,\dots ,q-1$ one has $L_{\lambda }{L}_F^{i}H\left(X\right)=0$. Next, the disturbance vector components $D_i$ are not expected to affect the initial $q$ equations of the observability Byrnes–Isidori form, which is similar to the controllability canonical one. The other equations concerning the ZD would depend on the disturbance components vector $D$.

Presume that the subsequent feedback control input is selected:

$$U=-\frac{B\left(Z\right)}{A\left(Z\right)}+\frac{v}{A\left(Z\right)}$$

(11)

Then, the feedback control is defined by Equation (8) and:

$$\dot{\vartheta }=Q\left(Z\right)+K\left(Z\right)D_i$$

(12)

where it may be observed that the output ($Z$) is entirely disconnected from the disturbance term $D_i$. Here, the condition $C_i>q$ must be fulfilled if the output is to not influence $D_i$, while $U$ is the linearizing control input.

Consider $U=a\left(X\right)+b\left(X\right)v$ so such extent that the system output $y\left(t\right)$ has no influence of $D_i$. The closed-loop system can be expressed as:

$$\left\{\begin{array}{l}\dot{X}=F\left(X\right)+G\left(X\right)b\left(X\right)v+G\left(X\right)a\left(X\right)+\lambda \left(X\right)D_i\\ y=H\left(X\right)\end{array}\right.$$

(13)

Next,

$$y^{\left(1\right)}\left(t\right)=Z_2\left(t\right)=L_{F+G\alpha }H\left(X\right)+L_{\lambda }H\left(X\right)D_i$$

(14)

becomes autonomous from the disturbance $D$ if and only if $L_{\lambda }H\left(X\right)=0$. Assuming this is obtained,

$$y^{\left(2\right)}\left(t\right)=Z_3\left(t\right)=L_{F+G\alpha }^{2}H\left(X\right)+L_{\lambda }{L}_{F+G\alpha }H\left(X\right)D_i$$

(15)

where $L_T=L_{F+G\alpha }$

Once again, $L_{\lambda }{L}_T^{q-1}H\left(X\right)$ should be different from zero. Calculate iteratively:

$$y^{\left(q\right)}\left(t\right)=L_T^{q}H\left(X\right)+L_{\lambda }{L}_T^{q-1}H\left(X\right)D_i$$

(16)

where $L_{\lambda }{L}_T^{q-1}H\left(X\right)$ is equal to zero. Consequently, it can be concluded that $L_{\lambda }{L}_T^{q-1}H\left(X\right)=0$ so far as $i=0,1,\dots ,q-1$, $C_i>q$.

Then, Equation (16) is written

$$\begin{array}{l}{y}^{\left(q\right)}\left(t\right)={\displaystyle \sum _{l\ge 1}{\mathsf{\Lambda }}_l^q{X}^{\left[l\right]}},\end{array}$$

(17)

where $\left\{\begin{array}{l}{\mathsf{\Lambda }}_l^0=H_l\\ {\mathsf{\Lambda }}_l^q={\displaystyle \sum _{j=1}^l{\mathsf{\Lambda }}_{l-j+1}^{q-1}{V}^{\left(l-j+1\right)}\left(T_j\otimes I_{n^{\left(l-j\right)}}\right)}\end{array}\right.$.

Overall, there is no term in the control law $U$ to discard case 1 disturbances because the state vector contains all pertinent information.

Lemma 3.

If$C_i=q$the control input is written as [38]:

$$U=a\left(X\right)+b\left(X\right)v+\beta \left(X\right)D_i$$

(18)

where$\left\{\begin{array}{ll}a\left(X\right)={\displaystyle \sum _{i=1}}{a}_i{X}^{\left[i\right]},& a_i={\mathsf{\Pi }}_0^{-1}\left[{\mathsf{\Lambda }}_i-{\displaystyle \sum _{p=1}^{i-1}{\mathsf{\Pi }}_{i-p}}\otimes a_p\right]\\ b\left(X\right)={\displaystyle \sum _{j=1}}{b}_j{X}^{\left[j\right]},& b_j=-{\mathsf{\Pi }}_0^{-1}{\displaystyle \sum _{p=1}^{i-1}{\mathsf{\Pi }}_{i-p}}\otimes b_p\\ \beta \left(X\right)=-\frac{{\displaystyle \sum _{s=0}^{q-1}{J}_s^p{X}^{\left[s\right]}}}{{\displaystyle \sum _{k=0}^{q-1}{\mathsf{\Pi }}_k^l{X}^{\left[k\right]}}}& \end{array}\right.$.

Proof. 

If $C_i=q$, the system output is similarly impacted by the control input and disturbance, there is a need for feed-forward steps to facilitate decoupling.

The control law specified by Equation (18) will be considered, whereby there is feed-forward action specific to $D_i$. The original system after such control can be represented as:

$$\left\{\begin{array}{l}\dot{X}=F\left(X\right)+G\left(X\right)b\left(X\right)v+G\left(X\right)a\left(X\right)+\left(G\left(X\right)\beta \left(X\right)+\lambda \left(X\right)\right)D_i\\ y=H\left(X\right)\end{array}\right.$$

(19)

Consequently, the initial $(q-1)$ state equations under the Byrnes–Isidori form appear similarly to the equations derived for an undisturbed model. However:

$$y^{\left(q\right)}\left(t\right)=L_{T1}^{q}H\left(X\right)+L_{T_2}{L}_F^{q-1}H\left(X\right)D_i$$

(20)

where $T_1=F+G\left(a+bv\right)$ and $T_2=G\beta +\lambda$

$$\begin{array}{ll}{L}_{T_2}{L}_F^{q-1}H\left(X\right)& =L_G{L}_F^{q-1}H\left(X\right)\beta \left(X\right)+L_{\lambda }{L}_F^{q-1}H\left(X\right)\\ & ={\displaystyle \sum _{k=0}^{q-1}{\mathsf{\Pi }}_k^i{X}^{\left[k\right]}}\beta \left(X\right)+{\displaystyle \sum _{s=0}^{q-1}{J}_s^p{X}^{\left[s\right]}}=0\end{array}$$

(21)

where ${\mathsf{\Pi }}_k^l={\displaystyle \sum _{i=0}^k{\mathsf{\Pi }}_{k-i+l}^{q-1}}{V}^{\left(k-i+1\right)}\left(G_{l^i}\otimes I_{n^{\left(k-l\right)}}\right)$ and $J_s^p={\displaystyle \sum _{k=0}^s{\mathsf{\Lambda }}_{s-k+1}^{q-1}{V}^{\left(s-k+1\right)}\left({\lambda }_{p^k}\otimes I_{n^{\left(p-k\right)}}\right)}$.

Next, if $y\left(t\right)$ is not dependent on $D_i$, and the input $U$ should be defined so that:

$$y^{\left(q\right)}\left(t\right)=\dot{Z_q}=v,$$

(22)

The function of decoupling $\beta \left(X\right)$ is chosen as:

$$\beta \left(X\right)=-\frac{{\displaystyle \sum _{s=0}^{q-1}{J}_s^p{X}^{\left[s\right]}}}{{\displaystyle \sum _{k=0}^{q-1}{\mathsf{\Pi }}_k^l{X}^{\left[k\right]}}}$$

(23)

wherein matrixes $J_i^p$ and ${\mathsf{\Pi }}_k^l$ are represented in Equation (21).

Lemma 4.

If$C_i<q$the control input is obtained by [38]:

$$U=a\left(X\right)+b\left(X\right)v+\beta \left(X\right)D_i$$

(24)

• where$\left\{\begin{array}{ll}a\left(X\right)={\displaystyle \sum _{i=1}}{a}_i{X}^{\left[i\right]},& a_i={\mathsf{\Pi }}_0^{-1}\left[{\mathsf{\Lambda }}_i-{\displaystyle \sum _{p=1}^{i-1}{\mathsf{\Pi }}_{i-p}}\otimes a_p\right]\\ b\left(X\right)={\displaystyle \sum _{j=1}}{b}_j{X}^{\left[j\right]},& b_j=-{\mathsf{\Pi }}_0^{-1}{\displaystyle \sum _{p=1}^{i-1}{\mathsf{\Pi }}_{i-p}}\otimes b_p\\ \beta \left(X\right)=-\frac{{\displaystyle \sum _{k=0}^{q-c_i}{\displaystyle \sum _{l\ge 0}{\mathsf{\Psi }}_l^i}}}{{\displaystyle \sum _{k=0}^{q-1}{\mathsf{\Pi }}_k^l{X}^{\left[k\right]}}}& \end{array}\right.$
• where:${\mathsf{\Pi }}_k^l={\displaystyle \sum _{i=0}^k{\mathsf{\Pi }}_{k-i+1}^{q-1}{V}^{\left(k-i+1\right)}\left(G_{l^i}\otimes I_{n^{\left(k-l\right)}}\right)}$and$\left\{\begin{array}{l}{\mathsf{\Psi }}_l^0={\Delta }_l\\ {\mathsf{\Psi }}_l^i={\displaystyle \sum _{j=1}^l{\mathsf{\Psi }}_{l-j+1}^{i-1}{V}^{\left(l-j+1\right)}\left(F_j\otimes I_{n^{\left(l-j\right)}}\right)}\end{array}\right.$.

Proof. 

In the case where $C_i<q$, the disturbance has a higher impact on the output compared to the control input. It is necessary to take “anticipative action” to fulfill disturbance-rejection.

The control rule specified in Equation (18) is considered since the order of disturbance appearance is the $C_i$ derivative corresponding to the output. It is established that:

$$Z_2(t)=y^{\left(1\right)}(t)=L_{T}H\left(X\right)+\beta \left(X\right)D_i{L}_{G}H\left(X\right)+L_{\lambda }H\left(X\right)D_i$$

(25)

For $C_i>1$, one has:

$$Z_3\left(t\right)=y^{\left(2\right)}\left(t\right)=L_T^{}H\left(X\right)+L_{\lambda }{L}_{F}H\left(X\right)D_i+\beta \left(X\right)D_i{L}_G{L}_{F}H\left(X\right)$$

(26)

For $C_i>2$, the previous Equation (26) is rewritten as:

$$Z_3\left(t\right)=y^2\left(t\right)=L_F^{2}H\left(X\right)={\displaystyle \sum _{l\ge 1}^{}{\mathsf{\Lambda }}_l^2{X}^{\left[l\right]}},$$

(27)

Stepping forward to:

$$y^{\left(C_i\right)}\left(t\right)=L_T^{}{L}_F^{C_i-1}H\left(X\right)+L_{\lambda }{L}_F^{C_i-1}H\left(X\right)D_i+\beta \left(X\right)D_i{L}_G{L}_F^{C_i-1}H\left(X\right)$$

(28)

and seeing that $q>C_i$, one has:

$$y^{\left(C_i\right)}\left(t\right)=L_F^{C_i}H\left(X\right)+L_{\lambda }{L}_F^{C_i-1}H\left(X\right)D_i,$$

(29)

Then,

$$\begin{array}{ll}{y}^{\left(C_i+1\right)}\left(t\right)& =L_T^{}{L}_F^{C_i}H\left(X\right)+\beta \left(X\right)D_i{L}_G{L}_F^{C_i}H\left(X\right)+L_{\lambda }{L}_F^{C_i}H\left(X\right)D_i\\ & +\frac{d}{dt}\left(L_{\lambda }{L}_F^{C_i-1}H\left(X\right)D_i\right)\end{array}$$

(30)

In the case where $q>C_i+1$, the computation is repeated until the $q^{th}$ derivative corresponding to the output is reached; the following expression results:

$$\begin{array}{ll}{y}^{\left(q\right)}\left(t\right)& =L_F^{q}H\left(X\right)+a\left(X\right)L_G{L}_F^{q-1}H\left(X\right)\\ & +\beta \left(X\right)D_i{L}_G{L}_F^{q-1}H\left(X\right)+L_{\lambda }{L}_F^{q-1}H\left(X\right)D_i\\ & +\frac{d}{dt}\left(L_{\lambda }{L}_F^{q-2}H\left(X\right)D_i\right)+\dots +\frac{d^{q-C_i}}{d{t}^{q-C_i}}\left(L_{\lambda }{L}_F^{C_i-1}H\left(X\right)D_i\right)\end{array}$$

(31)

Then,

$$y^{\left(q\right)}\left(t\right)=L_T{L}_F^{q-1}H\left(X\right)+\beta \left(X\right)L_G{L}_F^{q-1}H\left(X\right)D_i+{\displaystyle \sum _{k=0}^{q-C_i}\frac{d^k}{d{t}^k}}\left(L_{\lambda }{L}_F^{q-k-1}H\left(X\right)D_i\right)$$

(32)

which gives:

$$y^{\left(q\right)}\left(t\right)={\displaystyle \sum _{k\ge 0}{O}_k^s{X}^{\left[k\right]}}+\beta \left(X\right)D_i{\displaystyle \sum _{k=0}^{q-1}{\mathsf{\Pi }}_k^l{X}^{\left[k\right]}}+{\displaystyle \sum _{k=0}^{q-c_i}\frac{d^k}{d{t}^k}\left(D_i{\displaystyle \sum _{p\ge 0}{\Delta }_p^i{X}^{\left[p\right]}}\right)}$$

(33)

where $O_s^k={\displaystyle \sum _{l=0}^k{\mathsf{\Lambda }}_{k-l+1}^{q-1}}{V}^{\left(k-l+1\right)}\left(T_{s^i}\otimes I_{n^{\left(k-l\right)}}\right)$, and ${\Delta }_p^i={\displaystyle \sum _{l=0}^p{\Delta }_{p-l+1}^{q-p-l}{V}^{\left(p-l+1\right)}}\left({\lambda }_{i^l}\otimes I_{n^{\left(p-l\right)}}\right)$.

The decoupling of the output and class $\zeta$ disturbance $D_i$ is ensured using:

$$\beta \left(X\right)=-\frac{{\displaystyle \sum _{k=0}^{q-c_i}{\displaystyle \sum _{l\ge 0}{\mathsf{\Psi }}_l^i}}}{{\displaystyle \sum _{k=0}^{q-1}{\mathsf{\Pi }}_k^l{X}^{\left[k\right]}}}$$

(34)

where $\left\{\begin{array}{l}{\mathsf{\Psi }}_l^0={\Delta }_l\\ {\mathsf{\Psi }}_l^i={\displaystyle \sum _{j=1}^l{\mathsf{\Psi }}_{l-j+1}^{i-1}{V}^{\left(l-j+1\right)}\left(F_j\otimes I_{n^{\left(l-j\right)}}\right)}\end{array}\right.$.

The flowchart given in Figure 1 illustrates the different cases related to both values of local relative degree $q$ and disturbance relative degree $C_i$.

The requirement is that the output $y\left(t\right)$ corresponds to a specific reference trajectory. Using the state variable transformation [6], the manipulated variable $U$ can be described as:

$$U=\frac{-L_F^{q}H\left(X\right)+v}{L_G{L}_F^{q-1}H\left(X\right)}+\beta \left(X\right)$$

(35)

This last equation is defined in the polynomial form by:

$$\left\{\begin{array}{l}\begin{array}{ll}U& =-\left[\frac{{\displaystyle \sum _{i=1}^q{\mathsf{\Lambda }}_l^i{X}^{\left[i\right]}}+K{\displaystyle \sum _{k=1}^q{\mathsf{\Gamma }}_k{X}^{\left[k\right]}}}{{\displaystyle \sum _{k=0}^q{\mathsf{\Pi }}_k^l{X}^{\left[k\right]}}}\right]+\beta \left(X\right)\\ & ={\displaystyle \sum _{i=1}{a}_i{X}^{\left[i\right]}}+{\displaystyle \sum _{j=1}{\mu }_i{X}^{\left[i\right]}}+\beta \left(X\right)\end{array}\\ v=-K^T\mathsf{\Gamma }\left(X\right)=-K{\displaystyle \sum _{k=1}^q{\mathsf{\Gamma }}_k{X}^{\left[k\right]}},\hspace{1em}\hspace{1em}{\mathsf{\Gamma }}_q=1\end{array}\right.$$

(36)

• where $\begin{array}{l}\left\{\begin{array}{l}{\mu }_1=\left({\mathsf{\Pi }}_0^{-1}\right)K{T}_1\\ ⋮\\ {\mu }_j={\mathsf{\Pi }}_0^{-1}\left[K{T}_j-{\displaystyle \sum _{p=1}^{j-1}\left({\mathsf{\Pi }}_{j-p}\otimes {\mu }_p\right)}\right]\end{array}\right.\end{array}$.
• where $v$ denotes a new reference varying set point that maybe computed to provide a designed-equivalent linear model with specific eigenvalues sets.

One challenge concerning this control technique is that only local robustness can be ensured. It should be noted that both modeling faults and parameter unpredictability are not accounted for at this point. The assumption is the nonlinear transformation is acknowledged in its exact form and that the entirety of the states is available. It is indicated that this very method produces globally robust output under parametric uncertainty and disturbance if it is integrated with the sliding mode formalism [40].

The emphasis is on solving the I/O FBL problem when there are undetermined states and disturbances. The upcoming section contains two control techniques that integrate this method and the SMC technique, thereby producing a highly robust output.

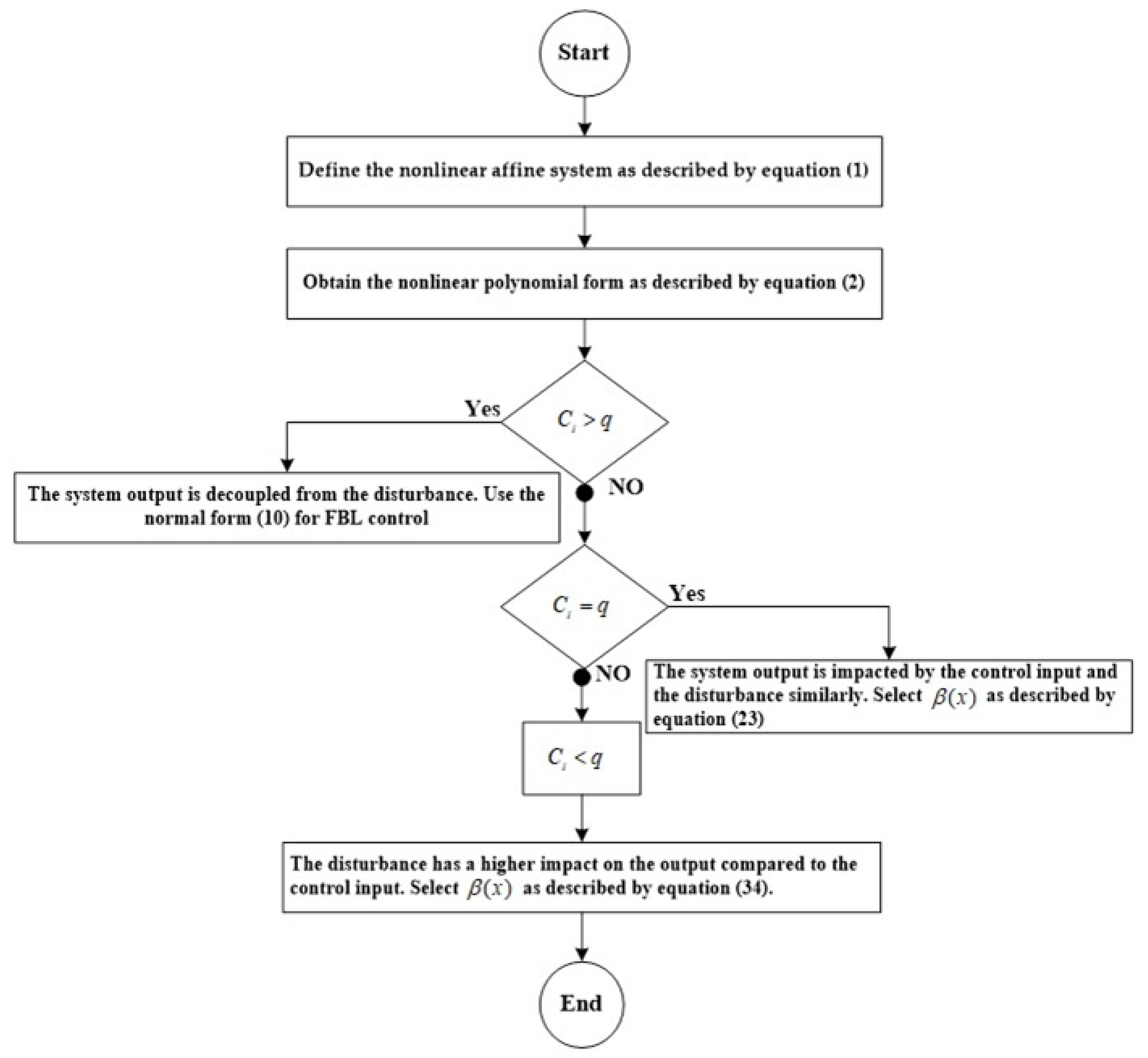
2.2. Analytical Design for the SMC and I/O FBL Control Technique

The SMC technique is an application of the relatively general variable structure control (VSC) technique that was first researched by [33]. This technique is interesting, especially because it can handle time-varying nonlinear systems and can deal with disturbances and uncertainties directly. Furthermore, it may facilitate the production of flexible control systems.

VSC systems comprise controls whose structure can be changed, i.e., movement among the elements of a group comprising continuous feasible functions corresponding to the state of the system. The design problem concerns a specific choice of the factors corresponding to every structure and specifying the travel logic. The ability to integrate useful characteristics pertaining to the structure is a suitable tradeoff for complexity.

Furthermore, a dynamic structure system can have characteristics, unlike individual structures. Hence, the sliding mode control approach is defined as such. Such control systems have been cemented by the efforts presented in [32].

The SMC process requires the definition of a sliding structure $P\left(t\right)$, which is typically locally asymptotically stable and linear time-varying; it is required that the sliding surface should be associated with the problem. The objective is to get to this surface and be present (slide) on the same. In the context of nonlinear systems having the Byrnes–Isidori standard form, the surface $P\left(t\right)$ is selected as a function that acts on a specific error variable:

$$P\left(t\right)={\left(d/dt+\theta \right)}^{q-1}E\left(t\right)$$

(37)

Here, $\theta$ denotes the bandwidth corresponding to error dynamics, representing system performance on $P\left(t\right)$. In the case where the process is not evolving on the sliding area $P\left(t\right)$, there must be a constraint that makes the system dynamics move to reach $P\left(t\right)$.

Furthermore, referred to as the reaching condition or the attractiveness equation, it may be selected to set the dynamics corresponding to the switching function directly. The goal is met under the conditions specified by the reaching law technique [8,9]. Consider the joining constraint seen as constant rate law and given by:

$$\dot{P}\le \vartheta {\left|P\right|}^{\rho }\mathrm{sgn}P$$

(38)

It can then be asserted that the system is expected to take a finite time to reach the surface $P\left(t\right)$ and move along it. This indicates that at a bandwidth of the variable, $\theta$ the error function $E\left(t\right)$ is close to zero.

If the objective is to integrate I/O FBL with SMC, the surface definition comprises a stable linear operator having an order $q-1$:

$$P={\displaystyle \sum _{k=0}^{q-1}{\displaystyle \sum _{i=0}^k{\mathsf{\Gamma }}_k{E}^{\left(i+1\right)}}}$$

(39)

$${\mathsf{\Gamma }}_{q-1}=1$$

From Equations (37) and (38), the altered control input is acquired as:

$$U=-\frac{1}{{\displaystyle \sum _{k=0}^{q-1}{\mathsf{\Pi }}_k^l{X}^{\left[l\right]}}}\left[\begin{array}{l}{\displaystyle \sum _{i=0}^q{\mathsf{\Lambda }}_l^i{X}^{\left[i\right]}}-\frac{d^q{y}_d}{d{t}_q}{\mathsf{\Gamma }}_k{\displaystyle \sum _{i=0}^q{\mathsf{\Lambda }}_l^i{X}^{\left[i\right]}}\\ -{\displaystyle \sum _{k=0}^q{\mathsf{\Gamma }}_k\frac{d^k{y}_d}{d{t}_k}-\vartheta {\left|P\right|}^{\rho }\mathrm{sgn}P}\end{array}\right]$$

(40)

The association between the SMC technique and I/O FBL is specified in Equation (40) under the condition where the error dynamics corresponding to the sliding surface are linear and time-invariant.

Sliding mode, in its original form, demonstrates chattering corresponding to the control signal, which is inadmissible for a majority of industrial applications. Some techniques help reduce chattering [8,9]. For example, the control signal can be smoothened by regulating the parameters $\vartheta$ and $\rho$ corresponding to Equation (38).

3. Trajectory Tracking Control of a Nonlinear Reactor: A Case Study

3.1. A Preliminary Simulation Analysis of the I/O FBL Control Design

As previously investigated by [40,41], the dimensionless modeling equations for a CSTR were considered in which an irreversible, first-order, exothermic reaction occurs:

$$\left\{\begin{array}{l}\dot{X_1}=-X_1+Da(1-X_1)\exp \left(\frac{X_2}{\left(\frac{X_2}{\sigma }\right)+1}\right)-D_2\\ \dot{X_2}=-X_2+T_{r}Da(1-X_1)\exp \left(\frac{X_2}{\left(\frac{X_2}{\sigma }\right)+1}\right)-\delta \left(X_2-X_{2c}\right)+\delta U+D_1\end{array}\right.$$

(41)

$D_2$ and $D_1$ refer to the disturbances pertaining to the concentration and inlet temperature, respectively. Reference [41] can be referred to for the original nomenclature. These disturbances were considered as steps.

Table 1. Dimensionless parameters for the CSTR model.

Description	Parameters
Activation energy	$\sigma =E/R{T}_0$
Adiabatic temperature rise	$T_r=\left(-\Delta H\right)c_{A{f}_0}/Q{c}_p{T}_{f_0}$
Damkohler number	$Da=k_0\exp \left(-\gamma V\right)/F_0$
Heat transfer coefficient	$\delta =hA/Q{c}_p{F}_0$
Dimensionless time	$t=t^{\prime }\left(F_0/V\right)$
Dimensionless conception	$X_1=\left(c_{A{f}_0}-c_A\right)/c_{A{f}_0}$
Dimensionless temperature	$X_2=\left(T-T_{f_0}\right)/T_{f_0}$
Dimensionless control input	$U=\left(T_c-T_{c_0}\right)/T_{f_0}$
Feed temperature disturbance	$D_1=\left(T_f-T_{f_0}\right)/T_{f_0}$
Feed composition disturbance	$D_2=\left(c_{Af}-c_{A{f}_0}\right)/c_{A{f}_0}$

lists out this system’s dimensionless parameters.

For the following set of the CSTR parameters: $T_r=8$, $\rho =0,3$, $\sigma =20$, $Da=0.078$ and $X_{2c}=0$, the process displays several stable and unstable steady states as:

• First stable equilibrium operating zone: ${\left(X_1,X_2\right)}_A=\left(0.14,0.89\right)$;
• Unstable equilibrium operating zone: ${\left(X_1,X_2\right)}_B=\left(0.447,2.75\right)$;
• Second Stable equilibrium operating zone: ${\left(X_1,X_2\right)}_C=\left(0.765,4.704\right)$.

The objective entails the development of a control input allowing the CSTR desired output to exhibit acceptable reference output trajectory tracking as well as disturbance elimination properties. Previously, [42] studied the control of the CSTR via feedback linearization that employed the concentration of the product as the available output. As the CSTR output, in this work, the temperature variable is investigated for two main reasons. First, industrial environments typically lack reliable concentration measurements, and second, the maximum admissible temperature is usually limited to avoid the occurrence of secondary reactions. Due to these constraints, the unstable equilibrium point is considered to conduct safe operating actions under control:

$$y=H\left(X\right)=X_2$$

(42)

For the selected output, the following parameters numerical values are considered $q=1$, $C_2=2$, and $C_1=1$. Therefore, the control input that allows I/O FBL of the system from the I/O point of view as well as allows decoupling of the output from measurable disturbances can be defined as:

$$U=\frac{-{\displaystyle \sum _{l\ge 1}{\mathsf{\Lambda }}_l^1{X}^{\left[i\right]}}-{\mathsf{\Gamma }}_1{\displaystyle \sum _{i=1}^n{H}_i{X}^{\left[i\right]}}+v}{{\displaystyle \sum _{k\ge 1}{\mathsf{\Pi }}_k^l{X}^{\left[k\right]}}}+\frac{{\displaystyle \sum _{k\ge 1}{J}_k^l{X}^{\left[k\right]}}}{{\displaystyle \sum _{k\ge 1}{\mathsf{\Pi }}_k^l{X}^{\left[k\right]}}}{D}_1$$

(43)

Substituting the Lie derivatives and considering the compensation for original settings because of the presence of unobservable ZD, Equation (43) gives:

$$U=\left[X_2-T_{r}Da\left(1-X_1\right)\exp \left(X_2/\left(\left(X_2/\sigma \right)+1\right)\right)+\delta X_2-y_d^{\left(1\right)}-{\mathsf{\Gamma }}_1\left(X_2-y_d\right)-B_1\right]{\delta }^{-1}$$

(44)

Since the ZD was seen as a minimum phase, confirmation of the asymptotic stability assumption is done, and thus, this method can be used.

In order to employ the state compensator provided in Equation (44), measurements regarding the system variable states are required. Particularly, the concentration needs to be known for the I/O FBL control law (44) to prevail. Since the possibility of concentration measurements has already been removed, this issue can be fixed by adopting a model-based control strategy. The CSTR model is employed as an observer in order to feed the control input with concentration value. It needs to be noted that the disturbance $D_2$ remains unmeasured.

In the beginning, this disturbance was taken into account for the process but not considered in the CSTR model. Moreover, since the output is already recognized, this information is employed for the model. The extraction of the manipulated variable to the plant ($U$) is established throughout the equivalent I/O FBL model to feed identical input to both Process and Model. Thus, the system and the model are impacted by bounds over the input naturally.

The I/O FBL approach had satisfactory performance when all the disturbances were measured and states are obtainable, provided that modeling errors and parameter uncertainty are not there. In order to offer a comparative analysis versus the case of a disturbed system, Figure 2 shows the system’s closed-loop stabilization in the neighborhood of the focused equilibrium point while employing the feedback control design (44). Should the measurable disturbance $D_1$ exist, modification is done only to the control law’s magnitude, while the output remains the same because of decoupling.

During startup, a predetermined trajectory needs to be adopted by the temperature towards the steady-state. This trajectory can generally be represented as:

$$y_d\left(t\right)=X_{2s}\left[1+k_1\exp \left(-k_{2}t\right)\right]$$

(45)

Here, $k_2$ and $k_1$ rely on real plant limitations and $X_{2s}$ represents the anticipated steady-state features. Figure 3 shows the CSTR state variables dynamics obtained for several values of $k_2$, when there are no disturbances.

Now, a 10% step disturbance is taken into account for the feed concentration $D_2$. At first, the system would tend to stray away from the equilibrium, but later, when the disturbance is gone, it proceeds to the steady state caused by the action of the controller. [38] contest there is no need to measure this disturbance, at most when all the CSTR states variables have become measurable.

Nevertheless, referring to this case study, the info on the disturbance $D_2$ is not entirely extant in the model variables since the concentration measurement has not been done. Subsequently, it is not possible to decouple this unmeasured disturbance without properly estimating the value of the concentration. This later condition becomes more complex when $D_2$ remains for a long time, which commits the system steady state to move towards another one (Figure 4).

To better interpret the problem, let a random disturbance be injected into the CSTR model. This later disturbance was considered for the process simulation, nonetheless, ignored in the CSTR control model calculation.

The result of this study is illustrated in Figure 5 and Figure 6 by the following figures:

It is obvious that the disturbance hardly affects the state variables and the control input dynamics. Equally important when implementing the SMC, the CSTR variables dynamics are largely improved. However, the chattering appears and affects the temperature dynamics, which is not accepted in terms of chemical process constraints.

The investigated control problem in this work is similar to the case of the uncertainty modeling problem. As stated in Section 2, plant/model inconsistency is a substantial restriction in the use of I/O FBL control methods since the controller design is attained based on the plant modeling outcomes [43,44]. Therefore, if the synthesized model is deemed not accurate, the system would not be linearized by the control law in the expected sense. However, analytical SMC combined with I/O FBL is expected to provide more robust results.

3.2. Second Simulation Analysis: Implementation of the Analytical SMC and I/O FBL Control Design

The aim is to ensure a perfect tracking between the CSTR output $y\left(t\right)$ and the reference desired input $y_d\left(t\right)$ even in the occurrence of the disturbance $D_2$. Next, after the aforementioned SMC method wherein $q=1$, the designed sliding surface is described by:

$$S\left(t\right)=y_d\left(t\right)-y\left(t\right)$$

(46)

By using the reaching law as provided in Equation (38), the control input gives:

$$U=\left[\begin{array}{l}{X}_2-T_{r}Da\left(1-X_1\right)\exp \left(X_2/\left(X_2/\sigma \right)+1\right)+\delta X_2-y_d^{\left(1\right)}\\ -{\mathsf{\Gamma }}_1\left(X_2-y_d\right)-D_1+\vartheta {\left|S\right|}^{\rho }\mathrm{sgn}\left(X_2-y_d\right)\end{array}\right]{\delta }^{-1}$$

(47)

Figure 7 displays the outcomes attained for several values of $D_2$, $\vartheta =0.5$, and $\rho =1$. The control input variable is not steady for all disturbance values. For $\rho =0.52$ and $\vartheta =0.5$, the chattering is suppressed (Figure 8).

The output was found to be near the desired value, thus preserving stability as well as representing better outcome robustness. Thus, complete elimination of the disturbing parameter $D_2$ did not happen because the model is incorrect. Thus, the computed value pertaining to the concentration, which also influences the SMC through the reaching law, remains incorrect. Consequently, some uncertainty could also be found associated with the derivative pertaining to the switching surface.

Another problem is that even when the parameters $\rho$ and $\vartheta$ are adjusted in an accurate manner, chattering could still impact the system. Moreover, the greater the chattering is reduced, the more the tracking error among $y\left(t\right)$ and $y_d\left(t\right)$ increases. To find the optimal controller gains pertaining to these above variables, one must reduce the length gap to the sliding surface, which is a delicate control task.

To conclude the above results, the concentration observer needs to be enhanced to achieve safe operation and good disturbance-rejection.

The stability and robustness characteristics are gained when the SMC loop is added to the I/O FBL controller, which made us contemplate applying SMC for determining the immeasurable disturbance.

To enhance the performance of the studied control design, a heuristic optimization technique combined with fuzzy logic will be implemented with the analytical SMC-based I/O FBL. The main objective is to preserve a high-quality steady-state regime while reducing the chattering phenomena under severe output desired trajectory dynamics.

4. A Fuzzy PSO-Based Control Design

4.1. Preliminaries on PSO

The PSO algorithm is evolutionary, and it uses several candidate solutions to produce the optimal solution fitting a specific problem. PSO is a stochastic optimization technique, and the changing behavior of social animals in swarms influences its concept. The technique models such social behaviors using equations to help the “particles” while they move. There are three aspects the influence particle movement: cognitive, social, and inertia components [45,46,47,48]. Each of these components reflects part of the equation. PSO has the advantage of being effective on a wide variety of problems without the user having to modify the basic structure algorithm. The literature specifies that PSO is among the highly efficient techniques employed for finding solutions to non-smooth global optimization problems. The primary benefits of the technique are specified below:

This technique does not rely on derivatives, unlike similar meta-heuristic optimization techniques.

• The literature specifies that PSO is a highly efficient technique employed to find solutions to non-smooth global optimization problems. The main benefits of the technique are listed below. This technique does not rely on derivatives, unlike similar meta-heuristic optimization techniques.
• The coding and theory corresponding to this method are straightforward, unlike other heuristic optimization techniques;
• It has considerably less sensitive to the aspects of the objective function, unlike traditionally used analytical and heuristic techniques;
• Unlike many heuristic optimization methods, PSO has relatively fewer parameters: inertia weight coefficient and acceleration coefficients. Furthermore, the parameters corresponding to the optimal solutions are relatively less sensitive compared to other heuristic methods;
• PSO is less contingent on the initial set of points compared to numerous evolutionary techniques; also, this algorithm has robust convergence characteristics;
• PSO-based techniques produce high-quality solutions at a lower time-cost but with better stability corresponding to the convergence aspects, as compared to other stochastic methods.

The PSO algorithm may be classified as an iterative (progressive movement towards the solution) technique. In contrast, stochastic techniques attempt to optimize the present solution by transitioning partially to other points following pre-specified rules to reach the desired solution ultimately [49].

There are prerequisites corresponding to PSO application: there should be a research space comprising particles associated with a cost function (also referred to as the objective function) that needs to be optimized. The algorithm is based on the fundamental that these particles must be moved in order to arrive at the optimal value [50,51,52]. All such particles are associated with:

• A set of defined coordinates specifying the position of the particle;
• Speed corresponding to the movement of the particle. There are several iterations when the particles have different positions. The characteristics evolve, considering the best position, neighbor position, and previous position. Such evolution of particles implies that several particles interact directly with a single particle, especially with the one having the optimal criteria.

A neighborhood where several particles interact with this particle directly, especially with the one having the most-optimal criteria. An optimization problem is associated with site quality in the search space being a function of the cost function corresponding to the point [53].

The choice of parameters of the PSO algorithm is imposed arbitrarily in which the number of particles. The decision values corresponding to parameters required to be assessed expressed in the form of the position vector corresponding to the i^th particle, as specified below:

$$X^{\left(i\right)}=\left[\begin{array}{c}{X}_1^{\left(i\right)}\\ X_2^{\left(i\right)}\end{array}\right], i\in \left\{1,\dots ,p\right\}$$

(48)

where $p$ denotes the swarm size (count of particles).

For each iteration k, the velocity corresponding to all the particles in the swarm is updated, while the positions are determined using the following set of equations

$$V_{k+1}^i=w_k{V}_k^i+R_1{L}_1\left(X_{pk}^{\left(i\right)}-X^i\left(k\right)\right)+R_2{L}_2\left(X_{gk}^{\left(i\right)}-X^i\left(k\right)\right)$$

(49)

$$X^i\left(k+1\right)=X^i\left(k\right)+V^i\left(k+1\right)$$

(50)

• $X^i\left(k\right)$ represents the present candidate solution comprising the position of the ith particle during the kth iteration, while $X^i\left(k+1\right)$ represents the new position of the particles;
• $V^i\left(k\right)$ and $V^i\left(k+1\right)$ represent the old and new velocities of the particles;
• $X_{pk}^{\left(i\right)}$ specifies the optimal position, also referred to as the “personnel best”, obtained in the past by the ith particle;
• $X_{gk}^{\left(i\right)}$ represents the ideal position corresponding to a particle’s neighbors and is called the global best;
• The $L_1$ and $L_2$ acceleration coefficients are generally equal and have values between 0 and 2. In order to achieve maximum acceleration $R_1$ and $R_2$ are random values generated at each iteration, they respect a uniform distribution;
• The number (k) of iterations is important information for the operation of PSO.

Finally, $w_k$ is inertia coefficient can be specified as:

$$w_k=w_{\max }-\left(\frac{w_{\max }-w_{\min }}{k_{\max }}\right)\times k$$

(51)

4.2. Computation of Fitness Function

The fitness function is the main operation, which should be conducted when implementing a PSO algorithm. Thus, the assessment of the particle quality is completed by utilizing the error between $y_d\left(t\right)$ and $y\left(t\right)$. Consider the following objective function (OF):

$$f={\displaystyle \underset{0}{\overset{\infty }{\int }}E{\left(t\right)}^2}dt$$

(52)

which should be minimized.

Considering the position $X^{\left(i\right)}$ for the ith particle, the procedure stated below may be utilized for assessing the fitness function for the ith particle.

4.3. Algorithm

• Activate the initial population: $X=X_0$;
  • For i = 1 up to the maximum number of populations, do:
  • For j = 1 until p do:
• Create the objective function for the particle “j” (or the individual “j”) defined by Equation (52);
• Obtain the polynomial system defined by Equation (2);
• Determine the function $\beta \left(X\right)$ defined by Equation (34);
• Calculate the control law defined by Equation (40);
• Evaluate the OF that should be minimized;
  • End of “j”
    • Classify the particles according to the above condition described by Equations (49) and (50).
  • End of “i”
• Return: $f_{\min }=\min \left\{{\displaystyle \underset{0}{\overset{\infty }{\int }}E{\left(t\right)}^2}dt\right\}$

4.4. Synthesis of the Fuzzy PSO Control

The Mamdani fuzzy inference system was employed for the enhancement of the control specified by Equation (40). This technique is beneficial because it has a straightforward implementation and has more comprehensive coverage concerning the variable-specific state models. The fuzzy-type inference is used for control systems because it facilitates smooth interpolation of the planned gains corresponding to the input state space. Thus, this fuzzy PSO controller essentially regulates the controller gain and offsets the undesirable nonlinearity that depends on the dynamic trajectory of the process.

The control variable fed to the plant is regulated in a way that there is fuzzy optimization pertaining to the SMC feedback gain while the system monitors the error dynamic and its first-order derivative. Then the optimization algorithm by PSO consists of adjusting the parameters of the fuzzy controller appurtenance function in order to improve its performance. The control strategy is illustrated in Figure 9.

The control of a given system is based on the use fuzzy controller. Fuzzy controller parameters are the membership functions exploited for Gaussian types for the input variables $E_i$ and $\Delta E_i$ also for the output variables. The selected membership functions are given by:

$$Gaussian\left(E_i,{\mathsf{\Theta }}_i,{\mathsf{\Omega }}_i\right)=e^{-\frac{1}{2}{\left(\frac{E_i-{\mathsf{\Theta }}_i}{{\mathsf{\Omega }}_i}\right)}^2}$$

(53)

$$Gaussian\left(\Delta E_i,{\mathsf{\Theta }}_i,{\mathsf{\Omega }}_i\right)=e^{-\frac{1}{2}{\left(\frac{\Delta E_i-{\mathsf{\Theta }}_i}{{\mathsf{\Omega }}_i}\right)}^2}$$

(54)

where ${\mathsf{\Theta }}_i$ is the center of the membership function and ${\mathsf{\Omega }}_i$ is the breadth of the membership function.

Unlike empirical control techniques, where controller gains are specified by process experts, fuzzy inference systems are designed to provide the control gains for the SMC while preserving its main features and structure. Each controlled gain is adjusted with an advanced stable and optimized system through PSO and fuzzy membership sets, which are well specified in Figure 10 and Figure 11. The fuzzy controller gains tuning rules are given in

Table 2. Fuzzy controller gains tuning rules.

$\dot{\mathit{E}}(\mathit{t})$
$E(t)$		NB	NM	NS	Z	PS	PM	PB
	NB	PB	PB	PB	PB	PM	PM	PM
	NM	PB	PB	PB	PM	PS	PS	PS
	NS	PM	PM	PM	PS	Z	Z	Z
	Z	PS	PS	PS	Z	NS	NS	NS
	PS	Z	Z	Z	NS	NM	NM	NM
	PM	NS	NS	NS	NM	NB	NB	NB
	PB	NM	NM	NM	NB	NB	NB	NB

.

These figures represent the membership functions of the controller, based on the tracking error and its derivative for the case of minimum phase plant characteristic.

The fuzzy PSO control strategy will be specified here. The formal description of the 9-step algorithm is as follows:

• Step 1: Activate all individuals;
• Step 2: Calculate the control gain defined by Equation (36);
• Step 3: Tune the regulator gains using the rules as demonstrated in the following table.
• Step 4: Calculate parameters of the Gaussian defined by Equations (53) and (54);
• Step 5: Apply the defuzzification formulas;
• Step 6: Calculate the objective function defined by Equation (50);
• Step 7: Update speed and position and iteration defined by Equation (49);
• Step 8: Update of $X_{pk}$ and $X_{gk}$ which are defined by Equation (48);
• Step 9: Go to step 2 to the stop criterion is met;
• Step 10: Determine the control $U$ defined by Equation (40);
• Step 11: Determine the fuzzy controller input expressed by:

  $$U_f=\frac{{\displaystyle \sum _{i=1}^N{\mu }_i{X}_i}}{{\displaystyle \sum _{i=1}^N{\mu }_i}}$$

  (55)
• Step 12: Calculate the control system defined by Equation (44).

4.5. Third Simulation Analysis: The Fuzzy Sliding Mode Controller Implementation

This part is dedicated to evaluating the performance of the designed PSO fuzzy control technique. A step change desired trajectory was considered. A second-order under-damped linear model was exploited to set the reference input for generating the desired trajectory $y_d$ as well as its first derivative ${\dot{y}}_d$:

$$y_d\left(t\right)=\left(1-\frac{\varsigma {\omega }_{n}t}{\sqrt{1-{\varsigma }^2}}\times \left(\varsigma \sin \left({\omega }_{n}dt\right)+\left(\sqrt{1-{\varsigma }^2}\right)\cos \left({\omega }_{n}dt\right)\right)\right)r\left(t\right)$$

(56)

The simulation parameters were specified as follows: ${\omega }_n=5rad/\min$ and $\varsigma =0.9$. The simulation illustrates in Figure 12.

For the PSO technique, the varying parameters $w_k$, $L_1$, and $L_2$ are considered as the crucial features that impact the algorithm convergence characteristics [54]. The steadiness between global examination and local searchability is controlled by the weight of inertia. While global exploration is preferred by a larger inertia weight, local searchability is preferred by a smaller weight of inertia.

The adopted parameters pertaining to the PSO algorithm are displayed in

Table 3. Parameters and settings of PSO algorithm.

Parameters	Values
Particle number	10
$L_1$	2
$L_2$	2
$R_1$ and $R_2$	Random
Iteration	20
$w_{\min }$	0.3
$w_{\max }$	1.1

.

Note that for the PSO algorithm, the simulations were repeats with other turning parameters, and each time, results are updated. Finally, it should be noted that the algorithm by PSO has been executed extensively. Figure 13 shows the process of minimizing the PSO coast function to determine the optimal fuzzy controller gains of the reactor system. Figure 14 illustrates the perfect tracking behavior improved SMC and Fuzzy PSO.

Figure 12 illustrates the tracking control performance and the impressive dynamic behavior of the designed strategy. Indeed, despite the severe step deviation on the desired reference input, the process output trajectory was under-damped with an attenuated rising time and settling. The steady-state accuracy of the response is quite satisfactory onward the reference trajectory alteration.

To assess the control scheme synthesized in this paper, a comparative analysis is established here to examine the performance of the fuzzy PSO regulator across the analytical SMC-based I/O FBL controller.

The outcomes of the simulation analysis are depicted in Figure 14 and Figure 15, which represent the system’s output dynamics as well as the resultant control inputs, respectively. Figure 12 illustrates the excellent dynamic performance of the advanced fuzzy logic SMC–I/O FBL controller evading attenuated chattering behavior. The synthesized control signal is represented in Figure 15. It appears that the excessive chattering dynamic is quite mitigated in assessment with the numerical simulation outcomes illustrated in Figure 15 for the several control inputs. Such achievement is justified by the significant additional benefit of the heuristic PSO fuzzy module implemented for the analytical SMC-based I/O FBL, where the controller gain settings are updated continuously. The synthesized scheme compensates for the uncertainties and unmeasurable external disturbances for the CSTR variables’ dynamics. The quantitative achievement of both regulators can be assessed by addressing the cumulative performance revealed in

Table 4. A comparative analysis.

Control Strategy	IAE	Control Effort	ISE	Maximum Overshoot
Fuzzy PSO	0.01	1152	0.000	0.11
SMC-based I/O FBL	0.15	1609	0.016	0.1

, which summarizes some main key control performance indicators once the tracking error convergence is achieved. Analyzing the results presented in Table 4, it easy to establish that besides ensuring swift steady-state requirements and asymptotical stabilization, the proposed fuzzy PSO scheme outperforms the analytical one in the selected key indicators. In fact, the steady-state error is significantly attenuated for the fuzzy PSO strategy, enabling augmented costs related to the control effort to be reduced in comparison to the analytical control method.

In this quantitative analysis, a fair assessment is performed to detail estimating the performance of the investigated control strategies. Besides the ISE performance indicator, the IAE index, which characterizes how close the dynamics are to the reference trajectory, is addressed as well. In Table 4, this evaluation is specified. The aim is to track the temperature trajectory of the CSTR in the occurrence of hard constrained setpoint variations as presented in [29,30]. The works were performed by designing those regulators and comparing them with results presented in [29]. The outcomes of the synthesized controllers have been analyzed based on (ISE), (IAE) and control effort criteria. The results clearly demonstrate that all investigated control schemes provide an acceptable achievement with respect to the hard constrained functional variations and fast-changing dynamics of the process temperature. This can be highlighted first in ensuring the asymptotic stability in the Lyapunov sense. Specifically, the robustness of the studied techniques in dealing with model uncertainties throughout the output tracking signal takes the emphasized point into account. The numerical values of the above-specified index are very comparable with an added value of saving energy costs. Still, fuzzy PSO SMC-based control structure provides better flexibility and accurate behavior in control action in comparison with peer approaches.

5. Conclusions

In this work, the I/O FBL method combined with the SMC technique was investigated in order to deal with control issues related to model parameter uncertainties and undetermined state disturbances under severe constraints.

The proposed analytical method provides better outcomes versus the I/O FBL alone. Nevertheless, complete decoupling of the desired output variable from the unmeasured disturbance could not be achieved.

The need to determine the exact value of the unmeasured state in order to define the manipulated control input for complete decoupling led to the implementation of advanced heuristic techniques to enhance the steady-state performance. In this respect, a novel and advanced nonlinear control strategy based on fuzzy logic combined with PSO has been developed. Using this approach, it was demonstrated that the tracking error could be made equal to zero. In spite of employing SMC, the undesirable chattering did not impact the system dynamics.

The designed scheme combines the state FBL technique to decouple the disturbance from the system output and an SMC technique to guarantee the robustness of the controller in addition to external disturbance-rejection, fast dynamic response and insensitivity to uncertainties in plant parameters and modeling. Moreover, to alleviate the SMC chattering, fuzzy logic was implemented. Indeed, fuzzy logic enables the tuning of the switching SMC gain, which guarantees the process stability and almost eliminates the effect of chattering. A PSO algorithm was applied to enhance the fuzzy logic control gain tuning, give more flexibility in adjusting the controller gains and reduce the steady-state error. As a result, the accuracy of the output trajectory tracking was significantly enhanced.

Future development work will focus on applying the proposed methodology in the discrete-time domain. Even though the control strategy made use of real-time application software, the effects of sampling period selection and process delays associated with the use of the control input were not specifically addressed in this work. Moreover, investigating the algorithm performance when exposed to constraints would be a promising research subject.