On the Use of Structured Prior Models for Bayesian Compressive Sensing of Modulated Signals

Abstract

The compressive sensing (CS) of mechanical signals is an emerging research topic for remote condition monitoring. The signals generated by machines are mostly periodic due to the rotating nature of its components. Often, these vibrations witness strong interactions among two or multiple rotating sources, leading to modulation phenomena. This paper is specifically concerned with the CS of this particular class of signals using a Bayesian approach. The main contribution of this paper is to consider the particular spectral structure of these signals through two families of hierarchical models. The first one adopts a block-sparse model that jointly estimates the sparse coefficients at identical or symmetrical positions around the carrier frequencies. The second is a spike-and-slab model where the spike component takes into account the symmetrical properties of the support of non-zero-coefficients in the spectrum. The resulting posterior distribution is approximated using a Gibbs sampler. Simulations show that considering the structure in the prior model yields better noise shrinkage and better reconstruction of small side-bands. Application to condition monitoring of a gearbox through CS of vibration signals highlights the good performance of the proposed models in reconstructing the signal, offering an accurate fault detection with relatively high compression rate.

1. Introduction

The condition monitoring (CM) of machines consists in observing the trend of physical quantities and identifying the health state of mechanical components in order to avoid system failures. Most CM systems in the industrial field are based on the analysis of the vibration signal, which is easy to acquire and provides complete information on the condition of the machines. In modern industries, online CM systems use cables with exorbitant costs and a huge footprint. CM systems that are based on wireless sensors, known as remote CM, are a new alternative and they offer easy installation and low power consumption [1]. However, remote CM based on the analysis of vibration signals has limitations. Indeed, the vibration signals are acquired at a high sampling frequency. That of gears, bearings, or reactor blades in aeronautics can reach tens of kilohertz, leading to an enormous amount of data. The challenge for remote monitoring is managing the transmission of these volumes of data.Therefore, there is a need to reduce the size of the samples that are acquired while preserving the useful information. In this context, an alternative to the sampling theory has recently emerged, which shows that data can be recovered from far fewer measurements than what the Shannon–Nyquist theorem states. This new theory, coined compressive sensing (CS) introduced in [2,3], relies on the sparsity or compressibility of data. This technique was applied in several fields, such as the medical, communication, presence detection, electromagnetic radiation, and structural health monitoring fields [4,5,6,7,8,9], respectively.

The theory of CS is a rising branch of signal processing, whose primary goal is to achieve compression during the sensing procedure, and to reconstruct the signal using just a small set of randomly acquired samples. Therefore, this theory concerns not only the reconstruction (decompression) of the signal, but also its sensing. The CS approach uses the sparse characteristic of the observation for the reconstruction process. It results in a representation of the observation in a specific dictionary, which is the set of elementary signals-or atoms-used to decompose the signal. The fundamental idea of the CS is that the observation must be sparse (or compressible) enough in the corresponding dictionary to reconstruct all important information. The choice of the dictionary that sparsifies the observation is one of the basic problems in the CS approach [10]. The Fourier dictionary, known as an orthogonal basis, is the most and probably the first used dictionary for periodic signals. In fact, the spectrum of a multi-sine waveform can be represented by a complex-weighted spike train. This means that sinusoidal components constructing the signal of interest are sparse in the Fourier transform basis [11,12]. Here, it is useful to report that this paper deals with the CS of smoothly modulated signals. These signals have a well known structure in the Fourier domain. The Fourier spectrum of such a signal only contains a family of harmonics (made up of carriers) around which sidebands appear. All the rest of the spectrum is zero or not significant. Such a representation is well sparse and offers an ideal basis for describing smoothly modulated signals. This is the reason why the Fourier basis will be exploited in the rest of this paper.

The problem of CS reconstruction, in a particular dictionary, is a linear inverse problem that is described by an underdetermined system of equation [13]. Two categories of approaches are used to solve the CS reconstruction problem. In the first category, the reconstruction problem is modeled as a minimization problem searching for the sparsest signal that yields the observations. One popular sparsity promoting penalization function is the ${\ell }^0$ pseudo-norm. The latter corresponds to the number of non-zero coefficients in the sparse domain. The solution to such an optimization problem is known to be computationally intractable or NP-Hard, so it is more realistic to solve a computationally tractable alternative. Greedy iterative methods attempt to find approximations to this minimization problems [14] like matching pursuit [15], orthogonal matching pursuit [16], and compressive sampling matching pursuit [17]. These algorithms are known to have low computational complexity, but they have the drawback of providing a large reconstruction error. Another attempt is based on convex optimization that relaxes the ${\ell }^0$ loss by using the ${\ell }^1$-norm [18], then solving the problem using the basis pursuit [19], linear programming [20], gradient projection sparse reconstruction [21], or shrinkage and selection operators [22].The second category covers the Bayesian methods. Unlike the first category, the Bayesian approaches treats unknown signal and model parameters as random variables by assigning them probability distributions and provides an entire posterior distribution [23,24].The latter can be used not only to compute point estimates, but also to provide additional information, such as credible regions. It has also shown that Bayesian methods outperform certain deterministic methods [25].

Other than the sparsity of the signal, structures on the sparse patterns of the signal have also been used as an additional prior in numerous works, in which the signal is described as a finite set of sparse vectors [26]. Those vectors share a common cluster (zero or non-zero coefficients) in the chosen dictionary, and this allows for considering the signal as the so-called block sparse structured signal [27]. The block sparse structure naturally arises for example when dealing with multi-band signal [28,29], measurement of gene expression [30], or magnetoencephalography signal [31]. Taking the block sparse structure in the signal into account reduces the number of required compressed measurement samples and enhances the recovery efficiency [32].Taking advantage of the signal structure, Bayesian approaches have been proposed to treat signals with block-sparse structure [33,34].

This paper concerns the block sparse Bayesian CS framework for the vibration data recovery in the context of mechanical condition monitoring. Vibration-based Condition monitoring is the process of observing the evolution of the vibrations that are generated by a mechanical component, aiming to identify a significant change that can be correlated with the health state of that component. The reason why CS is beneficial in such applications is that vibration data analysis is usually performed while using a relatively high sampling frequency. This results in a huge amount of data to be stored and transmitted. For example, a health monitoring system installed on a Vestas V47 wind turbine measures 2 terabytes per month [35]. In addition, such acquisition systems require high power consumption which can significantly affect the autonomy of the condition monitoring system. The latter point can be problematic in many applications, such as offshore wind turbines and airplanes remote monitoring. The use of CS for industrial signals is quite recent. Some works have been done on the condition monitoring of machine tools, structures [36,37], bearings, and gears [38,39,40] using traditional CS reconstruction algorithms. Few works have attached importance to the use of specific structures of the signal [39,41].

A gearbox is the monitored component addressed in this paper, being frequently used in mechanical systems to transmit and convert speed and torque into different part of the power transmission chain. The vibration signal that is generated by such a component is well studied in the literature and known from a signal point of view [42]. The CS of the gearbox vibration signal has already been addressed in previous works, since it is sparse in Fourier domain, Wigner-Ville distribution [38], and wavelet domain [43]. However, none of these works exploit the natural sparse structure of those types of signals. In fact, the resulting vibration manifests through amplitude and frequency modulations of a periodic carrier. The periodicity of the carrier is the same as that of the meshing phenomenon and it can be computed through a simple kinematic study. The occurrence of a fault results in an increase in the modulation, whose period depends on the faulty element. In the Fourier domain, the signal turns to a set of harmonics located at the (known) meshing frequency and its integer multiple, with (unknown) sidebands (location) around these harmonic representing the modulation effect. This natural structure allows for describing the gearbox vibration signal by a set of sparse block structures. Indeed, in the spectrum domain, the modulations are quasi-symmetrical and they appear at the same location around the carrier. To our knowledge, there is no proposed models that take the symmetrical structure of the spectrum of smoothly modulated signals into account.

This paper investigates the reconstruction of smoothly modulated signals in a Bayesian framework by exploiting, for the first time, the structured support of their spectrum. This paper is organized, as follows. Section 2 exposes the proposed method with an insight in the vibration signals and their structures in spectrum domain. Section 3 presents an application on both simulated and real gearbox vibration signal to evaluate the performance of the proposed method. Section 4 concludes the paper.

2. Proposed Method

The main contribution of our work consists in designing prior models that take advantage of not only the sparsity property, but also the structured form of the spectrum of periodically modulated signals. We also propose a Gibbs sampler that offers an efficient sampling of all parameters of the resulting model. In this section, we first formulate the compressive sensing problem of periodically modulated signals. Subsequently, we propose a structure of the support of the target spectrum through hierarchical models and their relevance for gearbox signal analysis is addressed. Finally, we discuss the difficulties of the sampling step of the model parameters and propose a solution for efficient sampling.

2.1. Problem Formulation

This part starts with a brief review of the characteristics of gearbox signals and points out at the relevance of non-regular sampling model. Next, the problem is formulated under the Bayesian framework.

2.1.1. Technical Background

Gearboxes are perhaps the most known component where modulations phenomena are encountered. The diagnosis of gears is well established in the literature. It is known that the vibration of the gears is mainly generated by the contact between two teeth; which leads to a periodic signal at the meshing period of the teeth. According to the Fourier series theory, this translates into a set of harmonics associated with the meshing frequency and its integer multiples [44].

Often, gears are subject to manufacturing errors, leading to (i) a non-uniform spacing between the teeth and (ii) irregularities on the contact surface of the teeth. These create local vibratory events during the contact phase. Because of the rotating motion of the gear, each of these events will reproduce after each complete revolution of the same gear. These (slower) periodic events interact with the (fast) meshing phenomenon through periodic modulations. We distinguish two types of modulations, namely amplitude and phase modulations, generated by different physical phenomena. Periodic amplitude modulations are often due to an uneven distribution of the stiffness along the teeth surface. Phase modulations are often the result of a change in the meshing period, defining the contact duration between two meeting teeth, which can be physically associated with the change in the spacing among the teeth. Amplitude and phase modulation are well modeled in the literature and they are characterized in the spectral domain by lateral bands around the meshing frequencies, as illustrated by Figure 1 [45].

In the presence of a defect, like a tooth spall or pittings, the vibratory event is stronger and more impulsive, and so are the modulations, resulting in stronger and richer sidebands around the meshing frequency and its harmonics. This explains why the information on the gears health state is mainly contained in the modulations which are traditionally estimated thanks to a demodulation around the meshing frequency [45]. It is worth noting that periodic amplitude modulations result in a perfectly symmetrical sidebands, as opposed to periodic phase modulations. However, amplitude modulations are more dominant in gearbox vibration analysis; thus, still leading to an inner symmetry in the sidebands. This property will be integrated in the proposed hierarchical model of the propose Bayesian CS approach.

Eventually, it should be remembered that meshing phenomena are generally fast and their frequency is often very high. For example, the meshing frequency of the driving gear of an ARRIEL helicopter powerturbine gearbox would reach 16 kHz, which means that a sampling frequency of 200 kHz is needed to ’see’ the first five meshing harmonics. This explains why a compressive sensing approach is needed to reduce the amount of data.

2.1.2. Observation Model

Let $\mathbf{s}$ be the target periodically modulated signal. As previously pointed out, these signals manifest in the spectrum through a set of harmonic with sidebands, thus being perfectly sparse in the Fourier domain. Therefore, the Discrete Fourier Transform (DFT) is well suited to analyze these signals. Precisely, these harmonics are located at the carrier frequency and its integer multiples, with sidebands equally spaced by the modulation frequencies. The carrier frequency is assumed to be known a priori and it will be denoted by $f_c$, while the frequency locations of the modulating signal are unknown. This is commonly the case when the modulating signal consists of many sinusoids of unknown frequencies, such as in vibration-based condition monitoring of planetary gearboxes [46] or in complex drive-trains. In some rare cases, the machine kinematics may be unknown, and so is the meshing frequency. This particular case is out of the scope of the present paper. The proposed method aims at estimating the target signal $\mathbf{s}\in {\mathbb{R}}^N$ from a non-regular sub-sampled signal $\mathbf{y}\in {\mathbb{R}}^M$ with $M<<N$ (i.e., samples are not taken as equally spaced in time). The considered problem can be formulated, as follows

$$\mathbf{y}=\mathbf{H}{\mathbf{\Phi }}^{-1}\mathbf{x}+\omega$$

(1)

where $\mathbf{\Phi }$ is the normalized DFT ( ${\varphi }_{k,n}=\frac{1}{\sqrt{N}}exp(-i\pi (k-1)n/N)$, so that ${\mathbf{\Phi }}^{†}\mathbf{\Phi }={\mathbf{I}}_N$, where ${\mathbf{\Phi }}^{†}$ denotes the conjugate transpose of matrix $\mathbf{\Phi }$ and ${\mathbf{I}}_N$ is the identity matrix of size N), $\mathbf{H}\in {\mathbb{R}}^{M\times N}$ is the non-regular sampling matrix being formed with 0 and 1, $\mathbf{x}\in {\mathbb{C}}^N$ is the vector of sparse unknown Fourier coefficients to be estimated (i.e., $\mathbf{x}=\mathbf{Œ}\mathbf{s}$), and $\omega$ is an additive noise.

It should be mentioned that the sparsity hypothesis in the DFT basis may be altered due the spectral leakage for a short or/and non-stationary observation. The spectral CS problem under these conditions has been addressed in a large number of works (see [12] for an example). In this paper, we assume that the signal to be recovered is sufficiently long to ensure a good frequency precision and that the speed variations are sufficiently small to be neglected.

2.1.3. Bayesian Framework

The CS problem is considered through a Bayesian framework. This will offer not only an automatic recovery algorithm to compute point estimates, but also a full posterior distribution to compute additional information, such as credible bars. Furthermore, Bayesian approaches with sparsity-inducing priors offer a large flexibility via hierarchical models and require less restrictions when compared to standard approaches involving ${\ell }^0$ and ${\ell }^1$ penalty functions [47].

In the sequel, the coefficients of $\omega$ are assumed to be i.i.d Gaussian variables of unknown variance $\tau >0$. The observation distribution density is then given by

$$\mathrm{p}\left(\mathbf{y}\right|\mathbf{x},\tau )={\left(2\pi \tau \right)}^{-\frac{M}{2}}exp\left(-\frac{\parallel \mathbf{y}-\mathbf{H}{\mathbf{\Phi }}^{-1}{\mathbf{x}\parallel }^2}{2\tau }\right)$$

(2)

We aim at estimating $\tau$ jointly with $\mathbf{x}$. Hence, we assign a non-informative Jeffrey prior for $\tau$: $p\left(\tau \right)\propto {\tau }^{-1}$ [48].

The use of sparsity-favoring prior distributions is the core of Bayesian CS modeling. In this paper, we particularly consider hierarchical models, as they exhibit large flexibility to take the structures of sparse coefficients through latent variables into account. In this paper, we will consider two families of models, namely continuous hierarchical models and spike-and-slab models (see Appendix A, for a review of these families of models). In the following, we will discuss their extensions to take the structure of the target spectrum into account.

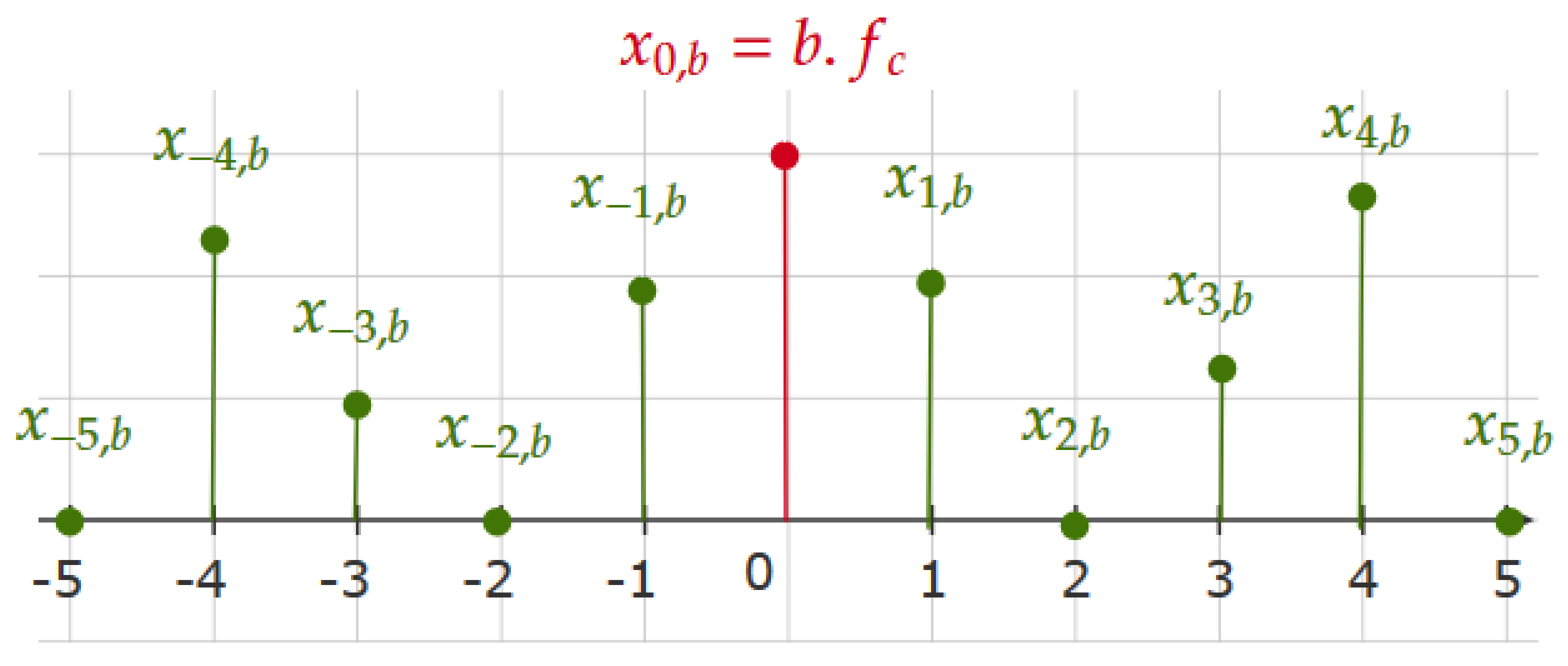
2.2. Structured Spectrum of Periodically Modulated Signals

Actually, the spectrum of periodically modulated signals exhibits the following properties. First, only few coefficients around the carrier frequency and its integer multiple harmonics are non-zero where the remaining coefficients can be considered as zero. Second, the spectrum is quasi-symmetrical around the carrier frequency. Third, the position of non-zero coefficients around the different harmonics of the carrier frequency remains almost identical. Consequently, given that the carrier frequency $f_c$ is known, the target spectrum can be modeled to be a block-sparse signal with partially-known active block positions. In fact, the center location of active blocks is known and equal to the carrier frequency, but the locations of non-zero coefficients inside the active block are unknown.

Let B be the number of carrier harmonics, i.e., the number of active groups. Each active group b is centered on the harmonic $b.f_c$. We further assume that active blocks are not overlapping and are quasi-symmetrical, i.e., each active block b contains the same number Q of coefficients on the left and the right side of $b.f_c$. This also means that we assume non-overlapping modulations, which is almost the case when the carrier frequency is very large when compared to the fundamental modulations frequencies. We also denote, by $\mathcal{A}$, the union of all active B groups, then $card\left(\mathcal{A}\right)=B(2Q+1)$. This means that we assume, at most, $B(2Q+1)$ non-zero coefficients (B carrier harmonics and $2Q$ non-zero coefficients around each carrier. It is worth noting that the number of non-zero coefficients around each carrier is actually much lower than $2Q$. Let $\overline{\mathcal{A}}$ denote the set of the remaining non-active coefficients, i.e., zero coefficients. In the following, for every $b\in \{1,\dots ,B\}$, we denote, by $x_{0,b}$, the coefficient at the frequency bin $b.f_c$ and, for every $q\in \{1,\dots ,Q\}$, we denote, by $x_{-q,b}$ and $x_{q,b}$, the $q^{th}$ coefficient at the left of $b.f_c$ and its symmetric with respect to $b.f_c$, respectively (see Figure 1). Note that each coefficient $x_{q,b}$ can be easily obtained from $\mathbf{x}$ by applying a suitable sparse matrix ${\mathbf{P}}_{q,b}$ containing one appropriate line of a permutation matrix i.e., $x_{q,b}={\mathbf{P}}_{q,b}\mathbf{x}$.

In this paper, we set that, for every $k\in \overline{\mathcal{A}}$, $x_k=0$. The following parts propose a model for the coefficients in active blocks $\mathcal{A}$ that takes the structure of spectrum into account.

2.3. Group Sparse Model for Modulated Signals

2.3.1. Related Works

One way to build a structured model is by jointly estimating the elements that are assumed to share the same inherent structure. In particular, this is achieved in Block Sparse Bayesian learning framework by modeling elements sharing the same group with a multivariate Gaussian distribution [34]. The correlation within each block was also encouraged in [49]. This model has been successfully applied to CS reconstruction of bearing vibration signals [39]. The constructed model in the latter work takes advantage of bearing signals spectrum structure, where non-zero coefficients tend to appear in small groups, rather than isolated peaks.

2.3.2. Hierarchical Model

In our case, the target spectrum exhibits modulations around the carrier frequency and its harmonics. Therefore, It is judicious to exploit the in-block quasi-symmetry of the spectrum in each active block b by jointly estimating coefficients $x_{-q,b}$ and $x_{q,b}$ belonging to symmetric frequency bins with respect to the $b^{th}$ harmonic of the carrier frequency $b{f}_c$ (see Figure 1). In fact, if a non-zero coefficient is related to a modulating signal, then there is a high probability that its symmetrical point with respect to the harmonic of the carrier frequency in this block is also nonzero with a quasi-similar magnitude. In that respect, we define the vector ${\mathbf{x}}_{q,b}\in {\mathbb{C}}^2$, where

$$\forall b\in \{1,\dots ,B\}\forall q\in \{1,\dots ,Q\},{\mathbf{x}}_{q,b}=[x_{-q,b},x_{q,b}]$$

(3)

We further aim to exploit the similarities across active blocks. Our idea is to capture such dependencies by jointly estimating the coefficients in the same position with respect to the carrier harmonics. To do this, we stack the coefficients of all B groups at the same position and their symmetrical points with respect to the carrier harmonics and then build the following vectors of multi-block coefficients of size $2B$

$$\forall q\in \{1,\dots ,Q\},{\mathbf{x}}_q={\left[{\mathbf{x}}_{q,1}^{\top },\dots ,{\mathbf{x}}_{q,B}^{\top }\right]}^{\top }$$

(4)

where ${\mathbf{x}}_{q,1}^{\top }$ is the transpose of vector ${\mathbf{x}}_{q,1}$. We also denote, by ${\mathbf{x}}_0$, the vector of size B containing the coefficients of the B carrier harmonics. The sparsity of the spectrum and the dependencies between the Fourier coefficients are captured by assuming that ${\left({\mathbf{x}}_q\right)}_{1⩽q⩽Q}$ are realizations of a heavy tailed multivariate distribution. We consider the class of scale mixture of multivariate Gaussian (SMG)

$$\forall q\in \{1,\dots ,Q\},{\mathbf{x}}_q\sim \mathcal{CN}\left(\mathbf{0},{\gamma }_q\mathbf{\Sigma }\right)$$

(5)

where $\mathcal{CN}$, here, denotes the multivariate complex normal distribution (As the covariance matrix is real-valued, (5) means that the real and imaginary parts of ${\mathbf{x}}_q$ follow the Gaussian distribution of zero mean and with covariance matrix $\tau {\gamma }_q\mathbf{\Sigma }$), ${\gamma }_q⩾0$ is the mixing parameter following some mixing distribution and $\mathbf{\Sigma }=\mathrm{Diag}\left(\mathbf{v}\right)⨂{\mathbf{I}}_2\in {\mathbb{R}}^{2B\times 2B}$ where ⨂ denotes the Kronecker product, ${\mathbf{I}}_2$ the identity matrix of size $2\times 2$, and $\mathbf{v}={[v_1,\dots ,v_B]}^{\top }\in {\left({\mathbb{R}}^{+}\right)}^B$. We further assume a Gaussian prior for the vector of carrier coefficients, i.e., ${\mathbf{x}}_0\sim \mathcal{CN}(\mathbf{0},\tau {\gamma }_0\mathrm{Diag}\left(\mathbf{v}\right))$, where ${\gamma }_0>0$. It is noteworthy that, although we have considered a diagonal covariance matrix, coefficients of ${\mathbf{x}}_q$ are uncorrelated but still dependent. Note that the block model (5), which is referred to as SMG-block, is a particular case of (A2) for which the variance of the Gaussian depends on the position of the Fourier coefficient, i.e., ${\lambda }_k=v_b{\gamma }_q$. The variable $v_b$ acts as a global indicator of the overall magnitude of harmonics in the active block b, while the local variable ${\gamma }_q$ controls the sparsity inside the blocks. In fact, if ${\gamma }_q$ is too small, then the spectrum coefficients in the position q and those in their symmetrical positions with respect to the carrier harmonics through the different B active groups approach zero. Inversely, if ${\gamma }_q$ is high, then all coefficients at positions q and $-q$ around the carrier harmonic in any active block b with non-zero $v_b$, they are also non-zero and then have a high probability to belong to modulations. It follows that the sparsity inside the active blocks is ensured if almost ${\gamma }_q$ are close to zero.

It is worth to note that model (5) promotes the structure of the spectrum through the dependency that it introduces between coefficients magnitudes with respect to their relative position to the carrier harmonics. One can interpret such dependency, as follows: coefficients in the same or symmetrical positions relatively to their carrier frequency contribute almost equally to the overall energy of the block where they lie. This is quite different from the Spike-and-Slab model dependency we will introduce later.

2.3.3. Setting the Mixing Hyperparameters

Setting the global and local parameters in the block sparse model (5) is quite important. In this paper, we propose the following hierarchical model for these parameters:

$$\begin{array}{cc}\hfill \forall b\in \{1,\dots ,B\},& v_b\sim \mathcal{IG}({\alpha }_b,{\beta }_b)\hfill \\ \hfill \forall q\in \{0,\dots ,Q\},& \sqrt{{\gamma }_q}|{\varphi }_q\sim {\mathcal{C}}^{+}(0,\sqrt{{\varphi }_q}),\sqrt{{\varphi }_q}\sim {\mathcal{C}}^{+}(0,1)\hfill \end{array}$$

where $\mathcal{IG}({\alpha }_b,{\beta }_b)$ is the inverse Gamma prior with positive constant parameters ${\alpha }_b$ and ${\beta }_b$ and ${\mathcal{C}}^{+}(0,e)$ denotes the half Cauchy distribution with location 0 and scale e. The intuition for this choice is explained, as follows. First, the global variables $v_b$ adapts the underlying sparsity in the active block: an appropriate small values of $v_b$ may lead to an over-shrinking of the active coefficients especially those with small amplitudes. Thus, we preferred to set its prior in such a way to avoid vanishing values of $v_b$ if active group b happens to be very sparse. This is motivated by our assumption of a known number of carrier harmonics, i.e., in each active block, there exists at least one non-zero coefficient. Note that, though, [48,50] recommend using the half Cauchy prior for both local and global parameters to improve shrinking, we found, in our experiments, that the half Cauchy prior for global parameters deteriorates the reconstruction of the small peaks as compared to the Inverse Gamma. We think that the Inverse Gamma is a suitable choice for two reasons: (1) its density vanishes in the origin that will artificially push away the values of $v_b$ from zero, and (2) it is a conjugate density for the Gaussian distribution that will facilitate the calculation afterwards. Second, unlike for the global scales, the local variables ${\gamma }_q$ are preferred to have vanishing values to appropriately model ultra-sparse signals. This is ensured while using the half Cauchy prior that, in addition to its Cauchy-like tails, has the merit when compared to the Inverse Gamma, of being non-zero at ${\gamma }_q=0$. This allows for the prior of ${\mathbf{x}}_q$ to have an infinitely tall spike in the origin resulting on good shrinking properties [51,52]. The hyperparameter ${\varphi }_q$ offers another degree of freedom in the mixing prior to ${\gamma }_q$. Third, the half-Cauchy prior does not bring additional difficulty in the posterior inference as compared to Inverse Gamma using the trick of parameter expansion [48,53]. In fact, the above model can be equivalently written, as follows

$$\begin{array}{cc}\hfill \forall b\in \{1,\dots ,B\},& v_b\sim \mathcal{IG}\left({\alpha }_b,{\beta }_b\right)\hfill \\ \hfill \forall q\in \{0,\dots ,Q\},& {\gamma }_q|{\eta }_q\sim \mathcal{IG}\left(\frac{1}{2},\frac{1}{{\eta }_q}\right),{\eta }_q|{\varphi }_q\sim \mathcal{IG}\left(\frac{1}{2},\frac{1}{{\varphi }_q}\right)\hfill \\ \hfill & {\varphi }_q|{\xi }_q\sim \mathcal{IG}\left(\frac{1}{2},\frac{1}{{\xi }_q}\right),{\xi }_q\sim \mathcal{IG}\left(\frac{1}{2},1\right)\hfill \end{array}$$

2.4. Structured Spike and Slab for Modulated Signals

2.4.1. Related Works

Spike and slab models that take the structure of the signals into account can be built by imposing a dependency between the model parameters of elements sharing the same cluster. For example, in [54], the authors exploit the statistical structure of the wavelet coefficients of their data by setting the model parameters ${\beta }_k$ of each wavelet coefficient according to the value of its parent in the wavelet tree, so that, if a parent coefficient is zero, its children coefficients are likely to also be zero. In [55], the authors consider relations between each coefficient of the signal and its neighbors by choosing ${\beta }_k$ from a set a different candidates according to the number of non-zero neighboring coefficients, yielding a high probability of a non-zero coefficients if all neighbors are non-zero. Such a model is motivated by sparse signals, where non-zero elements tend to appear in groups rather than isolated points. In [56,57], the authors take into account not only the spatial structure, but also the time evolving structure though an hierarchical Gaussian process. Such a model is convenient for temporal signals, where non-zero elements are clustered in groups for each timestamp and that these groups can move and evolve in time. These works are an inspiring point of our model.

In order to capture the structure form discussed above, the key idea is to set the model parameters ${\beta }_k$, $z_k$, and ${\lambda }_k$ in (A3), according to the position k of the Fourier coefficient $x_k$ in the spectrum. In fact, if the coefficient $x_k\in \mathcal{A}$, then it is located at some position q in an active block b, $b\in \{1,\dots ,B\}$, $q\in \{-Q,\dots ,Q\}$, and it follows that $z_k=z_{q,b}$ and ${\lambda }_k={\lambda }_{q,b}$. Therefore, we can add constraints on model parameters for the block b to be either equal or close for symmetrical positions q and $-q$ in order to assure the quasi-symmetry of the spectrum around a given carrier harmonic $b.f_c$. The similarity of the support of non-zero coefficients between actives blocks can be achieved while using additional constraints on model parameters at the same or symmetrical positions, but belonging to different active blocks b and $b^{\prime }$.

In the following, we propose different spike-and-slab models that range from weak to strong levels of prior symmetry assumptions and discuss their advantages and disadvantages. A spike-and-slab model is said to have a strong prior assumption on a given symmetrical structure if the latter is underlined through the binary selection variable $z_{q,b}$, while it has a weak prior assumption if it is only described through the prior probability of zero coefficient ${\beta }_{q,b}$ and/or the slab component parameters. In that respect, we can say that spike-and-slab models [54,55] are examples of models using a weak prior assumption, as they only take the structure of the target signals into account sthrough the spike probability ${\beta }_k$.

It seems interesting to note that, dealing with the structure in the spike-and-slab model is quite different from the continuous model (5), where the dependency is introduced in terms of energy contribution through the mixing variables. Here, instead, we are interested in the symmetrical properties of the support of non-zero coefficients in the spectrum rather than their contribution in the overall spectrum energy. However, nothing prevents us introducing energy constraints by setting the variance of the slab model well. This will discussed in the following parts.

2.4.2. Strong Assumptions on In-Block Symmetry and Inter-Block Similarity

One would set $z_{q,b}=z_{-q,b}$ in order to assure a perfect symmetry of the support around a given carrier harmonic $b.f_c$. In fact, if a non-zero coefficient is related to a modulating signal, then there is a high probability that its symmetric with respect to the harmonic of the carrier frequency in this block is also nonzero. Furthermore, in the ideal setting, the modulations tend to have a similar magnitude, so that one can assume ${\lambda }_{q,b}={\lambda }_{-q,b}$. We further aim to obtain a perfect similarity of the support across active blocks. One way to do this may be is to set $z_{q,b}=z_{q,b^{\prime }}$, $b^{\prime }\in \{1,\dots ,B\}$, so that the position of non-zero elements remains always the same for all groups. Under these strong prior assumptions, we propose the following spike-and-slab model (S&S):

$$\begin{array}{cc}\hfill \forall q\in \{1,\dots ,Q\},& {\mathbf{x}}_q\sim (1-z_q){\delta }_{\mathbf{0}}+z_q\mathcal{CN}\left(\mathbf{0},{\mathbf{\Lambda }}_q\right)\hfill \\ \hfill & z_q\sim \mathcal{B}\left(\varphi \left(g_q\right)\right)\hfill \\ \hfill & \mathbf{g}\sim \mathcal{N}(\mathbf{m},\mathbf{R})\hfill \end{array}$$

(6)

where $\mathcal{B}(.)$ stands for the Bernoulli distribution, ${\mathbf{\Lambda }}_q$ is the diagonal covariance matrix formed by the slab variable ${\lambda }_k$ of coefficients on position q, $\varphi$ is the cumulative function of the standard normal distribution ensuring a result on $(0,1)$ and the vector $\mathbf{g}$ is a Gaussian latent variable with mean $\mathbf{m}$ and covariance matrix $\mathbf{R}$. Regarding the latent variable, the mean value $\mathbf{m}$ controls the expected degree of sparsity inside the block and the covariance matrix $\mathbf{R}$ expresses the prior correlation regarding the support. For example, by choosing a covariance matrix $\mathbf{R}$ that has a non-zero positive correlation between two neighboring positions q and $q^{\prime }$, we promote slightly wide peaks in the spectrum (i.e., peaks over more than one frequency bin in the spectrum). Such a latent variable for the prior probability of the slab component is highly related to the latent Gaussian process in [56]. It may be also used to promote group-sparse vector recovery, similarly to [55].

It can be noted that letting ${\lambda }_{q,b}={\gamma }_q{v}_b$, where ${\gamma }_q$ and $v_b$ can be defined as in (5), coefficients at symmetrical and same positions in the spectrum are encouraged to have relatively close contributions to the energy of the block where they lie. Therein, model (6) can be seen as a multivariate Bernoulli-block sparse model that promotes perfectly symmetrical spectrum. The advantage of (6) compared to (5) is that it offers a strong level of sparsity, so that group of coefficients that do not belong to modulations are all set explicitly to be exactly zero, rather than small values.

2.4.3. Strong Assumptions on In-Block Symmetry and Weak Assumption for Inter-Block Similarity

The strong prior assumption on symmetry enable shrinking components that do not have their symmetrical counterparts in the spectrum. This can be particularly beneficial, when the measured signal is perturbed with external interfering components. However, this may fail in case of model mismatch, e.g., non-symmetrical components due to the noise level or the transfer function. In particular, it is common to observe in real industrial signals multiple modulations components around the first carrier harmonic, while their number decreases for higher carrier harmonics.

To offer more flexibility to the model to deal with this problem, we can relax the strong prior assumption regarding the perfect similarity of the support around all the carrier harmonics by setting

$$\begin{array}{cc}\hfill \forall b\in \{1,\dots ,B\}\forall q\in \{1,\dots ,Q\},{\mathbf{x}}_{q,b}& \sim (1-z_{q,b}){\delta }_{\mathbf{0}}+z_{q,b}\mathcal{CN}\left(\mathbf{0},{\mathbf{\Lambda }}_{q,b}\right)\hfill \\ \hfill z_{q,b}& \sim \mathcal{B}\left(\varphi \left(g_q\right)\right)\hfill \\ \hfill \mathbf{g}& \sim \mathcal{N}(\mathbf{m},\mathbf{R})\hfill \end{array}$$

(7)

where ${\mathbf{\Lambda }}_{q,b}$ is the diagonal matrix formed by elements ${\lambda }_k$ of the slab component lying in position q and $-q$ in the block b. In model (7), only the strong assumption regarding the symmetry around each carrier harmonic is kept unchanged while the similarity assumption of the support through the different blocks is relaxed by letting the spike variables in different blocks take different values. This means that the support is forced to be perfectly similar around the carrier harmonic, while it may slightly differ from one carrier harmonic to another, depending on the observed signal. Equivalently, the prior assumption on perfectly similar support is relaxed to give an additional degree of freedom to the observation in order to provide additional information as to whether the support is exactly the same or not.

While the relaxation of this hypothesis helps to handle the above problem of model mismatch, it may not help to recover low magnitude sidebands in a different block, especially in high noise levels. This may be compensated by adding, for instance, energy constraints. Similarly to (6), letting the slab component parameter ${\lambda }_{q,v}={\gamma }_q{v}_b$, we enforce symmetrical coefficients in the same block to have close magnitudes. In that way, the spectrum is forced to be perfectly quasi-symmetrical around the same carrier harmonic. Furthermore, coefficients lying in the same or symmetrical position will have close energy contribution in their relative active blocks if there are not zero.

2.4.4. Weak Assumptions on In-Block Symmetry and Inter-Block Similarity

Another concern about models (6) and (7) is that the perfect symmetry assumption about the support around the carrier harmonics may be somehow altered due to the sensor transfer function or phase modulations. In that case, we can further relax this assumption by letting either the local mixing value in the slab component or the selection variable in the spike component (or both of them) take different values. This yields the following model

$$\begin{array}{c}\hfill \forall b\in \{1,\dots ,B\}\forall q\in \{1,\dots ,Q\}\forall j\in \{1,-1\}\\ \hfill x_{j.q,b}& \sim (1-z_{j.q,b}){\delta }_0+z_{j.q,b}\mathcal{CN}(0,{\lambda }_{j.q,b})\hfill \\ \hfill z_{j.q,b}& \sim \mathcal{B}\left(\varphi \left(g_q\right)\right)\hfill \\ \hfill \mathbf{g}& \sim \mathcal{N}(\mathbf{m},\mathbf{R})\hfill \end{array}$$

(8)

Model (8) is very close to the univariate model (A2); the only difference is that a structured prior about the support is implicitly assumed through the latent variable $\mathbf{g}$. Similarly to (6) and (7), we can set ${\lambda }_{j.q,b}={\gamma }_q{v}_b$ to further upgrade the symmetry of the spectrum.

2.5. Practical Implementation

In this part, we only consider the structured spike-and-slab model that is defined in (8) for ${\lambda }_{j.q,b}={\gamma }_q{v}_b$. The derivation of the Gibbs sampler for the other models is straightforward.

Let $\mathbf{\Theta }=\underset{0⩽q⩽Q}{\cup }\{{\gamma }_q,{\eta }_q,{\varphi }_q,{\xi }_q\}\underset{1⩽b⩽B}{\cup }\left\{v_b\right\}\cup \{\mathbf{z},\mathbf{g}\}$ be the set of unknown parameters and hyperparameters of the proposed models. Figure 2 shows the generative graph of the proposed hierarchical model. The related joint prior distribution is given by

$$\mathrm{p}(\mathbf{x},\mathbf{\Theta })=\mathrm{p}\left(\mathbf{x}\right|\mathbf{\Theta }\left)\mathrm{p}\right(\mathbf{\Theta })$$

(9)

where

$$\mathrm{p}\left(\mathbf{\Theta }\right)=\prod _{q=0}^Q\mathrm{p}\left({\gamma }_q\right|{\eta }_q)\mathrm{p}\left({\eta }_q\right|{\varphi }_q)\mathrm{p}\left({\varphi }_q\right|{\xi }_q)\mathrm{p}\left({\xi }_q\right)\prod _{b=1}^B\mathrm{p}\left(v_b\right)\mathrm{p}\left(\mathbf{z}\right|\mathbf{g})\mathrm{p}\left(\mathbf{g}\right)$$

(10)

The resulting joint density reads

$$\mathrm{p}(\mathbf{x},\mathbf{\Theta },\tau ,\mathbf{y})=\mathrm{p}(\mathbf{x},\mathbf{\Theta })\mathrm{p}\left(\mathbf{x}\right|\tau \left)\mathrm{p}\right(\tau )$$

(11)

We propose designing a Gibbs sampler that is able to efficiently sample from the conditional distribution of the signal $\mathbf{x}$, $\tau$ and the set of hyperparameters $\mathbf{\Theta }$. The main challenge with industrial signals is their large size due to the high sample rate of the target signal. To give the reader an idea, a vibrating signal from a mechanical system that resonates at 5 kHz needs at least 10,000 samples per second. We propose adopting the data augmentation strategy in [58] in order to tackle the tractability of sampling in such a high dimensional problem. Appendix B provides the derivation of conditional distributions and details about sampling steps.

3. Experimental Results

In this section, experiments are first conducted on simulated signals to study the properties of the proposed models and the associated sampling algorithm. We also investigate, in our analysis, the choice of the proposed models and their effect on the structure of the reconstructed support set. Next, the potentiality of the proposed model is evaluated on real vibration data.

3.1. Simulated Example

The compression rate is one commonly used criterion to evaluate compressive sensing recovery. It is defined by $cr=\frac{N-M}{N}$. The noise level is a second important criterion for industrial vibrations signals. In fact, mechanical vibration signals are very often acquired by accelerometers that are mounted on operating mechanical components. Because of the harsh acquisition environment, mechanical signals are always contaminated with high levels of random noise as well as external interference, resulting in small signal-to-noise ratio. Therefore, it is important to investigate the ability of the reconstruction methods to reduce the noise and interfering components while providing an accurate estimate of the signal. For this reason, the simulation part is organized, as follows. First, we consider different compression rates and different Gaussian noise levels, and we aim to numerically investigate the contribution brought by the proposed structure models to the reconstruction quality. This is performed by comparing these models with their univariate versions. Finally, we study the shrinking properties for interfering components.

3.1.1. Test Signal

The test signal s is of length N = 50,000 and is simulated by multiplying two periodic signals $s_c$ and $s_m$ ($s=s_c\times s_m$). More specifically, we have used $B=3$ carrier harmonics with normalized fundamental frequency $f_c=0.07$ (the sampling frequency is $f_s$ = 5000 Hz) and 6 modulations with normalized fundamental frequency $f_m=0.005$. We have set $Q=1749$, so that each active block has a frequency bandwidth of size $f_c$. It is worth to note that the test signal is expressed in the unit of the actual experimental signal (e.g., [m/s${}^2$]), say [U].

The models that are followed in this paper can be applied to real applications in different fields such as telecommunication, electricity, mechanics and optics where modulated signals are frequently encountered. However, there is no versatile structured model. For each application, the prior model should be well adapted to the intrinsic structure shape of the considered spectrum (e.g., amplitude or phase modulations) and take possible symmetry mismatch into account. For instance, in our experiments, we are particularly interested in the modulated signals encountered in mechanical systems, such as Gearboxes. Modulations appear in the spectrum mainly due to amplitude and phase modulations (generated by transmission errors), leading to a quasi-symmetrical spectrum, as detailed in Section 2.1.1. Furthermore, the energy of such a structure becomes stronger when a damage appears in the gear pair. When the active blocs (composed each of a meshing frequency harmonic and its modulations) are considered, one can notice that there is no necessary rule concerning the energy of each bloc. Moreover, the transfer function between the source (e.g., the gear pair) and the accelerometer (i.e., transducer measuring transverse vibrations) alters the real signature that is produced by the source. All of these factors make the vibration signal structure unpredictable and the reconstruction task quite challenging, especially for small modulations in low signal-to-noise ratio (SNR) and high compression rate conditions. Accordingly, the adapted constraints to test signal should be imposed to approach the reality of vibration signals. In that respect, the test signal is set so as to have quasi-symmetrical spectrum around the carrier frequencies (symmetrical support, but with slightly different amplitude). Furthermore, the active blocks in the spectrum of the test signal have different energy levels.

3.1.2. Considered Models

We compare the proposed structured models to their univariate versions in order to study the contribution of the structured prior to the recovery performance. More specifically, we consider:

• Continuous models: we compare the proposed group sparse model (5) (SMG-block) with univariate models, namely the univariate Student’s t distribution (denoted by t-univ) and the Horseshoe prior defined by (A2) for Inverse Gamma and Half Cauchy mixing densities, respectively (denoted by H-univ).
• Discrete models: we consider the univariate spike-slab that is defined in (A3), where ${\lambda }_k$ is assumed to follow an Inverse Gamma density and the (unknown) prior probability of being non-zero is the same for all coefficients. We also compare six versions of the proposed structured spike-and-slab, namely $S\&S$-1A, $S\&S$-1B, $S\&S$-2A, $S\&S$-2B, $S\&S$-3A, and $S\&S$-3B, where the number $i\in \{1,2,3\}$ denotes the prior assumption (from weaker to stronger) given by models (6)–(8), respectively, and the letter B or A denotes the use or not of additional prior assumption on energy contribution (i.e., ${\lambda }_k$ can take any value as for the univariate model for A and ${\lambda }_k={\gamma }_q{v}_b$ for B).

Regarding the hyper-parameters of the structured Spike-and-Slab models, we have set the mean $\mathbf{m}$ to correspond to a prior probability of being non-zero of $0.15$ in order to promote ultra-sparse spectrum. We further choose a Gaussian kernel to build the covariance matrix $\mathbf{R}$ i.e., $R_{i,j}=a_{R}exp(-b_R^{-1}{|i-j|}^2)$ with $a_R=4$ and $b_R=0.5$, so that non-zero correlations span over two neighboring bins. It is worth noting that most of structured priors proposed for vibration monitoring deal with group sparse signals, where non-zero coefficients appear to be clustered rather than isolated peaks. To our knowledge, there is no proposed models that take the symmetrical structure of the spectrum of smoothly modulated signals into account, so we are not able to undertake a comparison with other structured models, as they are non-adapted to the structure of our signals.

3.1.3. Results

For the different models, we run the Gibbs algorithms for 6000 iterations, with the first 4000 iterations as burn-in. The last 2000 samples are used to empirically compute point estimates (maximum a posteriori). We begin with comparing the performance of the different models for different levels of Gaussian noise and compression rates. The noise level is given in terms of SNR. The reconstruction quality is evaluated in terms of normalized mean square error (NMSE) in Figure 3. The latter is defined as NMSE=$\frac{\parallel \mathbf{x}-\widehat{\mathbf{x}}{\parallel }_2^2}{{\parallel \mathbf{x}\parallel }_2^2}$, in which $\mathbf{x}$ is the real signal, $\widehat{\mathbf{x}}$ is its estimate, and ${\parallel .\parallel }_2$ stands for the ${\ell }^2$-norm.

A quick view of the NMSE plots shows that the proposed models (expect S&S-3A and expect S&S-3B) always improve the reconstruction error as compared to their univariate versions. We first discuss the results for continuous models then for spike-and-slab models and, finally, we compare both of them.

In the one hand, for continuous models, H-univ and t-univ lead approximately to the same reconstruction error, while the continuous SMG-block achieves almost the best results among all models. The contribution of the support structure in continuous models is mainly noticed for increasing noise levels. Using the SMG-block instead of H-univ and t-univ helps to decrease the error for $5\%$ for low noise levels until $20\%$ for higher noise levels. In order to evaluate the reconstruction error visually, we plot the reconstructed spectra using the H-univ, t-univ, and SMG-block in Figure 4 and in Figure 5 for the lowest noise level (13.97 dB) and a compression rate equal to $0.9$ and for a high noise level (0dB) and a compression rate equals $0.85$, respectively

We can see that, for very low noise levels, all of the continuous models recover the modulations, but the SMG-block better shrinks background noise, since we observe some peaks that are related to noise in the reconstructed spectrum by the univariate models. For the high noise level, although the NMSE values are close for continuous models, t-univ and H-univ fail to reconstruct modulations with small amplitudes, while SMG-block enhances the reconstruction of these small sidebands.

On the other hand, the addition of structure in the spike-and-slab model spectacularly improves the numerical results. In particular, we can see that S&S-1A and S&S-2A achieve a good improvement in the reconstruction error when compared to the S&S-univ. This means that adding the weak or strong assumption of the perfect symmetry of the support around the carrier frequencies is very advantageous, especially for low noise levels. The contribution of the assumption on support symmetry is less noticed for high noise levels, where the reconstitution error is only slightly improved when compared to S&S-univ. The use of additional constraints on the energy for S&S-1B and S&S-2B contributes to further enhance the results especially in high noise levels. In Figure 6, we display the reconstructed spectra using the S&S-1A and S&S-1B for initial SNR 1.93 dB and a compression rate equals 0.7. We can see that the addition of energy constraints in S&S-1B improves the recovering of the small sidebands as scompared to S&S-1A.

We can also note that a weak and strong assumption about support in-block symmetry (with the weak assumption about the support inter-block similarity) yields close results. The strong assumption does not bring additional improvement to the results. It is worth to recall that this the test signal exhibits perfectly symmetrical support. However, this perfect symmetry may sometimes be altered in real applications. Therein, we recommend adopting the default choice of the weak assumption about the in-block symmetry of the support.

In contrast, S&S-3A and S&S-3B generally yield less good results when compared to the other spike-and-slab models especially in low noise levels. This leads us to say that the strong assumption on the similarity of the support for the different carrier harmonic is not always advantageous. This can be explained by the relatively high shrinking power of such model that may be good to promote perfectly similar support, but which may not be adapted when modulations magnitudes are highly imbalanced.

When comparing these different families of models, the results show that the performance of spike-and-slab models are poorer than those of continuous models in low to medium noise levels. For example, the SMG-block yields better results than its discrete version, namely S&S-1B, S&S-2B, and S&S-3B for the first four noise levels, while, for medium and high noise levels (for SNR < 6 dB), theses discrete models achieve similar or slightly better results than the SMG-block. We may explain this observation, as follows. The assumption regarding the support increases the shrinking behavior of the model. This is beneficial, as it allows for impressively reducing the background noise by shrinking the unwanted components that do not have their symmetrical part in the spectrum, at the cost of an over-shrinking of the small coefficients. In high noise levels, the reconstruction error is mainly dominated by the shrinking effect of background noise. While, in low noise levels, the effect of over-shrinking the small components is more dominant. This can also explain the small value of correlation in low compression rates that were observed for S&S-univ when compared to continuous univariate models in low noise levels. Another concern that may explain our observations is the muli-modality of the posterior for spike-and-slab models, which makes the inference task more challenging for them than for continuous models. Therefore, the authors recommend the default use of continuous models for signals sharing the same properties as this test signal (only few non-zero coefficients, with symmetrical spectrum support and unbalanced amplitudes). More specifically, we recommend the SMG-block, since it achieved better performance for all scenarios in our experiments.

We now investigate the effect of presence of interfering components in the measured signal. Interfering components in real applications may come from external environment or simply other rotating components in the mechanical system, like fans, turbines, compressors, and so on. We simulate a small interfering sinusoidal signal $s_3$ of frequency $0.13$, and we add it to the test signal in addition to Gaussian noise. We investigate the shrinking behavior of the continuous models for a compression rate of 0.8 and for an initial signal-to-noise ration of 0 dB. Figure 7 shows zooms on the reconstructed spectra around frequency 0.13. We see that only the SMG-block succeeds in eliminating the interfering component. This can be also seen in the posterior marginal densities of the coefficient related to the interfering component. In fact, the additional symmetrical properties regarding the structure support included in SMG-block yield a marginal density, whose mass is concentrated at values near zero.

3.2. Application to Gearbox Vibrations

Here, we consider real data from CETIM (Centre technique des industries mécaniques, France). They consist of vibration signals, expressed in [m/s${}^2$], which were acquired at high sampling rate ($f_s$ = 20 KHz) with an accelerometer mounted in the vicinity of a gearbox reducer. The latter comprises two gears meshing together under constant speed. More specifically, one signal is acquired per day, during 12 days. A progressive fault in one wheel appeared around day 9. In such a system, the meshing forces are the main source of vibration that result from the teeth contact of the two wheels. The meshing force is naturally modulated by the rotation of the two wheels due to gears imperfection and the systematic variation of stiffness along the teeth. These modulations are typically weak for healthy signals, but their numbers and amplitude grow as the fault occurs and progresses. The energy of sidebands around the meshing frequencies in the spectrum are thus a good indicator about the health of the gear. In our test bench, the normalized meshing frequency is around $f_c=0.0165$. Given a sub-sampled vector of vibration measurements, the goal is to detect this fault by estimating the sidebands around the meshing frequencies. A standard practice in vibration-based condition monitoring is to track the evolution of some health indicators that tell us about the energy and the shape of the spectrum. We propose to use, as indicator, the root mean square of amplitude of the modulations that are induced by the faulty gear in the spectrum. Therefore, such an indicator tends to increase when a defect occurs. Because we are mainly interested in recovering the small sidebands rather than zeroing the background noise, we use the SMG-block model and run the proposed Gibbs sampler for 5000 iterations, where the first 3000 samples are discarded as a burn-in period. The proposed indicators are then computed on the amplitudes of the peaks that are associated with target modulations using the 2000 last samples generated by the Gibbs algorithm. Note that we do not have access to the noisy-free signal, the measured vibration signal may contain wide-band noise and frequency-sparse noise (interfering peaks from others sources that we do not know). Thus, it is difficult to quantitatively define the reconstruction error. However, the proposed indicator reflects and quantifies the reconstruction accuracy of sidebands. Rather than computing the indicators on point estimates (since we do not have the noisy-free signal to compare with it), we compute it on all samples and evaluate credible intervals. Figure 8 shows the evolution from day one to 12 of this indicator for different compression rates.

We can clearly see a progressive increase with the defect that is similar to the raw signal, even for low compression rates, which indicates a good recovery of sidebands from healthy case (small sidebands) to faulty cases (large sidebands), offering the possibility of monitoring gearboxes through compressive sensing.

4. Discussion and Conclusions

This paper concerns Bayesian CS of periodically modulated signals. This class of signals is in mechanical vibrations that are generated by rotating machines, and their analysis carries useful information regarding the health state of the component. The particularity of periodically modulated signals is that in addition to their sparsity in the Fourier basis, their spectrum exhibits two forms of symmetry. First, their spectrum is quasi-symmetrical around the carrier frequency. Second, the support of non-zero coefficients is almost identical around the different carrier harmonics. The main contribution of the paper is to consider the particular spectral structure of these signals in the design of prior models. More specifically, it proposes extensions of two families of hierarchical priors, namely continuous scale mixture of Gaussians and spike-and-slab model, to take the form of the target signal spectrum into account. First, a block-sparse model is proposed by jointly estimating coefficients being in similar or symmetrical positions relatively to the carrier harmonics. This form of dependency encourages such coefficients to contribute in an identical manner to the overall energy of the block to which they belong. Second, structured spike-and-slab models are built by letting the binary variable dependent on the position in the spectrum. This is ensured by introducing a Gaussian latent variable to decide for the prior probability of being non-zero. In that respect, different strength beliefs about the symmetrical properties of the spectrum lead to different hierarchical models. In fact, a strong assumption on the similarity of the support around the carrier harmonics leads us to set the same binary selection variable for all coefficients sharing symmetrical or same positions, while a weak assumption only introduces dependency through the prior probability of being non-zeros. This form of dependency promotes quasi-symmetrical and identical spectrum support. The proposed methods have been evaluated on both simulated signals and real gearbox vibration signal. It was shown that, for such signals, structured priors achieve better results when compared to their univariate versions. In particular, the continuous block-sparse model outperforms all of the tested priors for all the compression rates and noise levels. Moreover, the discrete structured priors give more accurate results when combined with the energy constraint. Overall, the consideration of the intrinsic structure of the spectrum support is a very successful strategy and has shown its advantage for the recovering of mechanical signals for diagnosis purposes. However, it is worth to note that the considered models are only adapted to mechanical signals under the hypothesis that they are sparse in the Fourier domain. This hypothesis can be, for example, altered if the speed variation or the spectral leakage are high as pointed in Section 2.1.1. Furthermore, some mechanical signals, such as bearings, may exhibit cyclostationarity in their second order moments, rather than in the Fourier spectrum. This means that they are not perfectly sparse in the Fourier domain and alternative representations should be considered. As a further investigation, we can study the performance of such models in other applications, where we also encounter modulated signals (e.g., telecommunication, electricity, optics). The investigation of cases where the carrier frequency and the number of its harmonics are unknown may be very attractive for other real applications as an extension of our work.