Seismic Performance Evaluation of Steel Buildings with Oil Dampers Using Capacity Spectrum Method
Abstract
:1. Introduction
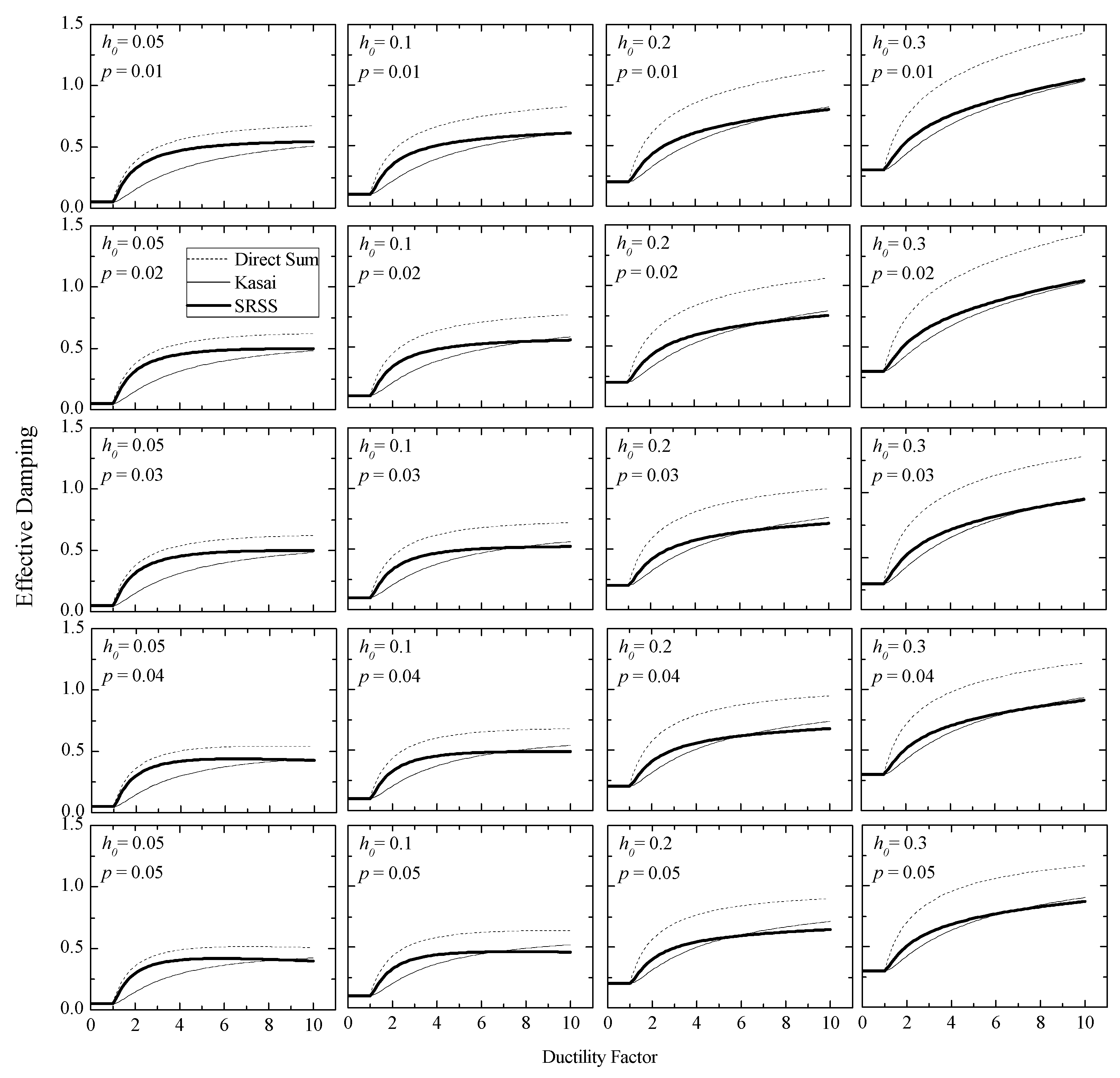
2. Proposal of the Square Root of Sum of Squares (SRSS) Effective Damping Ratio
3. Proposed CSM Procedure for Buildings Equipped with Oil Dampers
- The multi degree of freedom (MDOF) was converted to the ESDOF [29];
- For selected ductility factor values (e.g., μ = 1, 2, 3 …), the respective effective damping ratios (e.g., h1, h2, h3 …), not including the contribution of the oil damper devices, were computed using Equation (11) [3], and the demand spectra were adjusted by Equation (10), and plotted together with the capacity curve of the ESDOF as shown in Figure 4a;
- The spectral ordinates (spectral acceleration, SA, and displacement, SD) of the demand spectrum at the intersection points with equivalent stiffness lines were determined and named as initial performance points;
- For each initial performance point, the equivalent circular frequency of the ESDOF was estimated by Equation (12);
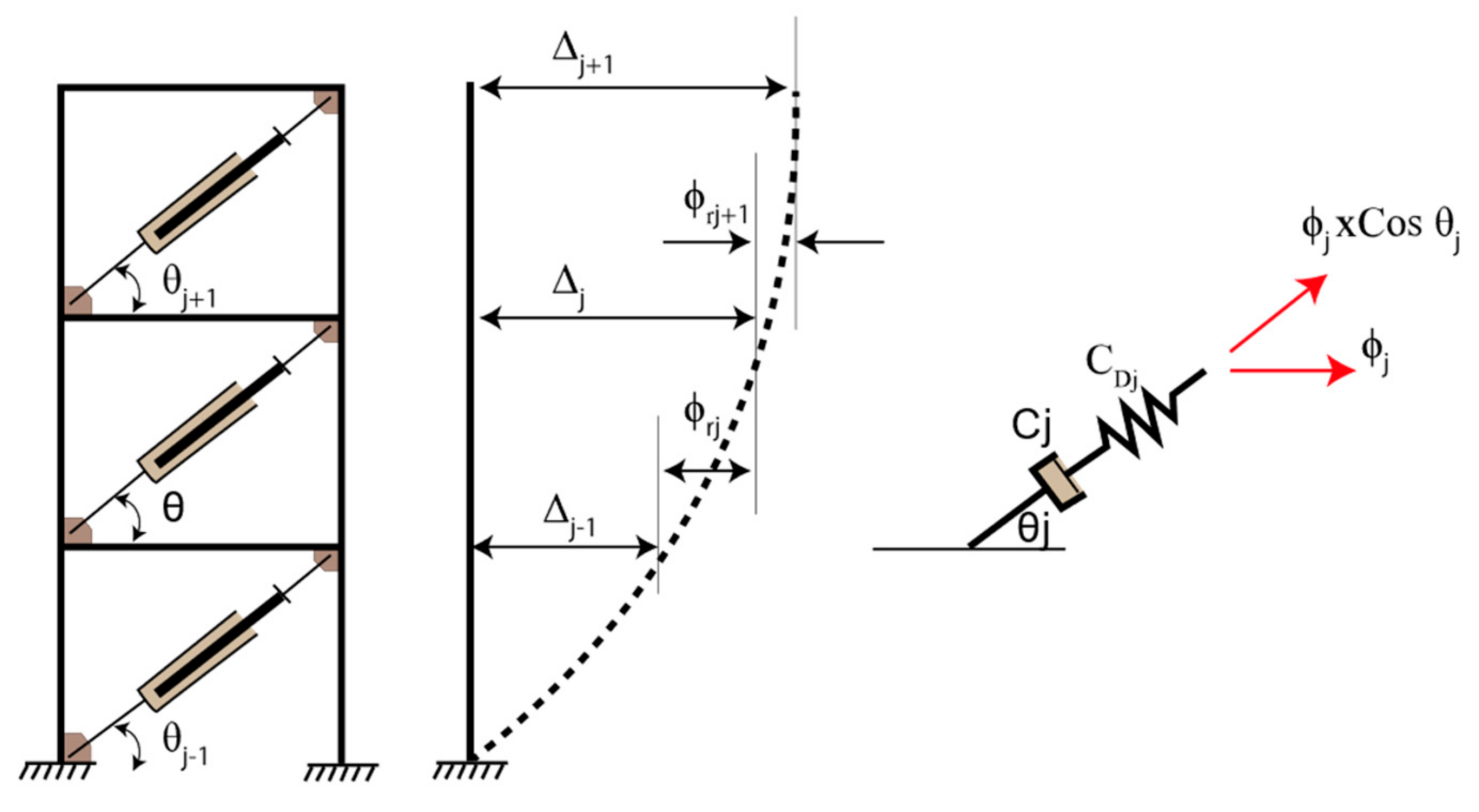
- The corresponding story displacements (δ1, δ2, δ3…) were computed from the ESDOF. Then, the maximum story velocities of the MDOF, Vmax, were estimated as following;
- Using Equations (8), (9) and (16) the effective damping of the system, heff,SRSS, the equivalent damping coefficient, Ceq, and the viscous damping of oil dampers, hV, were estimated, respectively;
- Demand spectra were updated for each ductility factor as shown in Figure 4b (dashed-line response spectra);
- The next performance points were considered, and the same process was repeated until convergence (the difference between successive effective damping ratios becomes negligible), as shown in Figure 4c (dashed-dotted-line response spectra);
- The final performance points were connected and the point of intersection of the formed curve (blue solid line in Figure 4d) with the capacity curve was defined as the ultimate performance point of the ESDOF;
- Maximum seismic performance of the corresponding MDOF could be deducted from the ultimate performance point of its ESDOF.
4. Application of the Proposed CSM on Steel Frame Buildings
4.1. Effective Damping Ratio of MDOF System
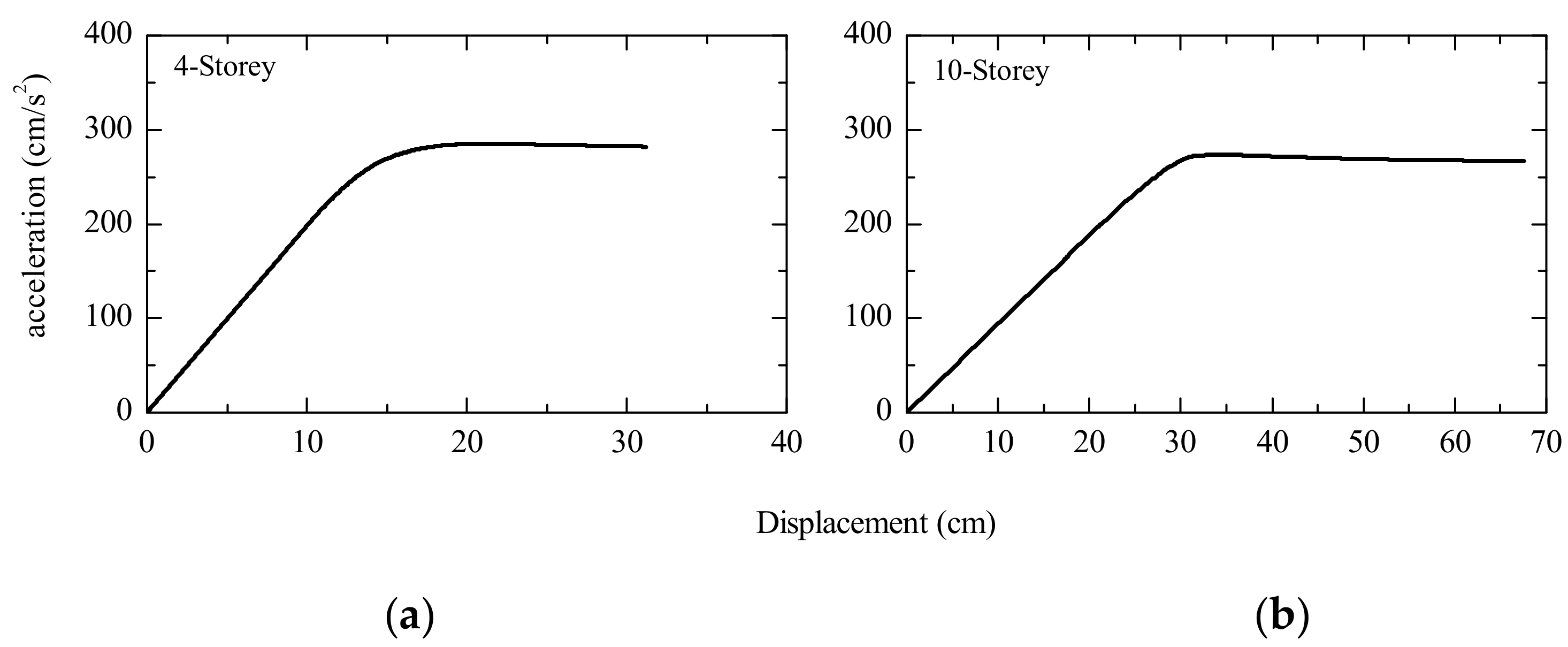
4.2. Description of Target Buildings
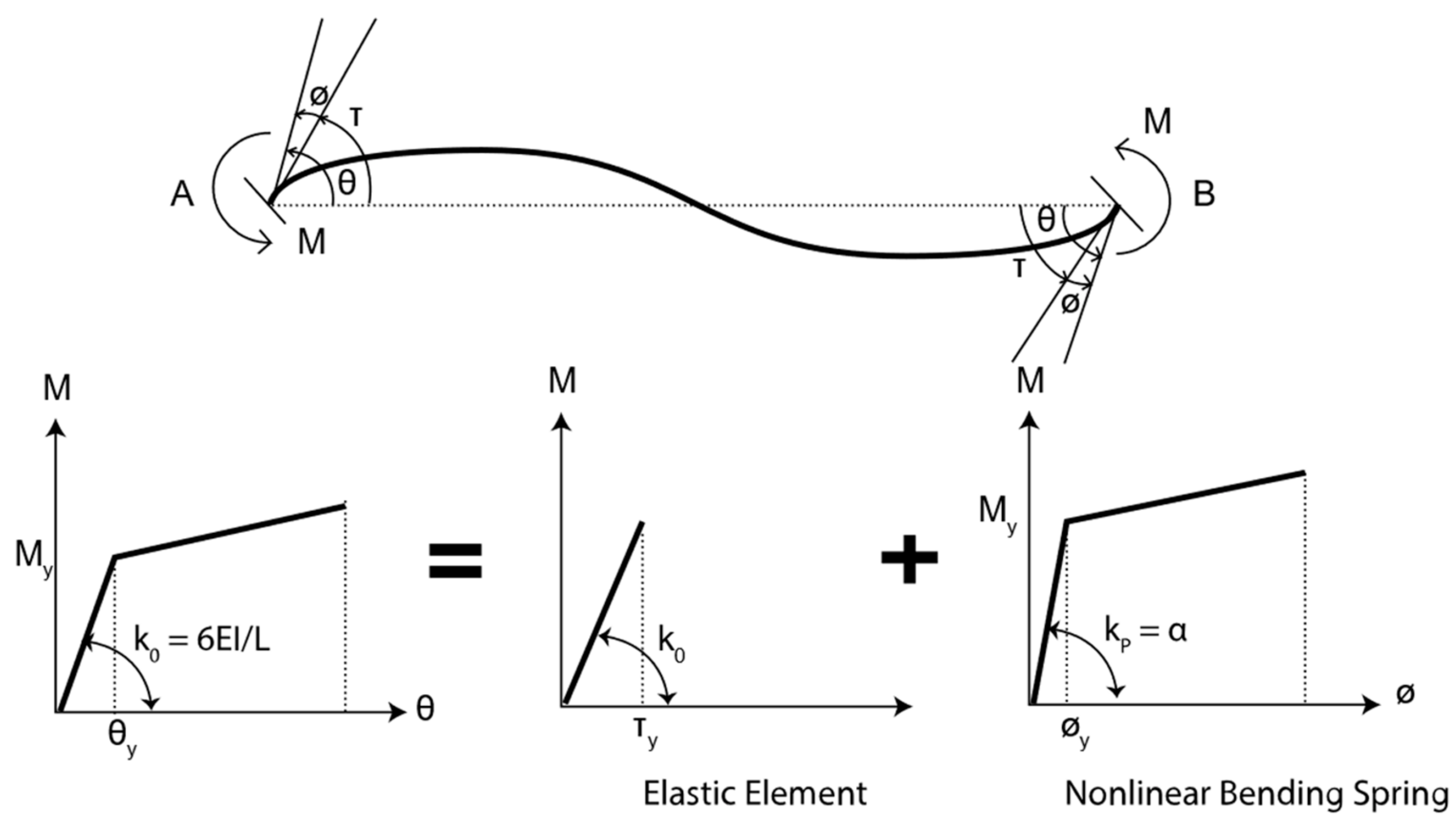
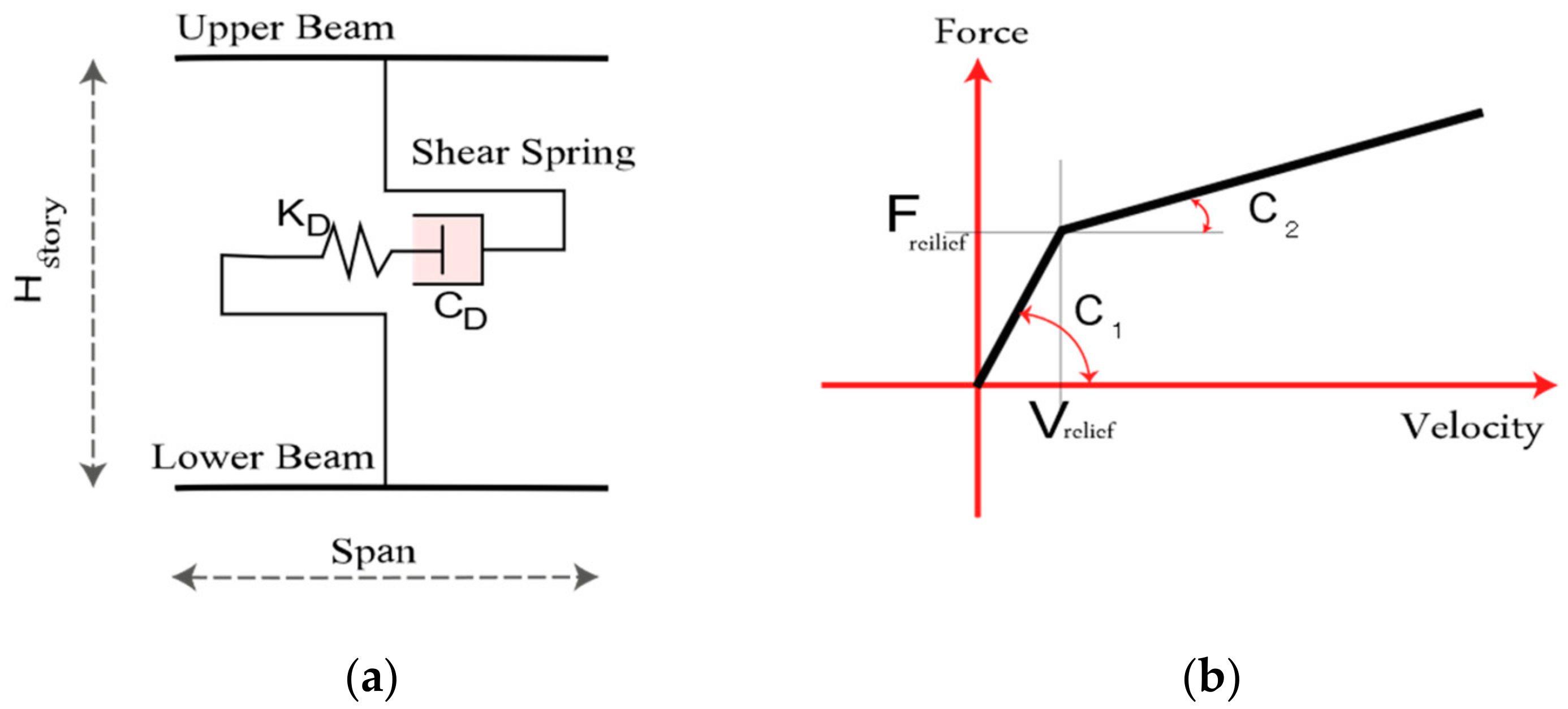
4.3. Frame Models of Target Buildings
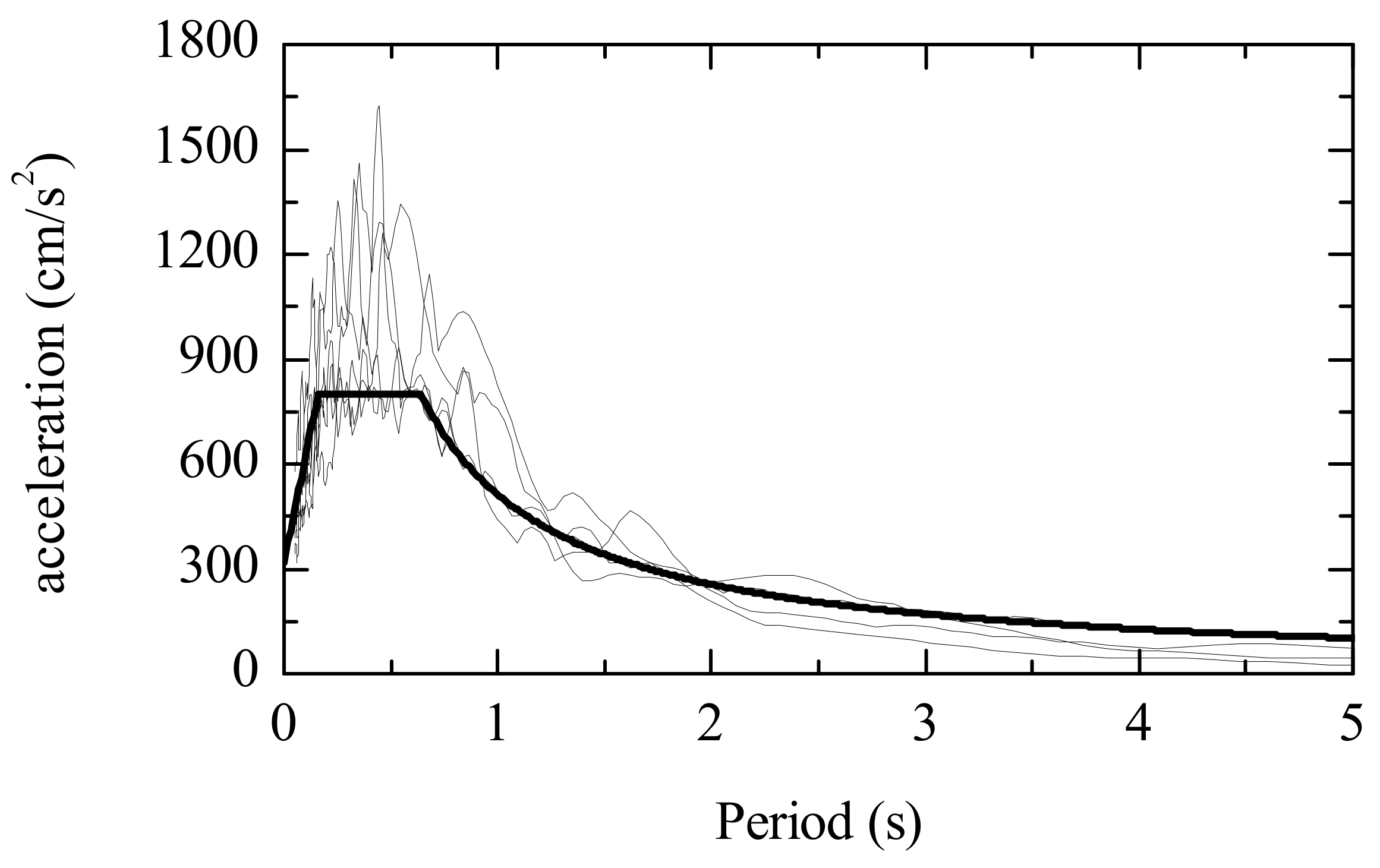
4.4. Demand Spectrum of Earthquake Ground Motions
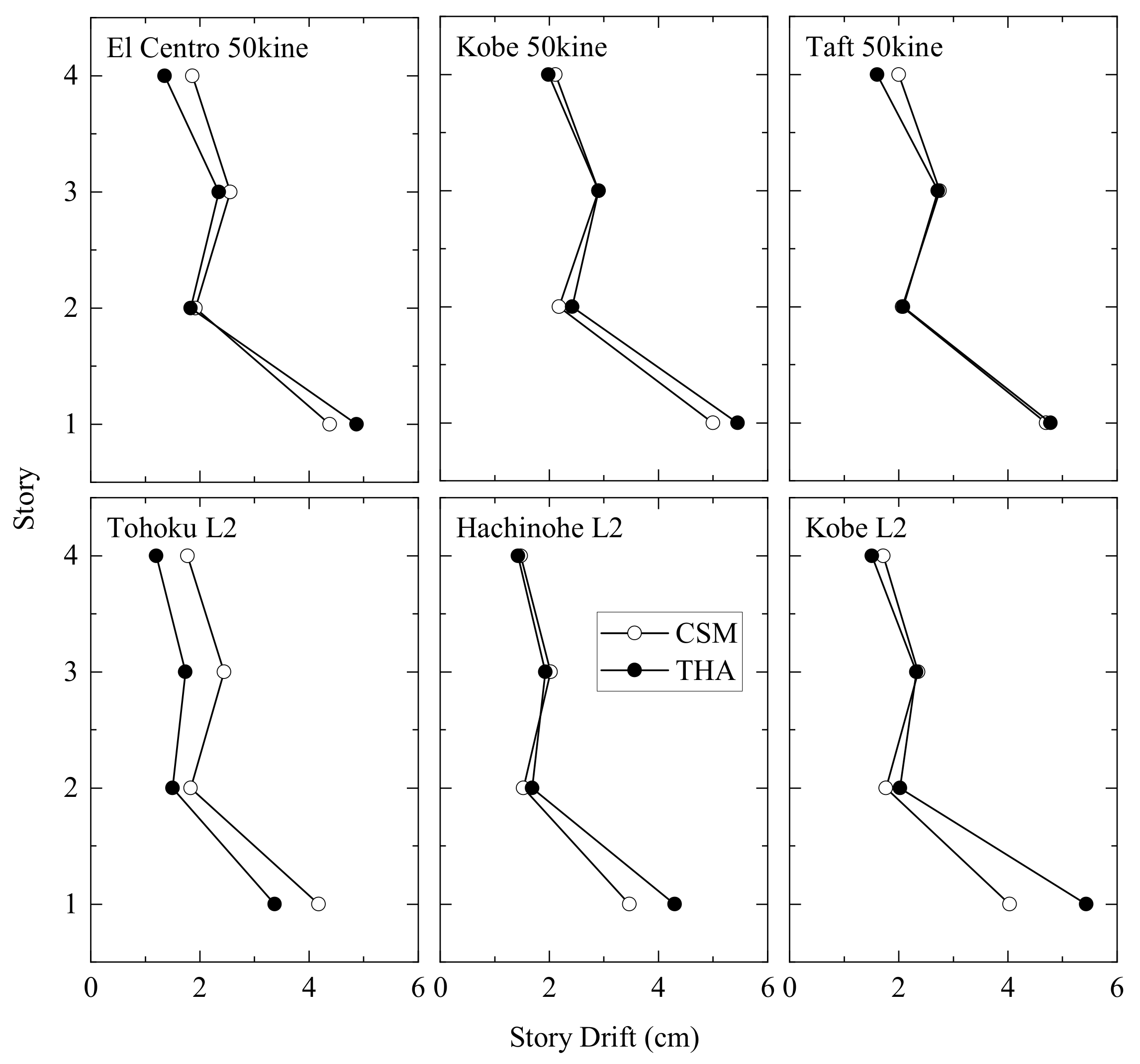
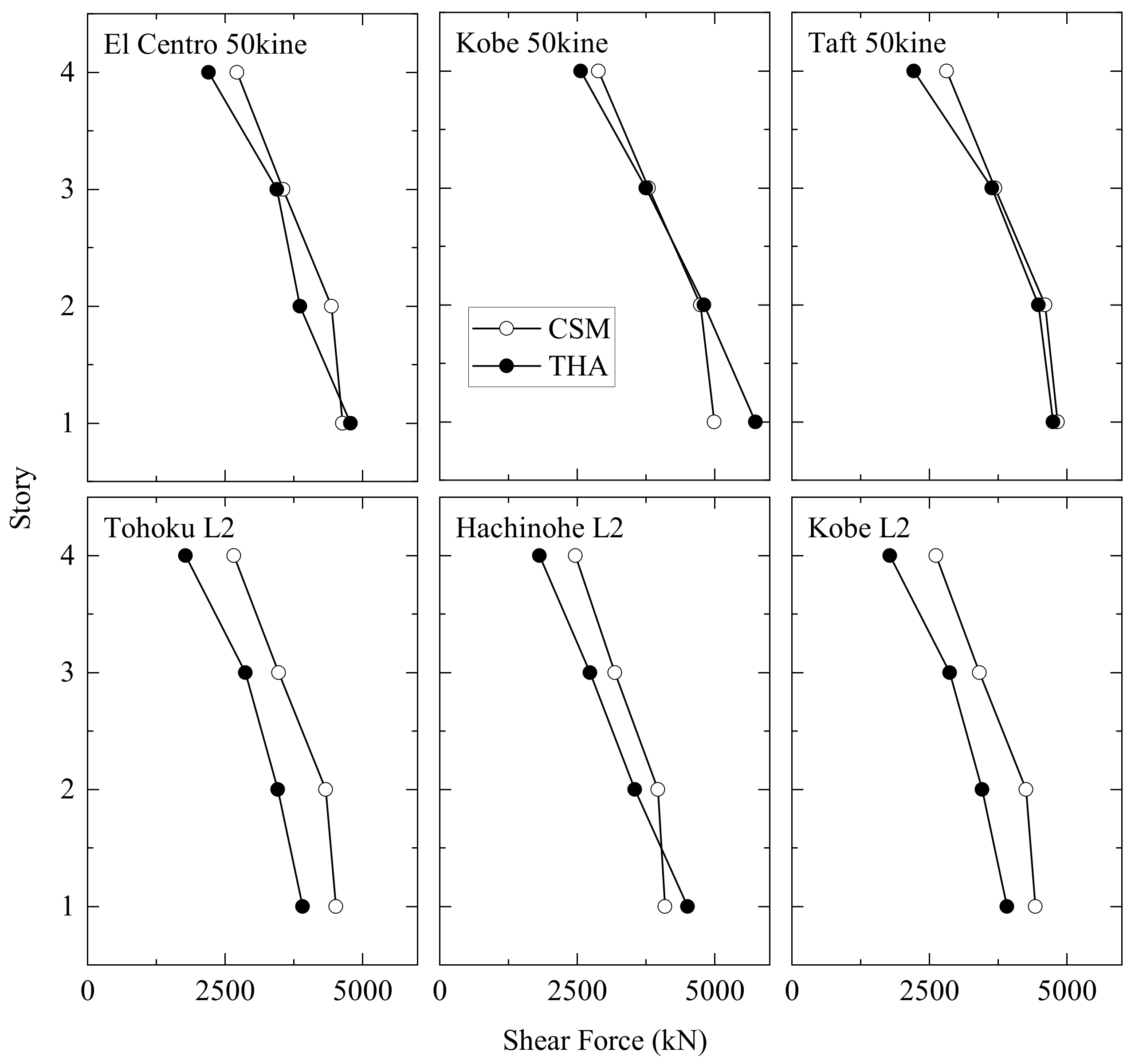
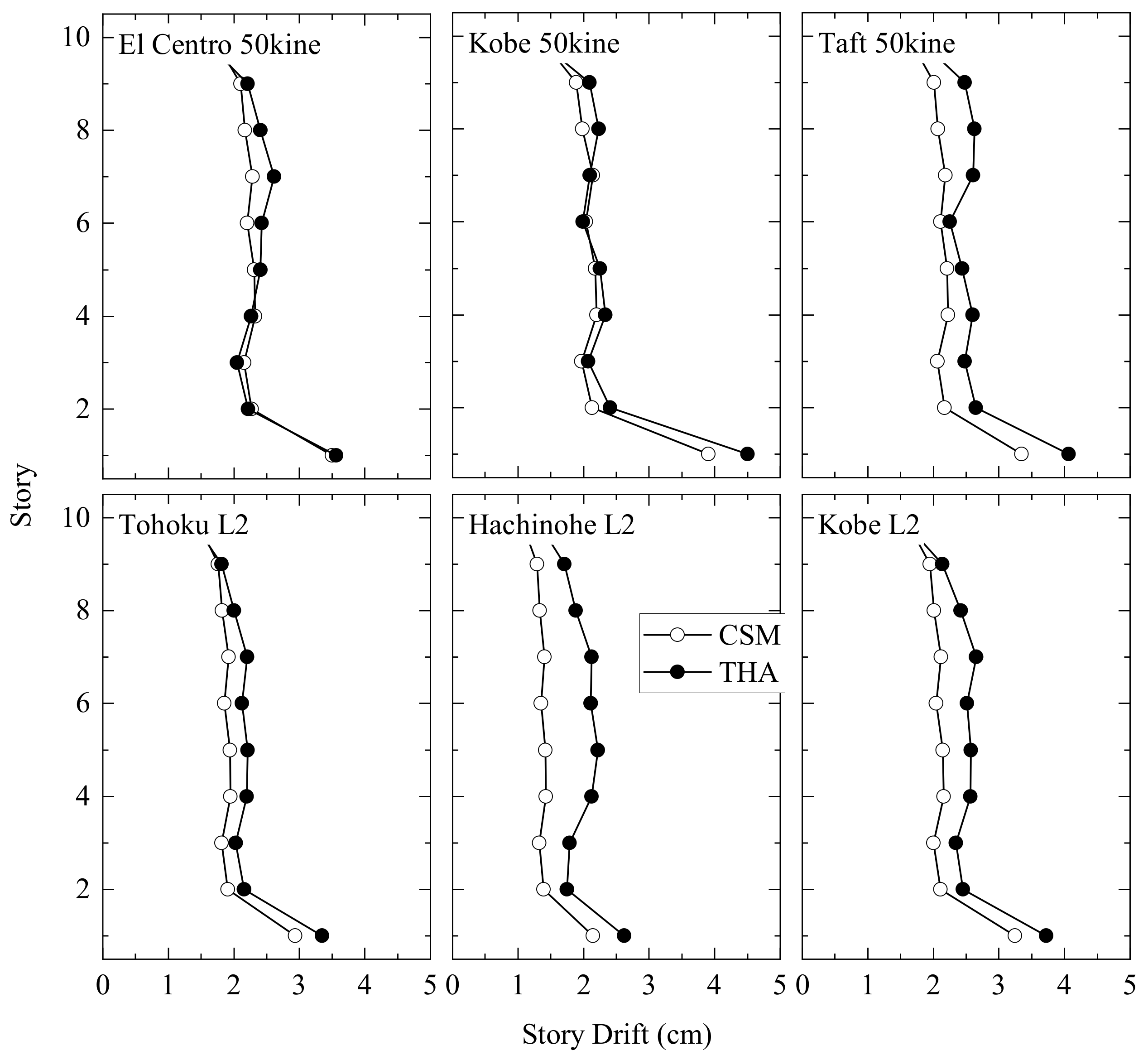
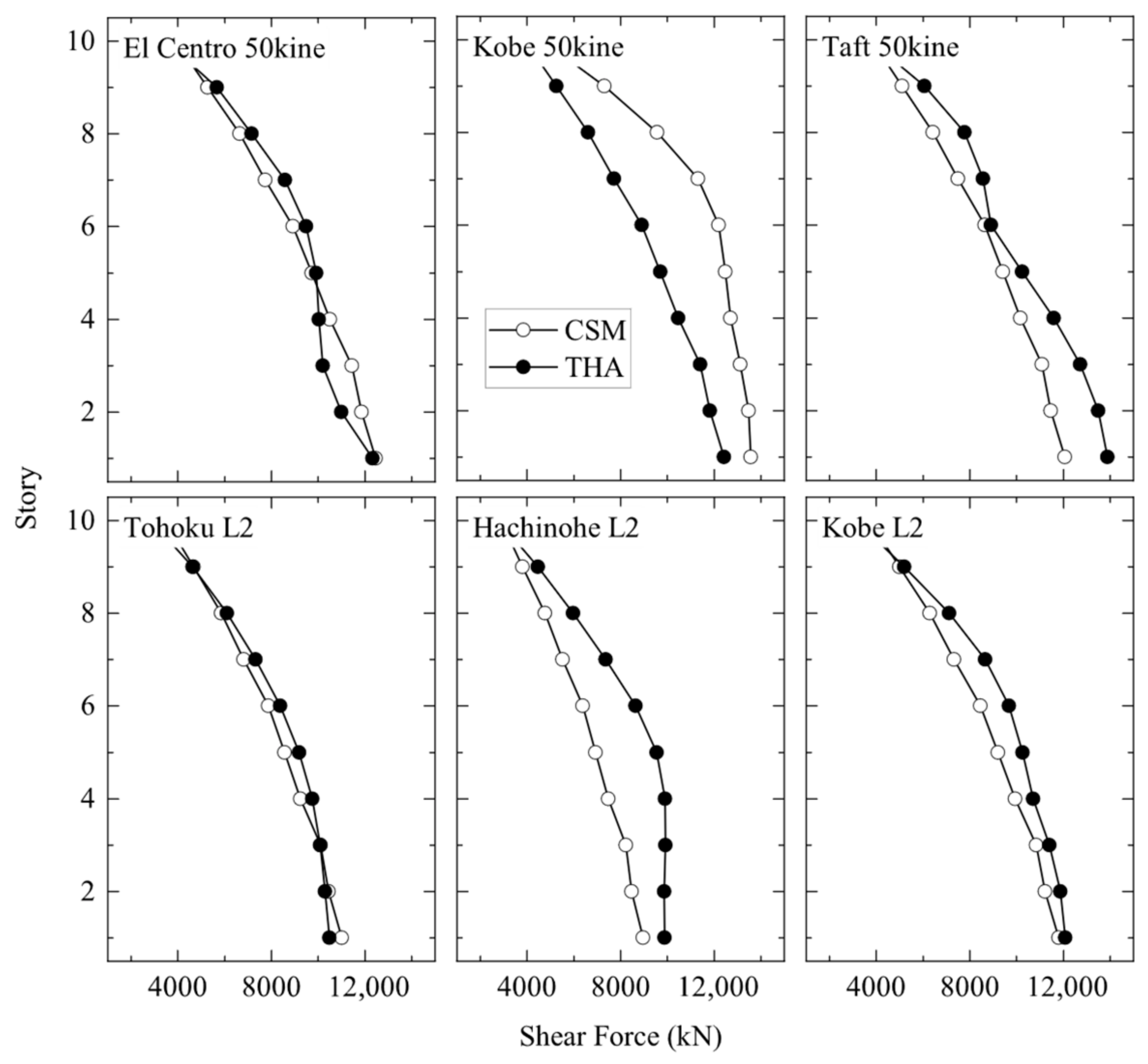
4.5. Comparison Results between CSM and THA
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Freeman, S.A. Review of the development of the capacity spectrum method. ISET J. Earthq. Tech. 2004, 4, 1–13. [Google Scholar]
- ATC. Seismic Evaluation and Retrofit of Concrete Buildings; Report ATC-40; ATC: Redwood City, CA, USA, 1996. [Google Scholar]
- BSL. The Building Standard Law of Japan; The building center of Japan; BSL: Tokyo, Japan, 2004. [Google Scholar]
- Kim, H.; Min, K.-W.; Chung, L.; Park, M.; Lee, S.-H. Evaluation of capacity spectrum method for estimating the peak inelastic responses. J. Earthq. Eng. 2005, 9, 695–718. [Google Scholar] [CrossRef]
- Choi, H.H.; Kim, J. Evaluation of proper supplemental damping for a multi-story steel frame using capacity spectrum method. Adv. Earthq. Eng. 2001, 9, 25–34. [Google Scholar]
- Kim, J.; Choi, H.; Min, K.-W. Performance-based design of added viscous dampers using capacity spectrum method. J. Earthq. Eng. 2003, 7, 1–24. [Google Scholar] [CrossRef]
- Li, B.; Liang, X.-W. Design of supplemental viscous dampers in inelastic SDOF system based on improved capacity spectrum method. Struct. Eng. Mech. 2007, 27, 541–554. [Google Scholar] [CrossRef]
- Chen, B.-J.; Chung, L.L.; Tsai, C.S.; Chiang, T.-C. Applications of capacity spectrum method for buildings with metallic yielding dampers. In Proceedings of the ASME 2005 Pressure Vessels and Piping Conference, Denver, CO, USA, 17–21 July 2005; Volume 8, pp. 299–306. [Google Scholar]
- Han, J.; Yan, R.; Li, H. Performance-based seismic design for structures with viscoelastic dampers. J. Earthq. Eng. Eng. Vibr. 2008, 28, 175–181. [Google Scholar]
- Benavent-Climent, A.; Escolano-Margarit, D. Shaking table tests of structures with hysteretic dampers: Experimental results versus prediction using non-linear static methods. Bull. Earthq. Eng. 2012, 10, 1857–1883. [Google Scholar] [CrossRef]
- Kim, J.; Kim, M.; Eldin, M.N. Optimal distribution of steel plate slit dampers for seismic retrofit of structures. Steel Comp. Struct. 2017, 25, 473–484. [Google Scholar]
- Bantilasa, K.E.; Kavvadias, I.E.; Vasiliadisb, L.K. Capacity spectrum method based on inelastic spectra for high viscous damped buildings. Earthq. Struct. 2017, 13, 337–351. [Google Scholar]
- João, M.C. Estêvão. An Integrated Computational Approach for Seismic Risk Assessment of Individual Buildings. Appl. Sci. 2019, 9, 5088. [Google Scholar]
- Ferraioli, M.; Lavino, A. A displacement-based design method for seismic retrofit of RC buildings using dissipative braces. Math. Probl. Eng. 2018, 2018, 1–28. [Google Scholar] [CrossRef]
- Naeem, A.; Kim, J. Seismic retrofit of structures using rotational friction dampers with restoring force. Adv. Struct. Eng. 2020, 23, 3525–3540. [Google Scholar] [CrossRef]
- Ramirez, O.M.; Constantinou, M.C.; Gomez, J.D.; Whittaker, A.S.; Chrysostomou, C.Z. Evaluation of Simplified Methods of Analysis of Yielding Structures with Damping Systems. Earthq. Spectra. 2002, 18, 501–530. [Google Scholar] [CrossRef]
- JSSI. Manual for design and construction of passively-controlled buildings. In The Japan Society of Seismic Isolation, 3rd ed.; JSSI: Tokyo, Japan, 2013. (In Japanese) [Google Scholar]
- Kasai, K.; Kibayashi, M. JSSI manual for building passive control technology, Part-1 manual contents and design/analysis methods. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. Paper No. 2989. [Google Scholar]
- Kibayashi, M.; Kasai, K.; Tsuji, Y.; Kikuchi, M.; Kimura, Y.; Kobayashi, T.; Nakamura, H.; Matsuba, Y. JSSI manual for building passive control technology, Part-2 criteria for implementation of energy dissipation devices. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. Paper No. 2990. [Google Scholar]
- Tsuyuki, Y.; Gofuku, Y.; Liyama, F.; Kotake, Y. JSSI manual for building passive control technology, Part-3 performance and quality control of oil damper. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. Paper No. 2468. [Google Scholar]
- Adachi, F.; Yoshitomi, S.; Tsuji, M.; Takewaki, I. Nonlinear optimal oil damper design in seismically controlled multi-story building frame. Soil Dyn. Earthq. Eng. 2013, 4, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Adachi, F.; Fujita, K.; Tsuji, M.; Takewaki, I. Importance of interstory velocity on optimal along-height allocation of viscous oil dampers in super high-rise buildings. Eng. Struc. 2013, 56, 489–500. [Google Scholar] [CrossRef] [Green Version]
- Ji, X.; Hikino, T.; Kasai, K.; Nakashima, M. Damping identification of a full-scale passively controlled five-story steel building structure. Earthq. Eng. Struct. Dyn. 2013, 42, 277–295. [Google Scholar] [CrossRef]
- Xie, L.; Cao, M.; Funaki, N.; Tang, H.; Xue, S. Performance study of an eight-story steel building equipped with oil dampers damaged during the 2011 great east japan earthquake part 1: Structural identification and damage reasoning. J. Asian Arch. Build. Eng. 2015, 14, 181–188. [Google Scholar] [CrossRef] [Green Version]
- Takabatake, H.; Kitada, Y. Approximate method of estimating seismic performance of high-rise buildings with oil-dampers. Struct. Desig. Tall. Spec. Build. 2018, 27, 1–28. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice Hall: Englewood Cliffs, NJ, USA, 2017. [Google Scholar]
- Kasai, K.; Fu, Y.; Watanabe, A. Passive control systems for seismic damage mitigation. J. Struct. Eng. 1998, 124, 501–512. [Google Scholar] [CrossRef]
- Kasai, K.; Kawanabi, Y. Equivalent linearization to predict dynamic properties and seismic peak responses of a structural system with high viscous damping and hysteretic damping. J. Struc. Cons. Eng. 2005, 591, 43–51. (In Japanese) [Google Scholar] [CrossRef] [Green Version]
- Kuramoto, H.; Teshigawara, M.; Lkuzono, T.; Koshika, N.; Takayama, M.; Hori, T. Predicting the earthquake response of buildings using equivalent single degree of freedom system. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. Paper No.1039. [Google Scholar]
- Fu, Y.; Kasai, K. Comparative study on frames using viscoelastic and viscous dampers. J. Struc. Eng. 1988, 124, 513–522. [Google Scholar] [CrossRef]
- Sekiya, E.; Mori, H.; Ohbuchi, T.; Yoshie, K.; Hara, H.; Arima, F.; Takeuchi, Y.; Saito, Y.; Ishii, M.; Kasai, K. Details of 4-, 10-, and 20-story theme structure used for passive control design examples. In The JSSI Response Control Committee Symposium on Passive Vibration Control; JSSI: Tokyo, Japan, 2004. (In Japanese) [Google Scholar]
- Saito, T. Structural Earthquake Response Analysis, STERA_3D Version 10.8. and STERA_WAVE Version 1.0. Available online: http://www.rc.ace.tut.ac.jp/saito/software-e.html (accessed on 24 December 2020).





| Natural Period (T) | Weight (W) | Damping (h0) | Stiffness (Kf) | Yielding Force (Fy) | |
|---|---|---|---|---|---|
| s | kN | % | kN/cm | kN | |
| 0.5 | 5000.0 | 5.0 | 805.68 | 1000.0 | 0.05 |
| Stiffness (KD) | Pre-Relief Damping Coef. (C1) | Relief Velocity (Vr) | C2/C1 * |
|---|---|---|---|
| kN/cm | kN-s/cm | cm/s | |
| 805.68 | 22.0 | 5.0 | 0.05 |
| Building | Story | Interior Column | Exterior Column | Corner Column |
|---|---|---|---|---|
| 4-story | 4 | 400 × 400 × 16 | 400 × 400 × 16 | 350 × 350 × 16 |
| 3 | 450 × 450 × 19 | 400 × 400 × 19 | 350 × 350 × 16 | |
| 2 | 450 × 450 × 22 | 450 × 450 × 19 | 400 × 400 × 19 | |
| 1 | 500 × 500 × 22 | 500 × 500 × 19 | 400 × 400 × 19 | |
| 10-story | 7–R | 550 × 550 × 22 | 500 × 500 × 22 | 500 × 500 × 19 |
| 5–6 | 600 × 600 × 28 | 550 × 550 × 25 | 550 × 550 × 22 | |
| 3–4 | 650 × 650 × 28 | 600 × 600 × 25 | 600 × 600 × 22 | |
| 2 | 650 × 650 × 28 | 600 × 600 × 28 | 600 × 600 × 25 |
| Building | Story | Longitudinal Direction | Transvers Direction | ||
|---|---|---|---|---|---|
| Interior Beam | Exterior Beam | Short Span | Long Span | ||
| 4-story | 4 | 550 × 200 × 9 × 16 | 550 × 250 × 12 × 22 | 700 × 300 × 12 × 22 | |
| 3 | 550 × 250 × 9 × 19 | 550 × 200 × 12 × 22 | 700 × 250 × 12 × 22 | ||
| 2 | 600 × 250 × 12 × 22 | 600 × 200 × 12 × 25 | 750 × 250 × 14 × 25 | ||
| 1 | 650 × 250 × 12 × 25 | 650 × 200 × 12 × 25 | 800 × 250 × 14 × 25 | ||
| 10-story | 10–R | 600 × 300 × 12 × 22 | 600 × 250 × 12 × 22 | 600 × 300 × 14 × 25 | 600 × 300 × 14 × 32 |
| 8–9 | 700 × 300 × 12 × 22 | 700 × 250 × 12 × 22 | 700 × 300 × 14 × 25 | 700 × 300 × 16 × 32 | |
| 6–7 | 750 × 300 × 16 × 25 | 750 × 250 × 14 × 25 | 750 × 300 × 16 × 28 | 750 × 300 × 16 × 32 | |
| 4–5 | 750 × 300 × 16 × 28 | 750 × 250 × 16 × 28 | 750 × 350 × 16 × 28 | 750 × 350 × 16 × 32 | |
| 3 | 750 × 300 × 16 × 28 | 750 × 300 × 16 × 28 | 750 × 350 × 16 × 28 | 750 × 350 × 16 × 32 | |
| 2 | 800 × 300 × 16 × 32 | 800 × 300 × 16 × 28 | 800 × 300 × 16 × 32 | 800 × 300 × 16 × 32 | |
| Story | Height (H) | Weight (Wf) | Story Stiffness (KF) | Damper Stiffness (KD) | Damping (C1) | Relief V. (Vr) | C2/C1 |
|---|---|---|---|---|---|---|---|
| m | kN | kN/mm | kN/mm | kN-s/mm | cm/s | ||
| 4 | 4.0 | 6622.0 | 328.2 | 56.50 | 11.75 | 38.6 | 0.02 |
| 3 | 4.0 | 6664.0 | 383.0 | 65.93 | 13.70 | 38.6 | 0.02 |
| 2 | 4.0 | 6680.0 | 383.5 | 66.02 | 13.72 | 38.6 | 0.02 |
| 1 | 6.0 | 6859.0 | 280.0 | 48.18 | 10.02 | 57.9 | 0.02 |
| Story | Height (H) | Weight (Wf) | Story Stiffness (KF) | Damper Stiffness (KD) | Damping (C1) | Relief V. (Vr) | C2/C1 |
|---|---|---|---|---|---|---|---|
| m | kN | kN/mm | kN/mm | kN-s/mm | cm/s | ||
| 10 | 4.0 | 8579.0 | 158.6 | 27.30 | 5.67 | 38.6 | 0.02 |
| 9 | 4.0 | 6365.0 | 180.1 | 31.00 | 6.45 | 38.6 | 0.02 |
| 8 | 4.0 | 6431.0 | 220.3 | 37.92 | 7.88 | 38.6 | 0.02 |
| 7 | 4.0 | 6470.0 | 244.8 | 42.13 | 8.77 | 38.6 | 0.02 |
| 6 | 4.0 | 6539.0 | 291.8 | 50.23 | 10.45 | 38.6 | 0.02 |
| 5 | 4.0 | 6567.0 | 306.2 | 52.70 | 10.95 | 38.6 | 0.02 |
| 4 | 4.0 | 6622.0 | 328.2 | 56.50 | 11.75 | 38.6 | 0.02 |
| 3 | 4.0 | 6664.0 | 383.0 | 65.93 | 13.70 | 38.6 | 0.02 |
| 2 | 4.0 | 6680.0 | 383.5 | 66.02 | 13.72 | 38.6 | 0.02 |
| 1 | 6.0 | 6859.0 | 280.0 | 48.18 | 10.02 | 57.9 | 0.02 |
| Building | Parameter | 1st Mode | 2nd Mode | 3rd Mode |
|---|---|---|---|---|
| 4-story | Natural period (s) | 1.40 | 0.49 | 0.25 |
| Effective mass (%) | 91.2 | 7.90 | 0.60 | |
| 10-story | Natural period (s) | 2.03 | 0.75 | 0.44 |
| Effective mass (%) | 82.8 | 11.3 | 3.40 |
| Categories | No. | Event | Year | Station |
|---|---|---|---|---|
| Scaled earthquake to be compatible of 50 cm/s | 1 | Imperial Valley | 1940 | El Centro |
| 2 | Kern County | 1952 | Taft | |
| 3 | Kobe | 1995 | JMA | |
| Artificially generated earthquake to be compatible of L2 | 4 | Tohoku | 1978 | Tohoku Univ. |
| 5 | Tokachi Oki | 1968 | Hachinohe | |
| 6 | Kobe | 1995 | JMA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naqi, A.; Saito, T. Seismic Performance Evaluation of Steel Buildings with Oil Dampers Using Capacity Spectrum Method. Appl. Sci. 2021, 11, 2687. https://doi.org/10.3390/app11062687
Naqi A, Saito T. Seismic Performance Evaluation of Steel Buildings with Oil Dampers Using Capacity Spectrum Method. Applied Sciences. 2021; 11(6):2687. https://doi.org/10.3390/app11062687
Chicago/Turabian StyleNaqi, Ahmad, and Taiki Saito. 2021. "Seismic Performance Evaluation of Steel Buildings with Oil Dampers Using Capacity Spectrum Method" Applied Sciences 11, no. 6: 2687. https://doi.org/10.3390/app11062687
APA StyleNaqi, A., & Saito, T. (2021). Seismic Performance Evaluation of Steel Buildings with Oil Dampers Using Capacity Spectrum Method. Applied Sciences, 11(6), 2687. https://doi.org/10.3390/app11062687







