Soft X-ray Transmission Microscopy on Lithium-Rich Layered-Oxide Cathode Materials
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Data Acquisition and Treatment
2.3. Stray Light Correction and Normalization
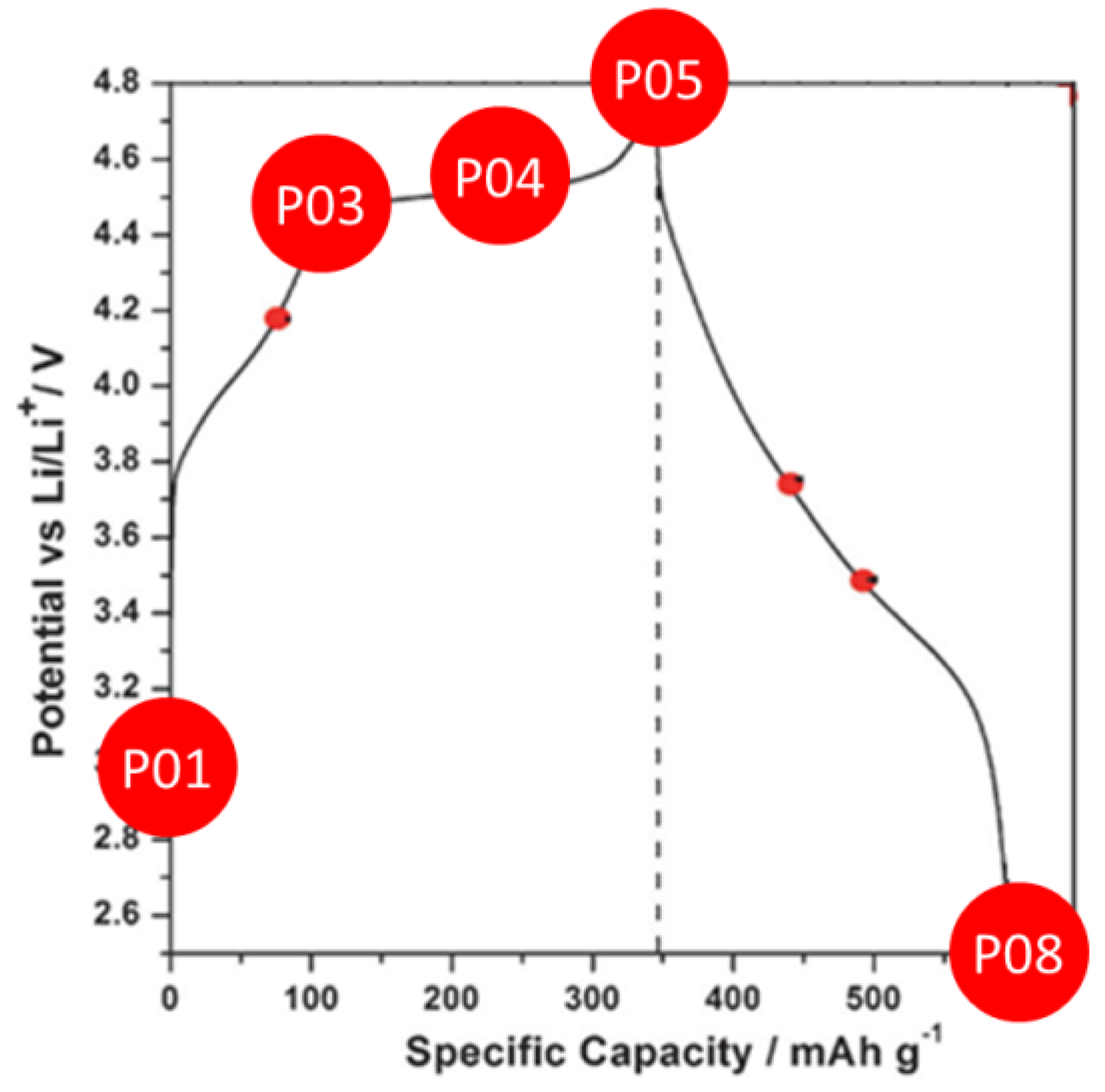
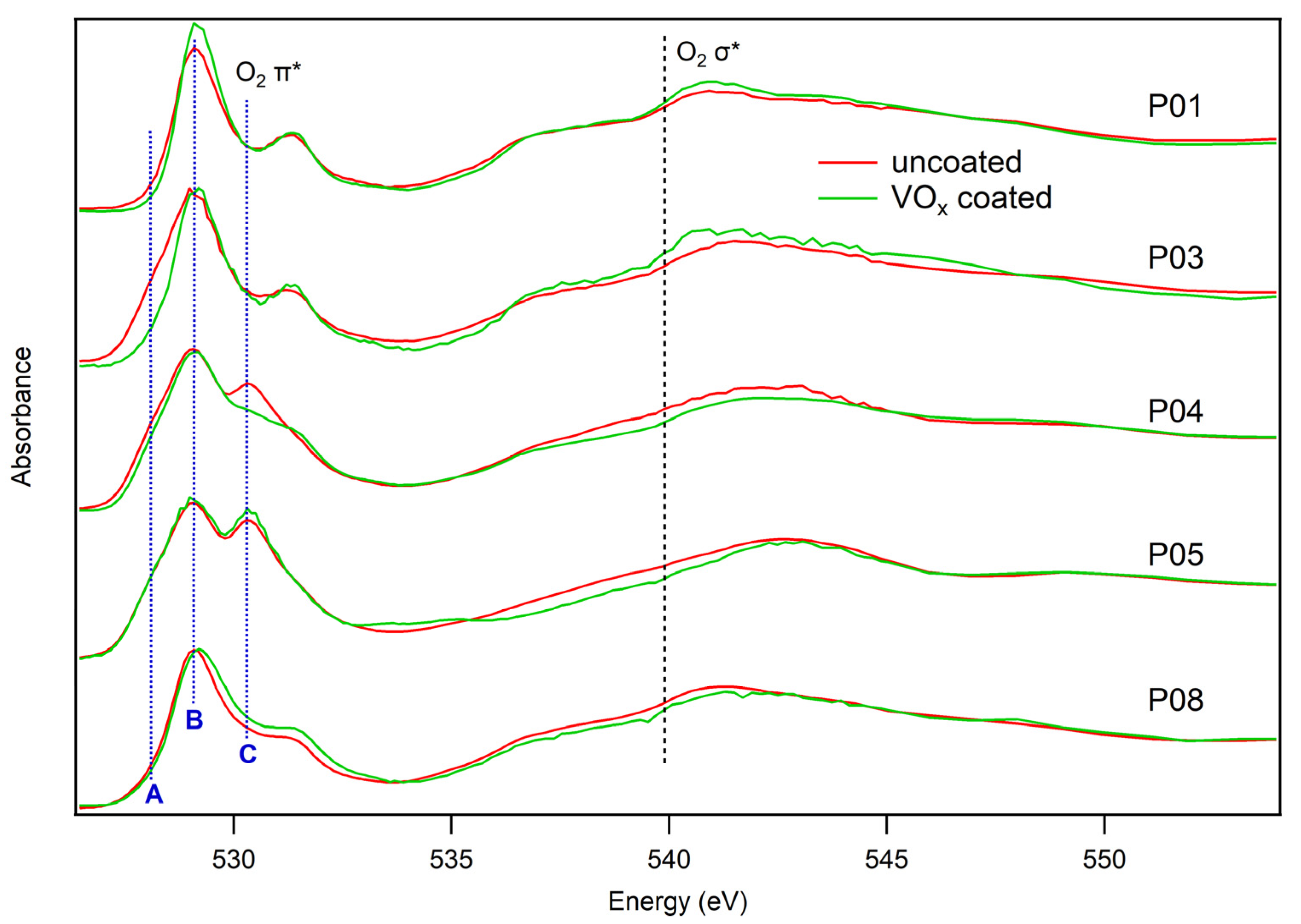
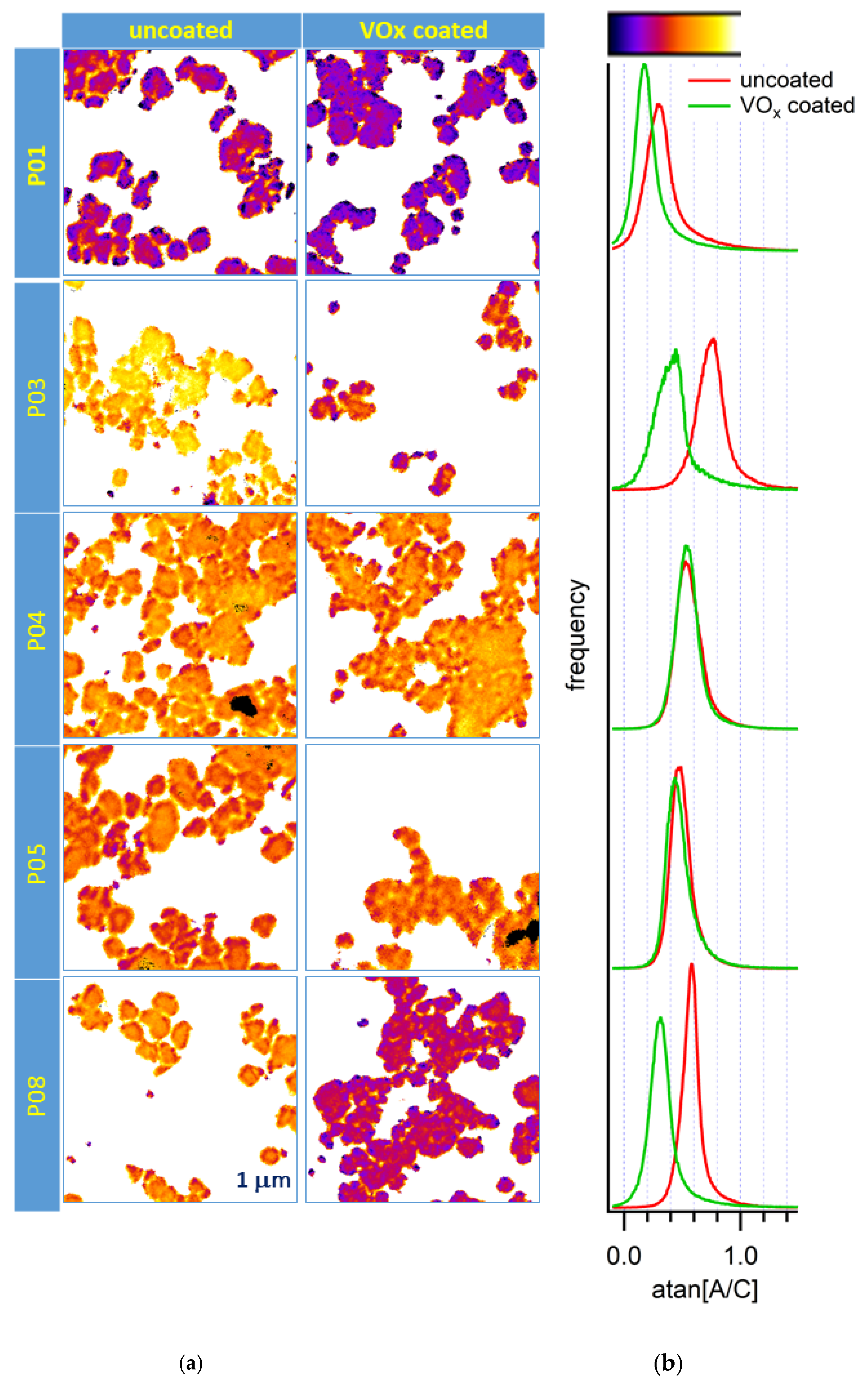
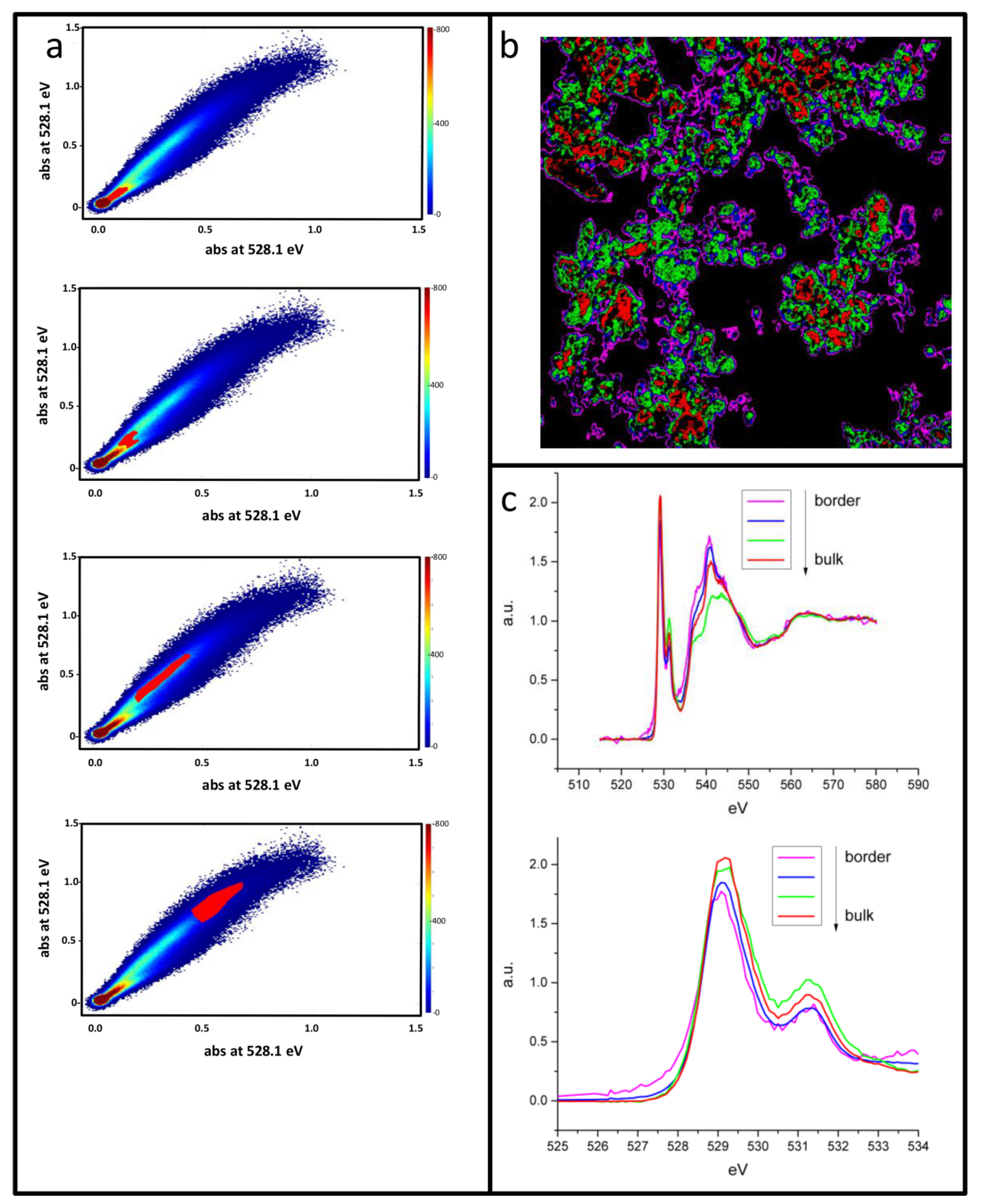
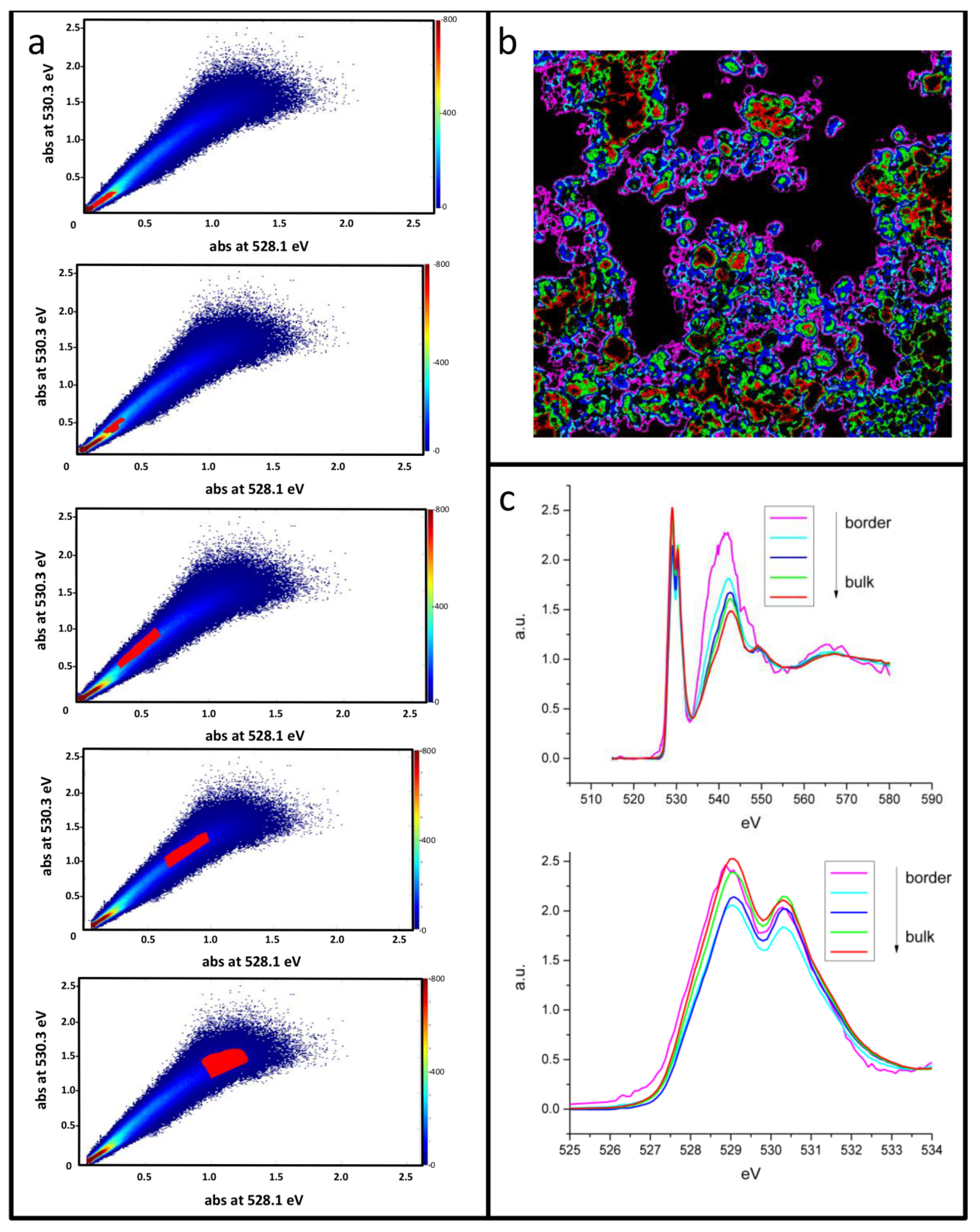
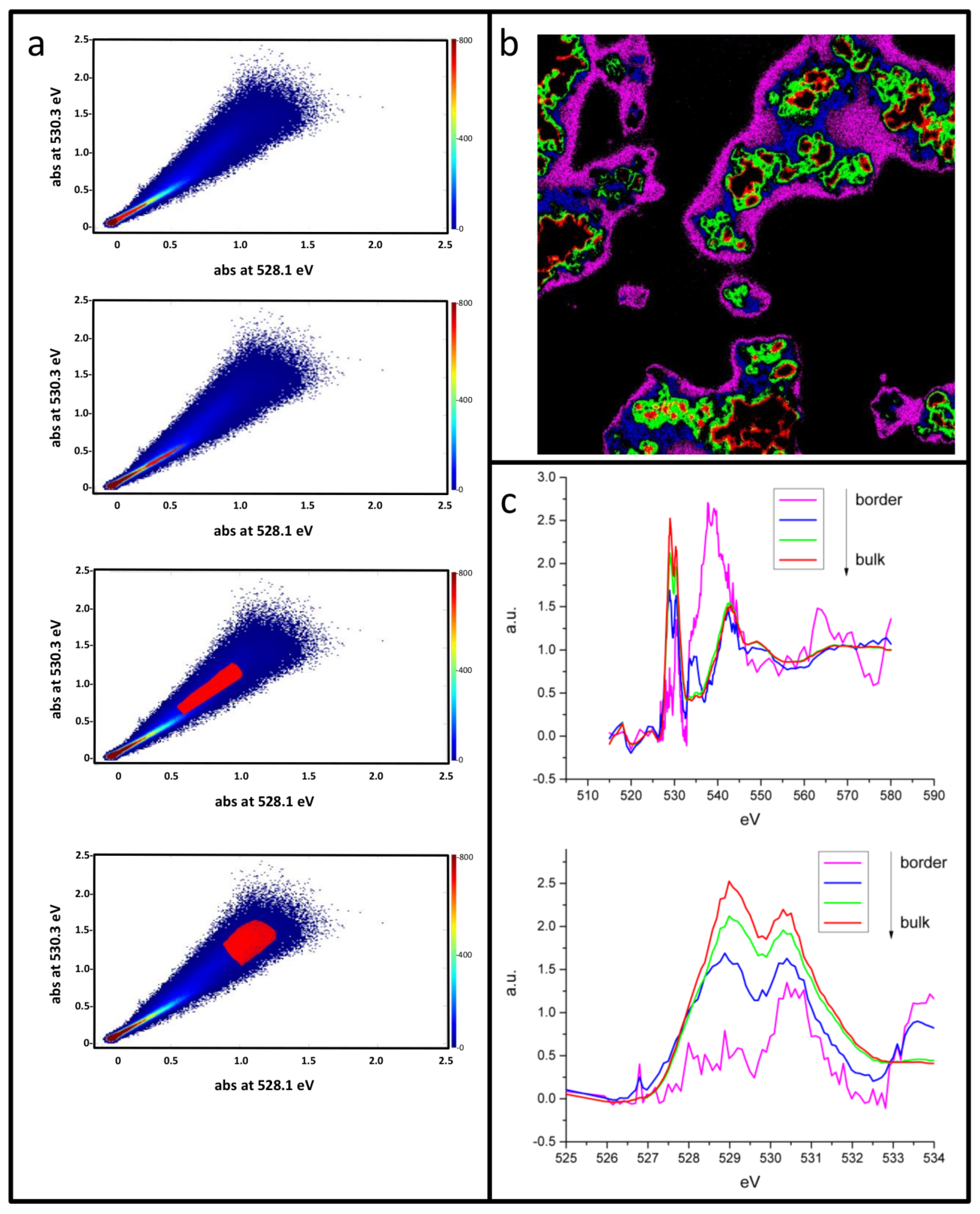
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Stray Light Correction
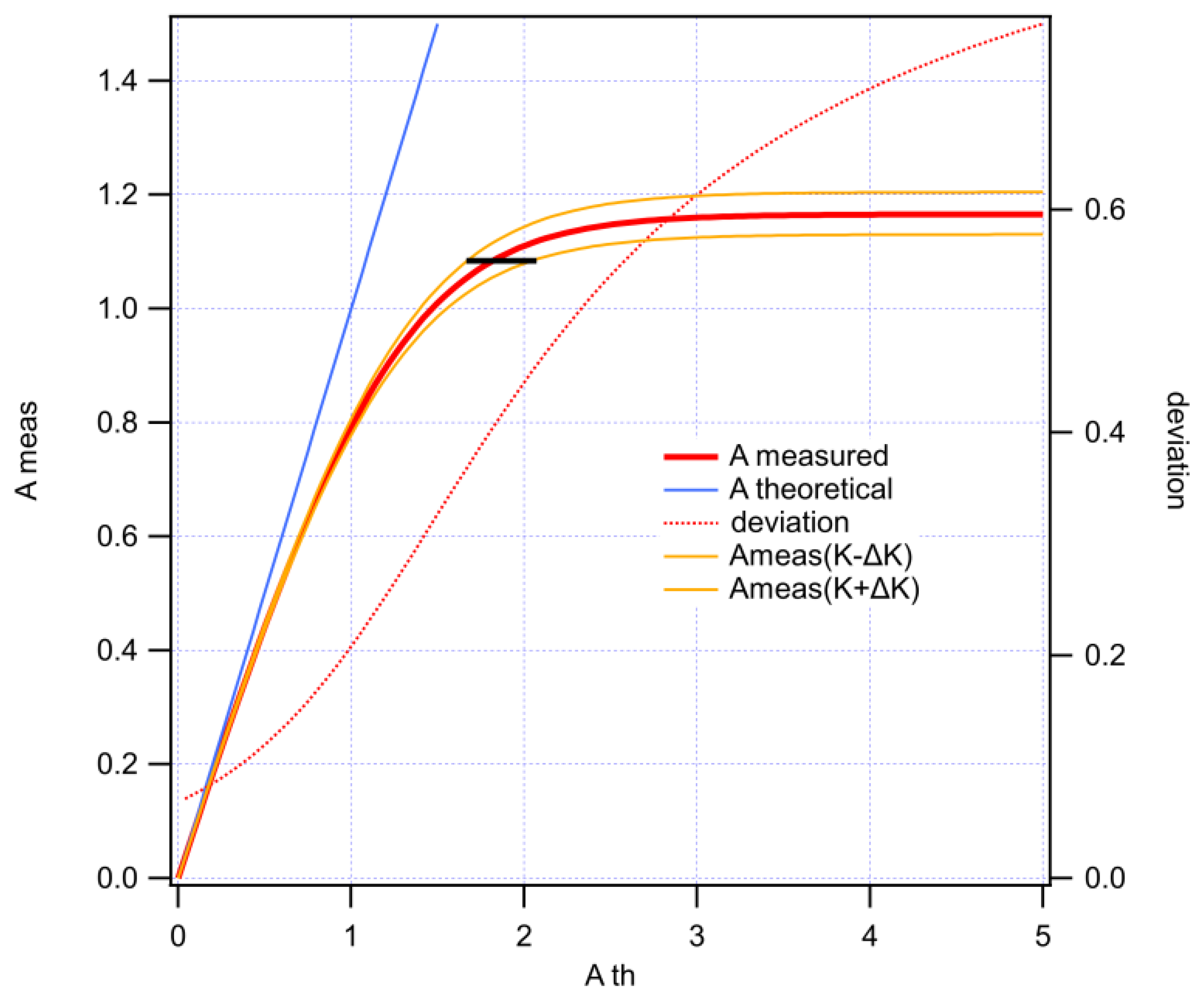
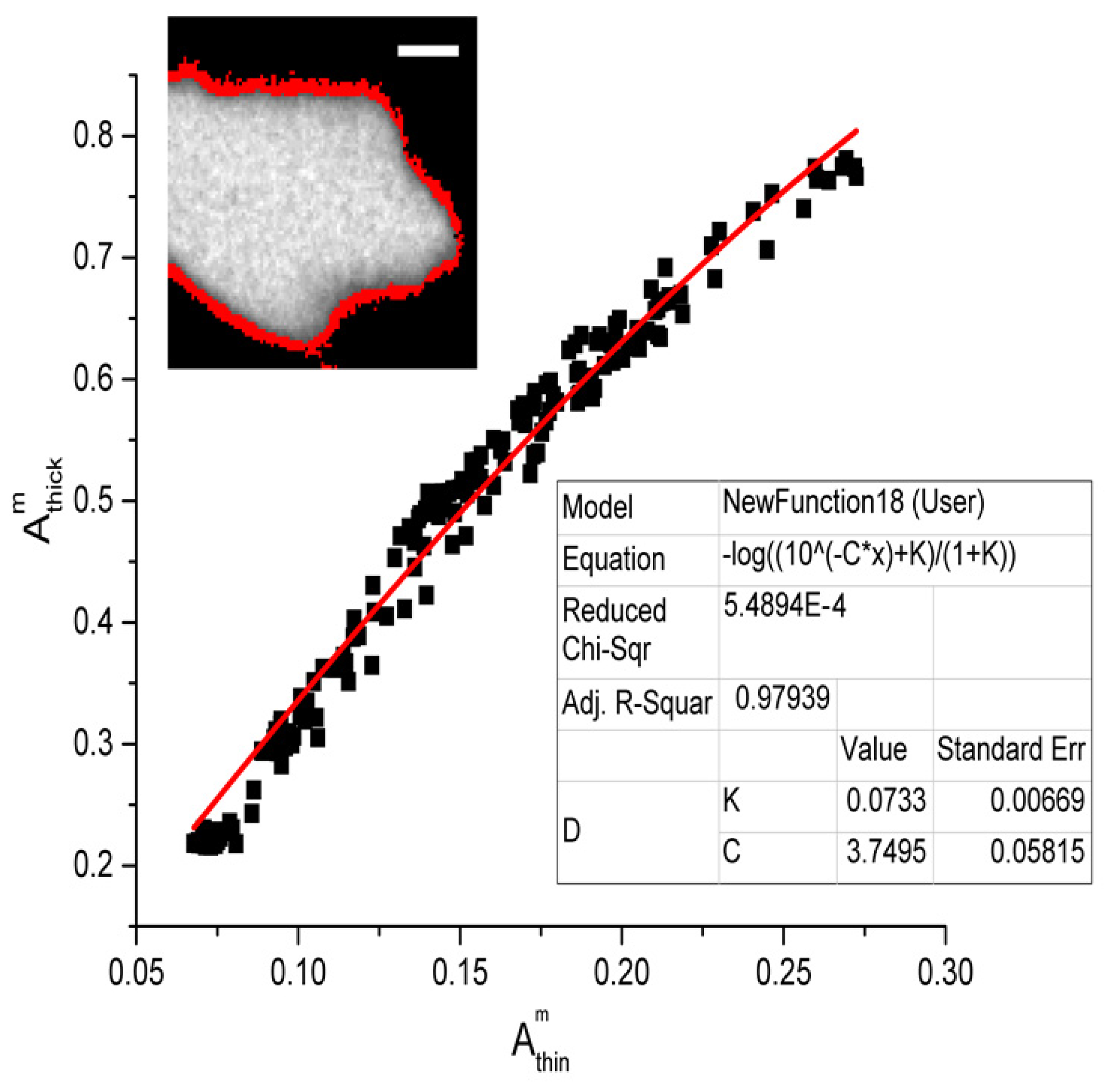

Appendix B. Ratio Correction

References
- Tonti, D.; Olivares-Marín, M.; Sorrentino, A.; Pereiro, E. Studies of Lithium-Oxygen Battery Electrodes by Energy- Dependent Full-Field Transmission Soft X-ray Microscopy. In X-ray Characterization of Nanostructured Energy Materials by Synchrotron Radiation; Petaccia, L., Ed.; IntechOpen: London, UK, 2017. [Google Scholar]
- Olivares-Marin, M.; Sorrentino, A.; Lee, R.C.; Pereiro, E.; Wu, N.L.; Tonti, D. Spatial Distributions of Discharged Products of Lithium-Oxygen Batteries Revealed by Synchrotron X-ray Transmission Microscopy. Nano Lett. 2015, 15, 6932–6938. [Google Scholar] [CrossRef]
- Olivares-Marín, M.; Sorrentino, A.; Pereiro, E.; Tonti, D. Discharge products of ionic liquid-based Li-O2 batteries observed by energy dependent soft X-ray transmission microscopy. J. Power Sources 2017, 359, 234–241. [Google Scholar] [CrossRef]
- Landa-Medrano, I.; Olivares-Marín, M.; Bergner, B.; Pinedo, R.; Sorrentino, A.; Pereiro, E.; Ruiz De Larramendi, I.; Janek, J.; Rojo, T.; Tonti, D. Potassium Salts as Electrolyte Additives in Lithium-Oxygen Batteries. J. Phys. Chem. C 2017, 121, 3822–3829. [Google Scholar] [CrossRef] [Green Version]
- Landa-Medrano, I.; Sorrentino, A.; Stievano, L.; Ruiz de Larramendi, I.; Pereiro, E.; Lezama, L.; Rojo, T.; Tonti, D. Architecture of Na-O2 battery deposits revealed by transmission X-ray microscopy. Nano Energy 2017, 37, 224–231. [Google Scholar] [CrossRef]
- Sathiya, M.; Rousse, G.; Ramesha, K.; Laisa, C.P.; Vezin, H.; Sougrati, M.T.; Doublet, M.L.; Foix, D.; Gonbeau, D.; Walker, W.; et al. Reversible anionic redox chemistry in high-capacity layered-oxide electrodes. Nat Mater 2013, 12, 827–835. [Google Scholar] [CrossRef] [PubMed]
- McCalla, E.; Sougrati, M.T.; Rousse, G.; Berg, E.J.; Abakumov, A.; Recham, N.; Ramesha, K.; Sathiya, M.; Dominko, R.; Van Tendeloo, G.; et al. Understanding the Roles of Anionic Redox and Oxygen Release during Electrochemical Cycling of Lithium-Rich Layered Li4FeSbO6. J. Am. Chem. Soc. 2015, 137, 4804–4814. [Google Scholar] [CrossRef] [PubMed]
- Assat, G.; Delacourt, C.; Corte, D.A.D.; Tarascon, J.M. Practical assessment of anionic redox in Li-rich layered oxide cathodes: A mixed blessing for high energy Li-ion batteries. J. Electrochem. Soc. 2016, 163, A2965–A2976. [Google Scholar] [CrossRef]
- Grimaud, A.; Hong, W.T.; Shao-Horn, Y.; Tarascon, J.M. Anionic redox processes for electrochemical devices. Nat. Mater. 2016, 15, 121–126. [Google Scholar] [CrossRef]
- Seo, D.H.; Lee, J.; Urban, A.; Malik, R.; Kang, S.; Ceder, G. The structural and chemical origin of the oxygen redox activity in layered and cation-disordered Li-excess cathode materials. Nat. Chem. 2016, 8, 692–697. [Google Scholar] [CrossRef]
- Luo, K.; Roberts, M.R.; Guerrini, N.; Tapia-Ruiz, N.; Hao, R.; Massel, F.; Pickup, D.M.; Ramos, S.; Liu, Y.S.; Guo, J.; et al. Anion Redox Chemistry in the Cobalt Free 3d Transition Metal Oxide Intercalation Electrode Li[Li0.2Ni0.2Mn0.6]O2. J. Am. Chem. Soc. 2016, 138, 11211–11218. [Google Scholar] [CrossRef] [Green Version]
- Ben Yahia, M.; Vergnet, J.; Saubanère, M.; Doublet, M.L. Unified picture of anionic redox in Li/Na-ion batteries. Nat. Mater. 2019, 18, 496–502. [Google Scholar] [CrossRef] [Green Version]
- House, R.A.; Maitra, U.; Pérez-Osorio, M.A.; Lozano, J.G.; Jin, L.; Somerville, J.W.; Duda, L.C.; Nag, A.; Walters, A.; Zhou, K.J.; et al. Superstructure control of first-cycle voltage hysteresis in oxygen-redox cathodes. Nature 2020, 577, 502–508. [Google Scholar] [CrossRef] [PubMed]
- House, R.A.; Rees, G.J.; Pérez-Osorio, M.A.; Marie, J.J.; Boivin, E.; Robertson, A.W.; Nag, A.; Garcia-Fernandez, M.; Zhou, K.J.; Bruce, P.G. First-cycle voltage hysteresis in Li-rich 3d cathodes associated with molecular O2 trapped in the bulk. Nat. Energy 2020, 5, 777–785. [Google Scholar] [CrossRef]
- Eum, D.; Kim, B.; Kim, S.J.; Park, H.; Wu, J.; Cho, S.P.; Yoon, G.; Lee, M.H.; Jung, S.K.; Yang, W.; et al. Voltage decay and redox asymmetry mitigation by reversible cation migration in lithium-rich layered oxide electrodes. Nat. Mater. 2020, 19, 419–427. [Google Scholar] [CrossRef] [Green Version]
- Kleiner, K.; Strehle, B.; Baker, A.R.; Day, S.J.; Tang, C.C.; Buchberger, I.; Chesneau, F.F.; Gasteiger, H.A.; Piana, M. Origin of High Capacity and Poor Cycling Stability of Li-Rich Layered Oxides: A Long-Duration in Situ Synchrotron Powder Diffraction Study. Chem. Mater. 2018, 30, 3656–3667. [Google Scholar] [CrossRef]
- Simonelli, L.; Sorrentino, A.; Marini, C.; Ramanan, N.; Heinis, D.; Olszewski, W.; Mullaliu, A.; Birrozzi, A.; Laszczynski, N.; Giorgetti, M.; et al. Role of Manganese in Lithium- and Manganese-Rich Layered Oxides Cathodes. J. Phys. Chem. Lett. 2019, 10, 3359–3368. [Google Scholar] [CrossRef]
- Ali, S.E.; Olszewski, W.; Sorrentino, A.; Marini, C.; Kazzazi, A.; Laszczynski, N.; Birrozzi, A.; Mullaliu, A.; Passerini, S.; Tonti, D.; et al. Local Interactions Governing the Performances of Lithium- and Manganese-Rich Cathodes. J. Phys. Chem. Lett. 2021, 1195–1201. [Google Scholar] [CrossRef] [PubMed]
- Buchholz, D.; Li, J.; Passerini, S.; Aquilanti, G.; Wang, D.; Giorgetti, M. X-ray Absorption Spectroscopy Investigation of Lithium-Rich, Cobalt-Poor Layered-Oxide Cathode Material with High Capacity. ChemElectroChem 2015, 2, 85–97. [Google Scholar] [CrossRef]
- Laszczynski, N.; von Zamory, J.; Kalhoff, J.; Loeffler, N.; Chakravadhanula, V.S.K.; Passerini, S. Improved Performance of VOx-Coated Li-Rich NMC Electrodes. ChemElectroChem 2015, 2, 1768–1773. [Google Scholar] [CrossRef]
- Ruckman, M.W.; Chen, J.; Qiu, S.L.; Kuiper, P.; Strongin, M.; Dunlap, B.I. Interpreting the near edges of O2 and O2- in alkali-metal superoxides. Phys. Rev. Lett. 1991, 67, 2533–2536. [Google Scholar] [CrossRef]
- Beer, A. Bestimmung der Absorption des rothen Lichts in farbigen Flüssigkeiten. Ann. Phys. 1852, 162, 78–88. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, B.K. X-ray Spectroscopy, 2nd ed.; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 1991; ISBN 978-3540507192. [Google Scholar]
- de Groot, F.; Kotani, A. Core Level Spectroscopy of Solids; Springer: Berlin, Germany, 2008; ISBN 9781420008425. [Google Scholar]
- Stöhr, J. NEXAFS Spectroscopy; Springer: Berlin/Heidelberg, Germany, 1992; Volume 25, ISBN 9783540544227. [Google Scholar]
- Sorrentino, A.; Nicolás, J.; Valcárcel, R.; Chichón, F.J.; Rosanes, M.; Avila, J.; Tkachuk, A.; Irwin, J.; Ferrer, S.; Pereiro, E. MISTRAL: A transmission soft X-ray microscopy beamline for cryo nano-tomography of biological samples and magnetic domains imaging. J. Synchrotron Radiat. 2015, 22, 1112–1117. [Google Scholar] [CrossRef]
- Kahil, K.; Varsano, N.; Sorrentino, A.; Pereiro, E.; Rez, P.; Weiner, S.; Addadi, L. Cellular pathways of calcium transport and concentration toward mineral formation in sea urchin larvae. Proc. Natl. Acad. Sci. USA 2020, 117, 30957–30965. [Google Scholar] [CrossRef]
- Sviben, S.; Gal, A.; Hood, M.A.; Bertinetti, L.; Politi, Y.; Bennet, M.; Krishnamoorthy, P.; Schertel, A.; Wirth, R.; Sorrentino, A.; et al. A vacuole-like compartment concentrates a disordered calcium phase in a key coccolithophorid alga. Nat. Commun. 2016, 7. [Google Scholar] [CrossRef]
- Gal, A.; Sorrentino, A.; Kahil, K.; Pereiro, E.; Faivre, D.; Scheffel, A. Native-state imaging of calcifying and noncalcifying microalgae reveals similarities in their calcium storage organelles. Proc. Natl. Acad. Sci. USA 2018, 115, 11000–11005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bertilson, M.; von Hofsten, O.; Hertz, H.M.; Vogt, U. Numerical model for tomographic image formation in transmission X-ray microscopy. Opt. Express 2011, 19, 11578–11583. [Google Scholar] [CrossRef] [PubMed]
- Frati, F.; Hunault, M.O.J.Y.; De Groot, F.M.F. Oxygen K-edge X-ray Absorption Spectra. Chem. Rev. 2020, 120, 4056–4110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DeVol, R.T.; Metzler, R.A.; Kabalah-Amitai, L.; Pokroy, B.; Politi, Y.; Gal, A.; Addadi, L.; Weiner, S.; Fernandez-Martinez, A.; Demichelis, R.; et al. Oxygen spectroscopy and polarization-dependent imaging contrast (PIC)-mapping of calcium carbonate minerals and biominerals. J. Phys. Chem. B 2014, 118, 8449–8457. [Google Scholar] [CrossRef] [PubMed]
- Hinkley, D.V. On the ratio of two correlated normal random variables. Biometrika 1969, 56, 635–639. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sorrentino, A.; Simonelli, L.; Kazzazi, A.; Laszczynski, N.; Birrozzi, A.; Mullaliu, A.; Pereiro, E.; Passerini, S.; Giorgetti, M.; Tonti, D. Soft X-ray Transmission Microscopy on Lithium-Rich Layered-Oxide Cathode Materials. Appl. Sci. 2021, 11, 2791. https://doi.org/10.3390/app11062791
Sorrentino A, Simonelli L, Kazzazi A, Laszczynski N, Birrozzi A, Mullaliu A, Pereiro E, Passerini S, Giorgetti M, Tonti D. Soft X-ray Transmission Microscopy on Lithium-Rich Layered-Oxide Cathode Materials. Applied Sciences. 2021; 11(6):2791. https://doi.org/10.3390/app11062791
Chicago/Turabian StyleSorrentino, Andrea, Laura Simonelli, Arefehsadat Kazzazi, Nina Laszczynski, Agnese Birrozzi, Angelo Mullaliu, Eva Pereiro, Stefano Passerini, Marco Giorgetti, and Dino Tonti. 2021. "Soft X-ray Transmission Microscopy on Lithium-Rich Layered-Oxide Cathode Materials" Applied Sciences 11, no. 6: 2791. https://doi.org/10.3390/app11062791
APA StyleSorrentino, A., Simonelli, L., Kazzazi, A., Laszczynski, N., Birrozzi, A., Mullaliu, A., Pereiro, E., Passerini, S., Giorgetti, M., & Tonti, D. (2021). Soft X-ray Transmission Microscopy on Lithium-Rich Layered-Oxide Cathode Materials. Applied Sciences, 11(6), 2791. https://doi.org/10.3390/app11062791








