3D Cavitation Shedding Dynamics: Cavitation Flow-Fluid Vortex Formation Interaction in a Hydrodynamic Torque Converter
Abstract
:1. Introduction
2. Methodology
2.1. Turbulence Model
2.2. Cavitation Model
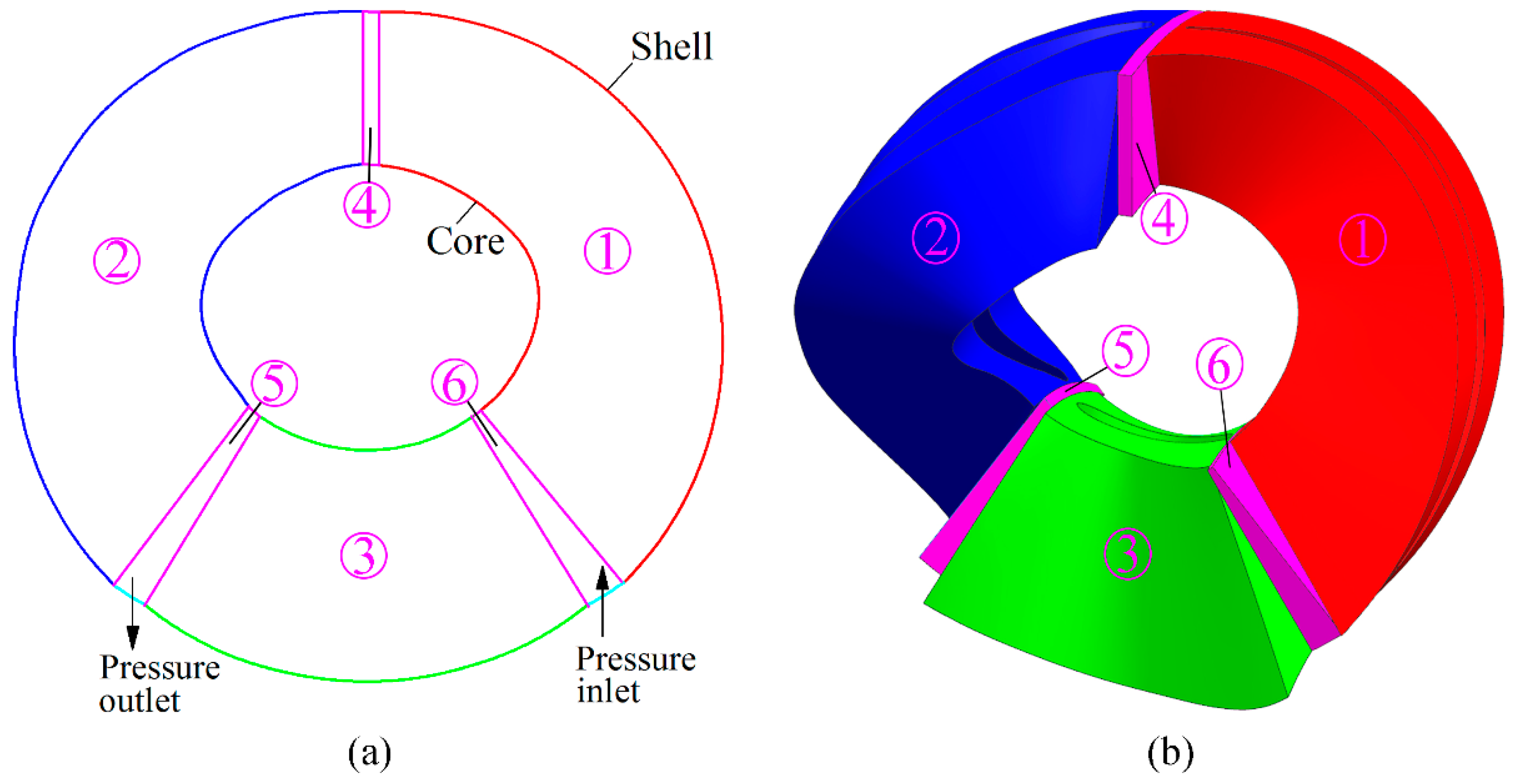
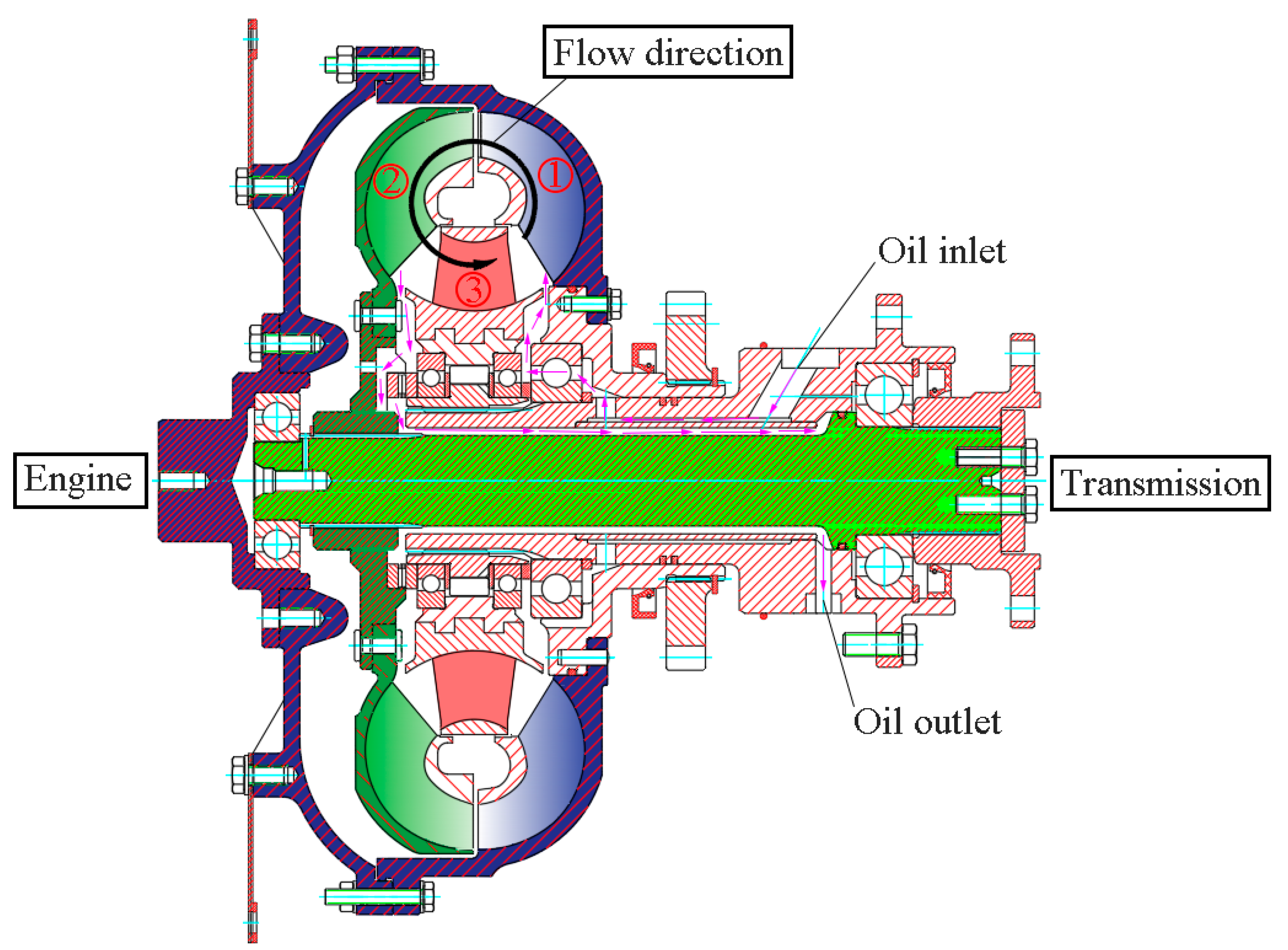
2.3. Simulation Setup
3. Transient Cavitation Behavior in a Hydrodynamic Torque Converter
3.1. Validation of the CFD Model
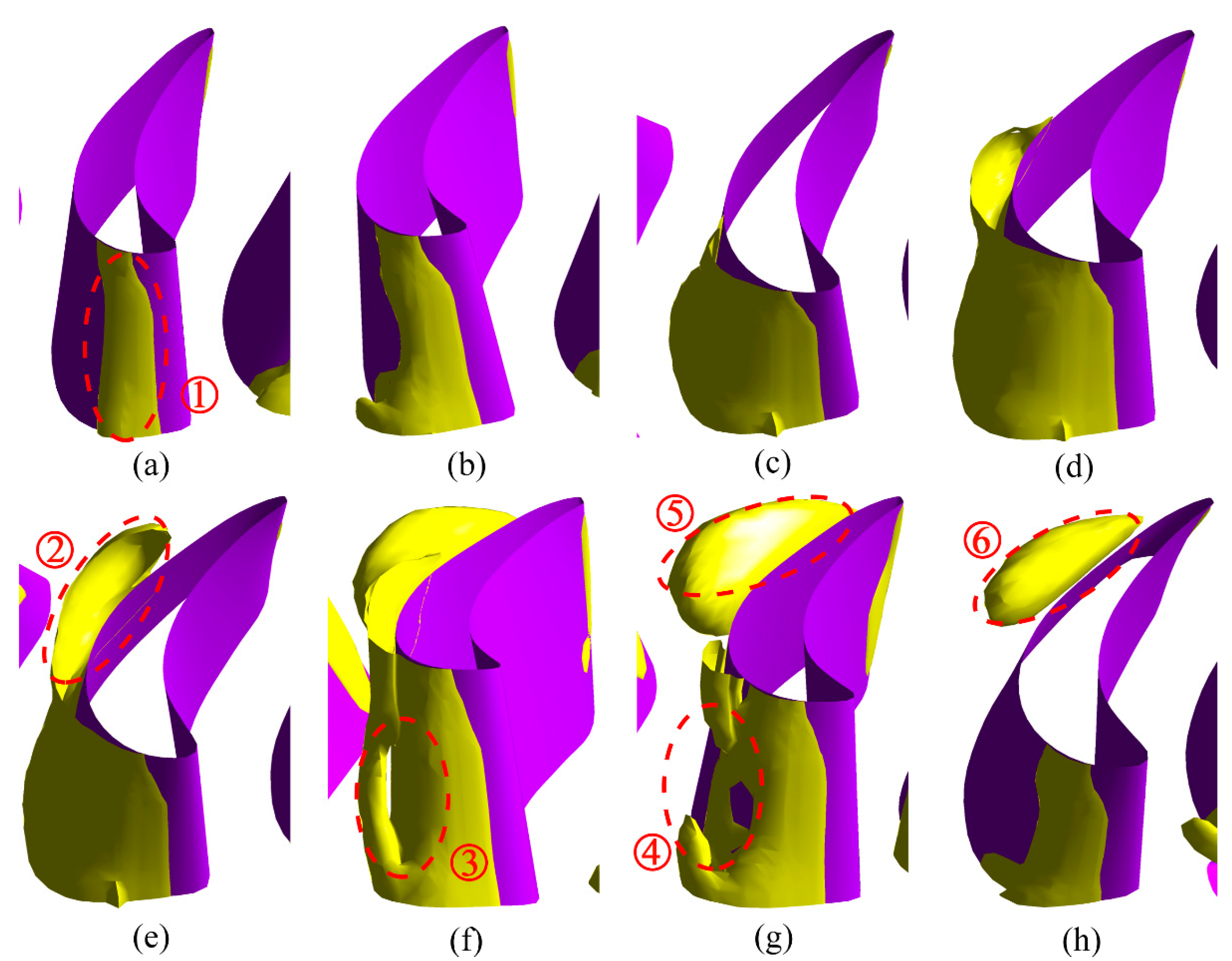
3.2. Transient Cavitation Behavior in the Hydrodynamic Torque Converter under the Stall Operating Condition
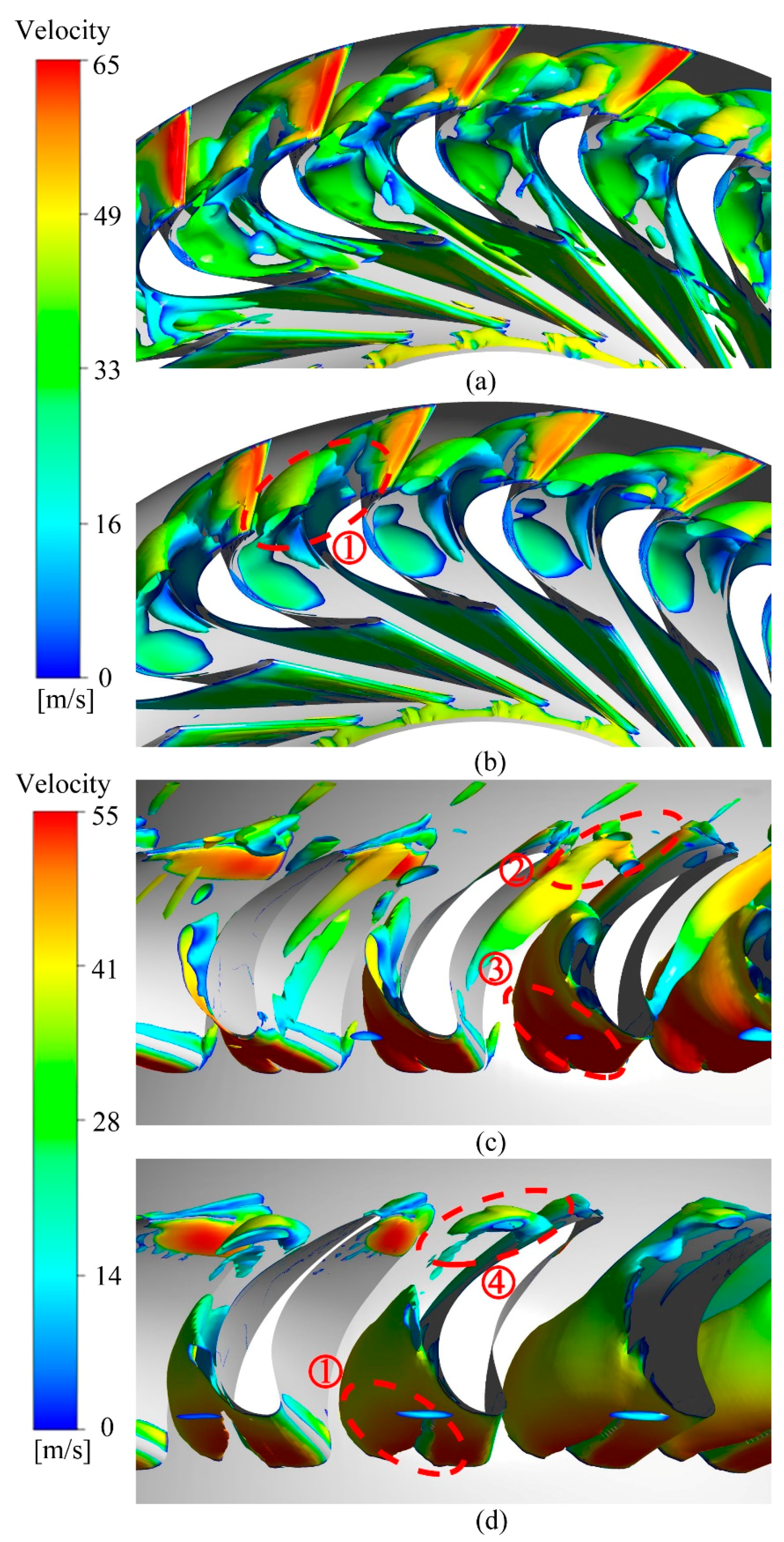
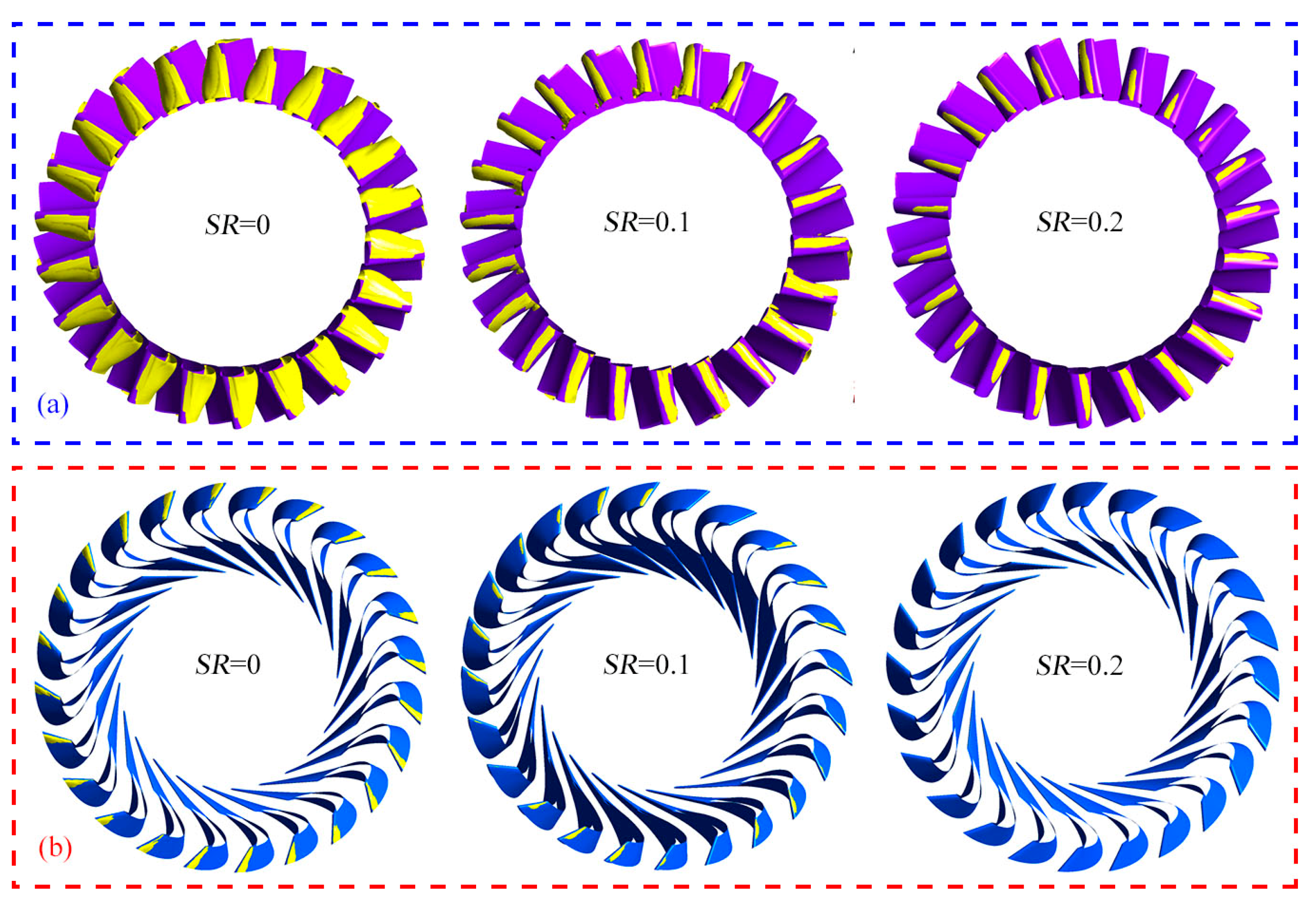
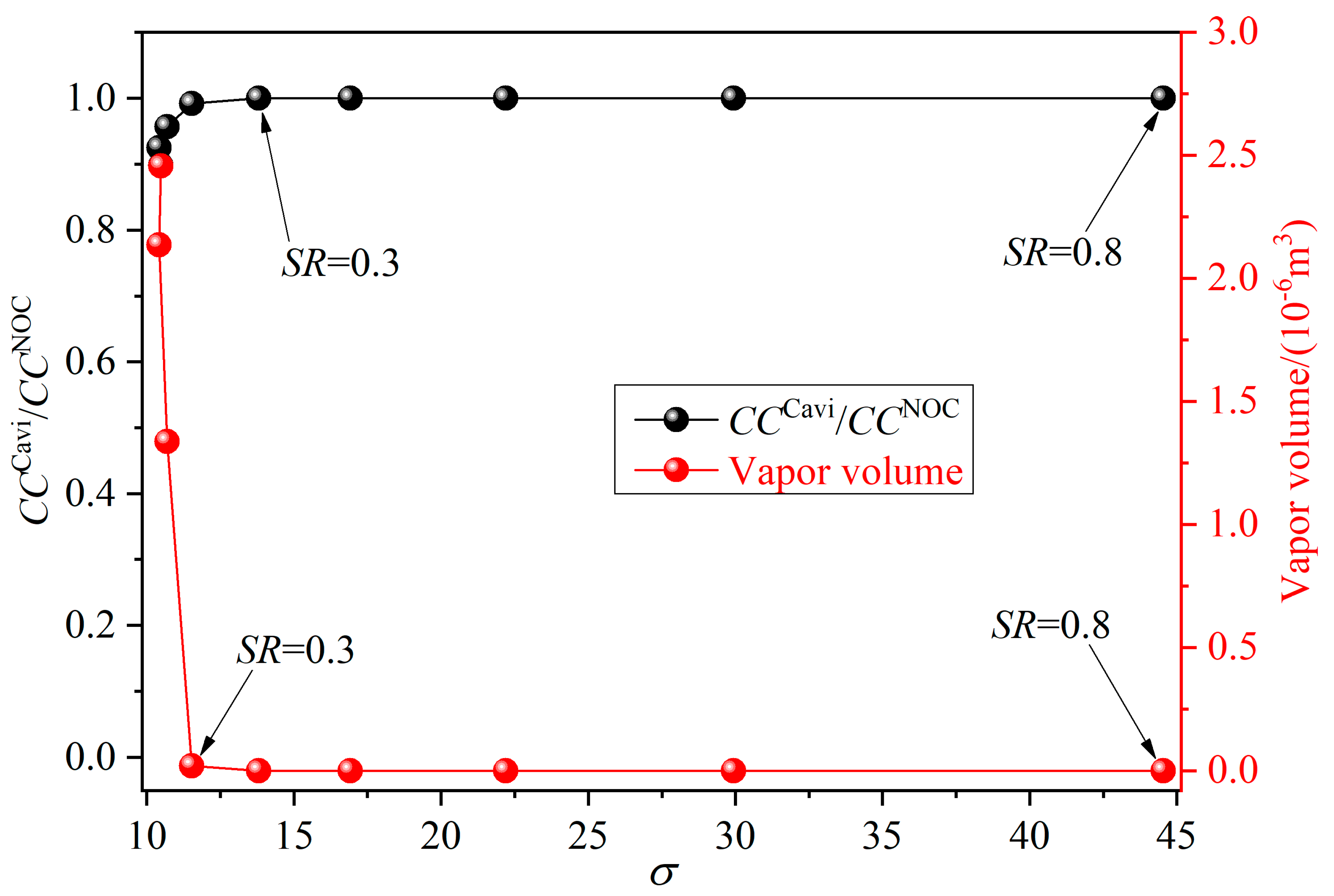
3.3. Cavitation Phenomena at Different SRs
4. Cavitation Effects
4.1. Pressure Distribution on the Stator Blade Surface According to the Two CFD Models
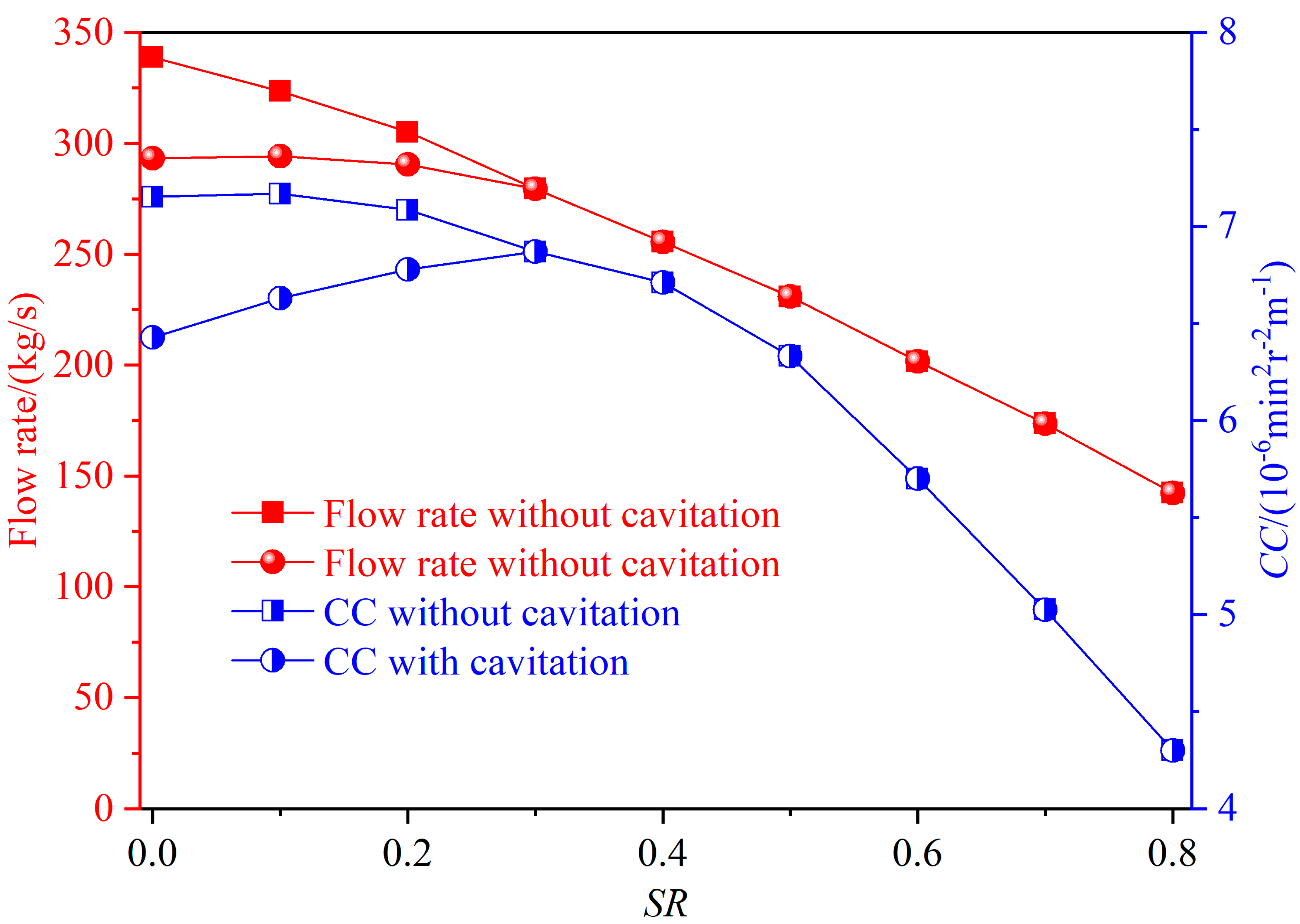
4.2. Mass Flow Rate and Capacity Loss in the Hydrodynamic Torque Converter
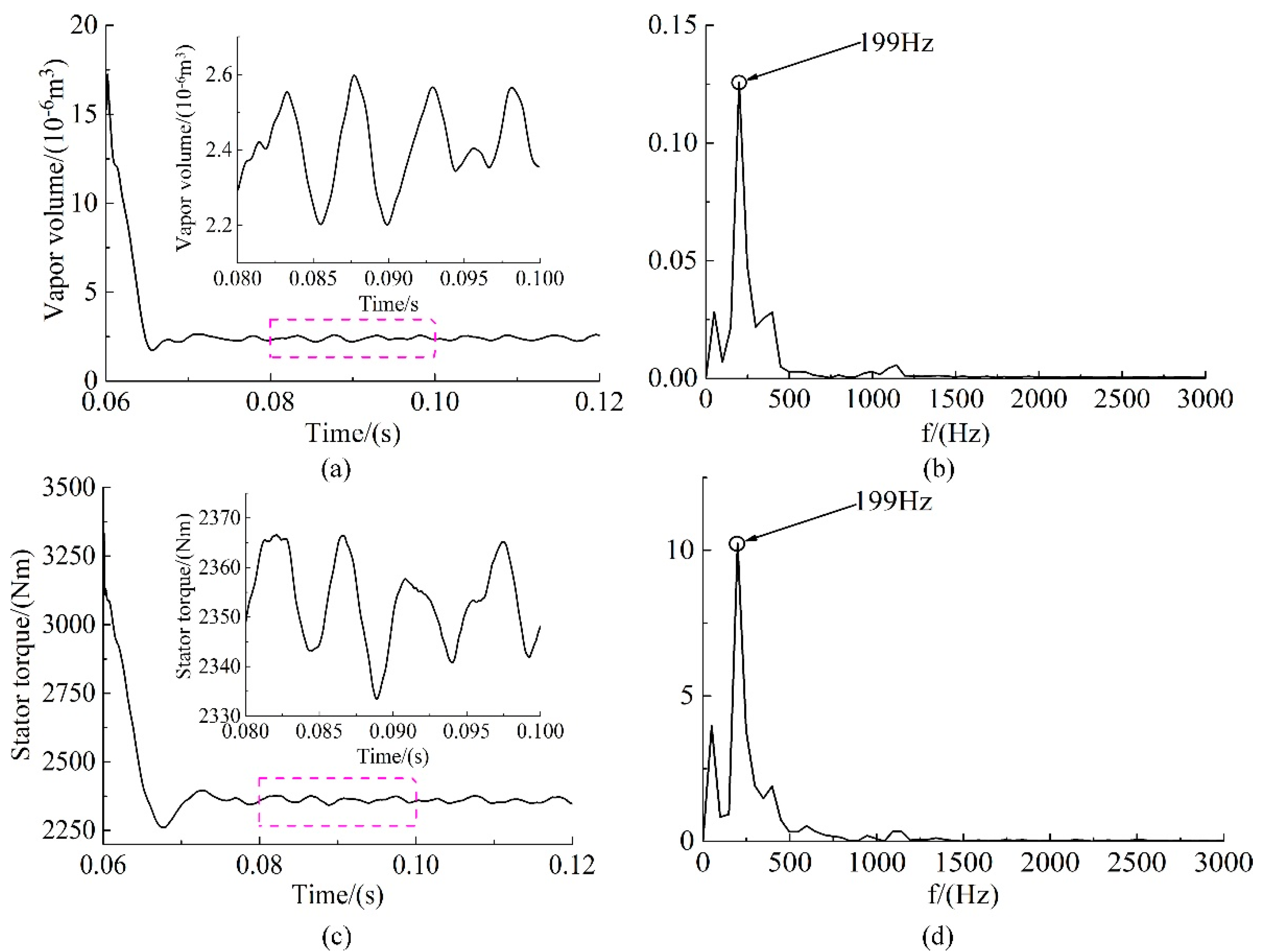
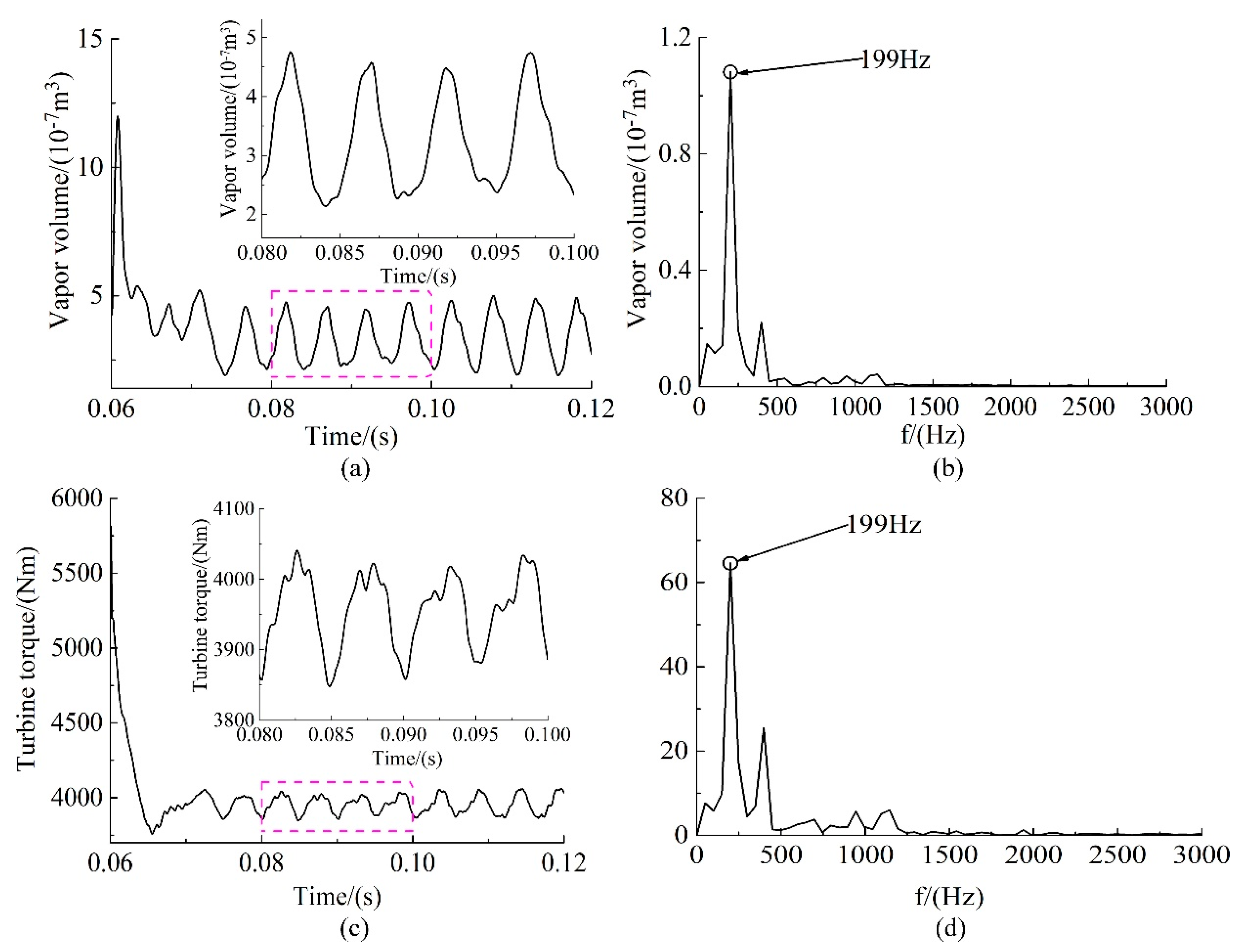
4.3. Spectral Analysis of the Stator and Turbine Torque
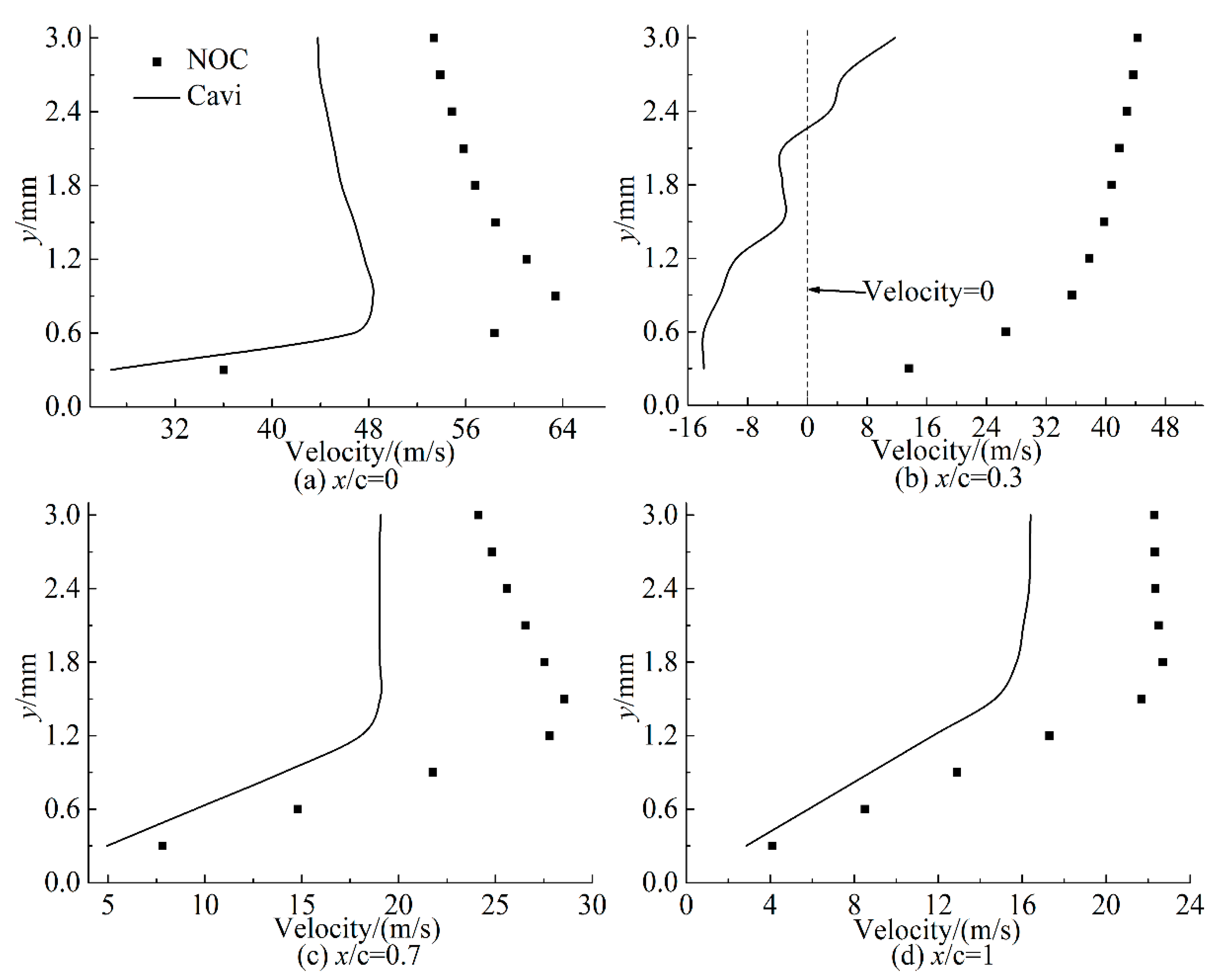
4.4. Normal Velocity Distribution at the Stator Surface with the Two CFD Models
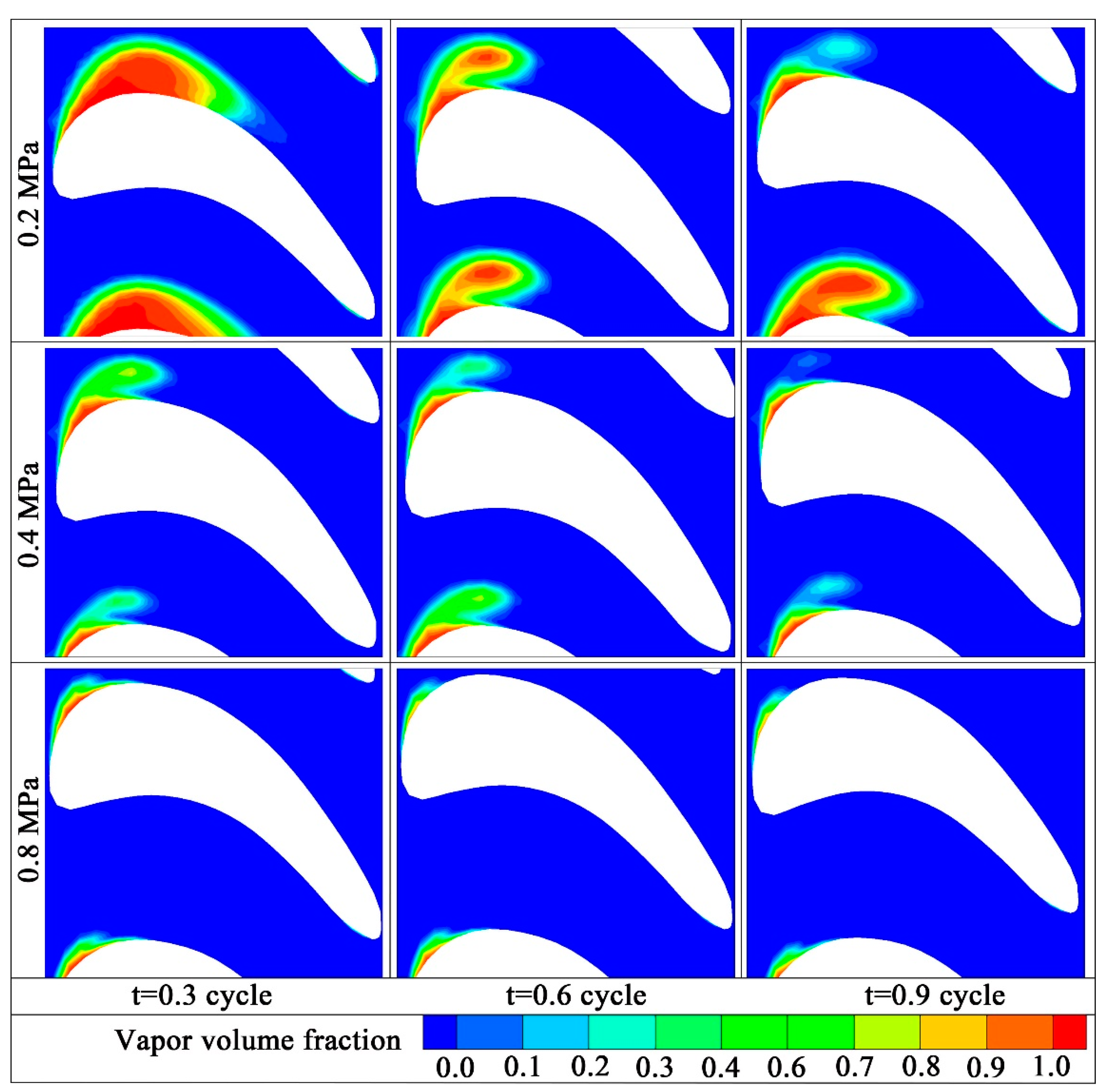
4.5. Effect of the Backpressure
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| speed ratio | |
| hydrodynamic torque converter torus diameter, mm | |
| turbine rotation speed, rpm | |
| pump rotation speed, rpm | |
| turbine torque, | |
| pump torque, | |
| torque ratio | |
| capacity constant, 10−6 | |
| efficiency | |
| charge pressure, Pa | |
| liquid volume fraction | |
| liquid density, kg m−3 | |
| velocity, m s−1 | |
| mass flow rate, kg s−1 | |
| bubble radius, m | |
| vapor pressure, Pa | |
| mixture pressure, Pa | |
| vapor volume fraction | |
| vapor density, kg m−3 | |
| volume fraction of the nucleation site | |
| vaporization constant | |
| condensation constant | |
| mixture density, kg m−3 | |
| mixture dynamic viscosity, Pa s | |
| liquid dynamic viscosity, Pa s | |
| vapor dynamic viscosity, Pa s | |
| cavitation number | |
| reference pressure, Pa | |
| reference velocity, m s−1 | |
| c | blade camberline length, mm |
| List of Sub-Indices | |
| Test | test data |
| NOC | non-cavitation CFD results |
| Cavi | cavitation CFD results |
References
- Liu, C.; Li, J.; Bu, W.; Ma, W.; Shen, G.; Yuan, Z. Large eddy simulation for improvement of performance estimation and turbulent flow analysis in a hydrodynamic torque converter. Eng. Appl. Comput. Fluid Mech. 2018, 12, 635–651. [Google Scholar] [CrossRef] [Green Version]
- Flack, R.; Brun, K. Fundamental analysis of the secondary flows and jet-wake in a torque converter pump—Part 1: Model and flow in a rotating passage. ASME J. Fluids Eng. 2003, 127, 1183–1191. [Google Scholar]
- Wu, G.Q.; Wang, L.J. Application of dual-blade stator to low-speed ratio performance improvement of torque converters. China J. Mech. Eng. 2016, 29, 293–300. [Google Scholar] [CrossRef]
- Bakir, F.; Rey, R.; Gerber, A.G.; Belamri, T.; Hutchinson, B. Numerical and experimental investigations of the cavitating behavior of an inducer. Int. J. Rotating Mach. 2007, 10, 15–25. [Google Scholar] [CrossRef] [Green Version]
- Brennen, C.E. A review of the dynamics of cavitating pumps. ASME J. Fluids Eng. 2012, 135, 301–311. [Google Scholar] [CrossRef]
- Park, S.I.; Lee, S.J.; You, G.S.; Suh, J.C. An experimental study on tip vortex cavitation suppression in a marine propeller. J. Ship Res. 2014, 58, 157–167. [Google Scholar] [CrossRef]
- Tsutsumi, K.; Watanable, S.; Tsuda, S.; Yamaguchi, T. Cavitation simulation of automotive torque converter using a homogeneous cavitation model. Eur. J. Mech. B Fluids 2016, 61, 263–270. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.S.; Shi, L.; Shi, W.D. Numerical simulation and experimental study on impeller tip region cavitation in axial flow pump. J. Hydraul. Eng. 2014, 45, 335–342. [Google Scholar]
- Bilus, I.; Predin, A. Numerical and experimental approach to cavitation surge obstruction in water pump. Int. J. Numer. Methods Heat Fluid Flow 2009, 19, 818–834. [Google Scholar] [CrossRef]
- Feng, X.R.; Lu, J.M. Effects of balanced skew and biased skew on the cavitation characteristics and pressure fluctuations of the marine propeller. Ocean. Eng. 2019, 184, 184–192. [Google Scholar] [CrossRef]
- Anderson, C.L.; Zeng, L.; Sweger, P.O.; Narain, A.; Blough, J.R. Experimental Investigation of Cavitation Signatures in an Automotive Torque Converter Using a Microwave Telemetry Technique. Int. J. Rotating Mach. 2003, 9, 403–410. [Google Scholar] [CrossRef] [Green Version]
- Mekkes, J.; Anderson, C.; Narain, A. Static Pressure Measurements and Cavitation Signatures on the Nose of a Torque Converter’s Stator Blades. In Proceedings of the 10th International Symposium on Rotating Machinery (ISROMAC-10), Honolulu, HI, USA, 7–11 March 2004. Paper no. ISROMAC10-2004-035. [Google Scholar]
- Kowalski, D.; Anderson, C.; Blough, J. Cavitation Detection in Automotive Torque Converters Using Nearfield Acoustical Measurements. SAE Trans. 2005, 114, 2796–2804. [Google Scholar]
- Foeth, E.J.; Van Doorne, C.W.H.; Van Terwisga, T.; Wieneke, B. Time resolved PIV and flow visualization of 3D sheet cavitation. Exp. Fluids 2006, 40, 503–513. [Google Scholar] [CrossRef]
- Kravtsova, A.Y.; Markovich, D.M.; Pervunin, K.S.; Timoshevskiy, M.; Hanjalić, K. High-speed visualization and PIV measurements of cavitating flows around a semi-circular leading-edge flat plate and NACA0015 hydrofoil. Int. J. Multiph. Flow 2014, 60, 119–134. [Google Scholar] [CrossRef]
- Kravtsova, A.Y.; Markovich, D.M.; Pervunin, K.S.; Timoshevskii, M.V.; Hanjalić, K. Cavitation on a semicircular leading-edge plate and NACA0015 hydrofoil: Visualization and velocity measurement. Therm. Eng. 2014, 61, 1007–1014. [Google Scholar] [CrossRef]
- Kravtsova, A.Y.; Markovich, D.M.; Pervunin, K.S.; Timoshevskiy, M.V. High-speed imaging and PIV measurements in turbulent cavitating flows around 2D hydrofoils. In International Symposium on Turbulence and Shear Flow Phenomena (TSFP); Elsevier: Amsterdam, Netherlands, 2013; Paper No. TSFP, 2. [Google Scholar]
- Robinette, D.; Anderson, C.; Blough, J.; Johnson, M.; Maddock, D.; Schweitzer, J. Characterizing the Effect of Automotive Torque Converter Design Parameters on the Onset of Cavitation at Stall. SAE Trans. 2007, 116, 1735–1746. [Google Scholar]
- Robinette, D.L.; Schweitzer, J.M.; Maddock, D.G.; Anderson, C.L.; Blough, J.R.; Johnson, M.A. Predicting the Onset of Cavitation in Automotive Torque Converters—Part I: Designs with Geometric Similitude. Int. J. Rotating Mach. 2008, 2008, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Robinette, D.L.; Schweitzer, J.M.; Maddock, D.G.; Anderson, C.L.; Blough, J.R.; Johnson, M.A. Predicting the Onset of Cavitation in Automotive Torque Converters—Part II: A Generalized Model. Int. J. Rotating Mach. 2008, 2008, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, S.; Otani, R.; Kunimoto, S.; Hara, Y.; Furukawa, A.; Yamaguchi, T. Vibration Characteristics due to Cavitation in Stator Element of Automotive Torque Converter at Stall Condition. In ASME Fluids Engineering Division Summer Meeting (FEDSM); ASME: New York, NY, USA; Rio Grande, PR, USA, 2013; pp. 535–541. [Google Scholar]
- Ju, J.; Jang, J.; Choi, M.; Baek, J.H. Effects of Cavitation on Performance of Automotive Torque Converter. Adv. Mech. Eng. 2016, 8, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Wei, W.; Yan, Q.; Weaver, B.K. Torque converter capacity improvement through cavitation control by design. ASME J. Fluids Eng. 2017, 139, 1101–1110. [Google Scholar] [CrossRef]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A Two-Phase Flow Model for Predicting Cavitation Dynamics. In Fifth International Conference on Multiphase Flow; Elsevier: Yokohama, Japan, 2004. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. ASME J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Liu, C.B.; Liu, C.S.; Ma, W.X. Mathematical model for elliptic torus of automotive torque converter and fundamental analysis of its effect on performance. Math. Probl. Eng. 2015, 2015, 1–13. [Google Scholar] [CrossRef]
- Long, X.P.; Cheng, H.Y.; Ji, B.; Arndt, R.E.; Peng, X. Large eddy simulation and Euler-Lagrangian coupling investigation of the transient cavitating turbulent flow around a twisted hydrofoil. Int. J. Multiph. Flow 2018, 100, 41–56. [Google Scholar] [CrossRef]
- Liu, C.; Yan, Q.D.; Wood, H.G. Numerical investigation of passive cavitation control using a slot on a three-dimensional hydrofoil. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 3585–3605. [Google Scholar] [CrossRef]
- Dubief, Y.; Delcayre, F. On coherent-vortex identification in turbulence. J. Turbul. 2000, 1, 1–12. [Google Scholar] [CrossRef]
- Liu, C.; Wei, W.; Yan, Q.D.; Weaver, B.K.; Wood, H.G. Influence of stator blade geometry on torque converter cavitation. ASME J. Fluids Eng. 2018, 140, 1101–1110. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.W.; Wu, Y.L.; Peng, X.; Duan, Y. Numerical analysis of unsteady cavitating turbulent flow and shedding horse-shoe vortex structure around a twisted hydrofoil. Int. J. Multiph. Flow 2013, 51, 33–43. [Google Scholar] [CrossRef] [Green Version]
- Ji, B.; Luo, X.W.; Wang, X.; Peng, X.; Wu, Y.; Xu, H. Unsteady numerical simulation of cavitating turbulent flow around a highly skewed model marine propeller. ASME J. Fluids Eng. 2011, 133, 1101–1108. [Google Scholar] [CrossRef]






| 0.09 | 5/9 | 3/40 | 0.85 | 0.5 | 0.44 | 0.0828 | 1 | 0.856 |
| Analysis Type | Transient |
|---|---|
| Fluid properties | = 860 kg m−3, = 0.0258 Pa s |
| Vapor properties | = 2.1 kg m−3, = 1.2 × 10−5 Pa s |
| Turbulence model | SST k–ω |
| Advection scheme | High resolution |
| Convergence target | RMS 1 × 10−4 |
| Pump status | Fixed at 2000 rpm |
| Turbine status | Variable within 0–1600 rpm |
| Stator status | Stationary |
| Charge pressure | 0.8 MPa |
| Backpressure | 0.4 MPa |
| Transient formulation | Second-order upwind |
| Other term spatial discretization | Second-order upwind |
| Time step | 1 × 10−4 s |
| Boundary details | No slip and smooth wall |
| Vapor pressure () | 110 Pa |
| Element | Inlet Angle | Outlet Angle | Number of Blades |
|---|---|---|---|
| Pump | 123° | 64° | 29 |
| Turbine | 32° | 157° | 24 |
| Stator | 120° | 33° | 22 |
| Charge Pressure (MPa) | Backpressure (MPa) | Vapor Volume (10−6 m3) | Mass Flowrate (kg s−1) | Cavitation Number |
|---|---|---|---|---|
| 0.8 | 0.2 | 4.1827145 | 308.50446 | 9.474 |
| 0.8 | 0.4 | 2.46 | 293.31395 | 10.480 |
| 0.8 | 0.6 | 2.4342955 | 287.00041 | 10.946 |
| 0.8 | 0.8 | 1.8027153 | 277.24304 | 11.731 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, Z.; Ma, W.; Liu, C. 3D Cavitation Shedding Dynamics: Cavitation Flow-Fluid Vortex Formation Interaction in a Hydrodynamic Torque Converter. Appl. Sci. 2021, 11, 2798. https://doi.org/10.3390/app11062798
Ran Z, Ma W, Liu C. 3D Cavitation Shedding Dynamics: Cavitation Flow-Fluid Vortex Formation Interaction in a Hydrodynamic Torque Converter. Applied Sciences. 2021; 11(6):2798. https://doi.org/10.3390/app11062798
Chicago/Turabian StyleRan, Zilin, Wenxing Ma, and Chunbao Liu. 2021. "3D Cavitation Shedding Dynamics: Cavitation Flow-Fluid Vortex Formation Interaction in a Hydrodynamic Torque Converter" Applied Sciences 11, no. 6: 2798. https://doi.org/10.3390/app11062798
APA StyleRan, Z., Ma, W., & Liu, C. (2021). 3D Cavitation Shedding Dynamics: Cavitation Flow-Fluid Vortex Formation Interaction in a Hydrodynamic Torque Converter. Applied Sciences, 11(6), 2798. https://doi.org/10.3390/app11062798







