Transient Analysis of Flow Unsteadiness and Noise Characteristics in a Centrifugal Compressor with a Novel Vaned Diffuser †
Abstract
:1. Introduction
2. Numerical Methods
2.1. Compressor Geometry
2.2. Computational Grid
2.3. Numerical Scheme and Boundary Condition
2.4. Numerical Sensitivity Analysis
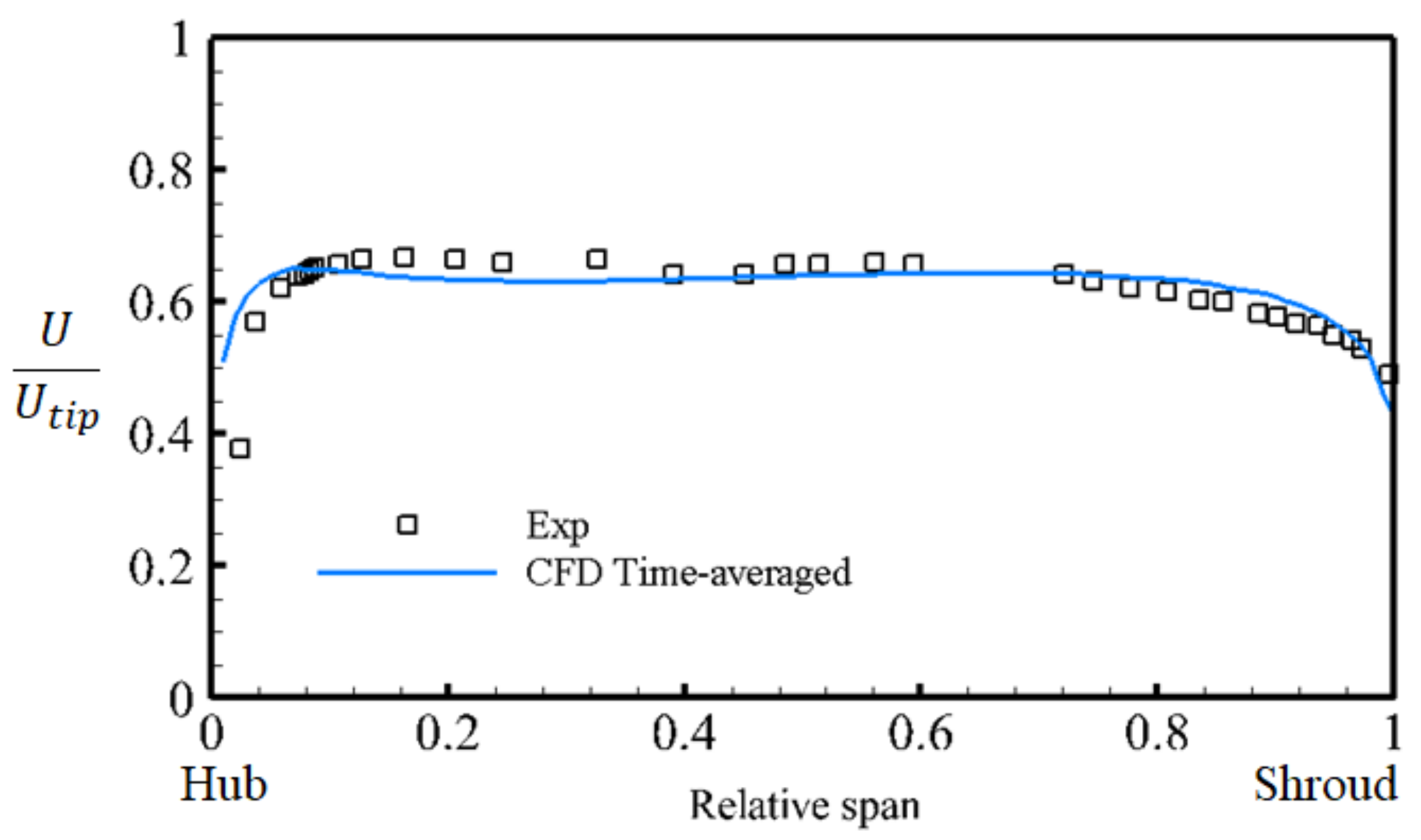
2.5. Validation and Consistency of the Numerical Simulation
2.6. Inclined Leading Edge in the Diffuser Vane
3. Results and Discussions
3.1. Aerodynamic Performance and Stall Margin
3.2. Flow-Field Analysis
3.3. Spectral Analysis
4. Conclusions
- (1)
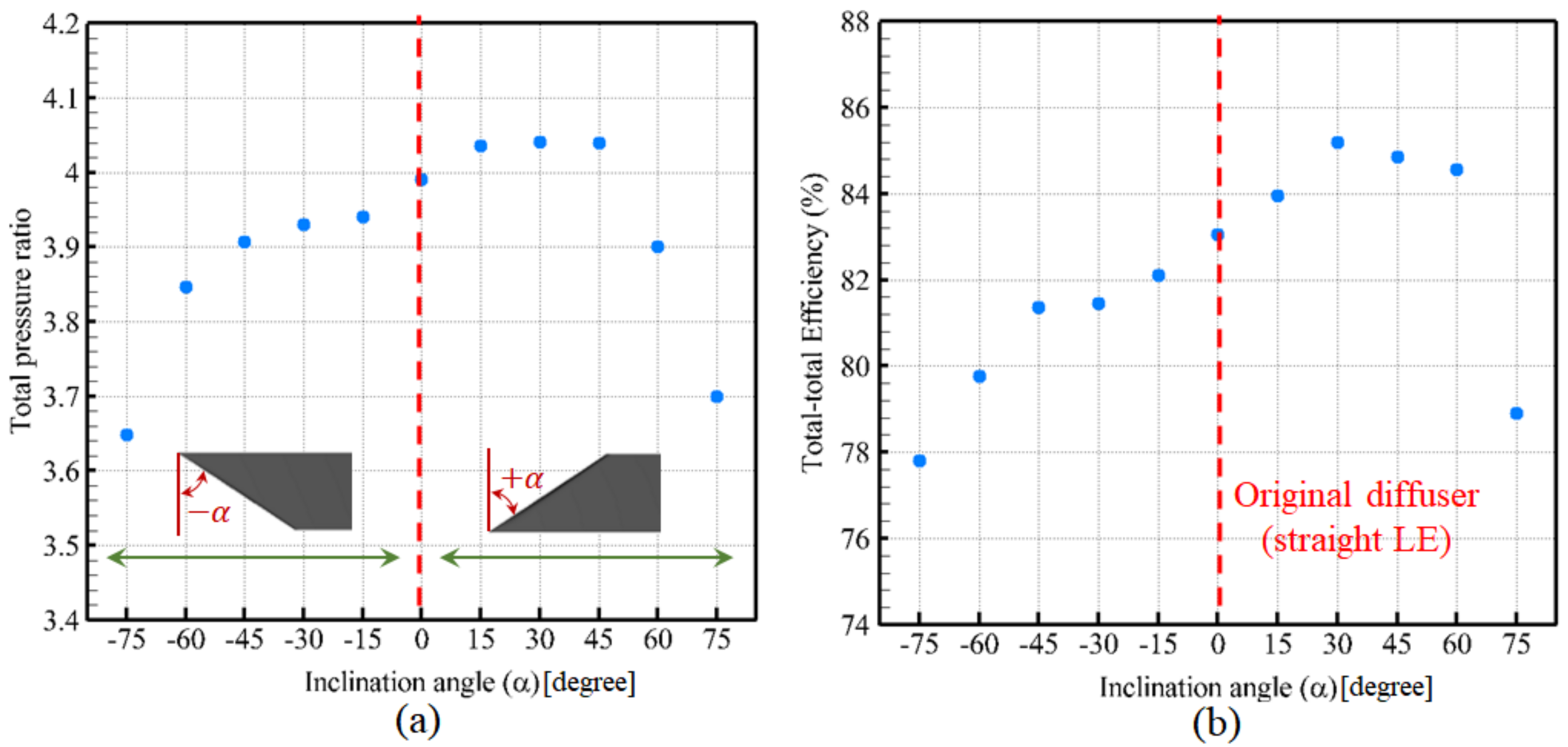
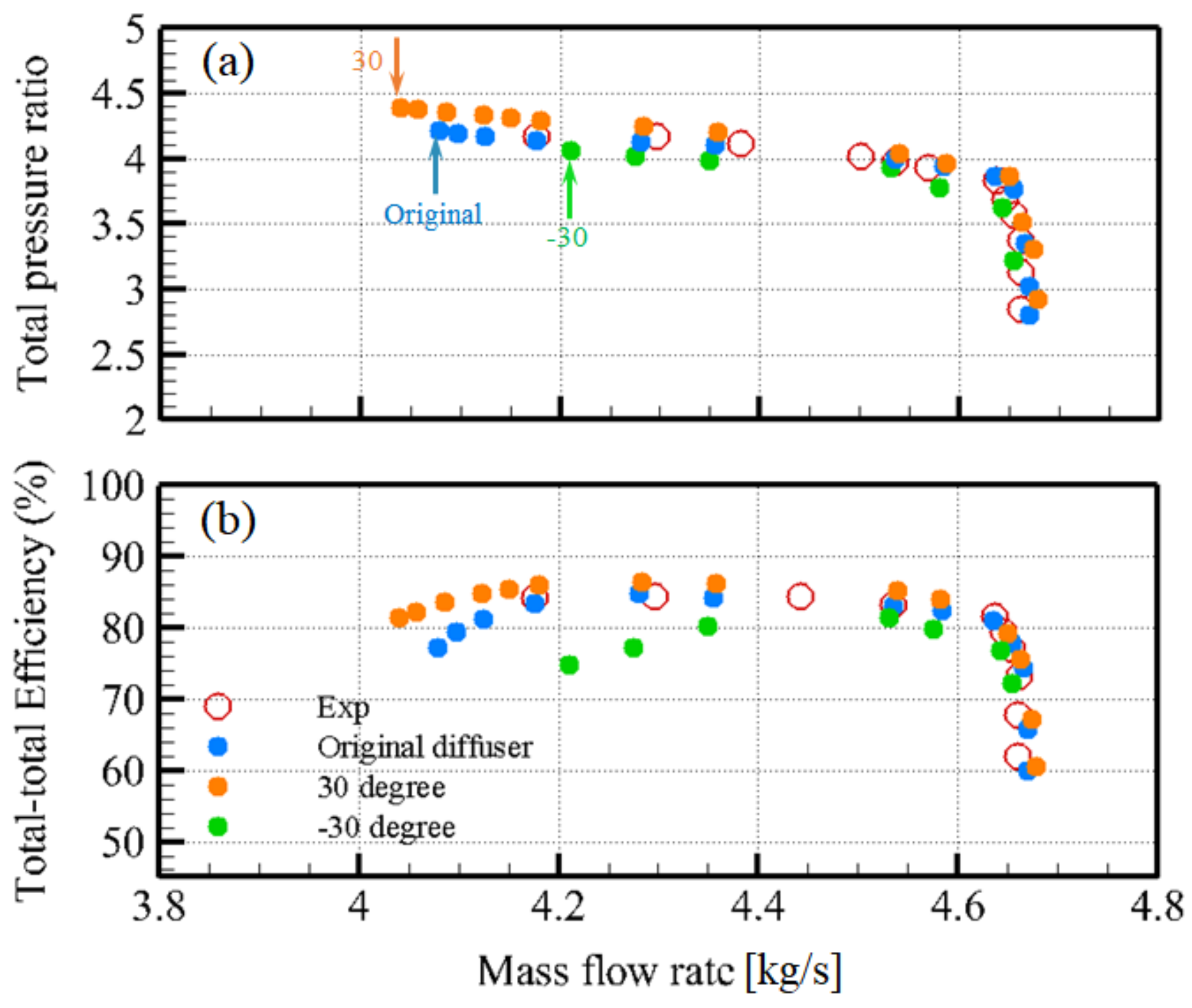
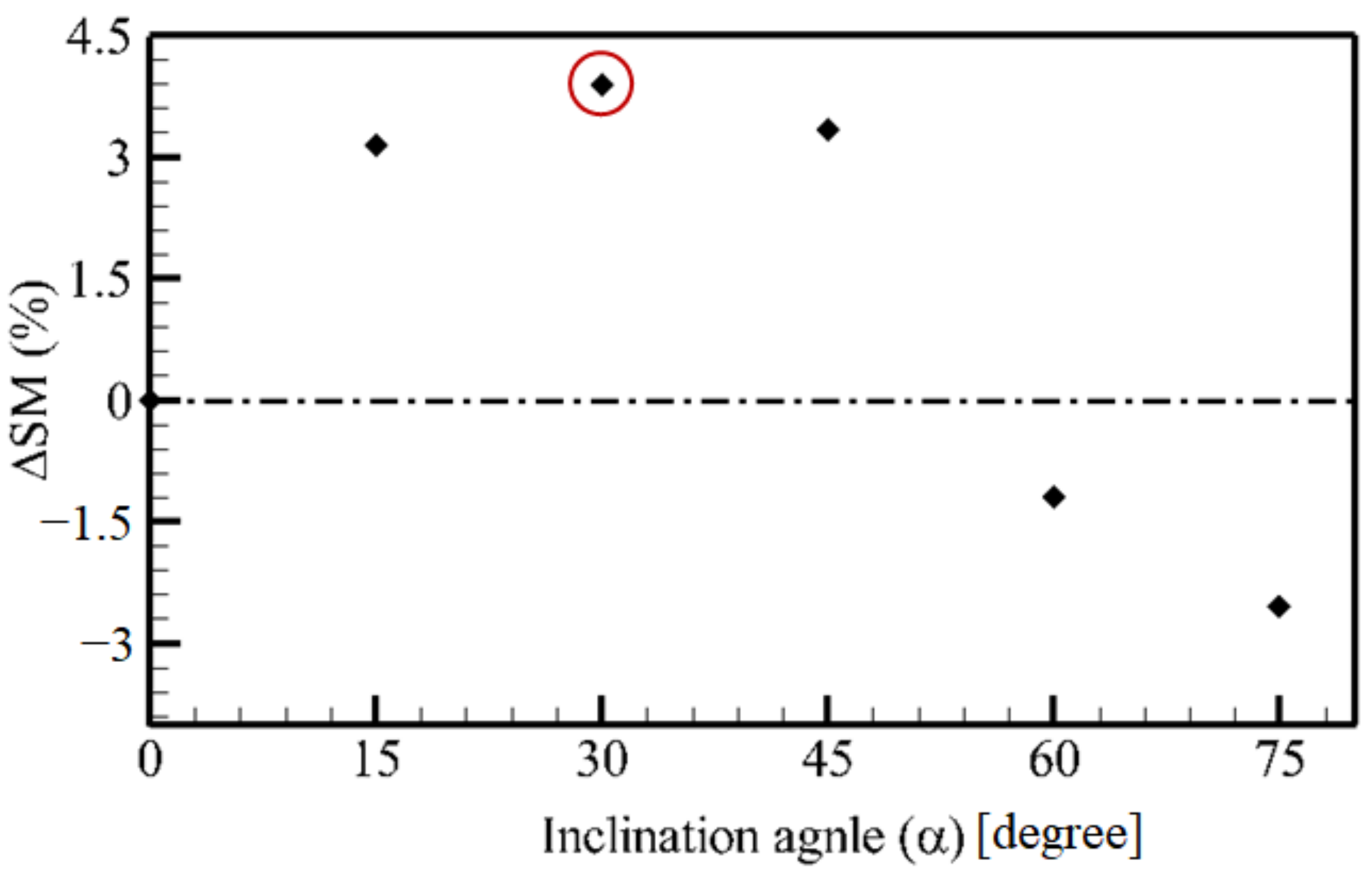
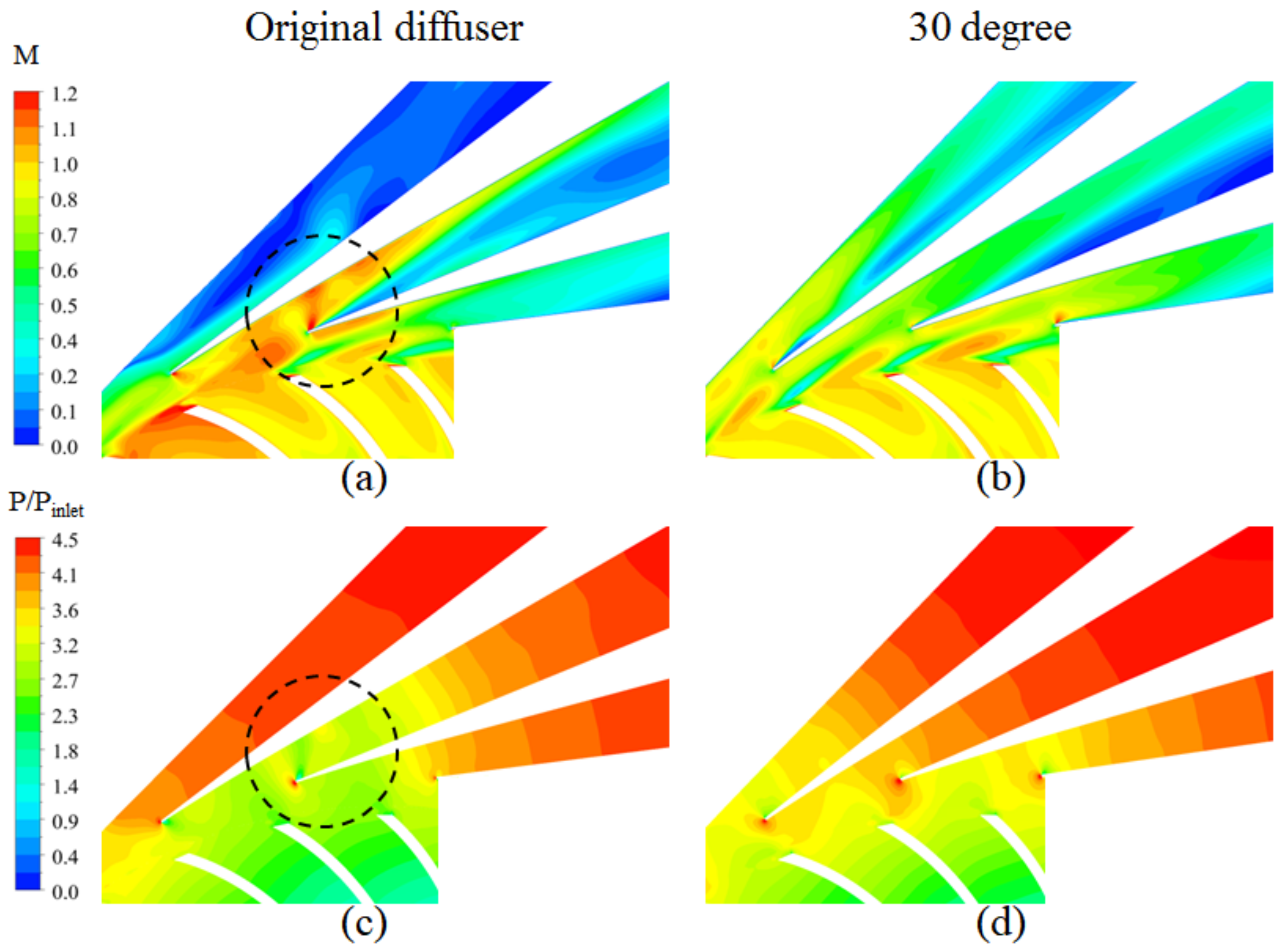
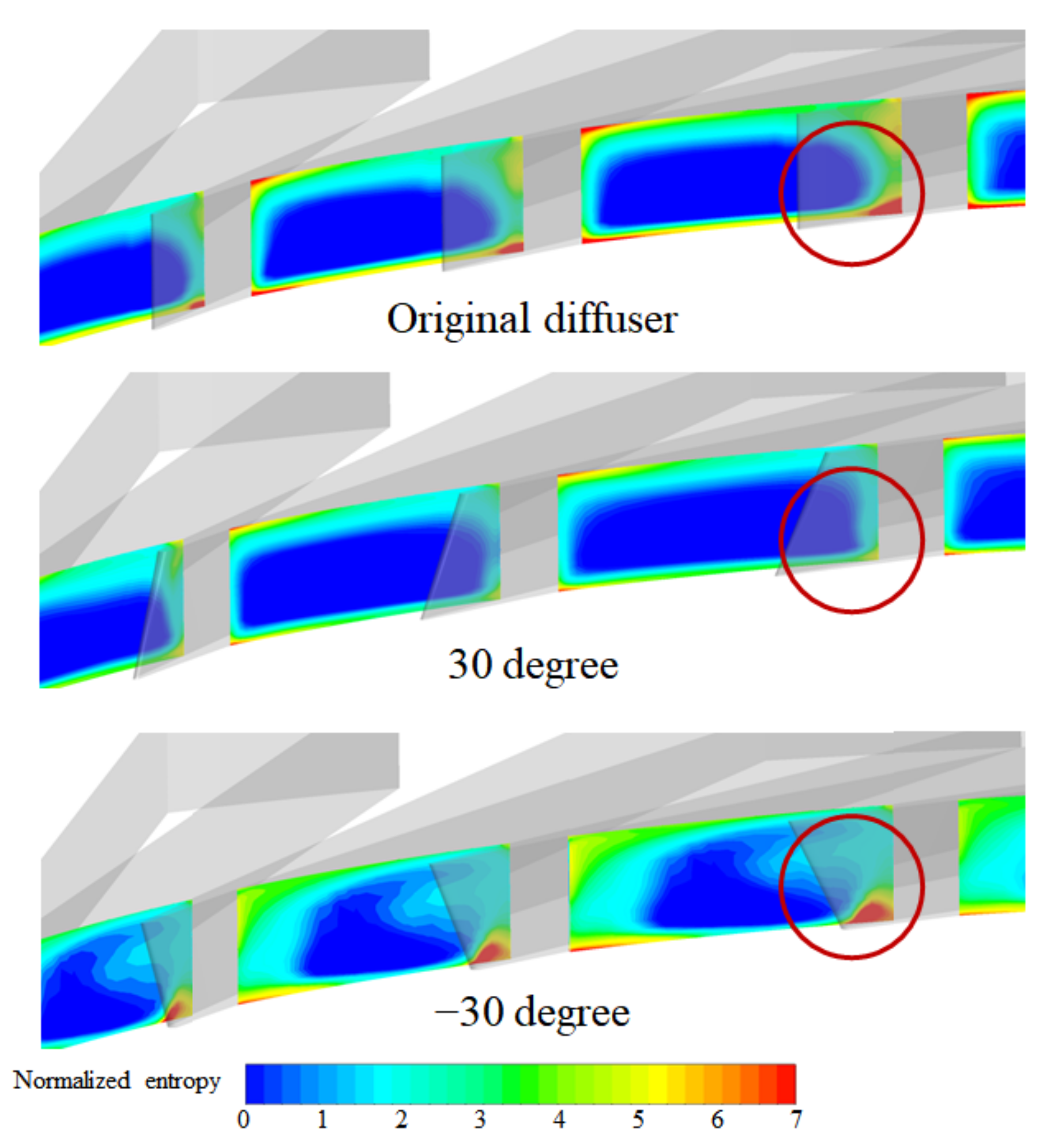
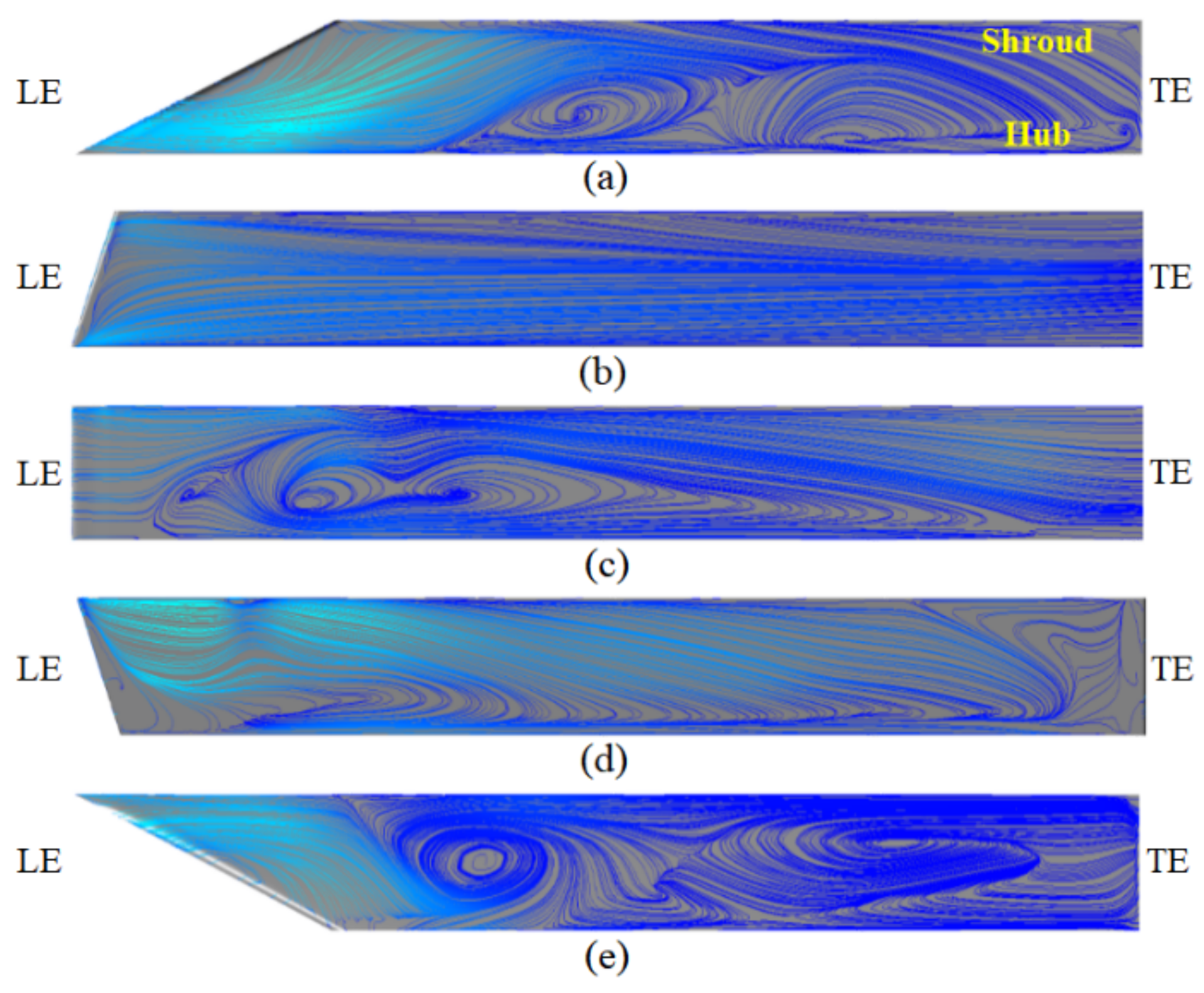
- The numerical results of various inclined leading edges showed that the inclination angles are effective tools for improving the efficiency of compressor and stall margin. With the optimal inclination angle of = 30° from hub-to-shroud, the performance at the design point increased by 2.6% and the stall margin by 3.88%, in comparison with the original diffuser. However, for accurate prediction of detailed flow physics near the stall point, transient approaches would be required. Detailed flow investigation inside the diffuser channels confirms that using the hub-to-shroud inclination angles can suppress the separated and secondary flows within the diffuser passage, especially on the vane pressure side.
- (2)
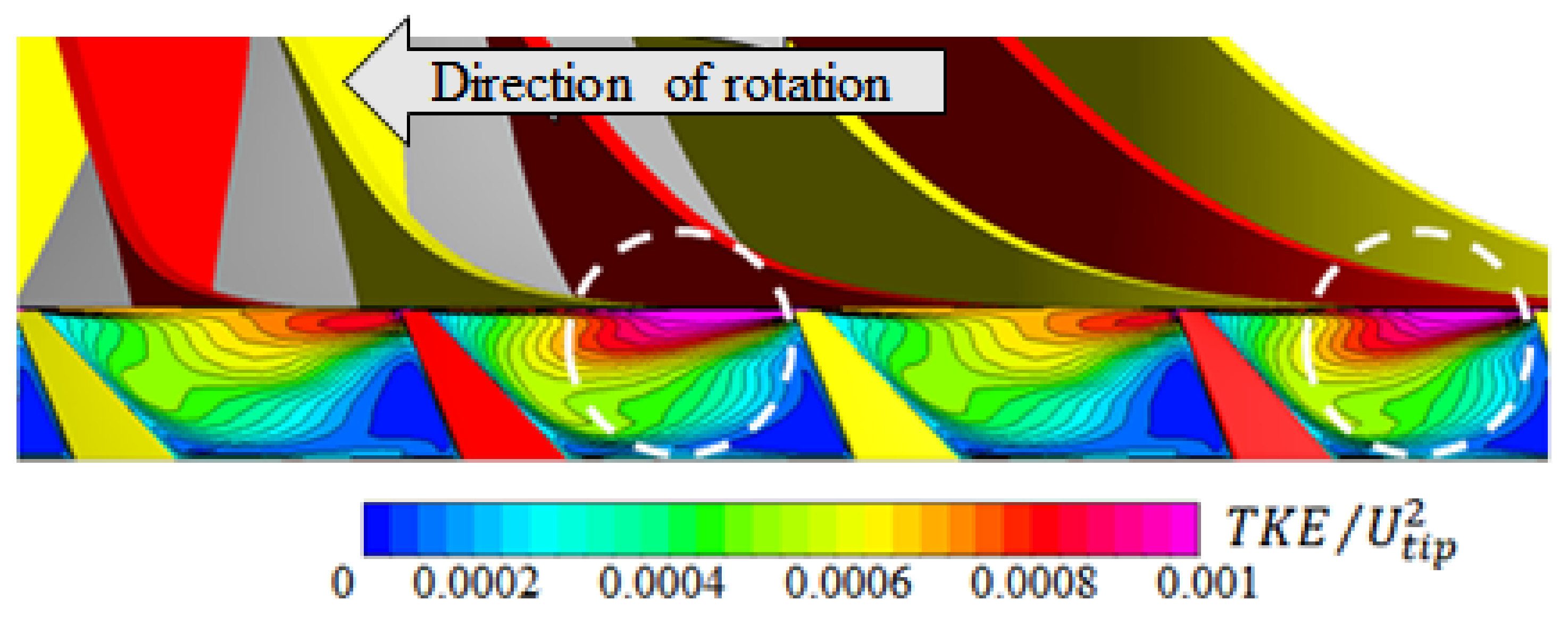
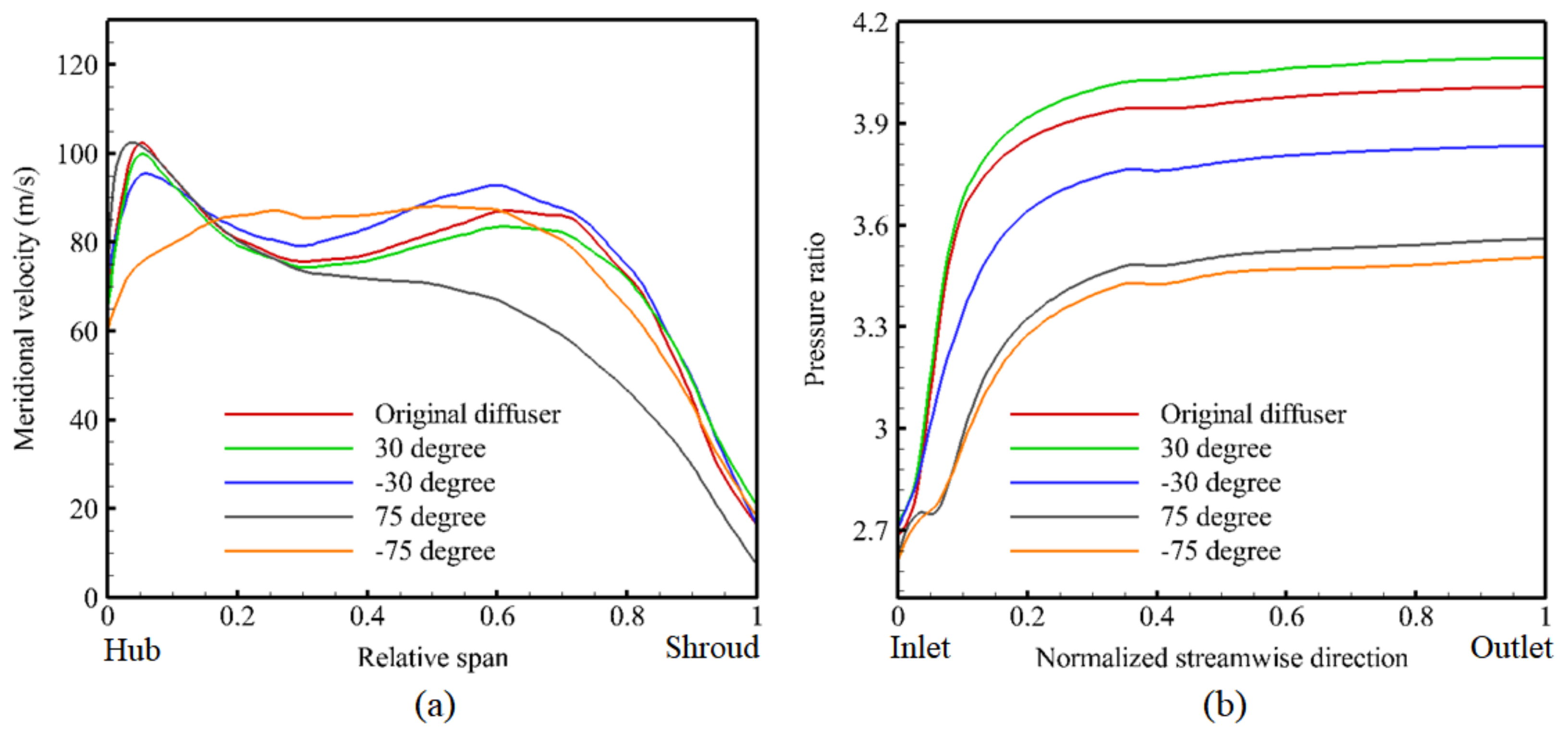
- The distribution of the static pressure and velocity contours in the diffuser channels demonstrated that the hub-to-shroud inclination angles reduced the flow unsteadiness. In addition, time-averaged streamlines on the surfaces of the diffuser vanes showed that the inclination angle in diffuser vane affects the boundary layer growth inside the diffuser channels, which leads to reduction of the recirculation zones, and thus the flow separations are postponed. It is evident that the hub-to-shroud inclined leading edges are very useful in mixing low and high-momentum flow regions.
- (3)
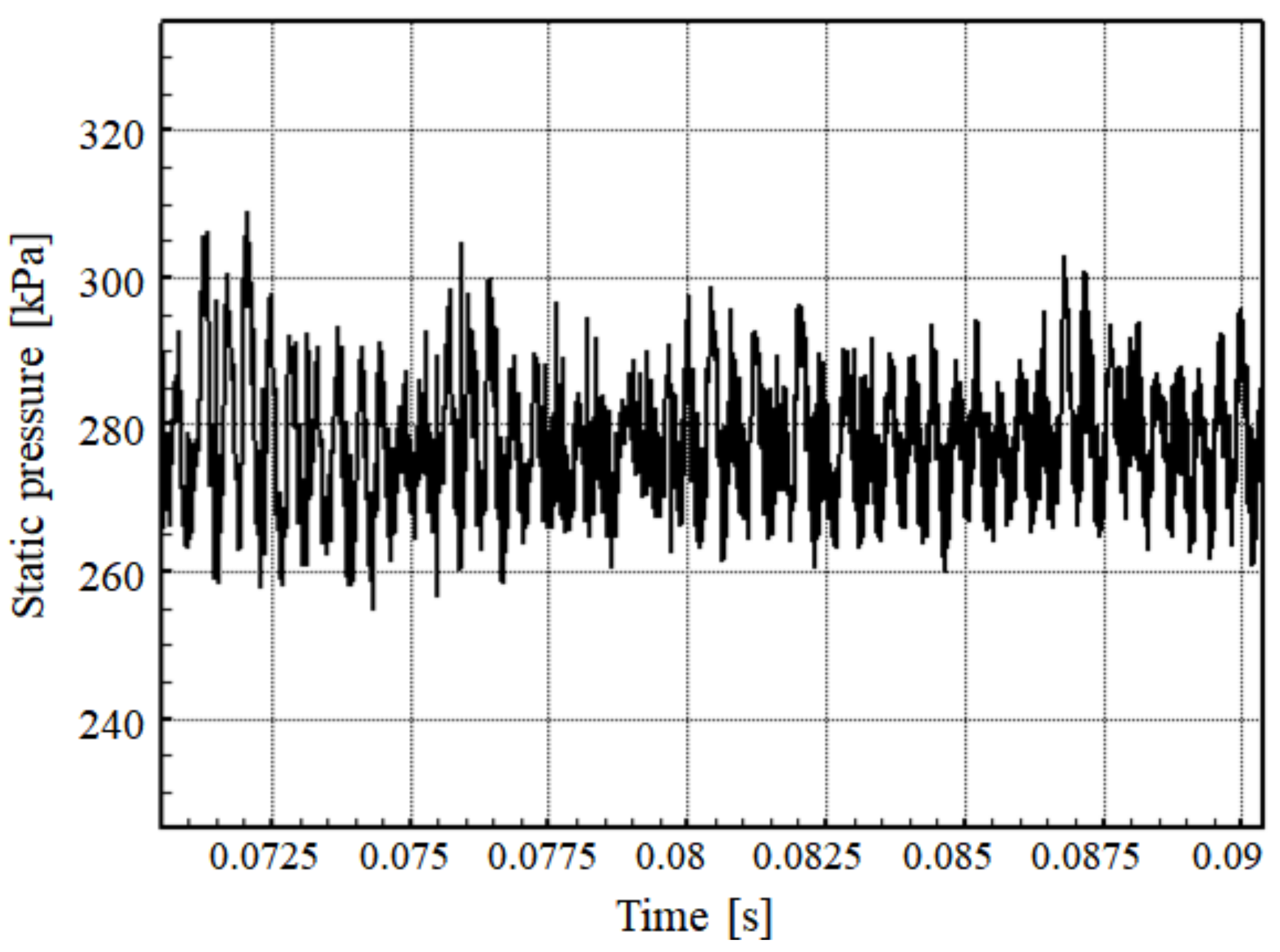
- The time/space pressure distribution at the midspan of the diffuser revealed that transient pressure waves mainly occur near the leading edges of the diffuser vanes, and decay very quickly along the diffuse passages. The number of these waves is the same as the number of impeller main and splitter blades, and their slope denotes the convective velocity. Instantaneous time/space distributions of the static pressure for various inclined leading edges confirmed that the 30° inclined leading edge had the maximum pressure level. Additionally, in the case of 30° inclination angle, in contrast with other cases, the pressure oscillations generated by the pseudo-periodic transient separation bubbles with various slopes were not observed on the time/space pressure distributions.
- (4)
- The spectrum of the near-field pressure fluctuation well predicted the fundamental frequencies corresponding to the first (5.4 kHz) and second (10.8 kHz) BPF harmonics. It is shown that the BPF tonal noise and its harmonics, generated by the interactions between the impeller and diffuser blades, are the dominant noise sources in the centrifugal compressors. The BPF noise and OASPL were decreased by 7.6 dB and 5.74 dB, respectively, by applying 30° inclination angle on the leading edges of the diffuser vanes. This confirms that the inclined leading edges are very effective technique, not only for the reduction of the tonal noise and OASPL, but also for the improvement of the aerodynamic performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| BPF | Blade passing frequency |
| CFD | Computational fluid dynamics |
| FFT | Fast Fourier transform |
| LE | Leading edge |
| OASPL | Overall sound pressure level, dB |
| P | Pressure, Pa |
| PR | Pressure ratio |
| PS | Pressure side |
| Q | Second invariant of velocity gradient |
| R | Radius, mm |
| SS | Suction side |
| T | Temperature, K |
| TE | Trailing edge |
| TPR | Total temperature ratio |
| c | Chord length |
| x | Coordinate, meridional and streamwise direction |
| Greek Letter | |
| Δ | Period of time |
| α | Inclination angle, degree |
| γ | Specific heat ratio of gas |
| Subscripts and superscripts | |
| 2 | Exit of impeller |
| D | Diffuser |
| s | Static |
| t | Total |
References
- Welch, G.E.; Hathaway, M.D.; Skoch, G.J.; Snyder, C.A. Rotary-Wing Relevant Compressor Aero Research and Technology Development Activities at Glenn Research Center, NASA TM-217280; Glenn Research Center: Cleveland, OH, USA, 2012. [Google Scholar]
- Sugimoto, T.; Kaeanishi, T.; Kumamaru, H.; Tohbe, Y. Performance Investigation into Supersonic Diffuser for a High Pressure Centrifugal Compressor. In Proceedings of the ASME Turbo Expo, GT2014-25104, Dusseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Braunscheidel, E.P.; Welch, G.E.; Skoch, G.J.; Medic, G.; Sharma, O.P. Aerodynamic Performance of a Compact, High Work-Factor Centrifugal Compressor at the Stage and Subcomponent Level. In Proceedings of the American Institute of Aeronautics and Astronautics, AIAA-2014-3632, Cleveland, OH, USA, 16–20 June 2014. [Google Scholar]
- Zheng, X.; Sun, Z.; Kawakubo, T.; Tamaki, H. Experimental Investigation of Surge and Stall in a Turbocharger Centrifugal Compressor with a vaned Diffuser. J. Appl. Therm. Eng. 2017, 82, 493–506. [Google Scholar] [CrossRef]
- Ziegler, K.U.; Gallus, H.E.; Niehuis, R. A Study on Impeller-Diffuser Interaction: Part I—Influence on the Performance. J. Turbomach. 2003, 125, 1. [Google Scholar] [CrossRef]
- Ziegler, K.U.; Gallus, H.E.; Niehuis, R. A Study on Impeller-Diffuser Interaction: Part II—Detailed Flow Analysis. J. Turbomach. 2003, 125, 1. [Google Scholar] [CrossRef]
- Gaetani, P.; Persico, G.; Mora, A.; Dossena, V.; Osnaghi, C. Impeller-Vaned Diffuser Interaction in a Centrifugal Compressor at the Best Efficiency Point. In Proceedings of the ASME Turbo Expo, GT2011-46223, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Zachau, U.; Buescher, C.; Niehuis, R.; Hoenen, H.; Wisler, D.C.; Moussa, Z.M. Performance Investigation into Supersonic Diffuser for a High Pressure Centrifugal Compressor. In Proceedings of the ASME Turbo Expo, GT2008-5153, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Inoue, M.; Cumpsty, N.A. Experimental Study of Centrifugal Impeller Discharge Flow in Vaneless and Vaned Diffuser. ASME J. Eng. Gas Turn. Power 1984, 2, 455–467. [Google Scholar] [CrossRef]
- Zamiri, A.; Lee, B.J.; Chung, J.T. Numerical Evaluation of Transient Flow Characteristics in a Transonic Centrifugal Compressor with Vaned Diffuser. J. Aerosp. Sci. Technol. 2017, 70, 244–256. [Google Scholar] [CrossRef]
- Zamiri, A.; Lee, B.J.; Chung, J.T. Influence of the Inclined Leading Edge Diffuser Vanes in the Aerodynamic Performance of a Transonic Centrifugal Compressor. J. Mech. Sci. Technol. 2017, 31, 5557–5568. [Google Scholar] [CrossRef]
- Shahin, I.; Alqaradawi, M.; Gadala, M.; Badr, O. On the Aero Acoustic and Internal Flows Structure in a Centrifugal Compressor with Hub Side Cavity Operating at Off Design Condition. J. Aerosp. Sci. Technol. 2017, 60, 68–83. [Google Scholar] [CrossRef]
- Jeong, T.B.; Kang, S.H.; Kim, H.J.; Won, K.M.; Park, C.Y.; Jung, W.Y.; Cho, K.S. Experimental Investigation on Aero-acoustic Characteristics of a Centrifugal Compressor for the Fuel-cell Vehicle. J. Mech. Sci. Technol. 2013, 27, 3287–3297. [Google Scholar]
- Ohta, Y.; Okutsu, Y.; Goto, T.; Outa, E. Aerodynamic Performance and Noise Characteristics of a Centrifugal Compressor with Modified Vaned Diffuser. J. Therm. Sci. 2006, 15, 289–298. [Google Scholar] [CrossRef]
- Wilkosz, B.; Zimmermann, M.; Schwarz, P.; Jeschke, P. Numerical Investigation of the Unsteady Interaction with a Close-Coupled Centrifugal Compressor Used in an Aero Engine. In Proceedings of the ASME Turbo Expo, GT2013-95644, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Zachau, U.; Buescher, C.; Niehuis, R.; Hoenen, H.; Wisler, D.C.; Moussa, Z.M. Experimental Investigation of a Centrifugal Compressor Stage with Focus in the Flow in the Pipe Diffuser Supported by particle Image Velocimetry (PIV) Measurement. In Proceedings of the ASME Turbo Expo, GT2008-51538, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Kunte, R.; Schwarz, P.; Wilkosz, B.; Jeschke, P.; Smythe, C. Experimental and numerical Investigations of the Tip Clearance and Bleed Effects in a Centrifugal Compressor Stage with Pipe Diffuser. J. Turbomach. 2013, 135, 1. [Google Scholar] [CrossRef]
- Vogel, K.; Abhari, R.S.; Zemp, A. Experimental and Numerical Investigation of the Unsteady Flow Field in a Vaned Diffuser of a High-Speed Centrifugal Compressor. In Proceedings of the ASME Turbo Expo, GT2014-25862, Dusseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Everitt, J.N.; Spakovszky, Z.S.; Rusch, D.; Schiffmann, J. The Role of Impeller Outflow Conditions on the Performance of Vaned Diffusers. J. Turbomach. 2017, 139. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Ai, Z.; Ji, Y.; Qin, G. Numerical Investigation of a Centrifugal Compressor with a Single Circumferential Groove in Different Types of Diffusers. In Proceedings of the ASME Turbo Expo, GT2017-63151, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Carretta, M.; Cravero, C.; Marsano, D. Numerical Prediction of Centrifugal Compressor Stability Limit. In Proceedings of the ASME Turbo Expo, GT2017-63352, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Adjei, R.A.; Wang, W.; Jiang, J.; Liu, Y.; Kawakubo, T. Numerical Investigation of Unsteady Shock Wave Motion in a Transonic Centrifugal Compressor. In Proceedings of the ASME Turbo Expo, GT2017-63887, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Krain, H. Unsteady Diffuser Flow in a Transonic Centrifugal Compressor. Int. J. Rotat. Mach. 2002, 8, 222–231. [Google Scholar] [CrossRef]
- Shum, Y.K.P.; Tan, C.S.; Cumpsty, N.A. Impeller-diffuser interaction in a Centrifugal Compressor. J. Turbomach. 2000, 4, 777–786. [Google Scholar] [CrossRef]
- Anish, S.; Sitaram, N.; Kim, H.D. A Numerical Study of the Unsteady Interaction Effects on Diffuser Performance in a Centrifugal Compressor. J. Turbomach. 2014, 136. [Google Scholar] [CrossRef]
- Fontanesi, S.; Paltrinieri, S.; Cantore, G. CFD Analysis of the Acoustic Behavior of a Centrifugal Compressor for high Performance Engine Application. J. Energy Procedia 2014, 45, 759–768. [Google Scholar] [CrossRef] [Green Version]
- Raitor, T.; Neise, W. Sound Generation in Centrifugal Compressors. J. Sound Vib. 2008, 314, 738–756. [Google Scholar] [CrossRef]
- Raitor, T.; Reutter, O.; Aulich, M.; Nicke, E. Aerodynamic Design Studies of a Transonic Centrifugal Compressor Impeller Based on Automated 3d-CFD Optimization. In Proceedings of the 10th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Lappeenranta, Finland, 15–19 March 2013. [Google Scholar]
- Skoch, G.J.; Prahst, P.S.; Wernet, M.P.; Strazisar, A.J. Laser Anemometer Measurements of the Flow Field in a 4:1 Pressure Ratio Centrifugal Impeller. In Proceedings of the International Gas Turbine & Aeroengine Congress & Exhibition, No. 97-GT-342, Orlando, FL, USA, 2–5 June 1997. [Google Scholar]
- McKain, T.F.; Holbrook, G.J. Coordinates for a High Performance 4:1 Pressure Ratio Centrifugal Compressor; NASA Contractor Report 204134; NASA Lewis Research Center: Cleveland, OH, USA, 1997. [Google Scholar]
- Bardina, J.; Huang, P.; Coakley, T. Turbulence Modeling Validation. In Proceedings of the 28th Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997. [Google Scholar]
- Jung, Y.; Jeon, H.; Jung, Y.; Lee, K.; Choi, M. Effects of Recessed Blade Tips on Stall Margin in a Transonic Axial Compressor. J. Aerosp. Sci. Technol. 2016, 54, 41–48. [Google Scholar] [CrossRef]
- Cui, M.; Hohlweg, W. Numerical and Experimental Investigation of Heat Transfer in a Low Flow Single Stage Centrifugal Compressor. In Proceedings of the ASME Turbo Expo, GT2016-57710, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Barth, T.J.; Jesperson, D.C. The Design and Application of Upwind Scheme on Unstructured Meshes. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989. [Google Scholar]
- Chen, H.; Huang, X.; Fu, S. CFD Investigation on Stall Mechanisms and Casing Treatment of a Transonic Compressor. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. [Google Scholar]
- Larosiliere, L.; Skoch, G.J. Aerodynamic Synthesis of a Centrifugal Impeller Using Computational Fluid Dynamics and Measurements. J. Propuls. Power 1999, 15, 623–632. [Google Scholar] [CrossRef]
- Cumpsty, N.A. Compressor Aerodynamics; Krieger Publishing Company: Malabar, FL, USA, 2004. [Google Scholar]
- Jeong, J.; Hussain, F. On the Identification of a Vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Grates, D.R.; Jeschke, P.; Niehuis, R. Numerical Investigation of the Unsteady Flow Inside a Centrifugal Compressor Stage with Pipe Diffuser. In Proceedings of the ASME Turbo Expo, GT2013-95465, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Marconcini, M.; Rubechini, F.; Arnone, A.; Ibaraki, S. Numerical Analysis of the Vaned Diffuser of a Transonic Centrifugal Compressor. J. Turbomach. 2010, 132. [Google Scholar] [CrossRef]
- Bulot, N.; Trébinjac, I. Effect of the Unsteadiness on the Diffuser Flow in a Transonic Centrifugal Compressor Stage. Int. J. Rotat. Mach. 2009, 2009, 932593. [Google Scholar] [CrossRef]
- Shahin, I.; Gadala, M.; Alwaradawi, M.; Badr, O. Large Eddy Simulation for a Deep Surge Cycle in a High-Speed Centrifugal Compressor with Vaned Diffuser. J. Turbomach. 2015, 137, 101007. [Google Scholar] [CrossRef]
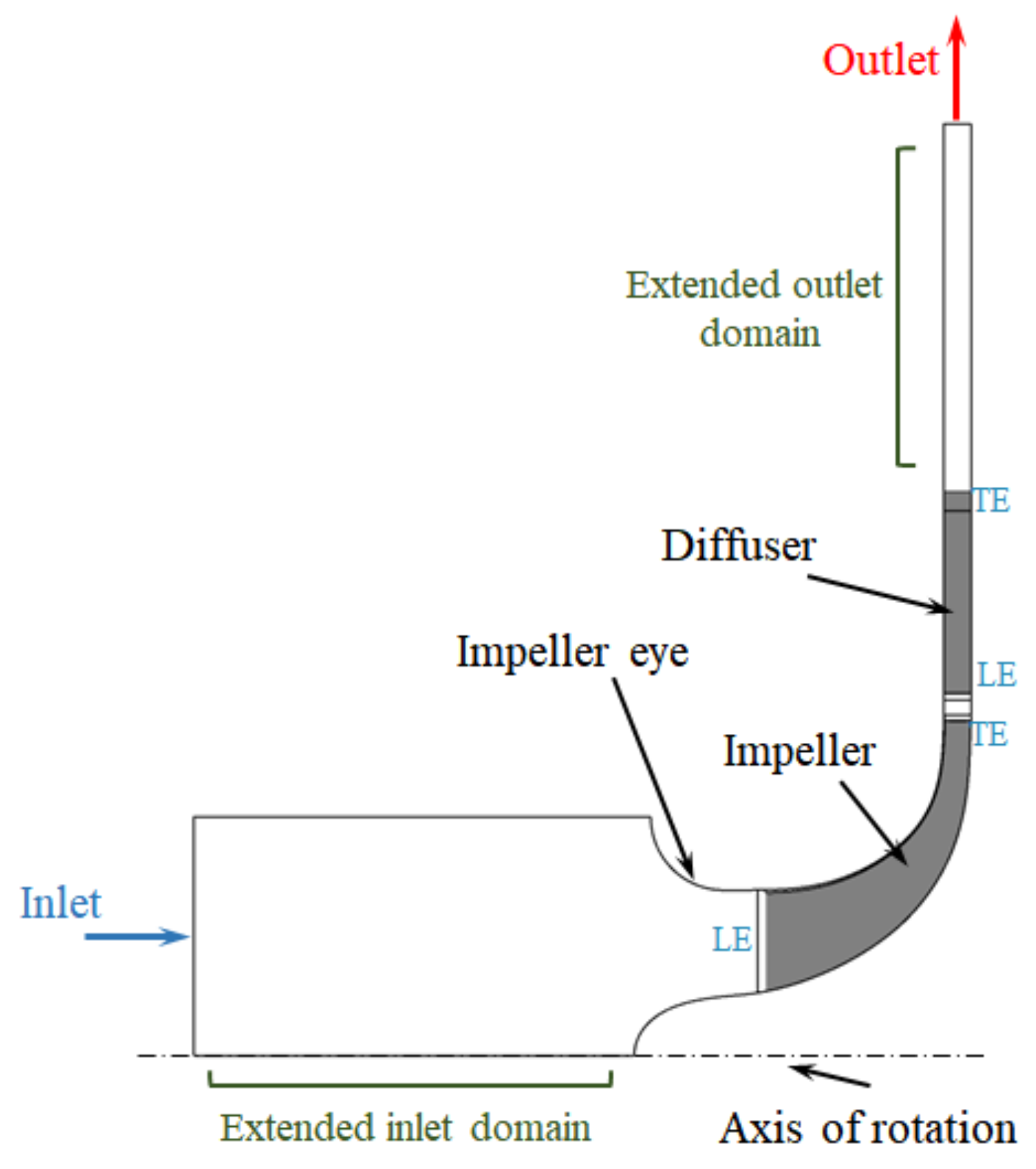
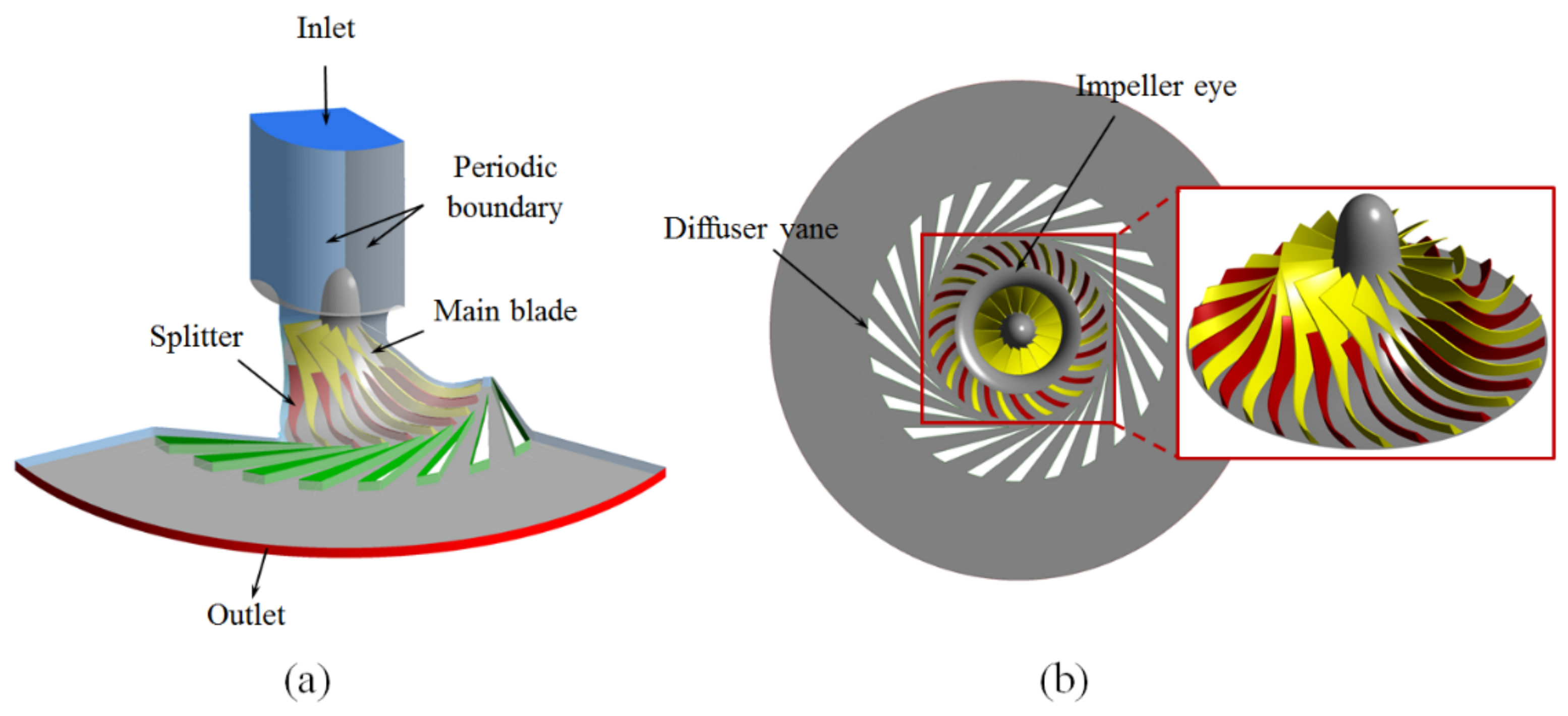

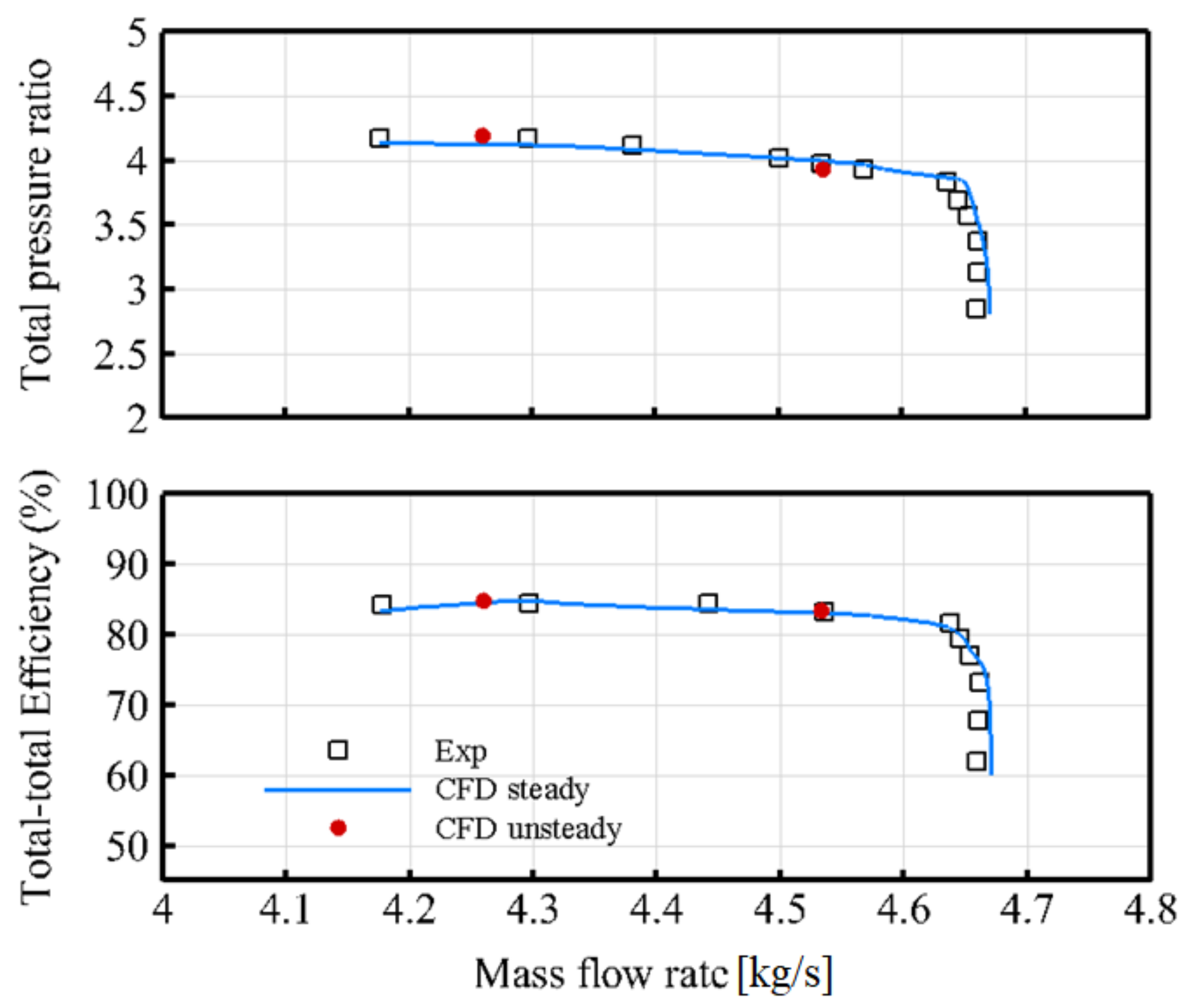






| Operating condition | |
| Inlet temperature | 288 K |
| Inlet pressure | 101,325 Pa |
| Total pressure ratio | 4:1 |
| Rotational speed at design point | 21,789 rpm |
| Mass flow rate at design point | 4.536 kg/s |
| Impeller configuration | |
| Number of main blades | 15 |
| Number of splitter blades | 15 |
| Radius at impeller inlet (R1) | 105 mm |
| Inlet blade height | 64 mm |
| Radius at impeller exit (R2) | 215.5 mm |
| Tip speed | 492 m/s |
| Blade height at exit | 17 mm |
| Backsweep angle | 50° |
| Vaned diffuser configuration | |
| Number of vanes | 24 |
| Divergence angle | 7.8° |
| Vane height | 17 mm |
| Inlet diameter | 431 mm |
| Outlet diameter | 714 mm |
| Flow Solver | ANSYS CFX V19.3 | |
|---|---|---|
| Spatial discretization | High resolution scheme (a hybrid of first order and second order upwind scheme) | |
| Temporal discretization | First order backward Euler scheme (steady) Second order backward Euler scheme (unsteady) | |
| Turbulence model | SST | |
| Working fluid | Air (treated as an ideal gas) | |
| Boundary conditions | Inlet duct | Total pressure (101,325 Pa) Total temperature (288 K) |
| Inlet duct/Impeller Impeller/Diffuser | Frozen rotor interface (steady) Transient rotor-stator interface (unsteady) | |
| Diffuser exit | Average static pressure | |
| Pressure Ratio | Efficiency (%) | Pressure Ratio % Difference | Efficiency % Difference | |
|---|---|---|---|---|
| Coarse | 4.124 | 84.32 | 3.33% | 1.48% |
| Moderate | 3.998 | 83.04 | 0.17% | 0.06% |
| Fine | 3.991 | 83.09 | - | - |
| Exp | |||
|---|---|---|---|
| Pressure ratio | 4.252 | 3.998 | 3.97 |
| Efficiency (%) | 86.17 | 83.04 | 83.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamiri, A.; Park, K.S.; Choi, M.; Chung, J.T. Transient Analysis of Flow Unsteadiness and Noise Characteristics in a Centrifugal Compressor with a Novel Vaned Diffuser. Appl. Sci. 2021, 11, 3191. https://doi.org/10.3390/app11073191
Zamiri A, Park KS, Choi M, Chung JT. Transient Analysis of Flow Unsteadiness and Noise Characteristics in a Centrifugal Compressor with a Novel Vaned Diffuser. Applied Sciences. 2021; 11(7):3191. https://doi.org/10.3390/app11073191
Chicago/Turabian StyleZamiri, Ali, Kun Sung Park, Minsuk Choi, and Jin Taek Chung. 2021. "Transient Analysis of Flow Unsteadiness and Noise Characteristics in a Centrifugal Compressor with a Novel Vaned Diffuser" Applied Sciences 11, no. 7: 3191. https://doi.org/10.3390/app11073191
APA StyleZamiri, A., Park, K. S., Choi, M., & Chung, J. T. (2021). Transient Analysis of Flow Unsteadiness and Noise Characteristics in a Centrifugal Compressor with a Novel Vaned Diffuser. Applied Sciences, 11(7), 3191. https://doi.org/10.3390/app11073191







