Effect of the Interfacial Dzyaloshinskii–Moriya Interaction on the Spin Waves Eigenmodes of Isolated Stripes and Dots Magnetized In-Plane: A Micromagnetic Study
Abstract
:1. Introduction
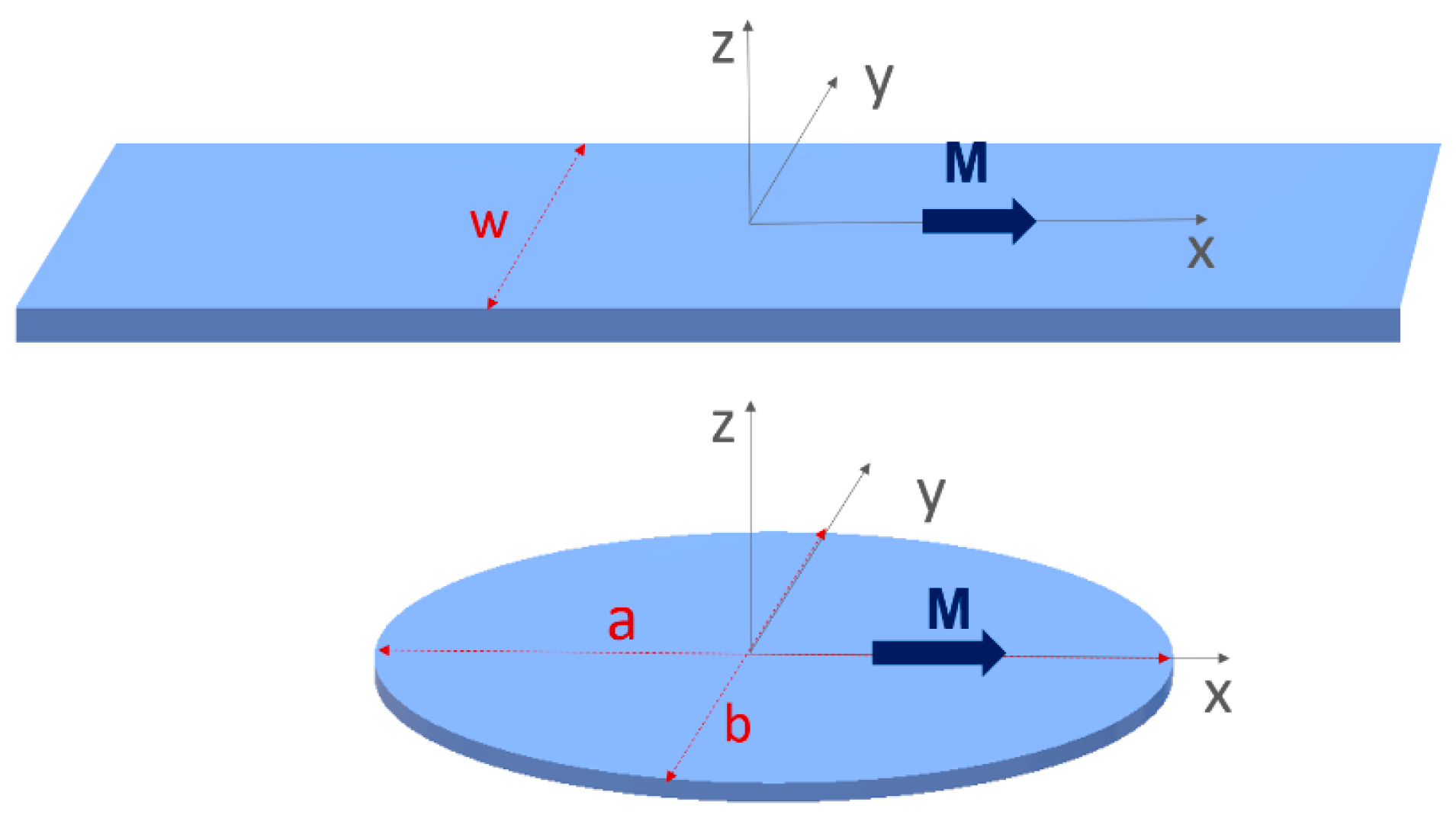
2. Theoretical Framework and Micromagnetic Simulations
3. Results
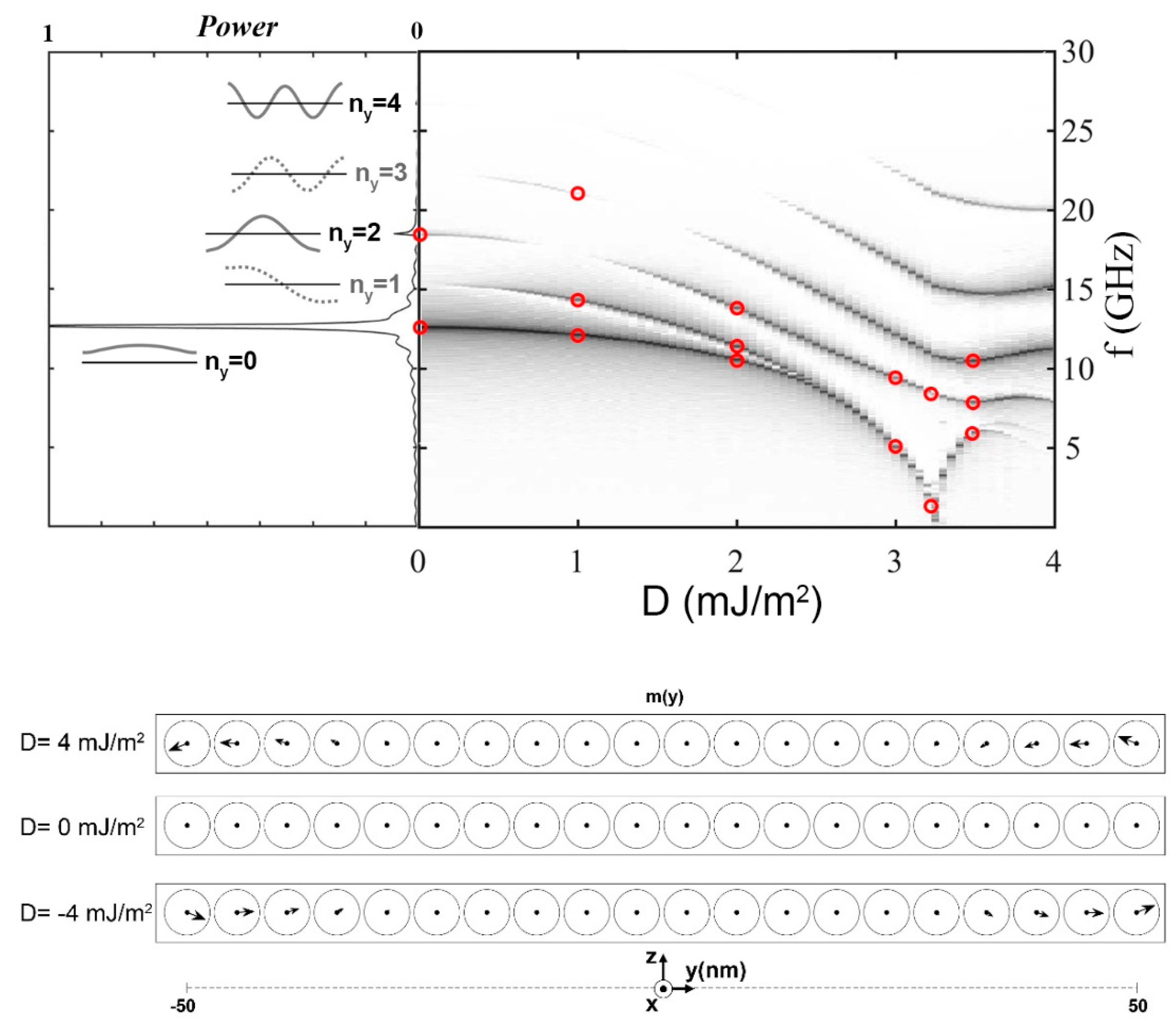
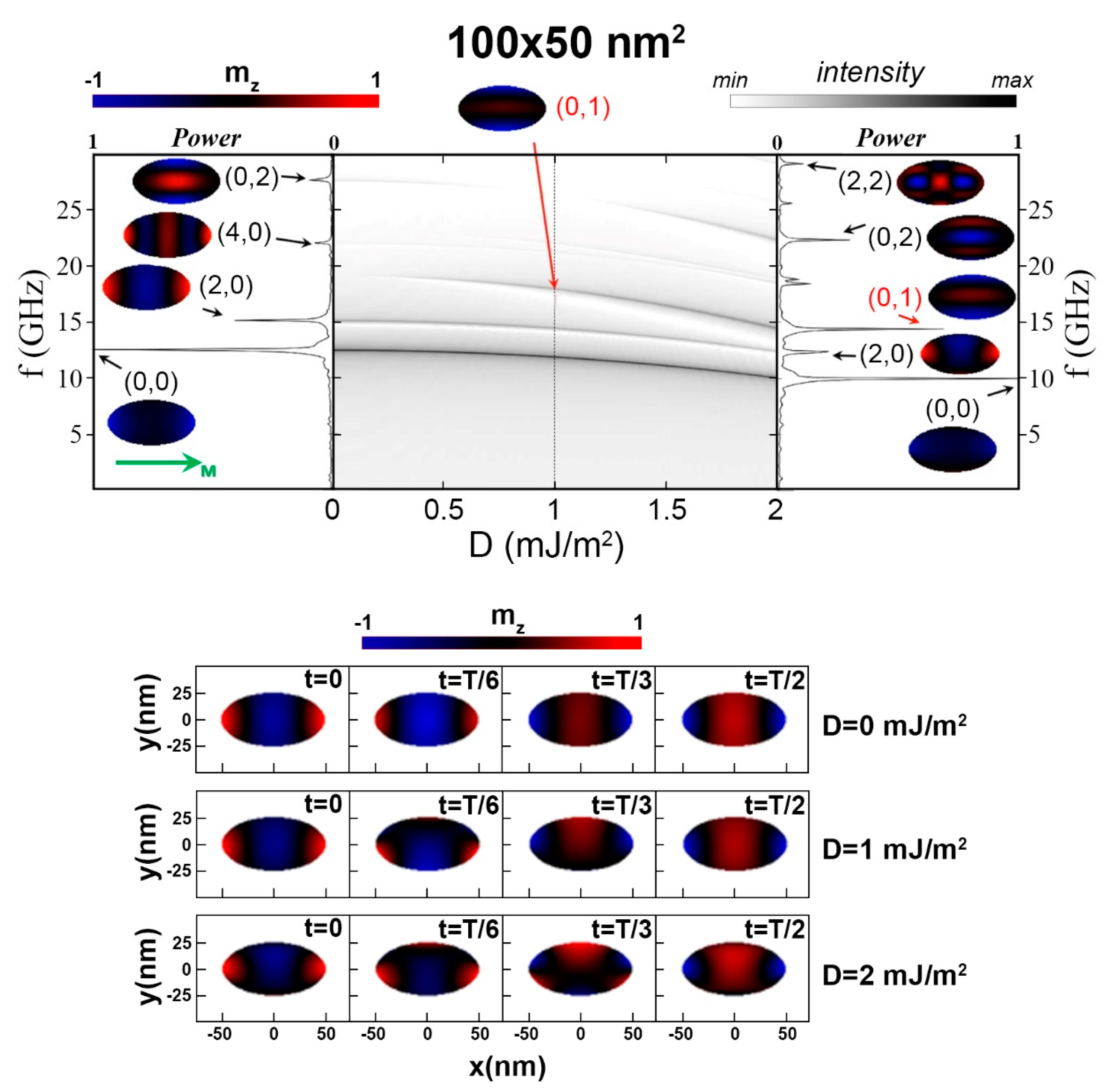
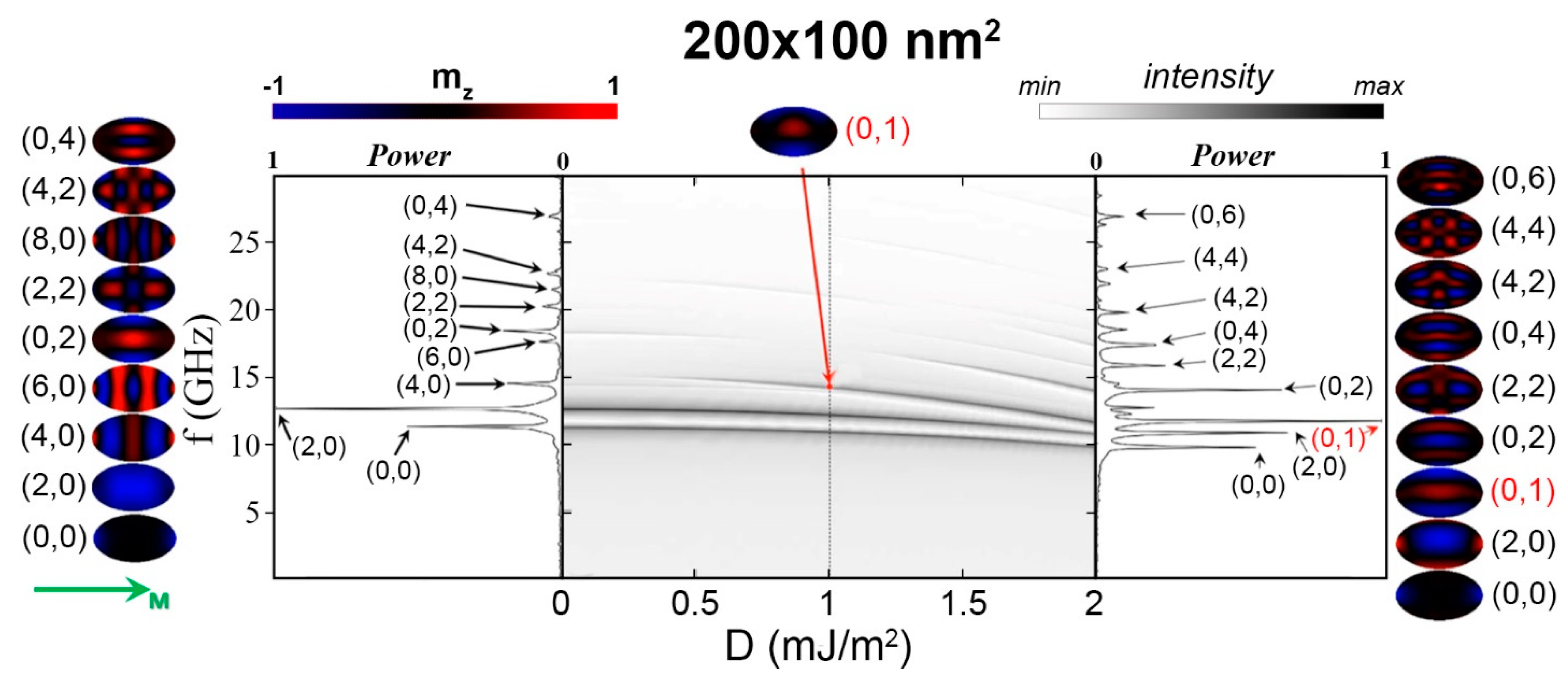
3.1. Eigenmodes of Isolated Stripes
3.2. Eigenmode of Isolated Elliptical Nanodots
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. New Mechanism of Anisotropic Superexchange Interaction. Phys. Rev. Lett. 1960, 4, 228–230. [Google Scholar] [CrossRef]
- Kashid, V.; Schena, T.; Zimmermann, B.; Mokrousov, Y.; Blügel, S.; Shah, V.; Salunke, H.G. Dzyaloshinskii-Moriya interaction and chiral magnetism in 3d−5d zigzag chains: Tight-binding model and ab initio calculations. Phys. Rev. B 2014, 90, 054412. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Thiaville, A.; Rohart, S.; Fert, A.; Chshiev, M. Anatomy of Dzyaloshinskii-Moriya Interaction at Co/Pt In-terfaces. Phys. Rev. Lett. 2015, 115, 267210. [Google Scholar] [CrossRef]
- Belabbes, A.; Bihlmayer, G.; Bechstedt, F.; Blügel, S.; Manchon, A. Hund’s Rule-Driven Dzyaloshinskii-Moriya Interaction at 3d−5d Interfaces. Phys. Rev. Lett. 2016, 117, 247202. [Google Scholar] [CrossRef] [Green Version]
- Boulle, O.; Vogel, J.; Yang, H.; Pizzini, S.; Chaves, D.D.S.; Locatelli, A.; Menteş, T.O.; Sala, A.; Buda-Prejbeanu, L.D.; Klein, O.; et al. Room-temperature chiral magnetic skyrmions in ultrathin magnetic nanostructures. Nat. Nanotechnol. 2016, 11, 449–454. [Google Scholar] [CrossRef] [Green Version]
- Khan, R.A.; Nembach, H.T.; Ali, M.; Shaw, J.M.; Marrows, C.H.; Moore, T.A. Magnetic domain texture and the Dzyaloshinskii-Moriya interaction in Pt/Co/IrMn and Pt/Co/FeMn thin films with perpendicular exchange bias. Phys. Rev. B 2018, 98, 064413. [Google Scholar] [CrossRef] [Green Version]
- Soucaille, R.; Belmeguenai, M.; Torrejon, J.; Kim, J.-V.; Devolder, T.; Roussigné, Y.; Chérif, S.-M.; Stashkevich, A.A.; Hayashi, M.; Adam, J.-P. Probing the Dzyaloshinskii-Moriya interaction in CoFeB ultrathin films using domain wall creep and Brillouin light spectroscopy. Phys. Rev. B 2016, 94, 104431. [Google Scholar] [CrossRef] [Green Version]
- Vaňatka, M.; Rojas-Sánchez, J.-C.; Vogel, J.; Bonfim, M.; Belmeguenai, M.; Roussigné, Y.; Stashkevich, A.; Thiaville, A.; Pizzini, S. Velocity asymmetry of Dzyaloshinskii domain walls in the creep and flow regimes. J. Physics: Condens. Matter 2015, 27, 326002. [Google Scholar] [CrossRef] [PubMed]
- Di, K.; Zhang, V.L.; Lim, H.S.; Ng, S.C.; Kuok, M.H.; Yu, J.; Yoon, J.; Qiu, X.; Yang, H. Direct observation of the Dzyaloshinskii-Moriya interaction in a Pt/Co/Ni film. Phys. Rev. Lett. 2015, 114, 047201. [Google Scholar] [CrossRef] [PubMed]
- Nembach, H.T.; Shaw, J.M.; Weiler, M.; Ju’e, E.; Silva, T.J. Linear relation between Heisenberg exchange and interfacial Dzyaloshinskii–Moriya interaction in metal films. Nat. Phys. 2015, 11, 825. [Google Scholar] [CrossRef]
- Chaurasiya, A.K.; Banerjee, C.; Pan, S.; Sahoo, S.; Choudhury, S.; Sinha, J.; Barman, A. Direct Observation of Interfacial Dzyaloshinskii-Moriya Interaction from Asymmetric Spin-wave Propagation in W/CoFeB/SiO2 Heterostructures Down to Sub-nanometer CoFeB Thickness. Sci. Rep. 2016, 6, 32592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tacchi, S.; Troncoso, R.E.; Ahlberg, M.; Gubbiotti, G.; Madami, M.; Åkerman, J.; Landeros, P. Interfacial Dzyaloshinskii-Moriya Interaction in Pt/CoFeB Films: Effect of the Heavy-Metal Thickness. Phys. Rev. Lett. 2017, 118, 147201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Belmeguenai, M.; Gabor, M.S.; Roussigńe, Y.; Petrisor, T.; Mos, R.B.; Stashkevich, A.; Chérif, S.M.; Tiusan, C. Interfacial Dzyaloshinskii-Moriya interaction sign in Ir/Co2FeAl systems investigated by Brillouin light scattering. Phys. Rev. B 2018, 97, 054425. [Google Scholar] [CrossRef] [Green Version]
- Bouloussa, H.; Yu, J.; Roussigné, Y.; Belmeguenai, M.; Stashkevitch, A.; Yang, H.; Cherif, S.M.; Mohamed, B.; Stachkevich, A. Brillouin light scattering investigation of interfacial Dzyaloshinskii–Moriya interaction in ultrathin Co/Pt nanostripe arrays. J. Phys. D Appl. Phys. 2018, 51, 225005. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Q.; Jia, J.; Zheng, Y.; Wang, Y.; Fan, X.; Cao, J. Tuning Slonczewski-like torque and Dzyaloshinskii–Moriya interaction by inserting a Pt spacer layer in Ta/CoFeB/MgO structures. Appl. Phys. Lett. 2018, 112, 232402. [Google Scholar] [CrossRef]
- Kim, G.W.; Samardak, A.S.; Kim, Y.J.; Cha, I.H.; Ognev, A.V.; Sadovnikov, A.V.; Nikitov, S.A.; Kim, Y.K. Role of the Heavy Metal’s Crystal Phase in Oscillations of Perpendicular Magnetic Anisotropy and the Interfacial Dzyaloshinskii-Moriya Interaction in W/Co−Fe−B/MgO Films. Phys. Rev. Appl. 2018, 9, 064005. [Google Scholar] [CrossRef]
- Gallardo, R.A.; Cortés-Ortuño, D.; Troncoso, R.E.; Landeros, P. Spin-waves in thin films and magnonic crystals with Dzyaloshinskii-Moriya interactions. In Three-Dimensional Magnonics: Layered, Micro- and Nanostructures; Gubbiotti, G., Ed.; Jenny Stanford Publishing, Pte. Ltd.: Singapore, 2019; pp. 121–160. [Google Scholar]
- Kuepferling, M.; Casiraghi, A.; Soares, G.; Durin, G.; Garcia-Sanchez, F.; Chen, L.; Back, C.H.; Marrows, C.H.; Tacchi, S.; Carlotti, G. Measuring interfacial Dzyaloshinskii-Moriya interaction in magnetic ultra thin films. arXiv 2020, arXiv:2009.11830. [Google Scholar]
- Ma, F.; Zhou, Y. Interfacial Dzialoshinskii–Moriya interaction induced nonreciprocity of spin waves in magnonic waveguides. RSC Adv. 2014, 4, 46454–46459. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Sanchez, F.; Borys, P.; Vansteenkiste, A.; Kim, J.V.; Stamps, R.L. Nonreciprocal spin-wave channeling along textures driven by the Dzyaloshinskii-Moriya interaction. Phys Rev. B 2014, 89, 224408. [Google Scholar] [CrossRef] [Green Version]
- Mruczkiewicz, M.; Krawczyk, M. Influence of the Dzyaloshinskii-Moriya interaction on the FMR spectrum of magnonic crystals and confined structures. Phys. Rev. B 2016, 94, 024434. [Google Scholar] [CrossRef] [Green Version]
- Zingsem, B.W.; Farle, M.; Stamps, R.L.; Camley, R.E. Unusual nature of confined modes in a chiral system: Directional transport in standing waves. Phys. Rev. B 2019, 99, 214429. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.-J.; Moon, J.-H.; Lee, H.-W.; Lee, K.-J. Spin-wave propagation in the presence of inhomogeneous Dzyaloshinskii-Moriya interactions. Phys. Rev. B 2017, 96, 184433. [Google Scholar] [CrossRef]
- Gallardo, R.A.; Cortés-Ortuño, D.; Schneider, T.; Roldán-Molina, A.; Ma, F.; Troncoso, R.E.; Lenz, K.; Fangohr, H.; Lindner, J.; Landeros, P. Flat Bands, Indirect Gaps, and Unconventional Spin-Wave Behavior Induced by a Periodic Dzyaloshinskii-Moriya Interaction. Phys. Rev. Lett. 2019, 122, 067204. [Google Scholar] [CrossRef] [Green Version]
- Chumak, A.V.; Vasyuchka, V.I.; Serga, A.A.; Hillebrands, B. Magnon spintronics. Nat. Phys. 2015, 11, 453–461. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef] [Green Version]
- Montoncello, F.; Giovannini, L.; Nizzoli, F.; Vavassori, P.; Grimsditch, M. Dynamic origin of first and second order phase transitions in magnetization reversal of elliptical nanodots. Phys. Rev. B 2008, 77, 214402. [Google Scholar] [CrossRef]
- Montoncello, F.; Giovannini, L.; Nizzoli, F.; Vavassori, P.; Grimsditch, M.; Ono, T.; Gubbiotti, G.; Tacchi, S.; Carlotti, G. Soft spin waves and magnetization reversal in elliptical Permalloy nanodots: Experiments and dynamical matrix results. Phys. Rev. B 2007, 76, 024426. [Google Scholar] [CrossRef]
- Carlotti, G. Pushing down the lateral dimension of single and coupled magnetic dots to the nanometric scale: Characteristics and evolution of the spin-wave eigenmodes. Appl. Phys. Rev. 2019, 6, 031304. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silvani, R.; Alunni, M.; Tacchi, S.; Carlotti, G. Effect of the Interfacial Dzyaloshinskii–Moriya Interaction on the Spin Waves Eigenmodes of Isolated Stripes and Dots Magnetized In-Plane: A Micromagnetic Study. Appl. Sci. 2021, 11, 2929. https://doi.org/10.3390/app11072929
Silvani R, Alunni M, Tacchi S, Carlotti G. Effect of the Interfacial Dzyaloshinskii–Moriya Interaction on the Spin Waves Eigenmodes of Isolated Stripes and Dots Magnetized In-Plane: A Micromagnetic Study. Applied Sciences. 2021; 11(7):2929. https://doi.org/10.3390/app11072929
Chicago/Turabian StyleSilvani, Raffaele, Michele Alunni, Silvia Tacchi, and Giovanni Carlotti. 2021. "Effect of the Interfacial Dzyaloshinskii–Moriya Interaction on the Spin Waves Eigenmodes of Isolated Stripes and Dots Magnetized In-Plane: A Micromagnetic Study" Applied Sciences 11, no. 7: 2929. https://doi.org/10.3390/app11072929






