Load Bearing Capacity of Cohesive-Frictional Soils Reinforced with Full-Wraparound Geotextiles: Experimental and Numerical Investigation
Abstract
:1. Introduction
2. Theoretical Background
3. Experimental and Numerical Procedures
3.1. Soil Samples
3.2. Geotextile Reinforcement
3.3. Load-Bearing Test Apparatus
3.4. Experimental and Numerical Programs
3.5. Construction and Test Methods
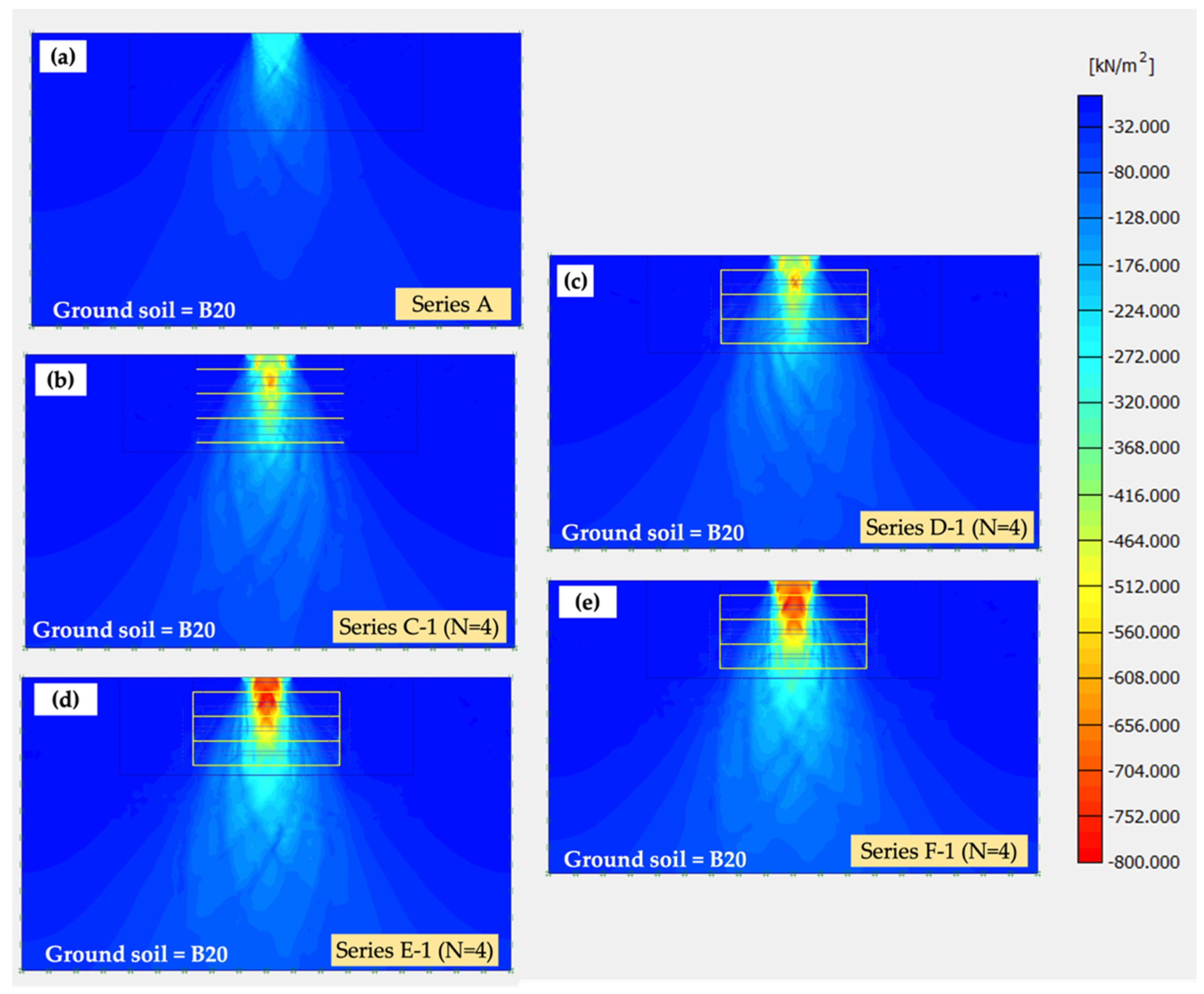
3.6. Numerical Modeling
4. Test Results and Discussion
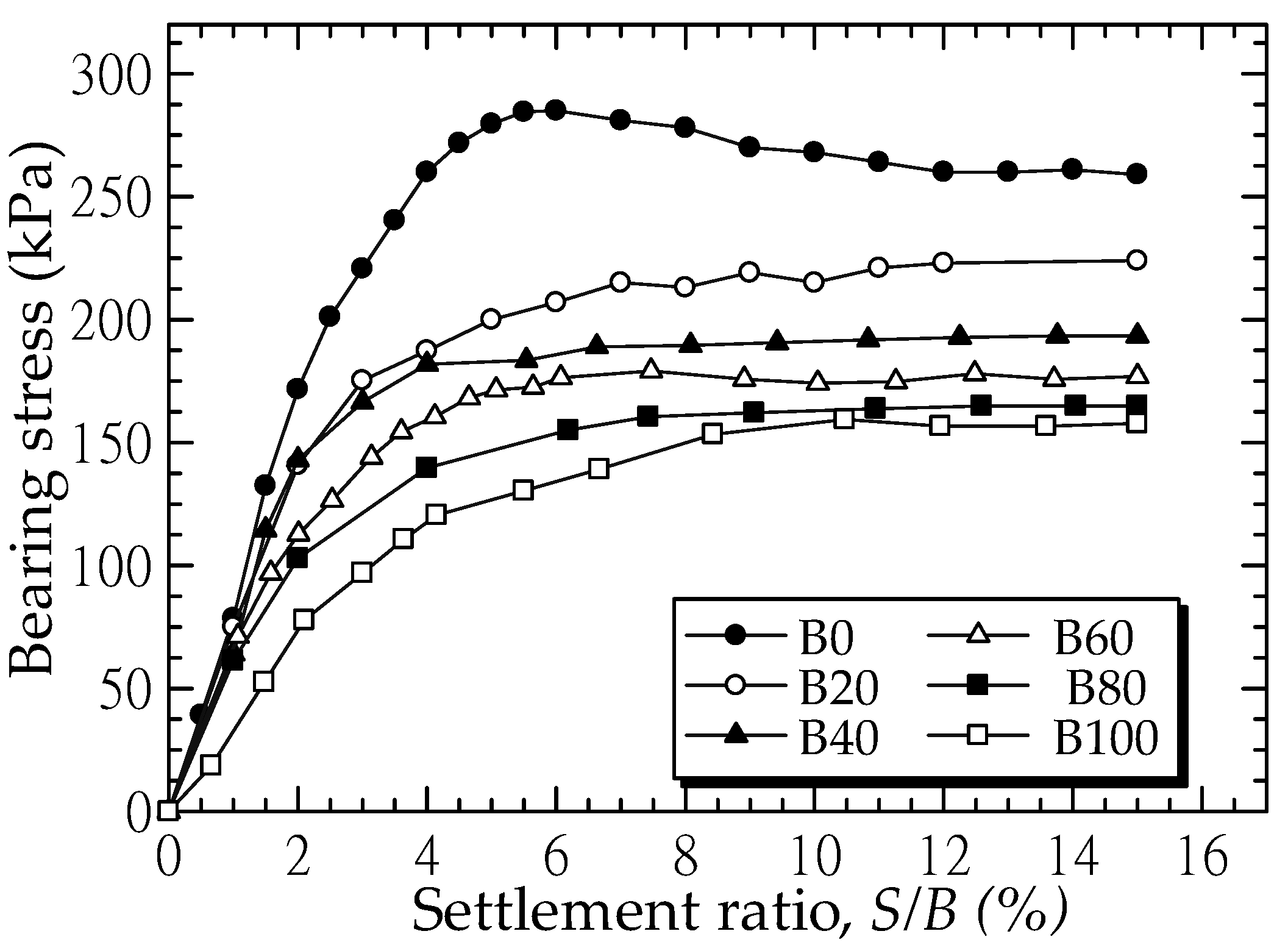
4.1. Load-Bearing Capacity of Unreinforced Soils (Series A)
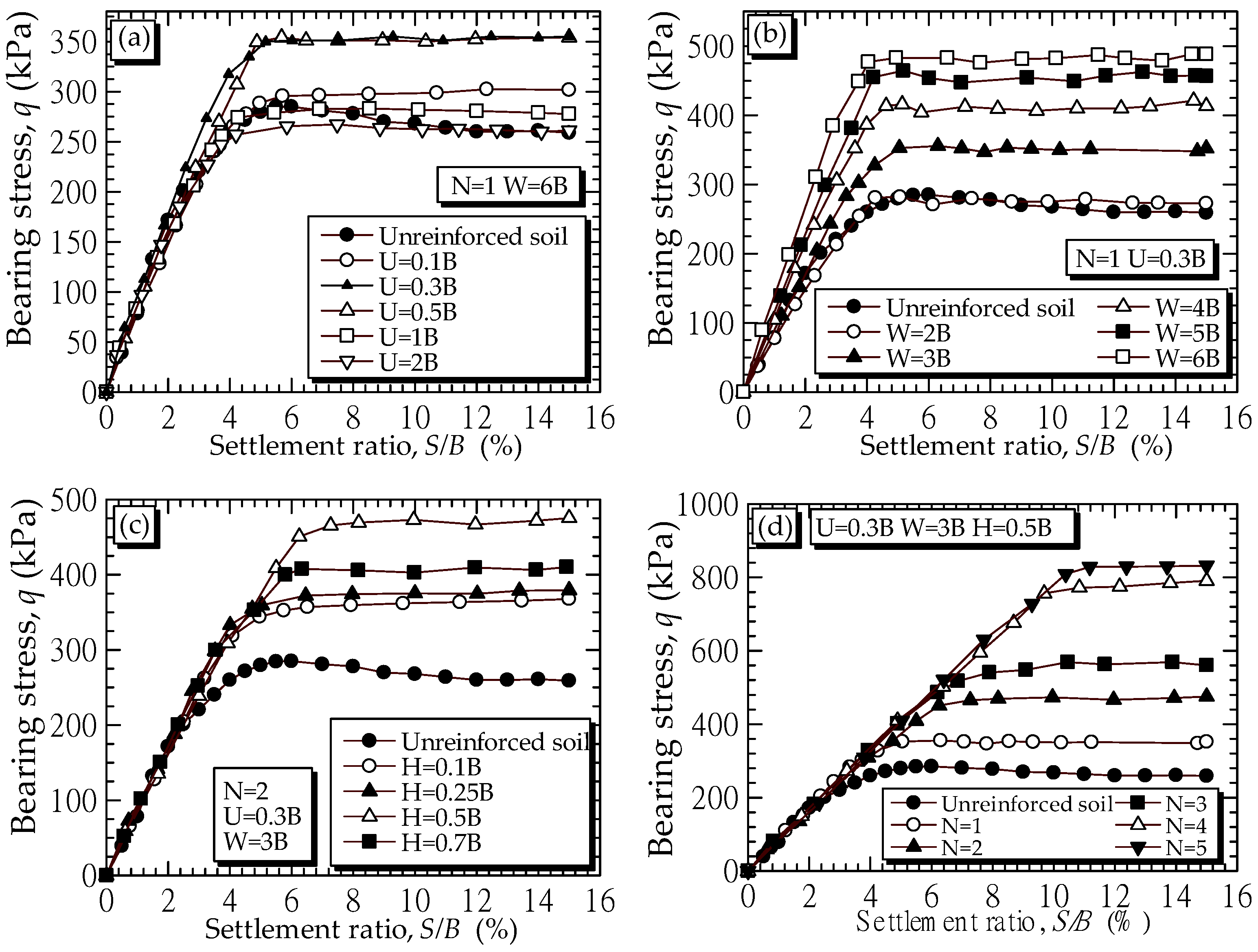
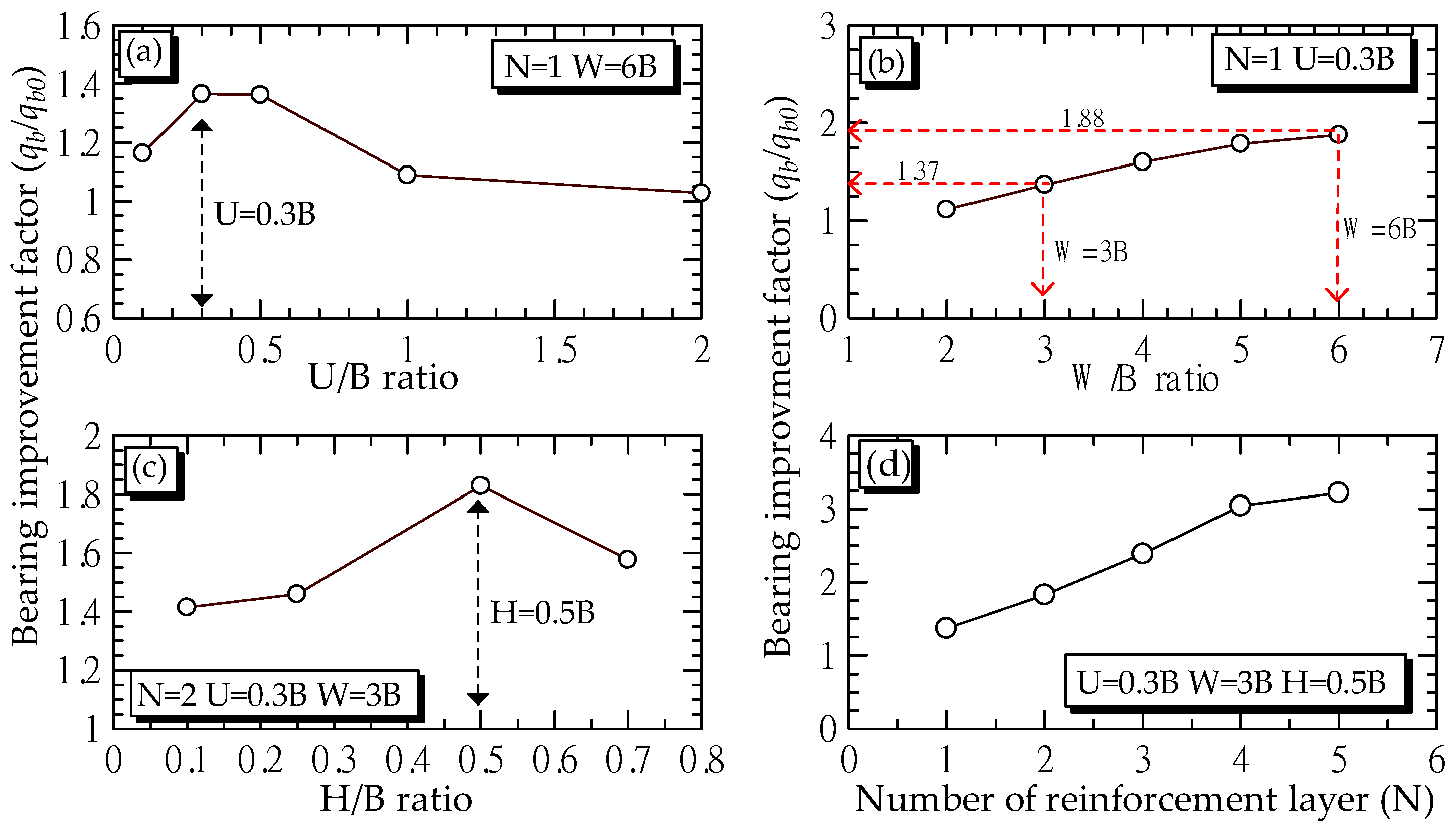
4.2. Load-Bearing Capacity of B0 Mixture Reinforced with Horizontal Planar Geotextile Reinforcement with N Layers (Series B)
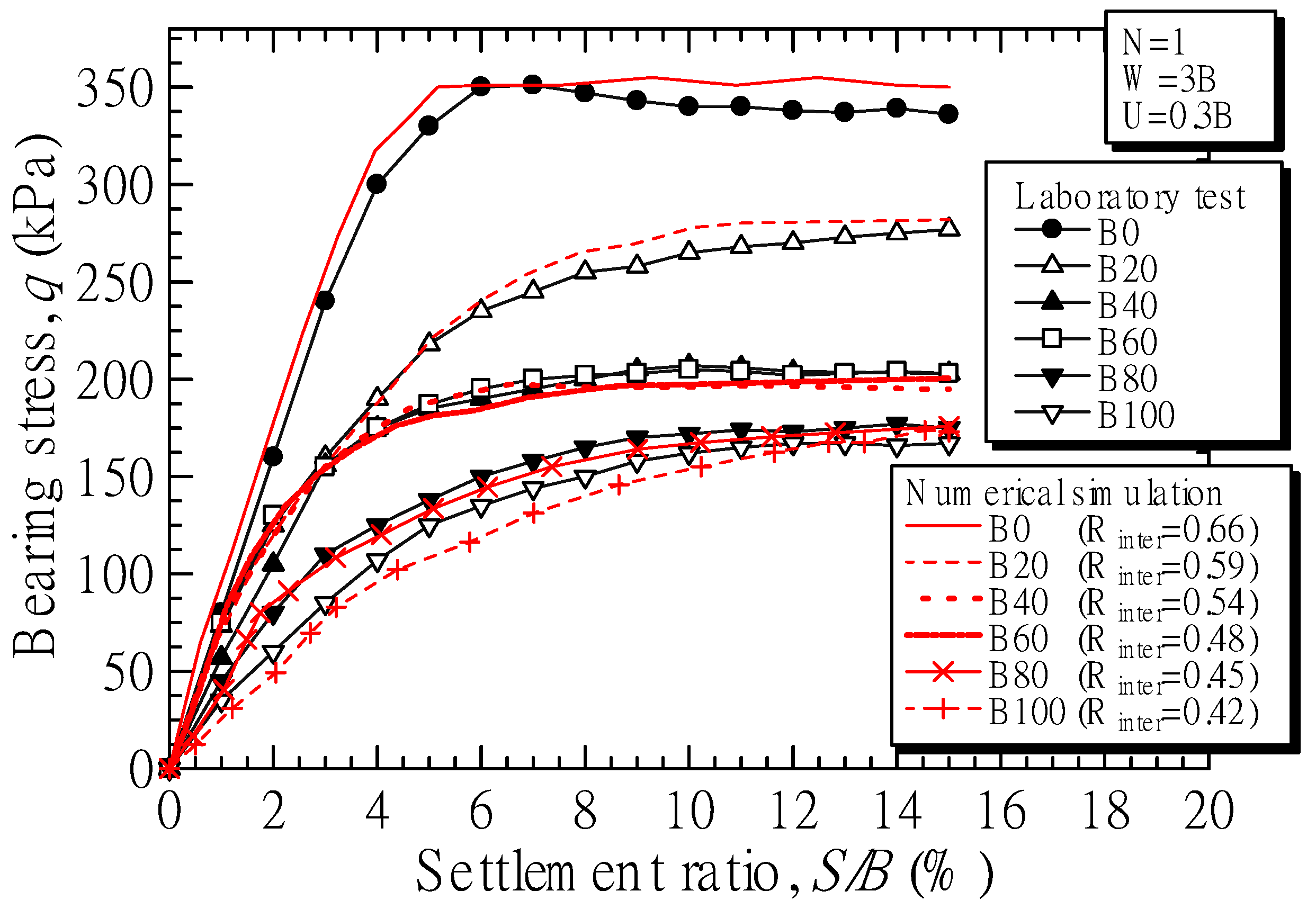
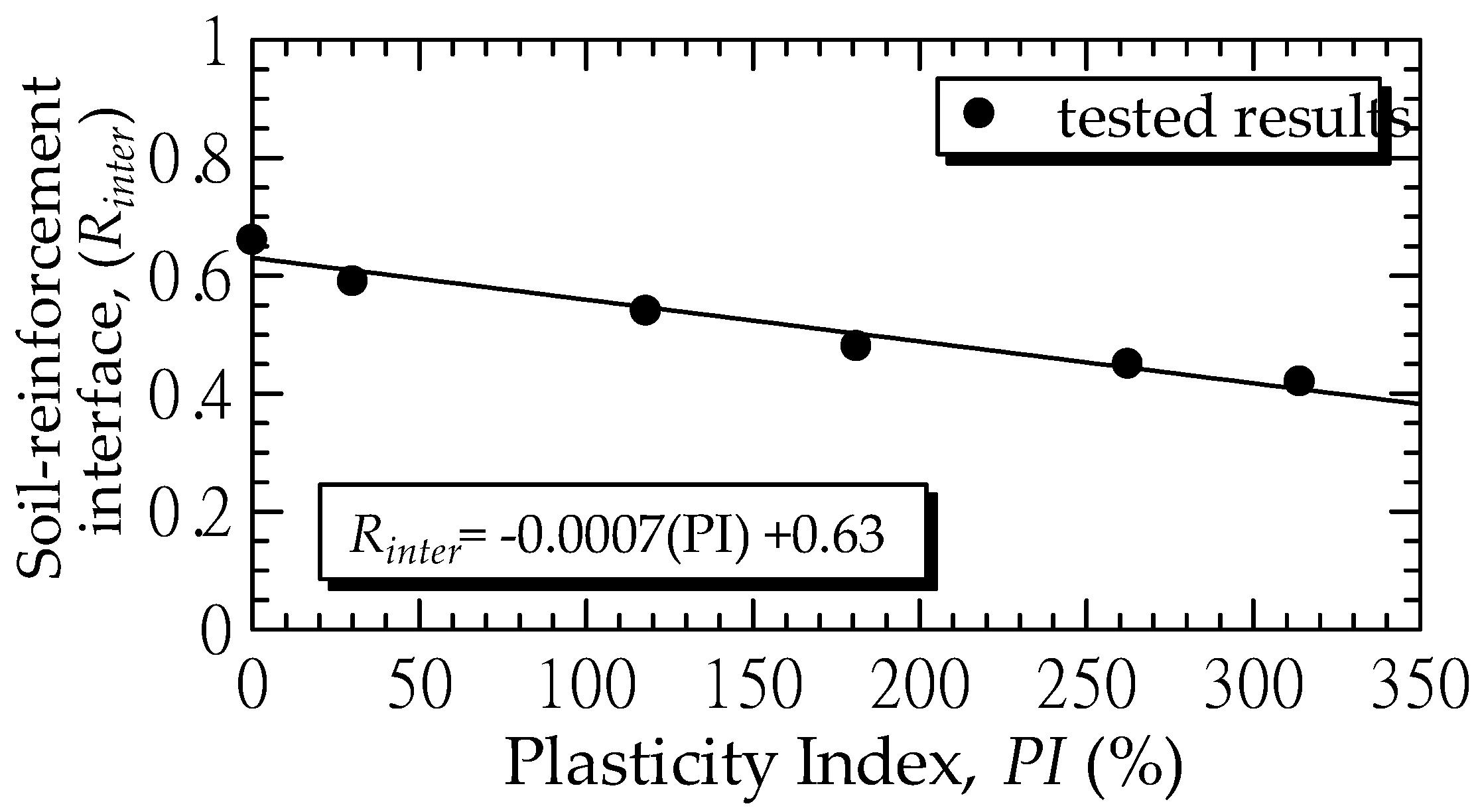
4.3. Interface Factor
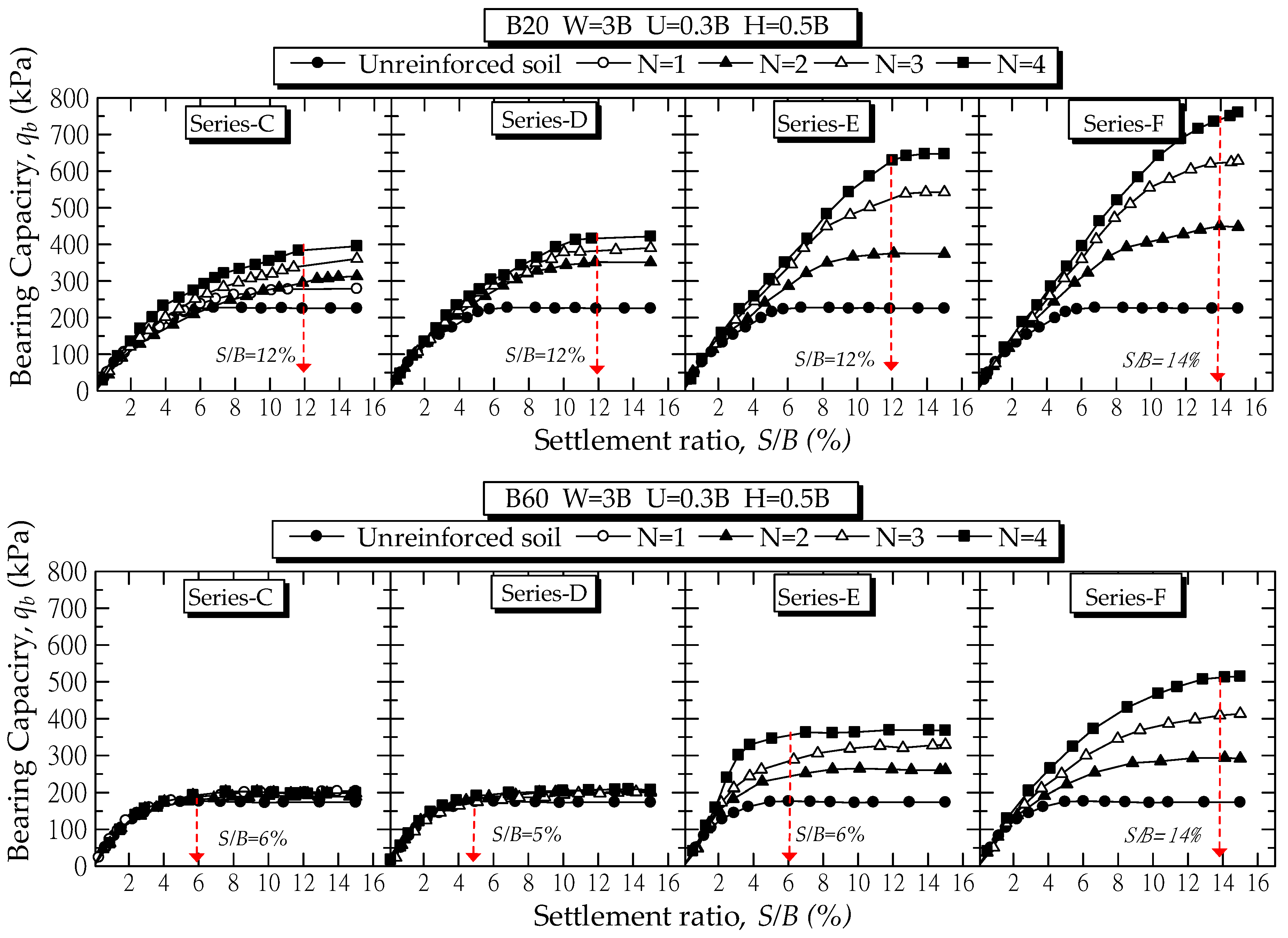
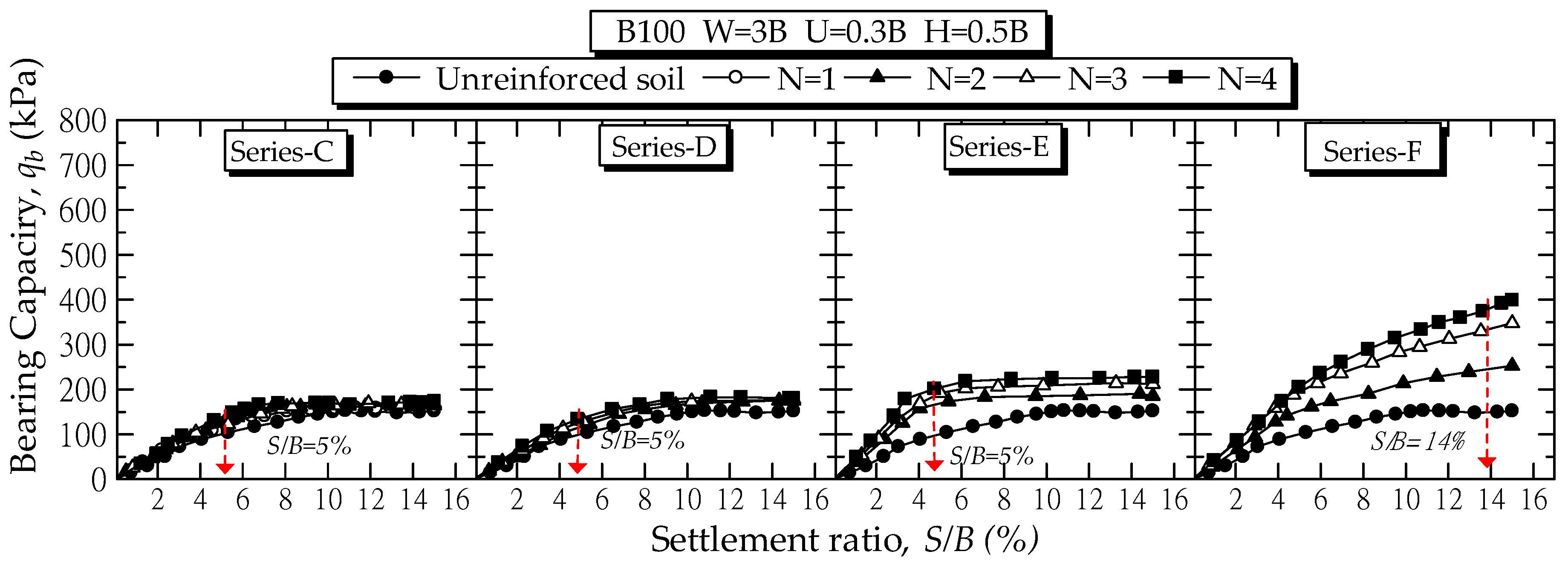
4.4. Performance of RSF with Different Reinforcing Techniques
5. Conclusions
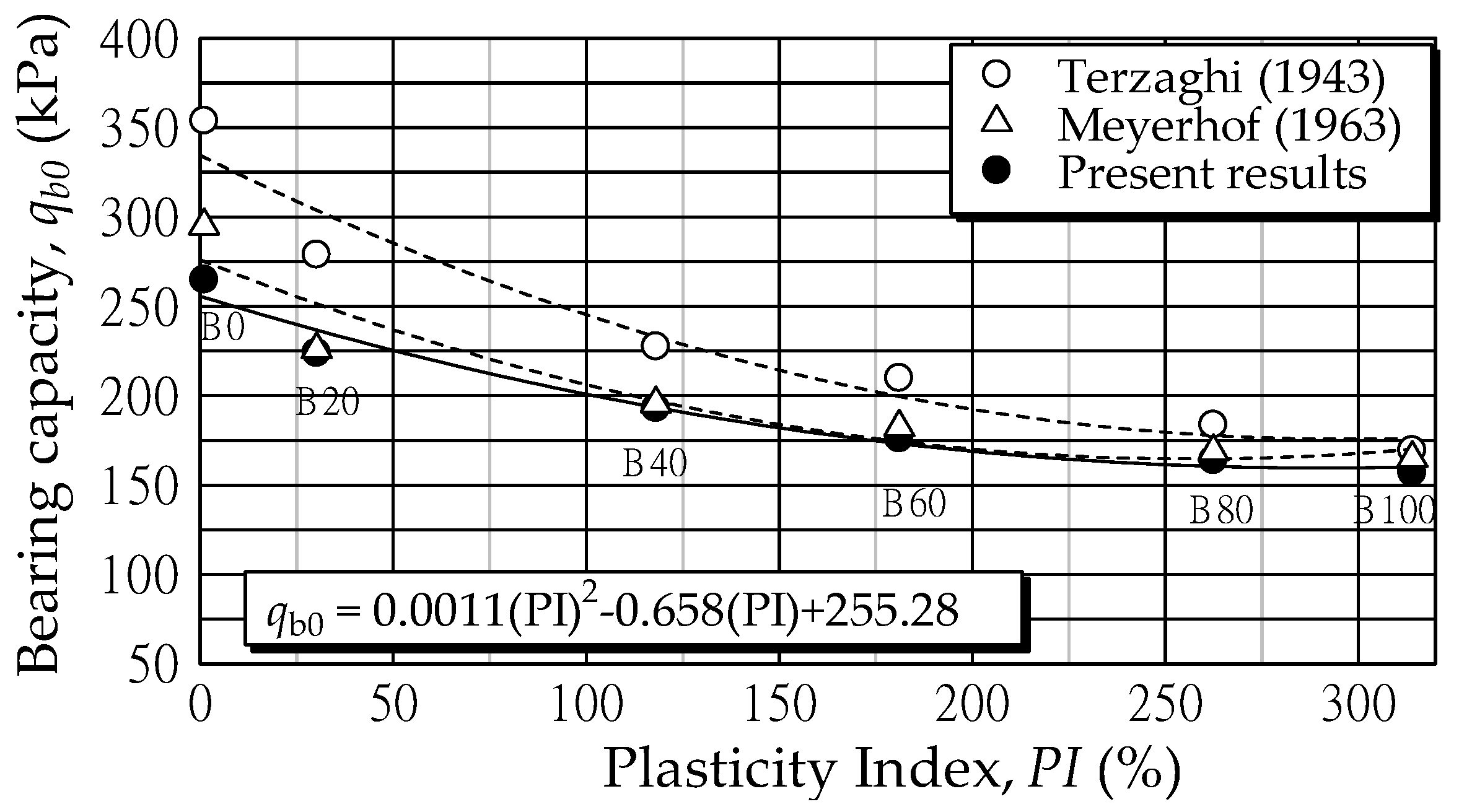
- For unreinforced soil, the qb0 decreased as the PI increased because of the reduction of soil shear strength. The qb0 can be predicted in terms of PI using a polynomial function: qb0 = 0.0011(PI)2 − 0.658(PI) + 255.28 when 0% < PI < 314%. The qb0 with various PI is satisfactorily predicted by Meyerhof (1963)’s equation. The laboratory investigation showed that the effective values of influence parameters for planar geotextile reinforcement were U/B = 0.3, W/B = 3.0, H/B = 0.5, and N = 4.
- For the horizontal planar form of geotextile reinforcement, when PI < 30, the qb/q0 increased with the increase in N from 1 to 4. The high soil-geotextile interface shear resistance tended to prevent the movement of soil particles and increased the bearing capacity. On the other hand, when PI > 30% (B40, B60, B80 and B100), the qb/q0 development was comparatively low with the additional N, because the soil movement highly occurred only on the first layer.
- For the full-wraparound ends of geotextile with filled-in foundation soils, when PI < 118%, the qb/q0 was improved in a range of 1.77 to 3.30 for B0, 1.45 to 1.90 for B20, and 1.44 to 1.75 for B40 when the N value increased from 2 to 4. Nevertheless, when PI > 118%, the qb/q0 was lower than 1.25 for all N values. When compared to the horizontal planar form of geotextile, the qb development in full-wraparound ends of geotextile was higher for the same foundation soils.
- For the full-wraparound ends of geotextile with filled-in sand, the qb/q0 value increased when the N increased from 2 to 4. For foundation soil with PI < 181%, the applied stress distributed through the foundation soil under the footing to the geotextiles effectively. However, the soil above the RSF was largely deformed with the low stiffness of soil with PI > 181% on the comparably stiffer RSF. With sand backfill under the footing, the qb/q0 increased linearly with the increase of N from 2 to 4. The qb/q0 varied from 1.35 to 3.34 for B20, 1.86 to 2.87 for B40, 1.66 to 2.91 for B60, 1.67 to 3.03 for B80, and 1.15 to 2.61 for B100.
- The horizontal planar reinforced soils, the full-wraparound ends of geotextile with filled-in foundation soil, and the full wraparound ends of geotextile with filled-in sand, were recommended for foundation soils with PI < 30%, PI < 118%, and PI < 181%, respectively. The sand backfill above the full wraparound ends of geotextile with filled-in sand can help effectively transfer the applied stress to RSF, hence the significant improvement in qb.
- It is kept in mind that the studied results are only valid for a woven geotextile. However, the knowledge gained from this research can be used as a guideline for further studies on different types of geosynthestics.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Chen, R.-H.; Wu, C.-P.; Huang, F.-C.; Shen, C.-W. Numerical analysis of geocell-reinforced retaining structures. Geotext. Geomembr. 2013, 39, 51–62. [Google Scholar] [CrossRef]
- Das, B.M.; Shin, E.C.; Omar, M.T. The bearing capacity of surface strip foundations on geogrid-reinforced sand and clay—A comparative study. Geotech. Geol. Eng. 1994, 12, 1–14. [Google Scholar] [CrossRef]
- Dash, S.K.; Krishnaswamy, N.R.; Rajagopal, K. Bearing capacity of strip footings supported on geocell-reinforced sand. Geotext. Geomembr. 2001, 19, 235–256. [Google Scholar] [CrossRef]
- Han, J. Principles and Practice of Ground Improvement; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hegde, A.M.; Sitharam, T.G. Three-dimensional numerical analysis of geocell-reinforced soft clay beds by considering the actual geometry of geocell pockets. Can. Geotech. J. 2015, 52, 1396–1407. [Google Scholar] [CrossRef]
- Kazi, M.; Shukla, S.K.; Habibi, D. Behavior of embedded strip footing on sand bed reinforced with multilayer geotextile with wraparound ends. Int. J. Geotech. Eng. 2015, 9, 437–452. [Google Scholar] [CrossRef]
- Kazi, M.; Shukla, S.K.; Habibi, D. An Improved Method to Increase the Load-Bearing Capacity of Strip Footing Resting on Geotextile-Reinforced Sand Bed. Indian Geotech. J. 2015, 45, 98–109. [Google Scholar] [CrossRef]
- Shirazi, M.G.; Rashid, A.S.A.; Nazir, R.B.; Rashid, R.H.B.A.; Moayedi, H.; Horpibulsuk, S.; Samingthong, W. Sustainable soil bearing capacity improvement using natural limited life geotextile reinforcement—A review. Minerals 2020, 10, 479. [Google Scholar] [CrossRef]
- Rashid, A.S.A.; Shirazi, M.G.; Nazir, R.; Mohamad, H.; Sahdi, F.; Horpibulsuk, S. Bearing capacity performance of soft cohesive soil treated by kenaf limited life geotextile. Mar. Georesour. Geotechnol. 2020, 38, 755–760. [Google Scholar] [CrossRef]
- Chakraborty, M.; Kumar, J. Bearing capacity of circular foundations reinforced with geogrid sheets. Soils Found. 2014, 54, 820–832. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Abu-Farsakh, M. Ultimate bearing capacity analysis of strip footings on reinforced soil foundation. Soils Found. 2015, 55, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Shahin, H.M.; Nakai, T.; Morikawa, Y.; Masuda, S.; Mio, S. Effective use of geosynthetics to increase bearing capacity of shallow foundations. Can. Geotech. J. 2017, 54, 1647–1658. [Google Scholar] [CrossRef]
- Benmebarek, S.; Djeridi, S.; Benmebarek, N.; Belounar, L. Improvement of bearing capacity of strip footing on reinforced sand. Int. J. Geotech. Eng. 2018, 12, 537–545. [Google Scholar] [CrossRef]
- Djeridi, S.; Benmebarek, N.; Benmebarek, S. Effect of Full Wrap-Around Ends of Geotextile on the Bearing Capacity of Sand. In Advances in Science, Technology & Innovation; IEREK Interdisciplinary Series for Sustainable Development; Springer: Berlin/Heidelberg, Germany, 2019; pp. 291–294. [Google Scholar] [CrossRef]
- Rao, P.; Liu, Y.; Cui, J. Bearing capacity of strip footings on two-layered clay under combined loading. Comput. Geotech. 2015, 69, 210–218. [Google Scholar] [CrossRef]
- Benmebarek, S.; Benmoussa, S.; Belounar, L.; Benmebarek, N. Bearing Capacity of Shallow Foundation on Two Clay Layers by Numerical Approach. Geotech. Geol. Eng. 2012, 30, 907–923. [Google Scholar] [CrossRef]
- Benmebarek, S.; Remadna, M.S.; Benmebarek, N.; Belounar, L. Numerical evaluation of the bearing capacity factor Nγ′ of ring footings. Comput. Geotech. 2012, 44, 132–138. [Google Scholar] [CrossRef]
- Conte, E.; Donato, A.; Troncone, A. Progressive failure analysis of shallow foundations on soils with strain-softening behaviour. Comput. Geotech. 2013, 54, 117–124. [Google Scholar] [CrossRef] [Green Version]
- Sukmak, K.; Sukmak, P.; Horpibulsuk, S.; Han, J.; Shen, S.-L.; Arulrajah, A. Effect of fine content on the pullout resistance mechanism of bearing reinforcement embedded in cohesive–frictional soils. Geotext. Geomembr. 2015, 43, 107–117. [Google Scholar] [CrossRef]
- Lupini, J.F.; Skinner, A.E.; Vaughan, P.R. The drained residual strength of cohesive soils. Géotechnique 1981, 31, 181–213. [Google Scholar] [CrossRef]
- Maio, C.D.; Fenellif, G.B. Residual strength of kaolin and bentonite: The influence of their constituent pore fluid. Géotechnique 1994, 44, 217–226. [Google Scholar] [CrossRef] [Green Version]
- Mesri, G.; Cepeda-Diaz, A.F. Residual shear strength of clays and shales. Géotechnique 1986, 36, 269–274. [Google Scholar] [CrossRef]
- Sridharan, A.; Rao, S.; Murthy, N. Liquid Limit of Montmorillonite Soils. Geotech. Test. J. 1986, 9, 156–159. [Google Scholar] [CrossRef]
- Tan, T.; Goh, T.; Karunaratne, G.; Lee, S. Shear Strength of Very Soft Clay-Sand Mixtures. Geotech. Test. J. 1994, 17, 27–34. [Google Scholar] [CrossRef]
- Bergado, D.T.; Youwai, S.; Teerawattanasuk, C.; Visudmedanukul, P. The interaction mechanism and behavior of hexagonal wire mesh reinforced embankment with silty sand backfill on soft clay. Comput. Geotech. 2003, 30, 517–534. [Google Scholar] [CrossRef]
- Khedkar, M.S.; Mandal, J.N. Pullout behaviour of cellular reinforcements. Geotext. Geomembr. 2009, 27, 262–271. [Google Scholar] [CrossRef]
- Suksiripattanapong, C.; Chinkulkijniwat, A.; Horpibulsuk, S.; Rujikiatkamjorn, C.; Tangsuttinon, T. Numerical Analysis of Bearing Reinforcement Earth (BRE) Wall. Geotext. Geomembr. 2012, 32, 28–37. [Google Scholar] [CrossRef] [Green Version]
- Sukmak, K.; Han, J.; Sukmak, P.; Horpibulsuk, S. Numerical parametric study on behavior of bearing reinforcement earth walls with different backfill material properties. Geosynth. Int. 2016, 23, 435–451. [Google Scholar] [CrossRef] [Green Version]
- Prandtl, L. Uber die eindringungstestigkeit plastisher baustoffe und die festigkeit von schneiden [in German]. Z. Fur Angew. Math. Mech. 1921, 1, 15–30. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1943. [Google Scholar]
- Meyerhof, G.G. Some recent research on the bearing capacity of foundations. Can. Geotech. J. 1963, 1, 16–26. [Google Scholar] [CrossRef]
- Burd, H.J.; Frydman, S. Bearing capacity of plane-strain footings on layered soils. Can. Geotech. J. 1997, 34, 241–253. [Google Scholar] [CrossRef]
- Hanna, A.M.; Meyerhof, G.G. Design charts for ultimate bearing capacity of foundations on sand overlying soft clay. Can. Geotech. J. 1980, 17, 300–303. [Google Scholar] [CrossRef]
- Ismail Ibrahim, K.M.H. Bearing capacity of circular footing resting on granular soil overlying soft clay. HBRC J. 2016, 12, 71–77. [Google Scholar] [CrossRef] [Green Version]
- Kumar, J.; Chakraborty, M. Bearing capacity of a circular foundation on layered sand–clay media. Soils Found. 2015, 55, 1058–1068. [Google Scholar] [CrossRef] [Green Version]
- Madhav Madhira, R.; Sharma, J.S.N. Bearing Capacity of Clay Overlain by Stiff Soil. J. Geotech. Eng. 1991, 117, 1941–1948. [Google Scholar] [CrossRef]
- Huang, C.-C.; Tatsuoka, F. Bearing capacity of reinforced horizontal sandy ground. Geotext. Geomembr. 1990, 9, 51–82. [Google Scholar] [CrossRef]
- Lovisa, J.; Shukla, S.K.; Sivakugan, N. Behaviour of prestressed geotextile-reinforced sand bed supporting a loaded circular footing. Geotext. Geomembr. 2010, 28, 23–32. [Google Scholar] [CrossRef]
- Yetimoglu, T.; Wu Jonathan, T.H.; Saglamer, A. Bearing Capacity of Rectangular Footings on Geogrid-Reinforced Sand. J. Geotech. Eng. 1994, 120, 2083–2099. [Google Scholar] [CrossRef]
- Khing, K.H.; Das, B.M.; Puri, V.K.; Cook, E.E.; Yen, S.C. The bearing-capacity of a strip foundation on geogrid-reinforced sand. Geotext. Geomembr. 1993, 12, 351–361. [Google Scholar] [CrossRef]
- Kumar, G.V.; Muir Wood, D. Fall cone and compression tests on clay-gravel mixtures. Geotechnique 1999, 49, 727–739. [Google Scholar] [CrossRef]
- Polidori, E. Relationship between the atterberg limits and clay content. Soils Found. 2007, 47, 887–896. [Google Scholar] [CrossRef] [Green Version]
- Skempton, A.W. The colloidal activity of clays. In Proceedings of the 3rd International Conference on Soil Mechanics and Foundation Engineering, Zurich, Switzerland, 16–27 August 1953; Volume 1, pp. 57–61. [Google Scholar]
- ASTM-D698 Standard Test. Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort (12,400 ft-lbf/ft3 (600 kN-m/m3)); ASTM International: West Conshohocken, PA, USA, 2012.
- Al-Shayea, N.A. The combined effect of clay and moisture content on the behavior of remolded unsaturated soils. Eng. Geol. 2001, 62, 319–342. [Google Scholar] [CrossRef]
- Tiwari, B.; Marui, H. A New Method for the Correlation of Residual Shear Strength of the Soil with Mineralogical Composition. Geotech. Geol. Eng. 2005, 131, 1139–1150. [Google Scholar] [CrossRef]
- Wang, S.; Chan, D.; Lam, K.C. Experimental study of the effect of fines content on dynamic compaction grouting in completely decomposed granite of Hong Kong. Constr Build. Mater. 2009, 23, 1249–1264. [Google Scholar] [CrossRef]
- Shadi, A.; Sanjay, K.S.; Alireza, M. Behaviour of sandy soil reinforced with geotextile having partially and fully wrapped ends. Ground Improvement. 2021, 174, 29–41. [Google Scholar] [CrossRef]
- Shadi, A.; Sanjay, K.S.; Alireza, M. Numerical Investigation of Wraparound Geotextile Reinforcement Technique for Strengthening Foundation Soil. Int. J. Geomech. 2019, 19. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J.; Broere, W.; Waterman, D. PLAXIS 2D—Version 8 Tutorial Manual; Plaxisbv: Delft, The Netherlands, 2006. [Google Scholar]
- ASTM-D4595 Standard Test. Method for Tensile Properties of Geotextiles by the Wide-Width Strip Method; ASTM International: West Conshohocken, PA, USA, 2017.
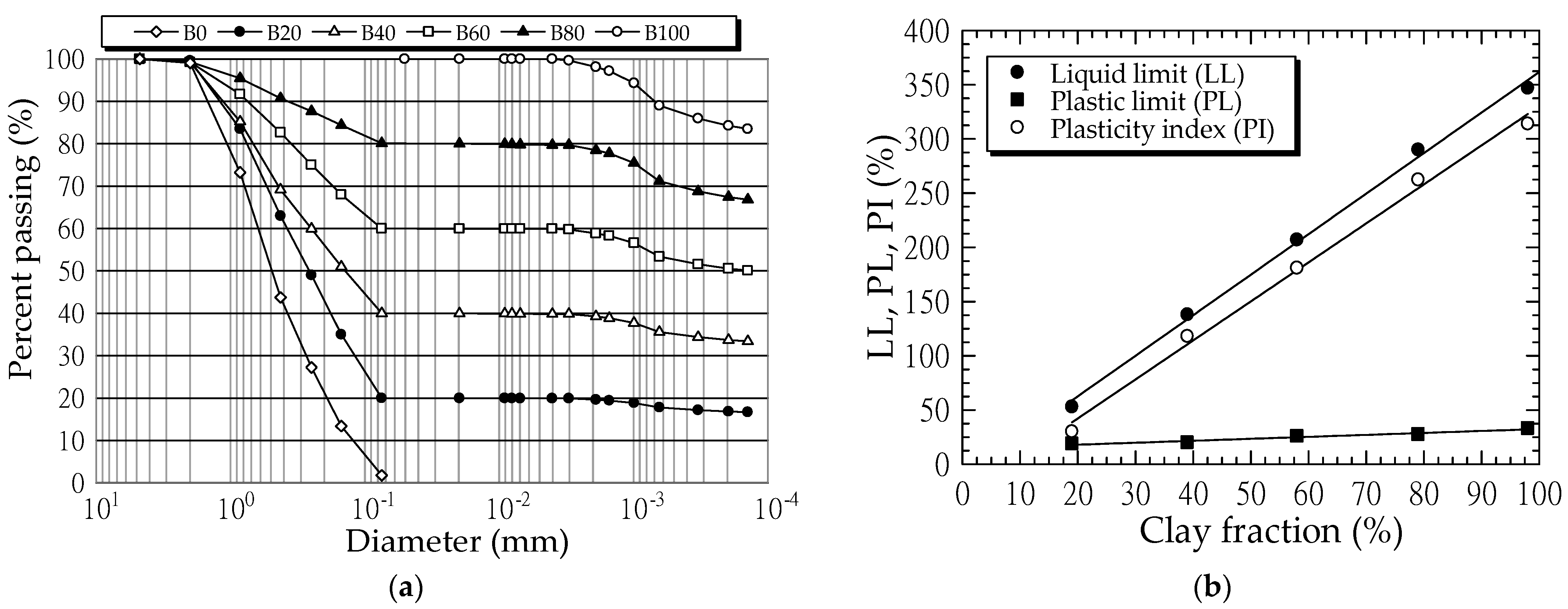
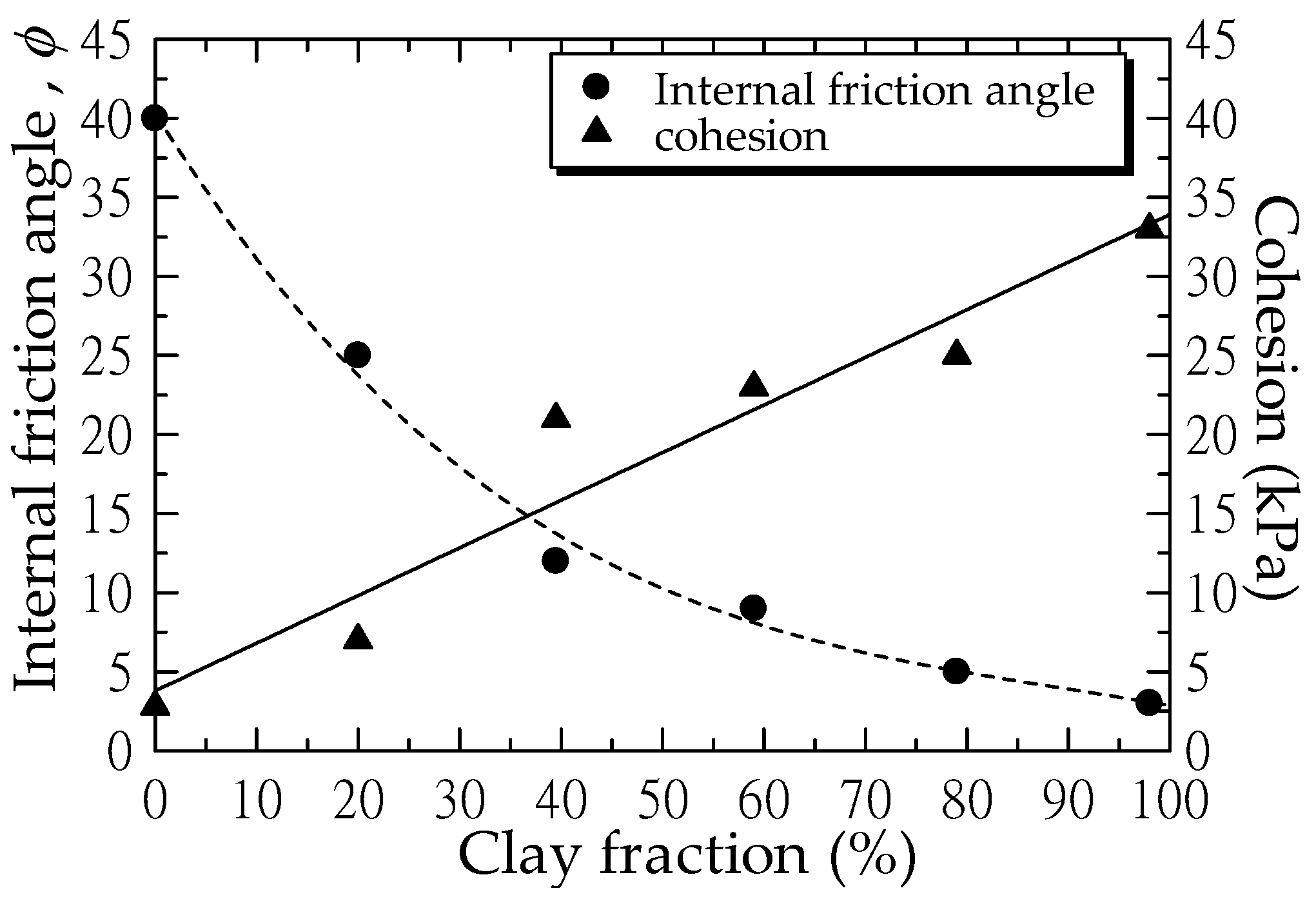








| Soil Mixtures | Total Unit Weight (kN/m3) | Dry Unit Weight (kN/m3) | Optimum Water Content (%) | Liquid Limit LL (%) | Plastic Limit PL (%) | Plasticity Index (PI) (%) | Internal Friction Angle (Degree) | Cohesion (kPa) |
|---|---|---|---|---|---|---|---|---|
| B0 | 17.66 | 17.14 | 3.0 | - | - | - | 40 | 2.8 |
| B20 | 18.69 | 16.87 | 10.8 | 49 | 19 | 30 | 30 | 7 |
| B40 | 17.40 | 15.01 | 16.0 | 138 | 20 | 118 | 12 | 21 |
| B60 | 16.17 | 13.32 | 21.4 | 207 | 26 | 181 | 9 | 23 |
| B80 | 15.81 | 12.65 | 25.0 | 290 | 28 | 262 | 5 | 25 |
| B100 | 14.17 | 10.99 | 29.0 | 347 | 33 | 314 | 0 | 33 |
| Investigation Cases | Reinforcement Layout Configurations | Test Series | Soil Ground | Filled Soil | Reinforcement Layout Configurations | Test Series |
|---|---|---|---|---|---|---|
| Experimental and numerical investigations | Unreinforced soil | A | B0, B20, B40, B60, B80, B100 | - | - | - |
| Horizontal planar reinforced soils | B-1 | B0 | - | N = 1, W/B = 6 | U/B = 0.1, 0.3, 0.5, 1 and 2 | |
| B-2 | - | N = 1, U/B = 0.3 | W/B = 2, 3, 4, 5 and 6 | |||
| B-3 | - | N = 2, U/B = 0.3, W/B = 3 | H/B = 0.1, 0.25, 0.5, 0.7 | |||
| B-4 | - | U/B = 0.3, W/B = 3, H/B = 0.5 | N = 1, 2, 3 and 4 | |||
| Horizontal planar reinforced soils | C-1 | B0 | - | U/B = 0.3, W/B = 3, N = 1, 2, 3 and 4 | Rinter= 0 to 1.0 | |
| C-2 | B20 | |||||
| C-3 | B40 | |||||
| C-4 | B60 | |||||
| C-5 | B80 | |||||
| C-6 | B100 | |||||
| Numerical investigations | Full wraparound ends of geotextile | D-1 | B0 | B0 | U/B = 0.3, W/B = 3, H/B = 0.5 | N = 2, 3 and 4 |
| D-2 | B20 | B20 | ||||
| D-3 | B40 | B40 | ||||
| D-4 | B60 | B60 | ||||
| D-5 | B80 | B80 | ||||
| D-6 | B100 | B100 | ||||
| Full wraparound ends of geotextile with filled-in sand | E-1 | B20 | B0 | U/B = 0.3, W/B = 3, H/B = 0.5 | N = 2, 3 and 4 | |
| E-2 | B40 | |||||
| E-3 | B60 | |||||
| E-4 | B80 | |||||
| E-5 | B100 | |||||
| Full wraparound ends of geotextile reinforcement with filled-in sand and sand backfill | F-1 | B20 | B0 | U/B = 0.3, W/B = 3, H/B = 0.5 | N = 2, 3 and 4 | |
| F-2 | B40 | |||||
| F-3 | B60 | |||||
| F-4 | B80 | |||||
| F-5 | B100 |
| Soil Mixtures | E (kN/m2) | υ | ϕ (Degree) | c (kPa) | ψ (Degree) | Rinter |
|---|---|---|---|---|---|---|
| B0 | 20,000 | 0.3 | 40 | 2 | 10 | 0.66 |
| B20 | 17,000 | 0.3 | 30 | 9 | 0 | 0.59 |
| B40 | 15,000 | 0.35 | 12 | 18 | 0 | 0.54 |
| B60 | 13,000 | 0.4 | 9 | 20 | 0 | 0.48 |
| B80 | 8000 | 0.4 | 5 | 25 | 0 | 0.45 |
| B100 | 5000 | 0.4 | 0 | 33 | 0 | 0.42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sukmak, G.; Sukmak, P.; Horpibulsuk, S.; Hoy, M.; Arulrajah, A. Load Bearing Capacity of Cohesive-Frictional Soils Reinforced with Full-Wraparound Geotextiles: Experimental and Numerical Investigation. Appl. Sci. 2021, 11, 2973. https://doi.org/10.3390/app11072973
Sukmak G, Sukmak P, Horpibulsuk S, Hoy M, Arulrajah A. Load Bearing Capacity of Cohesive-Frictional Soils Reinforced with Full-Wraparound Geotextiles: Experimental and Numerical Investigation. Applied Sciences. 2021; 11(7):2973. https://doi.org/10.3390/app11072973
Chicago/Turabian StyleSukmak, Gampanart, Patimapon Sukmak, Suksun Horpibulsuk, Menglim Hoy, and Arul Arulrajah. 2021. "Load Bearing Capacity of Cohesive-Frictional Soils Reinforced with Full-Wraparound Geotextiles: Experimental and Numerical Investigation" Applied Sciences 11, no. 7: 2973. https://doi.org/10.3390/app11072973
APA StyleSukmak, G., Sukmak, P., Horpibulsuk, S., Hoy, M., & Arulrajah, A. (2021). Load Bearing Capacity of Cohesive-Frictional Soils Reinforced with Full-Wraparound Geotextiles: Experimental and Numerical Investigation. Applied Sciences, 11(7), 2973. https://doi.org/10.3390/app11072973








