Numerical Modeling of Crack Growth under Mixed-Mode Loading
Abstract
:1. Introduction
2. ANSYS Mechanical APDL 19.2
3. Numerical Results and Discussions
3.1. Three-Point Bending Beam with Different Configurations
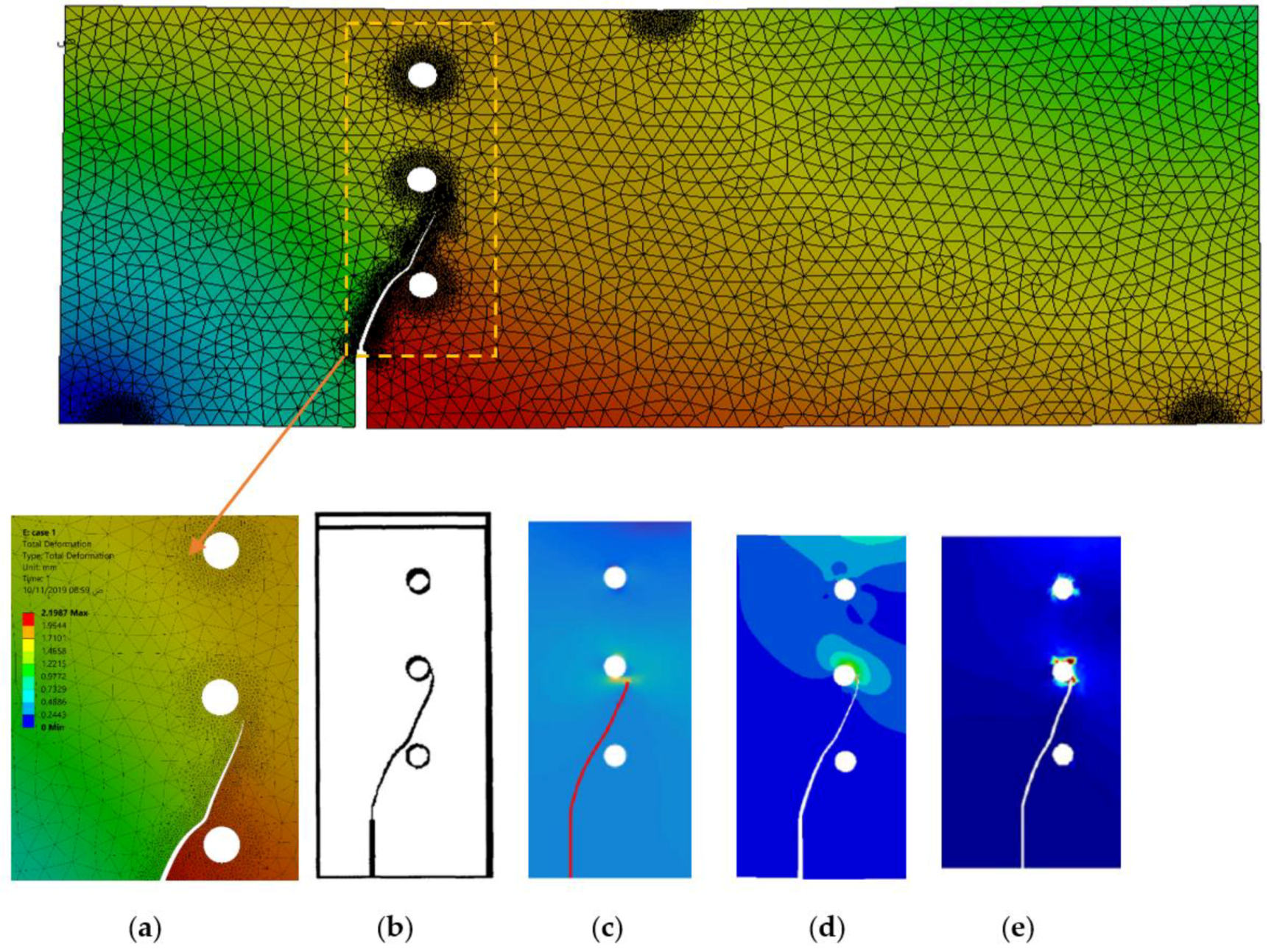
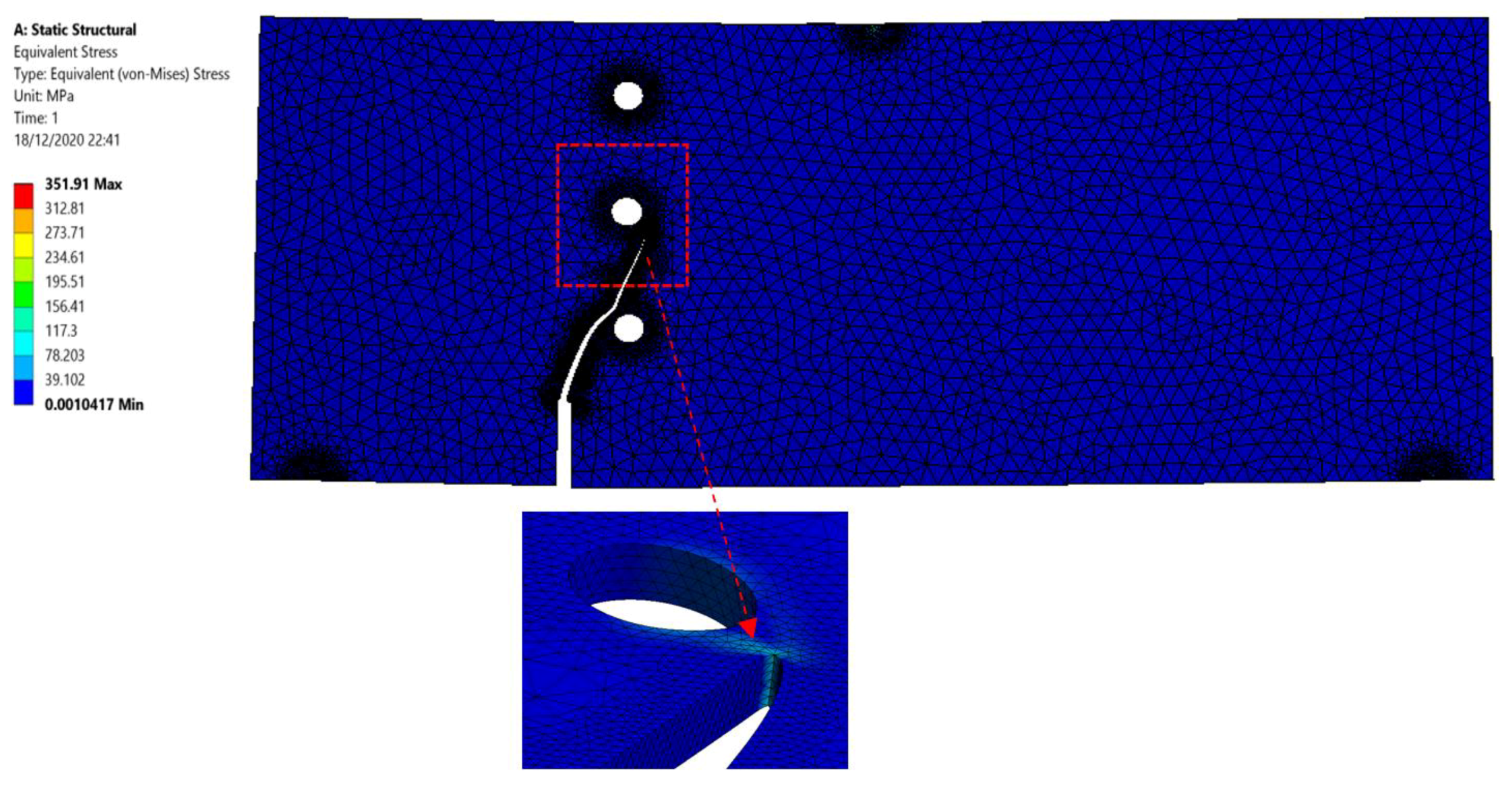
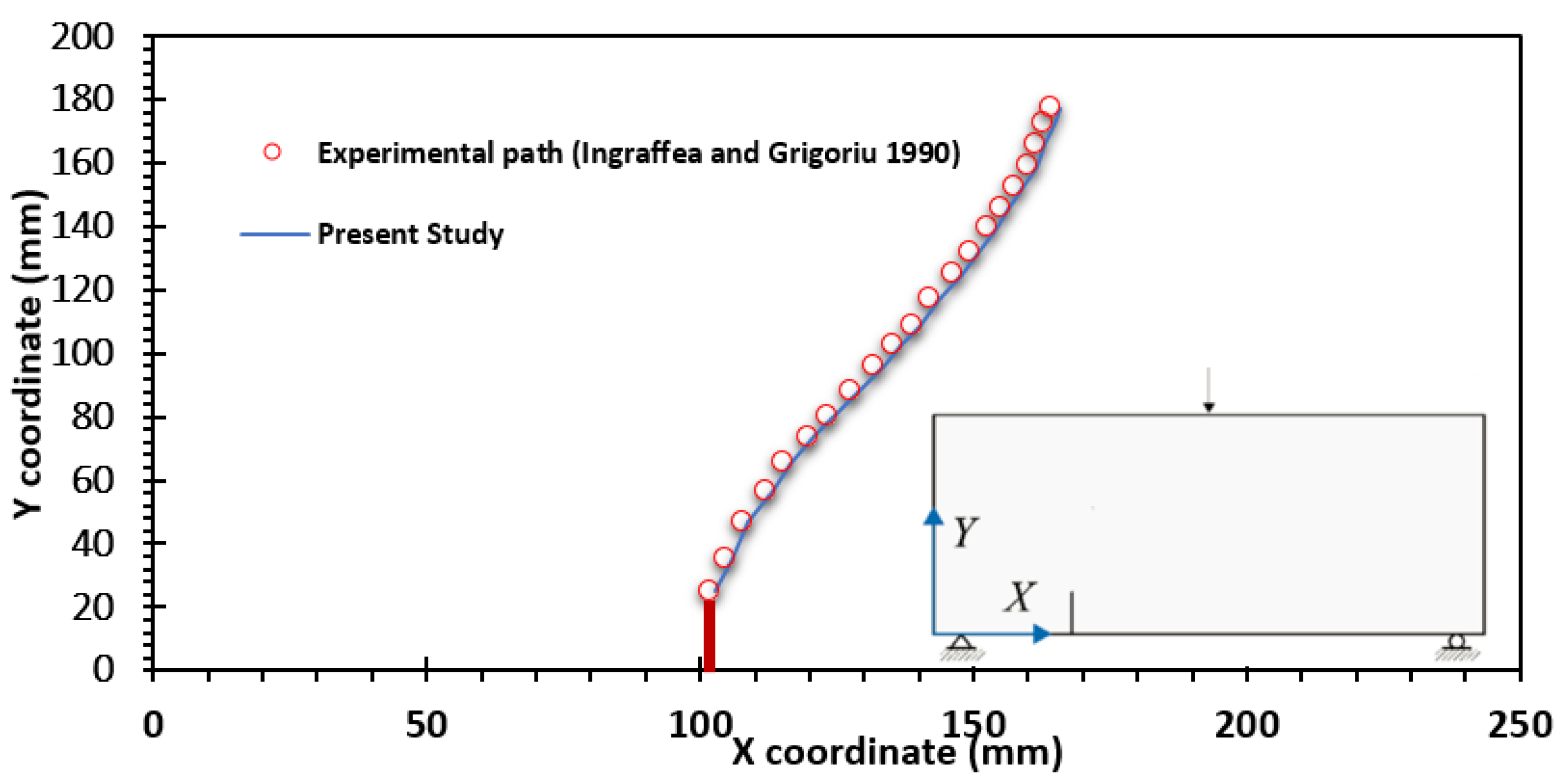
3.1.1. Specimen 1
3.1.2. Specimen 2
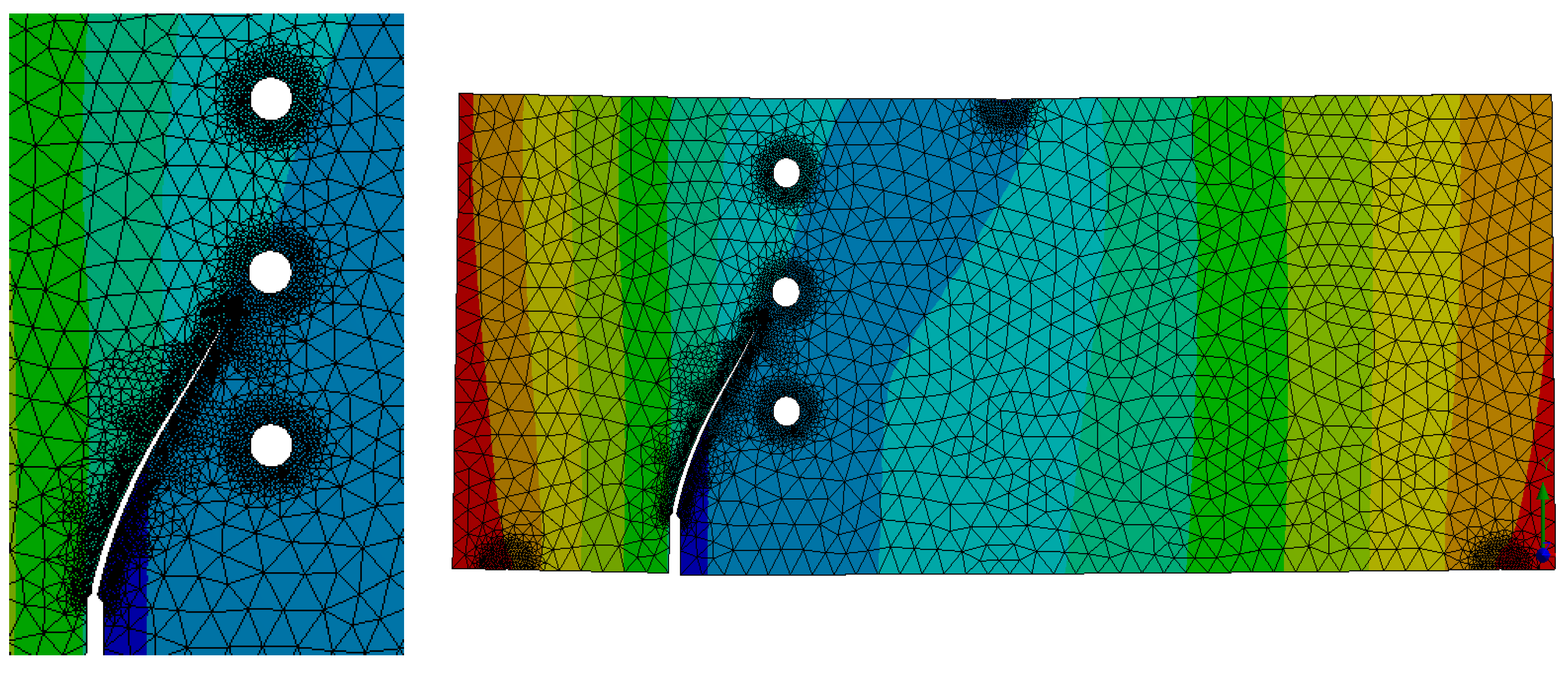
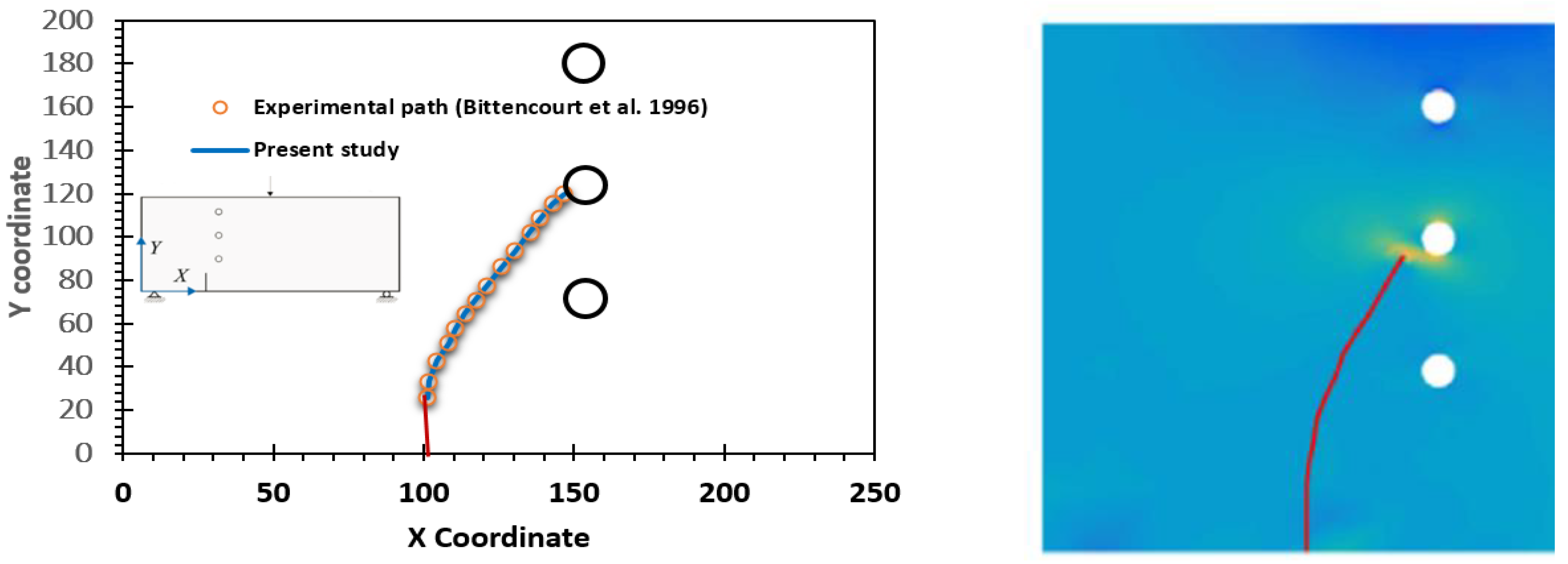
3.1.3. Specimen 3
3.1.4. Specimen 4
3.1.5. Specimen 5
3.1.6. Specimen 6
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Li, H.; Liu, L.; Liu, Y.; Ju, M.; Zhao, J. Investigating the Crack Initiation and Propagation Mechanism in Brittle Rocks Using Grain-Based Finite-Discrete Element Method. Int. J. Rock Mech. Min. Sci. 2020, 127, 104219. [Google Scholar] [CrossRef]
- Leclerc, W.; Haddad, H.; Guessasma, M. On the Suitability of a Discrete Element Method to Simulate Cracks Initiation and Propagation in Heterogeneous Media. Int. J. Solids Struct. 2017, 108, 98–114. [Google Scholar] [CrossRef]
- Shao, Y.; Duan, Q.; Qiu, S. Adaptive Consistent Element-Free Galerkin Method for Phase-Field Model of Brittle Fracture. Comput. Mech. 2019, 64, 741–767. [Google Scholar] [CrossRef]
- Kanth, S.A.; Harmain, G.; Jameel, A. Modeling of Nonlinear Crack Growth in Steel and Aluminum Alloys by the Element Free Galerkin Method. Mater. Today Proc. 2018, 5, 18805–18814. [Google Scholar] [CrossRef]
- Huynh, H.D.; Nguyen, M.N.; Cusatis, G.; Tanaka, S.; Bui, T.Q. A Polygonal XFEM with New Numerical Integration for Linear Elastic Fracture Mechanics. Eng. Fract. Mech. 2019, 213, 241–263. [Google Scholar] [CrossRef]
- Surendran, M.; Natarajan, S.; Palani, G.; Bordas, S.P. Linear Smoothed Extended Finite Element Method for Fatigue Crack Growth Simulations. Eng. Fract. Mech. 2019, 206, 551–564. [Google Scholar] [CrossRef]
- Rozumek, D.; Marciniak, Z.; Lesiuk, G.; Correia, J. Mixed Mode I/II/III Fatigue Crack Growth in S355 Steel. Procedia Struct. Integr. 2017, 5, 896–903. [Google Scholar] [CrossRef]
- Dekker, R.; van der Meer, F.; Maljaars, J.; Sluys, L. A Cohesive XFEM Model for Simulating Fatigue Crack Growth under Mixed-Mode Loading and Overloading. Int. J. Numer. Methods Eng. 2019, 118, 561–577. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, S.; Wulfinghoff, S.; Reese, S. Prediction of Fracture and Damage in Micro/Nano Coating Systems Using Cohesive Zone Elements. Int. J. Solids Struct. 2017, 121, 62–74. [Google Scholar] [CrossRef]
- Zhang, W.; Tabiei, A. An Efficient Implementation of Phase Field Method with Explicit Time Integration. J. Appl. Comput. Mech. 2020, 6, 373–382. [Google Scholar]
- Wu, J.-Y.; Qiu, J.-F.; Nguyen, V.P.; Mandal, T.K.; Zhuang, L.-J. Computational Modeling of Localized Failure in Solids: XFEM vs. PF-CZM. Comput. Methods Appl. Mech. Eng. 2019, 345, 618–643. [Google Scholar] [CrossRef]
- De Borst, R.R.; Verhoosel, C.V. Gradient Damage vs. Phase-Field Approaches for Fracture: Similarities and Differences. Comput. Methods Appl. Mech. Eng. 2016, 312, 78–94. [Google Scholar] [CrossRef] [Green Version]
- Harter, J.A. Afgrow Users Guide and Technical Manual. In Afgrow Users Guide and Technical Manual; Defense Technical Information Center: Fort Belvoir, VA, USA, 1999. [Google Scholar]
- Skorupa, M.; Machniewicz, T.; Schijve, J.; Skorupa, A. Application of the Strip-Yield Model from the NASGRO Software to Predict Fatigue Crack Growth in Alu-Minium Alloys Under Constant and Variable Amplitude Loading. Eng. Fract. Mech. 2007, 74, 291–313. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic Crack Growth in Finite Elements with Minimal Remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Baietto, M.-C.; Pierres, E.; Gravouil, A.; Berthel, B.; Fouvry, S.; Trolle, B. Fretting Fatigue Crack Growth Simulation Based on a Combined Experimental and XFEM Strategy. Int. J. Fatigue 2013, 47, 31–43. [Google Scholar] [CrossRef]
- Giner, E.; Sukumar, N.; Tarancón, J.; Fuenmayor, F. An Abaqus Implementation of the Extended Finite Element Method. Eng. Fract. Mech. 2009, 76, 347–368. [Google Scholar] [CrossRef] [Green Version]
- Qi, S.; Cai, L.; Bao, C.; Chen, H.; Shi, K.; Wu, H. Analytical Theory for Fatigue Crack Propagation Rates of Mixed-Mode I–II Cracks and its Application. Int. J. Fatigue 2019, 119, 150–159. [Google Scholar] [CrossRef]
- Barsom, J.; Rolfe, S. Fracture and Fatigue in Structure: Application of Fracture Mechanics; American Society for Testing and Materials: Philadelphia, PA, USA, 1999. [Google Scholar]
- Broek, D. Elementary Engineering Fracture Mechanics; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Sih, G.; Liebowitz, H. Mathematical Fundamentals, in Fracture; Academic Press: New York, NY, USA, 1968; pp. 67–190. [Google Scholar]
- Hellan, K.; Saunders, H. Introduction to Fracture Mechanics. J. Vib. Acoust. 1987, 109, 325–326. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, S.; Mianroodi, J.R.; Brepols, T.; Reese, S. Direction-Dependent Fracture in Solids: Atomistically Calibrated Phase-Field and Cohesive Zone Model. J. Mech. Phys. Solids 2021, 147, 104253. [Google Scholar] [CrossRef]
- Teichtmeister, S.; Kienle, D.; Aldakheel, F.; Keip, M.-A. Phase Field Modeling of Fracture in Anisotropic Brittle Solids. Int. J. Non linear Mech. 2017, 97, 1–21. [Google Scholar] [CrossRef]
- Nejati, M.; Aminzadeh, A.; Amann, F.; Saar, M.O.; Driesner, T. Mode I Fracture Growth in Anisotropic Rocks: Theory and Experiment. Int. J. Solids Struct. 2020, 195, 74–90. [Google Scholar] [CrossRef]
- Hakim, V.; Karma, A. Crack Path Prediction in Anisotropic Brittle Materials. Phys. Rev. Lett. 2005, 95, 235501. [Google Scholar] [CrossRef] [Green Version]
- Reuvers, M.C.; Rezaei, S.; Brepols, T.; Reese, S. Development of a Thermomechanically Coupled Damage Approach for Modeling Woven Ceramic Matrix Composites. Tech. Mech. Eur. J. Eng. Mech. 2020, 40, 59–65. [Google Scholar]
- Richard, H.; Sander, M.; Fulland, M.; Kullmer, G. Development of Fatigue Crack Growth in Real Structures. Eng. Fract. Mech. 2008, 75, 331–340. [Google Scholar] [CrossRef]
- Hussain, M.; Pu, S.; Underwood, J. Strain Energy Release Rate for a Crack under Combined Mode I and Mode II. In Fracture Analysis: Proceedings of the 1973 National Symposium on Fracture Mechanics, Part II; Irwin, G., Ed.; ASTM International: West Conshohocken, PA, USA, 1974; pp. 2–28. [Google Scholar]
- Demir, O.; Ayhan, A.O.; İriç, S. A New Specimen for Mixed Mode-I/II Fracture Tests: Modeling, Experiments and Criteria Development. Eng. Fract. Mech. 2017, 178, 457–476. [Google Scholar] [CrossRef]
- Tanaka, K. Fatigue Crack Propagation from a Crack Inclined to the Cyclic Tensile Axis. Eng. Fract. Mech. 1974, 6, 493–507. [Google Scholar] [CrossRef]
- Fageehi, Y.A.; Alshoaibi, A.M. Numerical simulation of mixed-mode fatigue crack growth for compact tension shear specimen. Adv. Mater. Sci. Eng. 2020, 2020, 5426831. [Google Scholar] [CrossRef] [Green Version]
- Alshoaibi, A.M.; Fageehi, Y.A. Numerical Analysis of Fatigue Crack Growth Path and Life Predictions for Linear Elastic Material. Materials 2020, 13, 3380. [Google Scholar] [CrossRef] [PubMed]
- Alshoaibi, A.M. Comprehensive comparisons of two and three dimensional numerical estimation of stress intensity factors and crack propagation in linear elastic analysis. Int. J. Integr. Eng. 2019, 11, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Alshoaibi, A.; Ghazwani, M.; Hakami, M. Fatigue life and reliability assessment of metal structures. Eng. Solid Mech. 2021, 9, 13–22. [Google Scholar] [CrossRef]
- Dirik, H.; Yalçinkaya, T. Crack Path and Life Prediction under Mixed Mode Cyclic Variable Amplitude Loading through XFEM. Int. J. Fatigue 2018, 114, 34–50. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. Dec. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Coffin, L. Cyclic Deformation and Fatigue of Metals; Fatigue and Staying Power of Metals, Izo: Moscow, IL, USSR, 1963. [Google Scholar]
- Wöhler, A. Versuche Zur Ermittlung der Auf Die Eisenbahnwagenachsen Einwirkenden Kräfte Und Die Widerstandsfähigkeit der Wagen-Achsen. Zeitschrift für Bauwesen 1860, 10, 583–614. [Google Scholar]
- Bjørheim, F. Practical Comparison of Crack Meshing in ANSYS Mechanical APDL 19.2; University of Stavanger: Stavanger, Norway, 2019. [Google Scholar]
- Lawrence, K. ANSYS Tutorial Release 2020; SDC Publications: Mission, KS, USA, 2020. [Google Scholar]
- Han, Q.; Wang, Y.; Yin, Y.; Wang, D. Determination of Stress Intensity Factor for Mode I Fatigue Crack Based on Finite Element Analysis. Eng. Fract. Mech. 2015, 138, 118–126. [Google Scholar] [CrossRef]
- Walters, M.C.; Paulino, G.H.; Dodds, R.H. Interaction Integral Procedures for 3-D Curved Cracks Including Surface Tractions. Eng. Fract. Mech. 2005, 72, 1635–1663. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
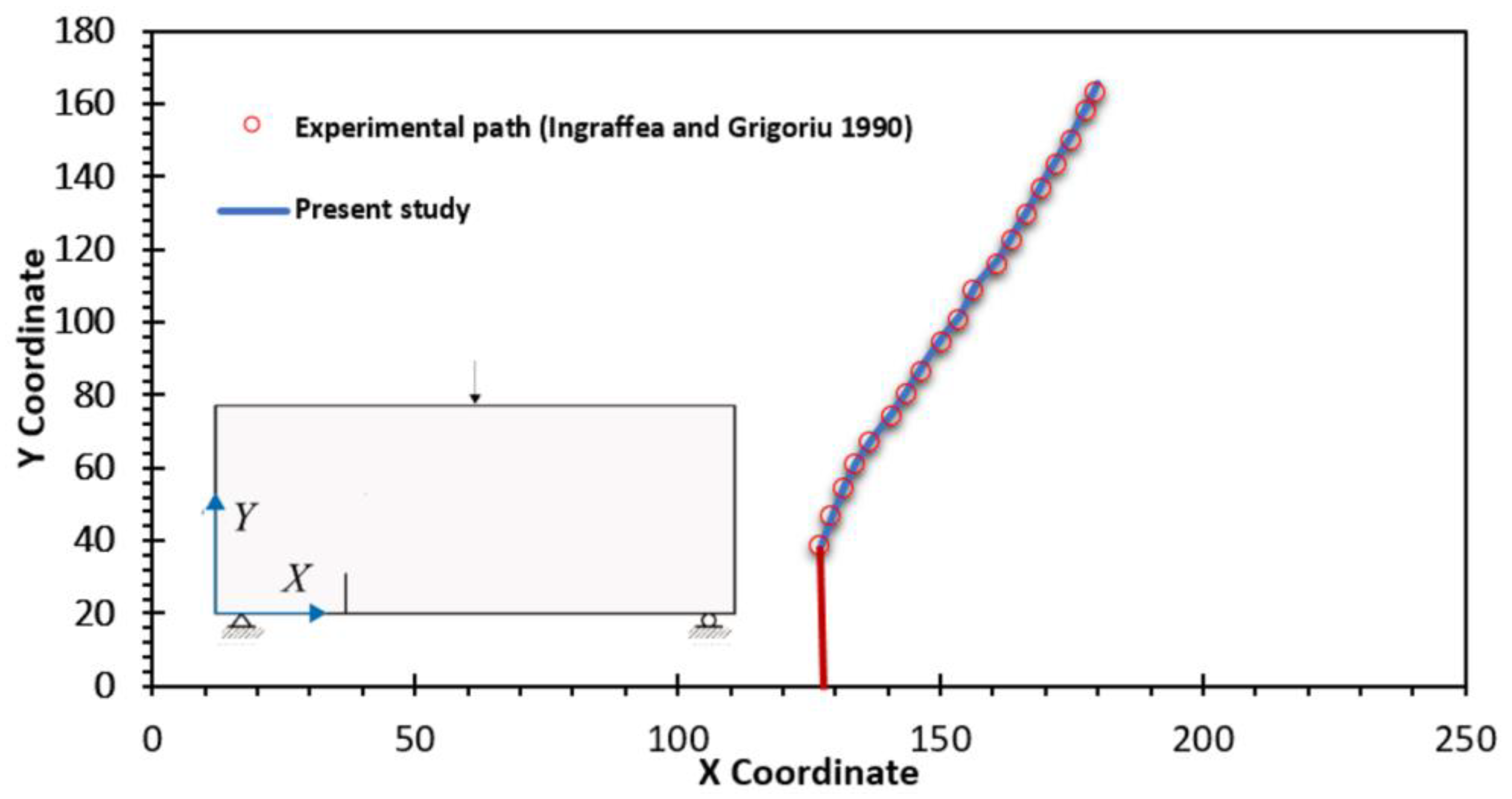
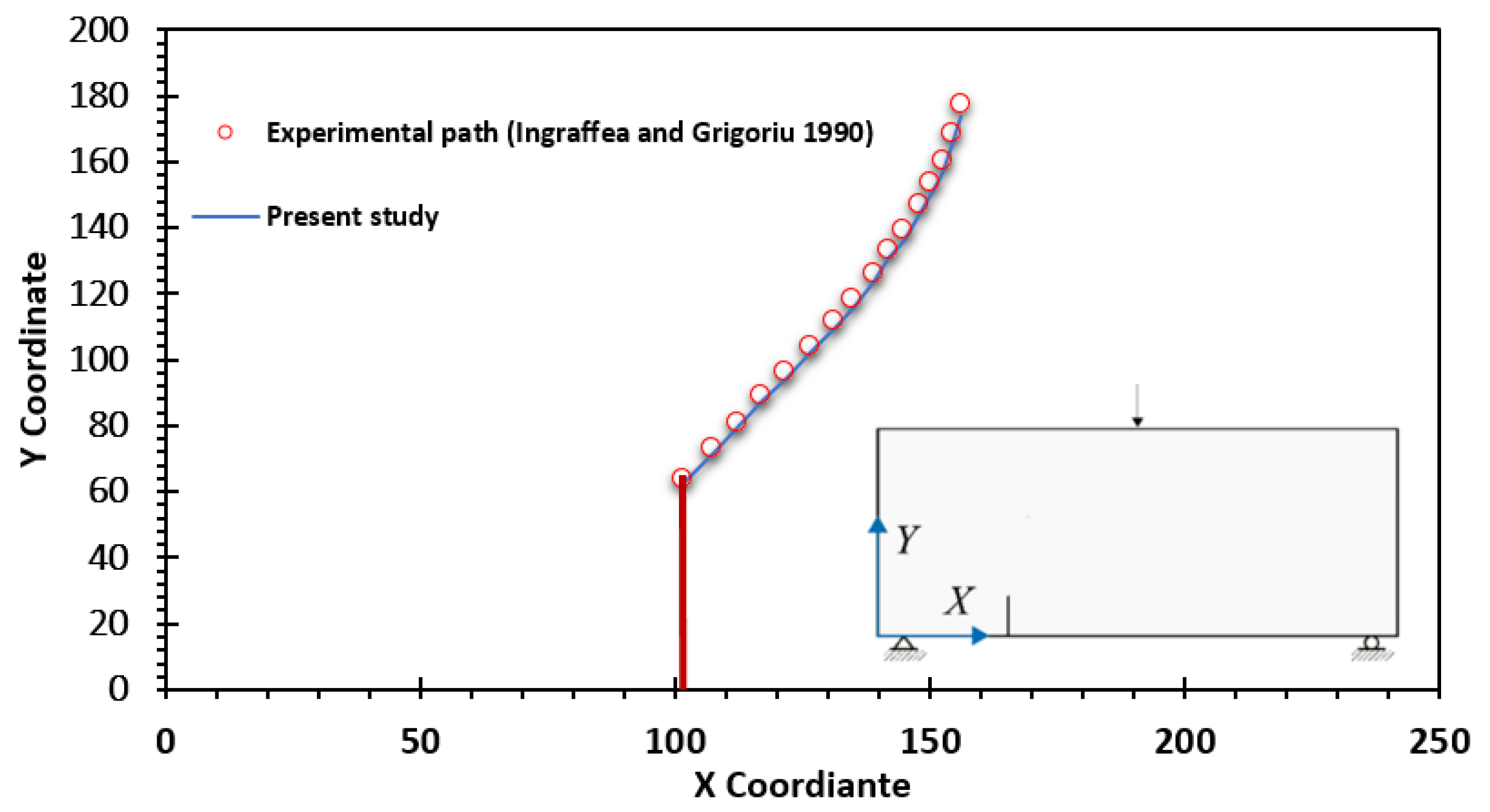
- Ingraffea, A.R.; Grigoriu, M. Probabilistic Fracture Mechanics: A Validation of Predictive Capability; Cornell University: Ithaca, NY, USA, 1990. [Google Scholar]
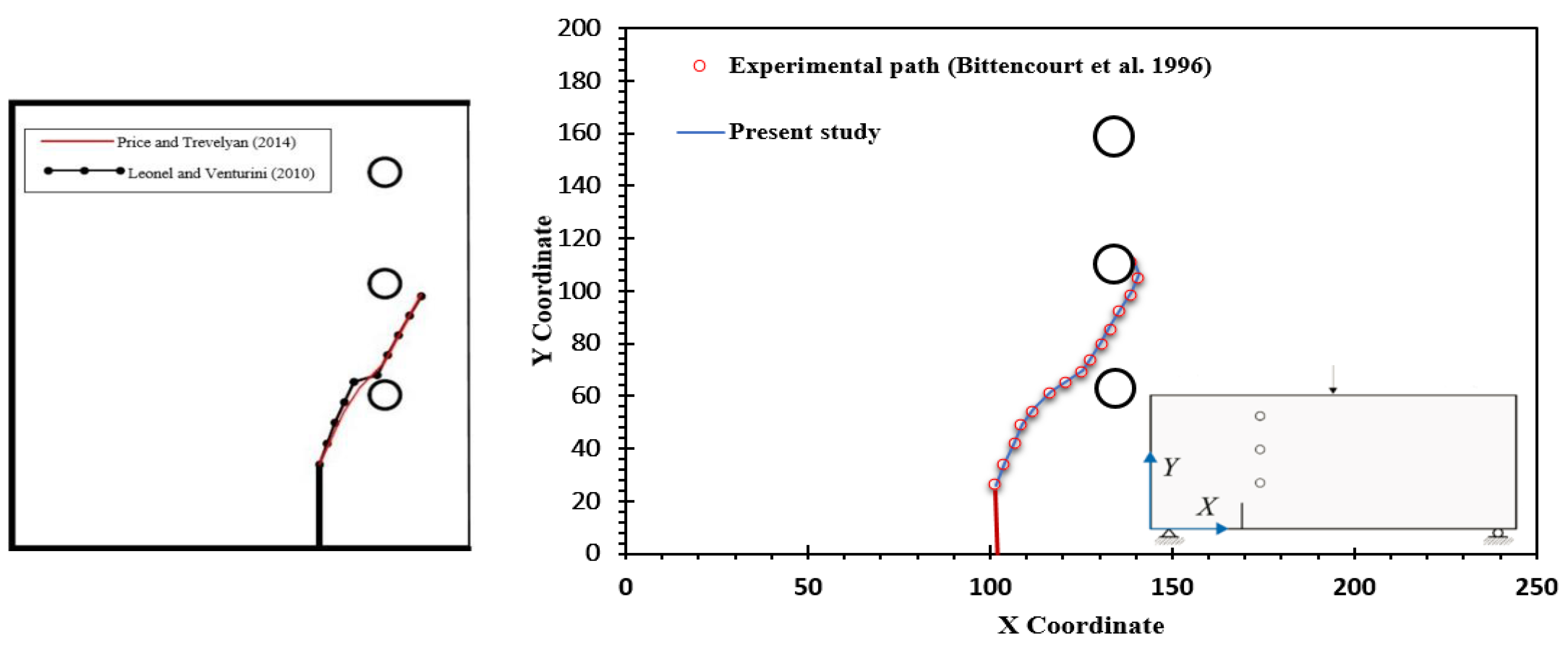
- Bittencourt, T.; Wawrzynek, P.; Ingraffea, A.; Sousa, J. Quasi-Automatic Simulation of Crack Propagation for 2D LEFM Problems. Eng. Fract. Mech. 1996, 55, 321–334. [Google Scholar] [CrossRef]
- Ma, W.; Liu, G.; Wang, W. A Coupled Extended Meshfree—Smoothed Meshfree Method for Crack Growth Simulation. Theor. Appl. Fract. Mech. 2020, 107, 102572. [Google Scholar] [CrossRef]
- Price, R.; Trevelyan, J. Boundary Element Simulation of Fatigue Crack Growth in Multi-Site Damage. Eng. Anal. Bound. Elem. 2014, 43, 67–75. [Google Scholar] [CrossRef] [Green Version]
- Leonel, E.D.; Venturini, W.S. Dual Boundary Element Formulation Applied to Analysis of Multi-Fractured Domains. Eng. Anal. Bound. Elem. 2010, 34, 1092–1099. [Google Scholar] [CrossRef]
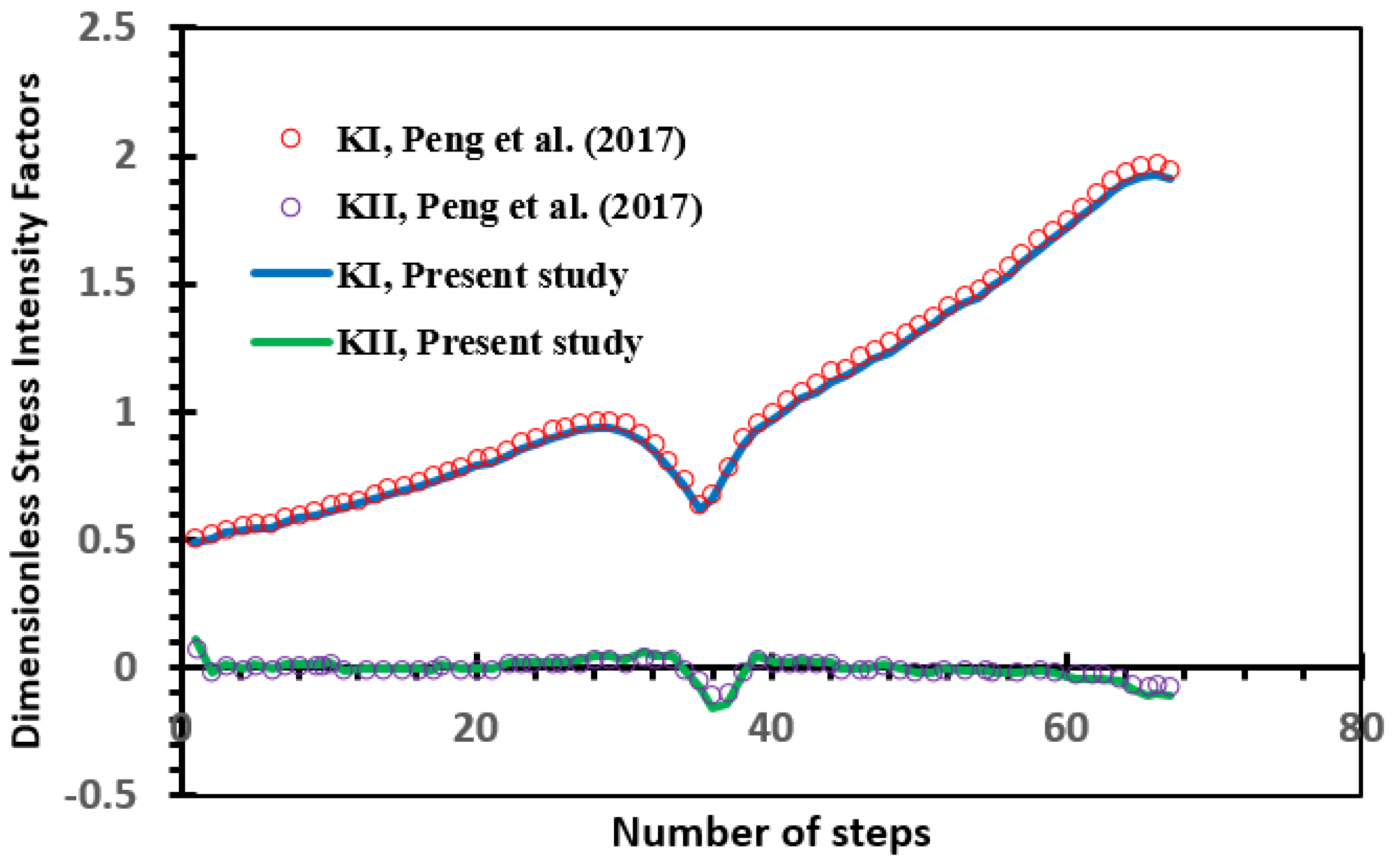
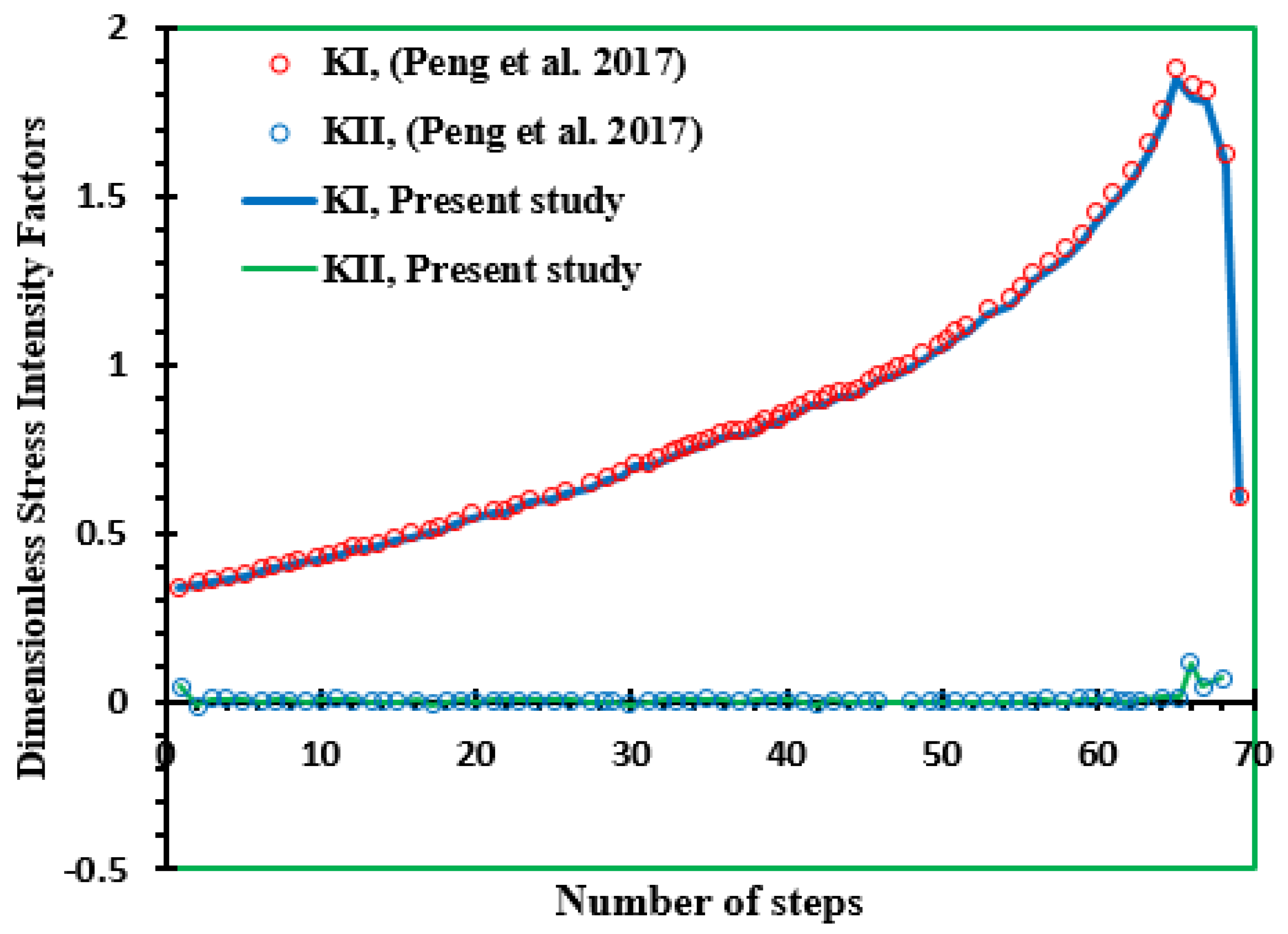
- Peng, X.; Kulasegaram, S.; Wu, S.; Bordas, S. An Extended Finite Element Method (XFEM) for Linear Elastic Fracture with Smooth Nodal Stress. Comput. Struct. 2017, 179, 48–63. [Google Scholar] [CrossRef] [Green Version]
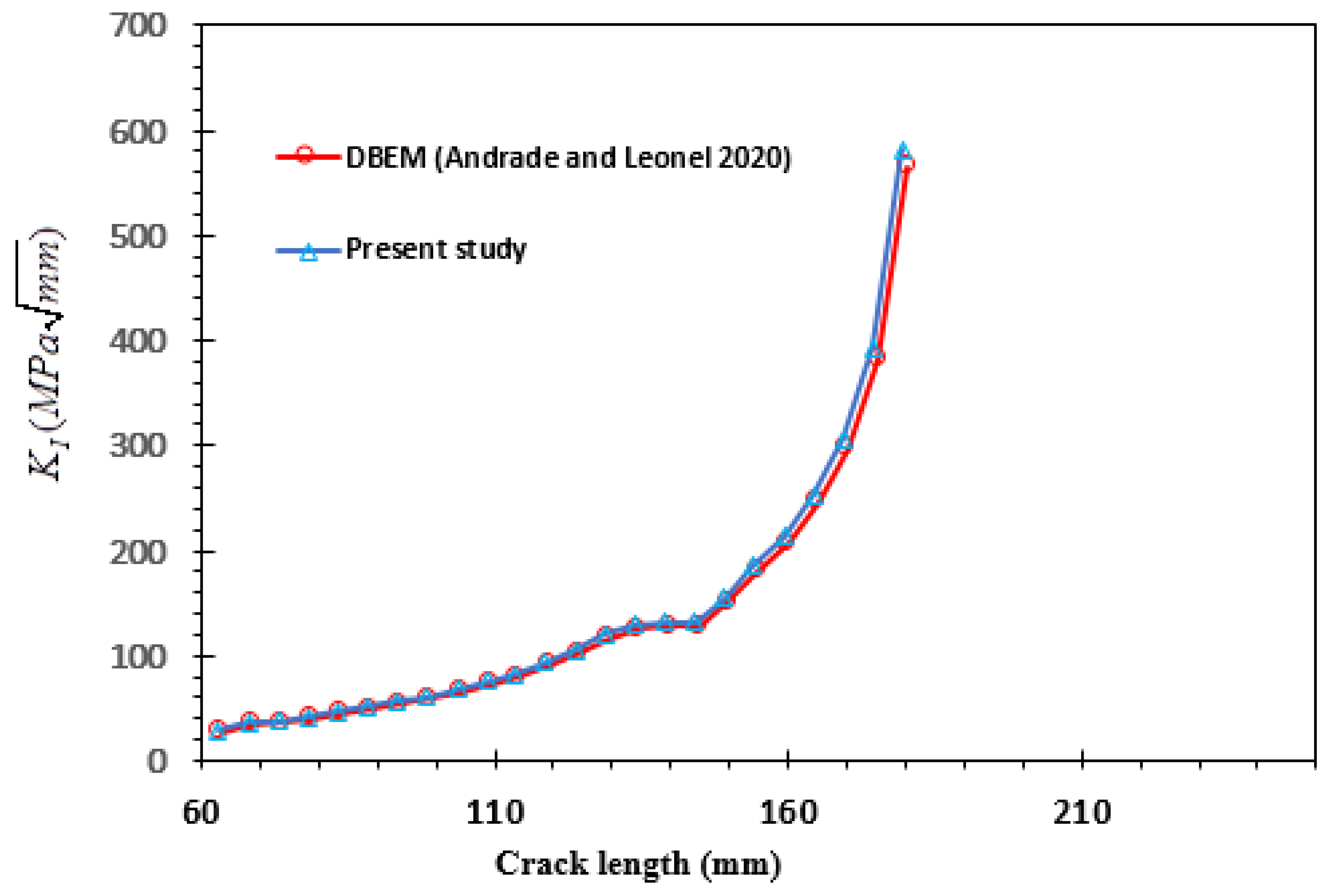
- Andrade, H.; Leonel, E. An Enriched Dual Boundary Element Method Formulation for Linear Elastic Crack Propagation. Eng. Anal. Bound. Elem. 2020, 121, 158–179. [Google Scholar] [CrossRef]
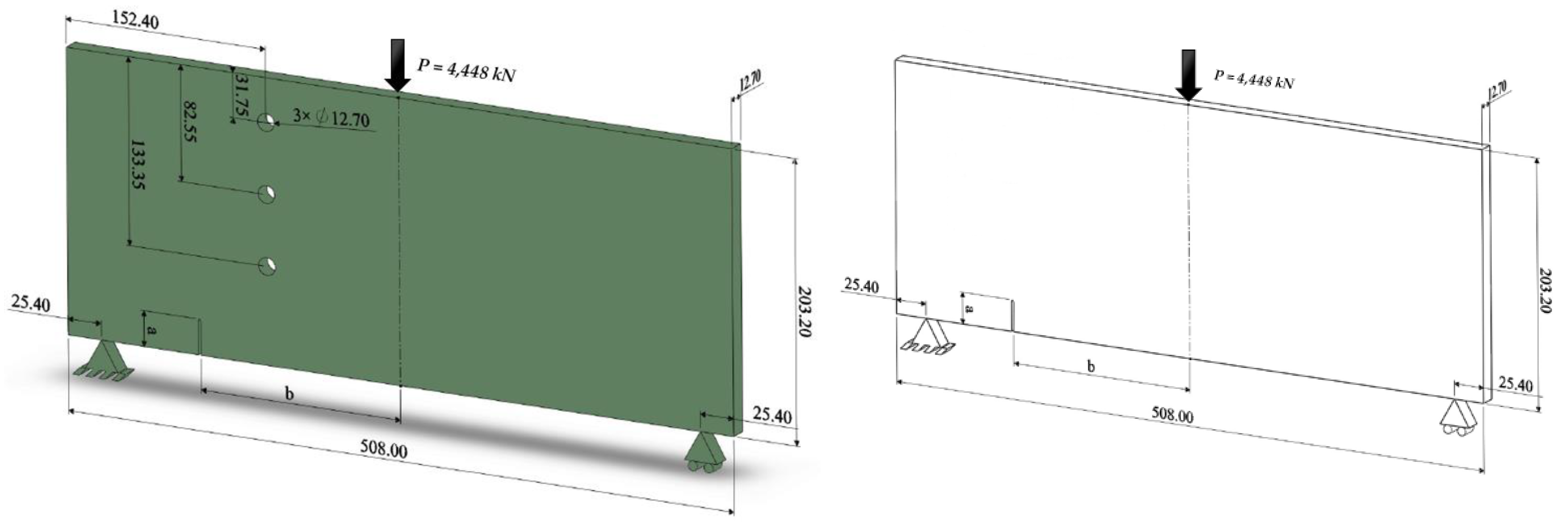







| Specimen No. | Length of Crack, a (mm) | Crack Position, b (mm) | Hole Layout |
|---|---|---|---|
| 1 | 25.4 | 152.4 | With hole |
| 2 | 25.4 | 152.4 | Without hole |
| 3 | 38.1 | 127 | With hole |
| 4 | 38.1 | 127 | Without hole |
| 5 | 63.5 | 152.4 | With hole |
| 6 | 63.5 | 152.4 | Without hole |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshoaibi, A.M. Numerical Modeling of Crack Growth under Mixed-Mode Loading. Appl. Sci. 2021, 11, 2975. https://doi.org/10.3390/app11072975
Alshoaibi AM. Numerical Modeling of Crack Growth under Mixed-Mode Loading. Applied Sciences. 2021; 11(7):2975. https://doi.org/10.3390/app11072975
Chicago/Turabian StyleAlshoaibi, Abdulnaser M. 2021. "Numerical Modeling of Crack Growth under Mixed-Mode Loading" Applied Sciences 11, no. 7: 2975. https://doi.org/10.3390/app11072975
APA StyleAlshoaibi, A. M. (2021). Numerical Modeling of Crack Growth under Mixed-Mode Loading. Applied Sciences, 11(7), 2975. https://doi.org/10.3390/app11072975






