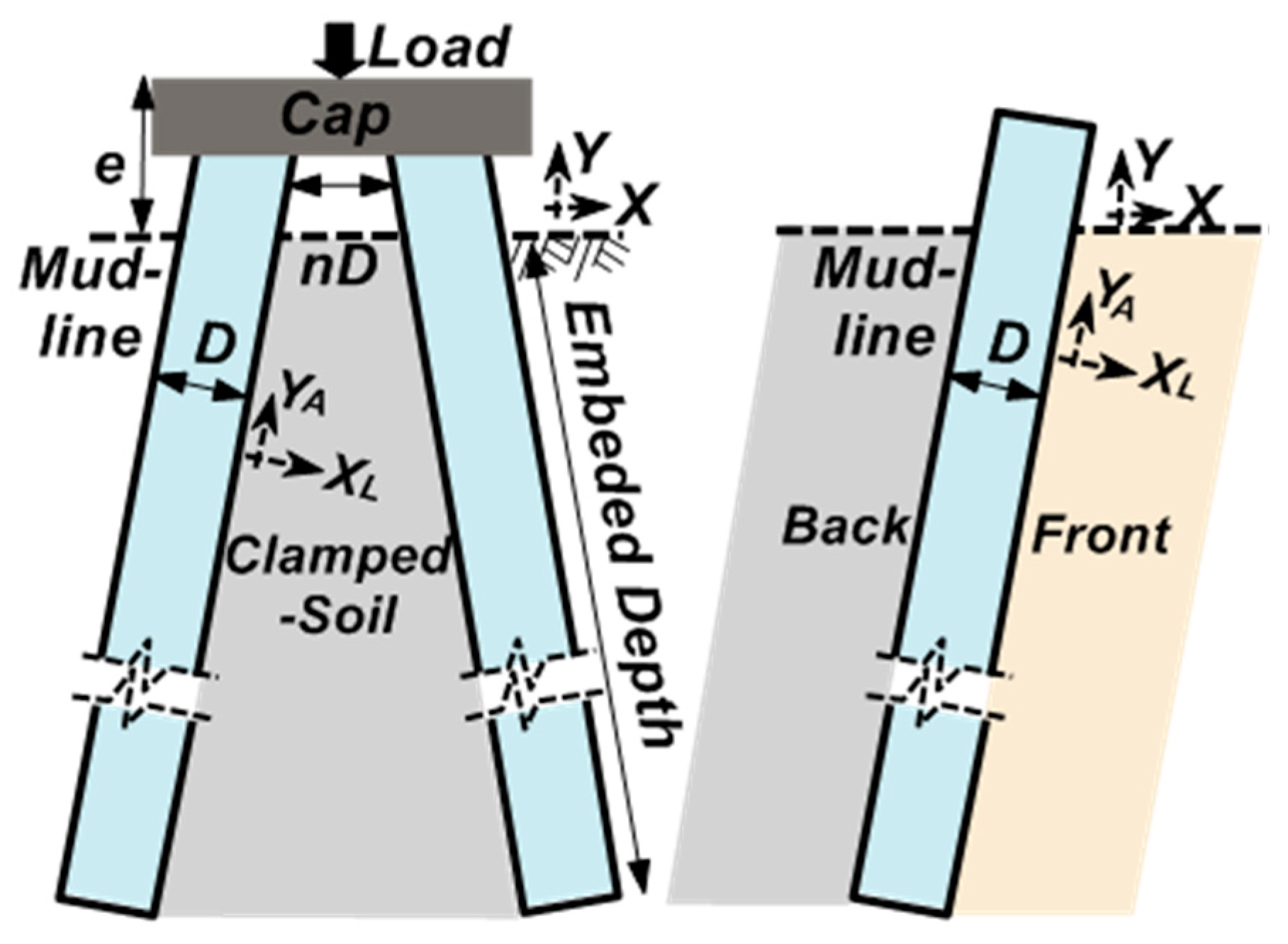
1. Introduction
Batter piles are widely used in infrastructure construction. Its high impedance to the lateral load makes it irreplaceable in the design of bridges, wharves, and transmission towers [
1]. They also have disadvantages, as it is generally accepted in academia that under vertical loads, batter piles will produce a sizeable additional bending moment and be accompanied by the horizontal and vertical displacements [
2,
3]. Therefore, some codes, such as Eurocode-8 [
4], do not recommend using batter piles in seismic-prone areas. Other scholars believe that the insufficient understanding of the batter piles’ working behavior and improper design are the main reasons for the occurrence of damage [
5]. If properly designed, the batter pile can be beneficial to both the superstructure and itself [
6,
7,
8]. The argument about whether the usage of batter piles is detrimental or beneficial is still unsettled. Its working behavior and load transfer mechanism are more complex than those of plumb piles.
Meyerhof [
9,
10] was the earliest to conduct a series of tests on single batter piles. The bearing capacity of the piles was found to depend on the layered structure, load inclination, and pile batter. Modified equations for displacement [
11] and the empirical formula for the ultimate bearing capacity under arbitrary inclined loads [
12] were proposed. As the pile inclination range was small, the method was obtained from the modification of the bearing capacity of the plumb pile. However, it is not suitable for piles with large inclinations, which are increasingly being used widely in engineering [
13]. Rao et al. [
14] considered the pile–soil separation and proposed an empirical formula that can predict the additional bending moment of a single batter pile caused by soil settlement. The comparison between the analytical and test results showed that the settlement would introduce a sizeable additional bending moment, which may lead to the failure of the batter pile.
In a centrifuge test, Zhang et al. [
15,
16] found that the vertical load had different influences on the lateral resistance of positive and negative batter piles. When a vertical load was applied, the lateral resistance of a negative battered pile was reduced because of the bending moment due to the vertical load component that causes an additional lateral displacement. The opposite was true for a positive battered pile as the bending moment counterbalance the lateral load component. However, the constraint of the cap and mirror-like batter was not considered in the test. This constraint may result in the redistribution of the internal force. In fact, it was found that in this paper, the symmetrical conformation could partially compensate for the disadvantage of the additional bending moment, thus reducing the concentration and maximum value of the additional bending moment. Moreover, batter piles rarely bear vertical load individually, which is inconsistent with engineering practice. Cao et al. [
17] investigated the influence of pile inclination on the single batter piles’ working behavior by laboratory tests. The results showed that the greater the inclination, the more rapidly the axial force decays. The maximum shear force appeared at the pile head and increased with the pile inclination. However, the test did not consider the mirror-like batter pile either, which is different from the engineering application.
Mroueh et al. [
18] explored the bearing capacity of a batter pile under the combination of vertical and horizontal loading by the finite element method. The relationships between the bearing capacity, the loading, and the pile inclination were given in a chart. However, the axial load caused the stiffness degradation of soil around the pile [
19], which could not be reflected by the Mohr–Coulomb constitutive model. The simple Coulomb friction criterion was used at the pile–soil interface; thus, the model is too simple to reflect the truth. Mohab et al. [
20] obtained the critical pile inclination of batter piles by analyzing the test and numerical results. They believe that when the pile inclination is less than 30°, the axial bearing capacity will change slightly, whereas when the inclination is greater than 30°, the axial bearing capacity will decrease with the pile inclination. Hanna et al. [
21] studied the influence of pile inclination on the skin-friction of batter piles through laboratory tests. However, they regarded the skin-friction in the entire pile as the same. The variation in skin-friction along the depth was not considered, which is inconsistent with the truth.
In summary, previous studies have mainly focused on the bearing capacity of batter piles. The working behavior, deformation mode, internal force distribution, and development under vertical loading have rarely been reported. The relevant tests are necessary. When subjected to vertical loading, horizontal and vertical displacements of the batter pile will occur simultaneously. Two important factors have been ignored in previous studies: First, the constraint of the pile cap and mirror-like batter; second, the interaction between the symmetrical batter and the soil clamped by the pile, namely, the “clamping” effect. All of the above two factors will introduce a redistribution of internal force and make the working behavior more complex. Therefore, symmetrical batter piles were set as the test object in this paper. The main purpose was to further understand the load transfer mechanism and the difference from the single pile.
3. The Deformation Mode and Bearing Capacity of Symmetrical Batter Piles
The deformation along the pile depth is an important aspect of the working behavior. This section first analyzes the deformation mode of symmetrical batter piles under vertical loading. On this basis, the load–displacement curve is corrected. The strain scatters of (−Δ
ε(z))/
d are fitted directly, and then quadratic integration is performed to obtain the pile deformation displacement in the X
L-Y
A coordinate system, as shown by Equation (2). In this way, the nonlinearity of the pile material can be considered, and errors introduced by the bending moment fitting and differentiation can be avoided, where Δ
ε is the difference between a pair of strain gauges and
d is the inner diameter of the pile.
Figure 4 shows the mean value of the deformation along the depth. All test results in the X
L-Y
A coordinate system are shown in
Figure 4a,b, which is the pile deformation with the same spacing and different inclination
β.
Figure 4c shows the pile deformation with the same inclination
β and different spacing
D.
Figure 4d shows the true deformation model of the symmetrical batter pile in the X-Y coordinate system. The result in the next section shows that when failure occurs, the maximum pile tip resistance is within 20% of the applied loading. Therefore, the deformation mode described here can be considered as the mode of floating symmetrical batter piles with a fixed pile head.
It can be seen from
Figure 4a that the deformation mainly occurs in the upper pile section (≤0.2
L). As shown in
Figure 5b,c, the maximum deformation value increases with the pile inclination
β and pile spacing
D. When the pile inclination
β changes from 10° to 20° or the pile spacing increases from 5
D to 7
D, the deformation value increases by more than twice. When the pile spacing increases to a certain value (7
D in this paper), negative deformation displacement appears, as shown in
Figure 4c.
There are two coordinate systems in
Figure 5d. The X and Y are parallel to the mud-line and gravity direction. X
L-Y
A is parallel to the lateral and axial directions of the pile. The deformation derived from strain occurs in the X
L-Y
A coordinate system (
Figure 5a–c). It should be noted that in the X-Y coordinate system, the boundary conditions at the joint between the pile and cap only allow the pile head to have displacement in the Y direction. Therefore, considering the boundary conditions and angular relationship, the true deformation mode in X-Y is shown in
Figure 4d.
In the tests, only one deformation mode is obtained (although the 7d test has negative deformation, it is essentially the same as the small pile spacing test group); namely, when the pile spacing is small, the upper batter pile section bends inward to compensate the displacement in the X-direction. With the increase in the pile spacing, the deformation develops deeper and is accompanied by the outward bulging deflection. The author believes that when subjected to the vertical loading, the flexible symmetrical floating batter piles has only one kind of deformation mode. The reasons are illustrated in
Figure 5.
Figure 5a shows the deformation mode assumed by Zhang et al. [
29]. The author believes it has limitations. When the symmetrical batter pile is subjected to the vertical loading, the settlement difference between the cap and pile tip must be compensated by the pile deformation. Due to the fixed pile head, the displacement along the X direction is not allowed. Therefore, only two kinds of deformation modes can meet the boundary conditions of the pile and cap connection. They are shown as
Figure 5b,c, called mode No. 1 and No. 2, respectively. The deformation of No. 2 is the same as the assumption of Zhang et al.
Due to the pile inclination and dead weight of the pile, the at-rest soil pressures in the front and back areas of the batter pile are different (
Figure 5d) [
21]. The pile front is higher than the pile back. From the perspective of force balance, deformation mode No. 2 is less likely to occur. Second, the “clamping” effect makes No.2 more difficult to occur. The “clamping” refers to the compression of soil between the piles caused by the deformation. This phenomenon is consistent with Li’s report [
30]. The symmetrical batter pile deforms in opposite directions. The greater the pile deforms, the greater the confining pressure on the trapezoidal soil (
Figure 5b) between the two piles. It is widely known that the increase in confining pressure will decrease the void ratio and increase the soil stiffness. Considering the above two reasons, only deformation No. 1 could occur, and it is also the only kind of deformation mode. Moreover, the “clamping” effect will enhance the pile–soil interaction. The variation in axial force, pile tip resistance ratio, and skin-friction are also affected. These issues will be discussed in the next section. For very flexible piles such as micro-piles, and batter piles of the high-piled wharf and super-long batter piles, the deformation mode mentioned above should be given sufficient attention.
According to the deformation value of the batter pile, the method in
Figure 6 was used to correct the displacement of the cap based on Equations (4) and (5).
Figure 6a,b show the correction method corresponding to deformations No.1 and No.2, respectively.
Figure 7 is the corrected result. The response of the pile cap only considers the factors of skin-friction and pile tip resistance, and the influence of deformation (Δ
L) is removed. The ultimate bearing capacity is also listed in the lower left corner.
It can be seen from
Figure 7a that when the pile inclination
β changes from 10° to 20°, the differentiation between the load–displacement curves is slight. The relative difference is less than 5%, which is quite different from the single pile test (the bearing capacity increases with the pile inclination). The author believes that this is due to the x-direction constraint weakening the influence of the pile inclination on the ultimate bearing capacity.
Although the pile spacing increases with the depth, the pile group effect is still obvious from the difference in ultimate bearing capacity between different pile spacings. In this paper, the test with a pile spacing of 7D was set as the reference to investigate the influence of pile spacing and inclination on the group effect.
The pile group effect is defined in Equation (5), where
UVnD and
UVsingle represent the loads of the symmetrical and single batter pile under the same displacement, respectively (below the failure load), and
n is the number of piles in the pile group, which equals 2 in this paper. The lower the coefficient, the more significant the pile group effect. The results are shown in
Figure 8b.
It can be seen from
Figure 8b that the increase in inclination and pile spacing will all reduce the pile group effect, but the influence of pile spacing is more significant. When the pile spacing is 3
D, the coefficient is only half of that when the spacing is 7
D. The increase in pile inclination
β helps to reduce the stress superposition area in soil. Therefore, when the inclination changes from 10° to 20° under the same pile spacing, the coefficient
COefv decreases by about 7%. In most codes, the critical pile spacing of plumb pile without the group effect is between S = 6
D and 8
D (Sandy soil). For example, the critical longitudinal pile spacing in American API code [
31] is 8
D. The pile foundation code of Poland [
32] is 6
D. For batter piles, the pile inclination will reduce the stress superposition area along the depth, thus reducing the pile group effect. In this paper, the pile group effect coefficient was already close to 1 when the pile spacing was 5
D. When the spacing was 7
D, the coefficient was greater than 1. Therefore, the pile group effect of the batter pile foundation should be modified considering the influence of inclination.
4. The Internal Force Distribution of Symmetrical Batter Piles and “Clamping” Effect
The distribution and variation in axial force, pile tip resistance ratio, skin-friction, and the influence of the ”clamping” effect on them will be analyzed in this section.
Figure 8 shows the variation in axial force along the depth of the batter pile, where
Figure 8a shows the axial force of all tests.
Figure 8b shows the variation in axial force under the same pile inclination and different pile spacings, while
Figure 8c shows the variation in axial force under the same pile spacing and different pile inclinations. It can be seen that the axial force decreases nonlinearly along the depth and presents as an inverted triangle, which is similar to the distribution of the plumb pile. It indicates that the activation sequence of the skin-friction is identical to the plumb pile.
However, it can be seen from
Figure 8a,b that in the upper pile section (the dotted circle), the attenuation rate of axial force gradually increases with the pile spacing. This tendency is more obvious when the load is greater, which is quite different from the symmetrical plumb pile. The author believes that this is caused by the “clamping” effect. The deformation of symmetrical batter piles leads to the compression of the soil between the piles. The pile–soil normal contact force increases and so does the friction coefficient. Moreover, the increase in confining pressure will result in the increase in the soil stiffness. All the reasons together will lead to an increase in the skin-friction attenuation rate. In terms of
Figure 4, the greater the pile spacing, the larger the deformation of the upper pile part, which will further aggravate the “clamping” effect. This is consistent with the phenomenon that the skin-friction attenuates rapidly in the upper part of the pile with greater pile spacing.
Figure 9c shows the influence of pile inclination on axial force. The influence area also appears on the upper part. The working principle is the same as the influence of the pile spacing on axial force, namely, the deformation of the upper section of the batter pile enhances the “clamping” effect. However, the influence of the pile inclination on the axial force is less than that of the pile spacing, and it is significant only when the load is greater.
The pile tip resistance ratio (the ratio between the pile head axial force and pile tip reaction force) is an important indicator for investigating the load transfer of the pile foundation [
33]. It is commonly used on plumb piles subjected to vertical loading, which can directly reflect the proportion of loading borne by the pile tip and skin-friction.
Figure 9 shows the variation in the pile tip resistance ratio under different loadings. The position indicated by the dashed arrow is near the ultimate bearing capacity of each test. It can be seen that when the loading is within 300–600 N, the pile tip resistance ratios are the same. This indicates that the pile skin-friction along the pile axis is not fully activated. As the load increases, the pile tip resistance shows a nonlinear increase. The ratio is negatively correlated with the pile spacing.
In terms of
Figure 5 and
Figure 6, the stronger the “clamping” effect, the earlier and more sufficient the skin-friction is mobilized. Therefore, the load transferred to the pile tip is reduced, which indirectly affects the pile tip resistance ratio.
The averaged skin-friction per unit length of the batter pile can be obtained from Equation (6), where
Qi is the axial force and
Zi is the depth corresponding to
Qi.
Figure 10 shows the variation in averaged skin-friction along the depth of each test, where the solid line represents the skin-friction near the failure load. It can be clearly seen from the figure that the skin-friction is divided into the deformation-affected zone and -nonaffected zones. The demarcation line depth is about 0.2–0.3
L.
In the nondeformation-affected zone, the skin-friction remains constant when it reaches the limit value, which is similar to that of plumb piles. However, in the deformation-affected zone, the limit value of skin-friction changes greatly due to the “clamping“ effect. It increases significantly with the pile spacing and inclination, especially in
Figure 10c,d. The phenomenon is consistent with the working principle of the “clamping” effect discussed above.
5. The Distribution and Development of the Bending Moment of Symmetric Batter Pile
Batter piles will generate additional bending moments under the action of dead weight or vertical load. This working behavior is significantly different from that of vertical piles, which is one of the main shortcomings pointed out by the community. In engineering practice, the conformation of symmetrical batter piles is widely used in wharves to bear the vertical loads of equipment and cargo. Therefore, it is necessary to explore the distribution of bending moments. The bending moment is obtained by Equation (7), where
EI is the bending stiffness of the pile section, Δε is the difference between a pair of strain gauges, and
d is the inner diameter of the pile.
Figure 11 is the distribution of bending moments along the depth under vertical loading, where
Figure 11a shows the bending moment of all tests and
Figure 11b,c show the comparison of bending moments when the pile inclination or pile spacing is the same. It can be seen that regardless of how the pile spacing or pile inclination changes, the distributions are similar. The maximum bending moment appears at the pile head, and the attenuation rate below 0.2
L is the same. When the pile spacing is 7
D, the maximum bending moment of the pile head is largest for all tests. This is because the upper deformation of the pile is largest in all tests, thus enhancing the P-Δ effect.
The additional bending moment of batter piles is the major disadvantage when comparing with plumb piles. However, when the batter pile appears in the conformation of symmetry, this disadvantage is not that prominent. The comparison of the bending moment between the symmetrical and single batter pile will support the conclusion. The experimental results of Cao et al. [
17] are also analyzed. (Cao et al. [
17] carried out a series of tests of a single batter under vertical loading. There are two testing groups, in which the material and dimension of the pile, embedded depth, loading height, and method are the same as in this paper.)
Figure 12 shows the comparison results, where
Figure 12a shows the test results of this paper with different loadings (only loads below 600 N are shown, because 600 N is close to the failure load of the single batter pile), and
Figure 12b shows the comparison between Cao and this paper under the load close to failure. It should be noted that in Cao’s experiment, the free length is basically zero, so only the bending moment below the mud-line is analyzed.
The disadvantage of an additional moment is fully displayed in the moment distribution of the single pile, namely, the large value and concentration of the bending moment. Due to the action of the free pile head and lateral load component, the P-Δ effect is enhanced, which results in the distribution of the bending moment under vertical loading being similar to that of the plumb pile under horizontal loading. Compared with the single batter pile, the symmetrical batter pile can activate deeper pile sections to resist loads either in the working state (
Figure 12a) or under ultimate load (
Figure 12a). The bending moment develops along the entire pile. Moreover, the P-Δ effect is reduced by the constraint of the pile cap and mirror-like pile. Therefore, the maximum bending moment decreases greatly. Even if the pile inclination of the symmetrical conformation is larger than that of the single pile, the maximum bending moment is reduced by 43% (
β = 20° compared with
β = 15°). In conclusion, under the vertical loading, the symmetrical batter pile can partially compensate for the disadvantage of additional bending moments and weakens the concentration.
7. Conclusions
The main conclusions of this paper are as follows.
(1) Under the vertical loading, there is only one kind of deformation mode of the flexible floating symmetric batter pile. When the pile spacing is small, the upper section of the pile bends inward. With the increase in the pile spacing, the deformation develops deeper and is accompanied by the outward bulging deflection.
(2) The greater the deformation, the more significant the soil “clamping” effect. The attenuation rate of the axial force and the limit value of skin-friction will increase, and the pile tip resistance ratio will decrease under the influence of the “clamping” effect.
(3) Under vertical loading, the additional bending moment caused by pile inclination is the main disadvantage of batter piles. Due to the constraint of the cap and mirror-like pile, the symmetrical conformation can reduce the influence of P-Δ and can partially compensate for the disadvantage of the additional bending moment. Moreover, the maximum value and concentration of the bending moment can also decrease, and the deeper pile section is activated to resist loads.
When the pile spacing is the same, the group effect of batter piles is smaller than that of plumb piles due to the pile inclination, and it becomes more significant with the increase in the pile inclination. At present, no study in the literature has given a method to describe the group effect of batter piles. However, based on experiments, using numerical and analytical methods, the pile group effect formula of plumb piles can be modified to describe the characteristic of the group effect of batter piles. This is also the focus of the author’s future studies.