2-D Seismic Response Analysis of a Slope in the Tyrrhenian Area (Italy)
Abstract
1. Introduction
2. Site Characterization
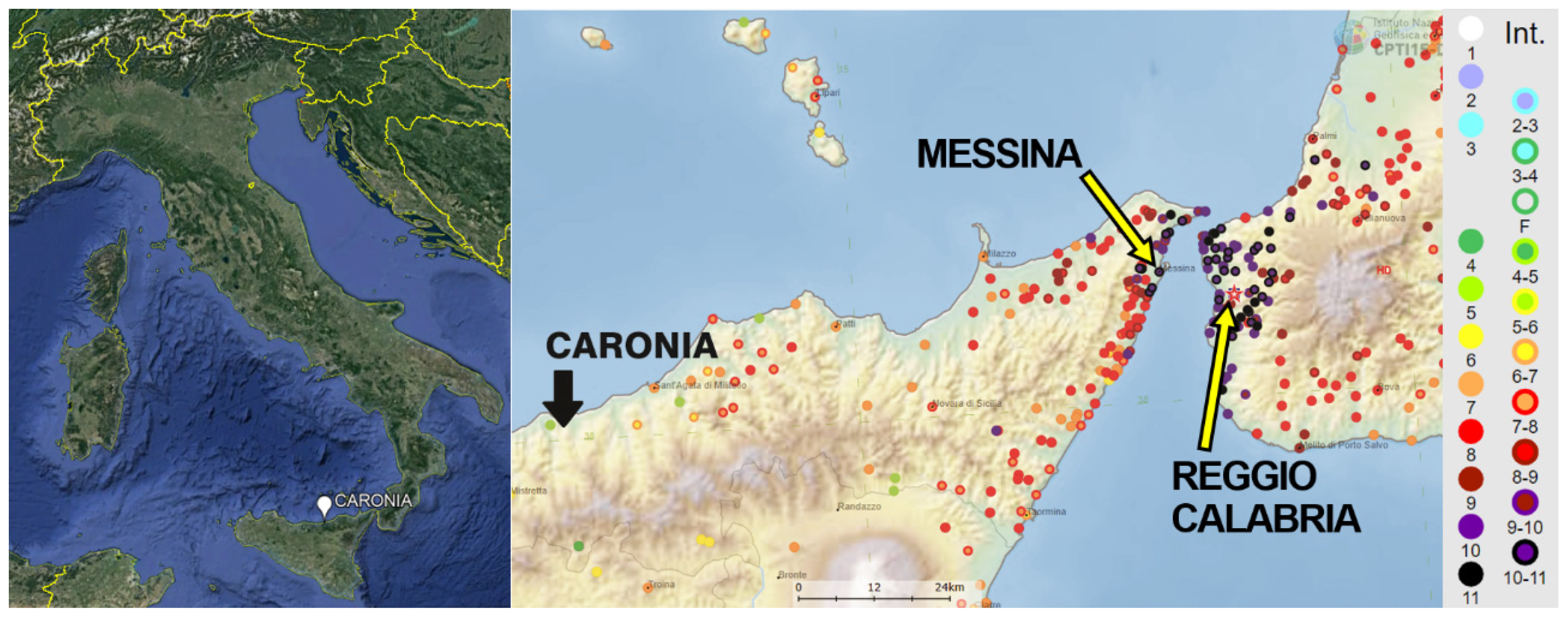
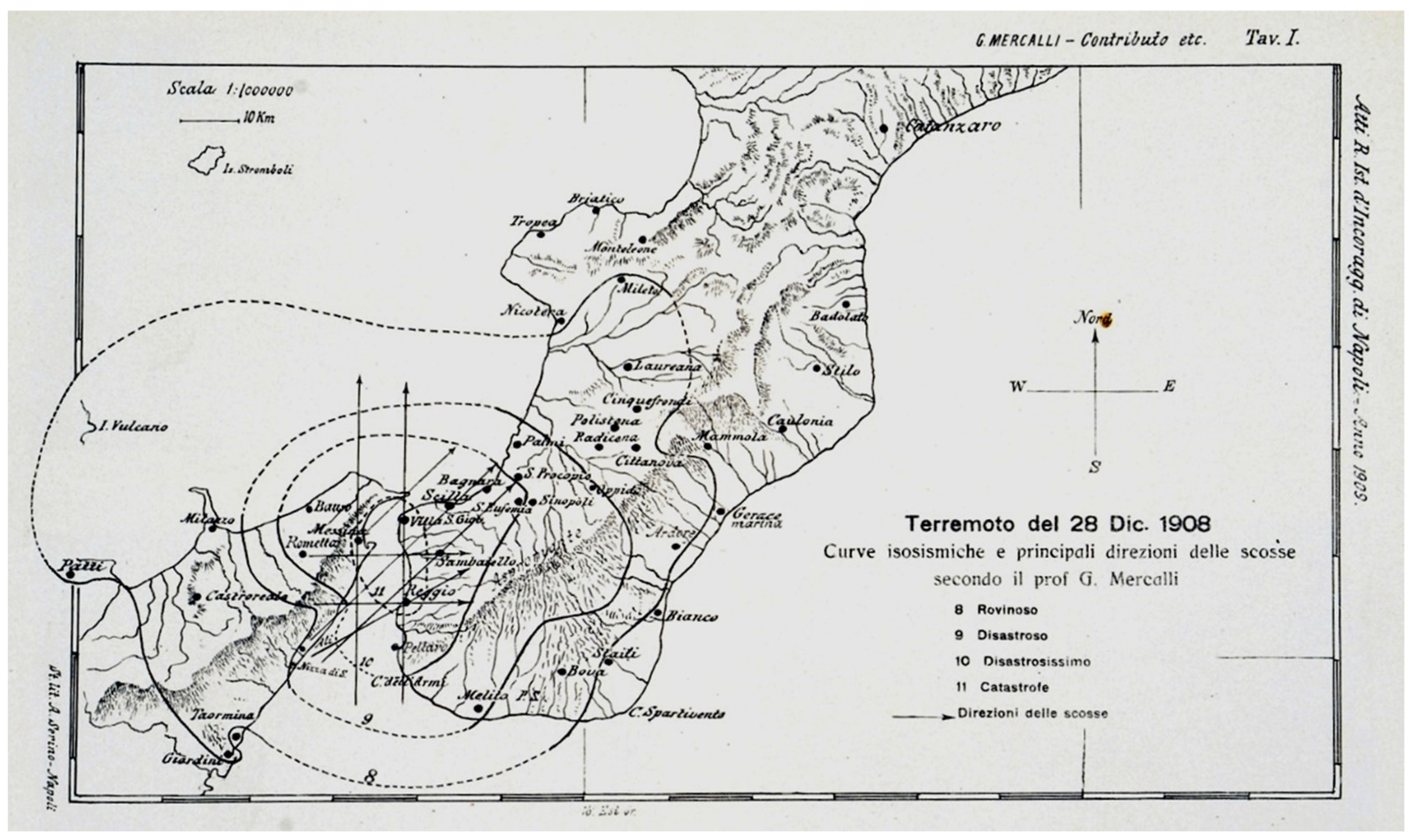
2.1. Seismicity of the Study Area
2.2. Geological Aspects
- (a)
- Tardorogene coverings unit—Reitano flysch: alternation of micaceous sandstones, of yellowish or gray-brown color, with intercalations of grayish or greenish marly clays (Ma and Mas in the geological map).
- (b)
- Sicilide complex—Upper scaly clays unit: marly clays and gray-blackish clayey marl with decimetric levels of gray marly limestone and grayish calcarenite (Cc in the geological map); Salici Mount—Castelli Mount unit: numidic flysch, blackish shafts (OM in the geological map) passing upwards to an alternation of brown clays and yellowish quartz arenites with local marly limestone and marl.
- (c)
- Panormide complex—numidic flysch, alternation of siliceous argillites and quartz arenites or quartz osyltites (Omi in the geological map).
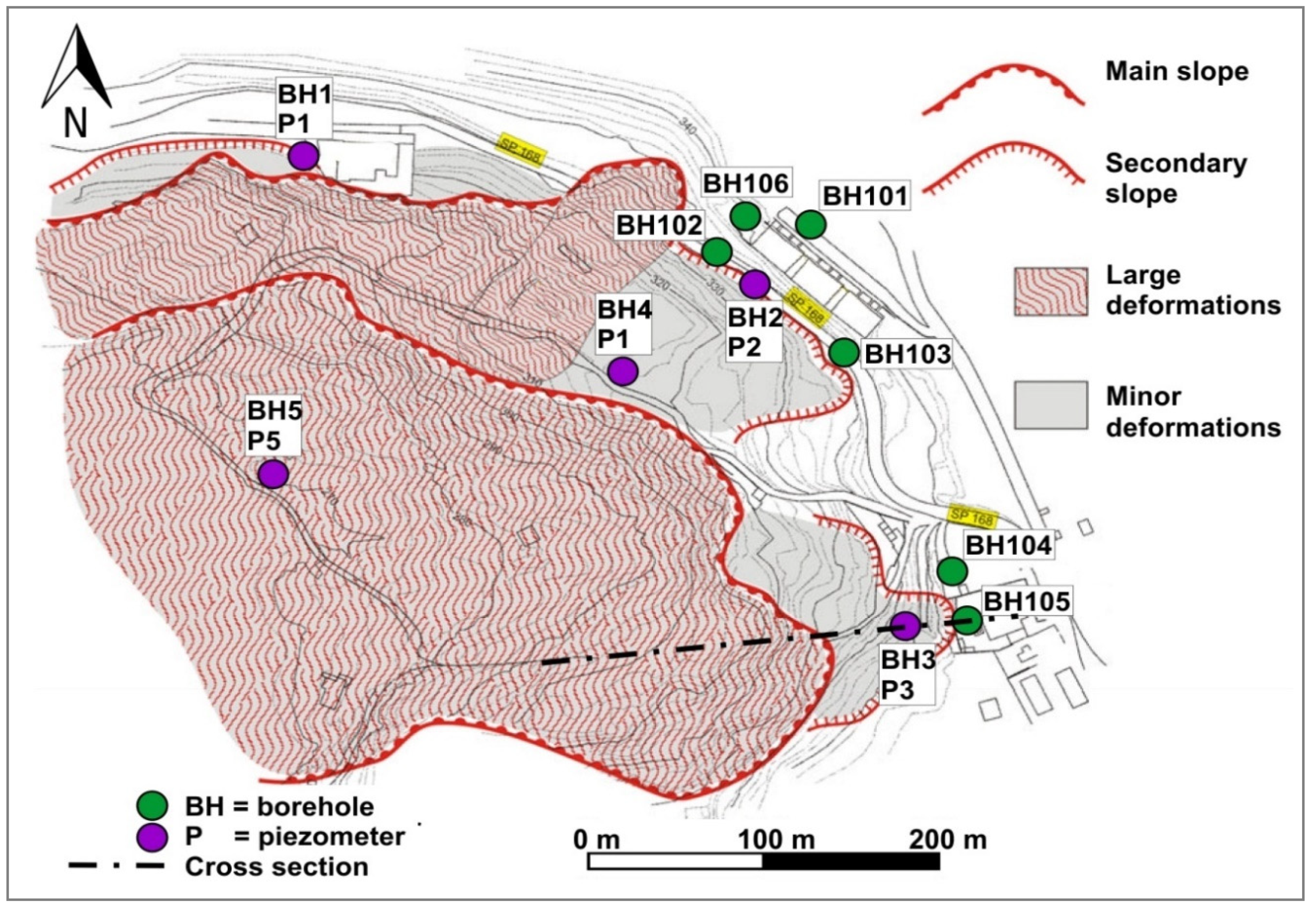
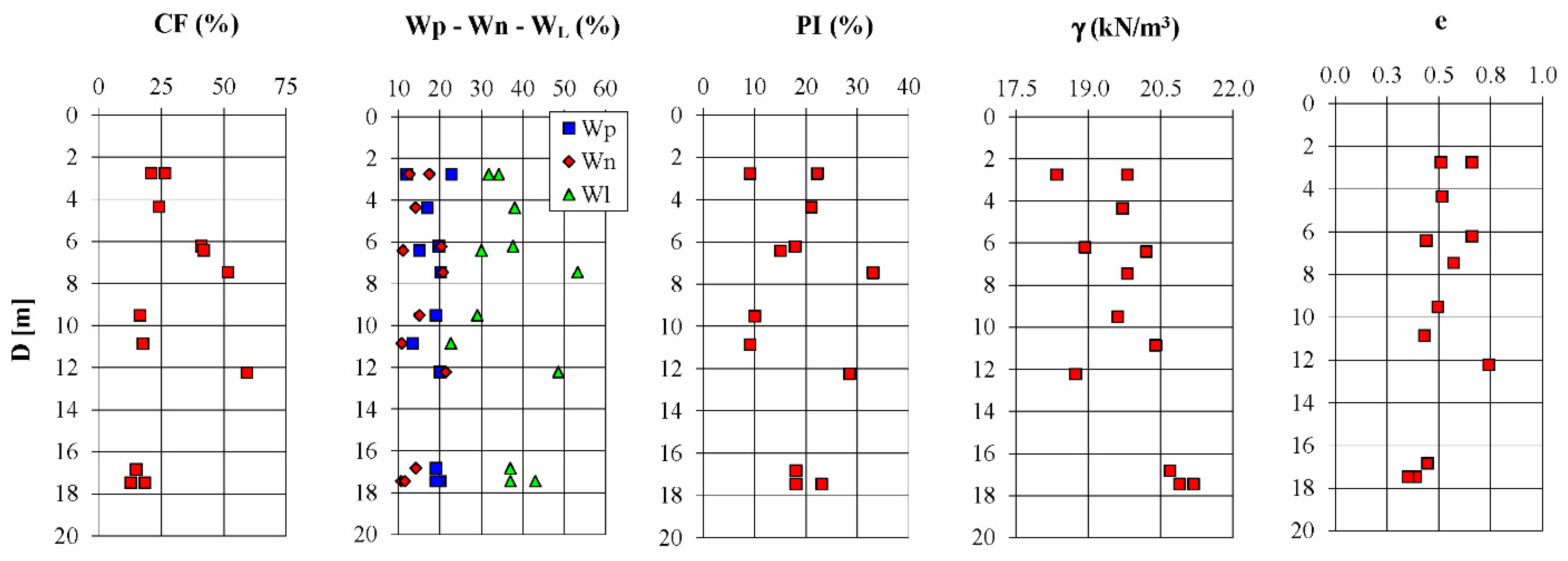
2.3. Investigation Program and Geotechnical Soil Properties
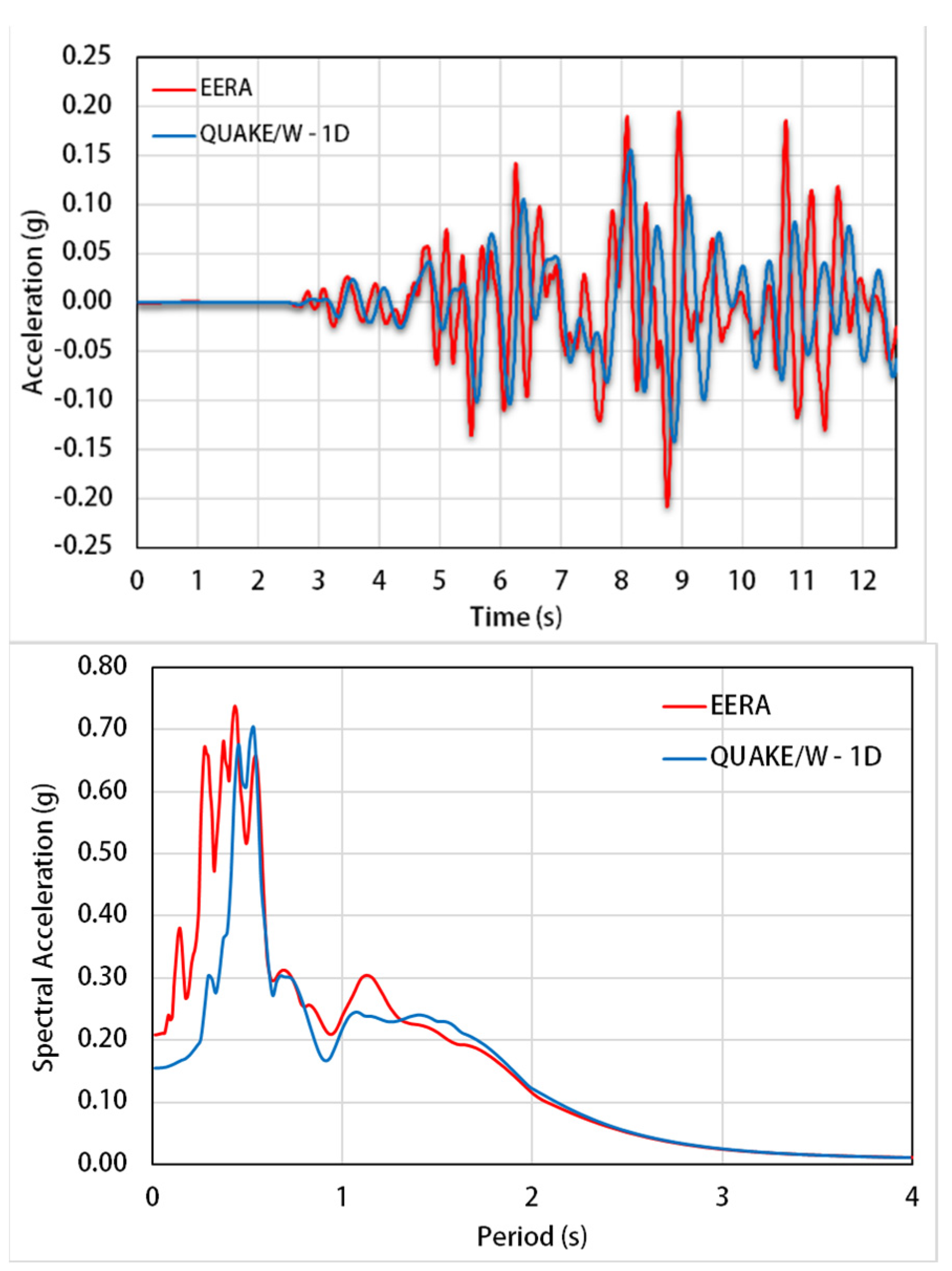
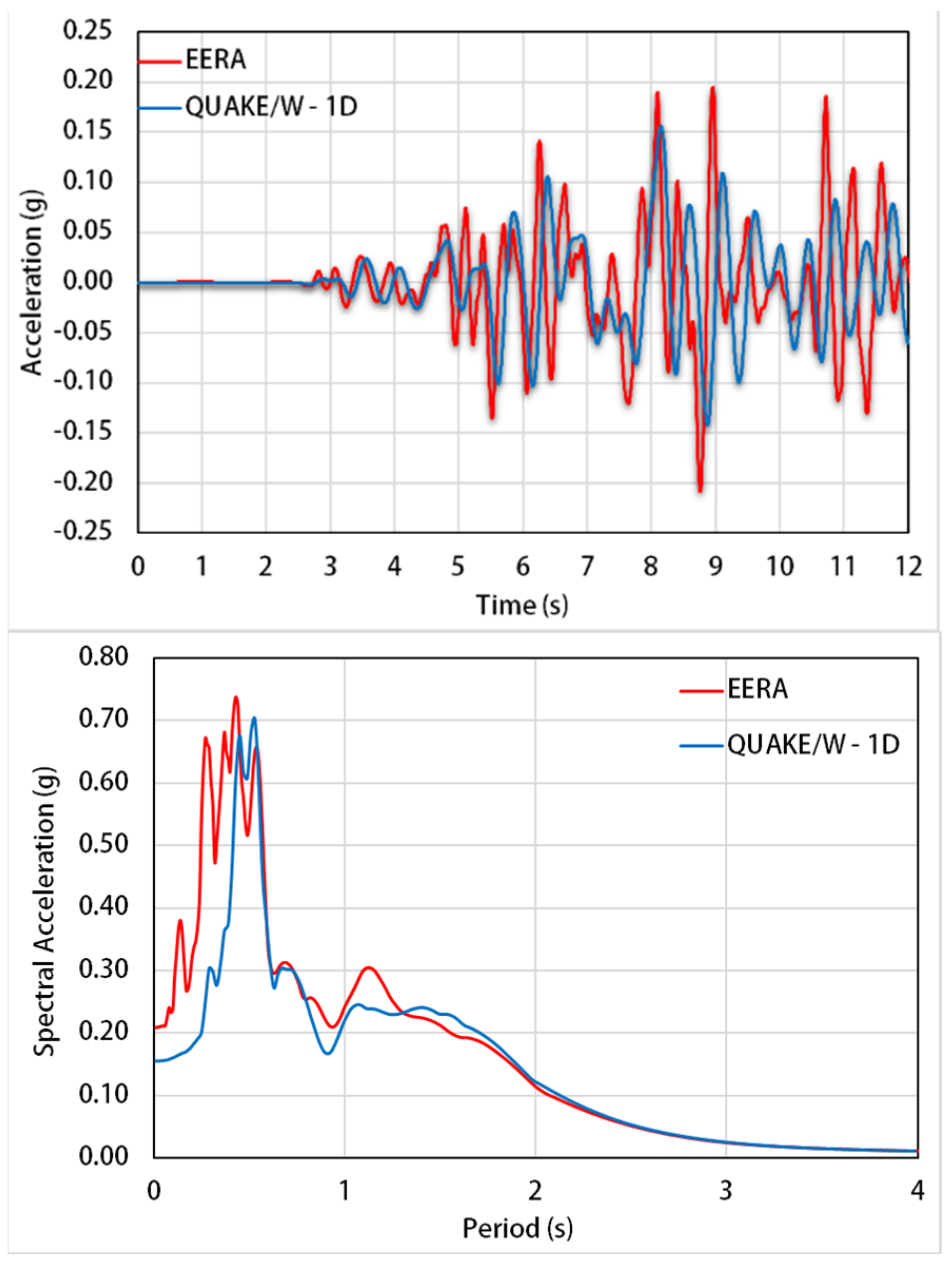
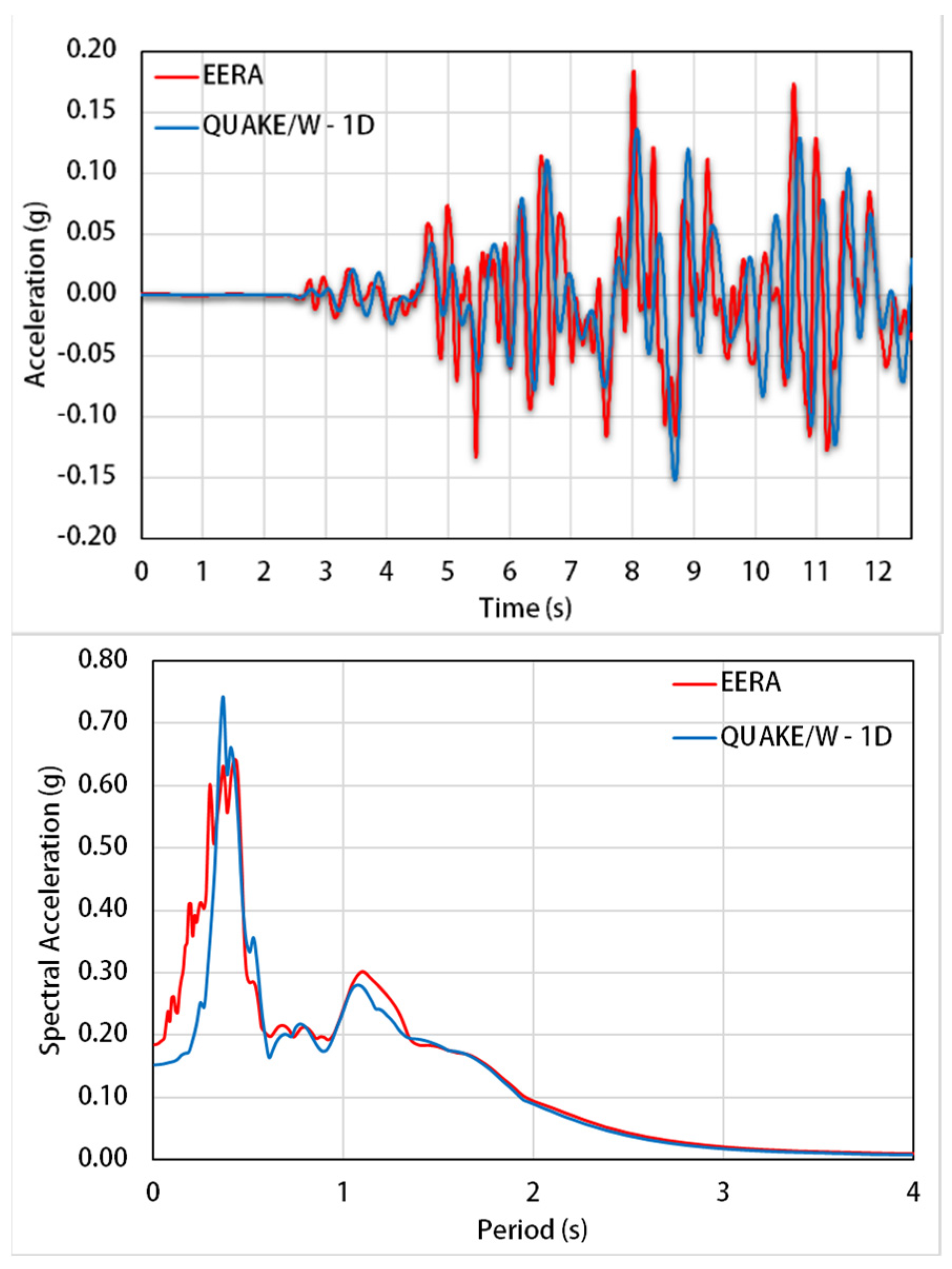
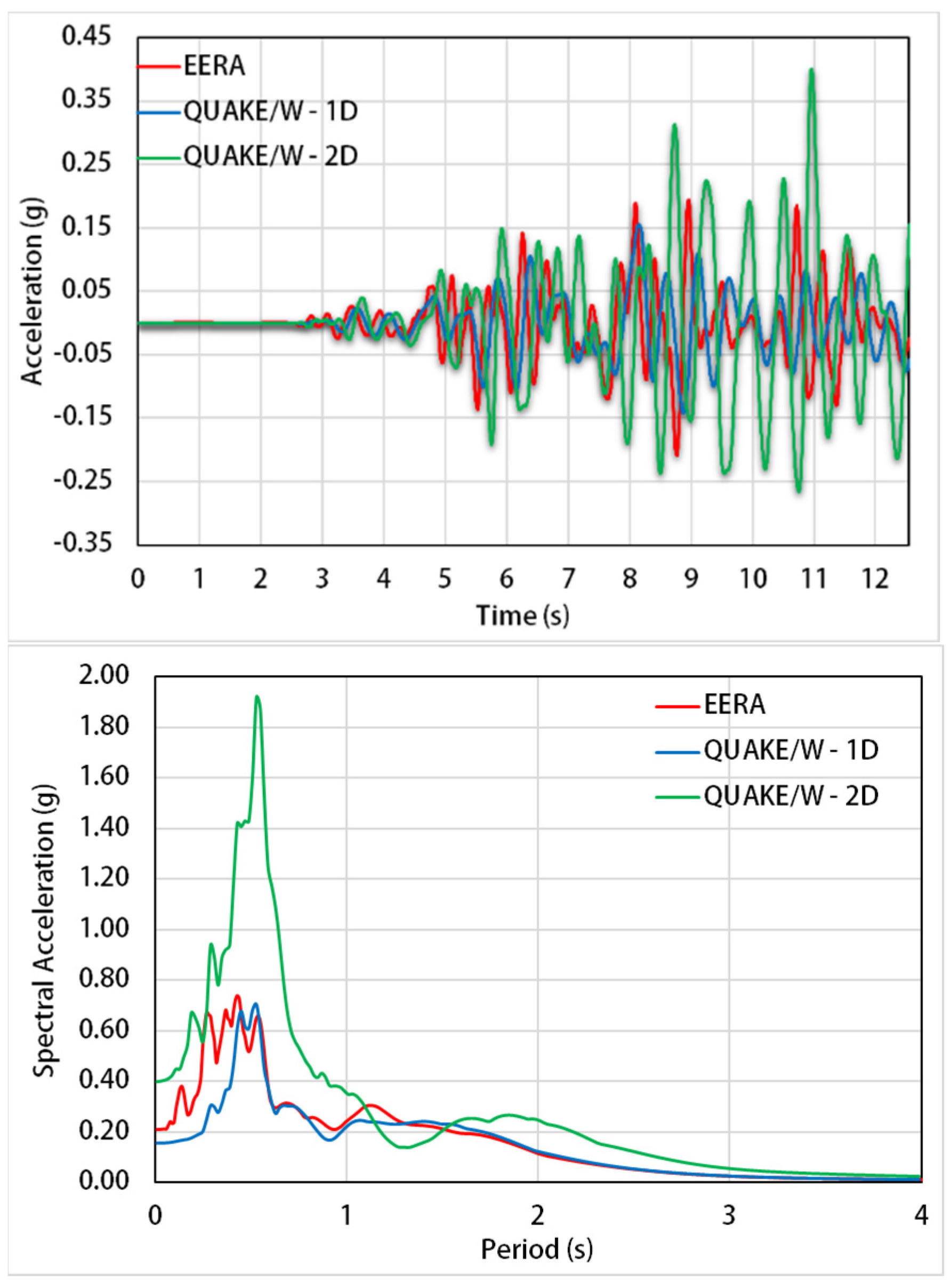
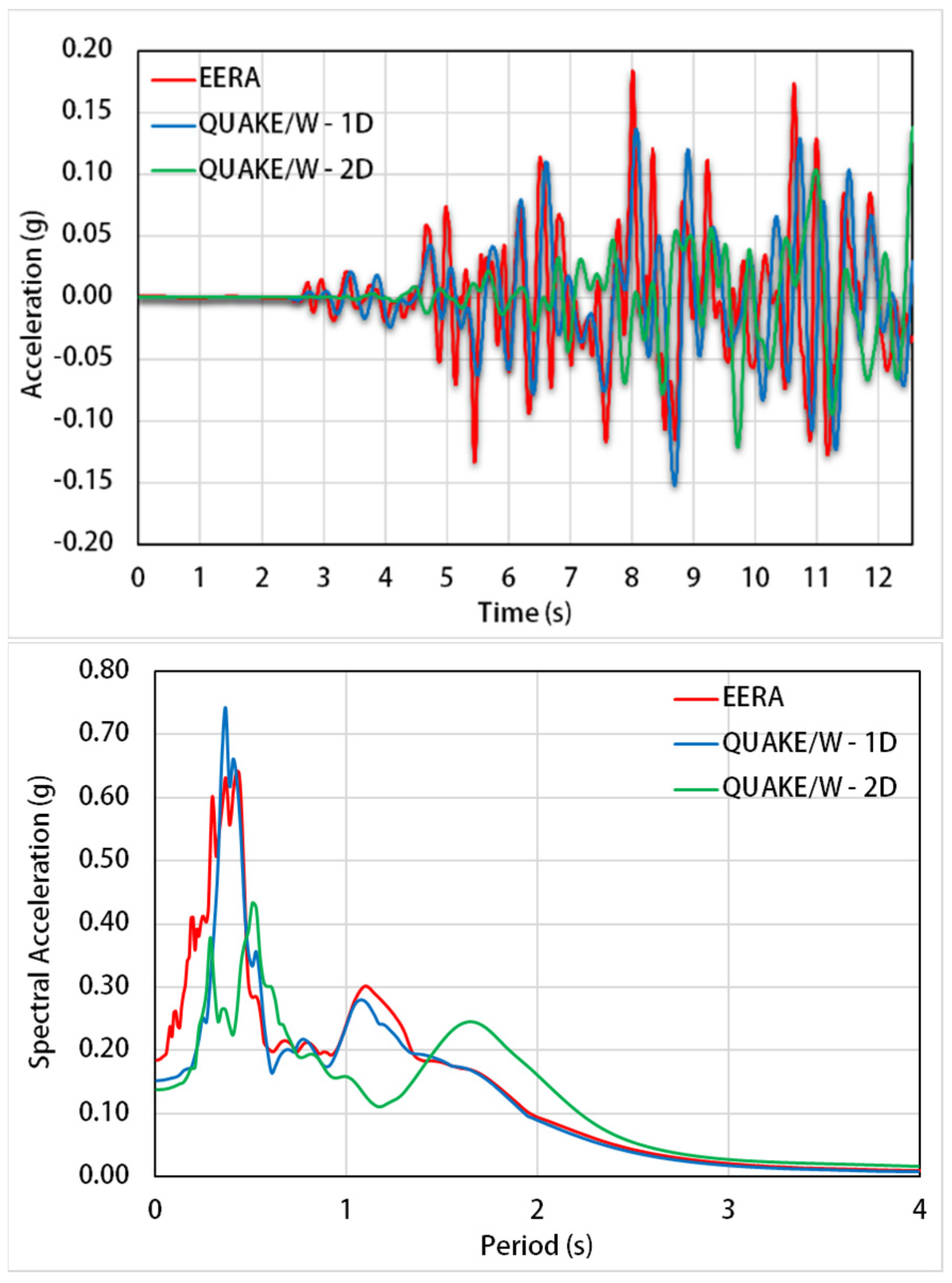
3. Site Response Analysis
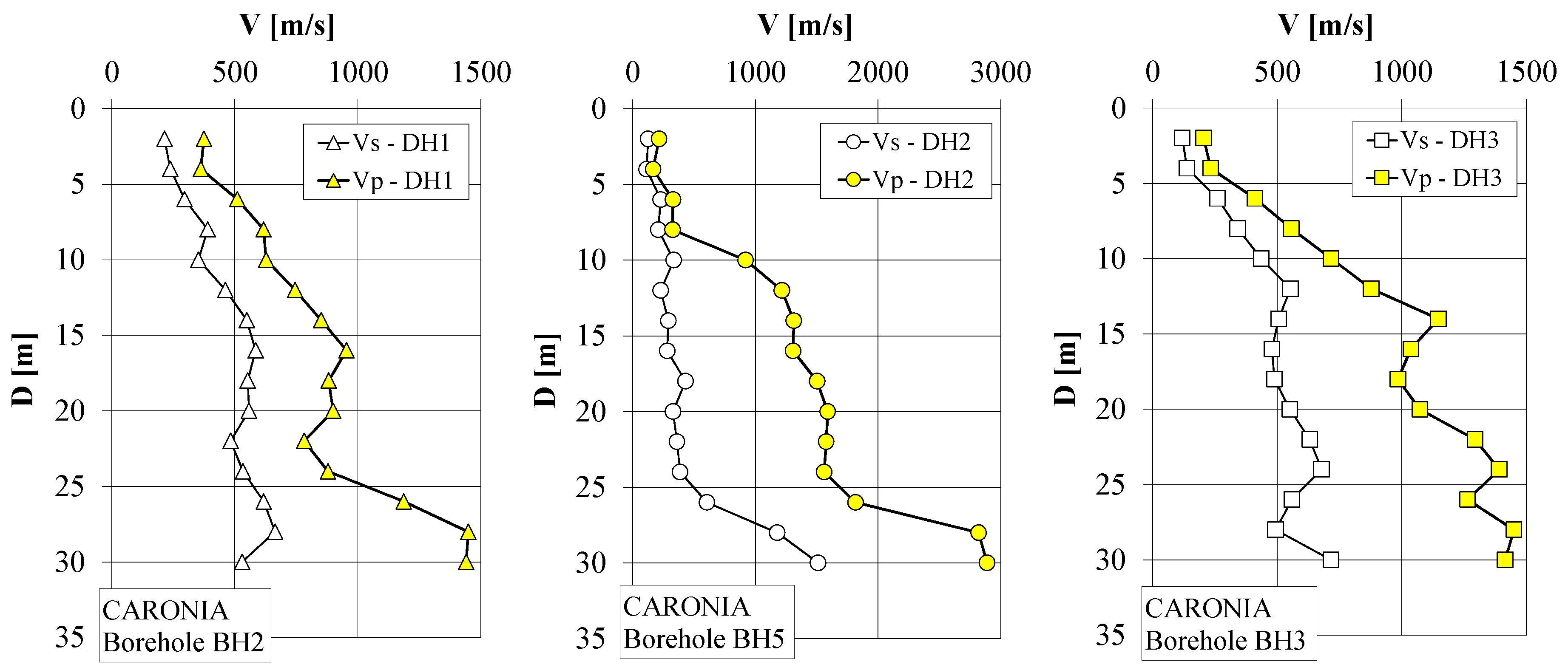
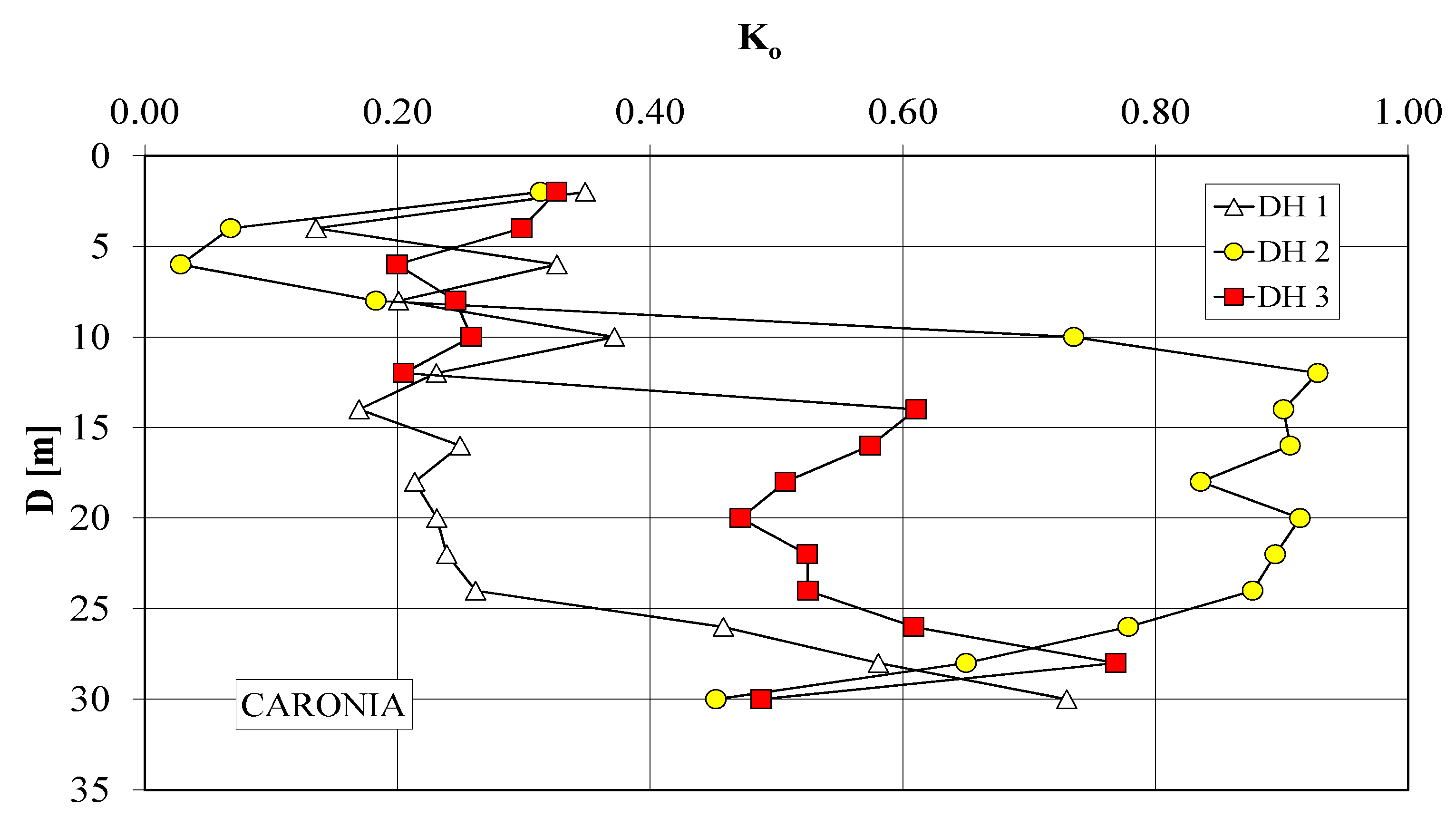
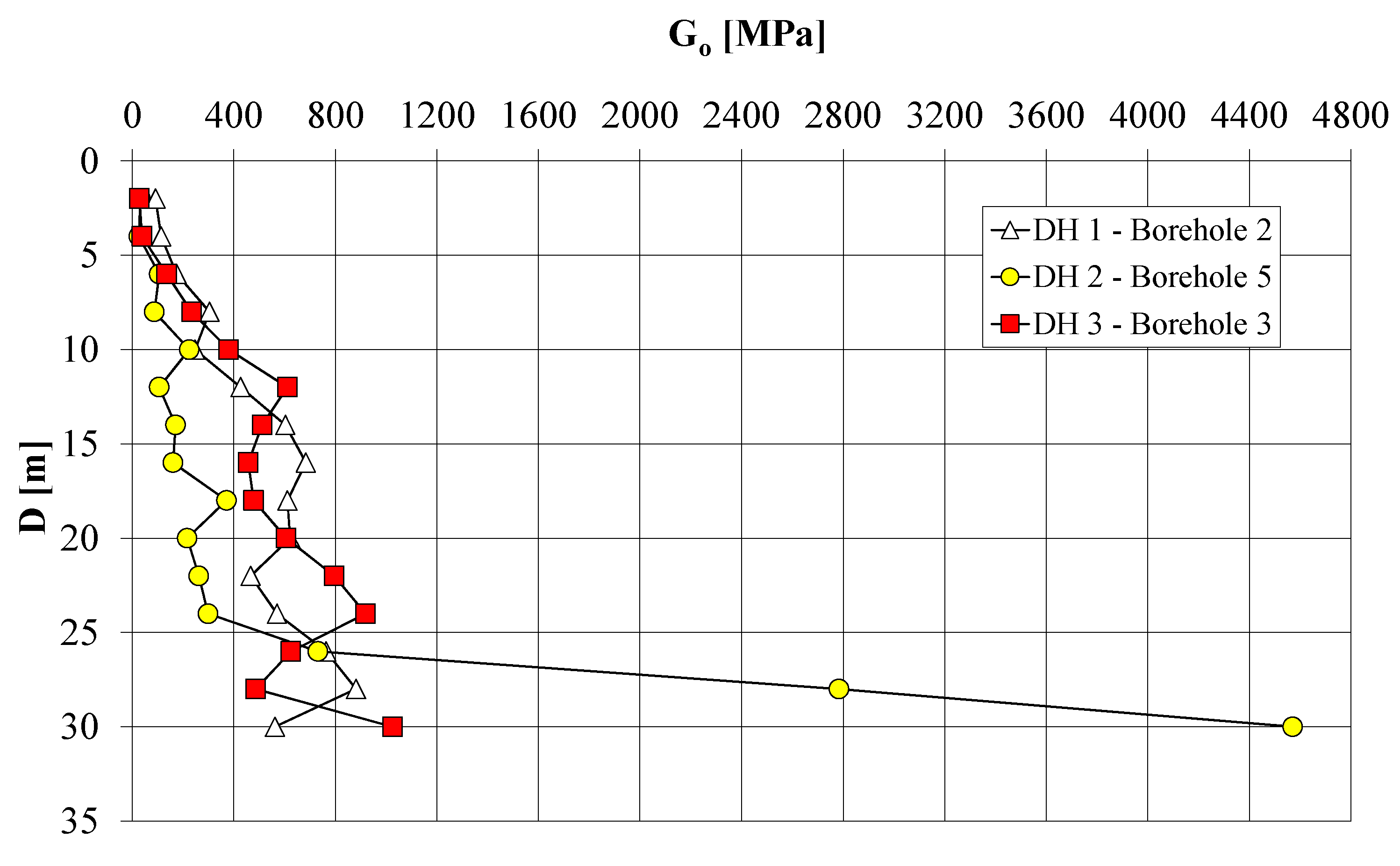
3.1. Seismic Input Motion and Soil Dynamic Properties
3.2. Numerical Analyses
3.3. 1-D Analysis
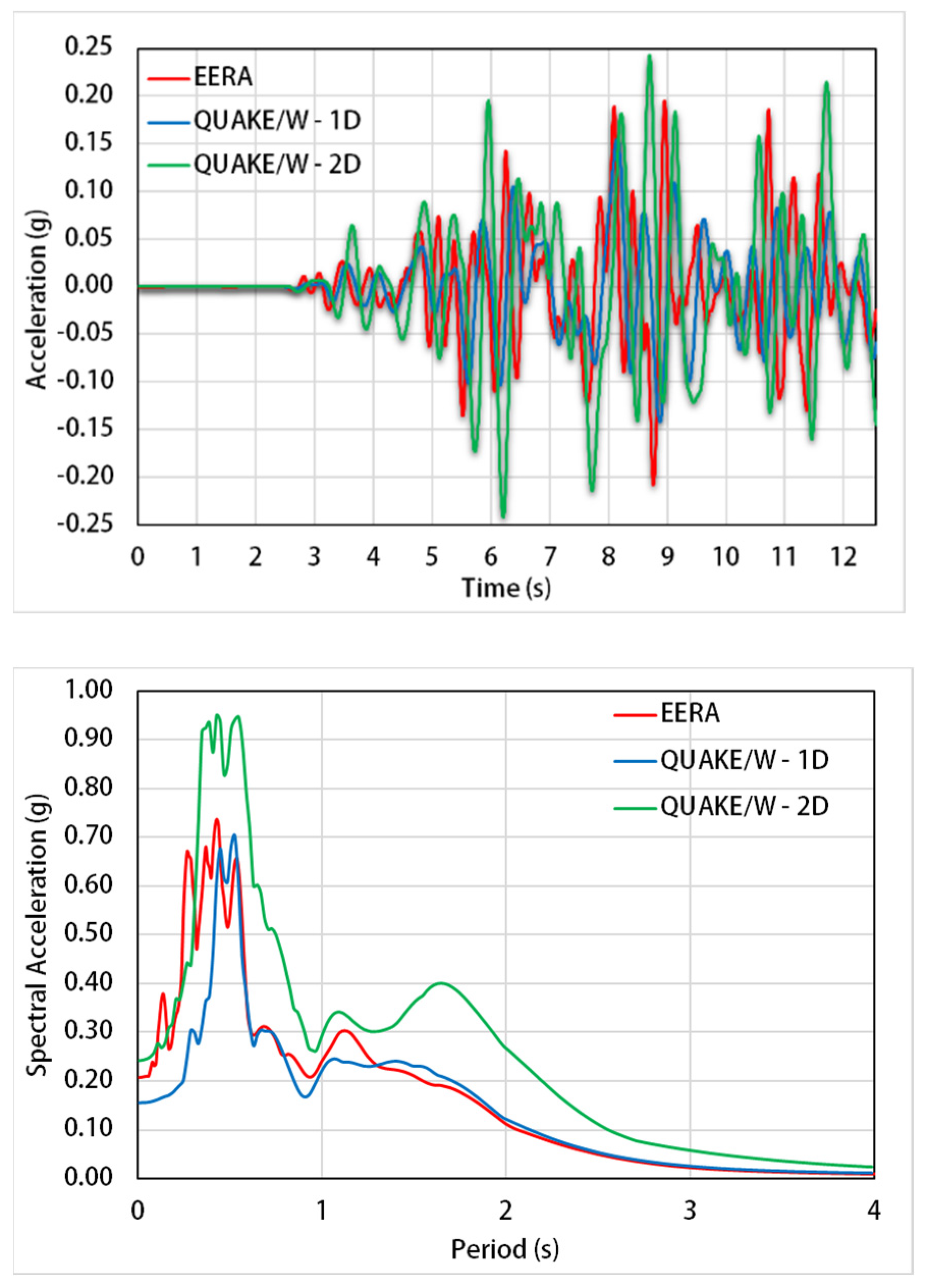
3.4. 2-D Analysis
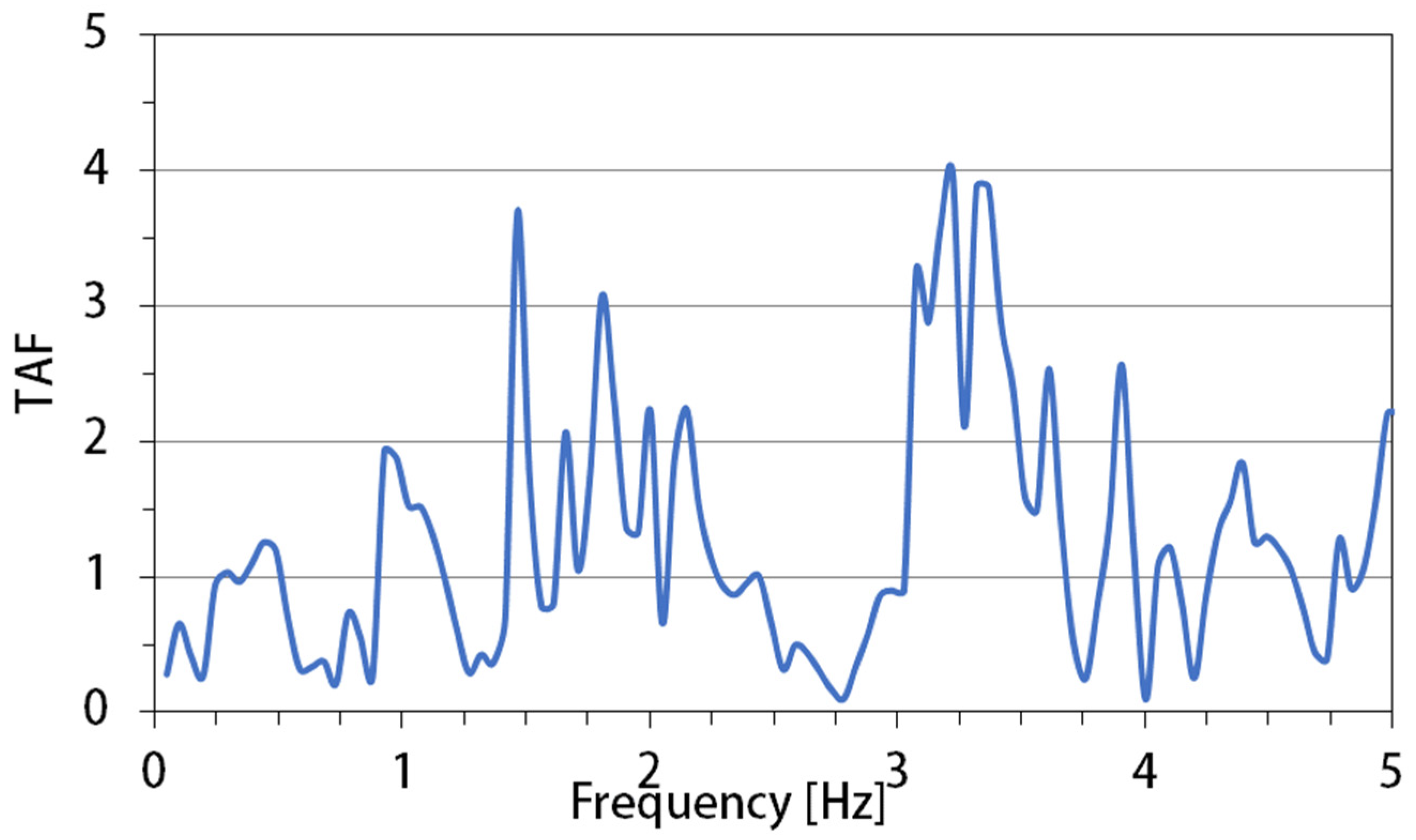
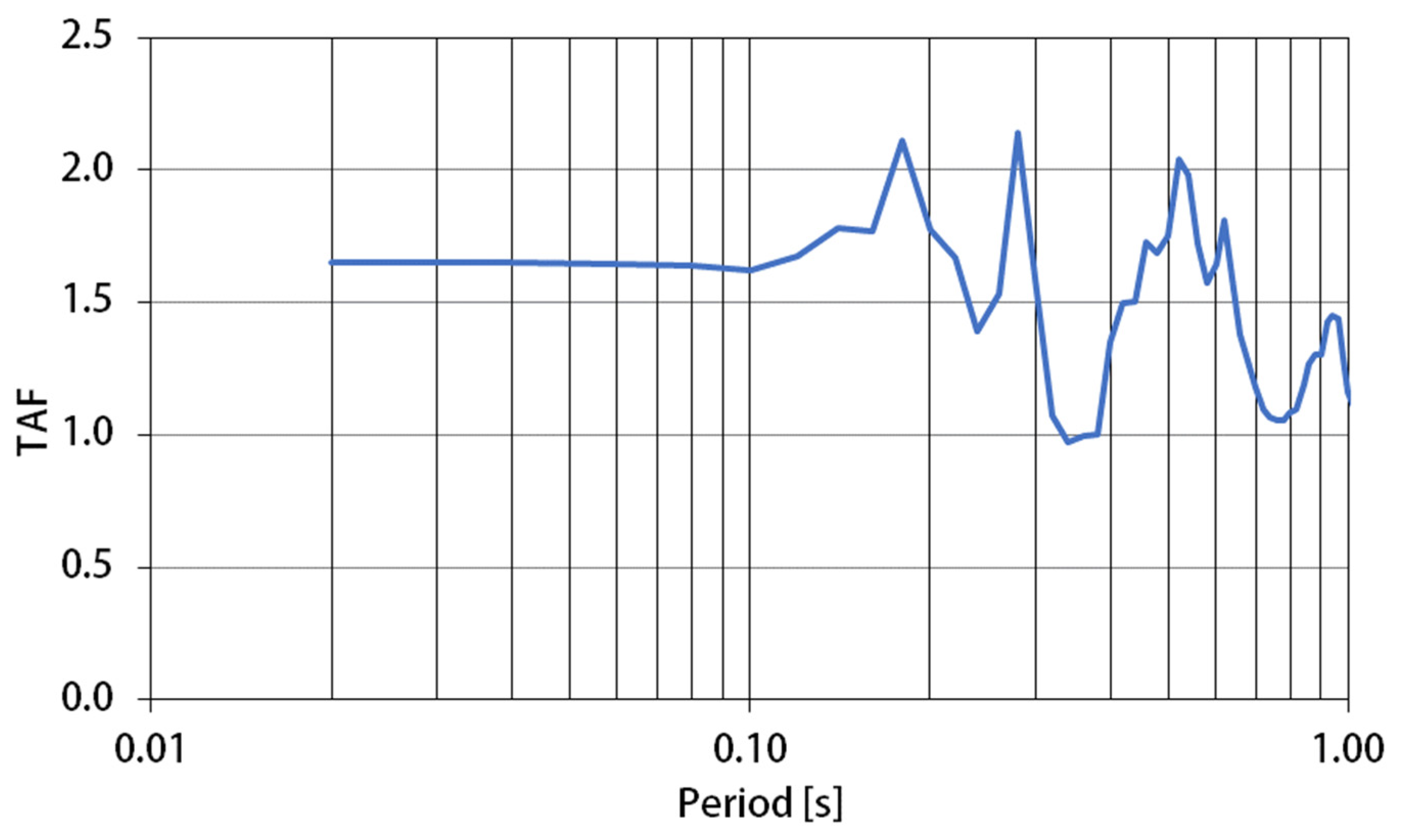
3.5. Topographic Effects
- -
- afft, the maximum free field acceleration in front of the toe;
- -
- affc, the maximum free field acceleration behind the crest see Equation (4);
- -
- amax, the maximum crest acceleration.
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EC8. Design Provisions for Earthquake Resistance of Structures, Part 1-1: General Rules-Seismic Actions and General Requirements for Structures. prEN 1998-5; European Committee for Standardization: Brussels, Belgium, 2000. [Google Scholar]
- Boore, D. The effect of simple topography on seismic waves: Implications for the accelerations recorded at Pacoima Dam, San Fernando Valley, California. Bull. Seismol. Soc. Am. 1973, 63, 1963–1973. [Google Scholar]
- Bouchon, M. Effect of topography on surface motion. Bull. Seismol. Soc. Am. 1973, 6, 615–632. [Google Scholar]
- Sepúlveda, S.; Murphy, W.; Jibson, R.; Petley, D. Seismically induced rock slope failures resulting from topographic amplification of strong ground motions: The case of Pacoima Canyon California. Eng. Geol. 2005, 80. [Google Scholar] [CrossRef]
- Assimaki, D.; Kausel, E.; Gazetas, G. Soil-dependent topographic effects: A case study from the 1999 Athens earthquake. Earthq. Spectra 2005, 21, 929–966. [Google Scholar] [CrossRef]
- Celebi, M. Topographical and geological amplifications determined from strong-motion and aftershock records of the 3 March 1985 Chile earthquake. Bull. Seism. Soc. Am. 1987, 77, 1147–1167. [Google Scholar]
- Geli, L.; Bard, P.Y.; Jullien, B. The effect of topography on earthquake ground motion: A review and new results. Bull. Seismol. Soc. Am. 1988, 78, 42–63. [Google Scholar]
- Wang, Y.; He, J.; Yonghong, L.; Cao, S.; He, Z. Seismic monitoring of a slope to investigate topographic amplification. Int. J. Geohazards Environ. 2015, 1, 101–109. [Google Scholar] [CrossRef]
- Glinsky, N.; Bertrand, E.; Régnier, J. Numerical simulation of topographical and geological site effects. Applications to canonical topographies and Rognes Hill, South East France. Soil Dyn. Earthq. Eng. 2018, 116, 620–636. [Google Scholar] [CrossRef]
- NCT 2018—Ministry of Infrastructure and Transport. Decree of the Ministry of Infrastructure and Transport (MIT) of the 01/17/2018; Ministry of Infrastructure and Transport: Rome, Italy, 2018.
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P. Catalogo Parametrico dei Terremoti Italiani (CPTI15), Version 2.0; Istituto Nazionale di Geofisica e Vulcanologia (INGV): Rome, Italy, 2019. [CrossRef]
- Meschis, M.; Roberts, G.P.; Mildon, Z.K.; Robertson, J.; Michetti, A.M.; Faure Walker, J.P. Slip on a mapped normal fault for the 28 December 1908 Messina earthquake (Mw 7.1) in Italy. Sci. Rep. 2019, 9, 6481. [Google Scholar] [CrossRef]
- Schambach, L.; Grilli, S.T.; Tappin, D.; Gangemi, M.D.; Barbaro, G. New simulations and understanding of the 1908 Messina Tsunami for a dual seismic and deep submarine mass failure source. Mar. Geol. 2020, 421, 106093. [Google Scholar] [CrossRef]
- Pino, N.A.; Piatanesi, A.; Valensise, G.; Boschi, E. The 28 December 1908 Messina strait earthquake (Mw 7.1): A great earthquake throughout a century of seismology. Seismol. Res. Lett. 2009, 80. [Google Scholar] [CrossRef]
- Boschi, E.; Ferrari, G.; Gasperini, P.; Guidoboni, E.; Smriglio, G.; Valensise, G. Catalogo dei Forti Terremoti in Italia dal 461 a.C. al 1980; ING-SGA: Bologna, Italy, 1995; p. 973. [Google Scholar]
- Mercalli, G. Contributo allo studio del terremoto calabro-messinese del 28 dicembre 1908. Coop. Tipogr. 1909, 7, 249–292. [Google Scholar]
- Guidoboni, E.; Ferrari, G.; Mariotti, D.; Comastri, A.; Tarabusi, G.; Valensise, G. CFTI4Med, Catalogue of Strong Earthquakes in Italy (461 B.C.–1997) and Mediterranean Area (760 B.C.–1500) 2007. Available online: http://CFTI5Med (ingv.it) (accessed on 21 November 2020).
- Cubito, A.; Ferrara, V.; Pappalardo, G. Landslide hazard in the Nebrodi mountains (Northeastern Sicily). Geomorphology 2005, 66, 359–372. [Google Scholar] [CrossRef]
- Pavano, F.; Romagnoli, G.; Tortorici, G.; Catalano, S. Active tectonics along the Nebrodi-Peloritani boundary in Northeastern Sicily (Southern Italy). Tectonophysics 2015, 659, 1–11. [Google Scholar] [CrossRef]
- Lentini, F.; Catalano, S.; Carbone, S. Geologic Map of The Messina Province; S.E.L.C.A: Firenze, Italy, 2000. [Google Scholar]
- Castelli, F.; Lentini, V.; Ferraro, A.; Grasso, S. Seismic risk evaluation for the emergency management. Ann. Geophys. 2018, 61, SE222. [Google Scholar] [CrossRef]
- Cavallaro, A.; Grasso, S.; Maugeri, M. Dynamic clay soils behaviour by different laboratory and in situ tests. In Solid Mechanics and its Applications, Proceedings of the Geotechnical Symposium on Soil Stress-Strain Behavior: Measurement, Modelling and Analysis to Celebrate Prof. Tatsuoka’s 60th Birthday, Roma, Italy, 16–17 March 2006; Springer: Dordrecht, The Netherlands, 2006; pp. 583–594. [Google Scholar]
- Bradley, B.A. Ground motions observed in the Darfield and Christ Church earthquakes and the importance of local site response effects. N. Z. J. Geol. Geophys. 2012, 55, 279–286. [Google Scholar] [CrossRef]
- Bottari, A.; Carapezza, E.; Carapezza, M.; Carveni, P.; Cefali, F.; Lo Giudice, E.; Pandolfo, C. The 1908 Messina strait earthquake in the regional geostructural framework. J. Geodyn. 1986, 5, 275–302. [Google Scholar] [CrossRef]
- Tortorici, L.; Monaco, C.; Tansi, C.; Cocina, O. Recent and active tectonics in the Calabrian Arc (Southern Italy). Tectonophysics 1995, 243, 37–55. [Google Scholar] [CrossRef]
- Amoruso, A.; Crescentini, L.; Scarpa, R. Source parameters of the 1908 Messina Strait, Italy, earthquake from geodetic and seismic data. J. Geophys. Res. 2002, 107, ESE 4-1–ESE 4-11. [Google Scholar] [CrossRef]
- Valensise, G.; Pantosti, D. Database of potential sources for earthquakes larger than M 5.5 in Italy. Ann. Geophys. 2001, 44, 1–964. [Google Scholar]
- Castelli, F.; Cavallaro, A.; Grasso, S.; Ferraro, A. In situ and laboratory tests for site response analysis in the ancient city of Noto (Italy). In Proceedings of the 1st IMEKO TC4 International Workshop on Metrology for Geotechnics, Benevento, Italy, 17–18 March 2016; pp. 85–90. [Google Scholar]
- Castelli, F.; Cavallaro, A.; Ferraro, A.; Grasso, S.; Lentini, V. A seismic geotechnical hazard study in the ancient city of Noto (Italy). In Procedia Engineering, Proceedings of the 6th Italian Conference of Researchers in Geotechnical Engineering (CNRIG), Bologna, Italy, 22–23 September 2016; Elsevier: Amsterdam, The Netherlands, 2016; pp. 535–540. [Google Scholar]
- Cavallaro, A.; Grasso, S.; Ferraro, A. Study on seismic response analysis in “Vincenzo Bellini” garden area by seismic dilatometer Marchetti tests. In Geotechnical and Geophysical Site Characterization, Proceedings of the 5th International Conference on Geotechnical and Geophysical Site Characterization, ISC’5, Queensland, Australia, 5–9 September 2016; Australian Geomechanics Society: Sydney, Australia, 2016; pp. 1309–1314. [Google Scholar]
- Capilleri, P.; Cavallaro, A.; Maugeri, M. Static and dynamic characterization of soils at Roio Piano (AQ). Ital. Geotech. J. 2014, 2, 38–52. [Google Scholar]
- Castelli, F.; Cavallaro, A.; Ferraro, A.; Grasso, S.; Lentini, V.; Massimino, M.R. Static and dynamic properties of soils in Catania (Italy). Ann. Geophys. 2018, 61, SE222. [Google Scholar] [CrossRef]
- Cavallaro, A.; Castelli, F.; Ferraro, A.; Grasso, S.; Lentini, V. Site response analysis for the seismic improvement of a historical and monumental building: The case study of Augusta Hangar. Bull. Eng. Geol. Environ. 2018, 77, 1217–1248. [Google Scholar] [CrossRef]
- Yokota, K.; Imai, T.; Konno, M. Dynamic deformation characteristics of soils determined by laboratory tests. OYO Tec. Rep. 1981, 3, 13–37. [Google Scholar]
- Ferraro, A.; Grasso, S.; Maugeri, M.; Totani, F. Seismic response analysis in the southern part of the historic centre of the city of L’Aquila (Italy). Soil Dyn. Earthq. Eng. 2016, 88, 256–264. [Google Scholar] [CrossRef]
- Madiai, C.; Facciorusso, J.; Gargini, E.; Baglione, M. 1D versus 2D site effects from numerical analyses on a cross section at Barberino di Mugello (Tuscany, Italy). Procedia Eng. 2016, 158, 499–504. [Google Scholar] [CrossRef]
- Bardet, J.P.; Ichii, K.; Lin, C.H. EERA: A Computer Program for Equivalent-Linear Earthquake Site Response Analyses of Layered Soil Deposits; University of Southern California: Los Angeles, CA, USA, 2000. [Google Scholar]
- Krahn, J. Dynamic Modeling with QUAKE/W: An Engineering Methodology; GEO-SLOPE International Ltd.: Calgary, AB, Canada, 2004. [Google Scholar]
- Ferraro, A.; Grasso, S.; Massimino, M.R. Site effects evaluation in Catania (Italy) by means of 1-D numerical analysis. Ann. Geophys. 2018, 61, 224. [Google Scholar] [CrossRef]
- Elton, D.J.; Shie, C.F.; Hadj-Hamou, T. One- and two-dimensional analysis of earth dams. In Proceedings of the International Conferences on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, Chicago, IL, USA, 11–15 March 1991; pp. 1043–1049. [Google Scholar]
- Schnabel, P.B.; Lysmer, J.; Seed, H.B. SHAKE–A Computer Program for Earthquake Response Analysis of Horizontally Layered Sites; Earthquake Engineering Research Center: Berkeley, CA, USA, 1972. [Google Scholar]
- Lysmer, J.; Udaka, T.; Tsai, C.; Seed, H.B. FLUSH–A Computer Program for Approximate 3-D Analysis of Soil-Structure Interaction Problems; Earthquake Engineering Research Center: Berkeley, CA, USA, 1975. [Google Scholar]
- Ji, J.; Wang, C.W.; Gao, Y.; Zhang, L.M. Probabilistic investigation of the seismic displacement of earth slopes under stochastic ground motion: A rotational sliding block analysis. Can. Geotech. J. 2020. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, W.; Zhang, F.; Gao, Y.; Lü, Q. Reliability analysis on permanent displacement of earth slopes using the simplified Bishop method. Comput. Geotech. 2020, 117, 103286. [Google Scholar] [CrossRef]
- Ashford, S.A.; Sitar, N. Seismic Response of Steep Natural Slopes; Earthquake Engineering Research Center: Berkeley, CA, USA, 1994. [Google Scholar]
- Ashford, S.A.; Sitar, N. Analysis of topographic amplification of inclined shear waves in a steep coastal bluff. Bull. Seism. Soc. Am. 1997, 87, 692–700. [Google Scholar]
- Ashford, S.A.; Sitar, N.; Asce, M. Simplified method for evaluating seismic stability of steep slopes. J. Geotech. Geo-Environ. Eng. 2002, 128, 119–128. [Google Scholar] [CrossRef]
- Kallou, P.V.; Gazetas, G.; Psarropoulos, P.N. A case history on soil and topographic effects in the 7 September 1999 Athens earthquake. In Proceedings of the International Conferences on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, San Diego, CA, USA, 26–31 March 2001; p. 32. [Google Scholar]
- Bouckovalas, G.; Kouretzis, G.P. Review of soil and topography effects in the 7 September 1999 Athens (Greece) earthquake. In Proceedings of the 4th International Conference on Recent Advences in Geotechnical Earthquake Engineering and Soil Dynamics and Symposium in Honor of Professor, San Diego, CA, USA, 26–31 March 2001. [Google Scholar]







| Borehole | D [m] | Soil Profile | VS [m/s] |
|---|---|---|---|
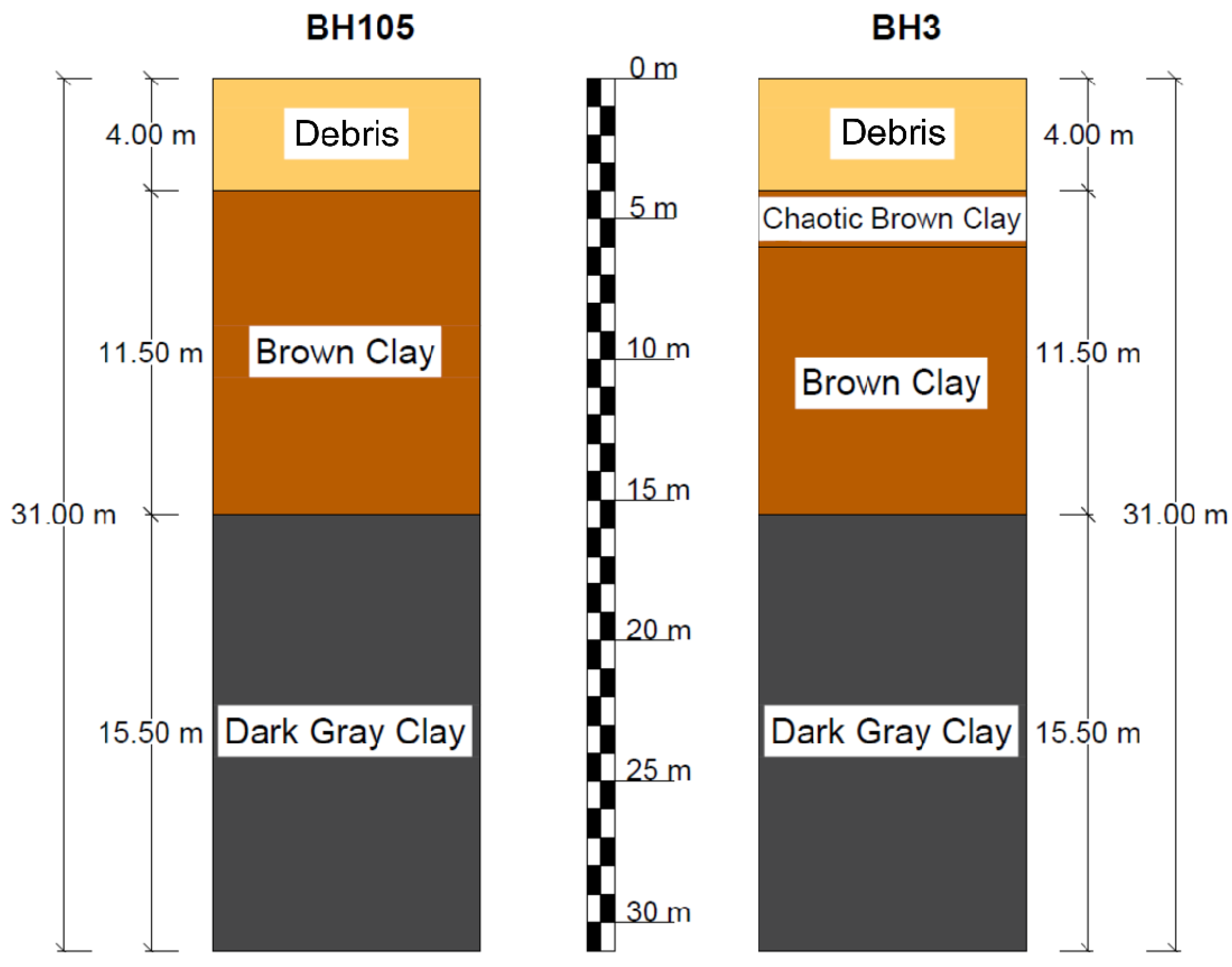
| BH105 | 0.00–4.00 | Debris: conglomerate screed, boulders and chaotic material. | <260 |
| BH105 | 4.00–15.50 | Tobacco brown clays, to the touch plastic and from medium consistent to consistent in the lower part (10.50–15.50 m); at times there are clay levels; overall, when cut, they present themselves with ferrous, rust-colored and alternatively gray alterations. | <350 |
| BH105 | 15.50–31.00 | Dark gray clay with very consistent sections, alternating with fractured and flattened layers; moreover, there are rare levels of clay with plastic behavior and dark color. | >450 <600 |
| BH3 | 0.00–4.00 | Plastic structureless clays (landslide debris). | <260 |
| BH3 | 4.00–6.00 | Chaotic structureless clay with occasional compact clay levels of brown color with plastic consistency and poor characteristics. | <350 |
| BH3 | 6.00–15.50 | Chaotic structureless clay with occasional compact clay levels of gray color with plastic consistency and mediocre characteristics. | >350 <450 |
| BH3 | 15.50–31.00 | Argillites with lytic tracts and sub-vertical fractures, dark gray or blackish in color with mediocre characteristics. | >450 <600 |
| Site | D [m] | γ [kN/m3] | Wn [%] | WL [%] | WP [%] | PI [%] | CI [%] | AI [%] |
|---|---|---|---|---|---|---|---|---|
| BH2CI1 | 2.50–3.00 | 19.81 | 12.54 | 34.17 | 11.98 | 22.19 | 0.97 | 1.07 |
| BH3CI1 | 2.50–3.00 | 19.71 | 26.21 | 31.78 | 22.71 | 9.07 | 1.58 | 0.34 |
| BH3CI2 | 6.00–6.40 | 19.61 | 22.65 | 37.63 | 19.74 | 17.89 | 0.97 | 0.44 |
| BH4CI1 | 7.30–7.60 | 18.24 | 15.78 | 53.27 | 20.20 | 33.07 | 0.99 | 0.64 |
| BH4CI2 | 10.70–11.00 | 19.22 | 24.45 | 22.58 | 13.42 | 9.16 | 1.29 | 0.52 |
| BH5CI1 | 12.00–12.45 | 19.12 | 26.35 | 48.56 | 20.06 | 28.50 | 0.96 | 0.48 |
| BH102-CM1 | 4.20–450 | 19.71 | 14.12 | 38.00 | 17.00 | 21.00 | 1.14 | 0.87 |
| BH2CI1 | 2.50–3.00 | 19.81 | 12.54 | 34.17 | 11.98 | 22.19 | 0.97 | 1.07 |
| BH3CI1 | 2.50–3.00 | 19.71 | 26.21 | 31.78 | 22.71 | 9.07 | 1.58 | 0.34 |
| BH3CI2 | 6.00–6.40 | 19.61 | 22.65 | 37.63 | 19.74 | 17.89 | 0.97 | 0.44 |
| BH4CI1 | 7.30–7.60 | 18.24 | 15.78 | 53.27 | 20.20 | 33.07 | 0.99 | 0.64 |
| BH4CI2 | 10.70–11.00 | 19.22 | 24.45 | 22.58 | 13.42 | 9.16 | 1.29 | 0.52 |
| Site | D [m] | e | n | Sr [%] | c’ [kPa] | φ‘ [°] |
|---|---|---|---|---|---|---|
| BH2CI1 | 2.50–3.00 | 0.51 | 0.34 | 66.58 | 4.88 | 31.6 |
| BH3CI1 | 2.50–3.00 | 0.66 | 0.40 | 69.89 | 5.86 | 27.6 |
| BH3CI2 | 6.00–6.40 | 0.66 | 0.40 | 81.96 | 6.93 | 23.4 |
| BH4CI1 | 7.30–7.60 | 0.57 | 0.36 | 95.58 | 19.95 | 28.1 |
| BH4CI2 | 10.70–11.00 | 0.43 | 0.30 | 67.06 | 21.73 | 15.8 |
| BH5CI1 | 12.00–12.45 | 0.74 | 0.43 | 78.96 | 2.41 | 16.0 |
| BH102-CM1 | 4.20–450 | 0.52 | 0.34 | 73.12 | 33.20 | 21 |
| BH2CI1 | 2.50–3.00 | 0.44 | 0.30 | 67.02 | 20.30 | 22 |
| BH3CI1 | 2.50–3.00 | 0.49 | 0.33 | 78.88 | 36.50 | 30 |
| BH3CI2 | 6.00–6.40 | 0.44 | 0.31 | 85.07 | 51.80 | 22 |
| BH4CI1 | 7.30–7.60 | 0.39 | 0.28 | 73.30 | 34.00 | 20 |
| BH4CI2 | 10.70–11.00 | 0.35 | 0.26 | 85.63 | 23.20 | 21 |
| Soil | α | β | η | λ |
|---|---|---|---|---|
| Debris | 65 | 1.15 | 34.8 | 1.9 |
| Brown Clay | 20 | 0.87 | 19 | 2.3 |
| Dark Gray Clay | 7.5 | 0.897 | 90 | 4.5 |
| PGAEERA [g] | PGAQUAKE/W 1-D [g] | |
|---|---|---|
| Point 1 | 0.228 | 0.207 |
| Point 2 | 0.228 | 0.207 |
| Point 3 | 0.168 | 0.141 |
| Tortorici et al. [25] | Bottari et al. [24] | DISS Messina Strait | ||||
|---|---|---|---|---|---|---|
| PGA EERA | PGA QUAKE/W 1-D | PGA EERA | PGA QUAKE/W 1-D | PGA EERA | PGA QUAKE/W 1-D | |
| [g] | [g] | [g] | [g] | [g] | [g] | |
| Point 1 | 0.208 | 0.193 | 0.208 | 0.156 | 0.195 | 0.269 |
| Point 2 | 0.208 | 0.193 | 0.208 | 0.156 | 0.195 | 0.269 |
| Point 3 | 0.176 | 0.147 | 0.184 | 0.152 | 0.165 | 0.151 |
| DISS Gioia Tauro | DISS Aspromonte Est | 1693 Catania Earthquake | ||||
| PGA EERA | PGA QUAKE/W 1-D | PGA EERA | PGA QUAKE/W 1-D | PGA EERA | PGA QUAKE/W 1-D | |
| [g] | [g] | [g] | [g] | [g] | [g] | |
| Point 1 | 0.257 | 0.203 | 0.206 | 0.266 | 0.179 | 0.142 |
| Point 2 | 0.257 | 0.203 | 0.206 | 0.266 | 0.179 | 0.142 |
| Point 3 | 0.202 | 0.157 | 0.181 | 0.167 | 0.154 | 0.117 |
| PGAEERA [g] | PGAQUAKE/W 1-D [g] | PGAQUAKE/W 2-D [g] | |
|---|---|---|---|
| Point 1 | 0.208 | 0.156 | 0.242 |
| Point 2 | 0.208 | 0.156 | 0.400 |
| Point 3 | 0.184 | 0.152 | 0.138 |
| Tortorici et al. [25] | Bottari et al. [24] | DISS Messina Strait | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PGA EERA | PGA QUAKE/W 1-D | PGA QUAKE/W 2-D | PGA EERA | PGA QUAKE/W 1-D | PGA QUAKE/W 2-D | PGA EERA | PGA QUAKE/W 1-D | PGA QUAKE/W 2-D | |
| [g] | [g] | [g] | [g] | [g] | [g] | [g] | [g] | [g] | |
| Point 1 | 0.208 | 0.193 | 0.311 | 0.228 | 0.207 | 0.336 | 0.195 | 0.269 | 0.403 |
| Point 2 | 0.208 | 0.193 | 0.400 | 0.228 | 0.207 | 0.370 | 0.195 | 0.269 | 0.493 |
| Point 3 | 0.176 | 0.147 | 0.083 | 0.168 | 0.141 | 0.064 | 0.165 | 0.151 | 0.140 |
| DISS Gioia Tauro | DISS Aspromonte Est | 1693 Catania Earthquake | |||||||
| PGA EERA | PGA QUAKE/W 1-D | PGA QUAKE/W 2-D | PGA EERA | PGA QUAKE/W 1-D | PGA QUAKE/W 2-D | PGA EERA | PGA QUAKE/W 1-D | PGA QUAKE/W 2-D | |
| [g] | [g] | [g] | [g] | [g] | [g] | [g] | [g] | [g] | |
| Point 1 | 0.257 | 0.203 | 0.369 | 0.206 | 0.266 | 0.493 | 0.179 | 0.142 | 0.121 |
| Point 2 | 0.257 | 0.203 | 0.373 | 0.206 | 0.266 | 0.536 | 0.179 | 0.142 | 0.140 |
| Point 3 | 0.202 | 0.157 | 0.197 | 0.181 | 0.167 | 0.156 | 0.154 | 0.117 | 0.054 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavallaro, A.; Ferraro, A.; Grasso, S.; Puccia, A. 2-D Seismic Response Analysis of a Slope in the Tyrrhenian Area (Italy). Appl. Sci. 2021, 11, 3180. https://doi.org/10.3390/app11073180
Cavallaro A, Ferraro A, Grasso S, Puccia A. 2-D Seismic Response Analysis of a Slope in the Tyrrhenian Area (Italy). Applied Sciences. 2021; 11(7):3180. https://doi.org/10.3390/app11073180
Chicago/Turabian StyleCavallaro, Antonio, Antonio Ferraro, Salvatore Grasso, and Antonio Puccia. 2021. "2-D Seismic Response Analysis of a Slope in the Tyrrhenian Area (Italy)" Applied Sciences 11, no. 7: 3180. https://doi.org/10.3390/app11073180
APA StyleCavallaro, A., Ferraro, A., Grasso, S., & Puccia, A. (2021). 2-D Seismic Response Analysis of a Slope in the Tyrrhenian Area (Italy). Applied Sciences, 11(7), 3180. https://doi.org/10.3390/app11073180








