Comparative Study of Aortic Wall Stress According to Geometric Parameters in Abdominal Aortic Aneurysms
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Experiment Details and Results
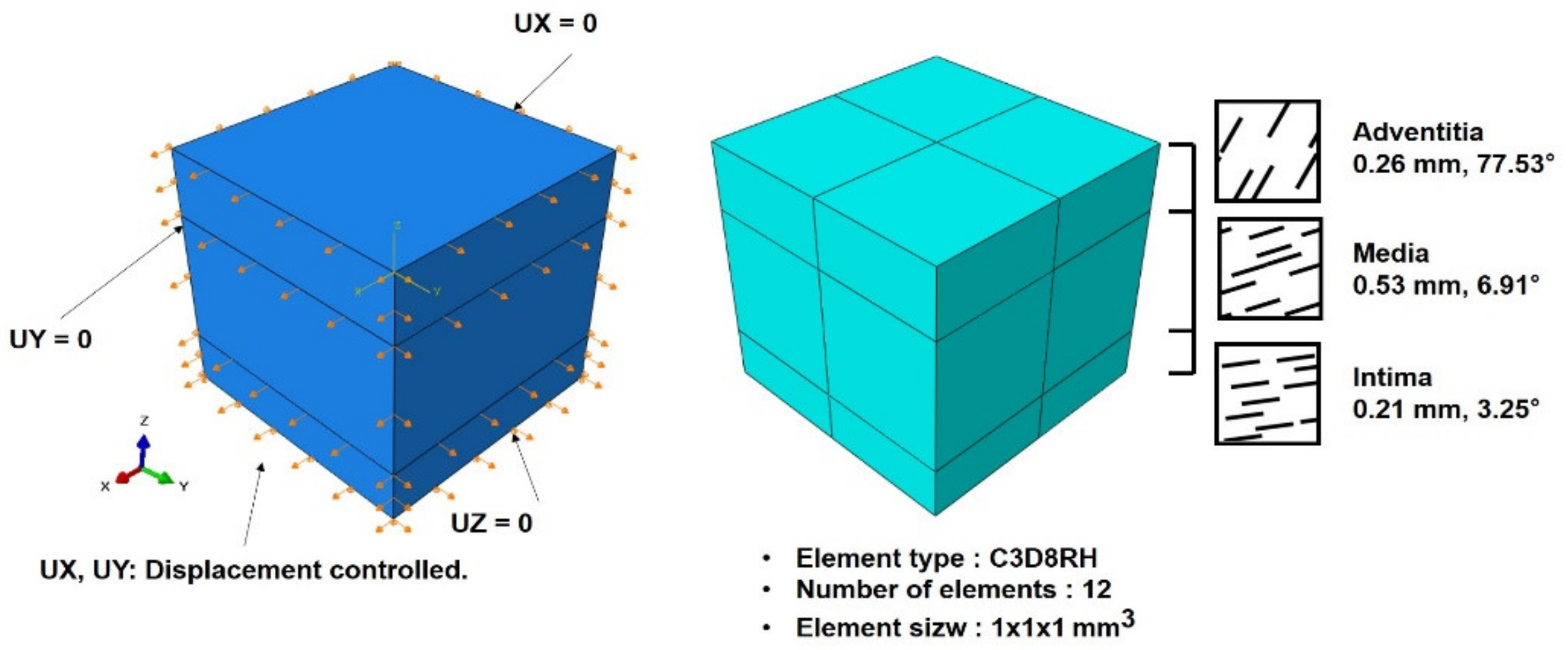
2.2. Numerical Model
2.3. Material Simulation Details
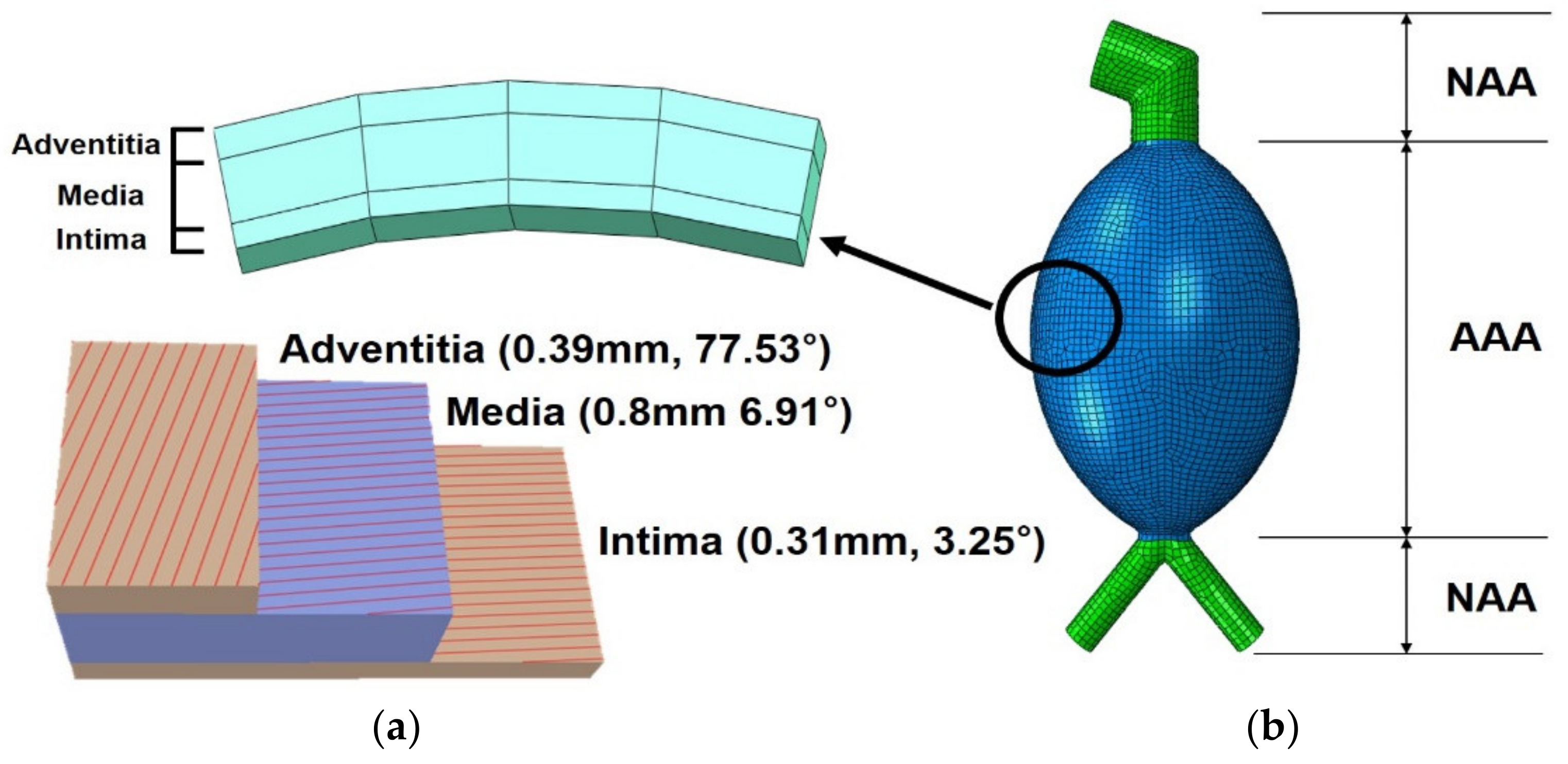
2.4. AAA Geometry Studies
2.5. Finite Element Model of AAA
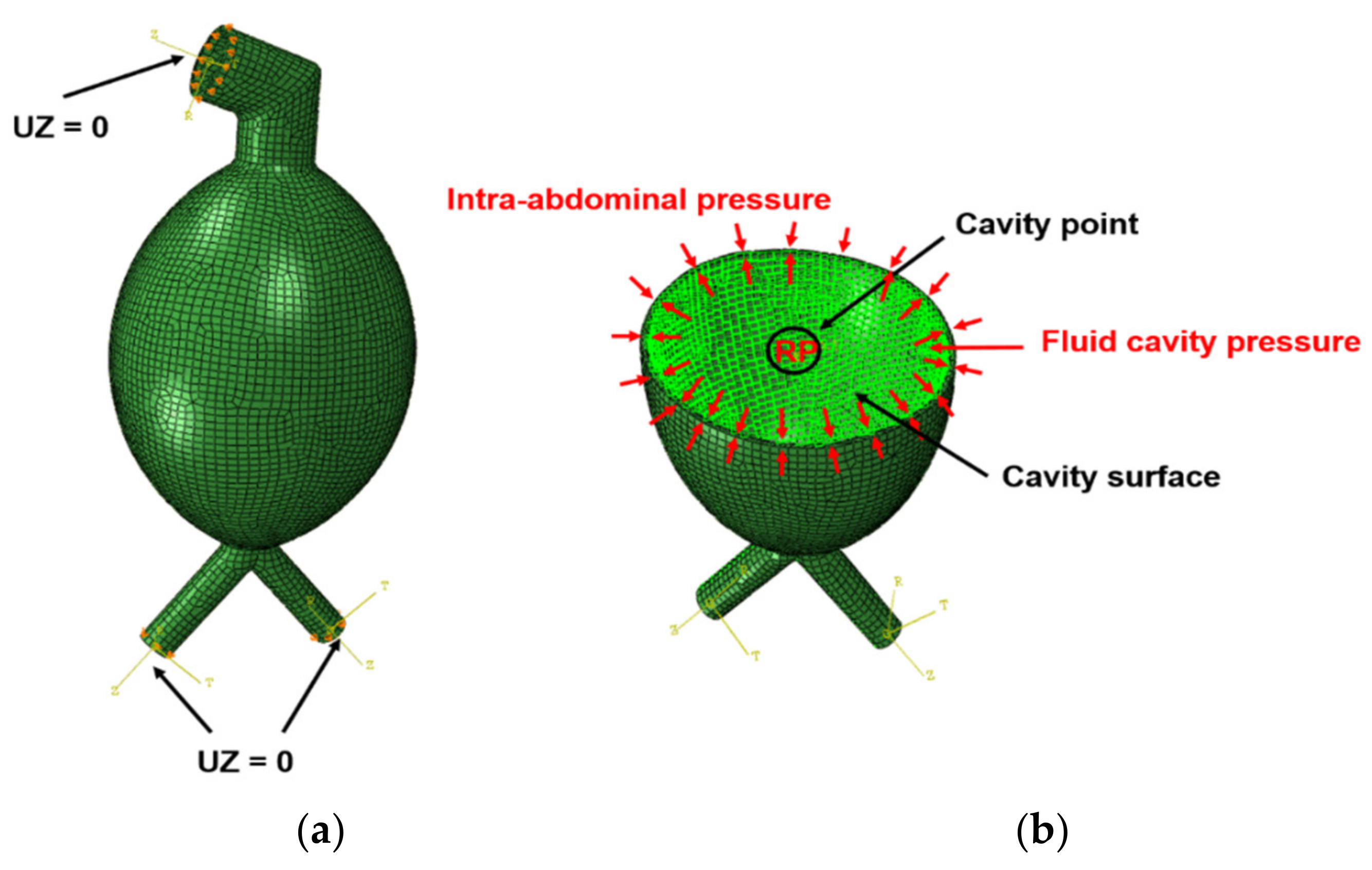
2.6. Loading and Boundary Condition of AAA Model
3. Results
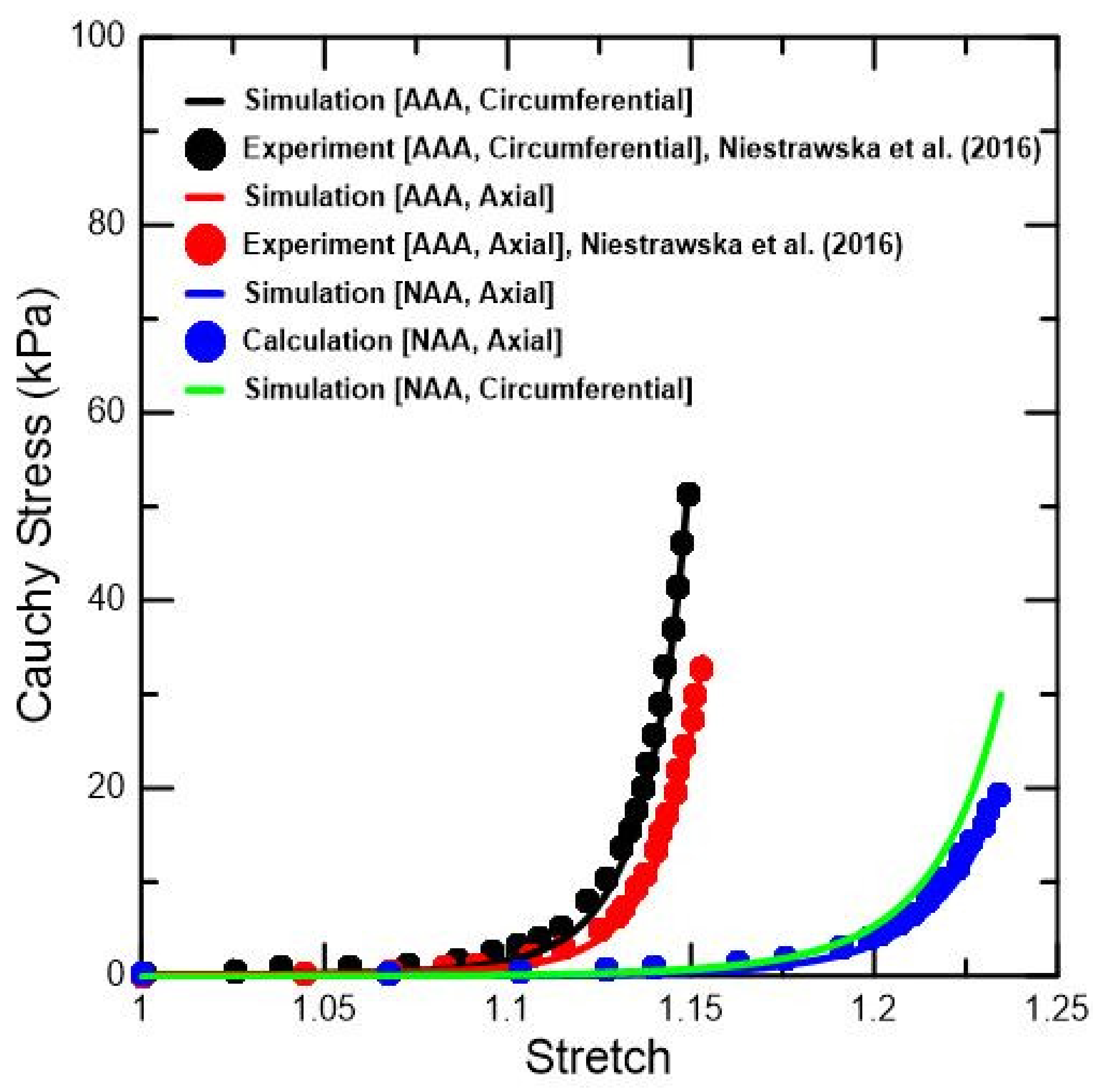
3.1. Material Contants of AAA
3.2. Measurements in Patients with AAA and Simulation Scenario Selection
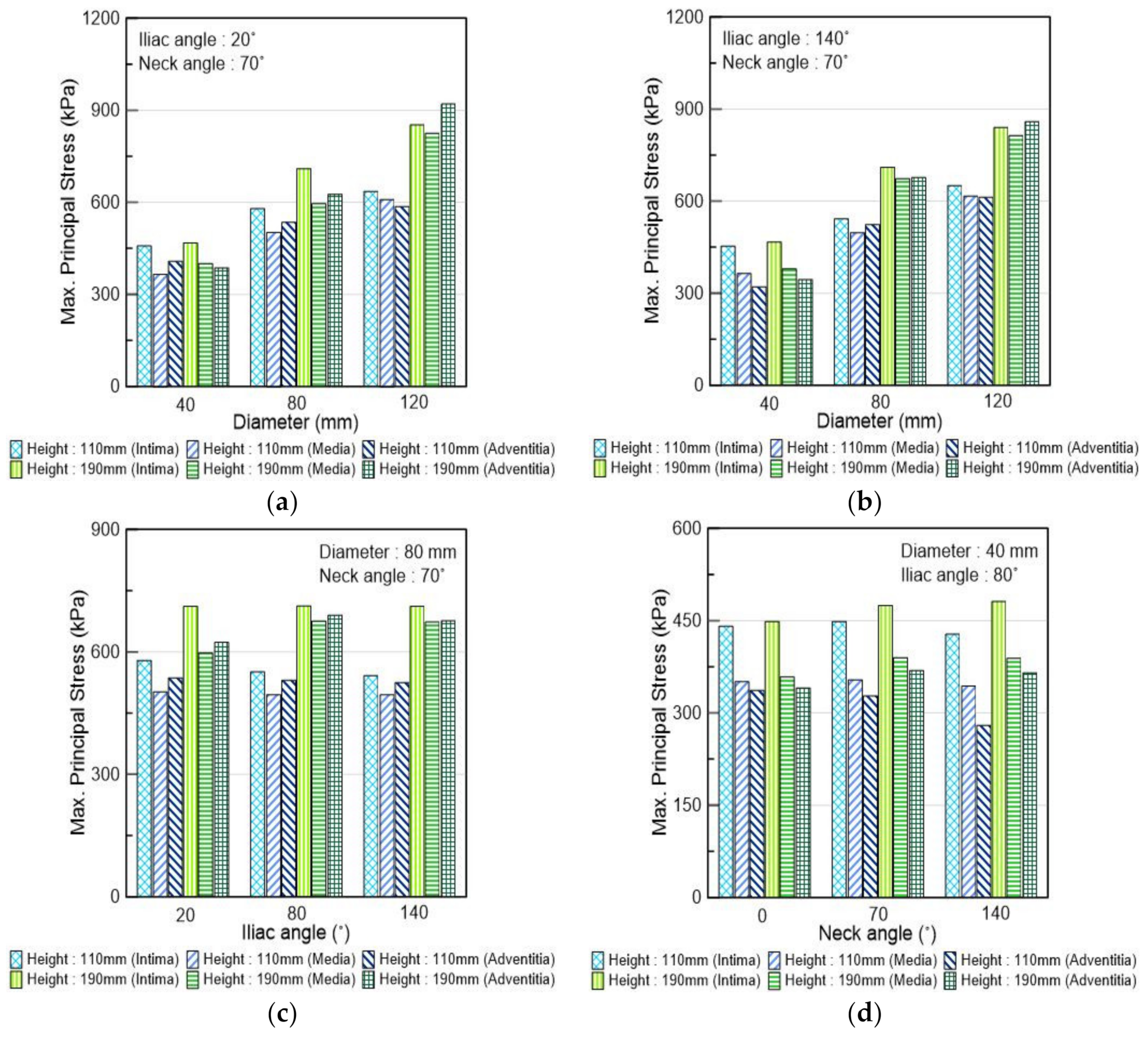
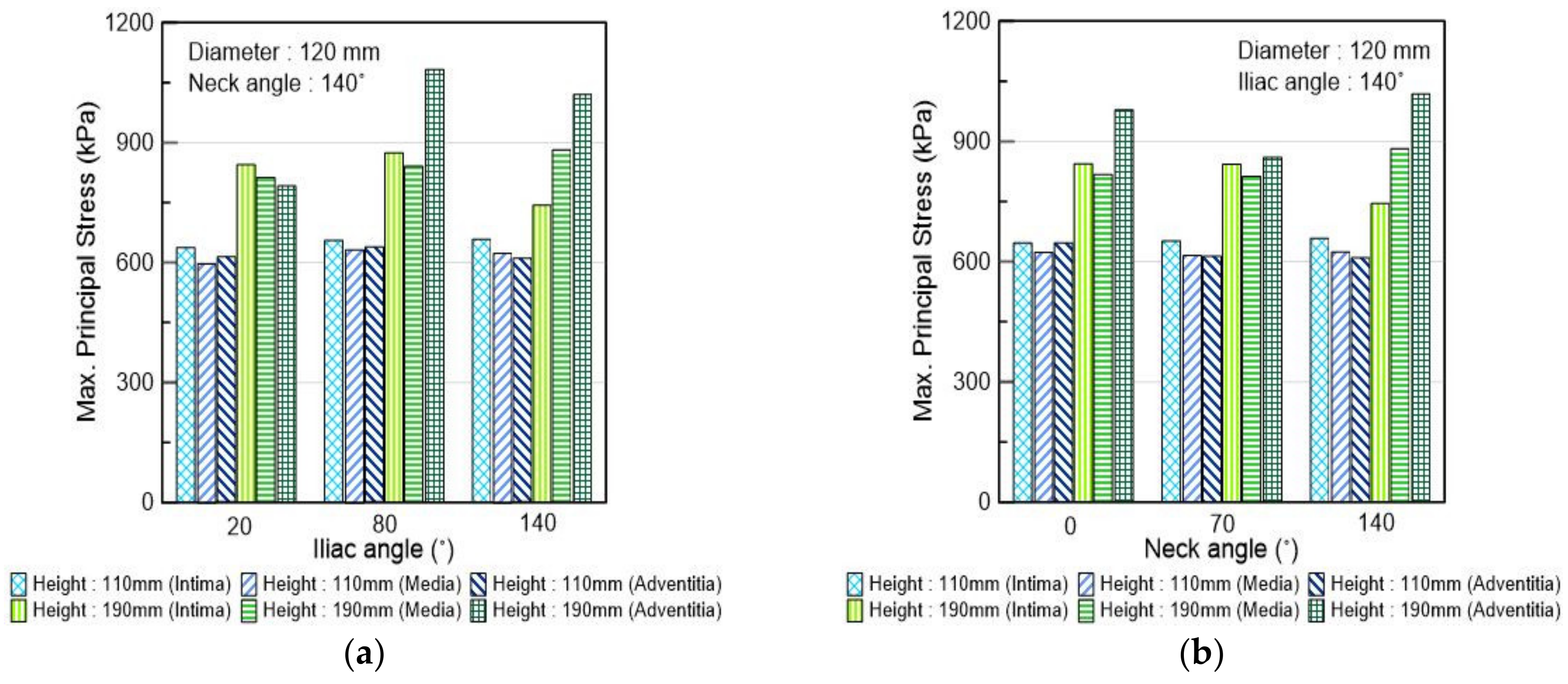
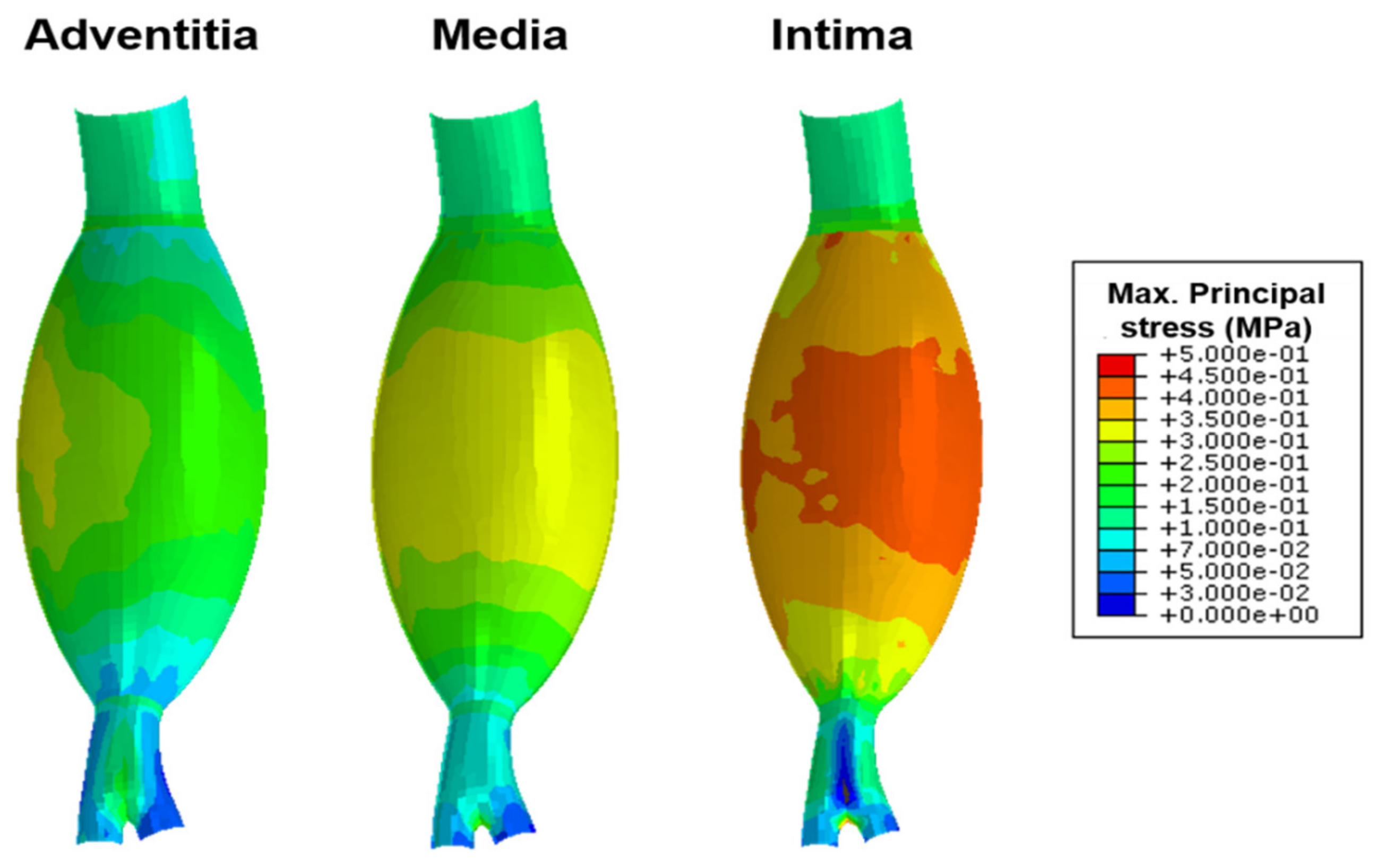
3.3. Scenario Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| DdHhNAnIAi | Adventitia (kPa) | Media (kPa) | Intima (kPa) |
|---|---|---|---|
| D40H110NA0IA20 | 357.856 | 357.064 | 444.306 |
| D40H110NA0IA80 | 336.68 | 350.636 | 440.584 |
| D40H110NA0IA140 | 344.756 | 359.684 | 441.998 |
| D40H190NA0IA20 | 366.868 | 376.335 | 464.93 |
| D40H190NA0IA80 | 341.025 | 358.598 | 449.266 |
| D40H190NA0IA140 | 370.371 | 381.259 | 398.85 |
| D40H110NA70IA20 | 408.545 | 366.859 | 458.022 |
| D40H110NA70IA80 | 327.661 | 353.739 | 448.409 |
| D40H110NA70IA140 | 321.392 | 362.292 | 453.608 |
| D40H190NA70IA20 | 384.403 | 401.012 | 468.754 |
| D40H190NA70IA80 | 369.512 | 389.926 | 475.351 |
| D40H190NA70IA140 | 344.925 | 377.789 | 467.515 |
| D40H110NA140IA20 | 428.71 | 420.968 | 484.413 |
| D40H110NA140IA80 | 279.652 | 343.531 | 427.682 |
| D40H110NA140IA140 | 358.445 | 365.581 | 451.361 |
| D40H190NA140IA20 | 442.726 | 400.205 | 509.011 |
| D40H190NA140IA80 | 365.698 | 388.783 | 481.649 |
| D40H190NA140IA140 | 393.411 | 398.98 | 491.017 |
| D80H110NA0IA20 | 525.382 | 502.761 | 531.946 |
| D80H110NA0IA80 | 595.655 | 505.547 | 549.219 |
| D80H110NA0IA140 | 514.826 | 501.778 | 548.356 |
| D80H190NA0IA20 | 721.917 | 683.943 | 730.629 |
| D80H190NA0IA80 | 685.424 | 672.681 | 721.127 |
| D80H190NA0IA140 | 714.781 | 679.127 | 718.698 |
| D80H110NA70IA20 | 535.609 | 503.137 | 579.57 |
| D80H110NA70IA80 | 529.957 | 495.819 | 551.566 |
| D80H110NA70IA140 | 524.229 | 495.498 | 542.27 |
| D80H190NA70IA20 | 624.29 | 596.221 | 710.945 |
| D80H190NA70IA80 | 690.938 | 674.51 | 712.007 |
| D80H190NA70IA140 | 677.435 | 671.997 | 711.378 |
| D80H110NA140IA20 | 634.462 | 504.617 | 560.634 |
| D80H110NA140IA80 | 550.968 | 496.806 | 577.645 |
| D80H110NA140IA140 | 575.293 | 495.328 | 541.099 |
| D80H190NA140IA20 | 725.316 | 675.627 | 730.46 |
| D80H190NA140IA80 | 712.872 | 671.491 | 716.558 |
| D80H190NA140IA140 | 737.953 | 706.509 | 748.335 |
| D120H110NA0IA20 | 634.736 | 605.533 | 637.874 |
| D120H110NA0IA80 | 635.262 | 624.018 | 659.785 |
| D120H110NA0IA140 | 646.979 | 623.436 | 645.982 |
| D120H190NA0IA20 | 886.176 | 821.801 | 842.241 |
| D120H190NA0IA80 | 765.492 | 790.705 | 815.276 |
| D120H190NA0IA140 | 979.02 | 817.703 | 843.217 |
| D120H110NA70IA20 | 587.573 | 610.675 | 635.772 |
| D120H110NA70IA80 | 599.654 | 633.134 | 644.765 |
| D120H110NA70IA140 | 613.574 | 615.103 | 651.245 |
| D120H190NA70IA20 | 918.297 | 826.263 | 853.297 |
| D120H190NA70IA80 | 929.279 | 854.259 | 871.757 |
| D120H190NA70IA140 | 859.846 | 812.894 | 841.455 |
| D120H110NA140IA20 | 613.079 | 598.188 | 636.752 |
| D120H110NA140IA80 | 638.058 | 633.682 | 654.637 |
| D120H110NA140IA140 | 609.531 | 624.385 | 657.826 |
| D120H190NA140IA20 | 790.219 | 812.858 | 845.014 |
| D120H190NA140IA80 | 1081.99 | 841.488 | 875.06 |
| D120H190NA140IA140 | 1019.02 | 882.521 | 743.775 |
References
- Fillinger, M.F.; Marra, S.P.; Raghavan, M.L.; Kennedy, F.E. Prediction of rupture risk in abdominal aortic aneurysm during observation: Wall stress versus diameter. J. Vasc. Surg. 2003, 37, 724–732. [Google Scholar] [CrossRef] [PubMed]
- Fillinger, M.F.; Raghavan, M.L.; Marra, S.P.; Cronenwett, J.L.; Kennedy, F.E. In vivo analysis of mechanical wall stress and abdominal aortic aneurysm rupture risk. J. Vasc. Surg. 2002, 36, 589–597. [Google Scholar] [CrossRef] [PubMed]
- Doyle, B.J.; Callanan, A.; Burke, P.E.; Grace, P.A.; Walsh, M.T.; Vorp, D.A.; McGloughlin, T.M. Vessel asymmetry as an additional diagnostic tool in the assessment of abdominal aortic aneurysms. J. Vasc. Surg. 2009, 49, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Giannoglou, G.; Giannakoulas, G.; Soulis, J.; Chatzizisis, Y.; Perdikides, T.; Melas, N.; Parcharidis, G.; Louridas, G. Predicting the risk of rupture of abdominal aortic aneurysms by utilizing various geometrical parameters: Revisiting the diameter criterion. Angiology 2006, 57, 487–494. [Google Scholar] [CrossRef] [PubMed]
- Geest, J.P.V.; di Martino, E.S.; Bohra, A.; Makaroun, M.S.; Vorp, D.A. A biomechanics-based rupture potential index for abdominal aortic aneurysm risk assessment: Demonstrative application. Ann. N. Y. Acad. Sci. 2006, 1085, 11–21. [Google Scholar] [CrossRef]
- Doyle, B.J.; Callanan, A.; Walsh, M.T.; Grace, P.A.; McGloughlin, T.M. A finite element analysis rupture index (FEARI) as an additional tool for abdominal aortic aneurysm rupture prediction. Vasc. Dis. Prev. 2009, 6, 114–121. [Google Scholar] [CrossRef][Green Version]
- Conlisk, N.; Geers, A.J.; McBride, O.M.; Newby, D.E.; Hoskins, P.R. Patient-specific modelling of abdominal aortic aneurysms: The influence of wall thickness on predicted clinical outcomes. Med. Eng. Phys. 2016, 38, 526–537. [Google Scholar] [CrossRef]
- Raut, S.S.; Jana, A.; de Oliveira, V.; Muluk, S.C.; Finol, E.A. The importance of patient-specific regionally varying wall thickness in abdominal aortic aneurysm biomechanics. J. Biomech. Eng. 2013, 135, 81010. [Google Scholar] [CrossRef]
- Shang, E.K.; Nathan, D.P.; Woo, E.Y.; Fairman, R.M.; Wang, G.J.; Gorman, R.C.; Gorman, J.H., III; Jackson, B.M. Local wall thickness in finite element models improves prediction of abdominal aortic aneurysm growth. J. Vasc. Surg. 2015, 61, 217–223. [Google Scholar] [CrossRef]
- Mower, W.R.; Quiñones, W.J.; Gambhir, S.S. Effect of intraluminal thrombus on abdominal aortic aneurysm wall stress. J. Vasc. Surg. 1997, 26, 602–608. [Google Scholar] [CrossRef]
- Wang, D.H.; Makaroun, M.S.; Webster, M.W.; Vorp, D.A. Effect of intraluminal thrombus on wall stress in patient-specific models of abdominal aortic aneurysm. J. Vasc. Surg. 2002, 36, 598–604. [Google Scholar] [CrossRef] [PubMed]
- Georgakarakos, E.; Ioannou, C.; Kamarianakis, Y.; Papaharilaou, Y.; Kostas, T.; Manousaki, E.; Katsamouris, A. The role of geometric parameters in the prediction of abdominal aortic aneurysm wall stress. Eur. J. Vasc. Endovasc. Surg. 2010, 39, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Polzer, S.; Gasser, T.C.; Swedenborg, J.; Bursa, J. The impact of intraluminal thrombus failure on the mechanical stress in the wall of abdominal aortic aneurysms. Eur. J. Vasc. Endovasc. Surg. 2011, 41, 467–473. [Google Scholar] [CrossRef] [PubMed]
- Haller, S.J.; Crawford, J.D.; Courchaine, K.M.; Bohannan, C.J.; Landry, G.J.; Moneta, G.L.; Azarbal, A.F.; Rugonyi, S. Intraluminal thrombus is associated with early rupture of abdominal aortic aneurysm. J. Vasc. Surg. 2018, 67, e1051–e1058. [Google Scholar] [CrossRef] [PubMed]
- Speelman, L.; Bohra, A.; Bosboom, E.M.H.; Schurink, G.W.H.; van de Vosse, F.N.; Makaroun, M.S.; Vorp, D.A. Effects of wall calcifications in patient-specific wall stress analyses of abdominal aortic aneurysms. J. Biomech. Eng. 2007, 129, 105–109. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-Y.; Jean, U.; Tang, T.Y.; Soh, E.; See, T.C.; Gillard, J.H. Impact of calcification and intraluminal thrombus on the computed wall stresses of abdominal aortic aneurysm. J. Vasc. Surg. 2008, 47, 928–935. [Google Scholar] [CrossRef]
- Vorp, D.A.; Raghavan, M.; Webster, M.W. Mechanical wall stress in abdominal aortic aneurysm: Influence of diameter and asymmetry. J. Vasc. Surg. 1998, 27, 632–639. [Google Scholar] [CrossRef]
- Shum, J.; Martufi, G.; di Martino, E.; Washington, C.B.; Grisafi, J.; Muluk, S.C.; Finol, E.A. Quantitative assessment of abdominal aortic aneurysm geometry. Ann. Biomed. Eng. 2011, 39, 277–286. [Google Scholar] [CrossRef]
- Urrutia, J.; Roy, A.; Raut, S.S.; Antón, R.; Muluk, S.C.; Finol, E.A. Geometric surrogates of abdominal aortic aneurysm wall mechanics. Med. Eng. Phys. 2018, 59, 43–49. [Google Scholar] [CrossRef]
- Azar, D.; Ohadi, D.; Rachev, A.; Eberth, J.F.; Uline, M.J.; Shazly, T. Mechanical and geometrical determinants of wall stress in abdominal aortic aneurysms: A computational study. PLoS ONE 2018, 13, e0192032. [Google Scholar] [CrossRef]
- Geest, J.P.V.; Sacks, M.S.; Vorp, D.A. The effects of aneurysm on the biaxial mechanical behavior of human abdominal aorta. J. Biomech. 2006, 39, 1324–1334. [Google Scholar] [CrossRef]
- Niestrawska, J.A.; Viertler, C.; Regitnig, P.; Cohnert, T.U.; Sommer, G.; Holzapfel, G.A. Microstructure and mechanics of healthy and aneurysmatic abdominal aortas: Experimental analysis and modelling. J. R. Soc. Interface 2016, 13, 20160620. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. Phys. Sci. Solids 2000, 61, 1–48. [Google Scholar]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef]
- Raghavan, M.L.; Hanaoka, M.M.; Kratzberg, J.A.; de Lourdes Higuchi, M.; Da Silva, E.S. Biomechanical failure properties and microstructural content of ruptured and unruptured abdominal aortic aneurysms. J. Biomech. 2011, 44, 2501–2507. [Google Scholar] [CrossRef] [PubMed]
- Brutin, D.; Sobac, B.; Loquet, B.; Sampol, J. Pattern formation in drying drops of blood. J. Fluid Mech. 2011, 667, 85–95. [Google Scholar] [CrossRef]
- Habibi, R.; Devendran, C.; Neild, A. Trapping and patterning of large particles and cells in a 1D ultrasonic standing wave. Lab Chip 2017, 17, 3279–3290. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, S.M.; Zhou, W.; Wu, J.G. Measurement and analysis of ultimate mechanical properties, stress-strain curve fit, and elastic modulus formula of human abdominal aortic aneurysm and nonaneurysmal abdominal aorta. J. Vasc. Surg. 2008, 48, 189–195. [Google Scholar] [CrossRef]
- De Lucio, M.; García, M.F.; García, J.D.; Rodríguez, L.E.R.; Marcos, F.Á. On the importance of tunica intima in the aging aorta: A three-layered in silico model for computing wall stresses in abdominal aortic aneurysms. Comput. Methods Biomech. Biomed. Eng. 2020, 1–18. [Google Scholar] [CrossRef]


| C10 (MPa) | K1 (MPa) | K2 | κ | |
|---|---|---|---|---|
| AAA | 0.03 | 150 | 250 | 0.261 |
| NAA | 0.1 | 20 | 61 | 0.226 |
| Diameter (mm) | Neck Angle (°) | Height (mm) | Iliac Angle (°) | |
|---|---|---|---|---|
| Minimum | 41.1 | 7.8 | 36 | 11.7 |
| Maximum | 118.1 | 136.9 | 188 | 143.5 |
| Average | 63.4 ± 14.2 | 49.3 ± 22.5 | 93.4 ± 28.6 | 68.34 ± 22.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, J.-H.; Lee, C.W.; Huh, U.; Lee, C.-S.; Ryu, D. Comparative Study of Aortic Wall Stress According to Geometric Parameters in Abdominal Aortic Aneurysms. Appl. Sci. 2021, 11, 3195. https://doi.org/10.3390/app11073195
You J-H, Lee CW, Huh U, Lee C-S, Ryu D. Comparative Study of Aortic Wall Stress According to Geometric Parameters in Abdominal Aortic Aneurysms. Applied Sciences. 2021; 11(7):3195. https://doi.org/10.3390/app11073195
Chicago/Turabian StyleYou, Ji-Hun, Chung Won Lee, Up Huh, Chi-Seung Lee, and Dongman Ryu. 2021. "Comparative Study of Aortic Wall Stress According to Geometric Parameters in Abdominal Aortic Aneurysms" Applied Sciences 11, no. 7: 3195. https://doi.org/10.3390/app11073195
APA StyleYou, J.-H., Lee, C. W., Huh, U., Lee, C.-S., & Ryu, D. (2021). Comparative Study of Aortic Wall Stress According to Geometric Parameters in Abdominal Aortic Aneurysms. Applied Sciences, 11(7), 3195. https://doi.org/10.3390/app11073195







