3D Snow Sculpture Reconstruction Based on Structured-Light 3D Vision Measurement
Abstract
:1. Introduction
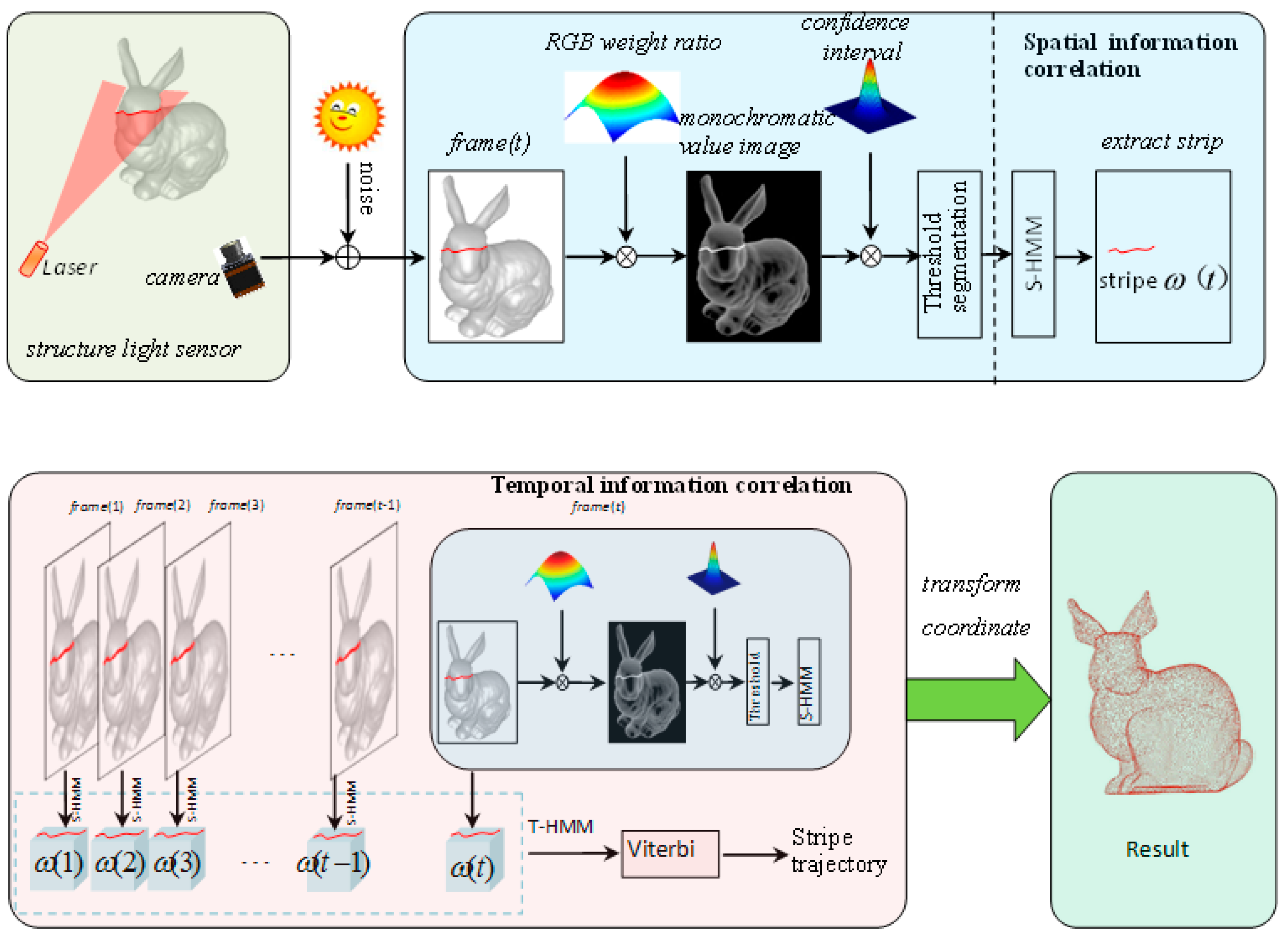
2. Methods
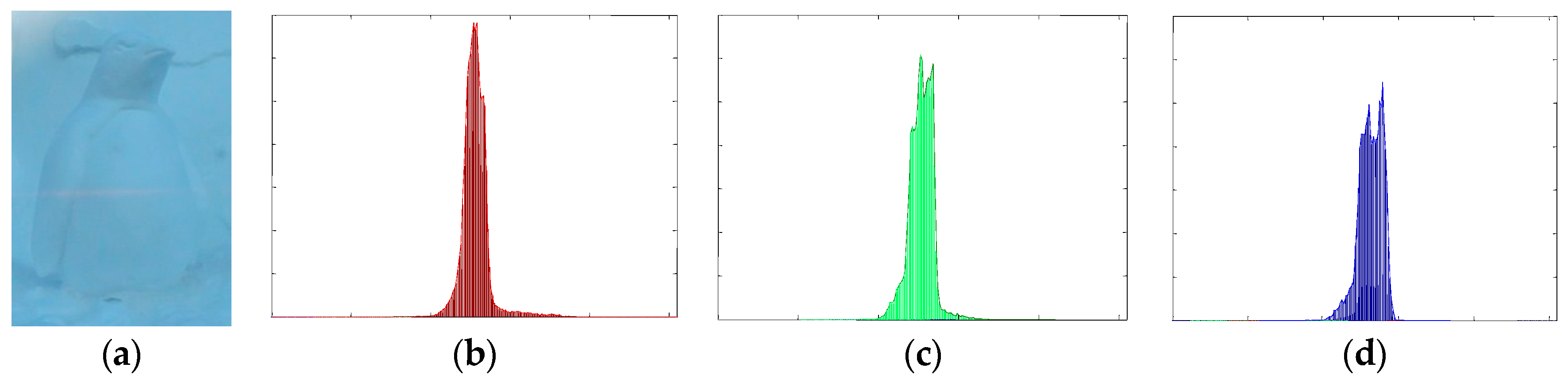
2.1. Noise Classification
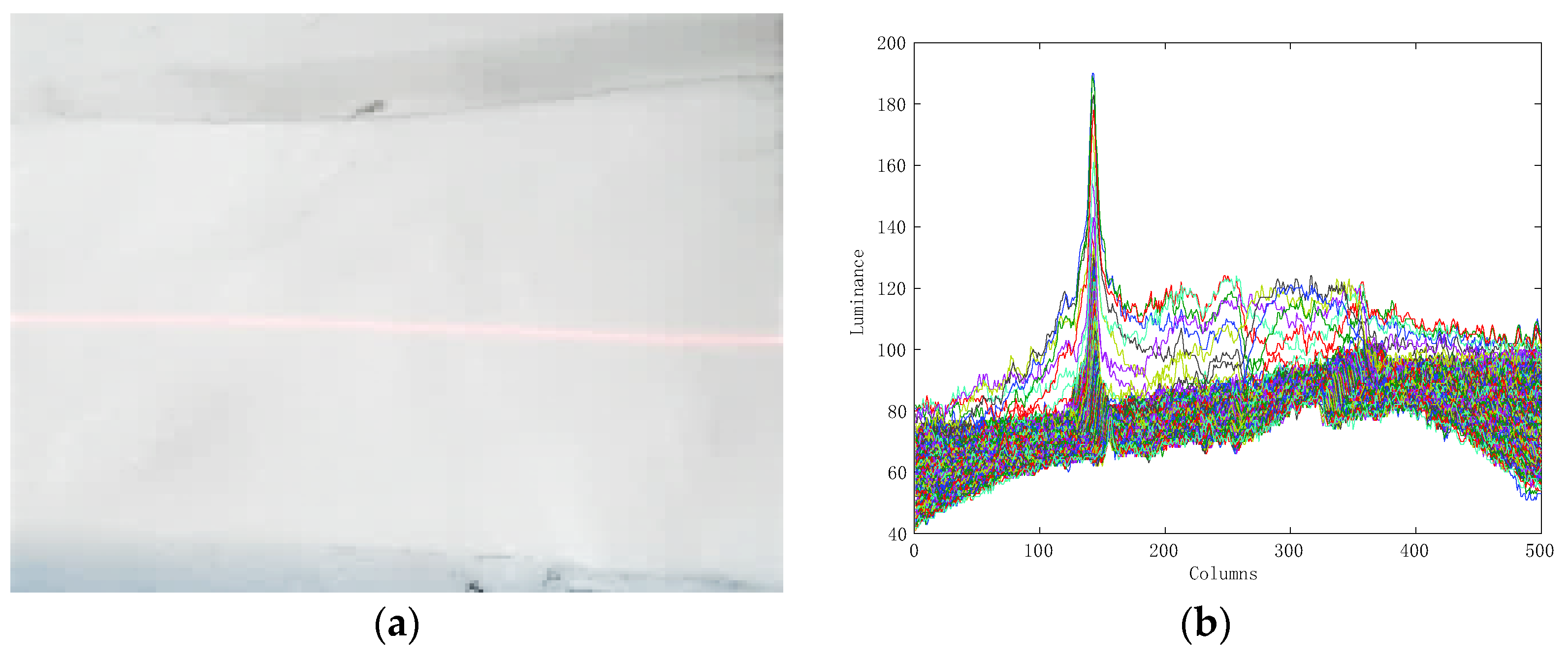
2.2. Monochromatic Value Space Transformation
2.3. Stripe Extraction and Tracking
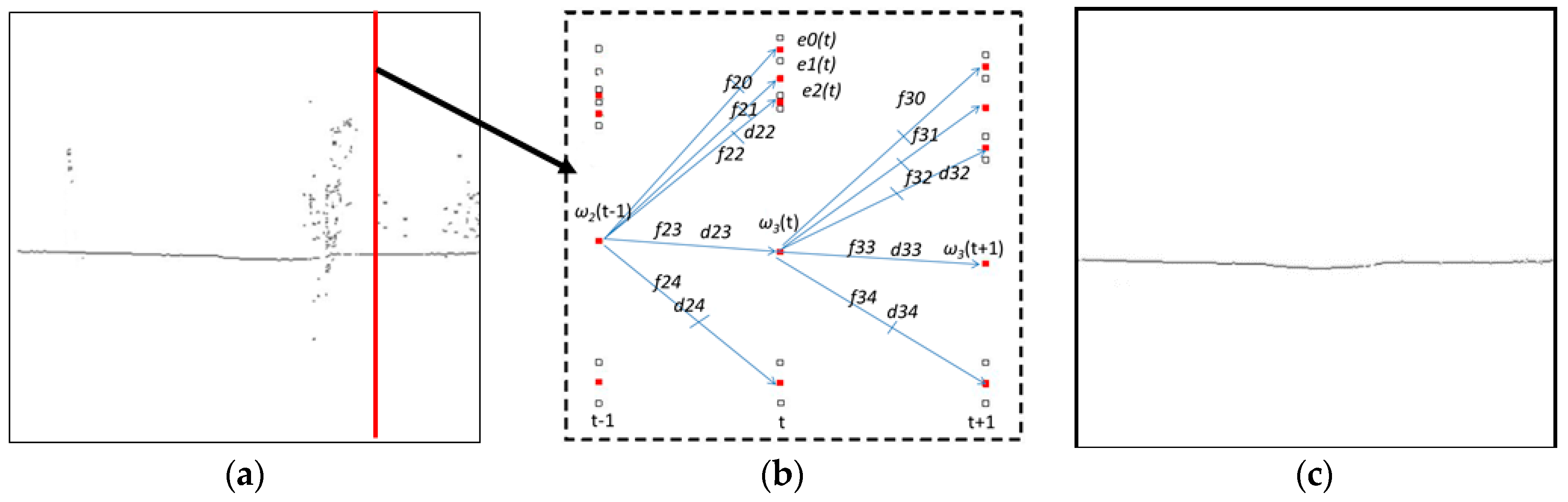
2.3.1. Establishment of aSpatial Decision Tree Model(S-DTM)
2.3.2. Establishment of aTemporal Decision Tree Model (T-DTM)
3. Results
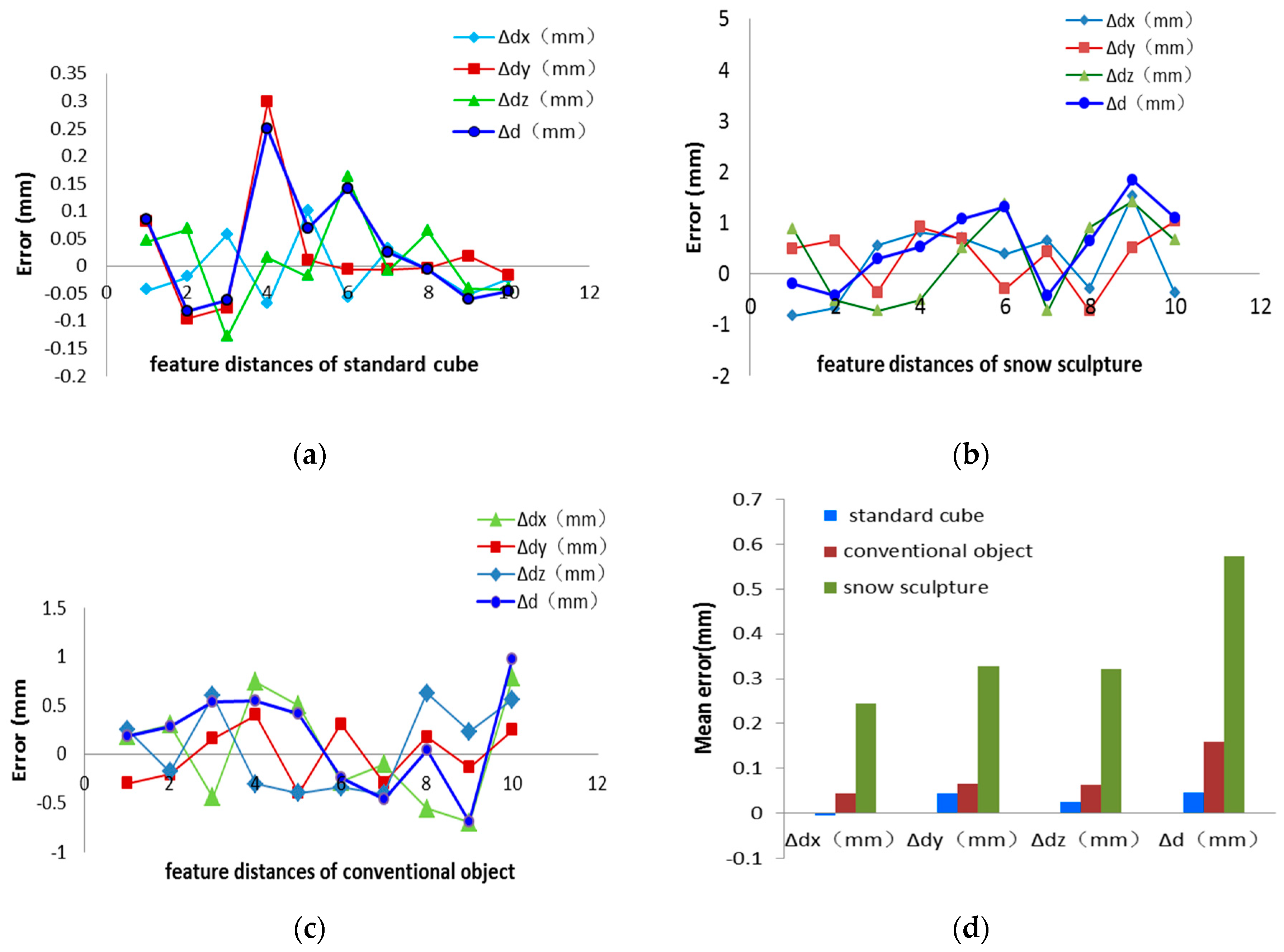
3.1. Accuracy Test
3.1.1. Standard Cube Measurement
3.1.2. Snow Sculpture Measurement
3.1.3. Conventional Object Measurement
3.2. Speed and Robustness Evaluation
4. Discussion
4.1. Light Environment and Optical Characteristics of the Measured Object Surfaces Affect the Measurement Accuracy
4.2. Large Local Error Is Related to Complex Texture and the Length of the Feature Distance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dewar, K.; Meyer, D.; Li, W.M. Lanterns of ice, sculptures of snow. Tour. Manag. 2001, 22, 523–532. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, L. Analysis of and Research into Foreign Factors That Drive China’s Ice-Snow Tourism. In Communications in Computer and Information Science, Proceedings of the Advances in Applied Economics, Business and Development, Dalian, China, 6–7 August 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 422–427. [Google Scholar]
- Li, Y.; Chen, Z.Y.; Wang, C.M. Research on the innovation and development of Harbin ice and snow tourism industry under the background of Beijing winter Olympic Games. China Winter Sports 2018, 2, 15. [Google Scholar]
- Di, H.N. On the digital technology in the protection of ancient buildings. Cult. Relics Apprais. Apprec. 2018, 3, 130–132. [Google Scholar]
- Koeva, M.; Luleva, M.; Maldjanski, P. Integrating Spherical Panoramas and Maps for Visualization of Cultural Heritage Objects Using Virtual Reality Technology. Sensors 2017, 17, 829. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuznetsova, I.; Kuznetsova, D.; Rakova, X. The use of surface laser scanning for creationof a three-dimensional digital model of monument. Procedia Eng. 2015, 100, 1625–1633. [Google Scholar] [CrossRef] [Green Version]
- Han, L.F.; Hou, Y.D.; Wang, Y.J.; Liu, X.B.; Han, J.; Xie, R.H.; Mu, H.W.; Fu, C.F. Measurement of velocity of sand-containing Oil-Water two-phase flow with super high water hold up in horizontal small pipe based on thermal tracers. Flow Meas. Instrum. 2019, 69, 101622. [Google Scholar] [CrossRef]
- Gupta, M.; Yin, Q.; Nayar, S.K.; Iso, D. Structured Light in Sunlight. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 3 March 2014; pp. 545–552. [Google Scholar]
- Gelabert, P. Comparison of fixed-pattern and multiple-pattern structured light imaging systems. Proc. Spie Int. Soc. Opt. Eng. 2014, 8979, 342–348. [Google Scholar]
- Kinect Outdoors. Available online: www.youtube.com/watch?v=rI6CU9aRDIo (accessed on 2 December 2015).
- O’Toole, M.; Mather, J.; Kutulakos, K.N. 3D Shape and Indirect Appearance by Structured Light Transport. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Steger, C. An unbiased detector of curvilinear structures. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 113–125. [Google Scholar] [CrossRef] [Green Version]
- Usamentiaga, R.; Molleda, J.; García, D.F. Fast and robust laser stripe extraction for 3D reconstruction in industrial environments. Mach. Vis. Appl. 2012, 23, 179–196. [Google Scholar] [CrossRef]
- Haverinen, J.; Röning, J. An Obstacle Detection System Using a Light Stripe Identification Based Method. In Proceedings of the IEEE International Joint Symposia on Intelligence and Systems, Rockville, MD, USA, 23 May 1998; pp. 232–236. [Google Scholar]
- Zhang, L.G.; Sun, J.; Yin, G. Across Structured Light Sensor and Stripe Segmentation Method for Visual Tracking of a WallClimbing Robot. Sensors 2015, 15, 13725–13751. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wiggins, R.A. Minimum entropy deconvolution. Geoexplorafion 1978, 16, 21–35. [Google Scholar] [CrossRef]
- Mcdonald, G.L.; Zhao, Q.; Zuo, M.J. Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection. Mech. Syst. Signal Process. 2012, 33, 237–255. [Google Scholar] [CrossRef]
- Mathis, H.; Douglas, S.C. Bussgang blind deconvolution for impulsive signals. IEEE Trans. Signal Process. 2003, 51, 1905–1915. [Google Scholar] [CrossRef]
- Collins, R.T.; Liu, Y.; Leordeanu, M. On-line selection of discriminative tracking features. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1631–1643. [Google Scholar] [CrossRef] [PubMed]
- Kai, Q.; Xiuhong, C.; Baiwei, S. Robust fast tracking via spatio-temporal context learning. Comput. Eng. Appl. 2016, 52, 163–167. [Google Scholar]
- Yuehua, L.; Jingbo, Z.; Fengshan, H.; Lijian, L. Sub-pixel extraction of laser stripe center using an improved gray-gravity method. Sensors 2017, 17, 814. [Google Scholar]
- Sun, J.H.; Wang, H.; Liu, Z.; Zhang, G.J. Fast extraction of laser strip center in dynamic measurement of rail abrasion. Opt. Precis. Eng. 2011, 19, 690–695. [Google Scholar]
- Li, Y.; Li, Y.F.; Wang, Q.L.; Xu, D.; Tan, M. Measurement and defect detection of the weld bead based on online vision inspection. IEEE Trans. Instrum. Meas. 2010, 59, 1841–1849. [Google Scholar]
- Zhang, L.; Ke, W.; Ye, Q.; Jiao, J. Anovel laser vision sensor for weld line detection on wall-climbing robot. Opt. Laser Technol. 2014, 60, 69–79. [Google Scholar] [CrossRef]
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multiview Stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef] [PubMed]






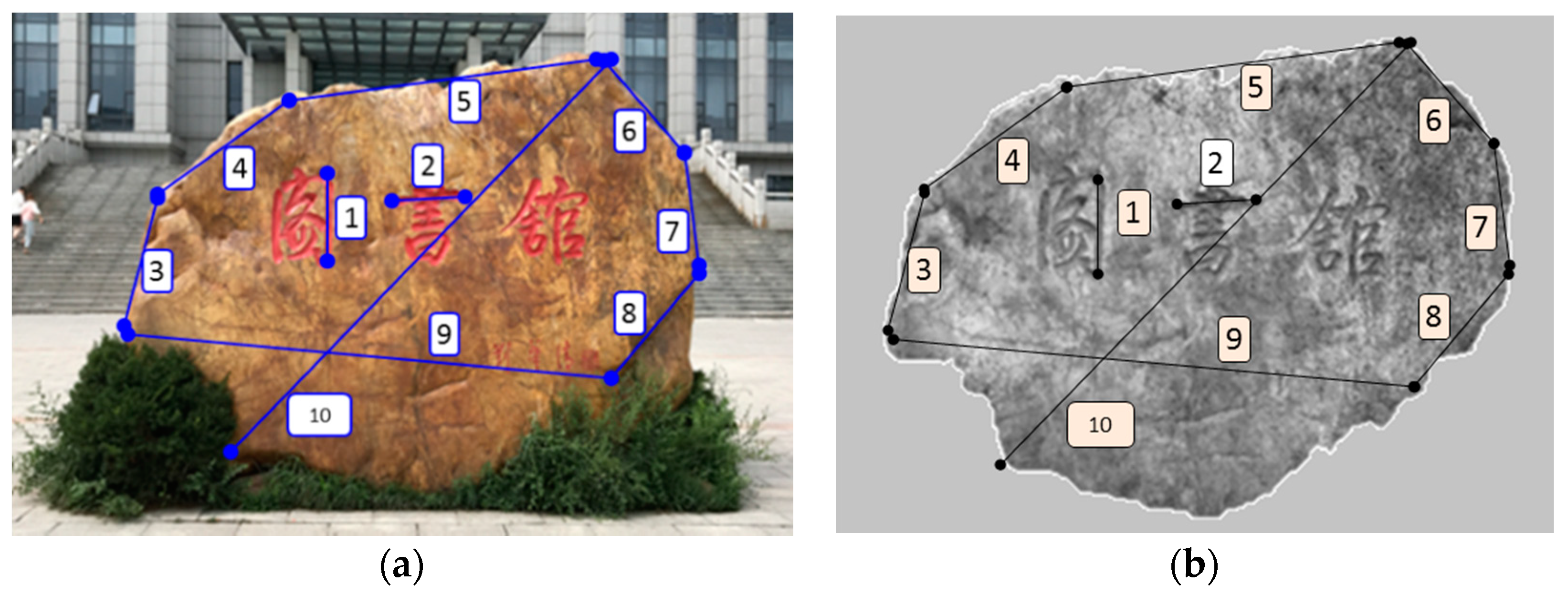


| Standard Value | Measurement Value | Error | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dx (mm) | dy (mm) | dz (mm) | d (mm) | d′x (mm) | d′y (mm) | d′z (mm) | d′ (mm) | Δdx (mm) | Δdy (mm) | Δdz (mm) | Δd (mm) | |
| 1 | 0.057 | 52.398 | 62.419 | 81.497 | 0.013 | 52.479 | 62.464 | 81.583 | −0.044 | 0.081 | 0.045 | 0.086 |
| 2 | 66.200 | 66.276 | 0.264 | 93.675 | 66.180 | 66.180 | 0.331 | 93.593 | −0.020 | −0.096 | 0.067 | −0.082 |
| 3 | 51.145 | 1.956 | 58.665 | 77.854 | 51.202 | 1.880 | 58.536 | 77.792 | 0.057 | −0.076 | −0.129 | −0.062 |
| 4 | 0.273 | 118.477 | 85.960 | 146.376 | 0.204 | 118.576 | 85.975 | 146.627 | −0.069 | 0.299 | 0.015 | 0.251 |
| 5 | 119.601 | 2.100 | 87.924 | 148.457 | 119.700 | 2.111 | 87.905 | 148.526 | 0.099 | 0.011 | −0.019 | 0.069 |
| 6 | 0.289 | 57.164 | 119.454 | 132.428 | 0.231 | 57.158 | 119.615 | 132.570 | −0.058 | −0.006 | 0.161 | 0.142 |
| 7 | 116.334 | 60.623 | 0.097 | 131.182 | 116.365 | 60.617 | 0.088 | 131.207 | 0.031 | −0.006 | −0.009 | 0.025 |
| 8 | 44.990 | 118.157 | 0.348 | 126.433 | 44.984 | 118.154 | 0.411 | 126.428 | −0.006 | −0.003 | 0.063 | −0.005 |
| 9 | 62.877 | 2.721 | 120.578 | 136.015 | 62.825 | 2.740 | 120.537 | 135.955 | −0.052 | 0.019 | −0.041 | −0.060 |
| 10 | 0.200 | 69.578 | 123.365 | 141.634 | 0.177 | 69.562 | 123.323 | 141.589 | −0.023 | −0.016 | −0.042 | −0.045 |
| 11 | 122.311 | 7.598 | 0.544 | 122.548 | 122.284 | 7.550 | 0.503 | 122.518 | −0.027 | −0.048 | −0.041 | −0.030 |
| 12 | 0.005 | 117.543 | 0.199 | 117.543 | 0.030 | 117.528 | 0.135 | 117.528 | 0.025 | −0.015 | −0.064 | −0.015 |
| 13 | 0.025 | 1.913 | 116.542 | 116.558 | 0.040 | 2.322 | 116.855 | 116.878 | 0.015 | 0.409 | 0.313 | 0.320 |
| Mean error (mm) | −0.006 | 0.043 | 0.025 | 0.046 | ||||||||
| RMS errors (mm) | 0.049 | 0.147 | 0.113 | 0.125 | ||||||||
| Standard Value | Measurement Value | Error | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dx (mm) | dy (mm) | dz (mm) | d (mm) | d′x (mm) | d′y (mm) | d′z (mm) | d′ (mm) | Δdx (mm) | Δdy (mm) | Δdz (mm) | Δd (mm) | |
| 1 | 394.526 | 285.011 | 105.542 | 498.017 | 393.696 | 285.502 | 106.424 | 497.829 | −0.830 | 0.491 | 0.882 | −0.188 |
| 2 | 402.012 | 153.214 | 22.123 | 430.787 | 401.328 | 153.858 | 21.599 | 430.352 | −0.684 | 0.644 | −0.524 | −0.435 |
| 3 | 408.995 | 179.562 | 34.856 | 448.034 | 409.543 | 179.190 | 34.130 | 448.330 | 0.548 | −0.372 | −0.726 | 0.296 |
| 4 | 333.785 | 389.215 | 486.671 | 706.930 | 334.598 | 390.123 | 486.156 | 707.460 | 0.813 | 0.908 | −0.515 | 0.530 |
| 5 | 494.594 | 390.996 | 190.462 | 658.617 | 495.294 | 391.669 | 190.962 | 659.687 | 0.700 | 0.673 | 0.500 | 1.070 |
| 6 | 265.123 | 314.014 | 1405.102 | 1463.969 | 265.510 | 313.717 | 1406.461 | 1465.280 | 0.387 | −0.297 | 1.359 | 1.311 |
| 7 | 164.920 | 97.126 | 534.857 | 568.070 | 165.572 | 97.549 | 534.124 | 567.643 | 0.652 | 0.423 | −0.733 | −0.427 |
| 8 | 158.152 | 299.102 | 1135.216 | 1184.563 | 157.859 | 298.376 | 1136.121 | 1185.208 | −0.293 | −0.726 | 0.905 | 0.645 |
| 9 | 852.156 | 256.983 | 2668.247 | 2812.784 | 853.678 | 257.492 | 2669.656 | 2814.628 | 1.522 | 0.509 | 1.409 | 1.844 |
| 10 | 225.562 | 1899.215 | 389.529 | 1951.827 | 225.187 | 1900.248 | 390.191 | 1952.921 | −0.375 | 1.033 | 0.662 | 1.094 |
| Mean error (mm) | 0.244 | 0.329 | 0.322 | 0.574 | ||||||||
| RMS errors (mm) | 0.755 | 0.588 | 0.862 | 0.722 | ||||||||
| Standard Value | Measurement Value | Error | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dx (mm) | dy (mm) | dz (mm) | d (mm) | d′x (mm) | d′y (mm) | d′z (mm) | d′ (mm) | Δdx (mm) | Δdy (mm) | Δdz (mm) | Δd (mm) | |
| 1 | 2.026 | 17.512 | 431.588 | 431.948 | 2.215 | 16.812 | 431.788 | 432.137 | 0.189 | 0.402 | 0.254 | 0.189 |
| 2 | 411.314 | 25.527 | 22.123 | 412.699 | 411.616 | 25.321 | 21.945 | 412.978 | 0.302 | −0.206 | −0.178 | 0.302 |
| 3 | 112.564 | 81.495 | 710.525 | 723.987 | 112.122 | 81.652 | 711.121 | 724.522 | −0.442 | 0.157 | 0.596 | −0.442 |
| 4 | 919.468 | 138.619 | 511.203 | 1061.115 | 920.210 | 139.021 | 510.899 | 1061.664 | 0.742 | 0.402 | −0.304 | 0.742 |
| 5 | 2412.852 | 215.665 | 262.421 | 2436.643 | 2413.352 | 215.268 | 262.021 | 2437.060 | 0.500 | −0.397 | −0.400 | 0.500 |
| 6 | 365.133 | 301.214 | 416.230 | 630.317 | 364.847 | 301.521 | 415.889 | 630.073 | −0.286 | 0.307 | −0.341 | −0.286 |
| 7 | 165.249 | 118.259 | 687.255 | 716.667 | 165.145 | 117.966 | 686.845 | 716.202 | −0.104 | −0.293 | −0.410 | −0.104 |
| 8 | 765.210 | 412.036 | 642.531 | 1080.817 | 764.652 | 412.214 | 643.156 | 1080.862 | −0.558 | 0.178 | 0.625 | −0.558 |
| 9 | 3215.365 | 168.249 | 215.223 | 3226.949 | 3214.665 | 168.112 | 215.456 | 3226.260 | −0.700 | −0.137 | 0.233 | −0.700 |
| 10 | 3016.230 | 215.266 | 2101.562 | 3682.465 | 3017.012 | 215.514 | 2102.122 | 3683.439 | 0.782 | 0.248 | 0.560 | 0.782 |
| Mean error (mm) | 0.043 | 0.066 | 0.064 | 0.159 | ||||||||
| RMS errors (mm) | 0.539 | 0.297 | 0.435 | 0.508 | ||||||||
| Index | Reflection | Shadow | Surface Color/ Color Light | Mean Error (mm) | Speed (ms/Frame) | |
|---|---|---|---|---|---|---|
| Measured Object | ||||||
| Standard cube(wood) | weak | none | weak | 0.046 | 18.9 | |
| Conventional object(stone) | middle | strong | strong | 0.159 | 20.7 | |
| Snow sculpture(snow) | very strong | very strong | strong | 0.574 | 21.3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Zhang, L.; Zhang, X.; Han, L. 3D Snow Sculpture Reconstruction Based on Structured-Light 3D Vision Measurement. Appl. Sci. 2021, 11, 3324. https://doi.org/10.3390/app11083324
Liu W, Zhang L, Zhang X, Han L. 3D Snow Sculpture Reconstruction Based on Structured-Light 3D Vision Measurement. Applied Sciences. 2021; 11(8):3324. https://doi.org/10.3390/app11083324
Chicago/Turabian StyleLiu, Wancun, Liguo Zhang, Xiaolin Zhang, and Lianfu Han. 2021. "3D Snow Sculpture Reconstruction Based on Structured-Light 3D Vision Measurement" Applied Sciences 11, no. 8: 3324. https://doi.org/10.3390/app11083324
APA StyleLiu, W., Zhang, L., Zhang, X., & Han, L. (2021). 3D Snow Sculpture Reconstruction Based on Structured-Light 3D Vision Measurement. Applied Sciences, 11(8), 3324. https://doi.org/10.3390/app11083324





