COVID-19: Worldwide Profiles during the First 250 Days
Abstract
:1. Introduction
- H1: Are there different types of behavior among countries/territories?
- H1a: If so, how many behavior clusters can be identified?
- H1b: If so, are there any significant features associated with such clusters?
- H1c: If so, what are the characteristics of countries/territories in each cluster?
2. Materials and Methods
2.1. Data Understanding
- The variables geoId, countryterritoryCode, popData2019, and Cumulative_number_for_14_days_of_COVID-19_cases_per_100,000 have missing values.
- The minimum values of the variables cases and deaths are negative, something that by definition is not possible.
2.2. Data Preparation
- Correction of the ISO 3166 alpha 3 codes in the Namibia and Taiwan observations
- Removal of observations with missing values in the countriesAndTerritories, which were related to two small territories (Wallis and Futuna and “Cases on an international conveyance Japan”)
- Replacement of the character “_” by a space in countries’ names (variable countriesAndTerritories)
- total_cases: Total cumulative cases
- total_deaths: Total cumulative deaths
- cases_100K: Daily cases normalized by 100,000 of the population
- deaths_100K: Daily deaths normalized by 100,000 of the population
- total_cases_100K: Total cumulative cases normalized by 100,000 of the population
- total_deaths_100K: Total cumulative deaths normalized by 100,000 of the population
- t: Number of days since the first case was identified (0 being the first day)
2.3. Modeling
2.3.1. Analysis of Temporal Sequences
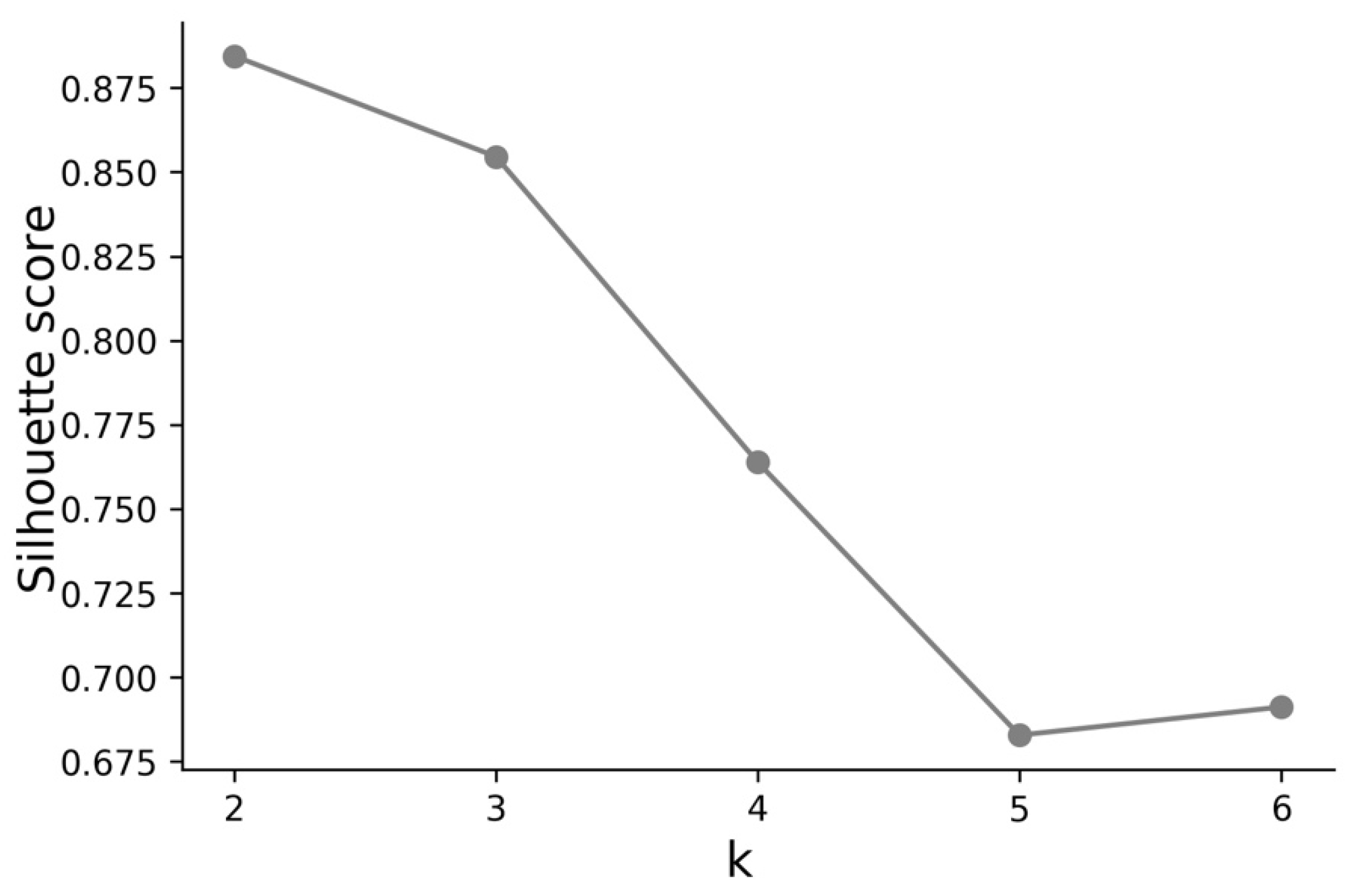
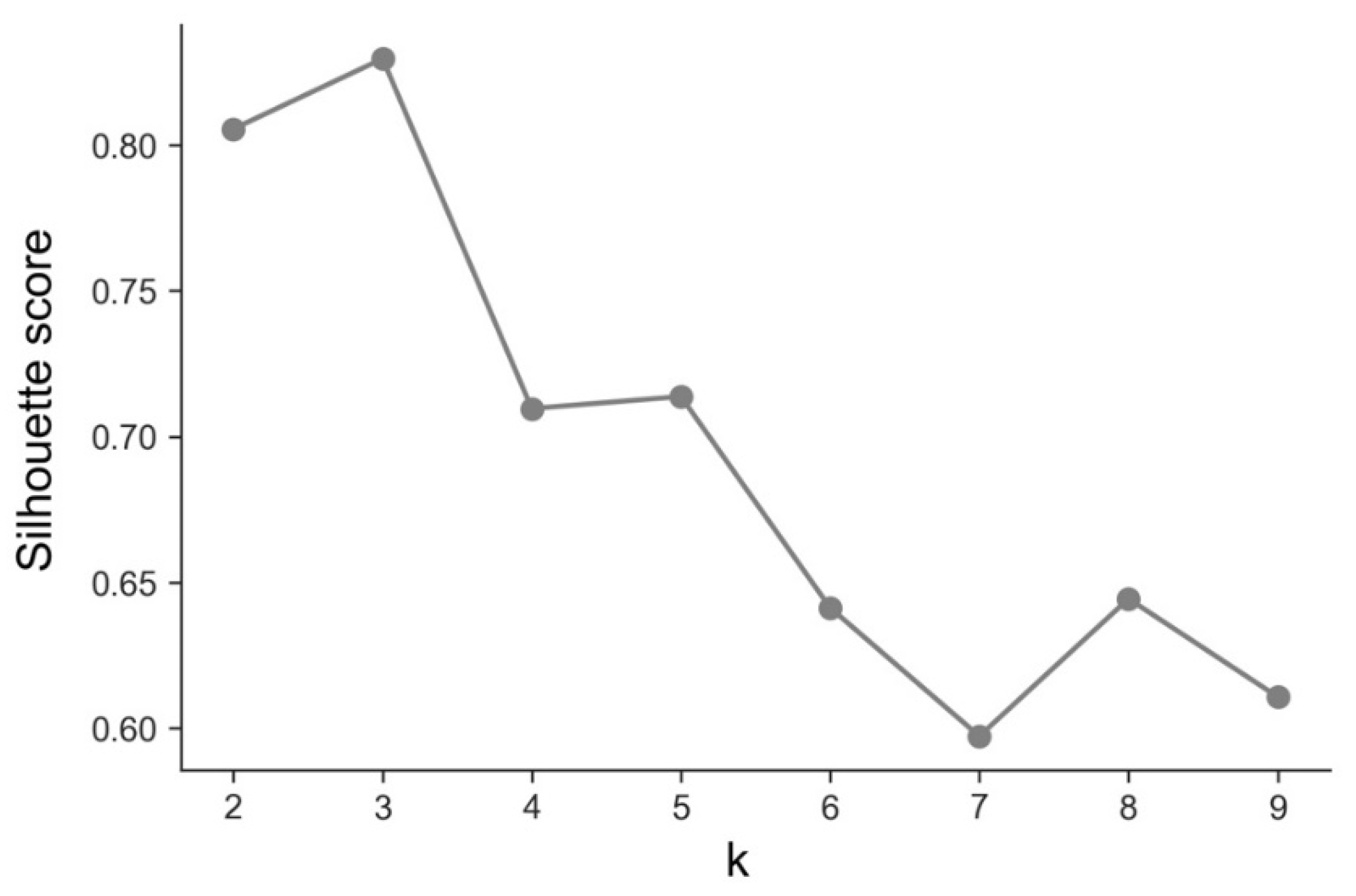
2.3.2. Analysis at Day 250
3. Results and Discussion
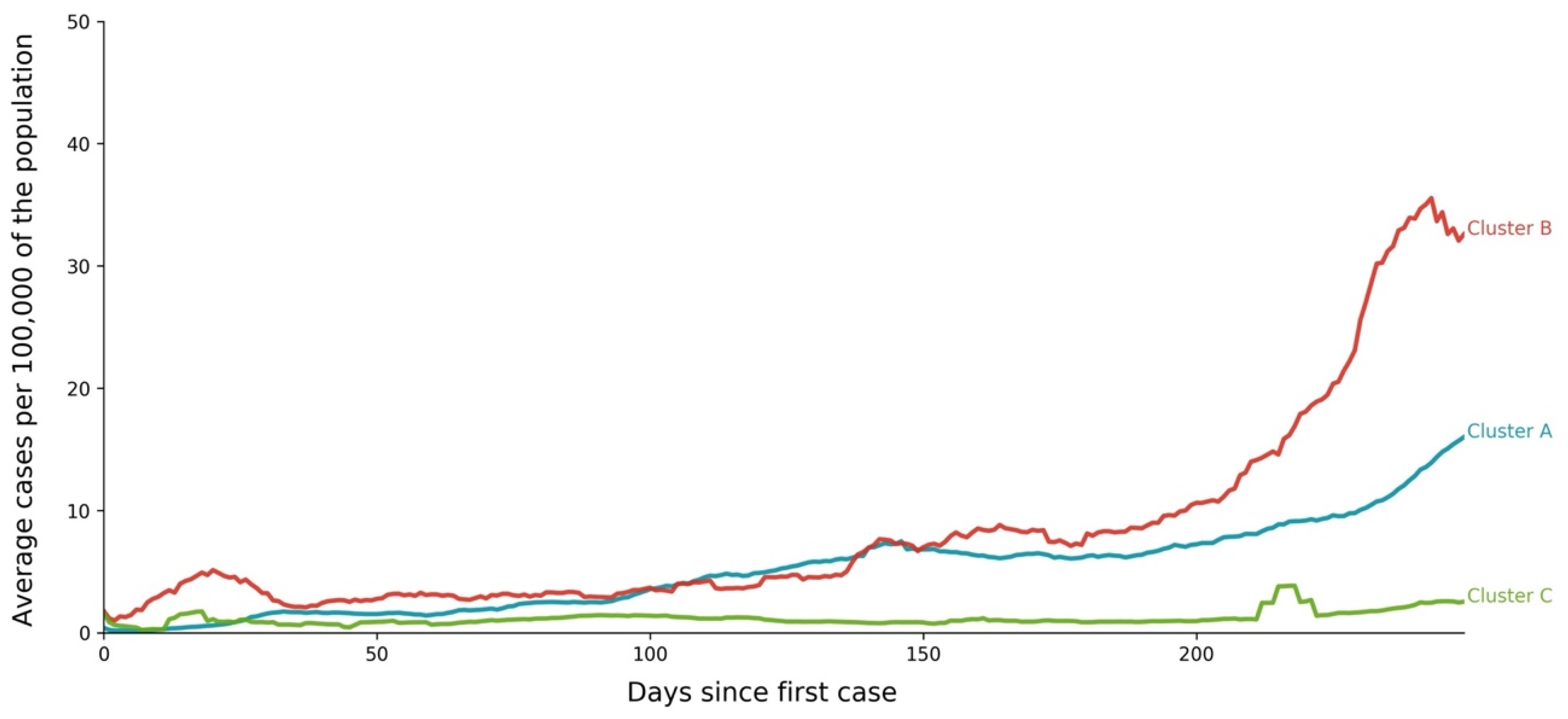
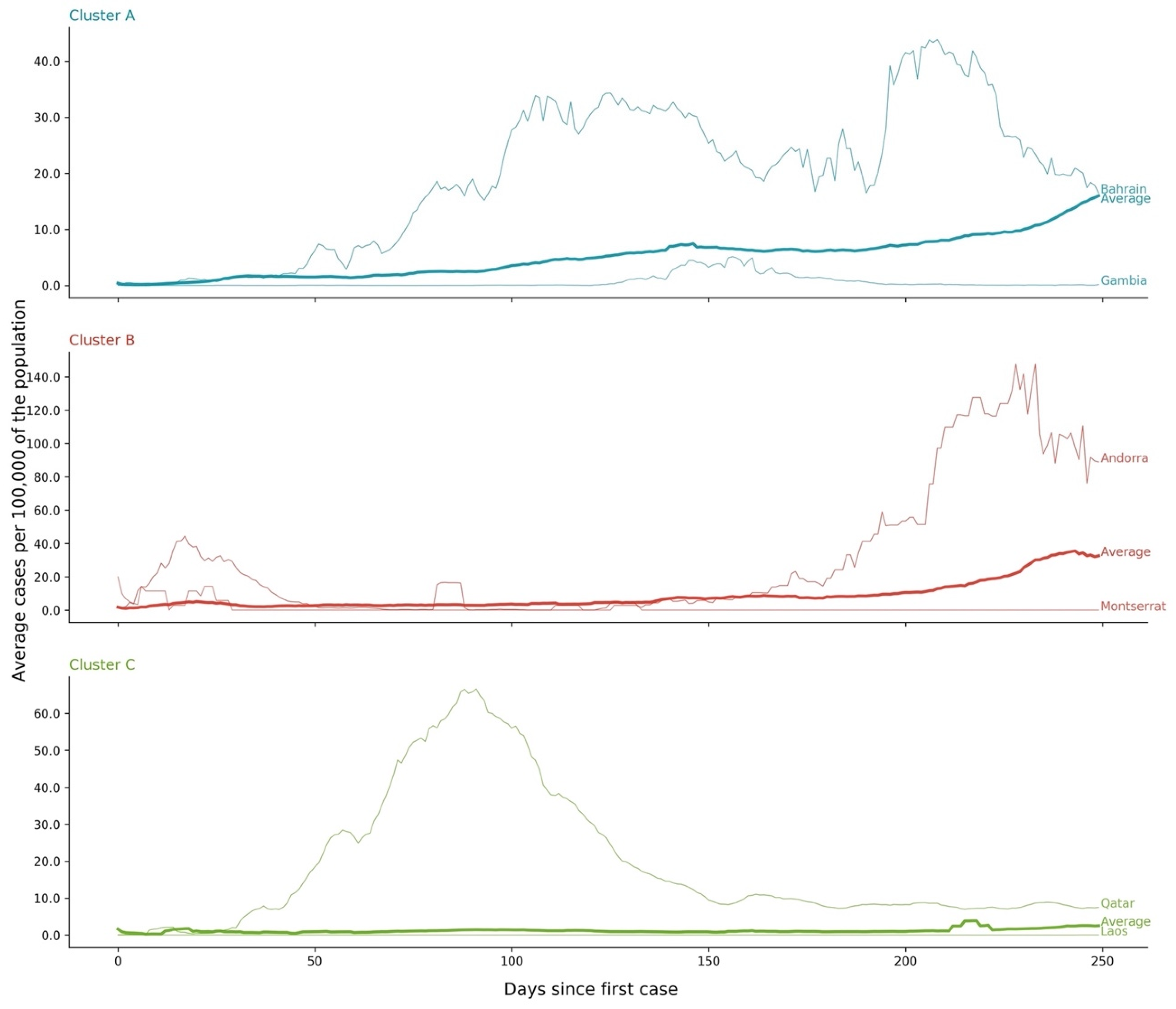
3.1. Cases—Temporal Sequence
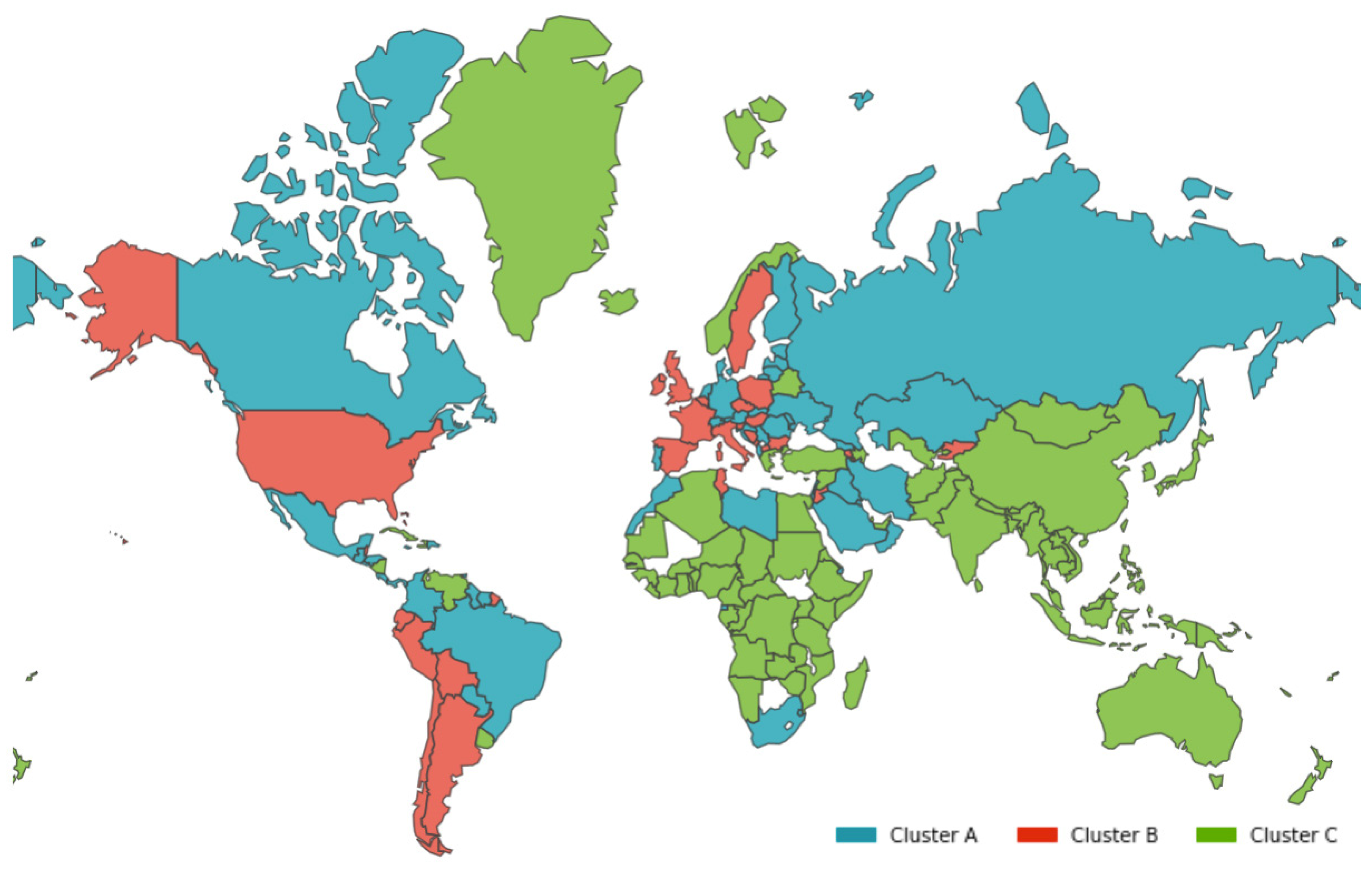
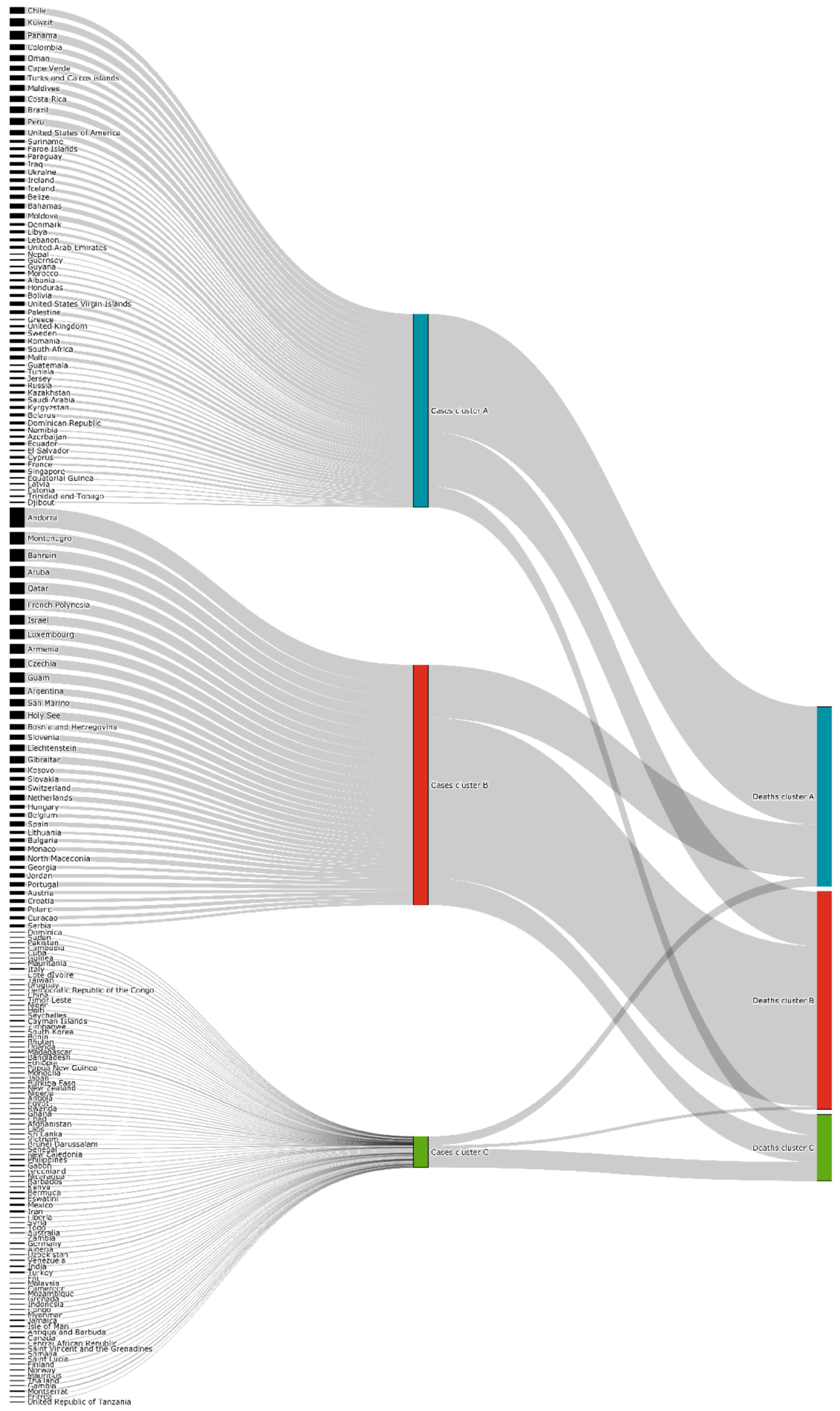
- Cluster A corresponds to a two-wave profile, with the first peak at around Day 140, and values reaching 7 cases per 100,000 of the population. The second wave started around Day 240 and seems not to have peaked yet at Day 250. The daily average number of cases per 100,000 of the population was now 10.919. This cluster comprises countries from a large variety of geographies and sizes, with an average population of 23 million people.
- Cluster B average profile indicates incidences that seem to have peaked only at around Day 240, at values above 35 cases per 100,000 of the population. This profile shows a different time constant and slower temporal dynamic with small slope linear growth until around Day 220, followed only after that by what seems to be exponential growth that has only recently reached a peak. The daily average number of cases per 100,000 of the population was 45.808. Except for Argentina, this cluster is composed mostly of small countries, much of them from Europe. The average population for these countries is seven million people.
- Cluster C average time profiles correspond to countries with new cases that have always been below 6 cases per 100,000 of the population and clearly showing smaller numbers of people with confirmed infection (either less testing, less incidence, or both). The first small peak was reached around Days 30–40, and a second small peak seems to take place at around Day 115, but more recently an apparent third peak started at Day 240. The daily average number of cases per 100,000 of the population was 0.923. Similar to Cluster A, this cluster is also composed of countries from a large variety of geographies and sizes. However, this is the cluster with the highest average population, 66 million people.
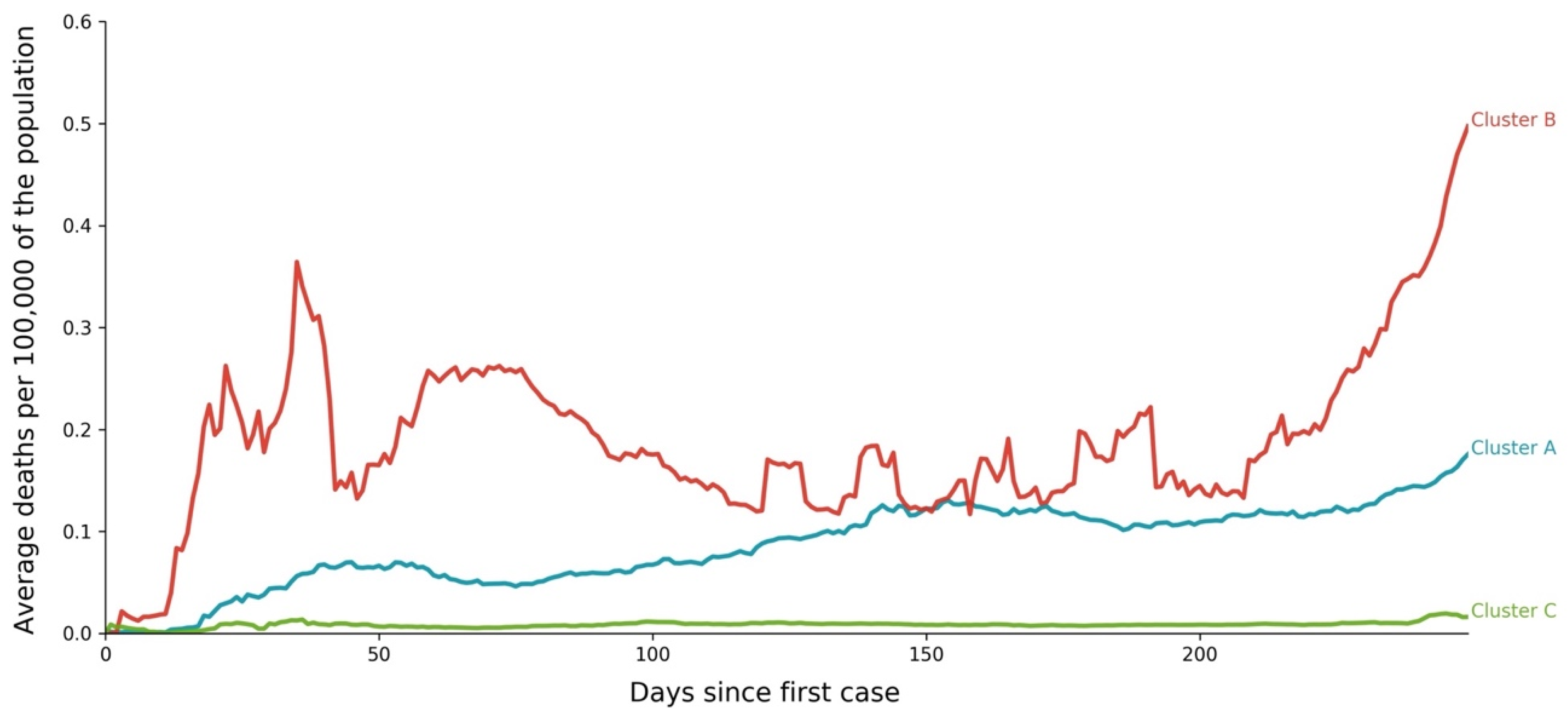
3.2. Deaths—Temporal Sequence
- Cluster A presents two waves of its average time profile. The first peak happens at around Day 50 and the second about 100 days later. However, another 100 days later, a third wave seems to be forming again. This cluster shows a slight trend line, with the average number of deaths increasing over time. The daily average number of deaths per 100,000 of the population was 0.190. This cluster is composed of countries from a diversity of geographies and sizes. The average population of the countries in this cluster is about 21 million people.
- Cluster B is the cluster with the highest daily average deaths per 100,000 of the population, 0.562. It presents one first wave of average time profile before Day 50 and a second one around Day 70, followed by a period of irregularity, and, then, after Day 210, a rapid increase of deaths that did not slow down up to Day 250. This cluster includes several small countries and larger countries such as the United States of America, United Kingdom, Spain, Italy, and Sweden, as well as other countries known publicly for being highly impacted by the pandemic. The countries’ average population in this cluster is very similar to Cluster A, at around 20 million people.
- Cluster C is the cluster with the lowest daily average deaths per 100,000 of the population, 0.029, which is six times less than Cluster A and 19 times less than Cluster B. This cluster presents a very flat average profile with no significant waves. Similar to Equatorial Guinea in Cluster A of cases, the country with the lowest number of deaths per 100,000 of the population, Aruba, seems to report data intermittently, thus causing spikes. Apart from some exceptions, this cluster is mostly comprised of countries from Africa, Asia, and Oceania. The countries’ average population in Cluster C is almost three times greater than the ones reported in Clusters A and B, reaching 61 million people.
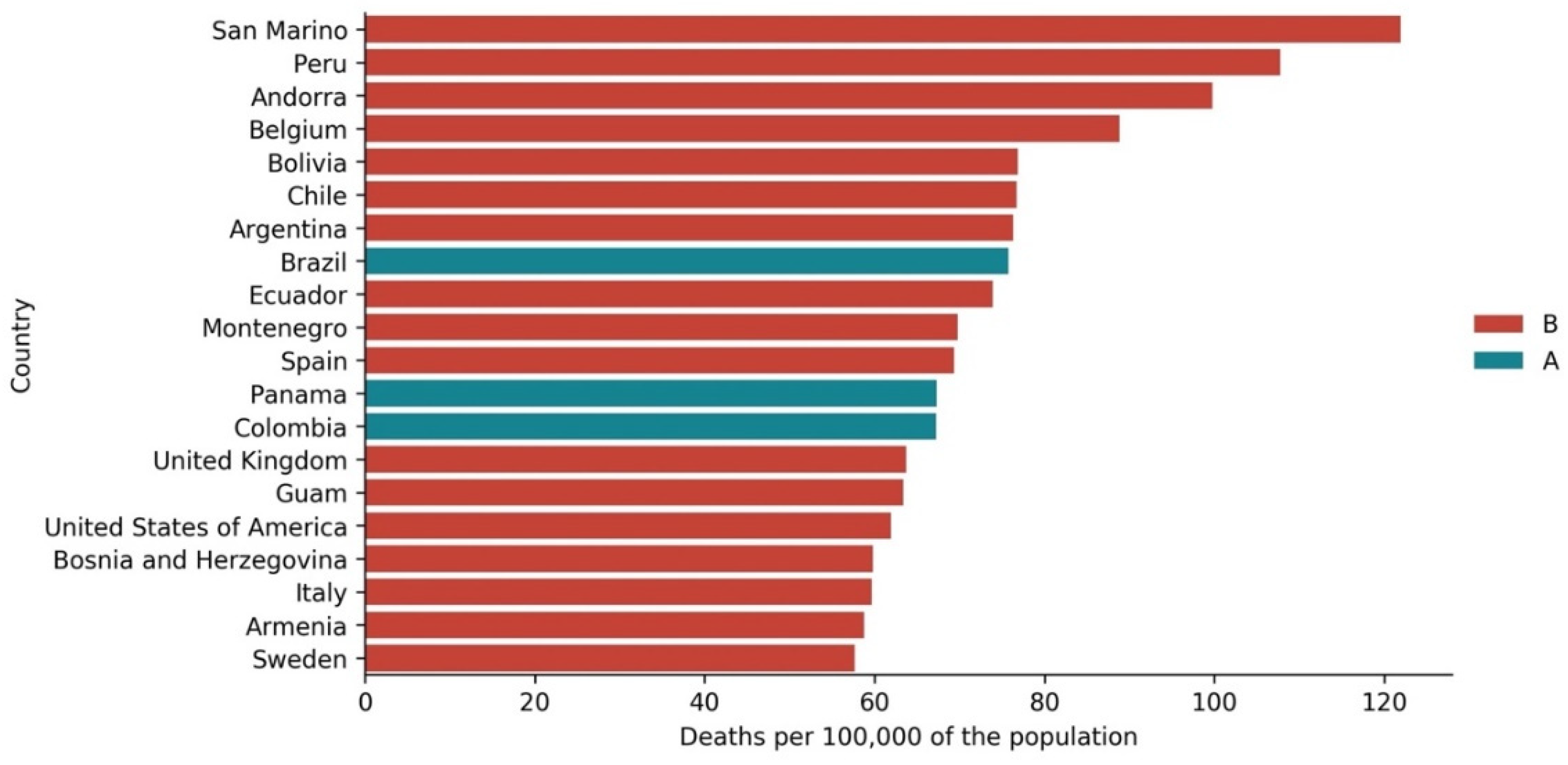
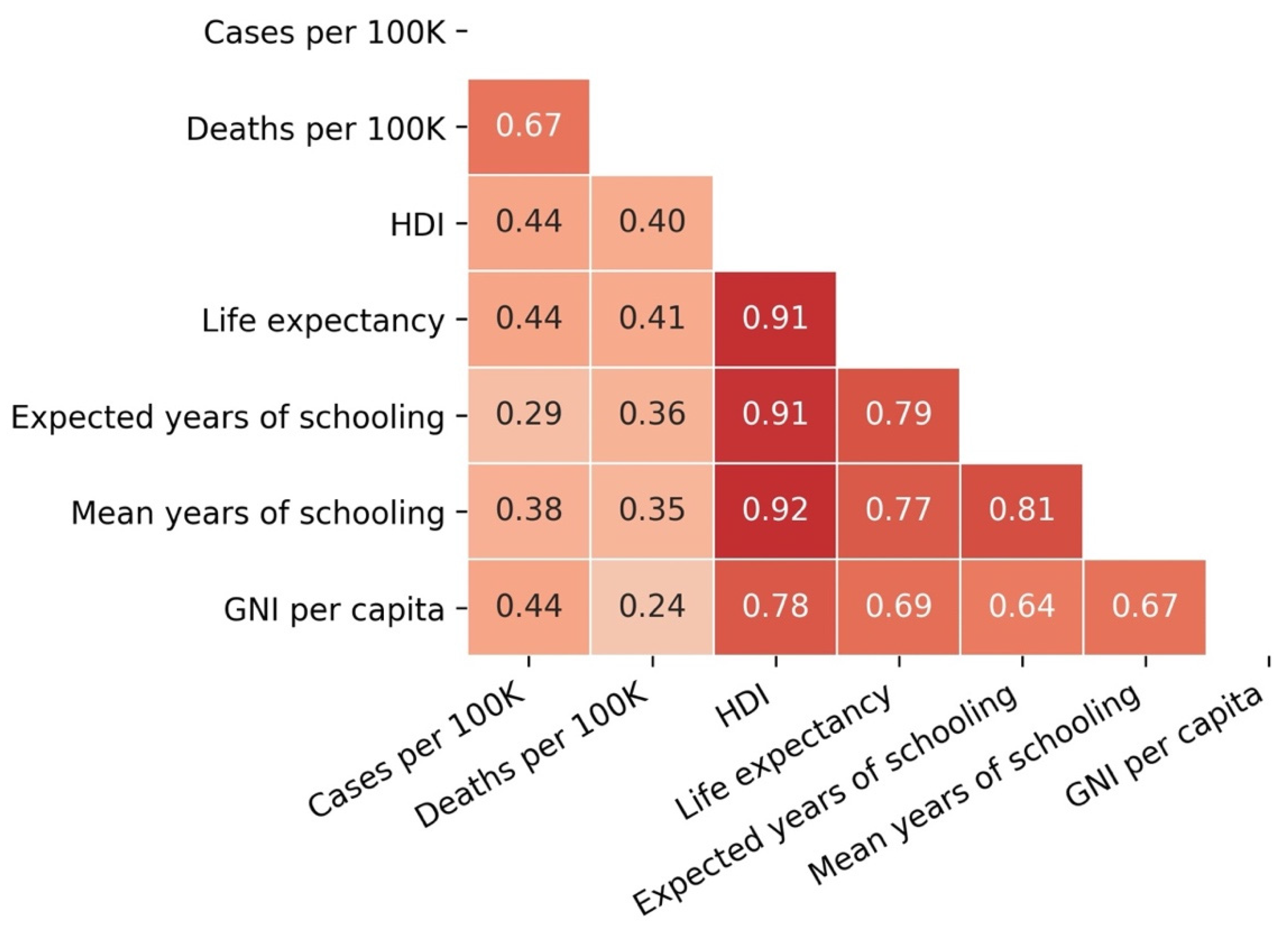
3.3. Cases vs. Deaths
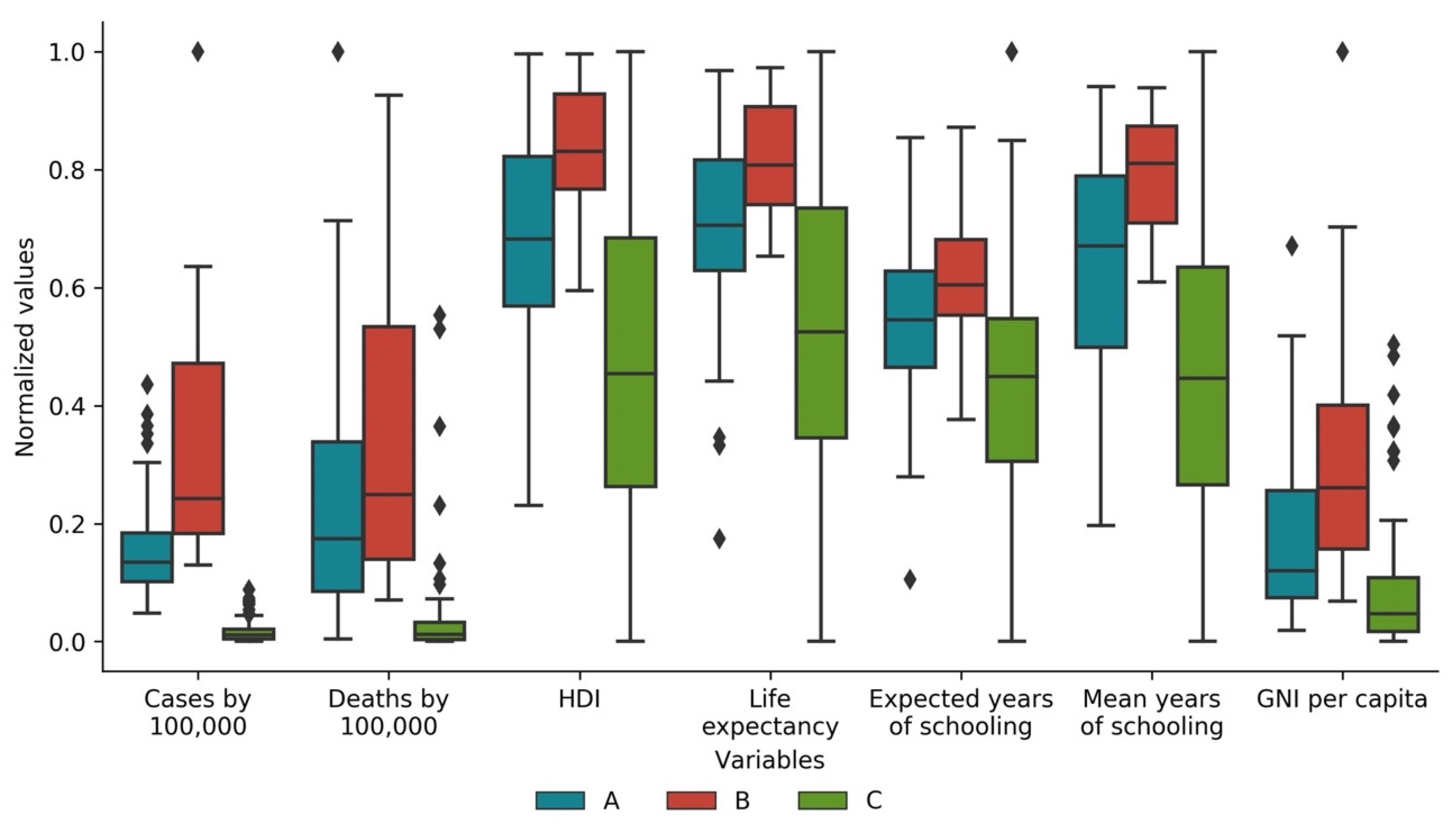
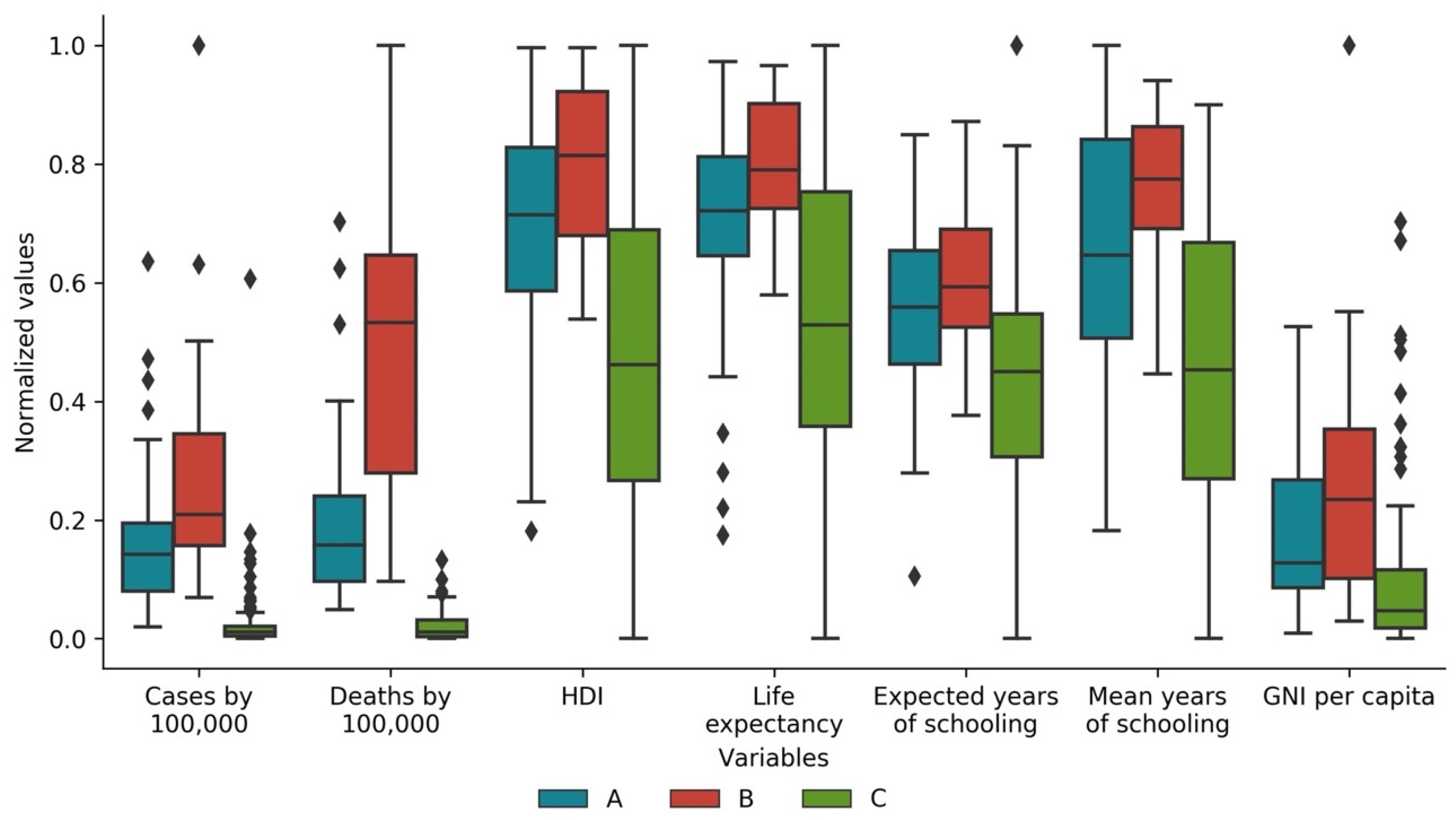
3.4. Cases and Deaths vs. Development Indicators
4. Conclusions
5. Limitations and Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Acronym
| ACAPS | Non-profit organization (previously known as “The Assessment CAPacitieS Project”) |
| CRISP-DM | CRoss-InduStry Process model for Data Mining |
| DTW | Dynamic Time Warping |
| ECDC | European Centre for Disease Control |
| GNI | Gross National Income |
| HDI | Human Development Index |
| ISO | International Organization for Standardization |
| OWID | Our World In Data |
| STD | Standard Deviation |
| UNDP | United Nations Development Program |
| WHO | World Health Organization |
| WTTC | World Travel & Tourism Council |
References
- Johns Hopkins University COVID-19 Map. Available online: https://coronavirus.jhu.edu/map.html (accessed on 31 December 2020).
- Nicola, M.; Alsafi, Z.; Sohrabi, C.; Kerwan, A.; Al-Jabir, A.; Iosifidis, C.; Agha, M.; Agha, R. The Socio-Economic Implications of the Coronavirus Pandemic (COVID-19): A Review. Int. J. Surg. 2020, 78, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Pak, A.; Adegboye, O.A.; Adekunle, A.I.; Rahman, K.M.; McBryde, E.S.; Eisen, D.P. Economic Consequences of the COVID-19 Outbreak: The Need for Epidemic Preparedness. Front. Public Health 2020, 8. [Google Scholar] [CrossRef] [PubMed]
- Antonio, N.; Rita, P. March 2020: 31 Days That Will Reshape Tourism. Curr. Issues Tour. 2020, 1–16. [Google Scholar] [CrossRef]
- Sarkodie, S.A.; Owusu, P.A. Global Assessment of Environment, Health and Economic Impact of the Novel Coronavirus (COVID-19). Environ. Dev. Sustain. 2020. [Google Scholar] [CrossRef] [PubMed]
- Shorten, C.; Khoshgoftaar, T.M.; Furht, B. Deep Learning Applications for COVID-19. J. Big Data 2021, 8, 18. [Google Scholar] [CrossRef] [PubMed]
- Zohner, Y.E.; Morris, J.S. COVID-TRACK: World and USA SARS-COV-2 Testing and COVID-19 Tracking. BioData Min. 2021, 14. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, E.; Brida, J.G.; Limas, E. Comparisons of COVID-19 Dynamics in the Different Countries of the World Using Time-Series Clustering. Health Econ. 2020. [Google Scholar] [CrossRef]
- Carrillo-Larco, R.M.; Castillo-Cara, M. Using Country-Level Variables to Classify Countries According to the Number of Confirmed COVID-19 Cases: An Unsupervised Machine Learning Approach. Wellcome Open Res. 2020, 5, 56. [Google Scholar] [CrossRef] [PubMed]
- Zarikas, V.; Poulopoulos, S.G.; Gareiou, Z.; Zervas, E. Clustering Analysis of Countries Using the COVID-19 Cases Dataset. Data Brief 2020, 31, 105787. [Google Scholar] [CrossRef] [PubMed]
- Rojas, I.; Rojas, F.; Valenzuela, O. Estimation of COVID-19 Dynamics in the Different States of the United States Using Time-Series Clustering. Health Inform. 2020. [Google Scholar] [CrossRef]
- Chandu, V. Identification of Spatial Variations in COVID-19 Epidemiological Data Using K-Means Clustering Algorithm: A Global Perspective. Epidemiology 2020. [Google Scholar] [CrossRef]
- Mahmoudi, M.R.; Baleanu, D.; Mansor, Z.; Tuan, B.A.; Pho, K.H. Fuzzy clustering method to compare the spread rate of Covid-19 in the high risks countries. Chaos Solitons Fractals 2020, 140, 110230. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Elsevier: Waltham, MA, USA, 2012. [Google Scholar]
- Chapman, P.; Clinton, J.; Kerber, R.; Khabaza, T.; Reinartz, T.; Shearer, C.; Wirth, R. CRISP-DM 1.0: Step-by-Step Data Mining Guide. Available online: https://the-modeling-agency.com/crisp-dm.pdf (accessed on 10 September 2015).
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Waskom, M.L. Seaborn: Statistical data visualization. Open J. 2021, 6, 3021. [Google Scholar] [CrossRef]
- ECDC Download Historical Data (to 14 December 2020) on the Daily Number of New Reported COVID-19 Cases and Deaths Worldwide. Available online: https://www.ecdc.europa.eu/en/publications-data/download-todays-data-geographic-distribution-covid-19-cases-worldwide (accessed on 27 December 2020).
- United Nations Human Development Reports. Available online: http://hdr.undp.org/en/composite/HDI (accessed on 27 December 2020).
- International Standards Organization Online Browsing Platform (OBP). Available online: https://www.iso.org/obp/ui/#search (accessed on 27 December 2020).
- Meert, W.; Hendrickx, K. Wannesm/Dtaidistance (Version v2.0.0). Available online: https://zenodo.org/record/3981067#.YHOqOT8RVPY (accessed on 27 December 2020).
- Novikov, A. PyClustering: Data Mining Library. J. Open Source Softw. 2019, 4, 1230. [Google Scholar] [CrossRef]
- Arora, P.; Varshney, S. Analysis of K-Means and K-Medoids Algorithm For Big Data. Procedia Comput. Sci. 2016, 78, 507–512. [Google Scholar] [CrossRef] [Green Version]
- Shamsuddin, N.R.; Mahat, N.I. Comparison Between k-Means and k-Medoids for Mixed Variables Clustering. In Proceedings of the Third International Conference on Computing, Mathematics and Statistics (iCMS2017); Kor, L.-K., Ahmad, A.-R., Idrus, Z., Mansor, K.A., Eds.; Springer: Singapore, 2019; pp. 303–308. ISBN 9789811372780. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Terpilowski, M. Scikit-Posthocs: Pairwise multiple comparison tests in Python. J. Open Source Softw. 2019, 4, 1169. [Google Scholar] [CrossRef]






| Authors (Date) | Main Purpose | Countries/ Territories | Period | Data Sources | Techniques |
| Alvarez et al. (2020) [8] | Identify groups of countries with a similar spread of the coronavirus | 191 countries | 100 days after the tenth case | OWID | Statistics tests, Hierarchical Clustering, Hierarchical Trees, Minimal, and Spanning Trees |
| Antonio and Rita (2020) [4] | Study the impact of the pandemic on tourism, particularly in hospitality | 12 European countries | March 2020 | ACAPS, D-EDGE, ECDC, OWID, STR, WTTC | Dynamic Time Warping, data characterization, statistics tests, and Hierarchical Clustering |
| Carrillo-Larco and Castillo-Cara, (2020) [9] | Understand the clustering of countries in groups using country-level pre-COVID-19 variables and COVID-19 cases and deaths | 155 countries | 23 March 2020 | John Hopkins University, Global Burden of Disease, Global Health Observatory, World Bank | Statistics tests, K-Means clustering |
| Chandu V. (2020) [12] | Identify the spatial variations in COVID-19 and relation to countries’ public health expenditure | 89 countries | Countries with 1000 confirmed cases at 6 May 2020 | WHO | K-Means clustering |
| Mahmoudi et al. (2020) [13] | Understand the spread of the coronavirus among different countries | 7 countries | 22 February 2020 to 18 April 2020 | WHO | Statistics tests, Fuzzy Clustering |
| Rojas et al. (2020) [11] | Determine the similarity of COVID-19 spread over time | States of the United States of America | Until 21 June 2020 | John Hopkins University | Dynamic Time Warping and Hierarchical Clustering |
| Zarikas et al. (2020) [10] | Understand the clustering of countries with respect to active cases | 208 countries with territories, but with several being excluded from the results | 22 January 2020 to 4 April 2020 | John Hopkins University | Hierarchical Clustering |
| Variable | Count | Type (Cat.) | Mean | Standard Deviation | Min. | 25% | 50% | 75% | Max. |
|---|---|---|---|---|---|---|---|---|---|
| dateRep | 58,919 | Cat. (336) | - | - | - | - | - | - | - |
| day | 58,919 | Num. | 16.0403 | 8.82002 | 1 | 8 | 16 | 24 | 31 |
| month | 58,919 | Num. | 6.81758 | 2.80696 | 1 | 5 | 7 | 9 | 12 |
| year | 58,919 | Num. | 2020 | 0.0337028 | 2019 | 2020 | 2020 | 2020 | 2020 |
| cases | 58,919 | Num. | 1066.9 | 6060.19 | −8261 | 0 | 14 | 247 | 207,913 |
| deaths | 58,919 | Num. | 24.801 | 126.707 | −1918 | 0 | 0 | 4 | 4928 |
| countries and Territories | 58,919 | Cat. (214) | - | - | - | - | - | - | - |
| geoId | 58,658 | Cat. (213) | - | - | - | - | - | - | - |
| country territory Code | 58,810 | Cat. (212) | - | - | - | - | - | - | - |
| popData 2019 | 58,810 | Num | 41.2304 × 106 | 153.732 × 106 | 815 | 1.32482 × 106 | 7.81321 × 106 | 28.6087 × 106 | 1.43378 × 109 |
| continent Exp | 58,919 | Cat. | - | - | - | - | - | - | - |
| Cumulative_number_ for_14_ days_of_ COVID19_ cases_per_ 100000 | 56,054 | Num. | 60.0217 | 150.082 | −147.42 | 0.682135 | 6.36797 | 47.3477 | 1900.84 |
| Variable | Count | Type (Cat.) | Mean | Standard Deviation | Min. | 25% | 50% | 75% | Max. |
|---|---|---|---|---|---|---|---|---|---|
| Country | 189 | Cat. (189) | - | - | - | - | - | - | - |
| HDI | 189 | Num. | 0.722 | 0.150 | 0.394 | 0.602 | 0.740 | 0.829 | 0.957 |
| Life Expectancy AtBirth | 189 | Num. | 72.712 | 7386 | 53.280 | 67.440 | 74.050 | 77.910 | 84.860 |
| Expected YearsOf Schooling | 189 | Num. | 13.325 | 2.941 | 5.005 | 11.431 | 13.188 | 15.227 | 21.954 |
| MeanYearsOf Schooling | 189 | Num. | 8728 | 3087 | 1644 | 6437 | 9032 | 11.326 | 14.152 |
| GrossNational IncomePer Capita | 189 | Num. | 20,219.726 | 21,229.049 | 753.909 | 4910.208 | 12,707.366 | 29,497.232 | 131,031.5 |
| Count | Mean | Standard Deviation | Min. | 25% | 50% | 75% | Max. |
|---|---|---|---|---|---|---|---|
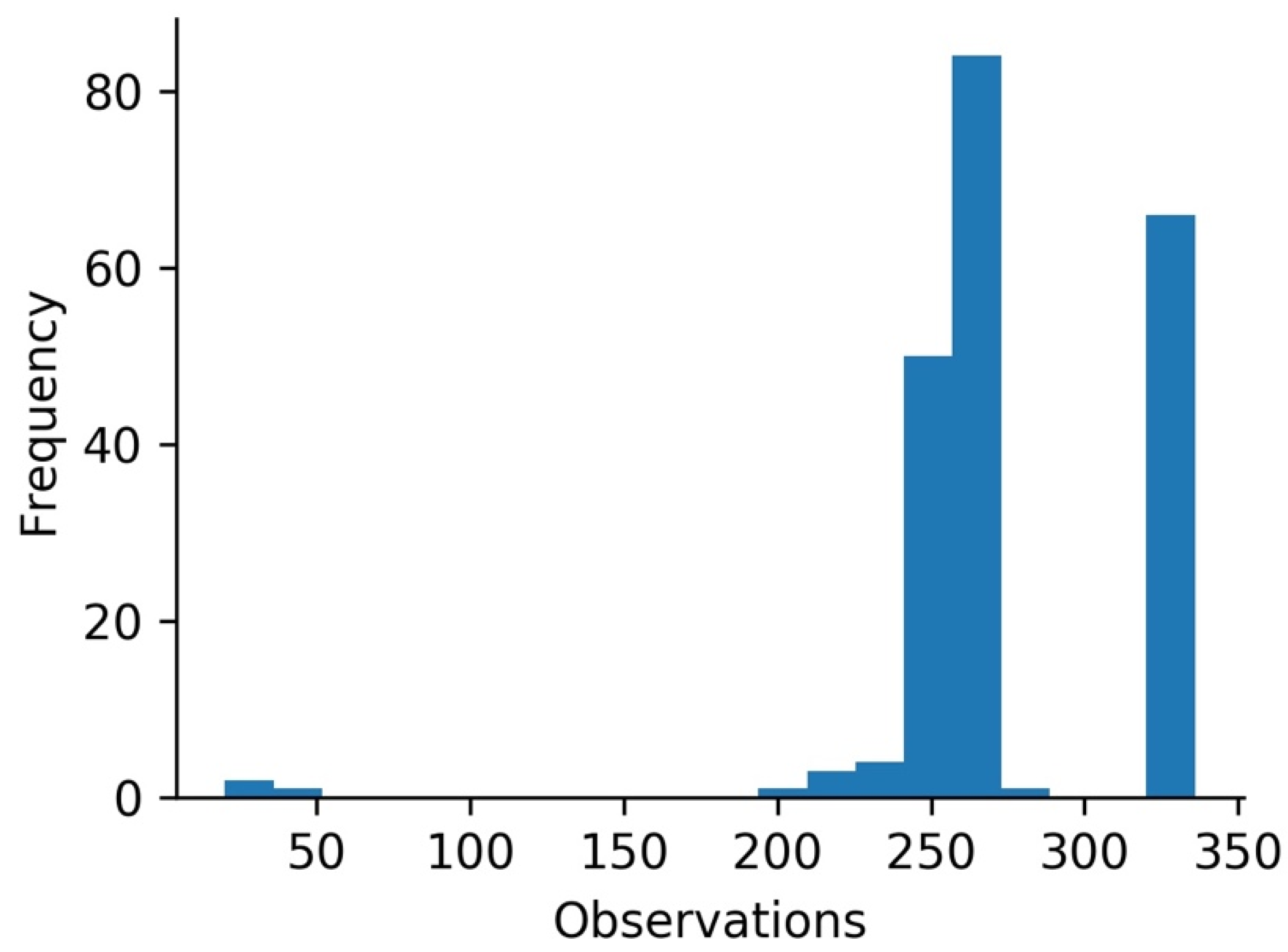
| 212 | 262.566 | 34.037 | 19.00 | 255.00 | 261.00 | 270.00 | 335.00 |
| Variable | Cluster A (Std) | Cluster B (Std) | Cluster C (Std) |
|---|---|---|---|
| Total cases by 100,000 of the population | 1267.782 (727.131) | 2639.816 (1525.025) | 140.471 (160.356) |
| Total deaths by 100,000 of the population | 26.871 (23.739) | 35.502 (29.556) | 4.705 (10.374) |
| Population | 22,979,074 (52,365,381) | 7,413,262 (11,664,577) | 65,751,558 (209,744,281) |
| Total cases by 100,000 of the population * | 1263.896 (737.867) | 2535.323 (1613.192) | 136.453 (157.875) |
| Total deaths by 100,000 of the population * | 27.309 (24.475) | 35.590 (26.512) | 4.357 (10.327) |
| Human Development Index * | 0.783 (0.102) | 0.863 (0.058) | 0.664 (0.151) |
| Life expectancy at birth * | 75.577 (5.042) | 78.915 (3.048) | 70.053 (7.698) |
| Expected years of schooling * | 14.253 (2.420) | 15.460 (1.912) | 12.501 (3.081) |
| Mean years of schooling * | 9.685 (2.377) | 11.580 (1.247) | 7.462 (3.061) |
| Gross national income per capita * | 25,111.109 (19,968.660) | 40,440.653 (26,746.722) | 13,377.740 (15,688.465) |
| Variable | Cluster A (Std) | Cluster B (Std) | Cluster C (Std) |
|---|---|---|---|
| Total cases by 100,000 of the population | 1307.134 (941.765) | 2161.559 (1536.914) | 296.200 (658.197) |
| Total deaths by 100,000 of the population | 21.771 (16.114) | 48.434 (27.677) | 2.124 (2.601) |
| Population | 21,259,945 (39,612,007) | 20,258,924 (53,000,847) | 60,766,034 (207,799,142) |
| Total cases by 100,000 of the population * | 1305.755 (962.065) | 2141.249 (1519.509) | 237.542 (575.844) |
| Total deaths by 100,000 of the population * | 21.390 (16.095) | 51.949 (25.883) | 2.251 (2.695) |
| Human Development Index * | 0.785 (0.108) | 0.842 (0.079) | 0.670 (0.152) |
| Life expectancy at birth * | 75.432 (5.509) | 78.378 (3.524) | 70.333 (7.649) |
| Expected years of schooling * | 14.204 (2.430) | 15.423 (2.079) | 12.538 (3.052) |
| Mean years of schooling * | 9.786 (2.602) | 11.148 (1.441) | 7.537 (3.308) |
| Gross national income per capita * | 24,960.222 (17,304.968) | 34,852.913 (26,739.551) | 15,312.351 (19,976.337) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
António, N.; Rita, P.; Saraiva, P. COVID-19: Worldwide Profiles during the First 250 Days. Appl. Sci. 2021, 11, 3400. https://doi.org/10.3390/app11083400
António N, Rita P, Saraiva P. COVID-19: Worldwide Profiles during the First 250 Days. Applied Sciences. 2021; 11(8):3400. https://doi.org/10.3390/app11083400
Chicago/Turabian StyleAntónio, Nuno, Paulo Rita, and Pedro Saraiva. 2021. "COVID-19: Worldwide Profiles during the First 250 Days" Applied Sciences 11, no. 8: 3400. https://doi.org/10.3390/app11083400
APA StyleAntónio, N., Rita, P., & Saraiva, P. (2021). COVID-19: Worldwide Profiles during the First 250 Days. Applied Sciences, 11(8), 3400. https://doi.org/10.3390/app11083400






