Analysis of La4Ni3O10±?-BaCe0.9Y0.1O3-? Composite Cathodes for Proton Ceramic Fuel Cells
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Microstructure
3.2. Equivalent Circuit Model (EQM)
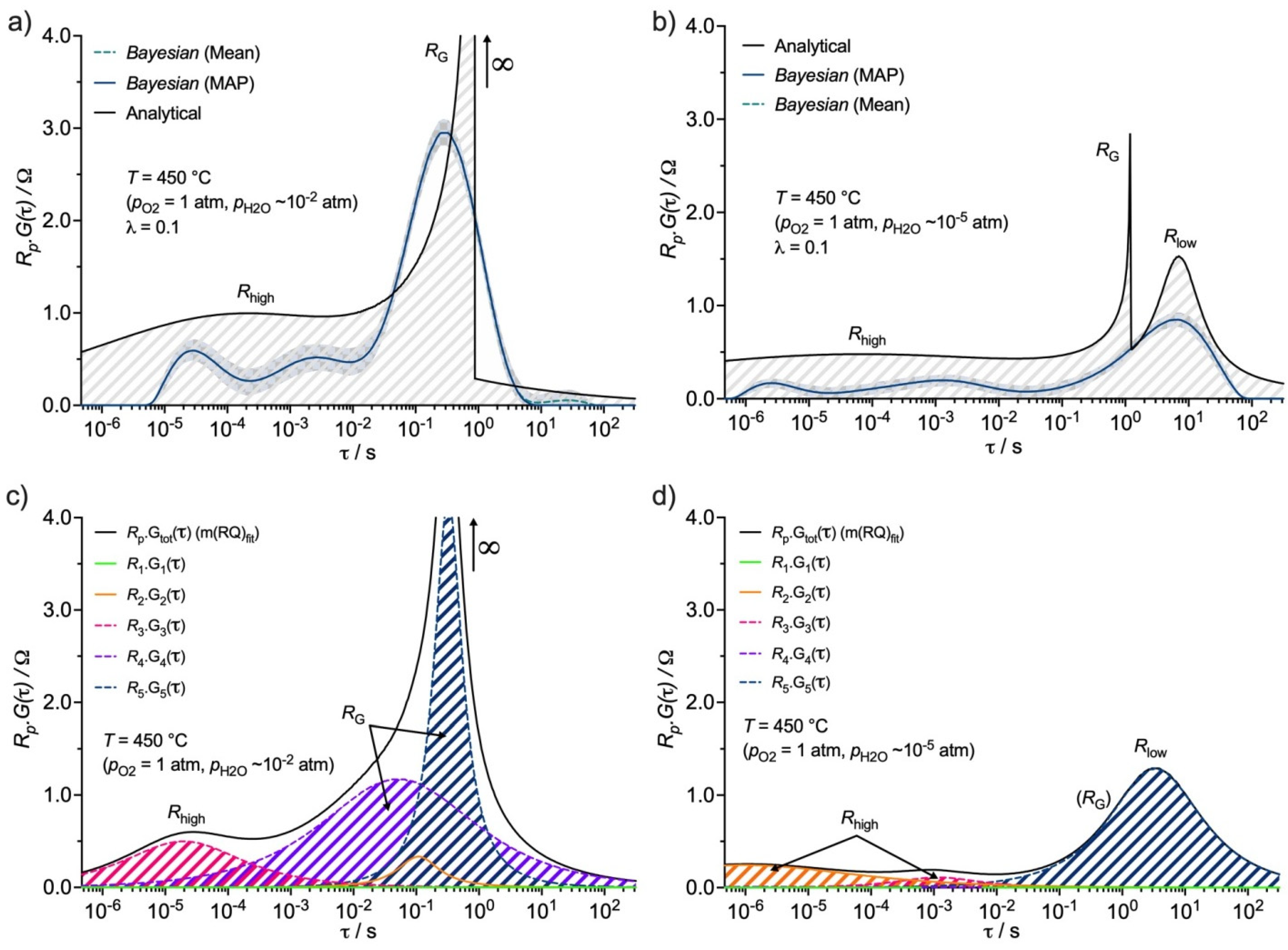
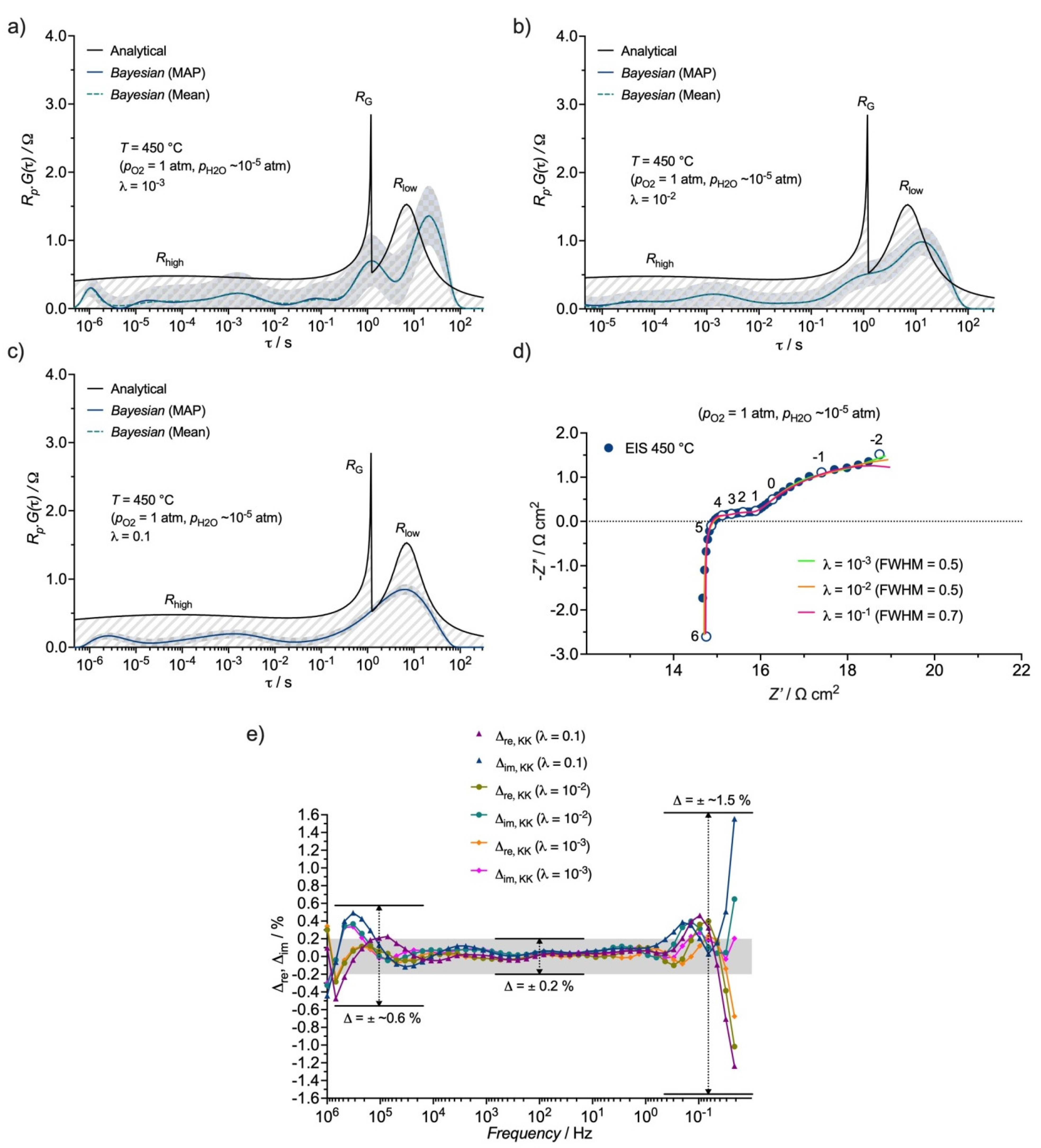
3.3. Distribution Function of Relaxation Times (DFRT) Analysis
3.4. Electronic Short-Circuiting through the BCY10 Electrolyte
3.5. Temperature Dependence of the Polarisation Resistances
3.6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Loureiro, F.J.A.; Nasani, N.; Reddy, G.S.; Munirathnam, N.R.; Fagg, D.P. A review on sintering technology of proton conducting BaCeO3-BaZrO3 perovskite oxide materials for Protonic Ceramic Fuel Cells. J. Power Sources 2019, 438, 226991. [Google Scholar] [CrossRef]
- Antunes, I.; Pérez-Coll, D.; Nasani, N.; Soares, H.S.; Mather, G.C.; Frade, J.R.; Fagg, D.P. Mechanochemical processing of BaZr1−yYyO3−δ (y = 0.15, 0.20) protonic ceramic electrolytes: Phase purity, microstructure, electrical properties and comparison with other preparation routes. Int. J. Hydrogen Energy 2020. [Google Scholar] [CrossRef]
- Fabbri, E.; Bi, L.; Pergolesi, D.; Traversa, E. Towards the Next Generation of Solid Oxide Fuel Cells Operating Below 600 °C with Chemically Stable Proton-Conducting Electrolytes. Adv. Mater. 2012, 24, 195–208. [Google Scholar] [CrossRef]
- Loureiro, F.J.A.; Macedo, D.A.; Nascimento, R.M.; Cesário, M.R.; Grilo, J.P.F.; Yaremchenko, A.A.; Fagg, D.P. Cathodic polarisation of composite LSCF-SDC IT-SOFC electrode synthesised by one-step microwave self-assisted combustion. J. Eur. Ceram. Soc. 2019, 39, 1846–1853. [Google Scholar] [CrossRef]
- Loureiro, F.J.A.; Yang, T.; Stroppa, D.G.; Fagg, D.P. Pr2O2SO4–La0.6Sr0.4Co0.2Fe0.8O3-δ: A new category of composite cathode for intermediate temperature-solid oxide fuel cells. J. Mater. Chem. A 2015, 3, 12636–12641. [Google Scholar] [CrossRef]
- Marinha, D.; Dessemond, L.; Djurado, E. Electrochemical investigation of oxygen reduction reaction on La0.6Sr0.4Co0.2Fe0.8O3−δ cathodes deposited by Electrostatic Spray Deposition. J. Power Sources 2012, 197, 80–87. [Google Scholar] [CrossRef]
- Loureiro, F.J.A.; Araújo, A.J.M.; Paskocimas, C.A.; Macedo, D.A.; Fagg, D.P. Polarisation mechanism of the misfit Ca-cobaltite electrode for reversible solid oxide cells. Electrochim. Acta 2021, 373, 137928. [Google Scholar] [CrossRef]
- Adler, S.B. Mechanism and kinetics of oxygen reduction on porous La1-xSrxCoO3-δ electrodes. Solid State Ion. 1998, 111, 125–134. [Google Scholar] [CrossRef]
- Hildenbrand, N.; Nammensma, P.; Blank, D.H.A.; Bouwmeester, H.J.M.; Boukamp, B.A. Influence of configuration and microstructure on performance of La2NiO4+δ intermediate-temperature solid oxide fuel cells cathodes. J. Power Sources 2013, 238, 442–453. [Google Scholar] [CrossRef]
- Zapata-Ramírez, V.; Dos Santos-Gómez, L.; Mather, G.C.; Marrero-López, D.; Pérez-Coll, D. Enhanced Intermediate-Temperature Electrochemical Performance of Air Electrodes for Solid Oxide Cells with Spray-Pyrolyzed Active Layers. ACS Appl. Mater. Interfaces 2020, 12, 10571–10578. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Coll, D.; Aguadero, A.; Escudero, M.J.; Daza, L. Effect of DC current polarization on the electrochemical behaviour of La2NiO4+δ and La3Ni2O7+δ-based systems. J. Power Sources 2009, 192, 2–13. [Google Scholar] [CrossRef]
- Loureiro, F.J.A.; Silva, V.D.; Simões, T.A.; Cesário, M.R.; Grilo, J.P.F.; Fagg, D.P.; Macedo, D.A. Misfit-layered Ca-cobaltite-based cathodes for intermediate-temperature solid oxide fuel cell. In Intermediate Temperature Solid Oxide Fuel Cells: Electrolytes, Electrodes and Interconnects; Elsevier: Amsterdam, The Netherlands, 2019; pp. 347–377. ISBN 9780128174456. [Google Scholar]
- Sharma, R.K.; Djurado, E. Functionally graded and homogeneous composites of La2NiO4+δ and Lan+1NinO3n+1 (n = 2 and 3) solid oxide fuel cell cathodes. J. Mater. Chem. A 2017, 5, 22277–22287. [Google Scholar] [CrossRef]
- Song, J.; Ning, D.; Boukamp, B.; Bassat, J.-M.; Bouwmeester, H.J.M. Structure, electrical conductivity and oxygen transport properties of Ruddlesden–Popper phases Lnn+1NinO3n+1 (Ln = La, Pr and Nd; n = 1, 2 and 3). J. Mater. Chem. A 2020, 8, 22206–22221. [Google Scholar] [CrossRef]
- Woolley, R.J.; Skinner, S.J. Functionally graded composite La2NiO4+δ and La4Ni3O10−δ solid oxide fuel cell cathodes. Solid State Ionics 2014, 255, 1–5. [Google Scholar] [CrossRef]
- Amow, G.; Davidson, I.J.; Skinner, S.J. A comparative study of the Ruddlesden-Popper series, Lan+1NinO3n+1 (n=1, 2 and 3), for solid-oxide fuel-cell cathode applications. Solid State Ionics 2006, 177, 1205–1210. [Google Scholar] [CrossRef] [Green Version]
- Grimaud, A.; Mauvy, F.; Marc Bassat, J.; Fourcade, S.; Marrony, M.; Claude Grenier, J. Hydration and transport properties of the Pr2−xSrxNiO4+δ compounds as H+-SOFC cathodes. J. Mater. Chem. 2012, 22, 16017–16025. [Google Scholar] [CrossRef]
- Grimaud, A.; Mauvy, F.; Bassat, J.M.; Fourcade, S.; Rocheron, L.; Marrony, M.; Grenier, J.C. Hydration Properties and Rate Determining Steps of the Oxygen Reduction Reaction of Perovskite-Related Oxides as H+-SOFC Cathodes. J. Electrochem. Soc. 2012, 159, B683–B694. [Google Scholar] [CrossRef]
- Loureiro, F.J.A.; Ramasamy, D.; Mikhalev, S.M.; Shaula, A.L.; Macedo, D.A.; Fagg, D.P. La4Ni3O10±δ-BaCe0.9Y0.1O3-δ cathodes for Proton Ceramic Fuel Cells; short-circuiting analysis using BaCe0.9Y0.1O3-δ symmetric cells. Int. J. Hydrogen Energy 2021, 46, 13594–13605. [Google Scholar] [CrossRef]
- Tarutin, A.P.; Lyagaeva, J.G.; Medvedev, D.A.; Bi, L.; Yaremchenko, A.A. Recent advances in layered Ln2NiO4+δ nickelates: Fundamentals and prospects of their applications in protonic ceramic fuel and electrolysis cells. J. Mater. Chem. A 2021, 9, 154–195. [Google Scholar] [CrossRef]
- Bannikov, D.O.; Cherepanov, V.A. Thermodynamic properties of complex oxides in the La–Ni–O system. J. Solid State Chem. 2006, 179, 2721–2727. [Google Scholar] [CrossRef]
- Santos, J.R.D.; Loureiro, F.J.A.; Grilo, J.P.F.; Silva, V.D.; Simões, T.A.; Fagg, D.P.; Macedo, D.A. Understanding the cathodic polarisation behaviour of the misfit [Ca2CoO3-δ]q[CoO2] (C349) as oxygen electrode for IT-SOFC. Electrochim. Acta 2018, 285, 214–220. [Google Scholar] [CrossRef]
- Loureiro, F.J.A.; Pérez-Coll, D.; Graça, V.C.D.; Mikhalev, S.M.; Ribeiro, A.F.G.; Mendes, A.; Fagg, D.P. Proton conductivity in yttrium-doped barium cerate in nominally dry reducing conditions for application in chemical synthesis. J. Mater. Chem. A 2019, 7, 18135–18142. [Google Scholar] [CrossRef]
- Loureiro, F.J.A.; Ramasamy, D.; Ribeiro, A.F.G.; Mendes, A.; Fagg, D.P. Underscoring the transport properties of yttrium-doped barium cerate in nominally dry oxidising conditions. Electrochim. Acta 2020, 334. [Google Scholar] [CrossRef]
- Loureiro, F.J.A.; Souza, G.S.; Graça, V.C.D.; Araújo, A.J.M.; Grilo, J.P.F.; Macedo, D.A.; Fagg, D.P. Nickel-copper based anodes for solid oxide fuel cells running on hydrogen and biogas: Study using ceria-based electrolytes with electronic short-circuiting correction. J. Power Sources 2019, 438. [Google Scholar] [CrossRef]
- Miyashita, T. Necessity of verification of leakage currents using Sm doped Ceria electrolytes in SOFCs. J. Mater. Sci. 2006, 41, 3183–3184. [Google Scholar] [CrossRef]
- Liu, M.; Hu, H. Effect of Interfacial Resistance on Determination of Transport Properties of Mixed-Conducting Electrolytes. J. Electrochem. Soc. 1996, 143, L109–L112. [Google Scholar] [CrossRef]
- Poetzsch, D.; Merkle, R.; Maier, J. Investigation of oxygen exchange kinetics in proton-conducting ceramic fuel cells: Effect of electronic leakage current using symmetric cells. J. Power Sources 2013, 242, 784–789. [Google Scholar] [CrossRef]
- Boukamp, B.A.; Rolle, A.; Vannier, R.N.; Sharma, R.K.; Djurado, E. Electrostatic spray deposited Ca3Co4O9+δ and Ca3Co4O9+δ/Ce0.9Gd0.1O1.95 cathodes for SOFC: A comparative impedance analysis study. Electrochim. Acta 2020, 362, 137142. [Google Scholar] [CrossRef]
- Osinkin, D.A.; Kolchugin, A.A.; Bogdanovich, N.M.; Beresnev, S.M. Performance and redox stability of a double–layer Sr2Fe1.5Mo0.5O6-δ-based electrode for solid state electrochemical application. Electrochim. Acta 2020, 361, 137058. [Google Scholar] [CrossRef]
- Pikalova, E.; Kolchugin, A.; Koroleva, M.; Vdovin, G.; Farlenkov, A.; Medvedev, D. Functionality of an oxygen Ca3Co4O9+δ electrode for reversible solid oxide electrochemical cells based on proton-conducting electrolytes. J. Power Sources 2019, 438, 226996. [Google Scholar] [CrossRef]
- Liu, J.; Wan, T.H.; Ciucci, F. A Bayesian view on the Hilbert transform and the Kramers-Kronig transform of electrochemical impedance data: Probabilistic estimates and quality scores. Electrochim. Acta 2020, 357, 136864. [Google Scholar] [CrossRef]
- Boukamp, B.A. A Linear Kronig-Kramers Transform Test for Immittance Data Validation. J. Electrochem. Soc. 1995, 142, 1885. [Google Scholar] [CrossRef]
- Melo, B.M.G.; Loureiro, F.J.A.; Fagg, D.P.; Costa, L.C.; Graça, M.P.F. DFRTtoEIS: An easy approach to verify the consistency of a DFRT generated from an impedance spectrum. Electrochim. Acta 2021, 366, 137429. [Google Scholar] [CrossRef]
- DFRTtoEIS. Available online: https://github.com/bmgmelo/DFRTtoEIS (accessed on 31 January 2021).
- DRTtool Toolbox. Available online: https://sites.google.com/site/drttools (accessed on 31 January 2021).
- Quarez, E.; Oumellal, Y.; Joubert, O. Optimization of the Lanthanum Tungstate/Pr2NiO4 Half Cell for Application in Proton Conducting Solid Oxide Fuel Cells. Fuel Cells 2013, 13, 34–41. [Google Scholar] [CrossRef]
- Solís, C.; Navarrete, L.; Serra, J.M. Study of Pr and Pr and Co doped La2NiO4+δ as cathodes for La5.5WO11.25−δ based protonic conducting fuel cells. J. Power Sources 2013, 240, 691–697. [Google Scholar] [CrossRef] [Green Version]
- Lyagaeva, J.; Medvedev, D.; Pikalova, E.; Plaksin, S.; Brouzgou, A.; Demin, A.; Tsiakaras, P. A detailed analysis of thermal and chemical compatibility of cathode materials suitable for BaCe0.8Y0.2O3−δ and BaZr0.8Y0.2O3−δ proton electrolytes for solid oxide fuel cell application. Int. J. Hydrogen Energy 2017, 42, 1715–1723. [Google Scholar] [CrossRef]
- Dailly, J.; Fourcade, S.; Largeteau, A.; Mauvy, F.; Grenier, J.C.; Marrony, M. Perovskite and A2MO4-type oxides as new cathode materials for protonic solid oxide fuel cells. Electrochim. Acta 2010, 55, 5847–5853. [Google Scholar] [CrossRef]
- Ricote, S.; Bonanos, N.; Lenrick, F.; Wallenberg, R. LaCoO3: Promising cathode material for protonic ceramic fuel cells based on a BaCe0.2Zr0.7Y0.1O3−δ electrolyte. J. Power Sources 2012, 218, 313–319. [Google Scholar] [CrossRef]
- Fulgêncio, E.B.G.A.; Loureiro, F.J.A.; Melo, K.P.V.; Silva, R.M.; Fagg, D.P.; Campos, L.F.A.; Macedo, D.A. Boosting the oxygen reduction reaction of the misfit [Ca2CoO3-δ]q[CoO2] (C349) by the addition of praseodymium oxide. J. Alloys Compd. 2019, 788, 148–154. [Google Scholar] [CrossRef]
- Nielsen, J.; Jacobsen, T.; Wandel, M. Impedance of porous IT-SOFC LSCF:CGO composite cathodes. Electrochim. Acta 2011, 56, 7963–7974. [Google Scholar] [CrossRef]
- Boukamp, B.A.; Rolle, A. Analysis and Application of Distribution of Relaxation Times in Solid State Ionics. Solid State Ionics 2017, 302, 12–18. [Google Scholar] [CrossRef]
- Boukamp, B.A.; Rolle, A. Use of a distribution function of relaxation times (DFRT) in impedance analysis of SOFC electrodes. Solid State Ionics 2018, 314, 103–111. [Google Scholar] [CrossRef]
- Ciucci, F.; Chen, C. Analysis of Electrochemical Impedance Spectroscopy Data Using the Distribution of Relaxation Times: A Bayesian and Hierarchical Bayesian Approach. Electrochim. Acta 2015, 167, 439–454. [Google Scholar] [CrossRef]
- Effat, M.B.; Ciucci, F. Bayesian and Hierarchical Bayesian Based Regularization for Deconvolving the Distribution of Relaxation Times from Electrochemical Impedance Spectroscopy Data. Electrochim. Acta 2017, 247, 1117–1129. [Google Scholar] [CrossRef]
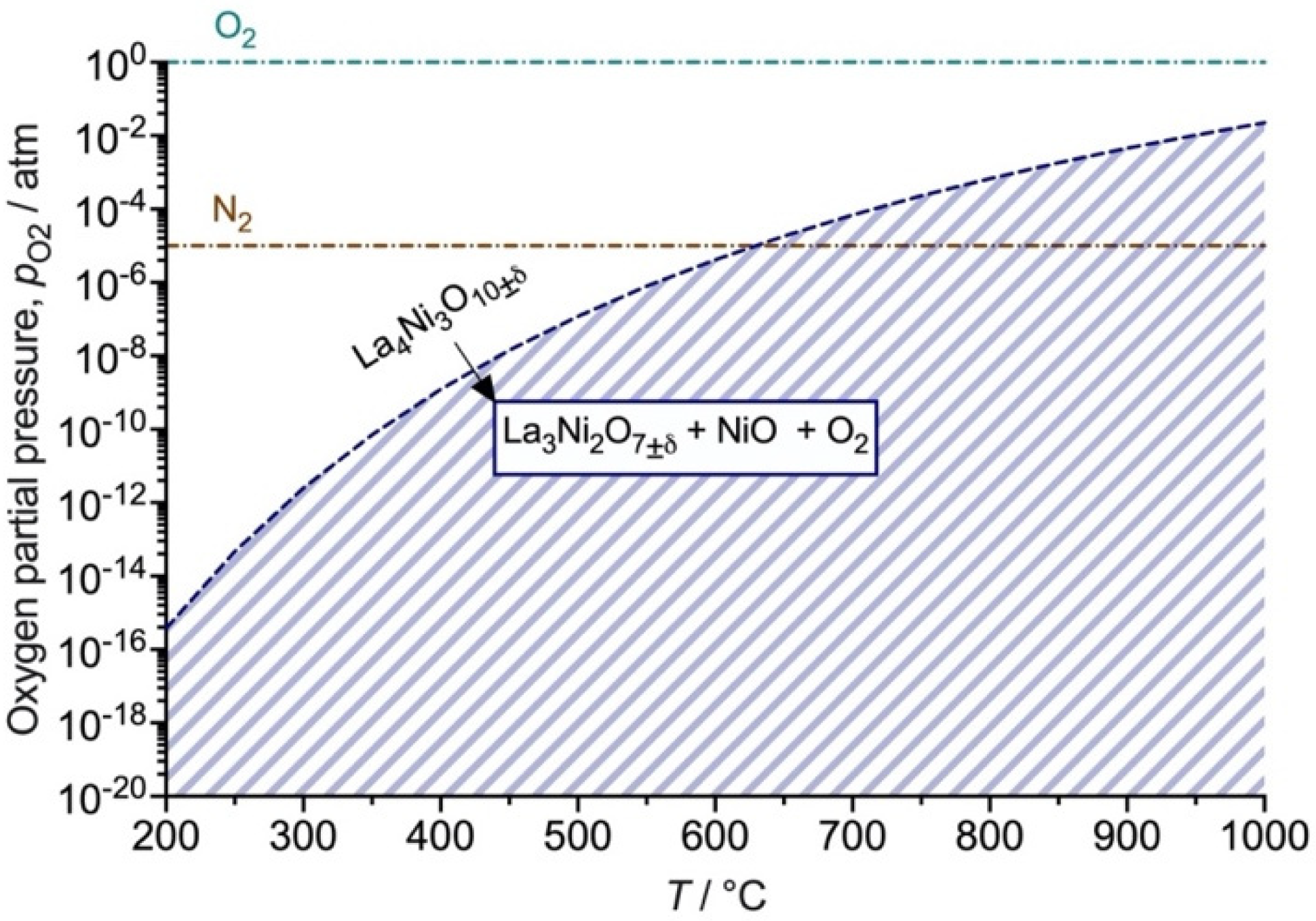

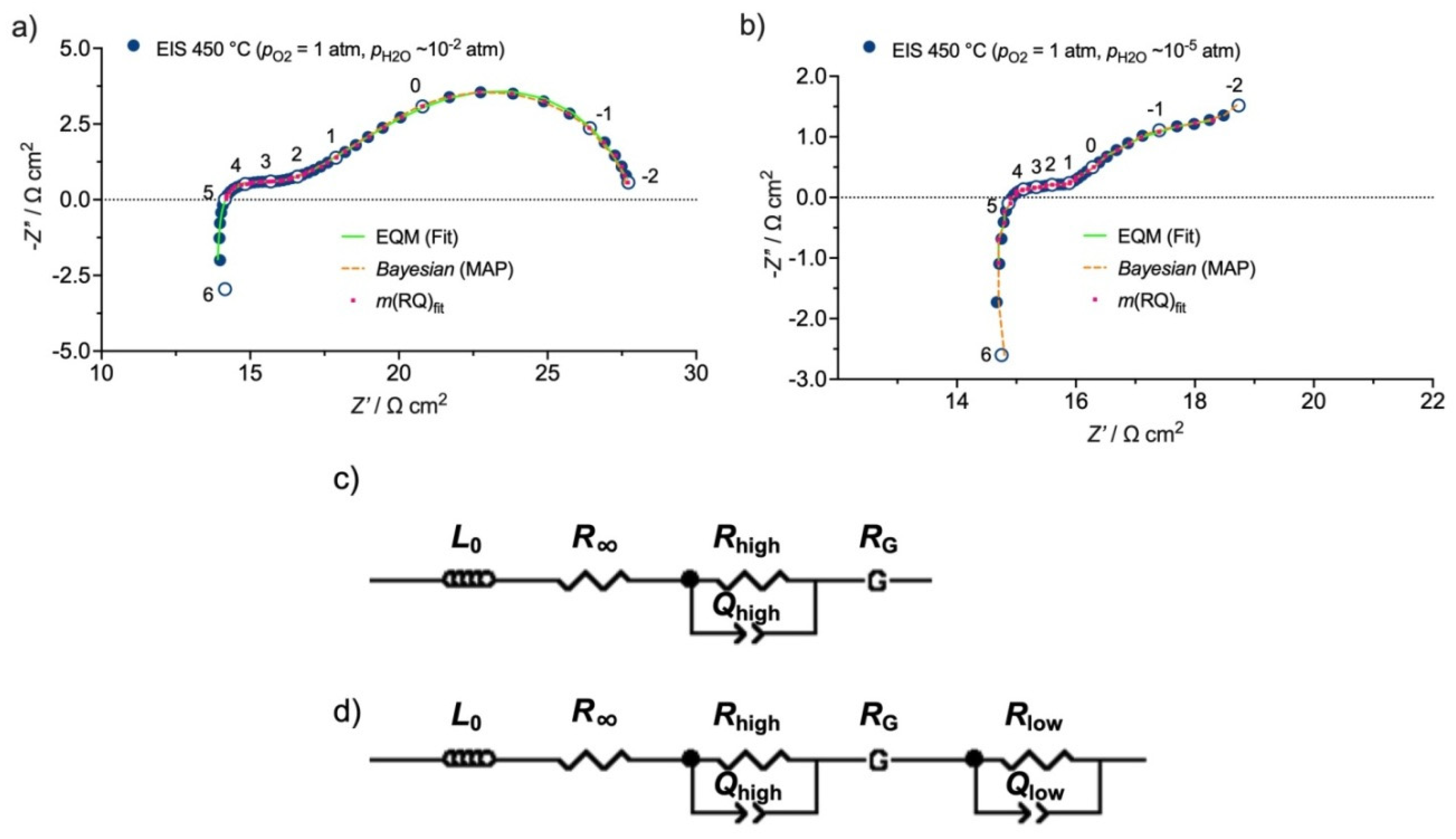
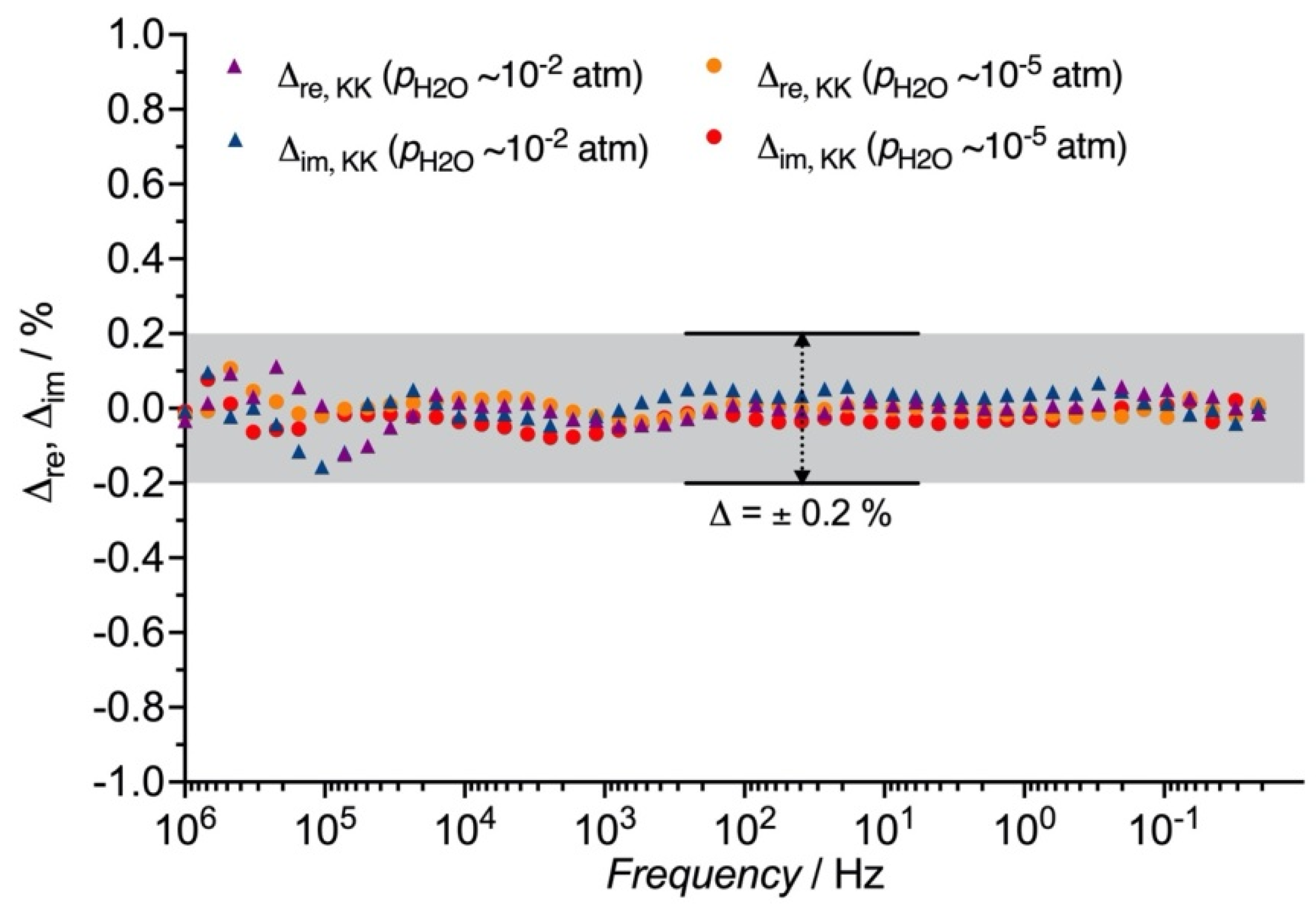
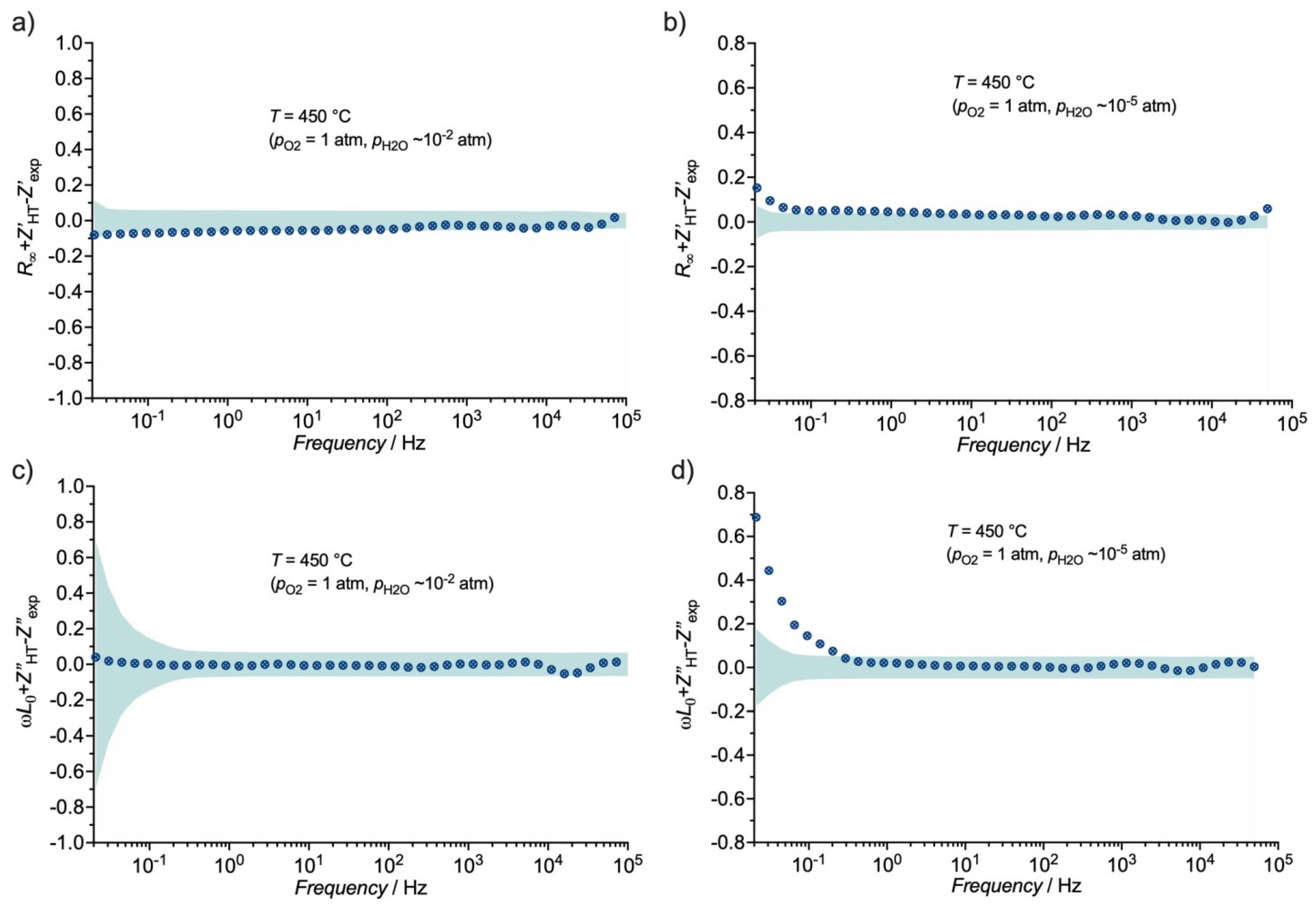


| Circuit Element | Wet | Low Humidity |
|---|---|---|
| L/H | 5.13 × 10−7 (2.33%) | 3.69 × 10−7 (2.41%) |
| R∞ /Ω | 12.28 (1.16%) | 13.25 (1.86%) |
| Rhigh/Ω | 4.79 (6.45%) | 2.40 (23.23%) |
| Qhigh/S sφ | 2.08 × 10−2 (11.90%) | 8.30 × 10−2 (21.76%) |
| high | 0.25 (7.06%) | 0.16 (21.88%) |
| Y0/S s−1/2 | 8.15 × 10−2 (1.36%) | 0.99 (93.56%) |
| KG/s−1 | 1.78 (1.38%) | 0.74 (73.81%) |
| Rlow/Ω | - | 2.99 (73.81%) |
| Qlow/S sφ | - | 1.49 (125.73%) |
| low | - | 0.76 (47.52%) |
| Metric | Score/% | |
|---|---|---|
| Wet | Low Humidity | |
| 76.19 | 76.19 | |
| 100.00 | 100.00 | |
| 99.58 | 98.39 | |
| 99.54 | 86.05 | |
| pH2O/atm | Activation Energy/eV | ||||
|---|---|---|---|---|---|
| Wet | 10−2 | Rhigh | RG | Rlow | Rp |
| 1.26 | 1.24 | - | 1.24 | ||
| Rhigh,eon | RG,eon | Rlow,eon | Rp,eon | ||
| 1.12 | 1.09 | - | 1.09 | ||
| Low humidity | 10−7 | Rhigh | RG | Rlow | Rp |
| 0.97 | 1.63 | 1.66 | 1.28 | ||
| Rhigh,eon | RG,eon | Rlow,eon | Rp,eon | ||
| 0.69 | 1.40 | 1.40 | 1.11 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loureiro, F.J.A.; Ramasamy, D.; Graça, V.C.D.; Holz, L.I.V.; Mikhalev, S.M.; Fagg, D.P. Analysis of La4Ni3O10±?-BaCe0.9Y0.1O3-? Composite Cathodes for Proton Ceramic Fuel Cells. Appl. Sci. 2021, 11, 3407. https://doi.org/10.3390/app11083407
Loureiro FJA, Ramasamy D, Graça VCD, Holz LIV, Mikhalev SM, Fagg DP. Analysis of La4Ni3O10±?-BaCe0.9Y0.1O3-? Composite Cathodes for Proton Ceramic Fuel Cells. Applied Sciences. 2021; 11(8):3407. https://doi.org/10.3390/app11083407
Chicago/Turabian StyleLoureiro, Francisco J. A., Devaraj Ramasamy, Vanessa C. D. Graça, Laura I. V. Holz, Sergey M. Mikhalev, and Duncan P. Fagg. 2021. "Analysis of La4Ni3O10±?-BaCe0.9Y0.1O3-? Composite Cathodes for Proton Ceramic Fuel Cells" Applied Sciences 11, no. 8: 3407. https://doi.org/10.3390/app11083407
APA StyleLoureiro, F. J. A., Ramasamy, D., Graça, V. C. D., Holz, L. I. V., Mikhalev, S. M., & Fagg, D. P. (2021). Analysis of La4Ni3O10±?-BaCe0.9Y0.1O3-? Composite Cathodes for Proton Ceramic Fuel Cells. Applied Sciences, 11(8), 3407. https://doi.org/10.3390/app11083407






