Development of Multi-Axis Crank Linkage Motion System for Synchronized Flight Simulation with VR Immersion
Abstract
:1. Introduction
2. Experimental Methods
2.1. Specification of Platform
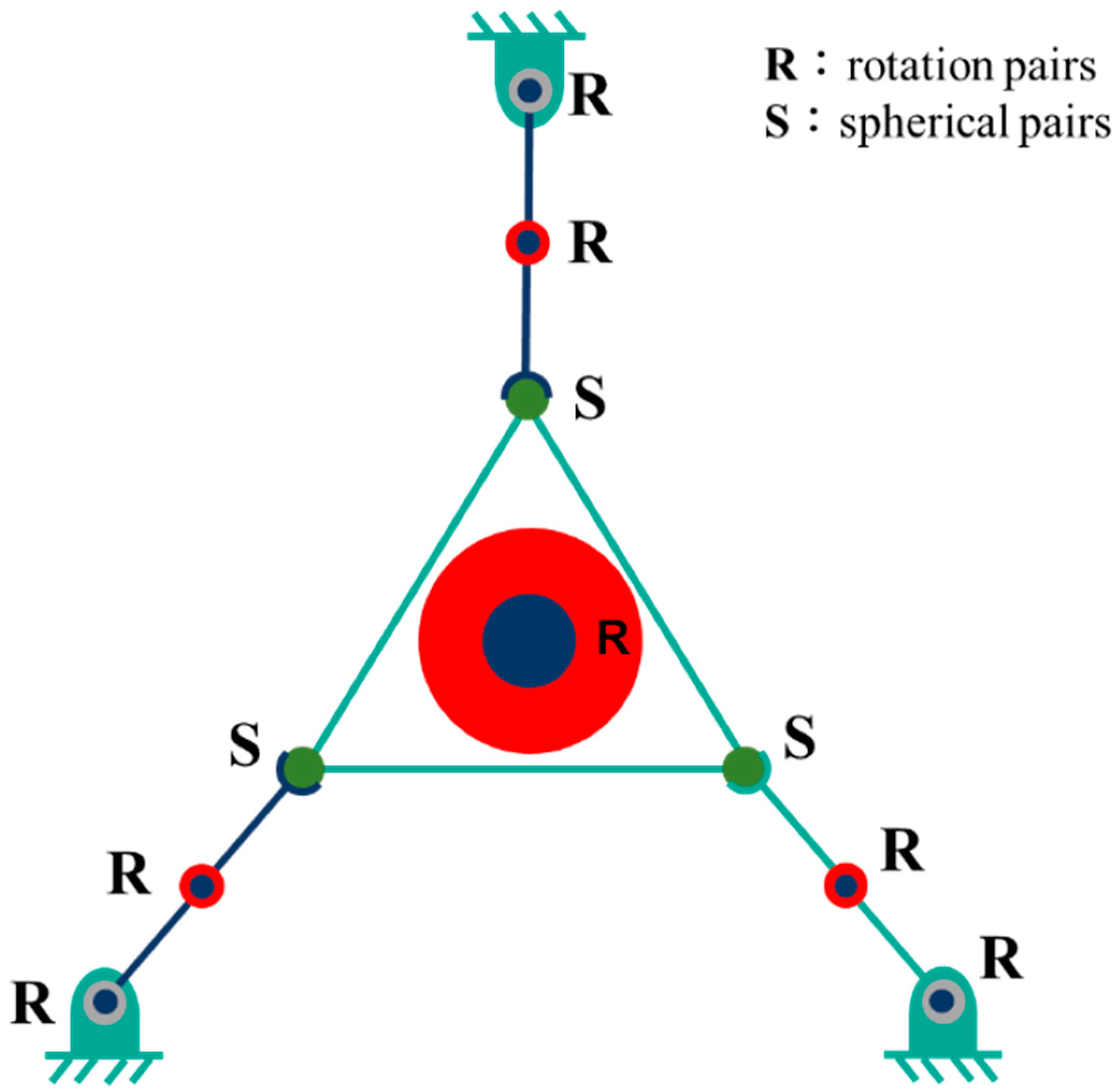
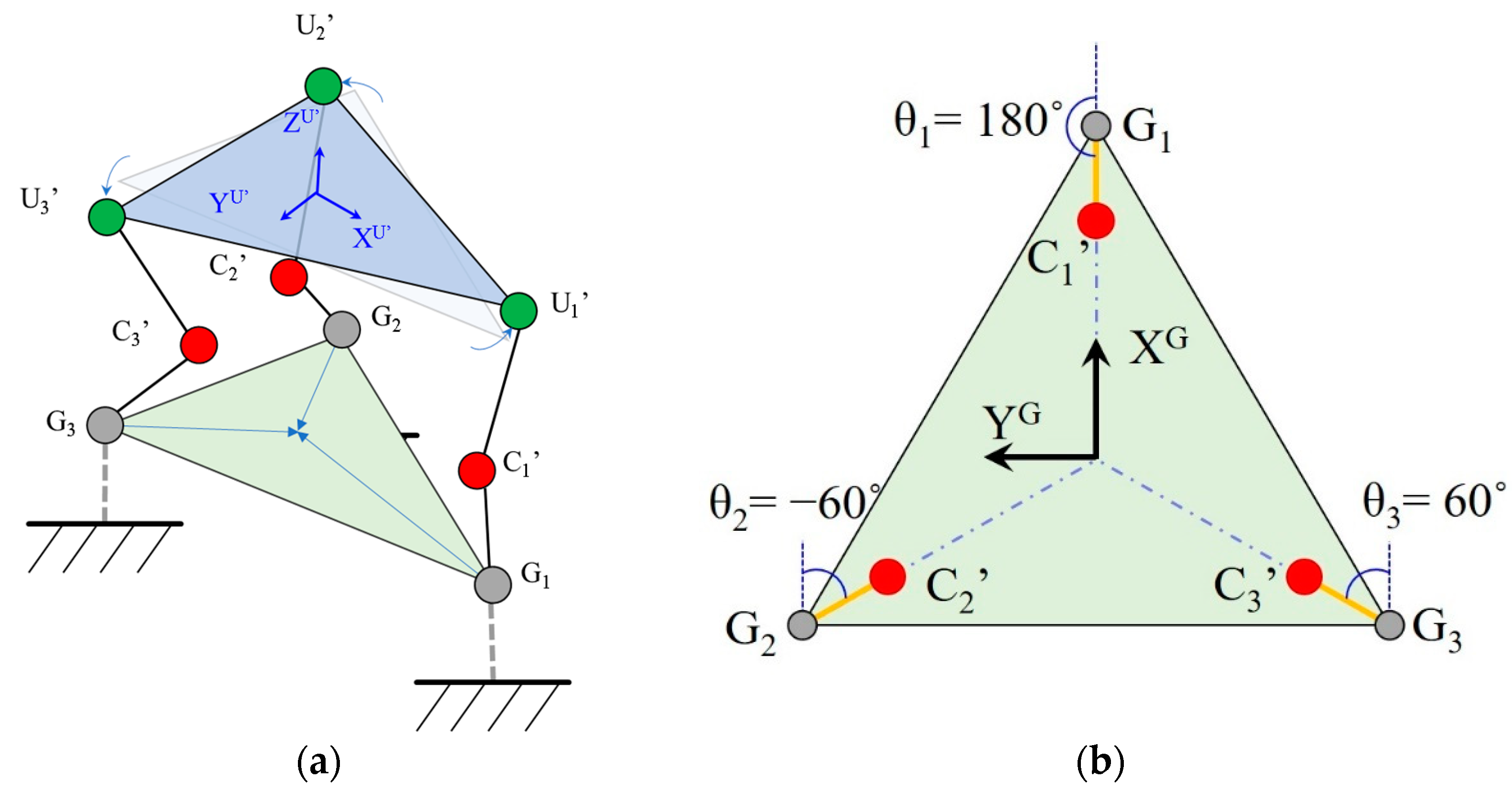
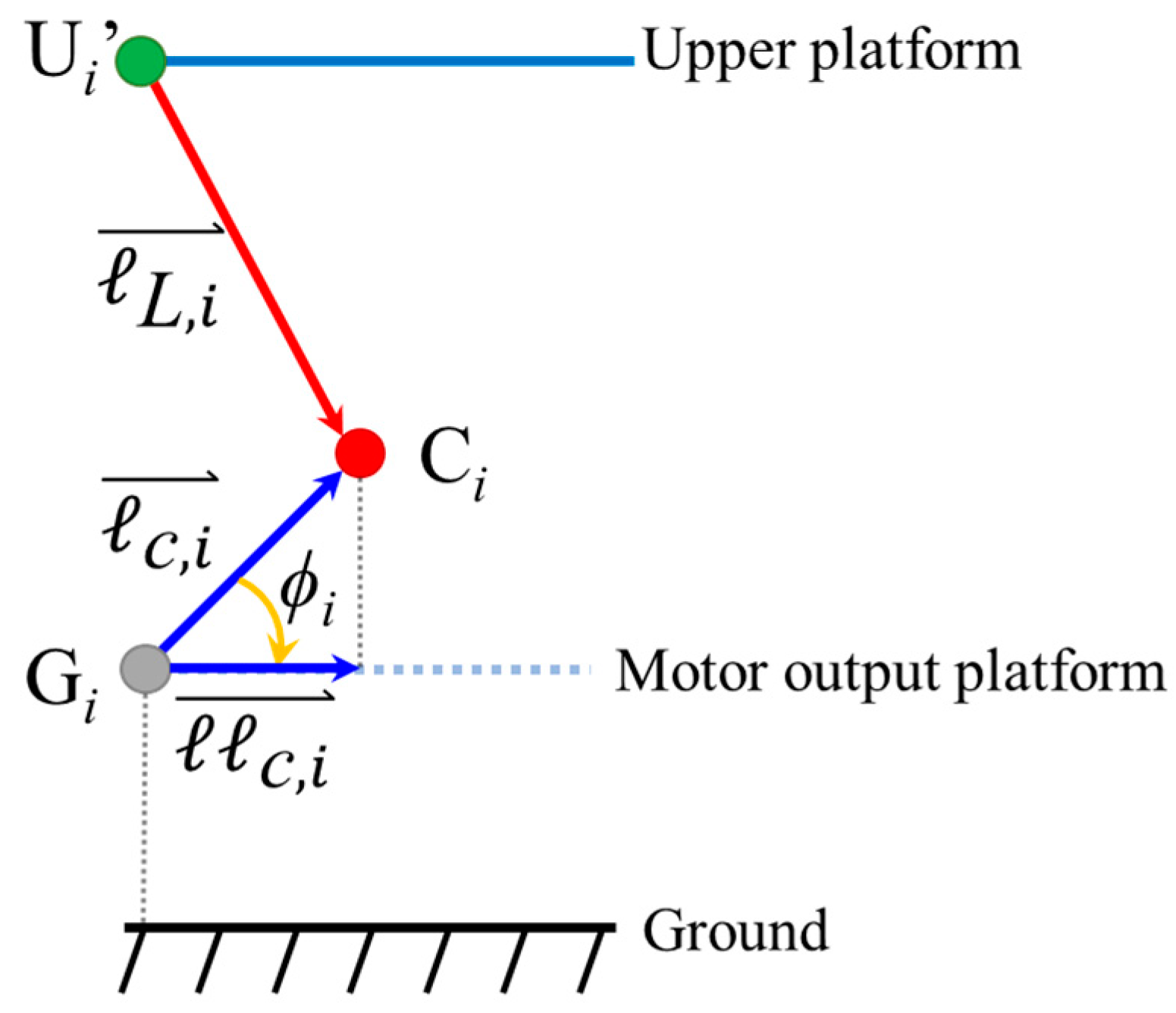
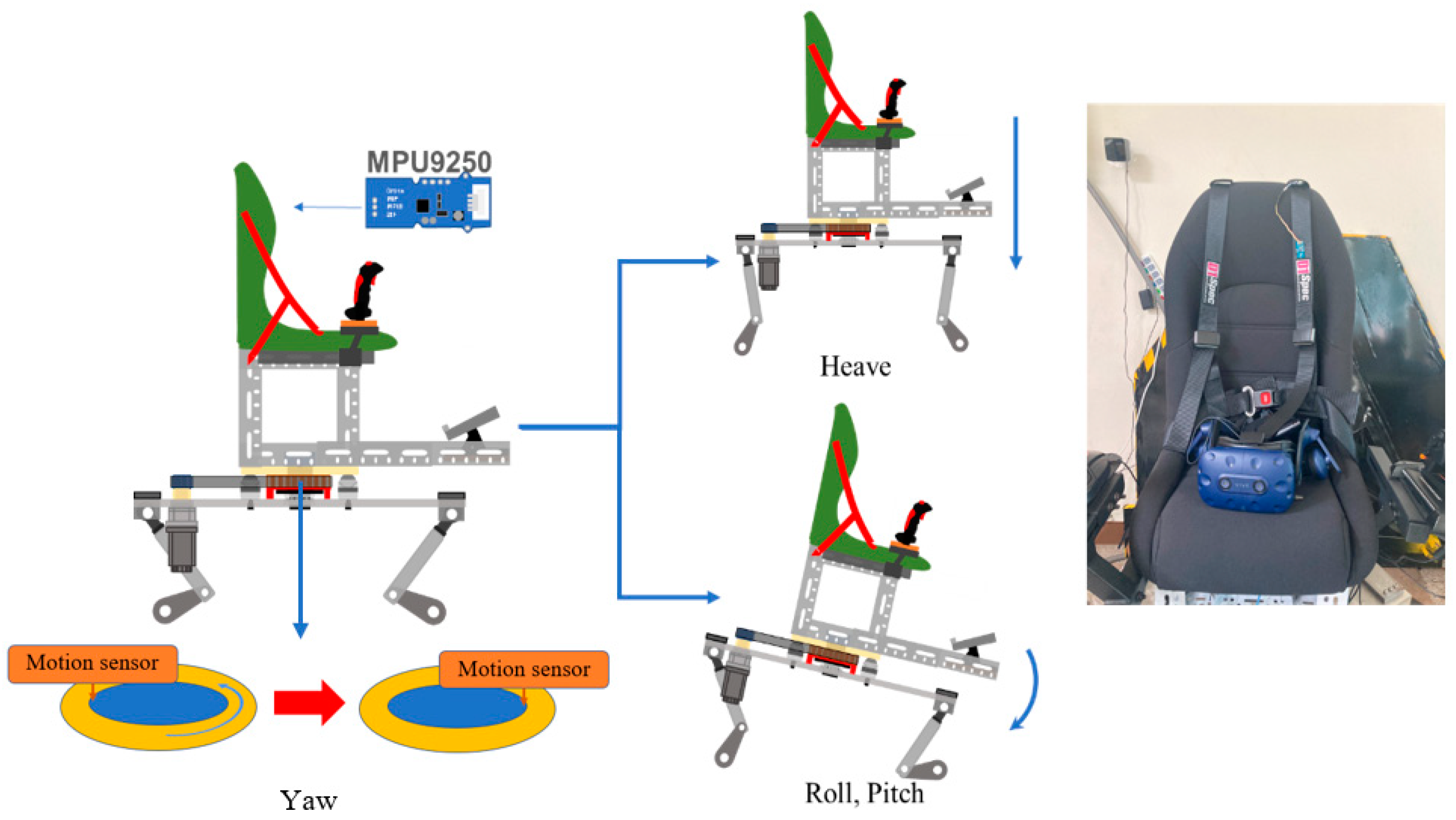
2.2. Design of the Platform
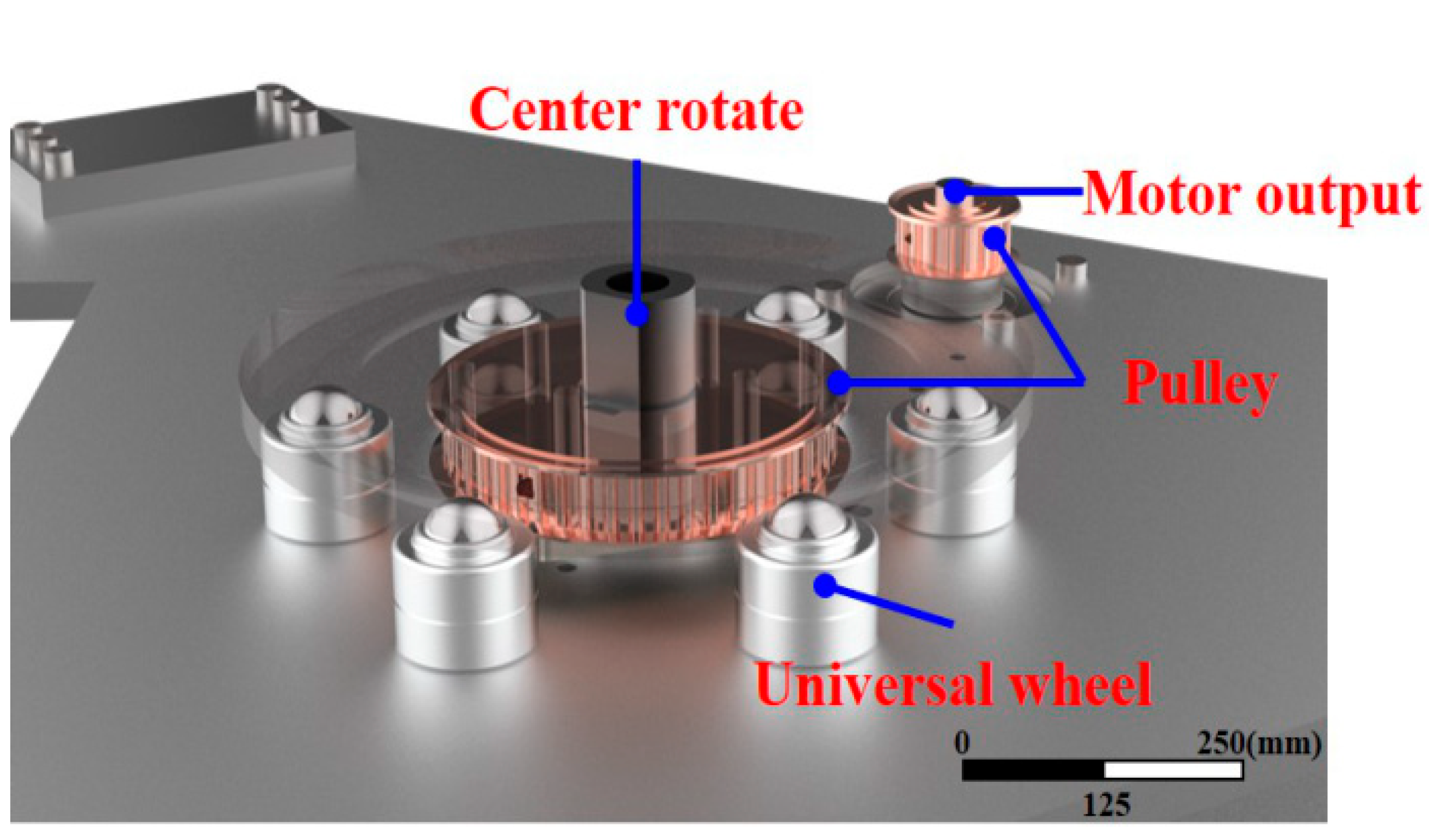
2.3. Central Rotating Mechanism Design
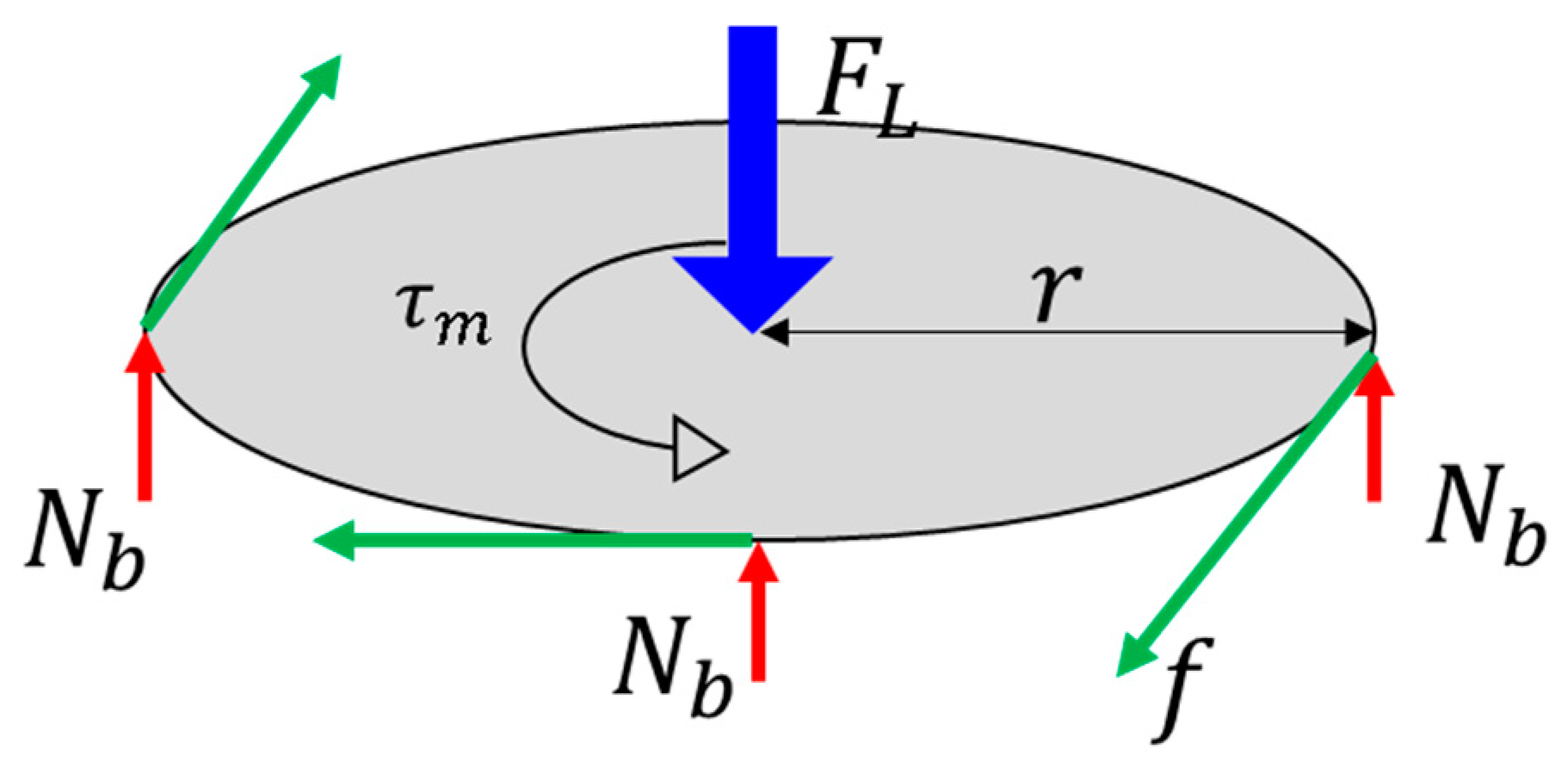
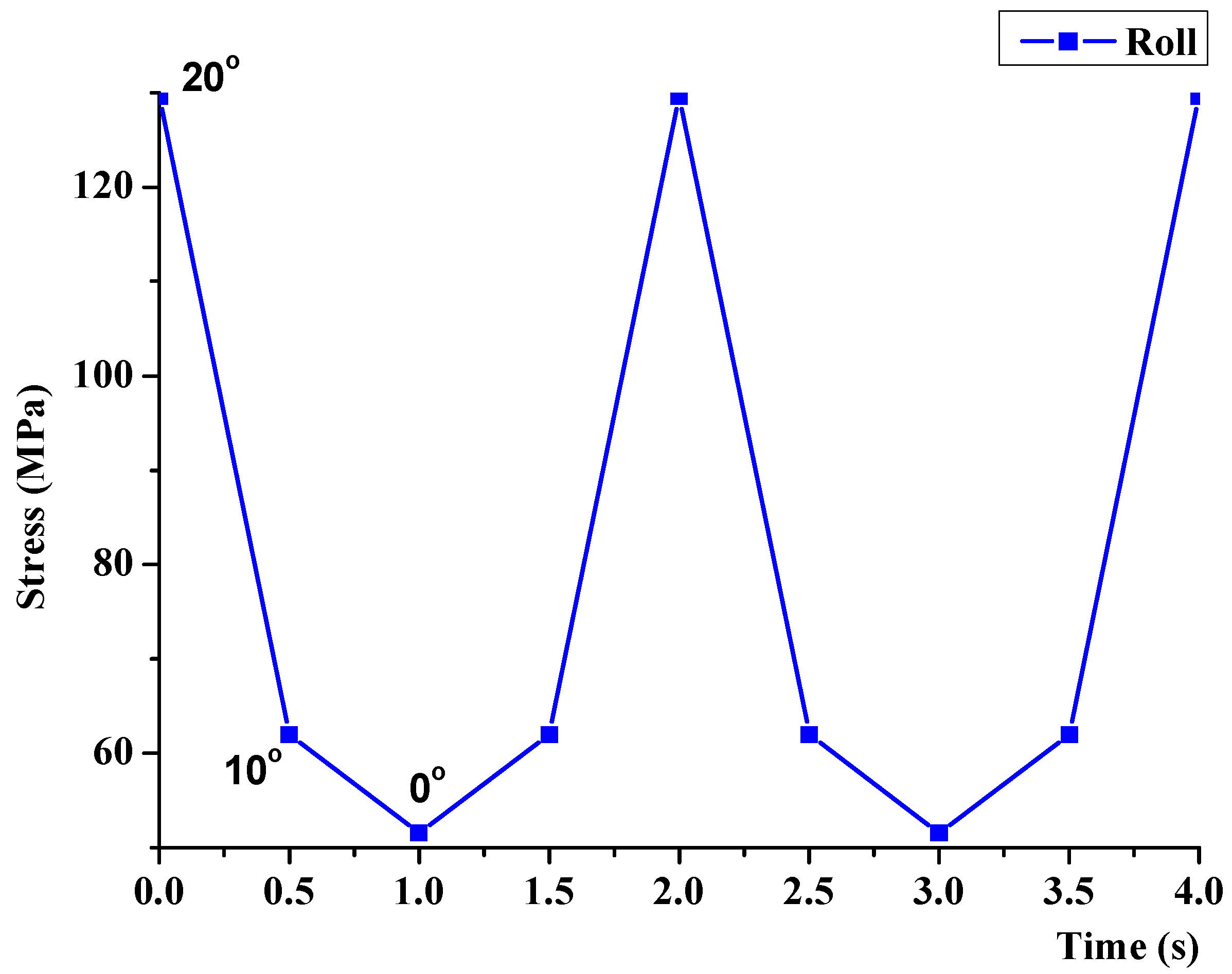
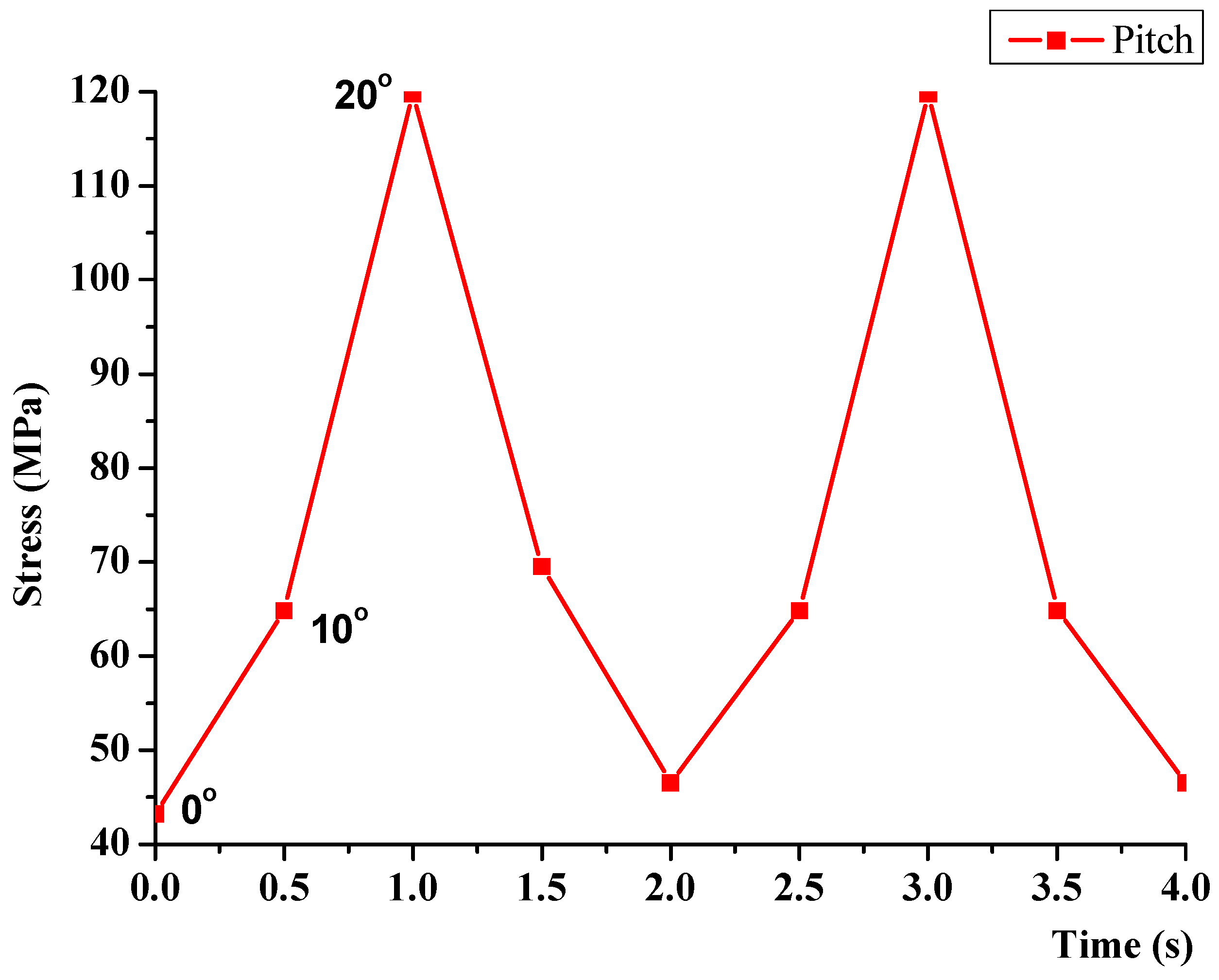
2.4. Stress Analysis
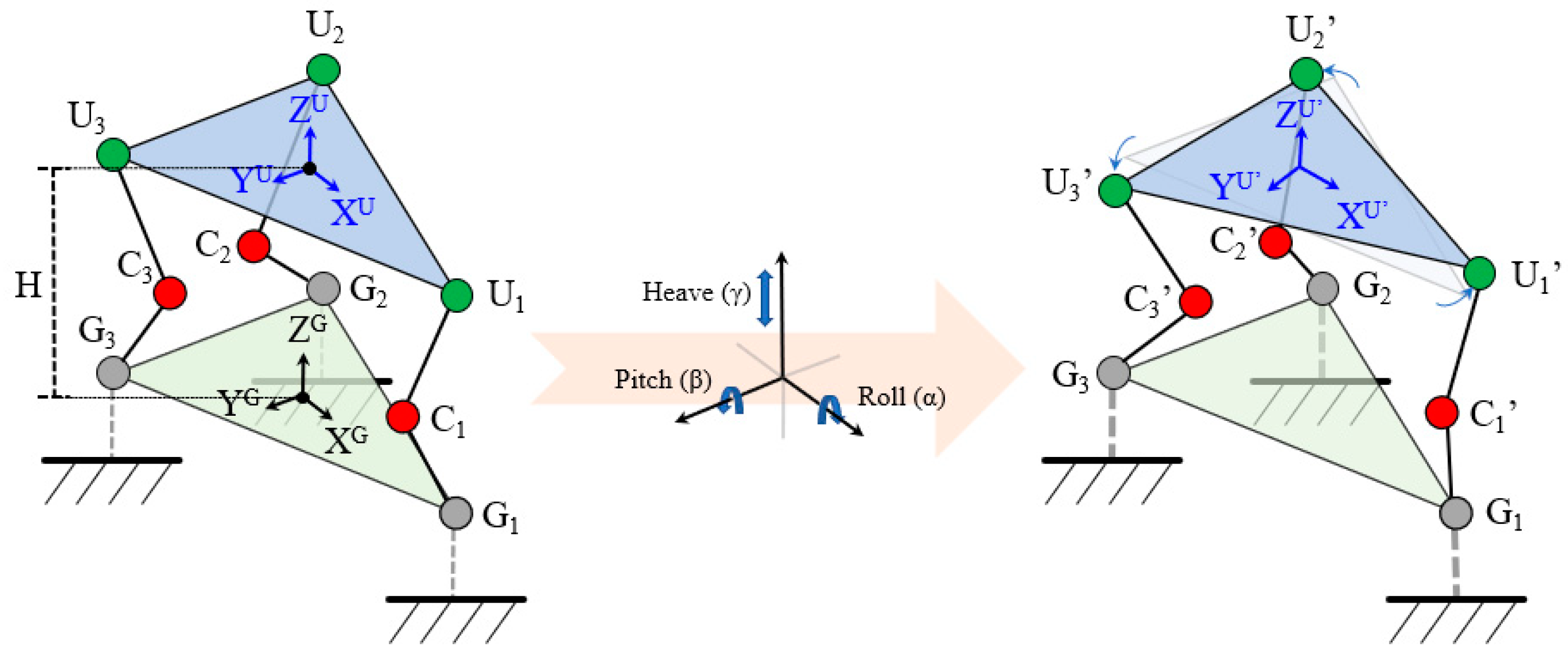
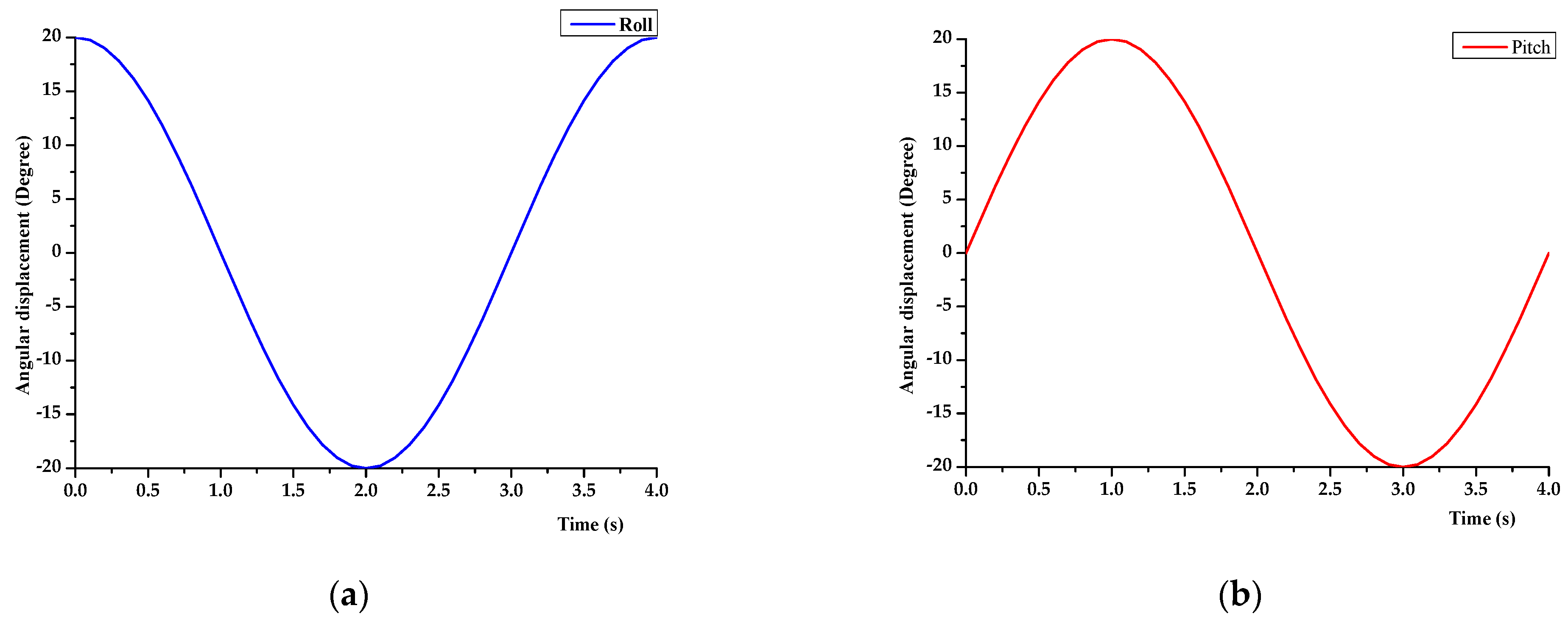
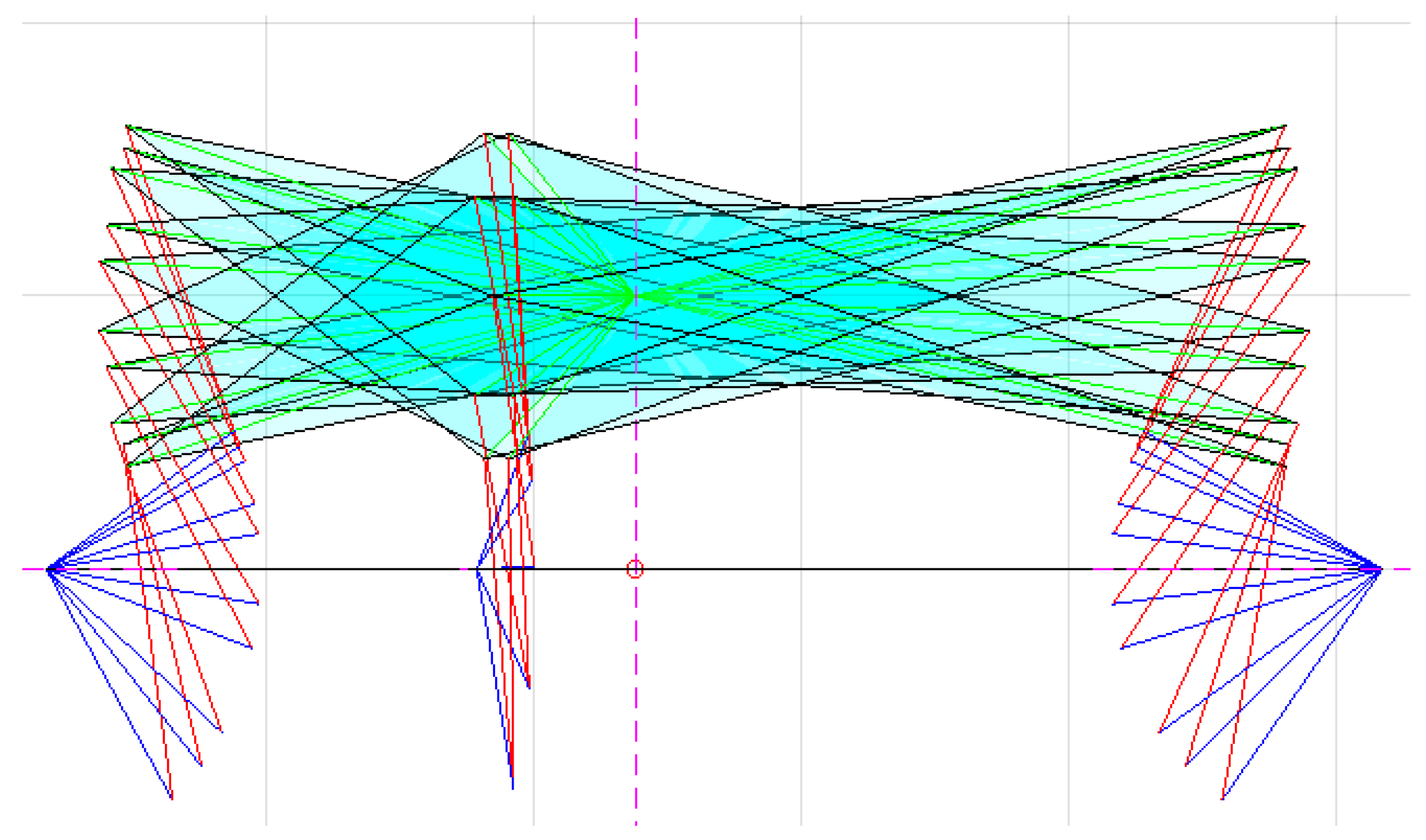
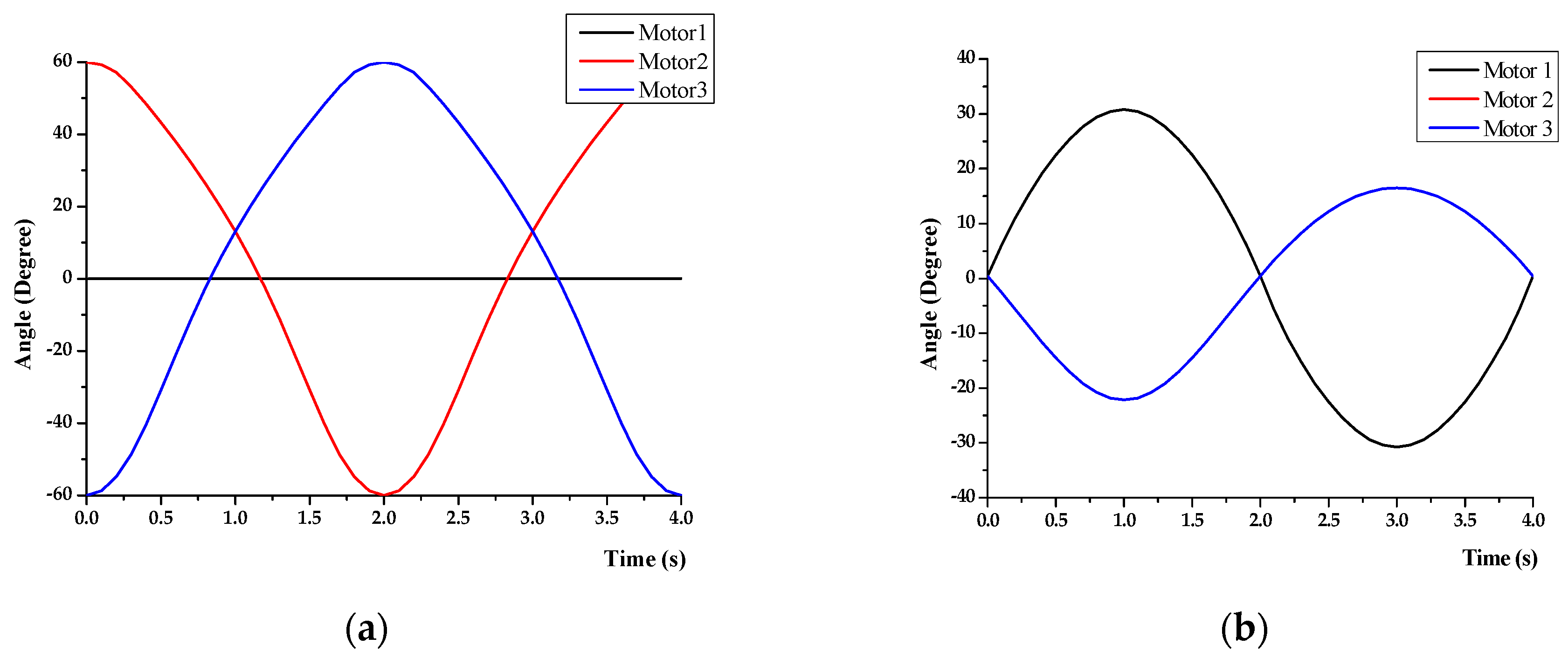
2.5. Motion Trajectory
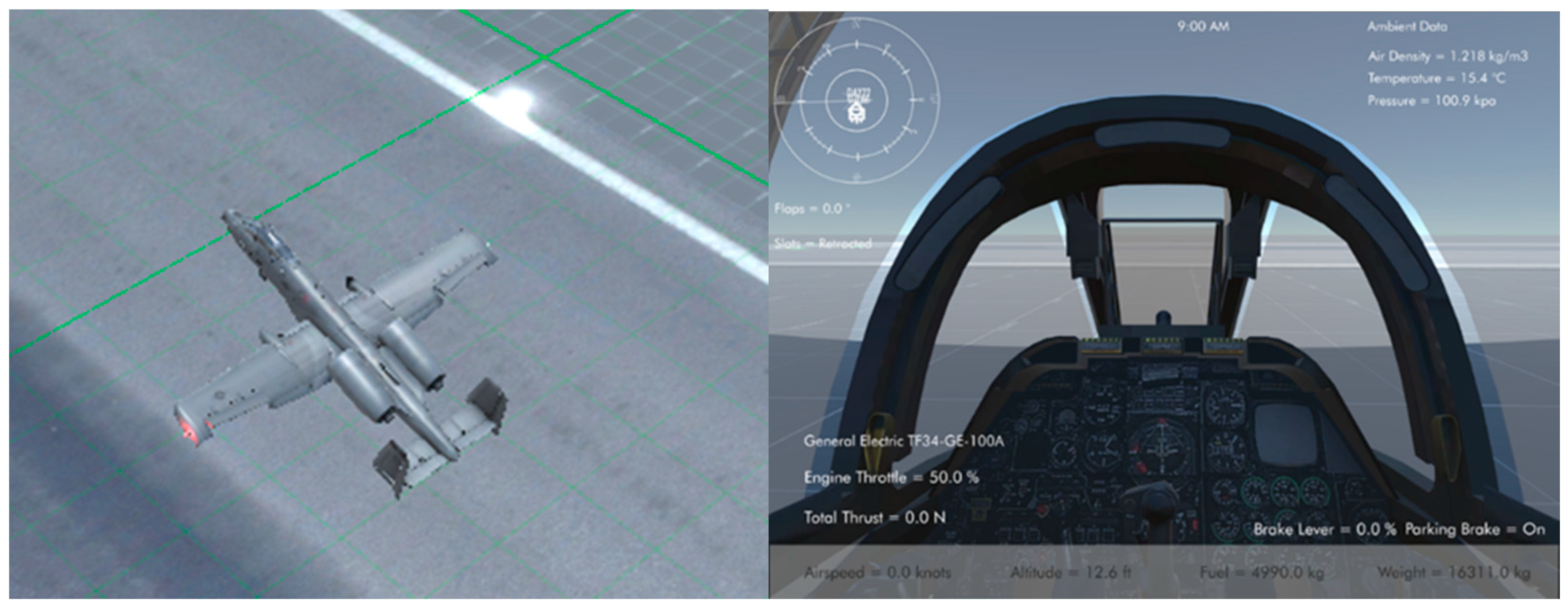
2.6. VR Image Design Method
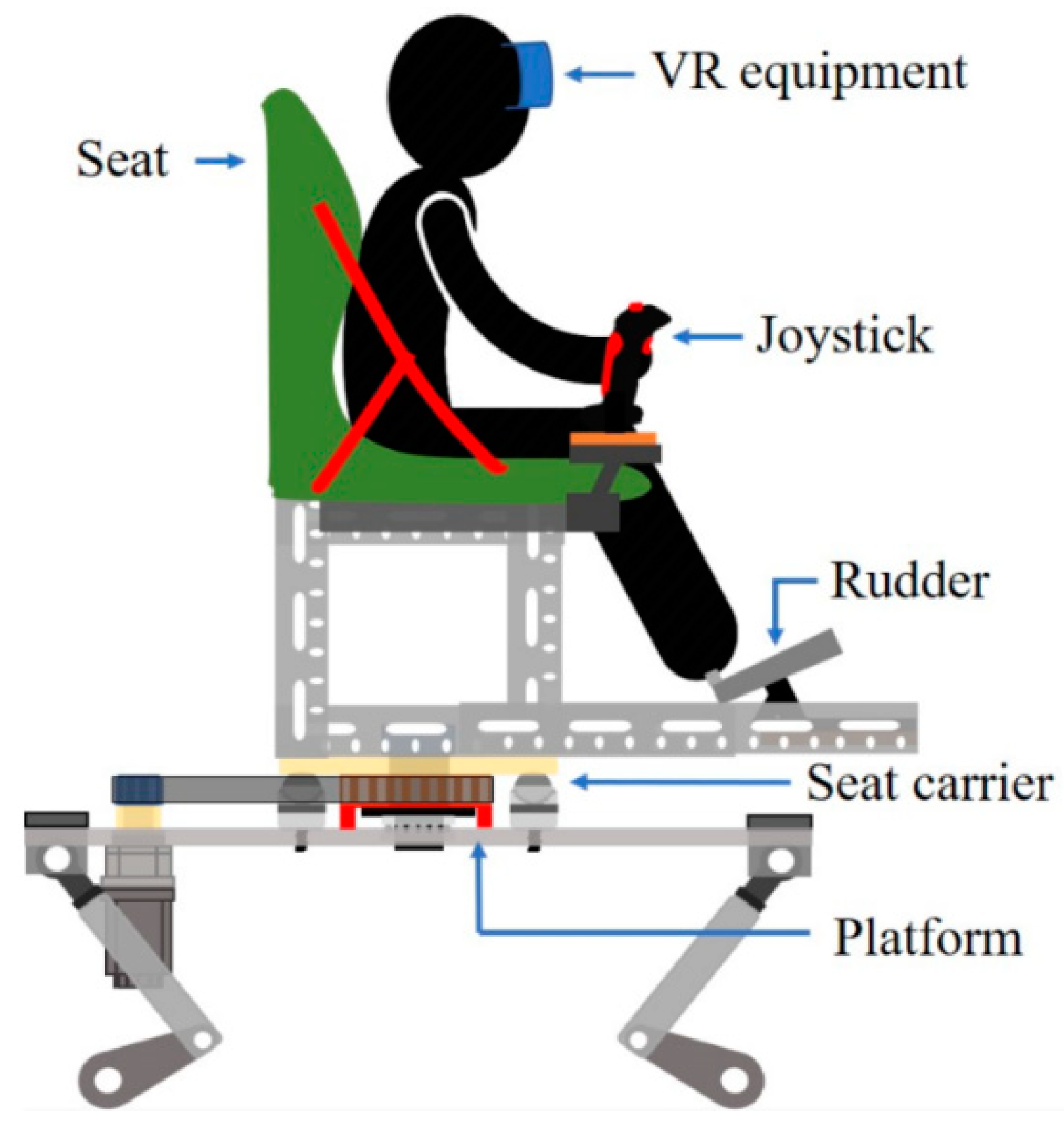
2.7. Platform Integrated with VR
3. Results and Discussion
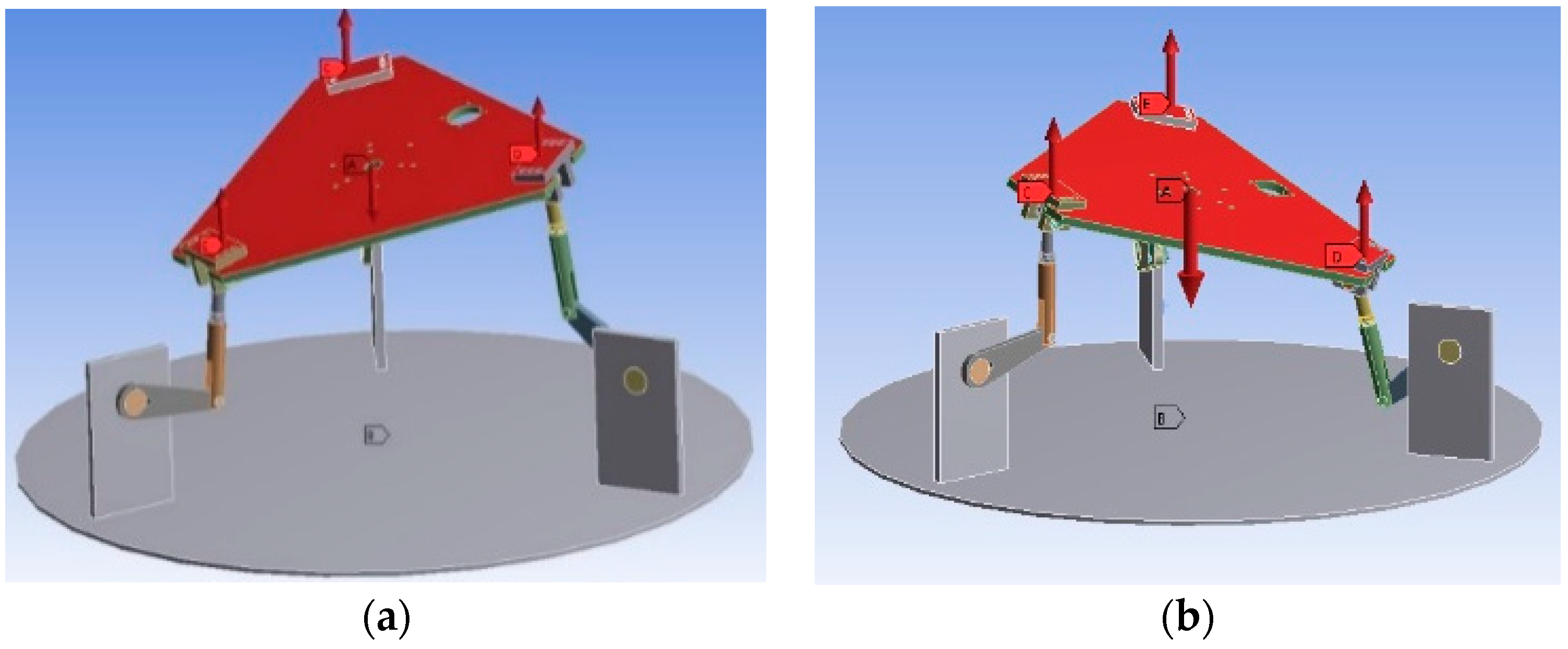
3.1. Multi-Axis Motion Platform Mechanism
3.2. Central Rotating Mechanism
3.3. Stress Analysis Results
3.4. Motion Trajectory Results
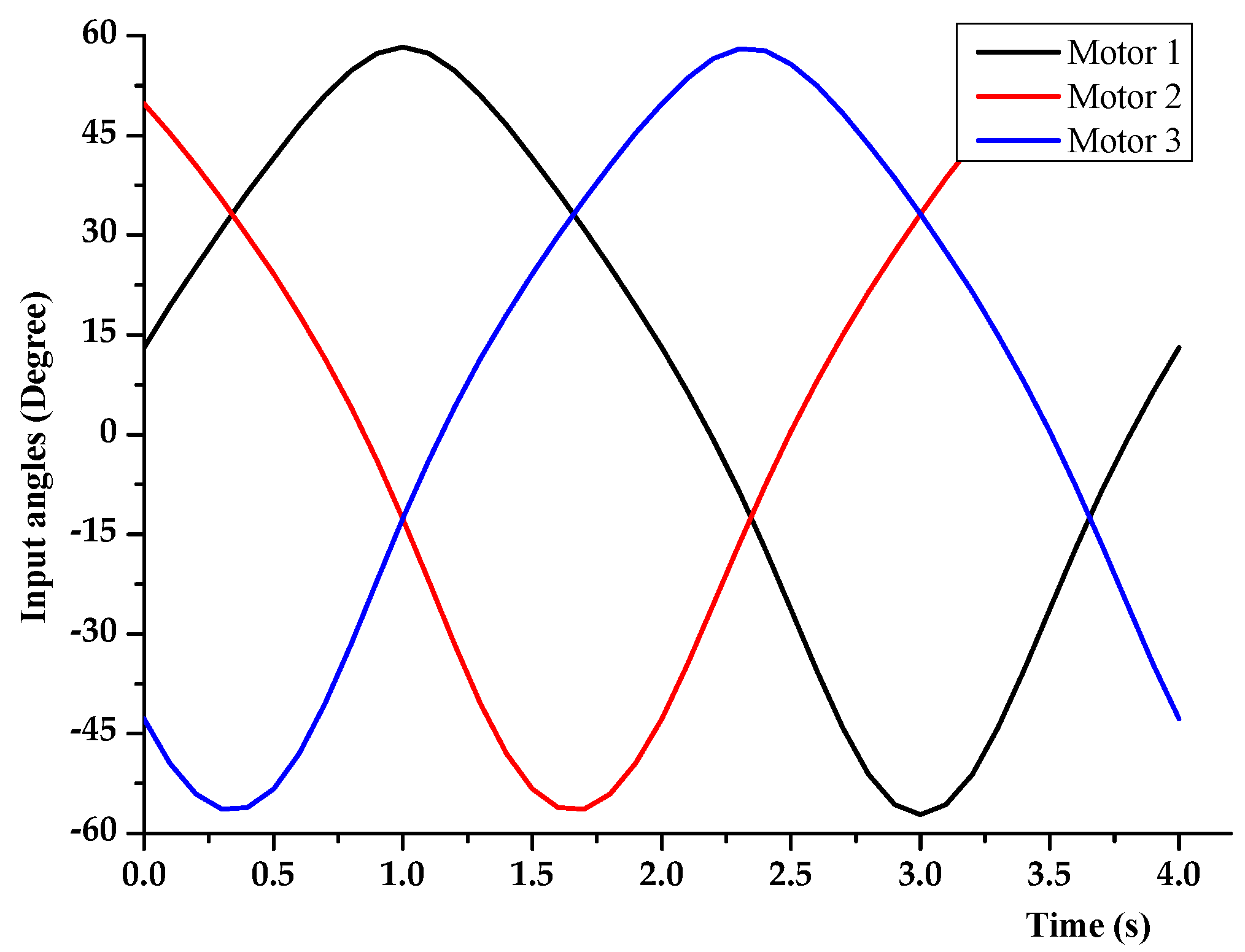
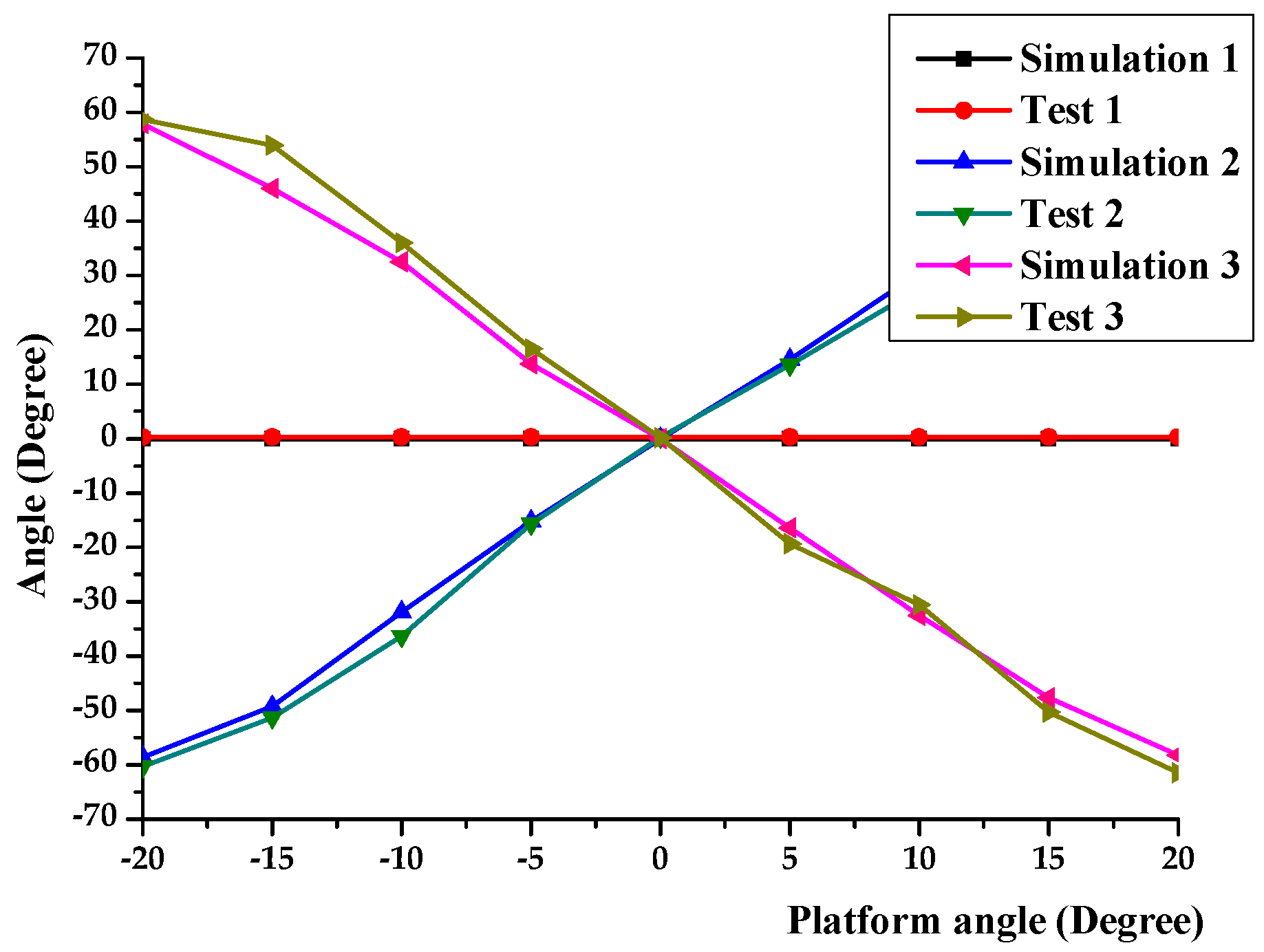
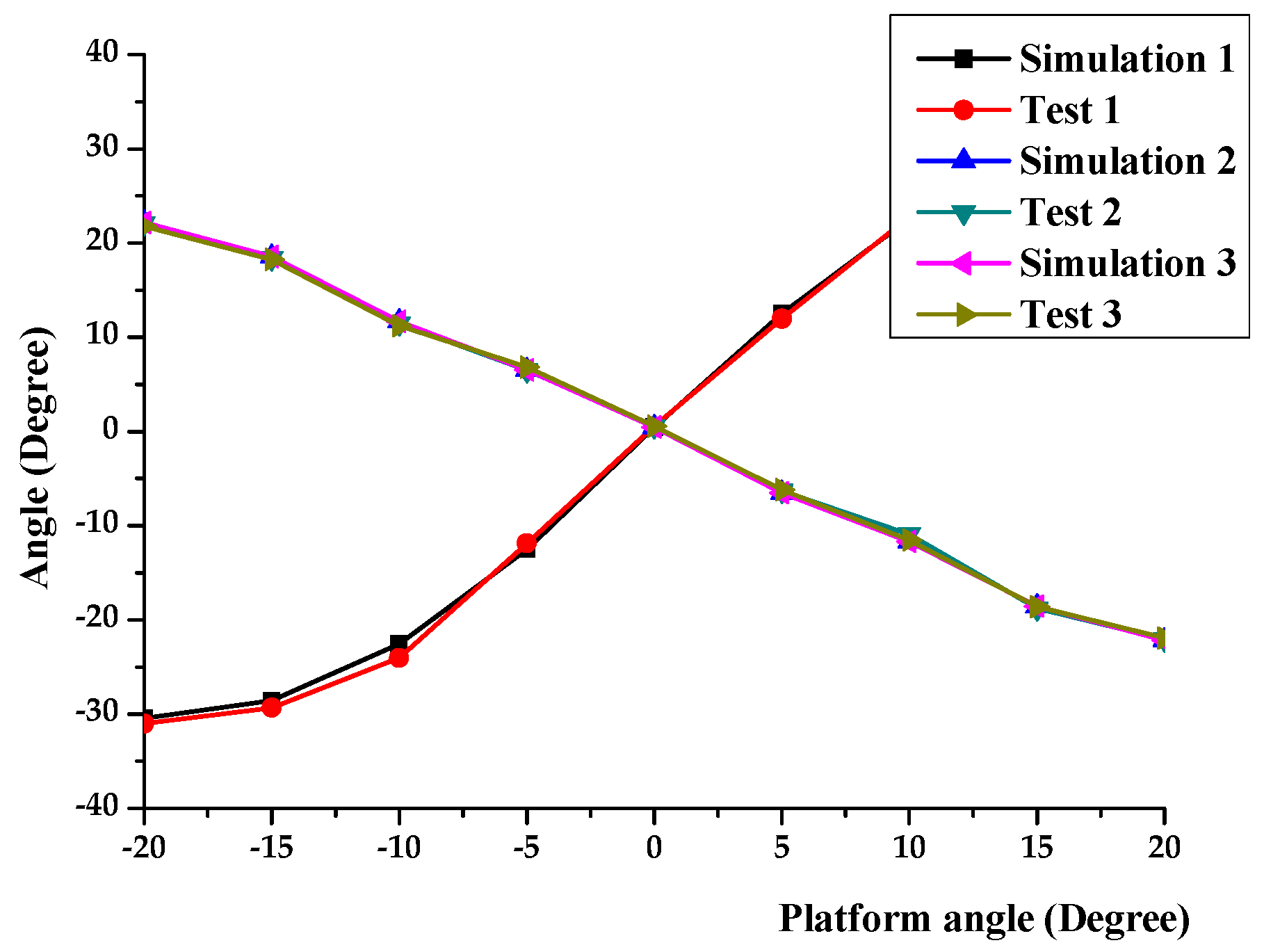
3.5. Motor Angle Trajectory Verification
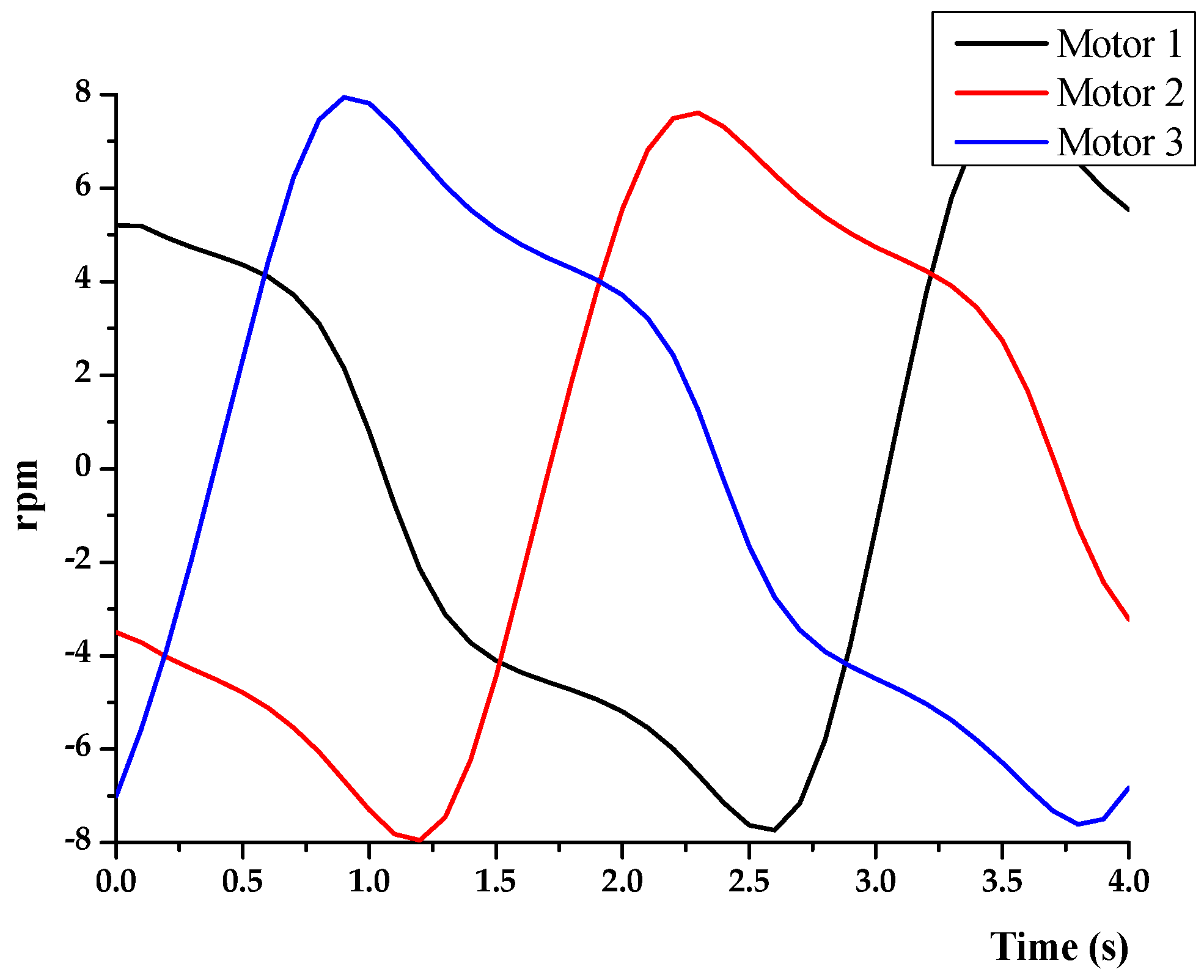
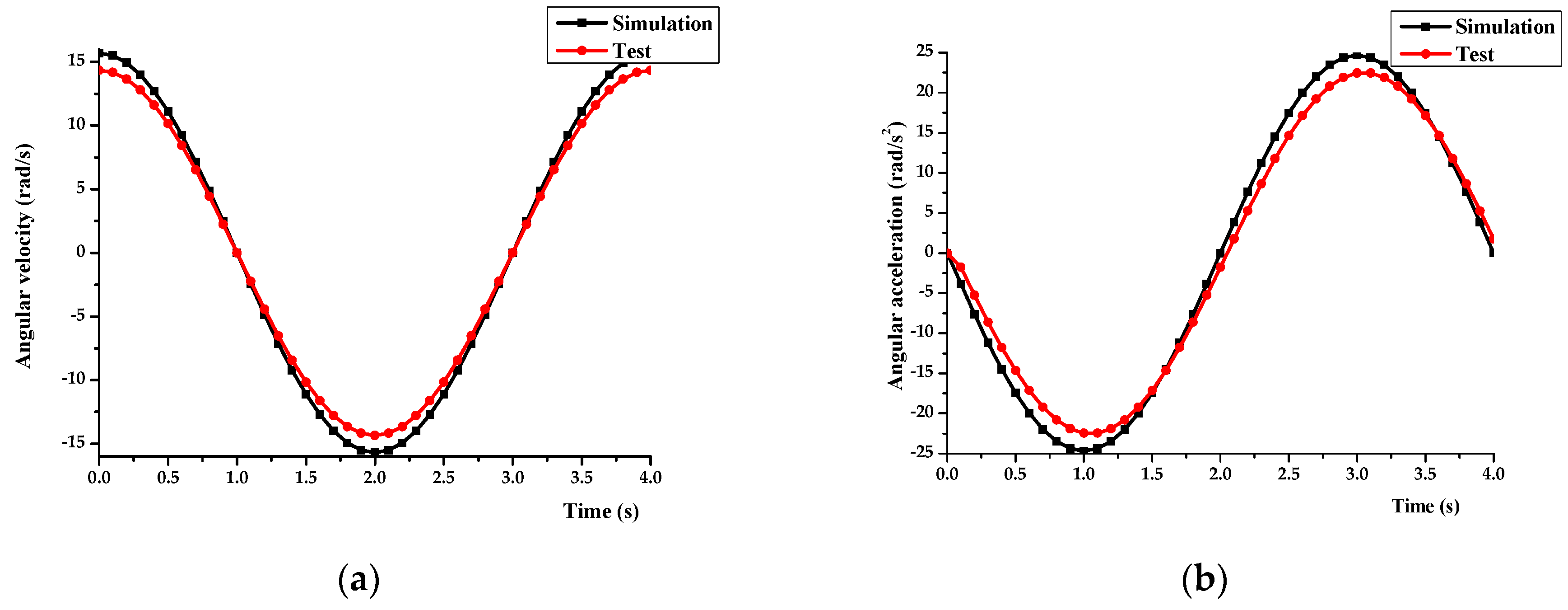
3.6. Motions Performance Test
3.7. Virtual Image Design
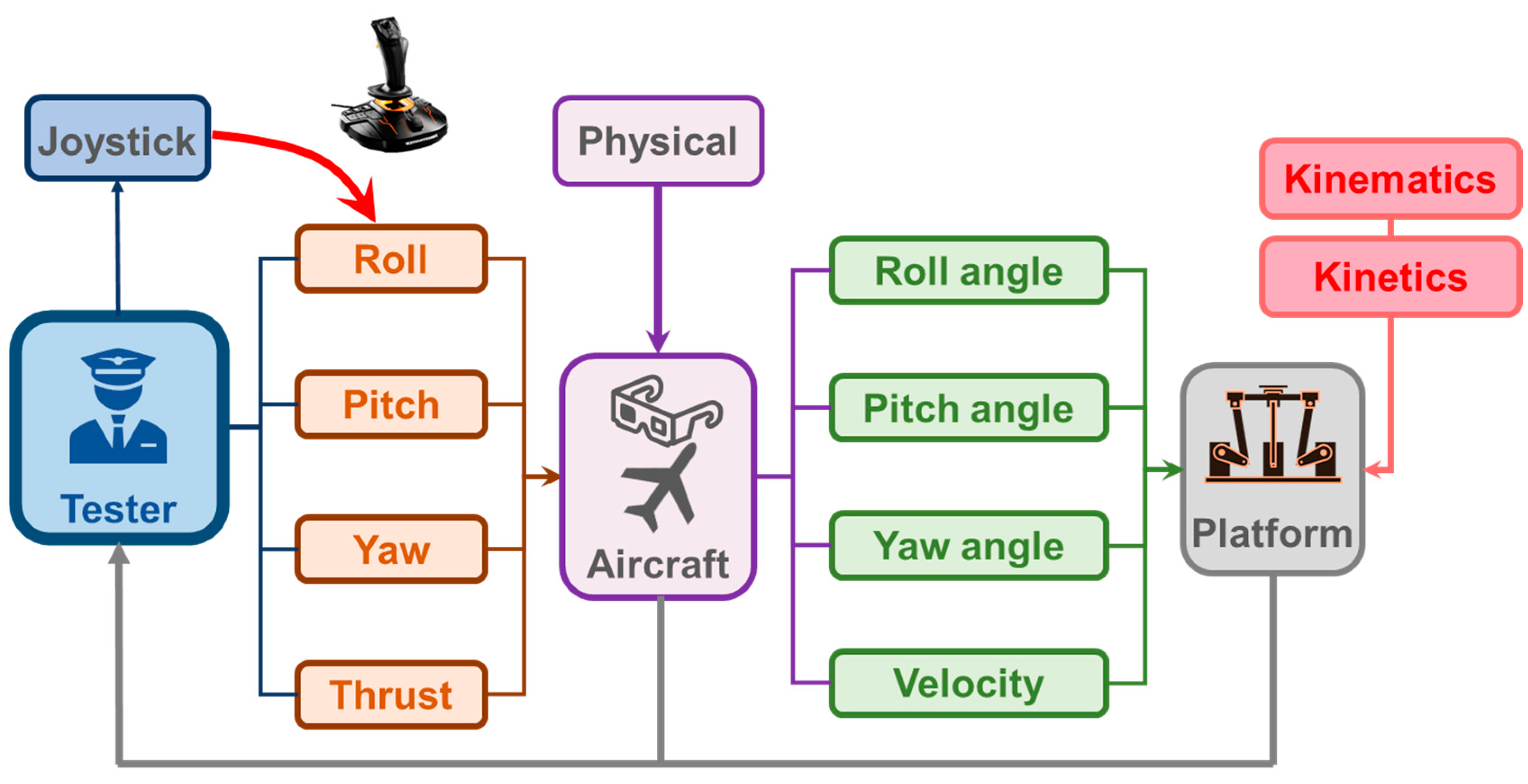
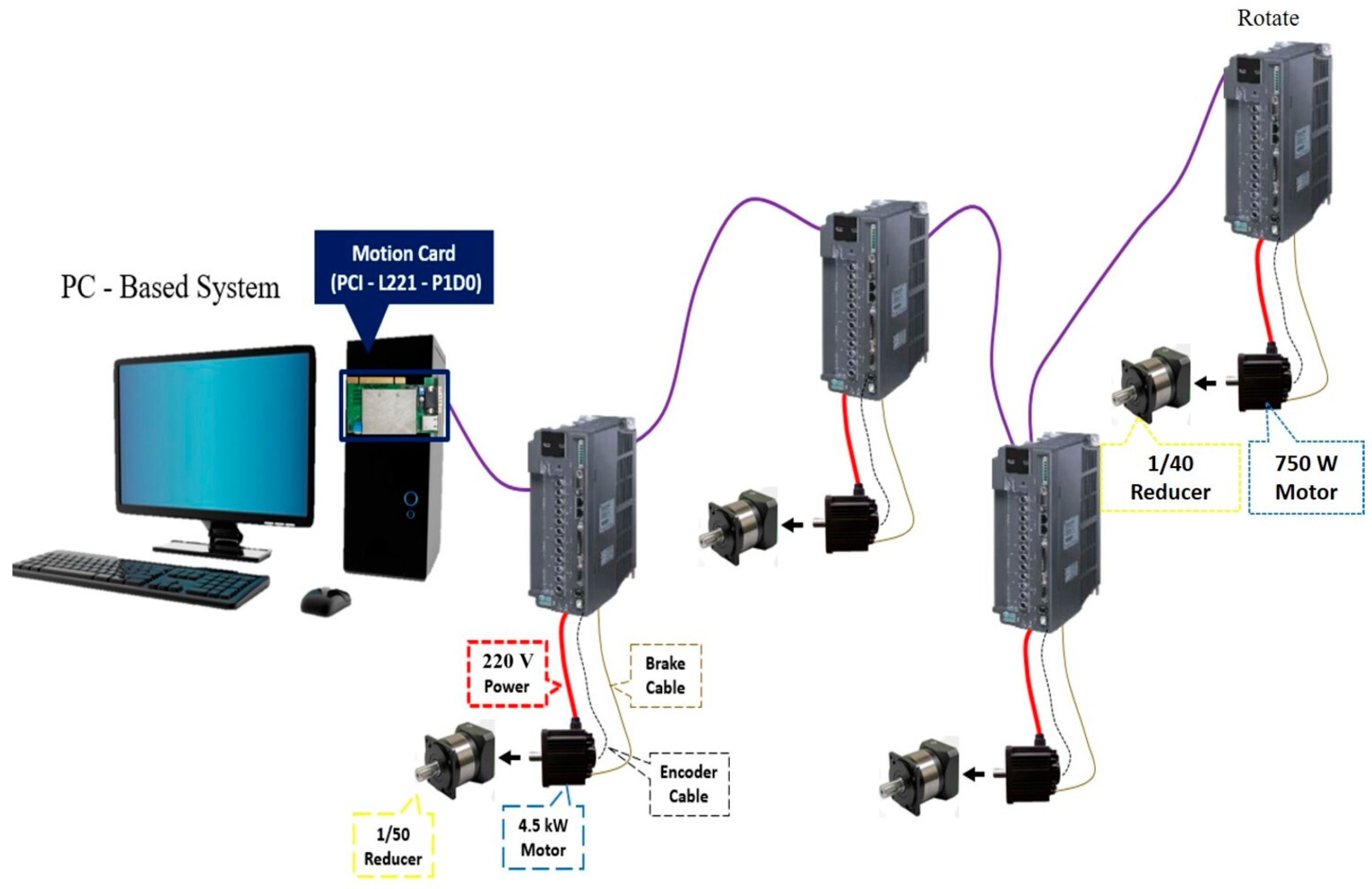
3.8. Control System
3.9. System Reliability
3.10. Rotatable Multi-Axis Motion Platform Combined with VR
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gough, V.; Whitehall, S. Universal tire test machine. In Proceedings of the FISITA 9th International Technical Congress, London, UK, 1 January 1962; Volume 11, pp. 117–137. [Google Scholar]
- Stewart, D. A platform with six Degrees of Freedom. Proceedings of the institution of mechanical engineers. Proc. Inst. Mech. Eng. 1965, 180, 371–386. [Google Scholar] [CrossRef]
- Hurt, K. Structural Kinematics of in Parallel Actuated Robot-Arms. ASME J. Mech. Transm. Autom. Des. 1983, 105, 705–712. [Google Scholar]
- Ammanagi, S.; Poornima, V.; Sera, A.; Sunder, R. Development of a digitally-controlled three-axis earthquake shake table. Curr. Sci. 2006, 91, 190–203. [Google Scholar]
- Itul, T.; Pisla, D. Dynamics of a 3-DoF parallel mechanism used for orientation applications. IEEE Int. Conf. Autom. Qual. Test. Robot. 2008, 2, 398–403. [Google Scholar] [CrossRef]
- Philip, E. Development of a 3-DOF motion simulation platform. Ph.D. Thesis, University of Stellenbosch, Stellenbosch, South Africa, 2010. [Google Scholar]
- Zhang, B.; Li, J.; Jiang, Z.; Wang, C.; Zhang, Z. Kinematics analysis of a 3-DoF hydraulic driven parallel mechanis. In IOP Conf. Series: Materials Science and Engineering; IOP Publishing: Kuala Lumpur, Malaysia, 2018; Volume 324. [Google Scholar]
- Ryszard, D.; Piotr, W. Design of a hydraulically actuated 3-DoF translational parallel manipulator. In Proceedings of the Fourth Huntsville Gamma-Ray Burst Symposium; AIP Publishing: Bydgoszcz, Poland, 2019; Volume 2077, p. 020015. [Google Scholar]
- Sukede, A.K.; Arora, J. Auto tuning of PID controller. In Proceedings of the 2015 International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; Institute of Electrical and Electronics Engineers (IEEE): Pune, India, 2015; Volume 2015, pp. 1459–1462. [Google Scholar] [CrossRef]
- Astrom, K.; Hagglund, T. Automatic Tuning of Simple Regulators with 12 Specifications on Phase and Amplitude Margins. Automatica 1984, 20, 645–651. [Google Scholar] [CrossRef] [Green Version]
- Valentino, K.; Christian, K.; Joelianto, E. Virtual reality flight simulator. Internetw. Indones. J. 2017, 9, 21–25. [Google Scholar]
- Dominic, M.; Halsmer, P.E. Development of a Virtual Reality Flight Simulator to Assist in the Design of Original Aircraft; ASEE Publishing: Tampa, Florida, 2018. [Google Scholar] [CrossRef]
- Halim, I.; Casey, J.; Baghaei, N. Designing a Virtual Reality Flight Simulator. In Proceedings of the 26th International Conference on Computers in Education (ICCE 2018), Manila, Philippines, 26–30 November 2018. [Google Scholar]
- Åstrom, K.J.; Klein, R.E.; Lennartsson, A. Bicycle Dynamics and Control. IEEE Control Syst. Mag. 2005, 25, 26–47. [Google Scholar]
- Bourke, P. Calculating Stereo Pairs. Retrieved 1999, 12, 2006. [Google Scholar]
- Villacís, C.; Fuertes, W.; Escobar, L.; Romero, F.; Chamorro, S. A New Real-Time Flight Simulator for Military Training Using Mechatronics and Cyber-Physical System Methods. Mil. Eng. 2020. [Google Scholar] [CrossRef] [Green Version]
- Ranky, R.; Sivak, M.; Lewis, J.; Gade, V.; Deutsch, J.E.; Mavroidis, C. VRACK virtual reality augmented cycling kit: Design and validation. In Proceedings of the 2010 IEEE Virtual Reality Conference (VR), Waltham, MA, USA, 22–24 March 2010; pp. 135–138. [Google Scholar]
- Herbuś, K.; Ociepka, P. Integration of the virtual model of a Stewart platform with the avatar of a vehicle in a virtual reality. IOP Conf. Ser. Mater. Sci. Eng. 2016, 145, 042018. [Google Scholar] [CrossRef]
- Fung, J.; Richards, C.L.; Malouin, F.; McFadyen, B.J.; Lamontagne, A. A Treadmill and Motion Coupled Virtual Reality System for Gait Training Post-Stroke. Cyberpsychol. Behav. 2006, 9, 157–162. [Google Scholar] [CrossRef] [PubMed]
- Keil, J.; Edler, D.; Schmitt, T.; Dickmann, F. Creating Immersive Virtual Environments Based on Open Geospatial Data and Game Engines. J. Cart. Geogr. Inf. 2021, 71, 1–13. [Google Scholar] [CrossRef]
- Virtanen, J.-P.; Hyyppä, H.; Kämäräinen, A.; Hollström, T.; Vastaranta, M.; Hyyppä, J. Intelligent Open Data 3D Maps in a Collaborative Virtual World. ISPRS Int. J. Geo-Inf. 2015, 4, 837–857. [Google Scholar] [CrossRef] [Green Version]
- Schmohl, S.; Tutzauer, P.; Haala, N. Stuttgart City Walk: A Case Study on Visualizing Textured DSM Meshes for the General Public Using Virtual Reality. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2020, 88, 147–154. [Google Scholar] [CrossRef]
- Vainio, T.; Kotala, O. Developing 3D information systems for mobile users: Some usability issues. In Proceedings of the Second Nordic Conference on Human-Computer Interaction, Aarhus, Denmark, 19–23 October 2002; pp. 231–234. [Google Scholar] [CrossRef]
- Hruby, F.; Sánchez, L.F.Á.; Ressl, R.; Escobar-Briones, E.G. An empirical study on spatial presence in immersive geo-environments. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2020, 88, 155–163. [Google Scholar] [CrossRef] [Green Version]
- Volkaner, B.; Sozen, S.N.; Omurlu, V.E. Realization of a Desktop Flight Simulation System for Motion-Cueing Studies. Int. J. Adv. Robot. Syst. 2016, 13, 85. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.I.; Chang, C.F.; Yu, M.Y.; Fu, L.C. Sliding-mode tracking control of the Stewart platform. In 2004 5th Asian Control Conference; IEEE Cat. No. 04EX904; IEEE: Melbourne, Australia, 2004; Volume 1, pp. 562–569. [Google Scholar]











| Item | Specification |
|---|---|
| Initial height | 0.3 m |
| Roll and pitch angle | ±20° |
| Heave stroke | ±20 cm |
| Yaw angle | ±180° |
| Supporting weight of platform (including tester) | 400 kg |
| Parameter Item | Specification |
|---|---|
| The length of the upper plate | 0.7 m |
| The drive motor output shaft | 1 m |
| The length of the crank | 0.21 m |
| The length of the linkage | 0.25 m |
| The initial height | 0.3 m |
| Heave stroke | ±20 cm |
| Roll angle | ±20° |
| Pitch angle | ±20° |
| Yaw angle | ±180° |
| Specification | Stewart Platform | Crank Linkage Platform |
|---|---|---|
| Structure | Linear actuator [8,12,25,26] | Crank linkage |
| Degrees of Freedom | 6 DoF [12,25,26] | 3 DoF |
| Initial height | 0.42 m [8] | 0.3 m |
| Heave stroke | +Z-axis [8,25,26] | ±20 cm |
| Roll angle | ±7°~±13° [25,26] | ±20° |
| Pitch angle | ±7°~±10.8° [25,26] | ±20° |
| Yaw angle | ±18.5° [26] | ±180° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.-T.; Sun, P.-Y.; Li, H.-J.; Hsieh, C.-H.; Hoe, Z.-Y.; Shiue, Y.-L. Development of Multi-Axis Crank Linkage Motion System for Synchronized Flight Simulation with VR Immersion. Appl. Sci. 2021, 11, 3596. https://doi.org/10.3390/app11083596
Pan C-T, Sun P-Y, Li H-J, Hsieh C-H, Hoe Z-Y, Shiue Y-L. Development of Multi-Axis Crank Linkage Motion System for Synchronized Flight Simulation with VR Immersion. Applied Sciences. 2021; 11(8):3596. https://doi.org/10.3390/app11083596
Chicago/Turabian StylePan, Cheng-Tang, Pei-Yuan Sun, Hao-Jan Li, Cheng-Hsuan Hsieh, Zheng-Yu Hoe, and Yow-Ling Shiue. 2021. "Development of Multi-Axis Crank Linkage Motion System for Synchronized Flight Simulation with VR Immersion" Applied Sciences 11, no. 8: 3596. https://doi.org/10.3390/app11083596
APA StylePan, C.-T., Sun, P.-Y., Li, H.-J., Hsieh, C.-H., Hoe, Z.-Y., & Shiue, Y.-L. (2021). Development of Multi-Axis Crank Linkage Motion System for Synchronized Flight Simulation with VR Immersion. Applied Sciences, 11(8), 3596. https://doi.org/10.3390/app11083596






