Pressure-Driven Nitrogen Flow in Divergent Microchannels with Isothermal Walls
Abstract
:1. Introduction
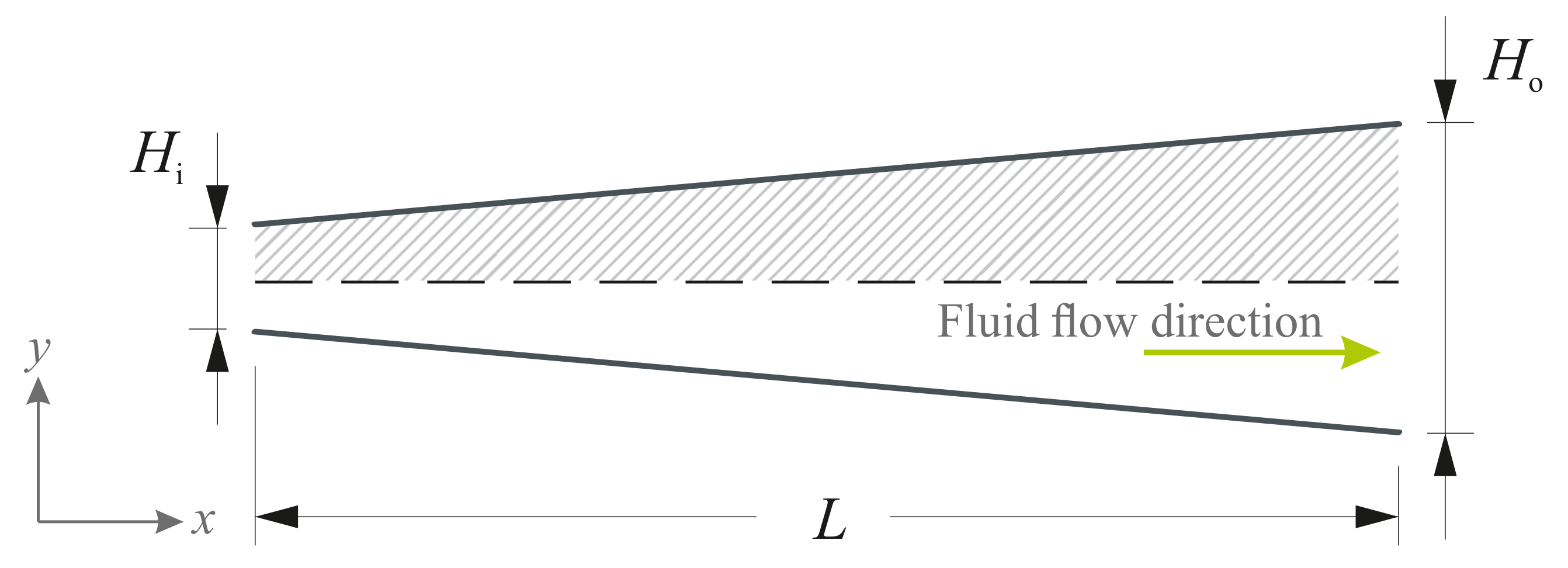
2. Problem Description
3. Numerical Procedure
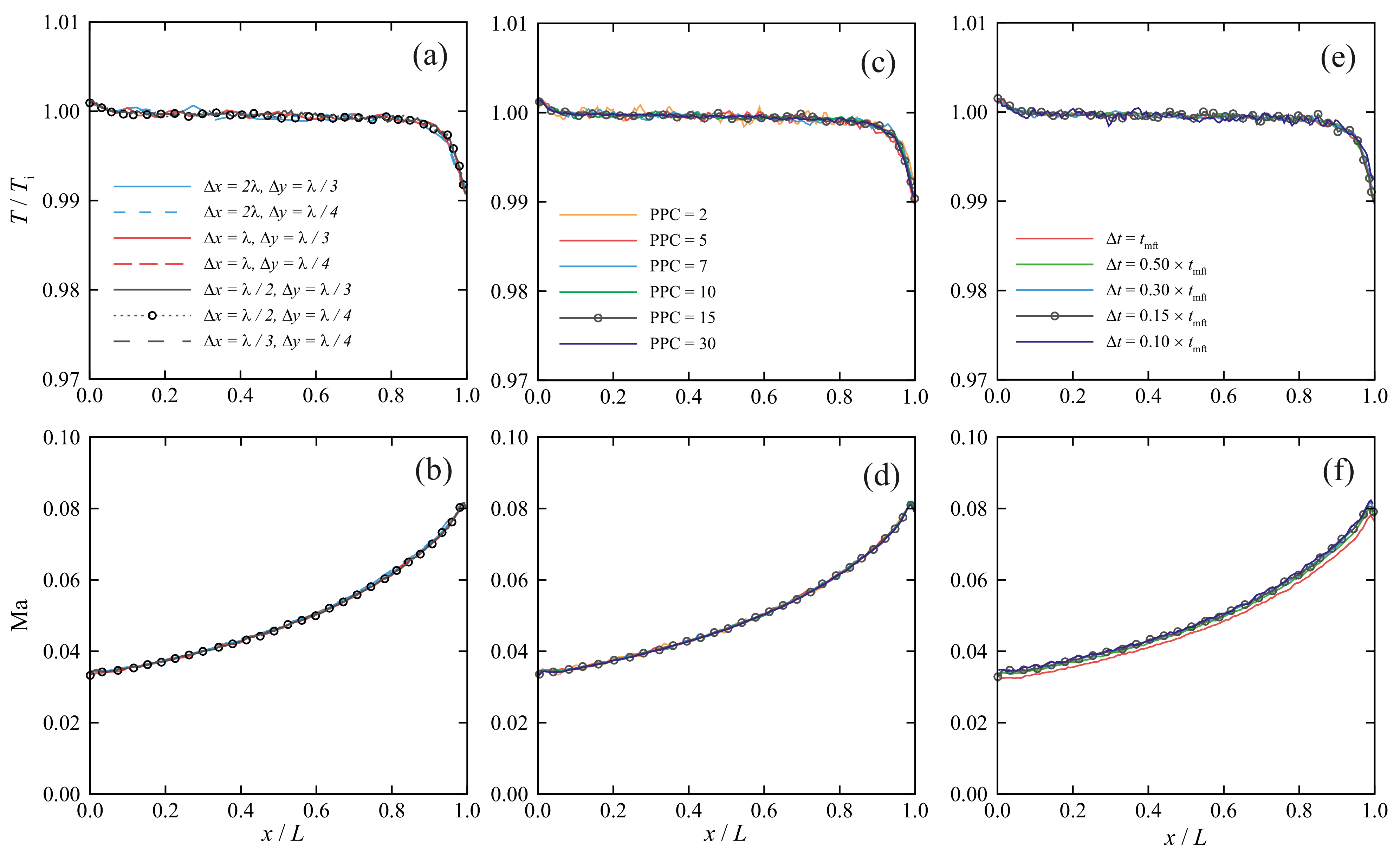
4. Model Validation and Verification
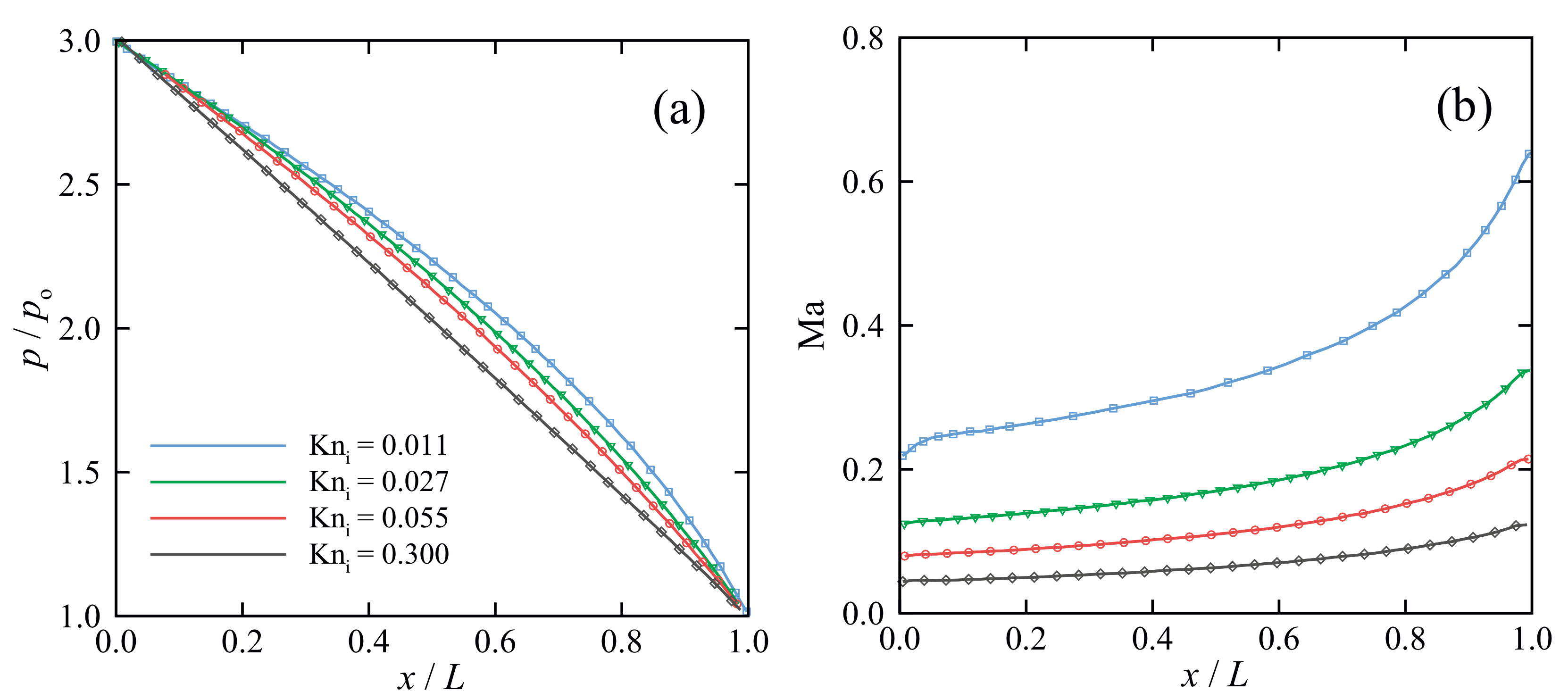
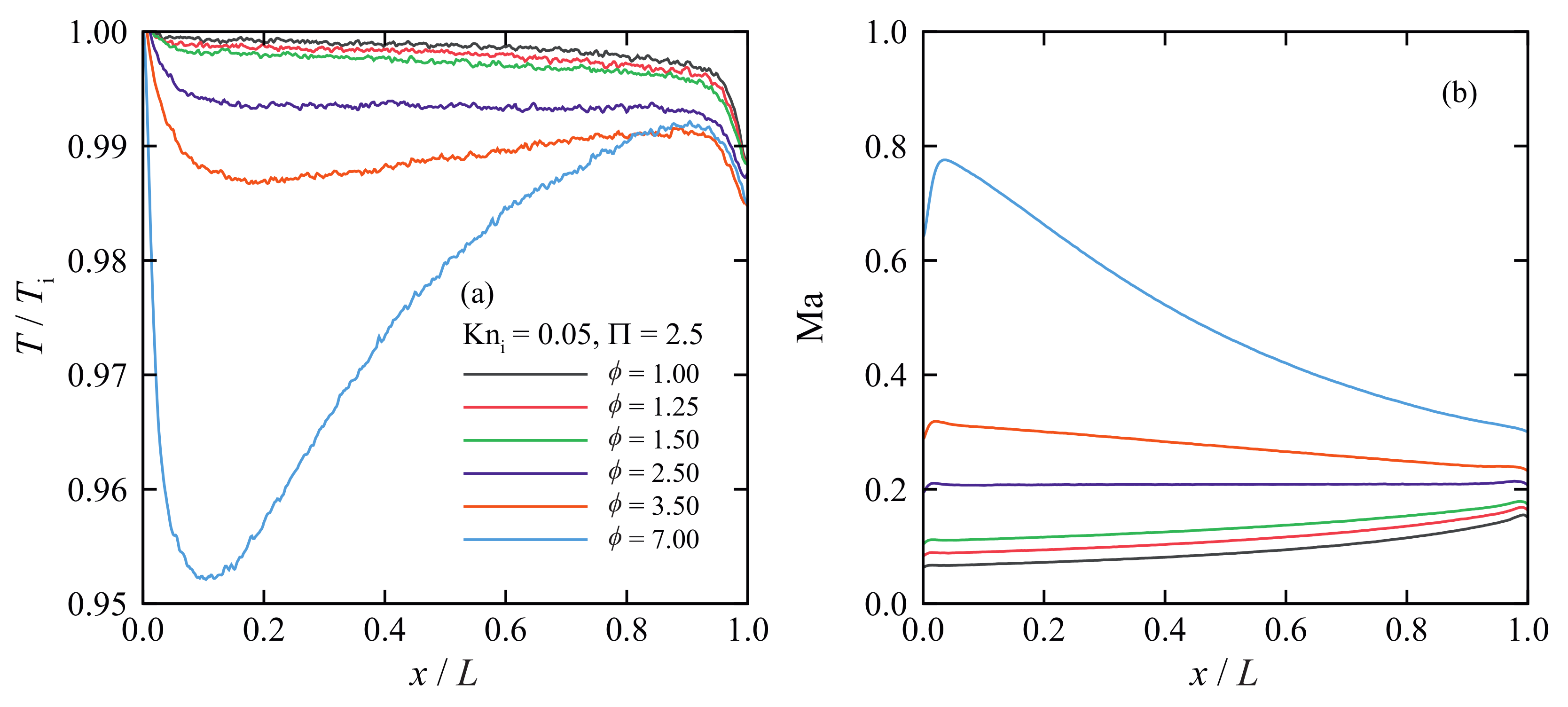
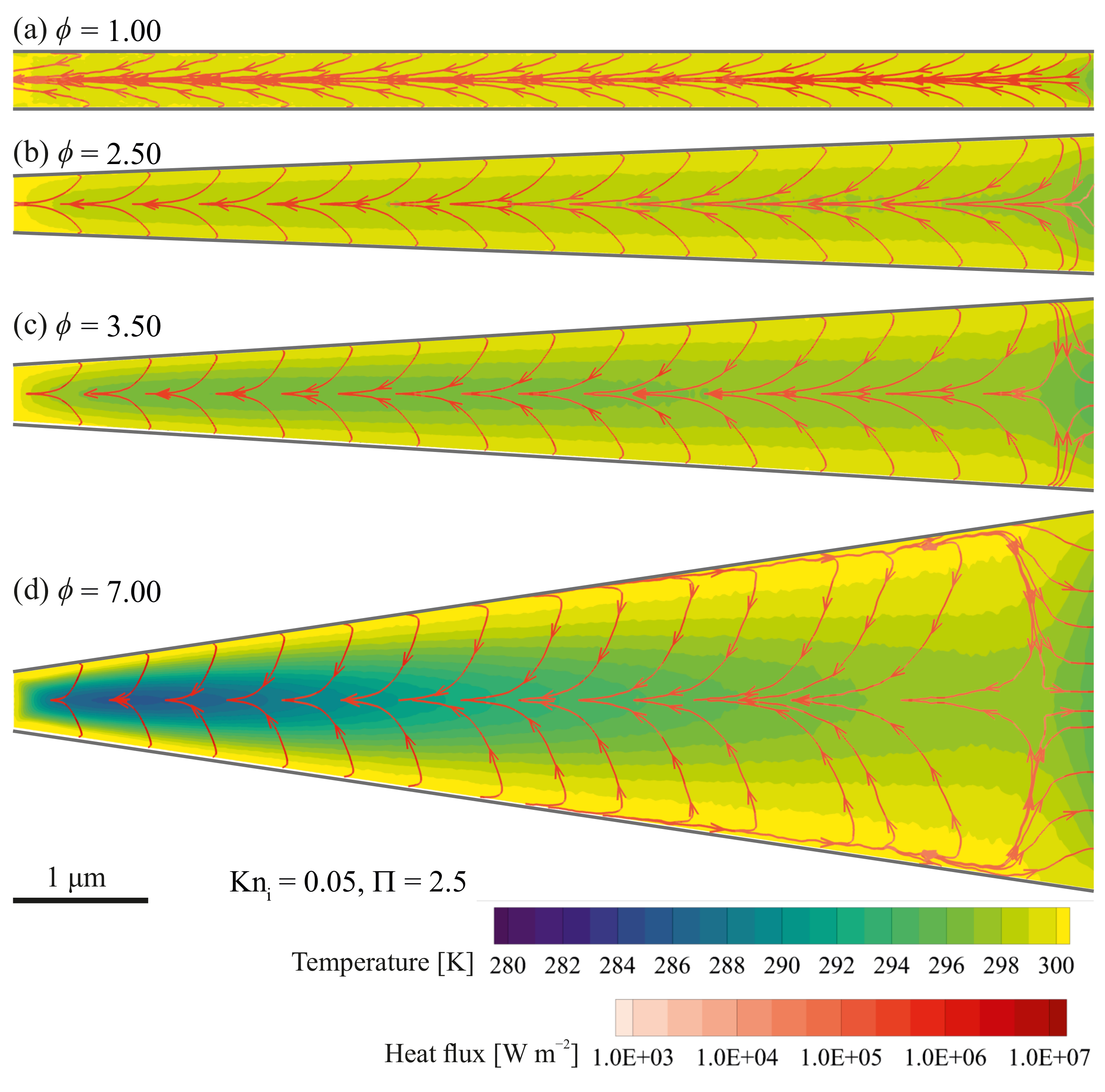
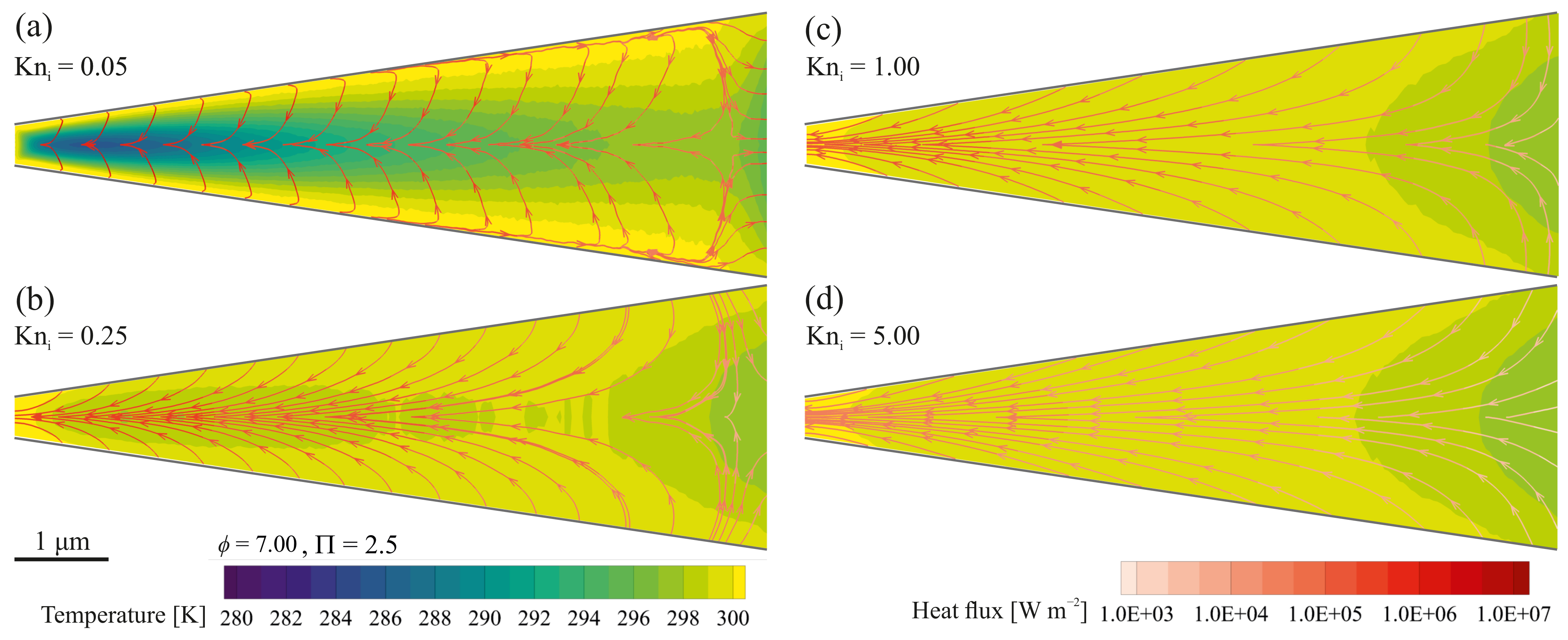
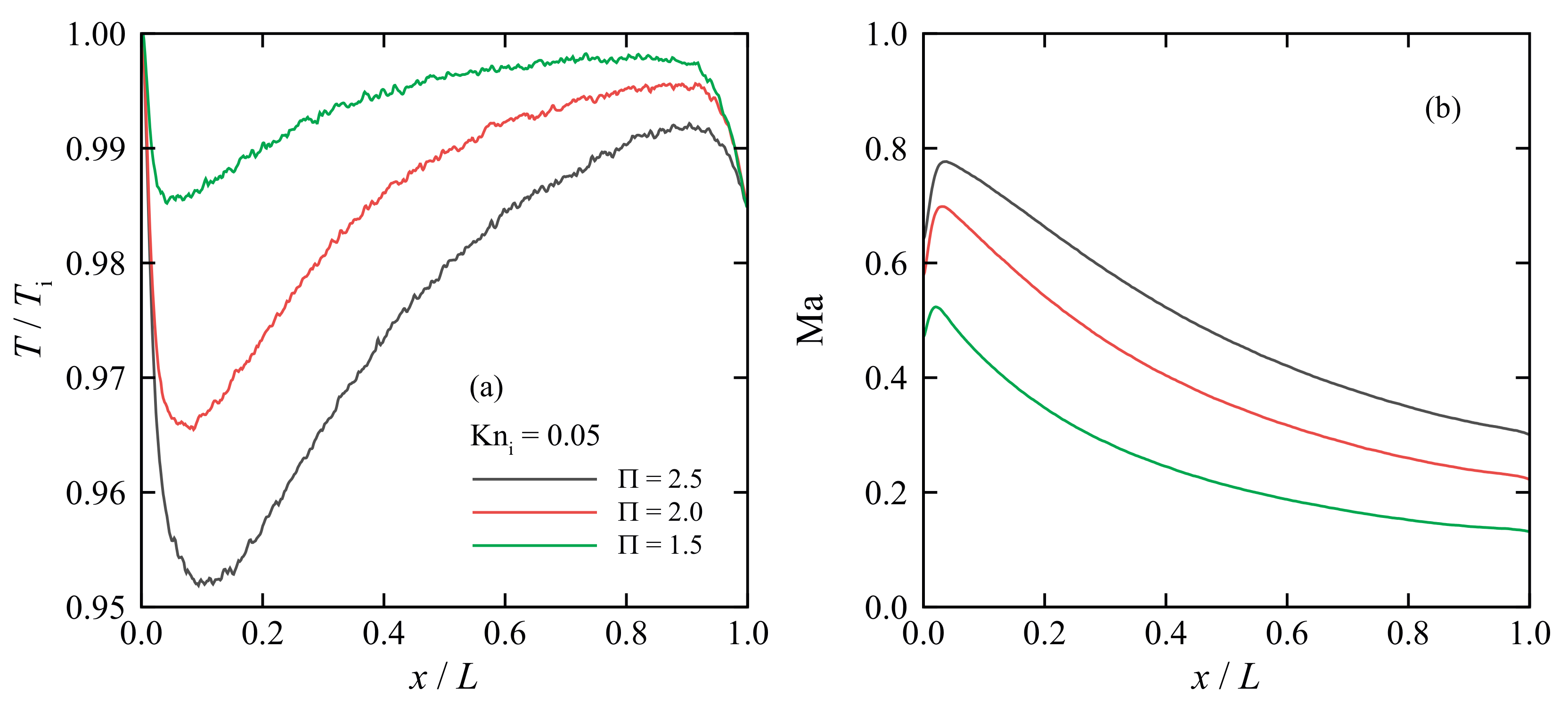
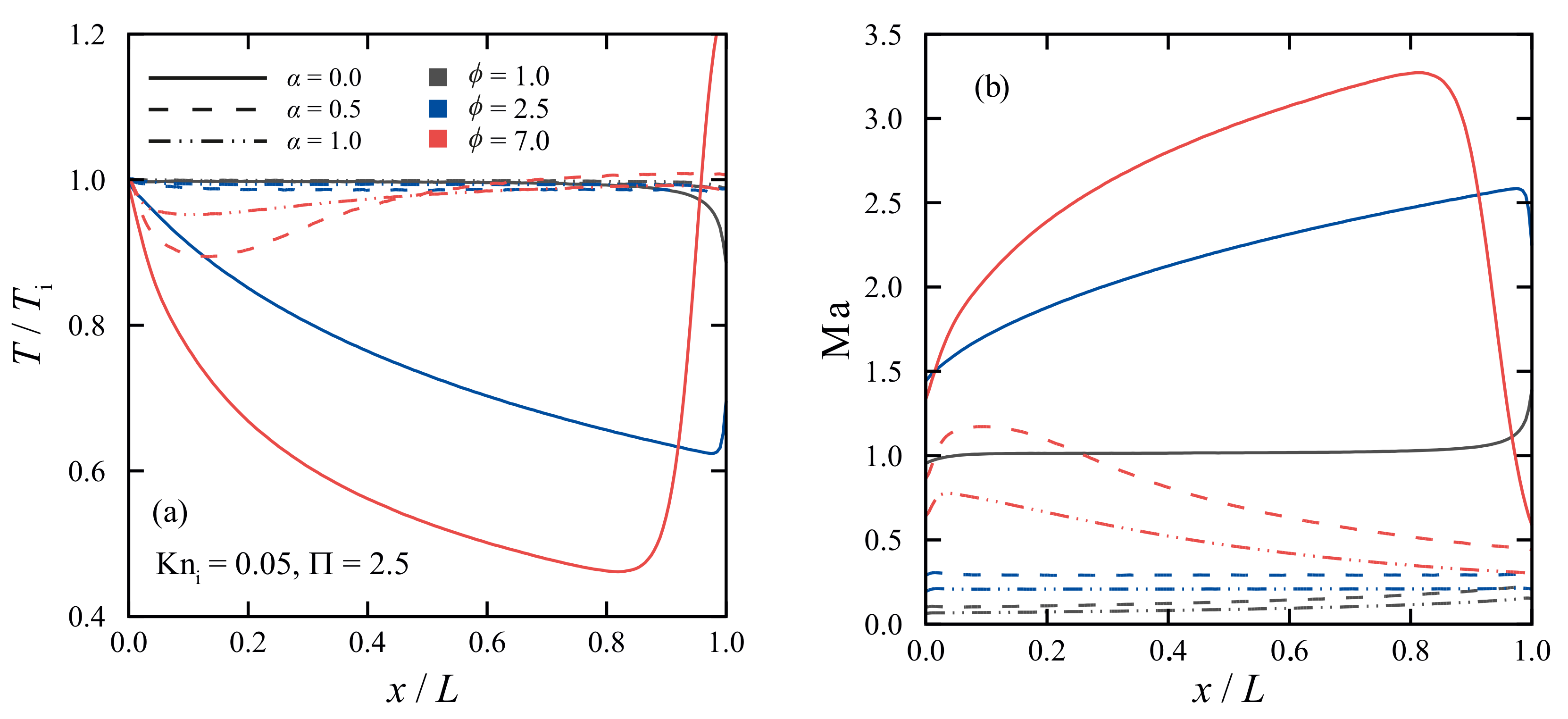
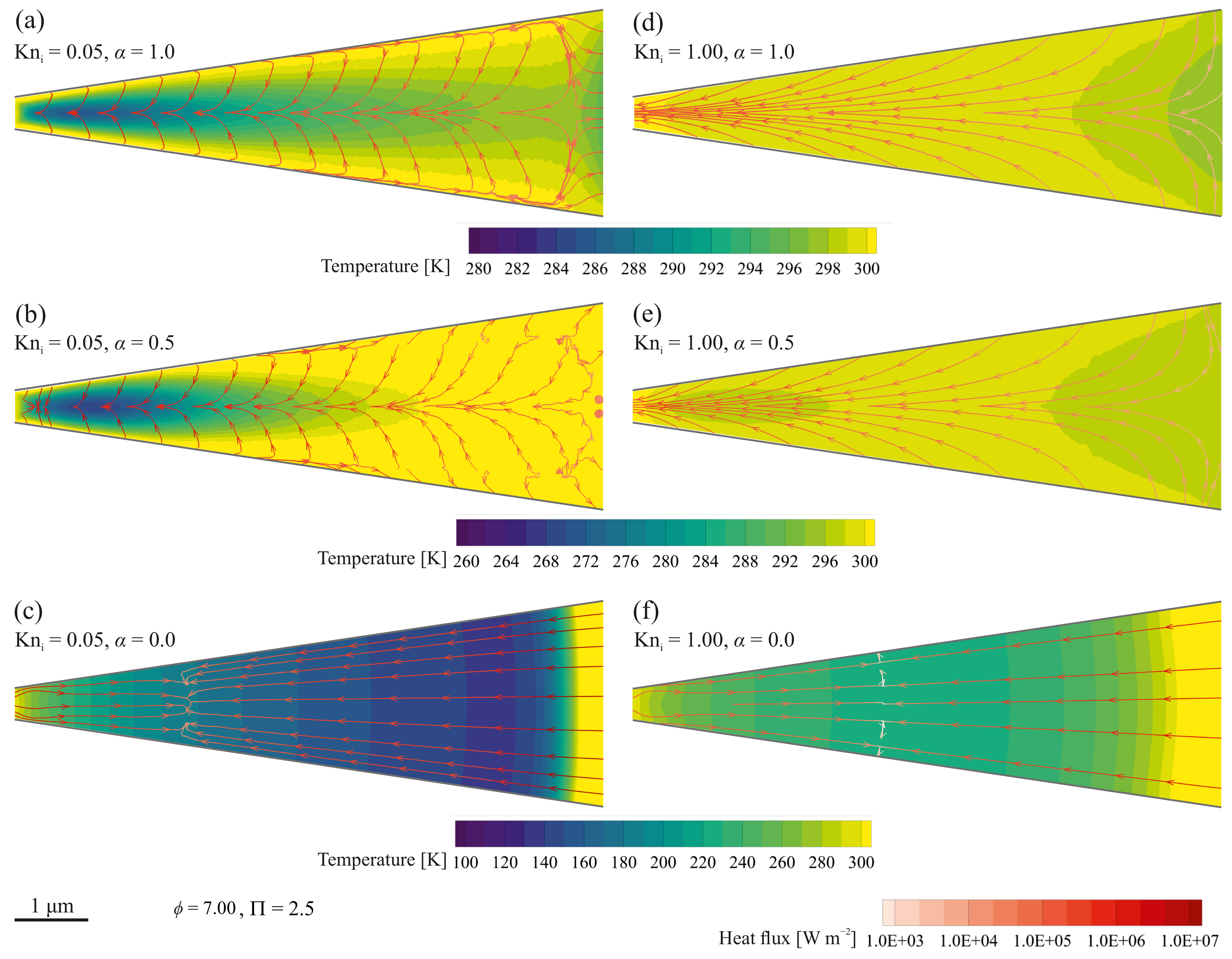
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DSMC | Direct simulation Monte Carlo |
| NTC | No time counter |
| TAS | Transient adaptive sub-celling |
| VHS | Variable hard sphere |
| PPC | Particle per cell |
| NSF | Navier–Stokes–Fourier |
| MEMS | Micro-electromechanical systems |
| OpenFOAM | Open Source Field Operation and Manipulation |
References
- Würger, A. Leidenfrost Gas Ratchets Driven by Thermal Creep. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef] [Green Version]
- Gebhard, U.; Hein, H.; Schmidt, U. Numerical investigation of fluidic micro-oscillators. J. Micromech. Microeng. 1996, 6, 115–117. [Google Scholar] [CrossRef]
- Jiang, X.; Zhou, Z.; Huang, X.; Li, Y.; Yang, Y.; Liu, C. Micronozzle/diffuser flow and its application in micro valveless pumps. Sens. Actuators A Phys. 1998, 70, 81–87. [Google Scholar] [CrossRef]
- Duryodhan, V.S.; Singh, A.; Singh, S.G.; Agrawal, A. A simple and novel way of maintaining constant wall temperature in microdevices. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Ripoll, M. Thermoosmotic microfluidics. Soft Matter 2016, 12, 8564–8573. [Google Scholar] [CrossRef] [PubMed]
- Bordbar, A.; Kheirandish, S.; Taassob, A.; Kamali, R.; Ebrahimi, A. High-viscosity liquid mixing in a slug-flow micromixer: A numerical study. J. Flow Chem. 2020, 10, 449–459. [Google Scholar] [CrossRef]
- Agrawal, A. A Comprehensive Review on Gas Flow in Microchannels. Int. J. Micro Nano Scale Transp. 2011, 2, 1–40. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Roohi, E.; Kheradmand, S. Numerical study of liquid flow and heat transfer in rectangular microchannel with longitudinal vortex generators. Appl. Therm. Eng. 2015, 78, 576–583. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, A.; Rikhtegar, F.; Sabaghan, A.; Roohi, E. Heat transfer and entropy generation in a microchannel with longitudinal vortex generators using nanofluids. Energy 2016, 101, 190–201. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Kaper, H.G.; Gross, E.P. Mathematical Theory of Transport Processes in Gases. Am. J. Phys. 1973, 41, 601–603. [Google Scholar] [CrossRef]
- Johnson, R.W. Handbook of Fluid Dynamics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Gad-el-Hak, M. The MEMS Handbook; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Kirby, B.J. Micro- and Nanoscale Fluid Mechanics; Cambridge University Press: Leiden, The Netherlands, 2010. [Google Scholar]
- Roy, S.; Raju, R.; Chuang, H.F.; Cruden, B.A.; Meyyappan, M. Modeling gas flow through microchannels and nanopores. J. Appl. Phys. 2003, 93, 4870–4879. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Beskok, A.; Aluru, N. Microflows and Nanoflows; Springer: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Shen, C. Rarefied Gas Dynamics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Kara, V.; Yakhot, V.; Ekinci, K. Generalized Knudsen Number for Unsteady Fluid Flow. Phys. Rev. Lett. 2017, 118. [Google Scholar] [CrossRef] [Green Version]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Jakobsen, H.A. Chemical Reactor Modeling; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Zheng, Y.; Garcia, A.L.; Alder, B.J. Comparison of Kinetic Theory and Hydrodynamics for Poiseuille Flow. J. Stat. Phys. 2002, 109, 495–505. [Google Scholar] [CrossRef]
- Arkilic, E.B.; Breuer, K.S.; Schmidt, M.A. Mass flow and tangential momentum accommodation in silicon micromachined channels. J. Fluid Mech. 2001, 437, 29–43. [Google Scholar] [CrossRef]
- Arlemark, E.J.; Dadzie, S.K.; Reese, J.M. An Extension to the Navier-Stokes-Fourier Equations by Considering Molecular Collisions With Boundaries. In Proceedings of the ASME 2008 6th International Conference on Nanochannels, Microchannels, and Minichannels, Darmstadt, Germany, 23–25 June 2008; ASME: New York, NY, USA, 2008. [Google Scholar] [CrossRef] [Green Version]
- Zade, A.Q.; Ahmadzadegan, A.; Renksizbulut, M. A detailed comparison between Navier–Stokes and DSMC simulations of multicomponent gaseous flow in microchannels. Int. J. Heat Mass Transf. 2012, 55, 4673–4681. [Google Scholar] [CrossRef]
- Torrilhon, M.; Struchtrup, H. Modeling Micro Mass and Heat Transfer for Gases Using Extended Continuum Equations. J. Heat Transf. 2009, 131, 033103. [Google Scholar] [CrossRef] [Green Version]
- Varoutis, S.; Day, C.; Sharipov, F. Rarefied gas flow through channels of finite length at various pressure ratios. Vacuum 2012, 86, 1952–1959. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Colin, S.; Peles, Y.; Garimella, S.; Pease, R.F.; Brandner, J.J.; Tuckerman, D.B. Heat Transfer in Microchannels—2012 Status and Research Needs. J. Heat Transf. 2013, 135, 091001. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Liou, W.W. Computations of the Flow and Heat Transfer in Microdevices Using DSMC With Implicit Boundary Conditions. J. Heat Transf. 2002, 124, 338. [Google Scholar] [CrossRef]
- Liou, W.; Fang, Y. Heat transfer in microchannel devices using DSMC. J. Microelectromech. Syst. 2001, 10, 274–279. [Google Scholar] [CrossRef]
- Zhang, M.; Day, C.; Varoutis, S.; Cai, G. Rarefied gas flow into vacuum through short tubes at variable wall temperatures. J. Vac. Sci. Technol. A Vacuum Surfaces Film 2017, 35, 021604. [Google Scholar] [CrossRef]
- Hemadri, V.; Duryodhan, V.S.; Agrawal, A. Liquid and gas flows in microchannels of varying cross section: A comparative analysis of the flow dynamics and design perspectives. Microfluid. Nanofluid. 2018, 22. [Google Scholar] [CrossRef]
- Varade, V.; Duryodhan, V.; Agrawal, A.; Pradeep, A.; Ebrahimi, A.; Roohi, E. Low Mach number slip flow through diverging microchannel. Comput. Fluids 2015, 111, 46–61. [Google Scholar] [CrossRef]
- Varade, V.; Agrawal, A.; Pradeep, A.M. Slip flow through a converging microchannel: Experiments and 3D simulations. J. Micromech. Microeng. 2015, 25, 025015. [Google Scholar] [CrossRef]
- Hemadri, V.; Varade, V.V.; Agrawal, A.; Bhandarkar, U.V. Investigation of rarefied gas flow in microchannels of non-uniform cross section. Phys. Fluids 2016, 28, 022007. [Google Scholar] [CrossRef]
- Hemadri, V.; Varade, V.V.; Agrawal, A.; Bhandarkar, U.V. Rarefied gas flow in converging microchannel in slip and early transition regimes. Phys. Fluids 2017, 29, 032002. [Google Scholar] [CrossRef]
- Milićev, S.S.; Stevanović, N.D. Gas Flow in Microchannels and Nanochannels With Variable Cross Section for All Knudsen and All Mach Number Values. J. Fluids Eng. 2020, 143. [Google Scholar] [CrossRef]
- Ohwada, T.; Sone, Y.; Aoki, K. Numerical analysis of the Poiseuille and thermal transpiration flows between two parallel plates on the basis of the Boltzmann equation for hard-sphere molecules. Phys. Fluids A Fluid Dyn. 1989, 1, 2042–2049. [Google Scholar] [CrossRef]
- John, B.; Gu, X.J.; Emerson, D.R. Nonequilibrium gaseous heat transfer in pressure-driven plane Poiseuille flow. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Roohi, E. Flow and Thermal Fields Investigation in Divergent Micro/Nano Channels. J. Therm. Eng. 2016, 2, 709–714. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Roohi, E. DSMC investigation of rarefied gas flow through diverging micro- and nanochannels. Microfluid. Nanofluid. 2017, 21. [Google Scholar] [CrossRef] [Green Version]
- Guerrieri, D.C.; Cervone, A.; Gill, E. Analysis of Nonisothermal Rarefied Gas Flow in Diverging Microchannels for Low-Pressure Microresistojets. J. Heat Transf. 2016, 138, 112403. [Google Scholar] [CrossRef]
- Kannan, A.S.; Narahari, T.S.B.; Bharadhwaj, Y.; Mark, A.; Sardina, G.; Maggiolo, D.; Sasic, S.; Ström, H. The Knudsen Paradox in Micro-Channel Poiseuille Flows with a Symmetric Particle. Appl. Sci. 2020, 11, 351. [Google Scholar] [CrossRef]
- Taassob, A.; Kamali, R.; Bordbar, A. Investigation of rarefied gas flow through bended microchannels. Vacuum 2018, 151, 197–204. [Google Scholar] [CrossRef]
- Shah, N.; Agrawal, A.; Bhandarkar, U. 3D study of temperature drop behavior of subsonic rarefied gas flow in microchannel. Numer. Heat Transf. Part A Appl. 2018, 73, 654–665. [Google Scholar] [CrossRef]
- Balaj, M.; Roohi, E.; Mohammadzadeh, A. Regulation of anti-Fourier heat transfer for non-equilibrium gas flows through micro/nanochannels. Int. J. Therm. Sci. 2017, 118, 24–39. [Google Scholar] [CrossRef]
- Gavasane, A.; Agrawal, A.; Pradeep, A.M.; Bhandarkar, U. Simulation of a temperature drop for the flow of rarefied gases in microchannels. Numer. Heat Transf. Part A Appl. 2017, 71, 1066–1079. [Google Scholar] [CrossRef]
- Hong, C.; Yamamoto, T.; Asako, Y.; Suzuki, K. Heat Transfer Characteristics of Compressible Laminar Flow Through Microtubes. J. Heat Transf. 2012, 134, 011602. [Google Scholar] [CrossRef]
- Roohi, E.; Darbandi, M.; Mirjalili, V. Direct Simulation Monte Carlo Solution of Subsonic Flow Through Micro/Nanoscale Channels. J. Heat Transf. 2009, 131, 092402. [Google Scholar] [CrossRef]
- Hong, C.; Asako, Y. Heat Transfer Characteristics of Gaseous Flows in a Microchannel and a Microtube with Constant Wall Temperature. Numer. Heat Transf. Part A Appl. 2007, 52, 219–238. [Google Scholar] [CrossRef]
- Zhen, C.E.; Hong, Z.C.; Lin, Y.J.; Hong, N.T. Comparison of 3-D and 2-D DSMC Heat Transfer Calculations of Low-Speed Short Microchannel Flows. Numer. Heat Transf. Part A Appl. 2007, 52, 239–250. [Google Scholar] [CrossRef]
- Acharya, T.; Falgoust, J.; Schoegl, I.; Martin, M.J. Measurement of Variation of Momentum Accommodation Coefficients with Molecular Mass and Structure. J. Thermophys. Heat Transf. 2019, 33, 773–778. [Google Scholar] [CrossRef]
- Graur, I.A.; Perrier, P.; Ghozlani, W.; Méolans, J.G. Measurements of tangential momentum accommodation coefficient for various gases in plane microchannel. Phys. Fluids 2009, 21, 102004. [Google Scholar] [CrossRef] [Green Version]
- White, C.; Borg, M.; Scanlon, T.; Longshaw, S.; John, B.; Emerson, D.; Reese, J. dsmcFoam+: An OpenFOAM based direct simulation Monte Carlo solver. Comput. Phys. Commun. 2018, 224, 22–43. [Google Scholar] [CrossRef]
- Scanlon, T.J.; White, C.; Borg, M.K.; Palharini, R.C.; Farbar, E.; Boyd, I.D.; Reese, J.M.; Brown, R.E. Open-Source Direct Simulation Monte Carlo Chemistry Modeling for Hypersonic Flows. AIAA J. 2015, 53, 1670–1680. [Google Scholar] [CrossRef] [Green Version]
- Palharini, R.C.; White, C.; Scanlon, T.J.; Brown, R.E.; Borg, M.K.; Reese, J.M. Benchmark numerical simulations of rarefied non-reacting gas flows using an open-source DSMC code. Comput. Fluids 2015, 120, 140–157. [Google Scholar] [CrossRef] [Green Version]
- Su, C.; Tseng, K.; Cave, H.; Wu, J.; Lian, Y.; Kuo, T.; Jermy, M. Implementation of a transient adaptive sub-cell module for the parallel-DSMC code using unstructured grids. Comput. Fluids 2010, 39, 1136–1145. [Google Scholar] [CrossRef]
- Oran, E.; Oh, C.; Cybyk, B. DIRECT SIMULATION MONTE CARLO: Recent Advances and Applications. Annu. Rev. Fluid Mech. 1998, 30, 403–441. [Google Scholar] [CrossRef]
- Alexander, F.J.; Garcia, A.L.; Alder, B.J. Cell size dependence of transport coefficients in stochastic particle algorithms. Phys. Fluids 1998, 10, 1540–1542. [Google Scholar] [CrossRef] [Green Version]
- Cai, C.; Boyd, I.D.; Fan, J.; Candler, G.V. Direct Simulation Methods for Low-Speed Microchannel Flows. J. Thermophys. Heat Transf. 2000, 14, 368–378. [Google Scholar] [CrossRef]
- Shen, C.; Fan, J.; Xie, C. Statistical simulation of rarefied gas flows in micro-channels. J. Comput. Phys. 2003, 189, 512–526. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.X.; Tang, Z.; He, Y.L.; Tao, W.Q. Proper cell dimension and number of particles per cell for DSMC. Comput. Fluids 2011, 50, 1–9. [Google Scholar] [CrossRef]
- Shu, C.; Mao, X.; Chew, Y. Particle number per cell and scaling factor effect on accuracy of DSMC simulation of micro flows. Int. J. Numer. Methods Heat Fluid Flow 2005, 15, 827–841. [Google Scholar] [CrossRef]
- Radtke, G.A.; Hadjiconstantinou, N.G.; Wagner, W. Low-noise Monte Carlo simulation of the variable hard sphere gas. Phys. Fluids 2011, 23, 030606. [Google Scholar] [CrossRef] [Green Version]
- Hadjiconstantinou, N.G.; Garcia, A.L.; Bazant, M.Z.; He, G. Statistical error in particle simulations of hydrodynamic phenomena. J. Comput. Phys. 2003, 187, 274–297. [Google Scholar] [CrossRef] [Green Version]
- White, C.; Borg, M.K.; Scanlon, T.J.; Reese, J.M. A DSMC investigation of gas flows in micro-channels with bends. Comput. Fluids 2013, 71, 261–271. [Google Scholar] [CrossRef] [Green Version]
- Hadjiconstantinou, N.G.; Simek, O. Constant-Wall-Temperature Nusselt Number in Micro and Nano-Channels. J. Heat Transf. 2001, 124, 356–364. [Google Scholar] [CrossRef] [Green Version]
- Sone, Y. (Ed.) Molecular Gas Dynamics; Birkhäuser: Boston, MA, USA, 2007. [Google Scholar] [CrossRef]
- Gu, X.; Barber, R.; Emerson, D. How Far Can 13 Moments Go in Modeling Microscale Gas Phenomena? Nanoscale Microscale Thermophys. Eng. 2007, 11, 85–97. [Google Scholar] [CrossRef]
- Mahdavi, A.M.; Roohi, E. Investigation of cold-to-hot transfer and thermal separation zone through nano step geometries. Phys. Fluids 2015, 27, 072002. [Google Scholar] [CrossRef]
- Cercignani, C.; Lampis, M.; Lorenzani, S. Variational approach to gas flows in microchannels. Phys. Fluids 2004, 16, 3426–3437. [Google Scholar] [CrossRef]


| (m) | (kg) | (−) | (−) | (K) | (N s m) |
|---|---|---|---|---|---|
| 2 | 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebrahimi, A.; Shahabi, V.; Roohi, E. Pressure-Driven Nitrogen Flow in Divergent Microchannels with Isothermal Walls. Appl. Sci. 2021, 11, 3602. https://doi.org/10.3390/app11083602
Ebrahimi A, Shahabi V, Roohi E. Pressure-Driven Nitrogen Flow in Divergent Microchannels with Isothermal Walls. Applied Sciences. 2021; 11(8):3602. https://doi.org/10.3390/app11083602
Chicago/Turabian StyleEbrahimi, Amin, Vahid Shahabi, and Ehsan Roohi. 2021. "Pressure-Driven Nitrogen Flow in Divergent Microchannels with Isothermal Walls" Applied Sciences 11, no. 8: 3602. https://doi.org/10.3390/app11083602
APA StyleEbrahimi, A., Shahabi, V., & Roohi, E. (2021). Pressure-Driven Nitrogen Flow in Divergent Microchannels with Isothermal Walls. Applied Sciences, 11(8), 3602. https://doi.org/10.3390/app11083602








