Investigation of Magnetic Anisotropy and Barkhausen Noise Asymmetry Resulting from Uniaxial Plastic Deformation of Steel S235
Abstract
:1. Introduction
2. Materials and Methods
3. Results of Experiments and Their Discussion
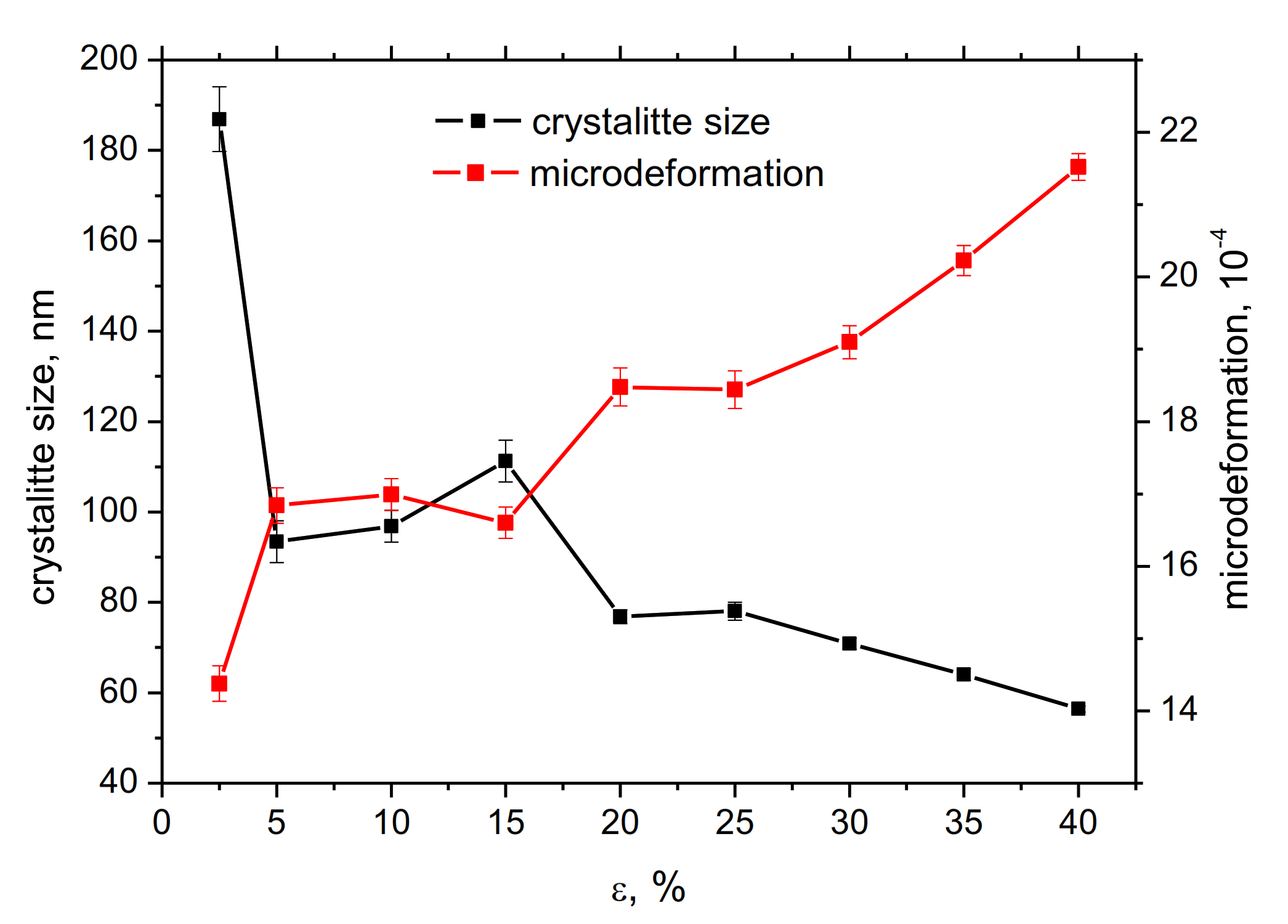
3.1. XRD Measurements
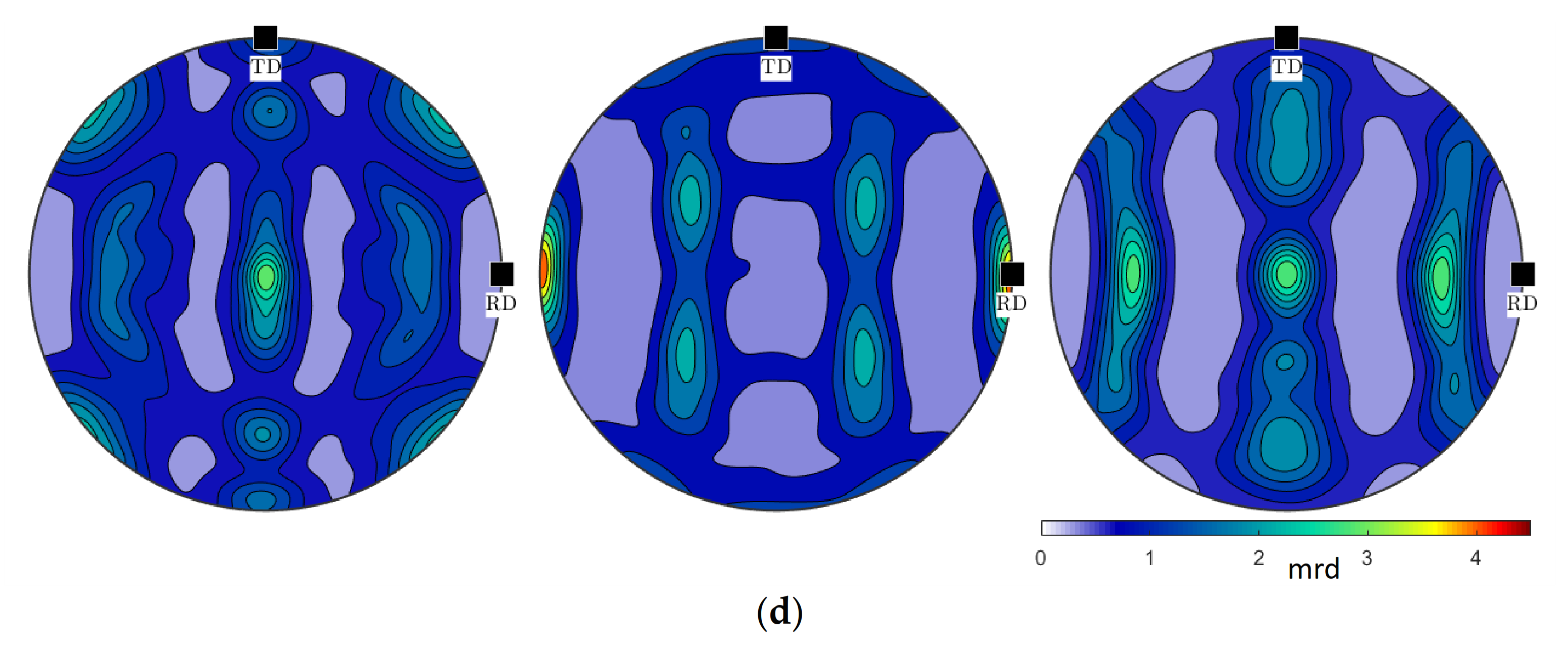
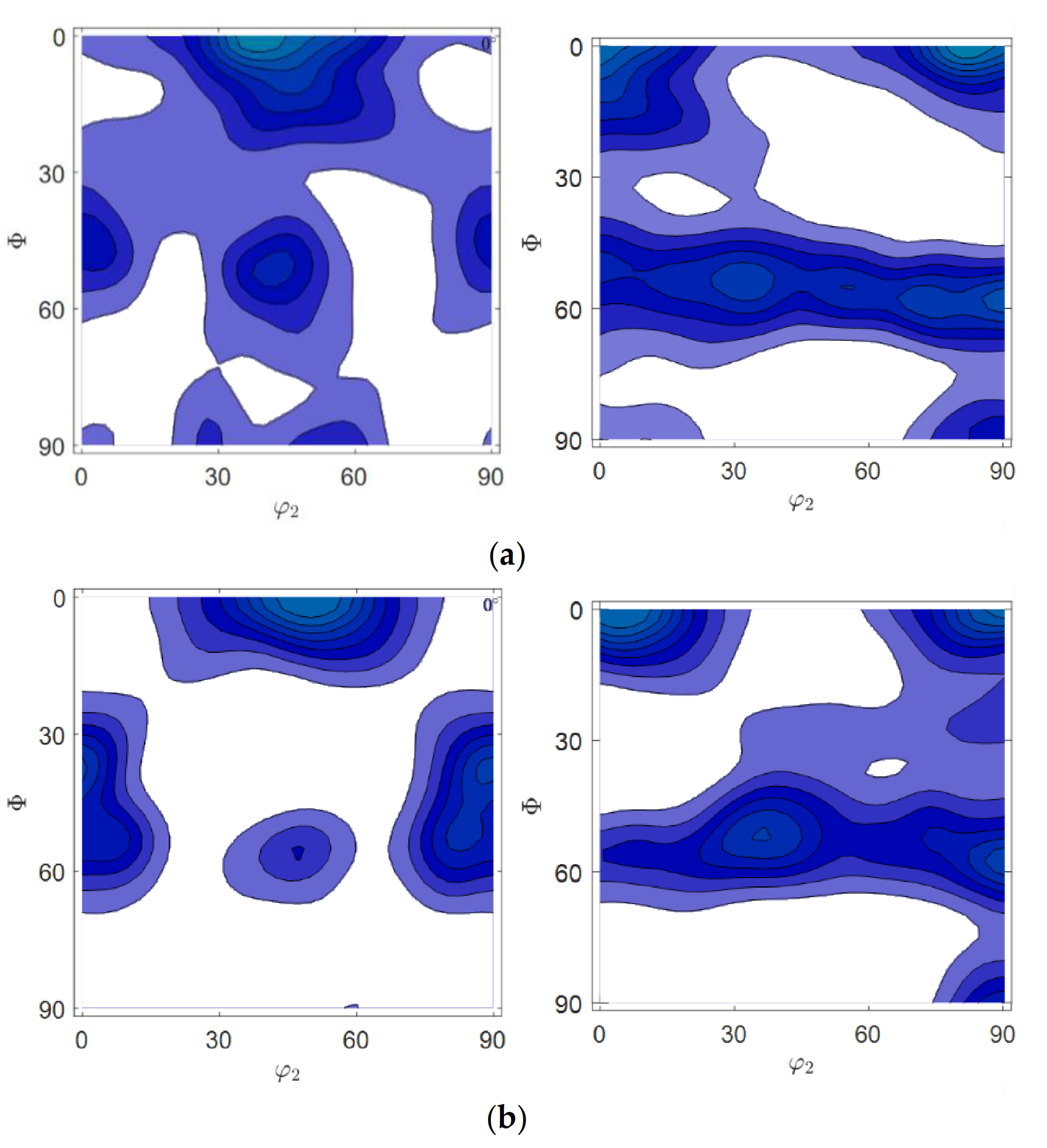
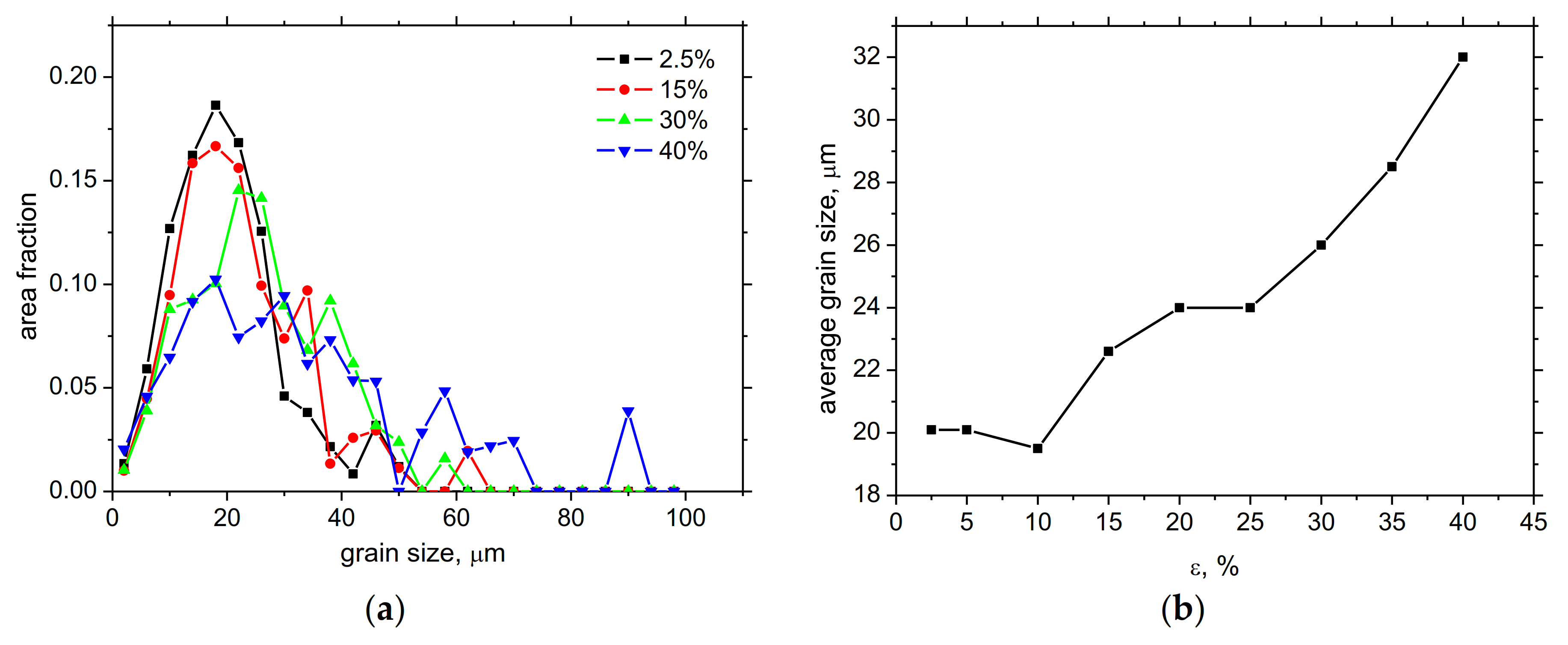
3.2. EBSD Observations
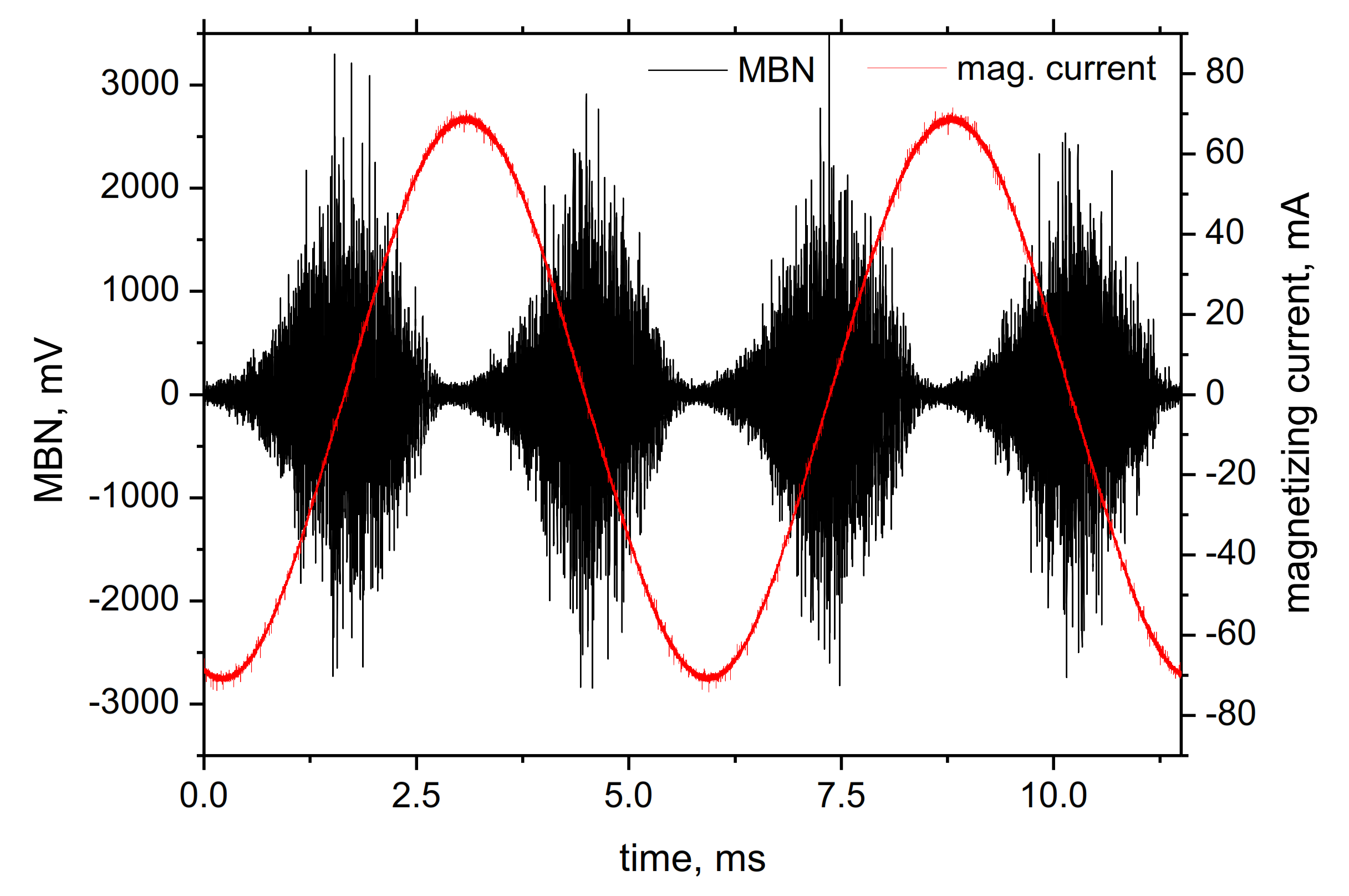
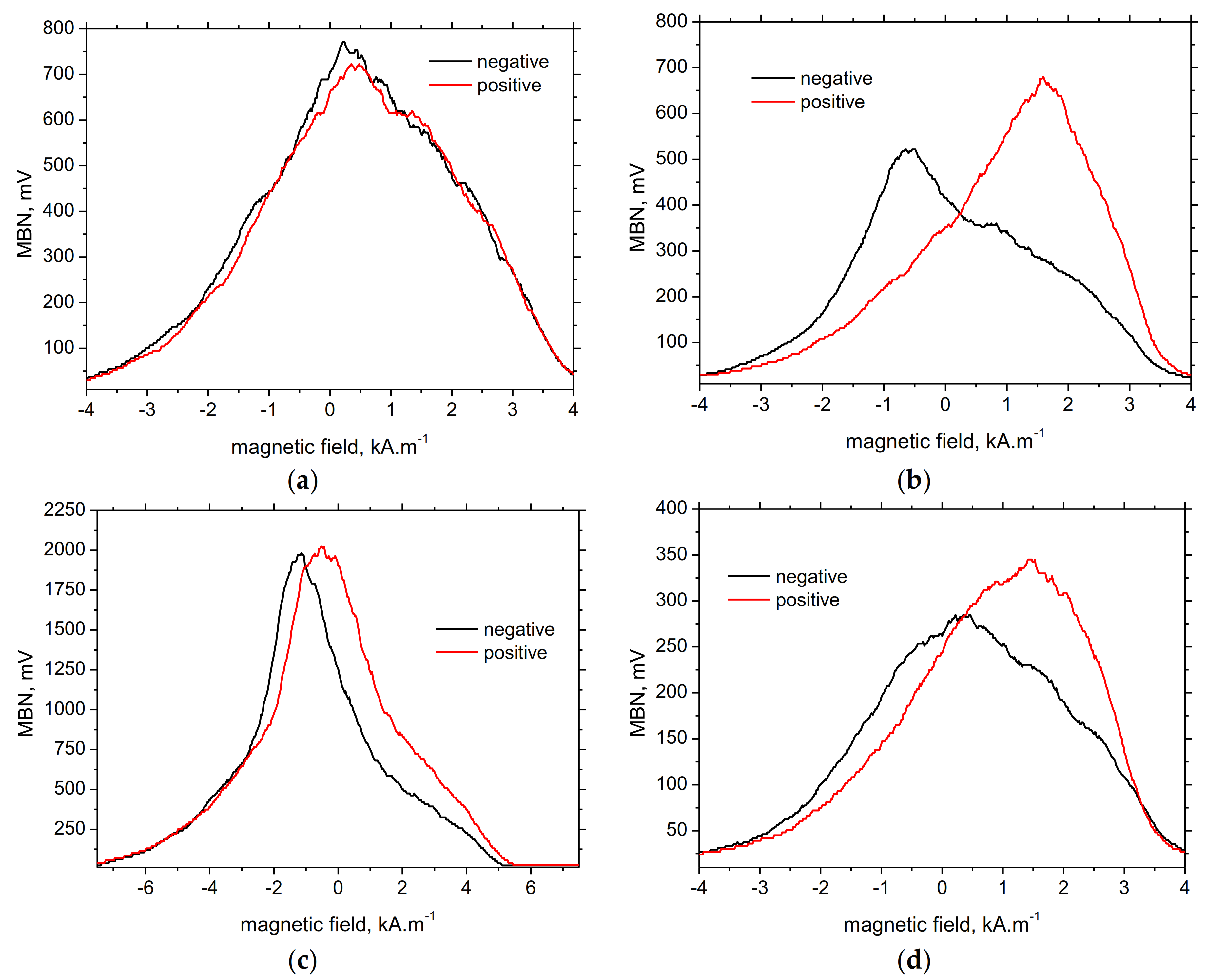
3.3. MBN Measurements
4. Conclusions
- -
- progressively developed ε markedly alters the magnetic anisotropy of S235 steel and makes the TD the easy axis of magnetisation due to the preferential crystallographic orientation in the TD,
- -
- MBN asymmetry becomes more apparent at the lower ε in the RD direction only, due to magnetic coupling between the heavily strained and the unaffected grains,
- -
- MBN asymmetry is more pronounced with respect to the PP of MBN envelopes as compared with the rms values of the MBN signal,
- -
- the degree of MBN asymmetry vanishes towards the TD as well as at higher ε,
- -
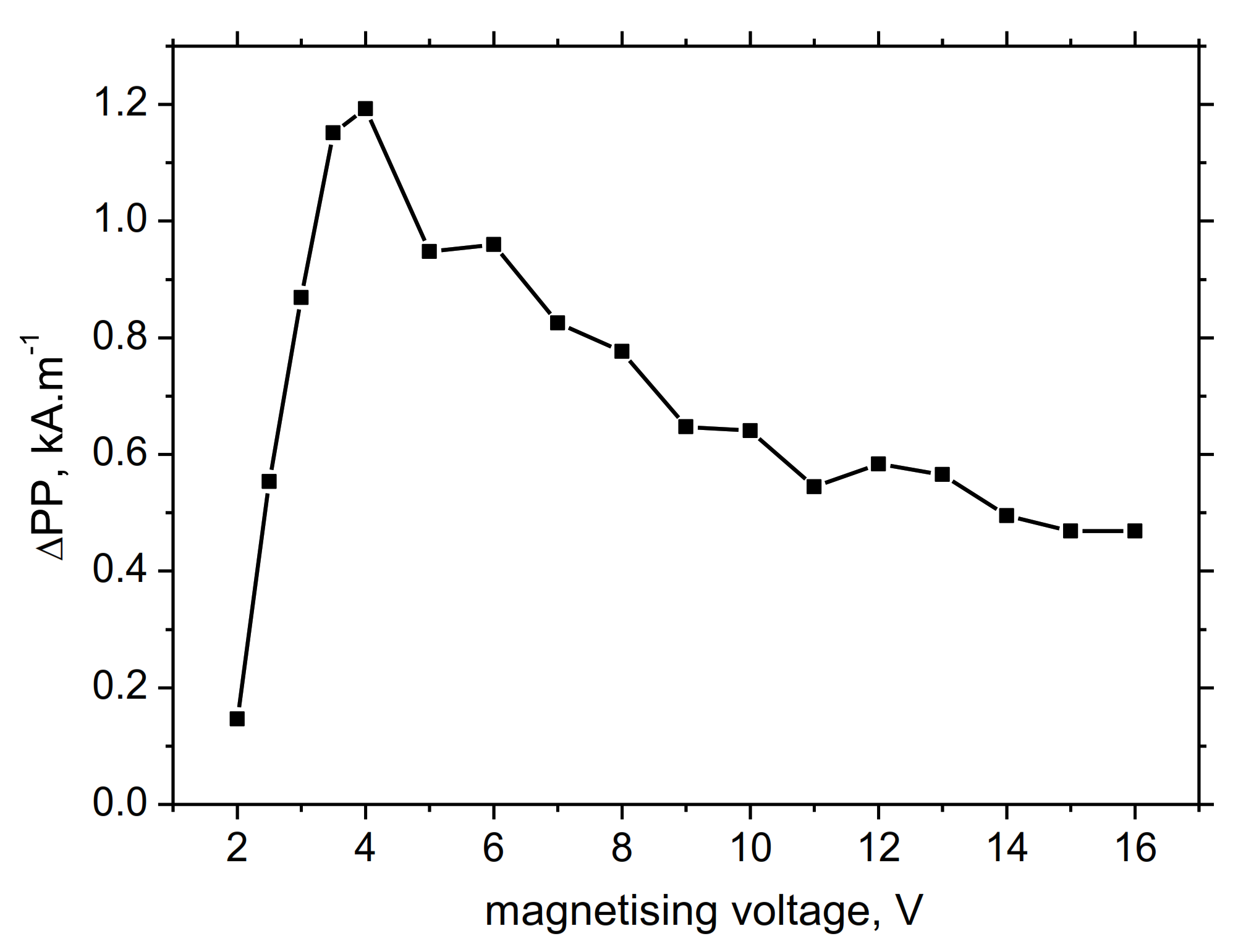
- the highest degree of MBN asymmetry can be found at the medium magnetising voltages as a result of good contrast between DWs unpinning in the different grains.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiles, D. Introduction to Magnetism and Magnetic Materials, 3rd ed.; Taylor & Francis Group: New York, NY, USA, 2016. [Google Scholar]
- Varga, R. Domain Walls and Their Dynamics, 1st ed.; Pavol Jozef Šafárik University: Košice, Slovakia, 2014. [Google Scholar]
- Chikazumi, S. Physics of Ferromagnetism, 2nd ed.; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Čížek, J.; Neslušan, M.; Čilliková, M.; Mičietová, A.; Melikhova, O. Modification of steel surfaces induced by turning: Non-destructive characterization using Barkhausen noise and positron annihilation. J. Phys. D Appl. Phys. 2014, 47, 1–17. [Google Scholar] [CrossRef]
- Bayramoglu, S.; Gür, C.H.; Alexandrov, I.V.; Abramova, M.M. Characterization of ultra-fine grained steel samples produced by high pressure torsion via magnetic Barkhausen noise analysis. Mater. Sci. Eng. A 2010, 527, 927–933. [Google Scholar] [CrossRef]
- Vértesy, G.; Gasparics, A.; Griffin, J.M.; Mathew, J.; Fitzpatrick, M.E.; Uytdenhouwen, I. Analysis of Surface Roughness Influence in Non-Destructive Magnetic Measurements Applied to Reactor Pressure Vessel Steels. Appl. Sci. 2020, 10, 8938. [Google Scholar] [CrossRef]
- Yamaura, S.; Furuya, Y.; Watanabe, T. The effect of grain boundary microstructure on Barkhausen noise in ferromagnetic materials. Acta Mater. 2001, 49, 3019–3027. [Google Scholar] [CrossRef]
- Neslušan, M.; Čížek, J.; Kolařík, K.; Minárik, P.; Čilliková, M.; Melikhová, O. Monitoring of grinding burn via Barkhausen noise emission in case-hardened steel in large-bearing production. J. Mater. Process. Technol. 2017, 240, 104–117. [Google Scholar] [CrossRef]
- Neslušan, M.; Bahleda, F.; Minárik, P.; Zgútová, K.; Jambor, M. Non-destructive monitoring of corrosion extent in steel rope wires via Barkhausen noise emission. J. Magn. Mater. 2019, 484, 179–187. [Google Scholar] [CrossRef]
- Sorsa, A.; Santa-Aho, S.; Wartiainen, J.; Souminen, L.; Vippola, M.; Leviskä, K. Effect of shot peening parameters to residual stress profiles and Barkhausen noise. J. Non-Destruct. Eval. 2018, 37, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Hang, C.; Liu, W.; Wang, P. A Method of Barkhausen Noise Feature Extraction Based on an Adaptive Threshold. Appl. Sci. 2019, 9, 2964. [Google Scholar] [CrossRef] [Green Version]
- Neslušan, M.; Jurkovič, M.; Kalina, T.; Pitoňák, M.; Zgútová, K. Monitoring of S235 steel over-stressing by the use of Barkhausen noise technique. Eng. Fail. Anal. 2020, 117, 104843. [Google Scholar] [CrossRef]
- White, S.A. A Barkhausen Noise Testing System for CANDU® Feeder Pipes. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2009. [Google Scholar]
- Neslušan, M.; Trško, L.; Minárik, P.; Čapek, J.; Bronček, J.; Pastorek, F.; Čížek, J.; Moravec, J. Non-destructive evaluation of steel surface after severe plastic deformation via Barkhausen noise technique. Metals 2018, 8, 1029. [Google Scholar] [CrossRef] [Green Version]
- Kleber, X.; Vincent, A. On the role of residual internal stresses and dislocations on Barkhausen noise in plastically deformed steel. NDTE Int. 2004, 37, 439–445. [Google Scholar] [CrossRef]
- Šrámek, J.; Neslušan, M.; Bahleda, F.; Zgútová, K.; Schenk, P. Influence of sample size and magnetizing voltage on Barkhausen noise during bending and uniaxial tensile test. Acta Phys. Pol. A 2020, 137, 640–643. [Google Scholar] [CrossRef]
- Haušild, P.; Kolařík, K.; Karlík, M. Characterization of strain-induced martensitic transformation in A301 stainless steel by Barkhausen noise measurement. Mater. Des. 2013, 44, 548–554. [Google Scholar] [CrossRef]
- Čilliková, M.; Mičietová, A.; Čep, R.; Neslušan, M.; Kejzlar, P. Asymmetrical Barkhausen noise of a hard milled surface. Materials 2021, 14, 1293. [Google Scholar] [CrossRef]
- Manh, T.L.; Caleyo, F.; Hallen, J.M.; Espina-Hernández, J.H.; Pérez-Benitez, J.A. Model for the correlation between magnetocrystalline energy and Barkhausen noise in ferromagnetic materials. J. Magn. Magn. Mater. 2018, 454, 155–164. [Google Scholar] [CrossRef]
- Ducharne, B.; Tene Deffo, Y.A.; Tsafack, P.; Nguedjang Kouakeuo, S.H. Directional magnetic Barkhausen noise measurement using the magnetic needle probe method. J. Magn. Magn. Mater. 2021, 519, 167453. [Google Scholar] [CrossRef]
- Neslušan, M.; Trojan, K.; Haušild, P.; Minárik, P.; Mičietová, A.; Čapek, J. Monitoring of components made of duplex steel after turning as a function of flank wear by the use of Barkhausen noise emission. Mater. Charact. 2020, 169, 110587. [Google Scholar] [CrossRef]
- Rivas, M.; Martinéz-García, J.C.; Škorvánek, I.; Švec, P.; Gorria, P. Magnetostatic interaction in soft magnetic bilayer ribbons unambiguously identified by first-order reversal curve analysis. Appl. Phys. Lett. 2015, 107, 132240. [Google Scholar] [CrossRef] [Green Version]
- Ribárik, G.; Ungár, T.; Gubicza, J. MWP-fit: A program for multiple whole-profile fitting of diffraction peak profiles by ab initio theoretical functions. J. Appl. Crystallogr. 2001, 34, 669–676. [Google Scholar] [CrossRef] [Green Version]
- Ribárik, G.; Ungár, T. Characterization of the microstructure in random and textured polycrystals and single crystals by diffraction line profile analysis. Mater. Sci. Eng. A 2010, 528, 112–121. [Google Scholar] [CrossRef]
- Scardi, P.; Leoni, M. Whole powder pattern modeling. Acta Crystallogr. A 2002, 58, 190–200. [Google Scholar] [CrossRef] [PubMed]
- Matěj, Z.; Kužel, R.; Nichtová, L. XRD total pattern fitting applied to study of microstructure of TiO2 films. Powder Diffr. 2010, 25, 125–131. [Google Scholar] [CrossRef]
- Ayers, J.E. The measurement of threading dislocation densities in semiconductor crystals by X-ray diffraction. J. Cryst. Growth 1994, 135, 71–77. [Google Scholar] [CrossRef]
- Ungár, T.; Borbély, A. The effect of dislocation contrast on x-ray line broadening: A new approach to line profile analysis. Appl. Phys. Lett. 1996, 69, 21. [Google Scholar] [CrossRef]
- Cullity, B.D.; Graham, C.D. Introduction to the Magnetic Materials, 2nd ed.; IEEE Press: Piscataway, NJ, USA, 2009. [Google Scholar]
- Čilliková, M.; Uríček, J.; Neslušan, M.; Ballo, V.; Mičietová, A. Monitoring of thermal damage after deposition of coatings via Barkhausen noise technique. Acta Phys. Polonica A 2020, 137, 637–640. [Google Scholar] [CrossRef]
- Neslušan, M.; Minárik, P.; Grenčík, J.; Trojan, K.; Zgútová, K. Non-destructive evaluation of the railway wheel surface damage after long-term operation via Barkhausen noise technique. Wear 2019, 420–421, 195–206. [Google Scholar] [CrossRef]
- Santa-Aho, S.; Vippola, M.; Sorsa, A.; Leiviskä, K.; Lindgren, M.; Lepistö, T. Utilization of Barkhausen noise magnetizing sweeps for case-depth detection from hardened steel. NDT&E Int. 2012, 52, 95–102. [Google Scholar] [CrossRef]
- MicroScan 600 Operating Instructions Manual V.5.4b (2015-0-06); Stresstech Group: Jyväskylä, Finland.
- Smallman, R.E. Modern Physical Metallurgy, 4th ed.; Butterworth-Heinemann: Oxford, UK, 1985. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pitoňák, M.; Neslušan, M.; Minárik, P.; Čapek, J.; Zgútová, K.; Jurkovič, M.; Kalina, T. Investigation of Magnetic Anisotropy and Barkhausen Noise Asymmetry Resulting from Uniaxial Plastic Deformation of Steel S235. Appl. Sci. 2021, 11, 3600. https://doi.org/10.3390/app11083600
Pitoňák M, Neslušan M, Minárik P, Čapek J, Zgútová K, Jurkovič M, Kalina T. Investigation of Magnetic Anisotropy and Barkhausen Noise Asymmetry Resulting from Uniaxial Plastic Deformation of Steel S235. Applied Sciences. 2021; 11(8):3600. https://doi.org/10.3390/app11083600
Chicago/Turabian StylePitoňák, Martin, Miroslav Neslušan, Peter Minárik, Jiří Čapek, Katarína Zgútová, Martin Jurkovič, and Tomáš Kalina. 2021. "Investigation of Magnetic Anisotropy and Barkhausen Noise Asymmetry Resulting from Uniaxial Plastic Deformation of Steel S235" Applied Sciences 11, no. 8: 3600. https://doi.org/10.3390/app11083600







