Importance of Microstructure in Carbonate Rocks: Laboratory and 3D-Imaging Petrophysical Characterization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Rocks Presentation
2.2. Petrophysical Properties from Laboratory Measurements
2.3. Petrophysical Properties Computed from Micro-Tomography Images
2.3.1. X-ray Tomography Data Acquisition
2.3.2. X-ray Tomography Data Processing
3. Results
3.1. Petrophysical Properties from Laboratory Measurements
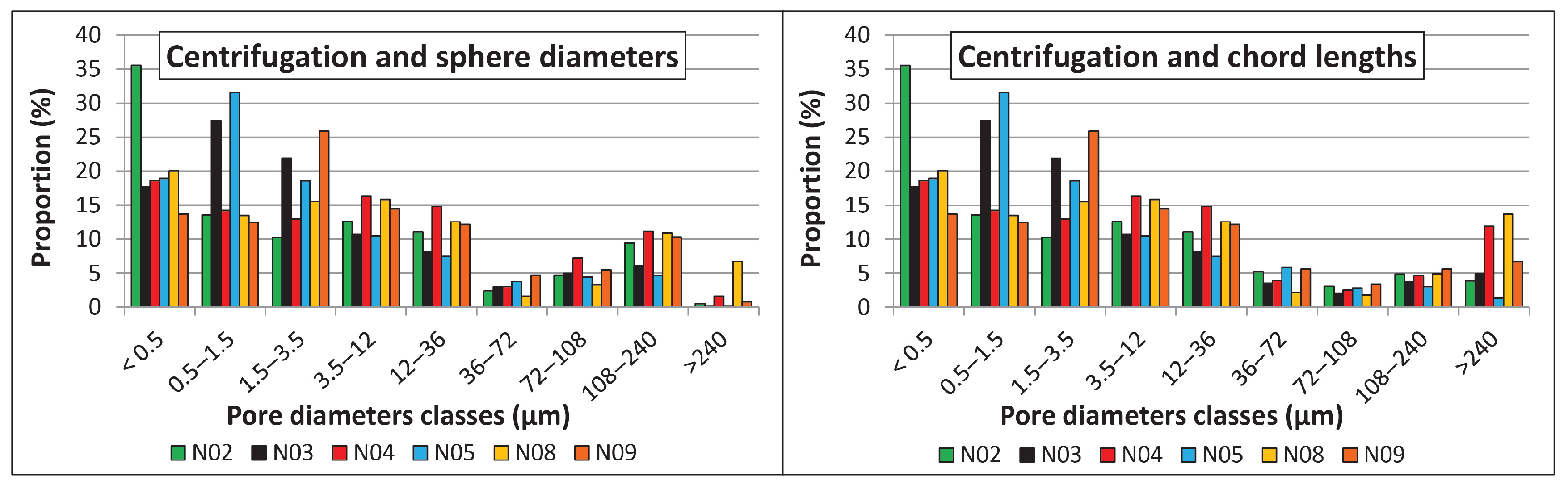
3.2. Petrophysical Calculations from Micro-Tomography Images
3.3. Comparison between Laboratory Measurements and Tomographic Images Calculations
4. Discussion
4.1. Validation of Calculated Parameters
4.2. Influence of Rock Structure on Elastic Properties
4.3. Influence of Rock Structure on Electrical Properties
4.4. Upscalling from Sample Measurements to Field Scale
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| N | Normandie |
| E | Euville |
| L | Lexos |
| XRD | X-ray Diffraction |
| SEM | Scanning Electron Microscopy |
| XRMT | X-ray Micro-Tomography |
| XRCT | X-ray Computed Tomography |
| PV | Percolating Volume |
| REV | Representative Elementary Volume |
| RHG | Raymer-Hunt-Gardner |
| WTA | Wyllie’s Time Average |
References
- Chilingarian, G.V.; Mazzullo, S.J.; Rieke, H.H. Carbonate Reservoir Characterization: A Geologic-Engineering Analysis; Number 30, 44 in Developments in Petroleum Science; Elsevier: Amsterdam, The Netherlands; New York, NY, USA, 1992. [Google Scholar]
- Moore, C.H.; Wade, W.J. Carbonate Reservoirs: Porosity and Diagenesis in a Sequence Stratigraphic Framework, 2nd ed.; Number 67 in Developments in Sedimentology; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Choquette, P.W.; Pray, L.C. Geologic Nomenclature and Classification of Porosity in Sedimentary Carbonates. Bulletin 1970, 54. [Google Scholar] [CrossRef]
- Lucia, F.J. Petrophysical parameters estimated from visual descriptions of carbonate rocks. J. Pet. Technol. 1983, 35, 629–637. [Google Scholar] [CrossRef]
- Lønøy, A. Making sense of carbonate pore systems. Bulletin 2006, 90, 1381–1405. [Google Scholar] [CrossRef]
- Regnet, J.; David, C.; Robion, P.; Menéndez, B. Microstructures and physical properties in carbonate rocks: A comprehensive review. Mar. Pet. Geol. 2019, 103, 366–376. [Google Scholar] [CrossRef]
- Eberli, G.P.; Baechle, G.T.; Anselmetti, F.S.; Incze, M.L. Factors controlling elastic properties in carbonate sediments and rocks. Lead. Edge 2003, 22, 654–660. [Google Scholar] [CrossRef]
- Verwer, K.; Eberli, G.P.; Weger, R.J. Effect of pore structure on electrical resistivity in carbonates. AAPG Bull. 2011, 95, 175–190. [Google Scholar] [CrossRef]
- Garing, C.; Luquot, L.; Pezard, P.A.; Gouze, P. Electrical and flow properties of highly heterogeneous carbonate rocks. Bulletin 2014, 98, 49–66. [Google Scholar] [CrossRef] [Green Version]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook, 3rd ed.; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- Dunham, R.J. Classification of Carbonate Rocks According to Depositional Textures; AAPG Special Volumes; AAPG: Tulsa, OK, USA, 1962. [Google Scholar]
- Lucia, F.J. Carbonate Reservoir Characterization: An Integrated Approach, 2nd ed.; Springer: Berlin, Germany; New York, NY, USA, 2007. [Google Scholar]
- Glover, P. What is the cementation exponent? A new interpretation. Lead. Edge 2009, 28, 82–85. [Google Scholar] [CrossRef]
- Archie, G. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Kozeny, J. Uber kapillare Leitung des Wassers im Boden. Sitzungberichte Akadamie Wiss. Wien Abt. Ila 1927, 136, 271–301. [Google Scholar]
- Carman, P.C. Fluid Flow through Granular Beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Wyllie, M.R.J.; Rose, W.D. Application of the Kozeny Equation to Consolidated Porous Media. Nature 1950, 165, 972. [Google Scholar] [CrossRef]
- Cornell, D.; Katz, D.L. Flow of gases through consolidated porous media. Ind. Eng. Chem. 1953, 45, 2145–2152. [Google Scholar] [CrossRef]
- Clennell, M.B. Tortuosity: A guide through the maze. Geol. Soc. Lond. Spec. Publ. 1997, 122, 299–344. [Google Scholar] [CrossRef]
- Holzer, L.; Wiedenmann, D.; Münch, B.; Keller, L.; Prestat, M.; Gasser, P.; Robertson, I.; Grobéty, B. The influence of constrictivity on the effective transport properties of porous layers in electrolysis and fuel cells. J. Mater. Sci. 2013, 48, 2934–2952. [Google Scholar] [CrossRef]
- Rembert, F.; Jougnot, D.; Guarracino, L. A fractal model for the electrical conductivity of water-saturated porous media during mineral precipitation-dissolution processes. Adv. Water Resour. 2020, 145, 103742. [Google Scholar] [CrossRef]
- Bourbie, T.; Coussy, O.; Zinszner, B. Acoustics of Porous Media; Gulf Publishing Company: Houston, TX, USA, 1987. [Google Scholar]
- Thompson, A.; Katz, A.; Krohn, C. The microgeometry and transport properties of sedimentary rock. Adv. Phys. 1987, 36, 625–694. [Google Scholar] [CrossRef]
- Gueguen, Y.; Dienes, J. Transport properties of rocks from statistics and percolation. Math. Geol. 1989, 21, 1–13. [Google Scholar] [CrossRef]
- Anselmetti, F.S.; Eberli, G.P. The Velocity-Deviation Log: A tool to predict pore type and permeability trends in carbonate drill holes from sonic and porosity or density logs. AAPG Bull. 1999, 83, 450–466. [Google Scholar]
- Verwer, K.; Braaksma, H.; Kenter, J.A. Acoustic properties of carbonates: Effects of rock texture and implications for fluid substitution. Geophysics 2008, 73, B51–B65. [Google Scholar] [CrossRef]
- Weger, R.J.; Eberli, G.P.; Baechle, G.T.; Massaferro, J.L.; Sun, Y.F. Quantification of pore structure and its effect on sonic velocity and permeability in carbonates. Bulletin 2009, 93, 1297–1317. [Google Scholar] [CrossRef]
- Regnet, J.B.; Robion, P.; David, C.; Fortin, J.; Brigaud, B.; Yven, B. Acoustic and reservoir properties of microporous carbonate rocks: Implication of micrite particle size and morphology. J. Geophys. Res. Solid Earth 2015, 120, 790–811. [Google Scholar] [CrossRef]
- Japsen, P.; Bruun, A.; Fabricius, I.L.; Rasmussen, R.; Vejbæk, O.V.; Pedersen, J.M.; Mavko, G.; Mogensen, C.; Høier, C. Influence of porosity and pore fluid on acoustic properties of chalk: AVO response from oil, South Arne Field, North Sea. Pet. Geosci. 2004, 10, 319–330. [Google Scholar] [CrossRef] [Green Version]
- Le Ravalec, M.; Darot, M.; Reuschlé, T.; Guéguen, Y. Transport properties and microstructural characteristics of a thermally cracked mylonite. Pure Appl. Geophys. 1996, 146, 207–227. [Google Scholar] [CrossRef]
- Ramakrishnan, T.S.; Rabaute, A.; Fordham, R.J.; Ramamoorthy, R.; Herron, M.; Matteson, A.; Raghurman, B. A petrophysical and petrographic study of carbonate cores from the Thamama Formation. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 11–14 November 1998. [Google Scholar] [CrossRef]
- Hebert, V.; Garing, C.; Luquot, L.; Pezard, P.A.; Gouze, P. Multi-scale X-ray tomography analysis of carbonate porosity. Geol. Soc. Lond. Spec. Publ. 2015, 406, 61–79. [Google Scholar] [CrossRef]
- Luquot, L.; Hebert, V.; Rodriguez, O. Calculating structural and geometrical parameters by laboratory measurements and X-ray microtomography: A comparative study applied to a limestone sample before and after a dissolution experiment. Solid Earth 2016, 7, 441–456. [Google Scholar] [CrossRef] [Green Version]
- Luquot, L.; Rodriguez, O.; Gouze, P. Experimental Characterization of Porosity Structure and Transport Property Changes in Limestone Undergoing Different Dissolution Regimes. Transp. Porous Med. 2014, 101, 507–532. [Google Scholar] [CrossRef]
- Rötting, T.S.; Luquot, L.; Carrera, J.; Casalinuovo, D.J. Changes in porosity, permeability, water retention curve and reactive surface area during carbonate rock dissolution. Chem. Geol. 2015, 403, 86–98. [Google Scholar] [CrossRef]
- Torquato, S.; Lu, B. Chord-Length Distribution Function for Two-Phase Random Media. Phys. Rev. E 1993, 47, 2950. [Google Scholar] [CrossRef] [PubMed]
- Gouze, P.; Luquot, L. X-ray microtomography characterization of porosity, permeability and reactive surface changes during dissolution. J. Contam. Hydrol. 2011, 120–121, 45–55. [Google Scholar] [CrossRef] [PubMed]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. II. Higher Frequency Range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Gassmann, F. Elastic waves through a packing of spheres. Geophysics 1951, 16, 673–685. [Google Scholar] [CrossRef]
- Waxman, M.; Smits, L. Electrical conductivities in oil-bearing shaly sands. Soc. Pet. Eng. J. 1968, 8, 107–122. [Google Scholar] [CrossRef]
- Reatto, A.; Da Silva, E.M.; Bruand, A.; Souza Martins, E.; Lima, J.E.F.W. Validity of the Centrifuge Method for Determining the Water Retention Properties of Tropical Soils. Soil Sci. Soc. Am. J. 2008, 72, 1547–1553. [Google Scholar] [CrossRef] [Green Version]
- Espinoza, D.N.; Santamarina, J.C. Water-CO2-mineral systems: Interfacial tension, contact angle, and diffusion - Implications to CO2 geological storage. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Gouze, P.; Melean, Y.; Le Borgne, T.; Dentz, M.; Carrera, J. Non-Fickian dispersion in porous media explained by heterogeneous microscale matrix diffusion. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Ghanbarian, B.; Hunt, A.G.; Ewing, R.P.; Sahimi, M. Tortuosity in Porous Media: A Critical Review. Soil Sci. Soc. Am. J. 2013, 77, 1461–1477. [Google Scholar] [CrossRef]
- Tanikawa, W.; Shimamoto, T. Klinkenberg effect for gas permeability and its comparison to water permeability for porous sedimentary rocks. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 1315–1338. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media, 2nd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2009; OCLC: ocn268793772. [Google Scholar]
- Casteleyn, L.; Robion, P.; Collin, P.Y.; Menéndez, B.; David, C.; Desaubliaux, G.; Fernandes, N.; Dreux, R.; Badiner, G.; Brosse, E.; et al. Interrelations of the petrophysical, sedimentological and microstructural properties of the Oolithe Blanche Formation (Bathonian, saline aquifer of the Paris Basin). Sediment. Geol. 2010, 230, 123–138. [Google Scholar] [CrossRef]
- Casteleyn, L.; Robion, P.; David, C.; Collin, P.Y.; Menéndez, B.; Fernandes, N.; Desaubliaux, G.; Rigollet, C. An integrated study of the petrophysical properties of carbonate rocks from the “Oolithe Blanche” formation in the Paris Basin. Tectonophysics 2011, 503, 18–33. [Google Scholar] [CrossRef]
- Anselmetti, F.S.; Eberli, G.P. Controls on sonic velocity in carbonates. Pure Appl. Geophys. 1993, 141, 287–323. [Google Scholar] [CrossRef]
- Wyllie, M.R.J.; Gregory, A.R.; Gardner, L.W. Elastic wave veloticies in heterogeneous and porous media. Geophysics 1956, 21, 41–70. [Google Scholar] [CrossRef]
- Raymer, L.; Hunt, E.; Gardner, J.S. An Improved Sonic Transit Time-To-Porosity Transform. In Proceedings of the SPWLA 21st Annual Logging Symposium, Lafayette, Louisiana, 8–11 July 1980. [Google Scholar]
- Pickett, G. Acoustic Character Logs and Their Applications in Formation Evaluation. J. Pet. Technol. 1963, 15, 659–667. [Google Scholar] [CrossRef]
- Castagna, J.P.; Backus, M.M. (Eds.) Offset-Dependent Reflectivity—Theory and Practice of AVO Analysis; Society of Exploration Geophysicists: Houston, TX, USA, 1993. [Google Scholar] [CrossRef]
- Martys, N.S.; Torquato, S.; Bentz, D.P. Universal scaling of fluid permeability for sphere packings. Phys. Rev. E 1994, 50, 403–408. [Google Scholar] [CrossRef]
- Carman, P.C. Some physical aspects of water flow in porous media. Discuss. Faraday Soc. 1948, 3, 72–77. [Google Scholar] [CrossRef]
- Carman, P.C. Flow of Gases through Porous Media; Academic: Cambridge, MA, USA, 1956. [Google Scholar]
- Pape, H.; Clauser, C.; Iffland, J. Permeability prediction based on fractal pore-space geometry. Geophysics 1999, 64, 1447–1460. [Google Scholar] [CrossRef]
- Costa, A. Permeability-porosity relationship: A reexamination of the Kozeny-Carman equation based on a fractal pore-space geometry assumption. Geophys. Res. Lett. 2006, 33, L02318. [Google Scholar] [CrossRef]
- Paterson, M. The equivalent channel model for permeability and resistivity in fluid-saturated rock—A re-appraisal. Mech. Mater. 1983, 2, 345–352. [Google Scholar] [CrossRef]
- Walsh, J.B.; Brace, W.F. The effect of pressure on porosity and the transport properties of rock. J. Geophys. Res. Solid Earth 1984, 89, 9425–9431. [Google Scholar] [CrossRef]
- Fabricius, I.L.; Baechle, G.; Eberli, G.P.; Weger, R. Estimating permeability of carbonate rocks from porosity and vp/vs. Geophysics 2007, 72, E185–E191. [Google Scholar] [CrossRef] [Green Version]
- Fores, B. Gravimetry and Ambient Seismic Noise Monitoring for Hydrological Modeling: Application to the Durzon Karstic Basin (Larzac, France). Ph.D. Thesis, Université Montpellier, Montpellier, France, 2016. [Google Scholar]
- Fores, B.; Champollion, C.; Lesparre, N.; Pasquet, S.; Martin, A.; Nguyen, F. Variability of the water stock dynamics in karst: Insights from surface-to-tunnel geophysics. Hydrogeol. J. in press.


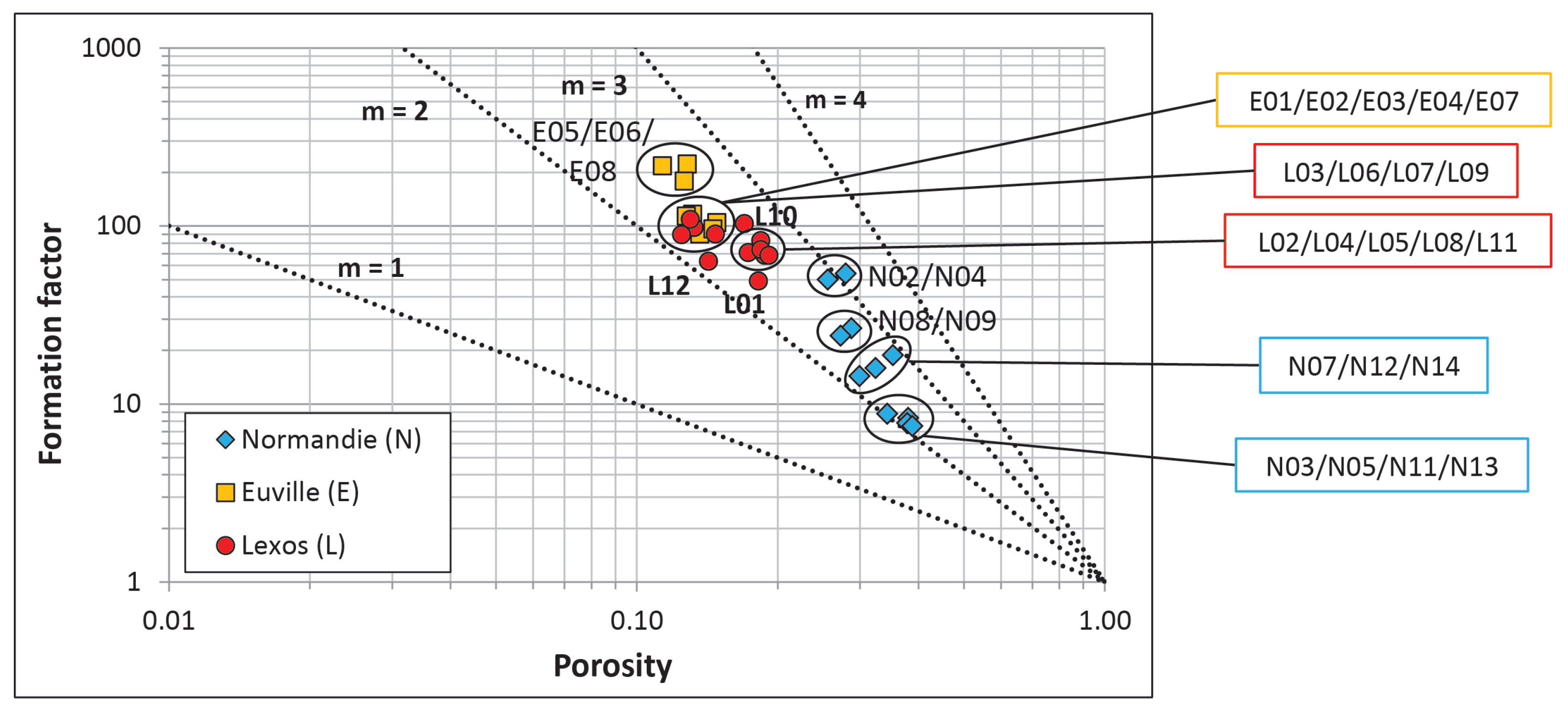

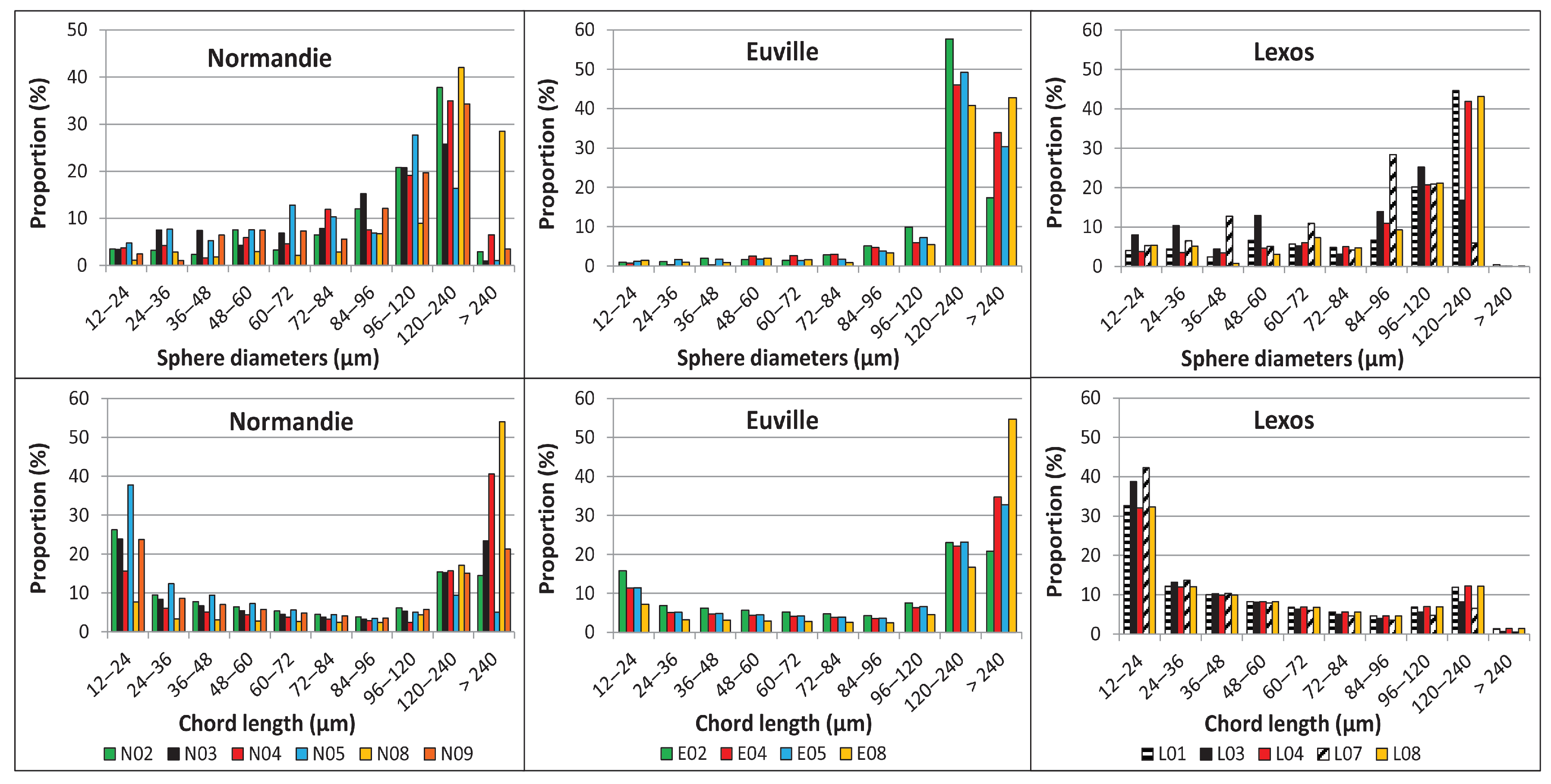
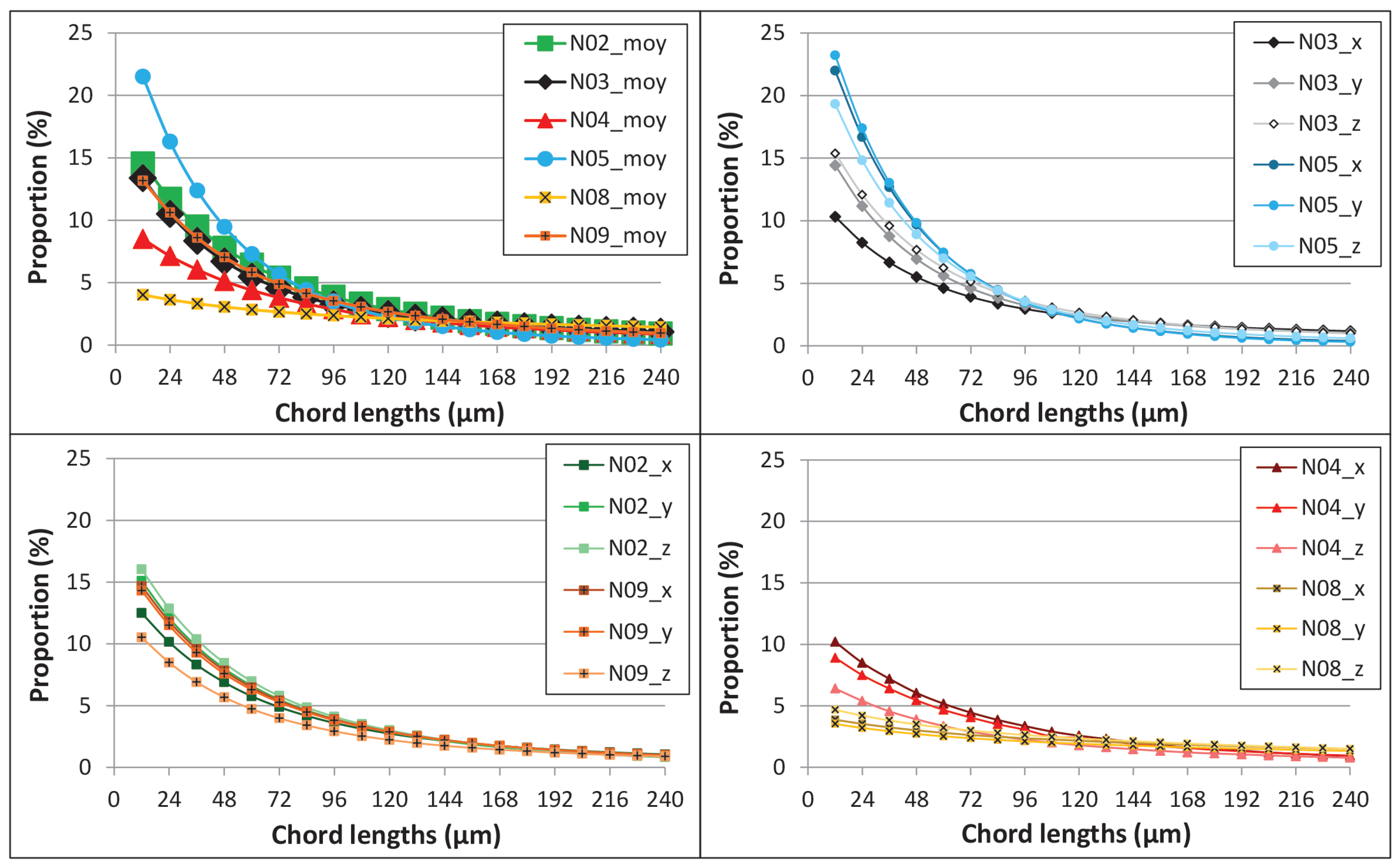

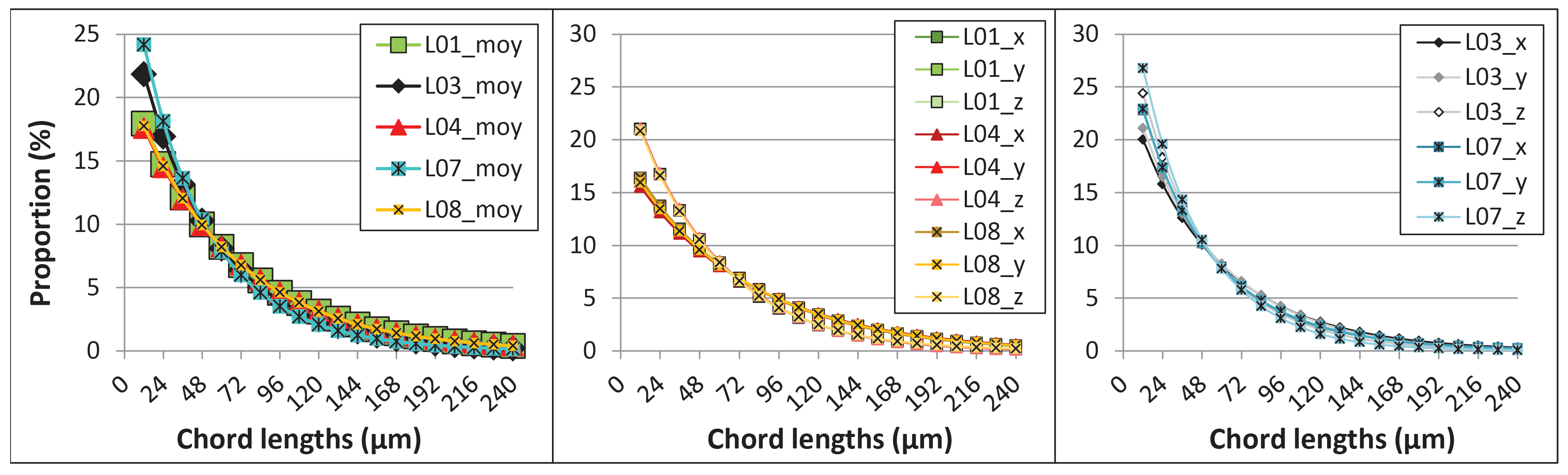




| Samples | (%) | (%) | (mD) | (mD) | (km/s) | (km/s) | K (GPa) | G (GPa) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| N02 | 30.0 | 27.9 | 5.7 | 3.7 | 54.1 | 3.13 | 3.89 | 2.40 | 1.31 | 12.22 | 6.01 |
| N03 | 39.9 | 38.0 | 12.5 | 11.2 | 8.3 | 2.19 | 1.78 | 2.36 | 1.18 | 12.47 | 4.67 |
| N04 | 27.0 | 25.6 | 4.6 | 1.3 | 50.0 | 2.87 | 3.58 | 3.27 | 1.78 | 22.93 | 11.24 |
| N05 | 40.9 | 37.8 | 12.1 | 9.1 | 7.8 | 2.12 | 1.72 | 2.35 | 1.25 | 11.78 | 5.29 |
| N07 | 35.0 | 32.4 | 39.8 | • | 15.9 | 2.45 | 2.27 | 2.32 | 1.26 | 11.01 | 5.28 |
| N08 | 30.6 | 28.8 | 16.4 | 8.4 | 26.6 | 2.63 | 2.77 | 2.33 | 1.30 | 11.07 | 5.89 |
| N09 | 28.5 | 27.2 | 6.0 | 1.9 | 24.2 | 2.45 | 2.57 | 2.97 | 1.64 | 18.32 | 9.43 |
| N11 | 34.6 | 34.3 | 10.4 | • | 8.8 | 2.03 | 1.74 | 2.30 | 1.00 | 13.70 | 3.46 |
| N12 | 36.3 | 35.3 | 20.5 | • | 18.8 | 2.81 | 2.57 | 2.28 | 1.33 | 9.86 | 6.05 |
| N13 | 39.6 | 38.8 | 23.5 | • | 7.5 | 2.13 | 1.71 | 2.29 | 1.35 | 9.20 | 6.07 |
| N14 | 30.7 | 29.9 | 22.4 | • | 14.4 | 2.21 | 2.07 | 2.35 | 1.42 | 9.83 | 7.05 |
| E01 | 14.3 | 13.2 | 7.9 | 0.5 | 116.3 | 2.35 | 3.91 | 3.80 | 1.90 | 17.40 | 13.44 |
| E02 | 14.3 | 14.8 | 12.1 | 1.0 | 104.2 | 2.43 | 3.93 | 2.32 | 1.42 | 10.03 | 7.40 |
| E03 | 12.6 | 13.6 | 6.1 | • | 90.1 | 2.26 | 3.51 | 2.70 | 1.42 | 17.00 | 7.43 |
| E04 | 14.1 | 14.6 | 26.2 | 4.0 | 96.2 | 2.37 | 3.74 | 2.56 | 1.42 | 14.33 | 7.46 |
| E05 | 12.7 | 12.8 | 17.5 | 1.6 | 222.2 | 2.63 | 5.34 | 3.73 | 2.04 | 31.30 | 15.57 |
| E06 | 10.8 | 11.4 | 8.9 | • | 217.4 | 2.47 | 4.97 | 2.72 | 1.41 | 17.61 | 7.41 |
| E07 | 14.7 | 12.8 | 1.1 | • | 113.6 | 2.30 | 3.81 | 3.73 | 1.86 | 34.62 | 12.90 |
| E08 | 11.7 | 12.6 | 2.3 | 0.05 | 178.6 | 2.51 | 4.75 | 3.86 | 2.10 | 33.77 | 16.59 |
| L01 | 18.6 | 18.2 | • | 1.9 | 49.0 | 2.29 | 2.99 | 3.40 | 2.00 | 23.44 | 15.12 |
| L02 | 18.9 | 18.4 | • | • | 82.7 | 2.61 | 3.90 | 2.58 | 1.64 | 11.74 | 10.07 |
| L03 | 13.8 | 13.3 | • | 0.1 | 98.0 | 2.27 | 3.61 | 2.95 | 1.71 | 18.72 | 11.44 |
| L04 | 20.1 | 18.8 | • | 13.8 | 68.5 | 2.53 | 3.59 | 3.10 | 1.86 | 18.93 | 12.95 |
| L05 | 17.8 | 17.3 | • | • | 70.9 | 2.43 | 3.50 | 2.73 | 1.60 | 15.39 | 9.68 |
| L06 | 13.3 | 13.0 | • | • | 108.7 | 2.30 | 3.76 | 3.35 | 1.77 | 27.48 | 12.17 |
| L07 | 13.5 | 12.5 | • | 0.1 | 89.3 | 2.16 | 3.34 | 4.50 | 1.85 | 53.57 | 11.69 |
| L08 | 18.7 | 18.4 | • | 0.7 | 73.5 | 2.54 | 3.68 | 3.41 | 1.71 | 29.12 | 11.09 |
| L09 | 14.7 | 14.7 | • | • | 90.1 | 2.35 | 3.64 | 3.78 | 1.82 | 37.82 | 12.65 |
| L10 | 17.1 | 17.0 | • | • | 103.1 | 2.61 | 4.18 | 3.04 | 1.87 | 17.40 | 13.27 |
| L11 | 18.8 | 19.2 | • | • | 68.5 | 2.56 | 3.62 | 3.78 | 1.60 | 40.78 | 9.65 |
| L12 | 13.9 | 14.2 | • | • | 63.3 | 2.13 | 3.00 | 3.90 | 2.01 | 37.65 | 15.55 |
| Samples | (%) | (%) | (%) | (mm) | (%) | |||
|---|---|---|---|---|---|---|---|---|
| N02 | 7.67 | 37.4 | 47.8 | 38.3 | 1.42 | 1.71 | 100.2 | 91.5 |
| N03 | 8.74 | 48.0 | 13.8 | 35.6 | 1.47 | 1.76 | 112.3 | 79.9 |
| N04 | 8.55 | 31.2 | 569 | 15.8 | 1.12 | 1.16 | 80.5 | 96.0 |
| N05 | 7.68 | 49.3 | 23.8 | 33.8 | 1.37 | 1.61 | 110.0 | 82.9 |
| N08 | 9.18 | 33.6 | 444 | 30.9 | 1.43 | 1.69 | 81.1 | 91.9 |
| N09 | 7.77 | 34.3 | 73.0 | 36.7 | 1.41 | 1.69 | 100.7 | 91.8 |
| E02 | 7.28 | 18.3 | 6.4 | 82.4 | 1.68 | 2.45 | 42.3 | 97.7 |
| E04 | 6.69 | 16.6 | 68.9 | 70.1 | 1.57 | 2.17 | 42.0 | 98.4 |
| E05 | 5.55 | 19.3 | 10.5 | 116.7 | 1.65 | 2.55 | 36.4 | 99.2 |
| E08 | 4.38 | 19.3 | 3.3 | 207.4 | 1.71 | 3.01 | 33.1 | 99.3 |
| L01 | 6.63 | 16.4 | 0.65 | 127.4 | 1.79 | 2.91 | 87.4 | 55.0 |
| L03 | - | - | - | - | - | - | 114.9 | - |
| L04 | 4.46 | 17.3 | 7.15 | 48.02 | 1.25 | 1.46 | 84.8 | 86.7 |
| L07 | - | - | - | - | - | - | 123.3 | - |
| L08 | 8.31 | 16.8 | 1.76 | 67.75 | 1.69 | 2.37 | 86.8 | 85.8 |
| Samples | f | Samples | f | Samples | f |
|---|---|---|---|---|---|
| N02 | 0.19 | E02 | 0.39 | L01 | 0.95 |
| N03 | 0.98 | E04 | 0.34 | L04 | 0.17 |
| N04 | 0.11 | E05 | 0.23 | L08 | 0.42 |
| N05 | 0.88 | E08 | 0.40 | ||
| N08 | 0.37 | ||||
| N09 | 0.43 |
| Nb | Equation | Rock Type | Variables | k (mD) Calculated | k (mD) Measured | References |
|---|---|---|---|---|---|---|
| chalk | 4–22 | 4–40 | ||||
| 1 | limestone | 4–8 | 2–26 | [15,16] | ||
| dolomite | 5–16 | |||||
| chalk | ; | 3–20 | 4–40 | |||
| 2 | limestone | ; | <1 | 2–26 | [54] | |
| dolomite | ; | <1 | ||||
| chalk | μm | 3–20 | 4–40 | |||
| 3 | limestone | μm | 4–10 | 2–26 | [15,16] | |
| dolomite | μm | 15–50 | ||||
| chalk | μm; | 7–85 | 4–40 | |||
| 4 | limestone | μm; | 7–30 | 2–26 | [22] | |
| dolomite | μm; | 3–45 | ||||
| chalk | μm | 30 | 4–40 | |||
| 5 | limestone | μm | 80 | 2–26 | [24] | |
| dolomite | μm | 170 | ||||
| chalk | μm | 4 | 4–40 | |||
| 6 | limestone | μm | 3 | 2–26 | [23] | |
| dolomite | μm | 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leger, M.; Luquot, L. Importance of Microstructure in Carbonate Rocks: Laboratory and 3D-Imaging Petrophysical Characterization. Appl. Sci. 2021, 11, 3784. https://doi.org/10.3390/app11093784
Leger M, Luquot L. Importance of Microstructure in Carbonate Rocks: Laboratory and 3D-Imaging Petrophysical Characterization. Applied Sciences. 2021; 11(9):3784. https://doi.org/10.3390/app11093784
Chicago/Turabian StyleLeger, Marie, and Linda Luquot. 2021. "Importance of Microstructure in Carbonate Rocks: Laboratory and 3D-Imaging Petrophysical Characterization" Applied Sciences 11, no. 9: 3784. https://doi.org/10.3390/app11093784
APA StyleLeger, M., & Luquot, L. (2021). Importance of Microstructure in Carbonate Rocks: Laboratory and 3D-Imaging Petrophysical Characterization. Applied Sciences, 11(9), 3784. https://doi.org/10.3390/app11093784






