Exploring 3D Wave-Induced Scouring Patterns around Subsea Pipelines with Artificial Intelligence Techniques
Abstract
:Featured Application
Abstract
1. Introduction
2. AI Predictive Techniques on Scouring below Seabed Pipeline: A Brief Review
2.1. Current-Induced-Pipeline Scour
2.2. Wave-Induced-Pipeline Scour
3. Analysis of Datasets: Dimensional Analysis and Experimental Tests
3.1. Dimensional Analysis
3.2. Experimental Data
4. Intelligent Computing Methods: Brief Descriptions and Implementations
4.1. Gene-Expression Programming (GEP)
4.2. Evolutonary Polynomial Regression (EPR)
4.3. Multivariate Adaptive Regression Spline (MARS)
4.4. M5 Model Tree (M5MT)
5. Results and Discussion
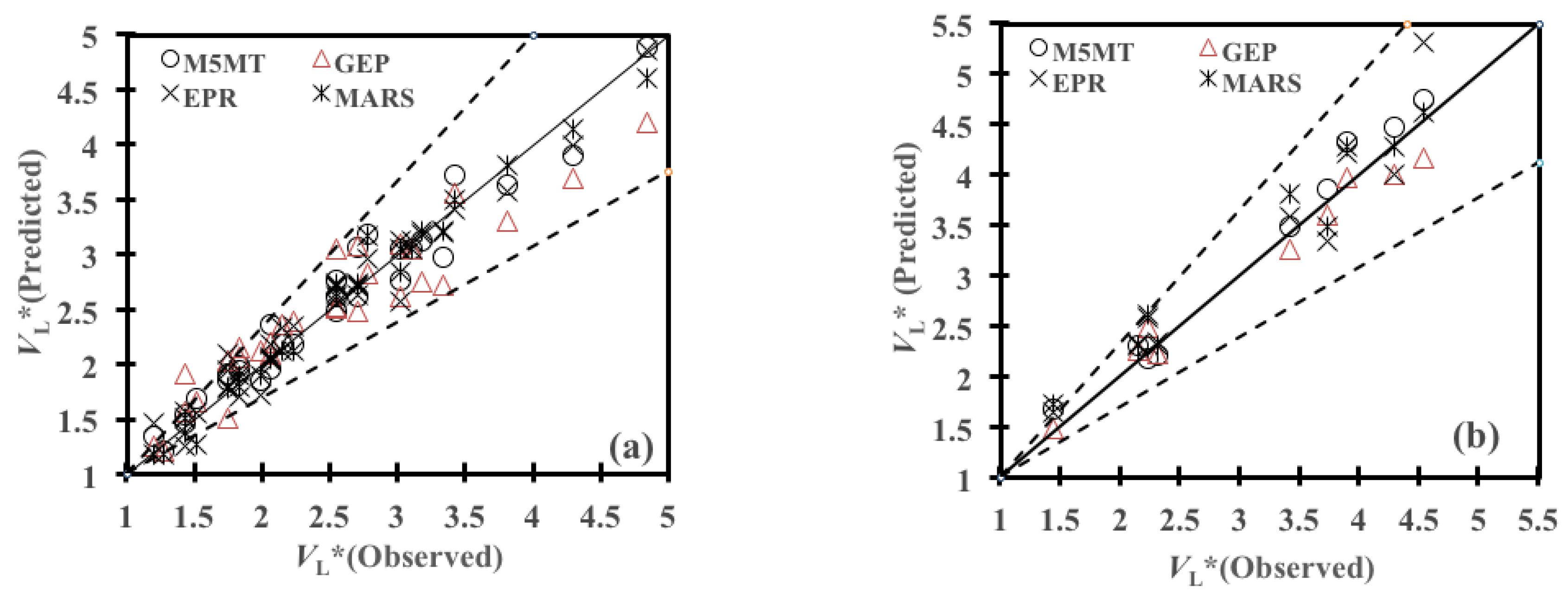
5.1. Performance Indices
5.2. Performance of Data-Driven Models under Study
5.3. Driving Physical Meaning of AI Results
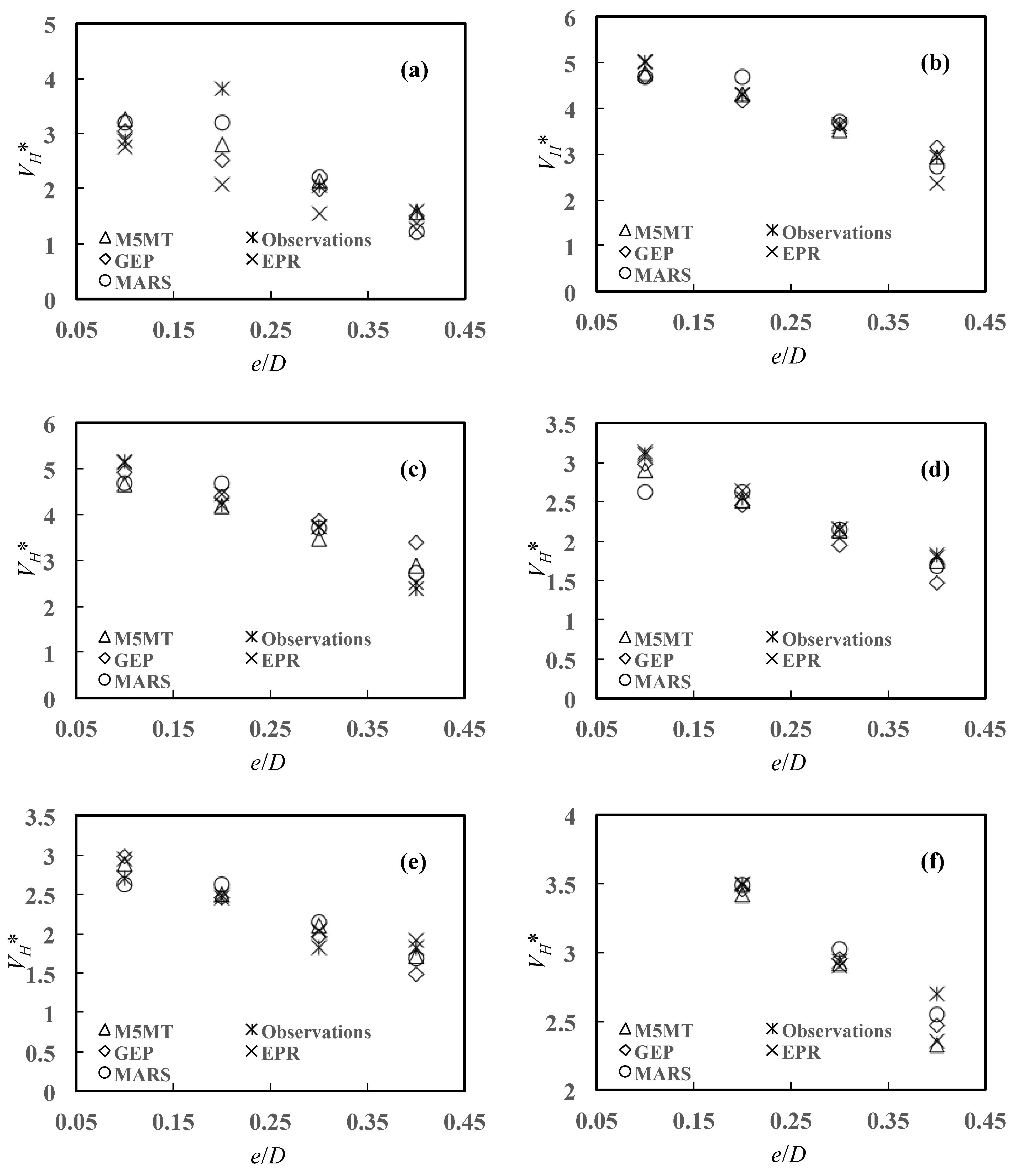
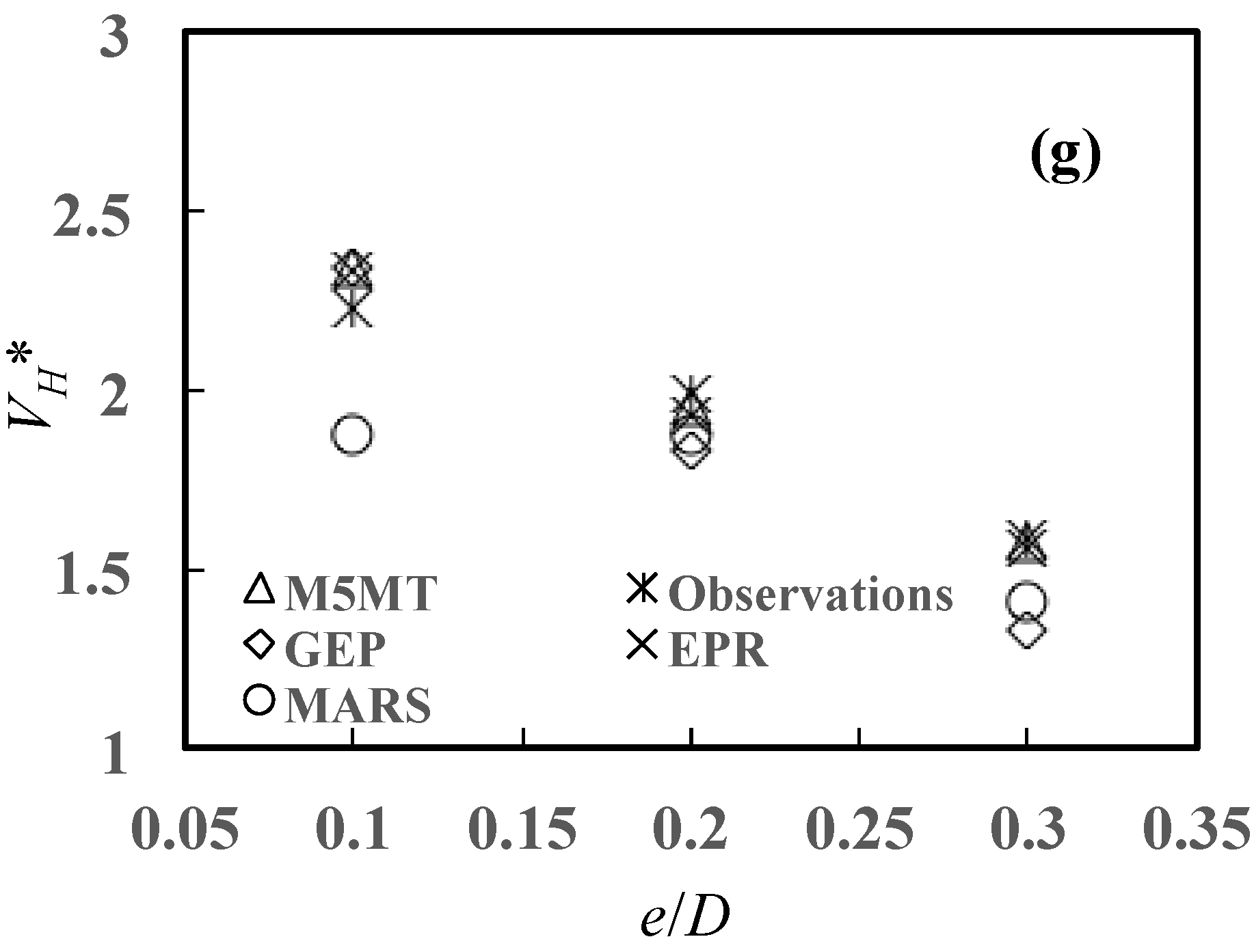
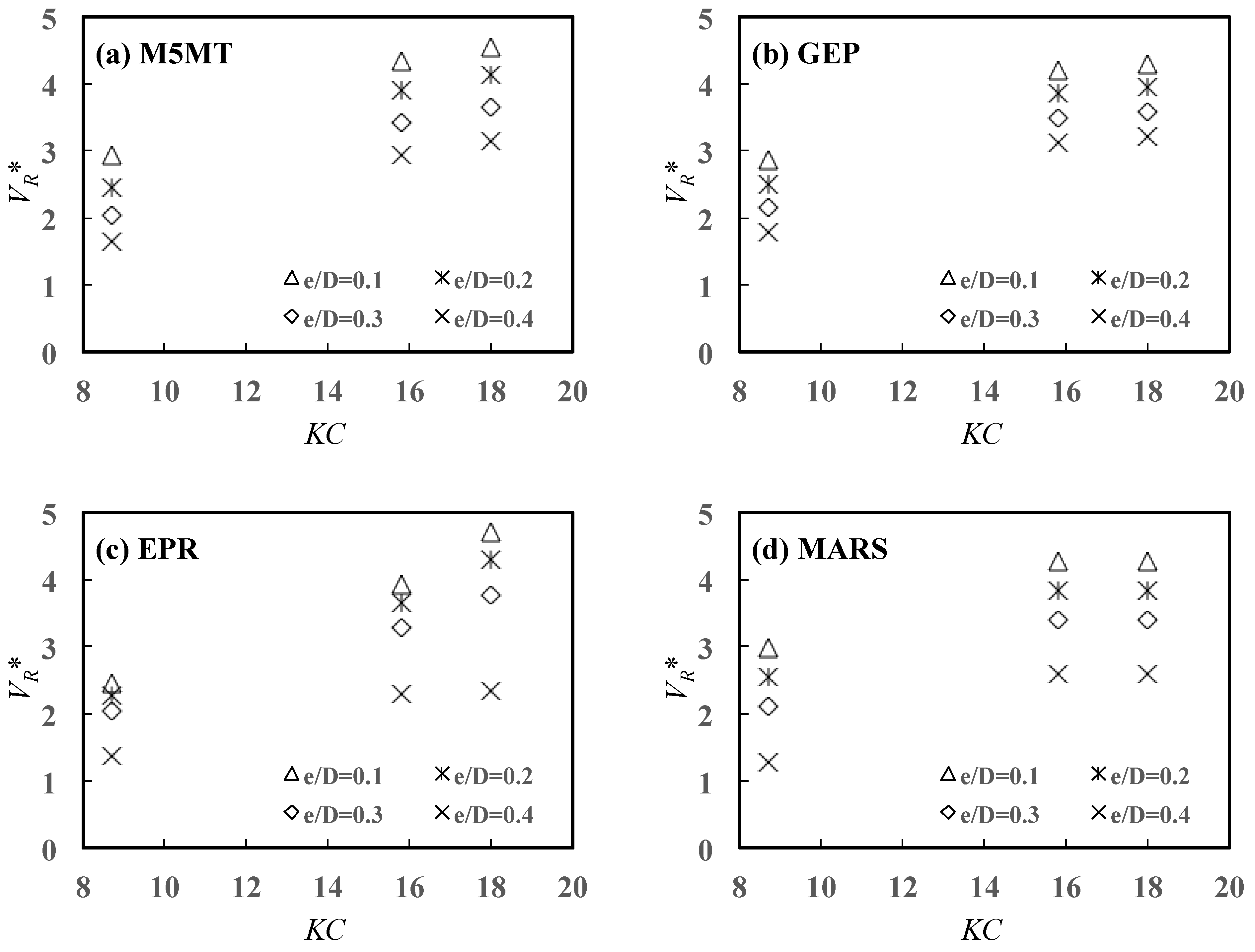
5.3.1. Effects of on
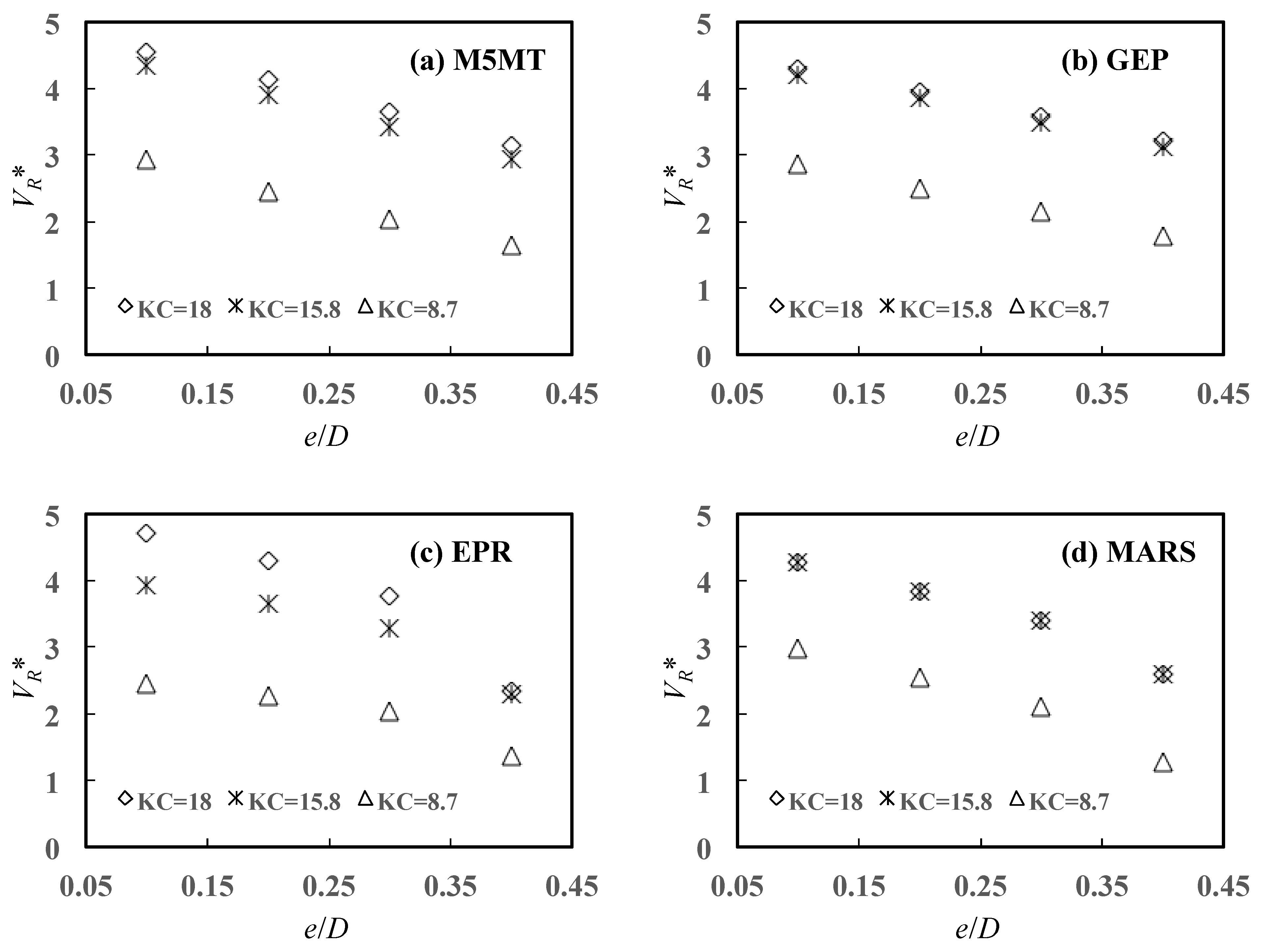
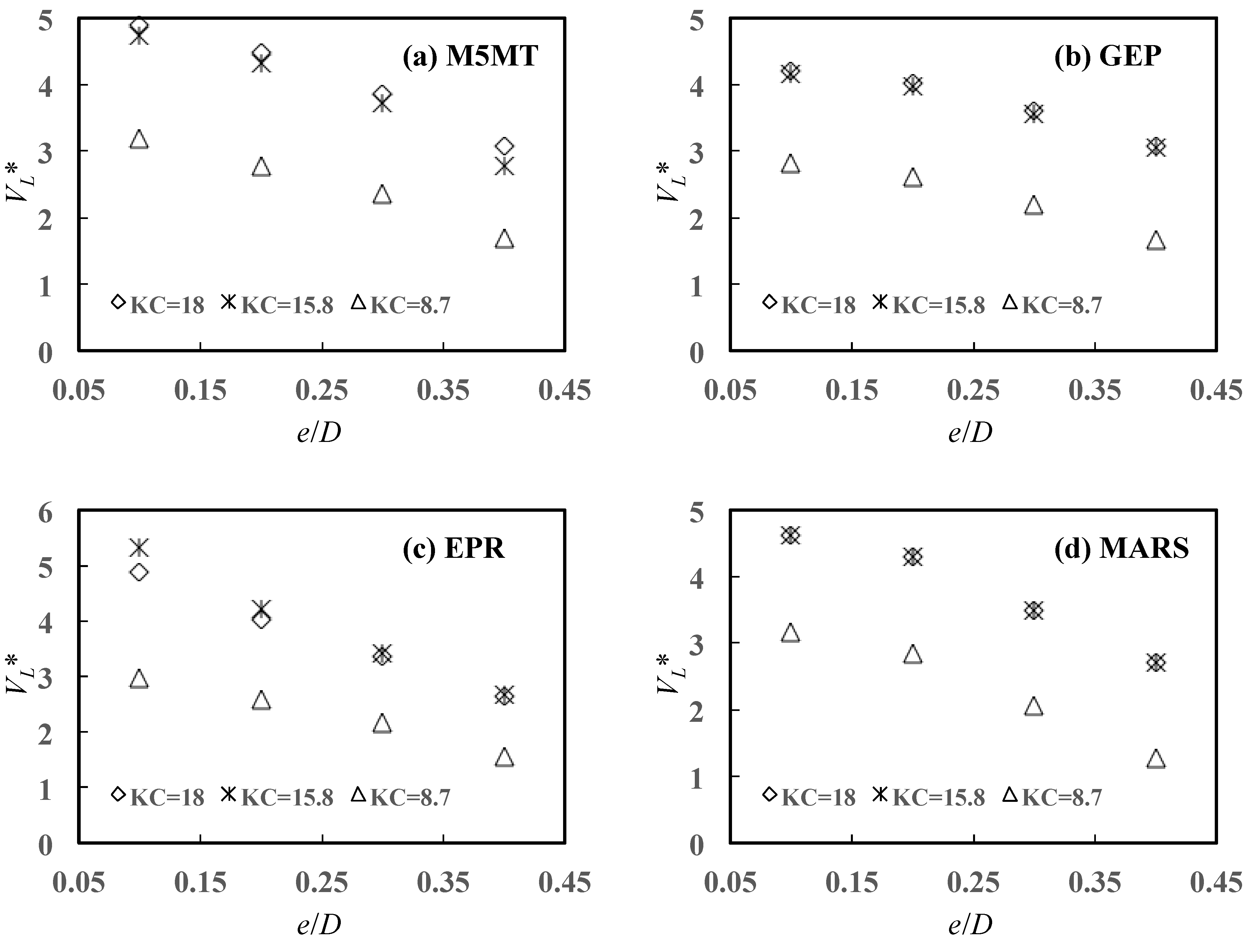
5.3.2. Effects of and on
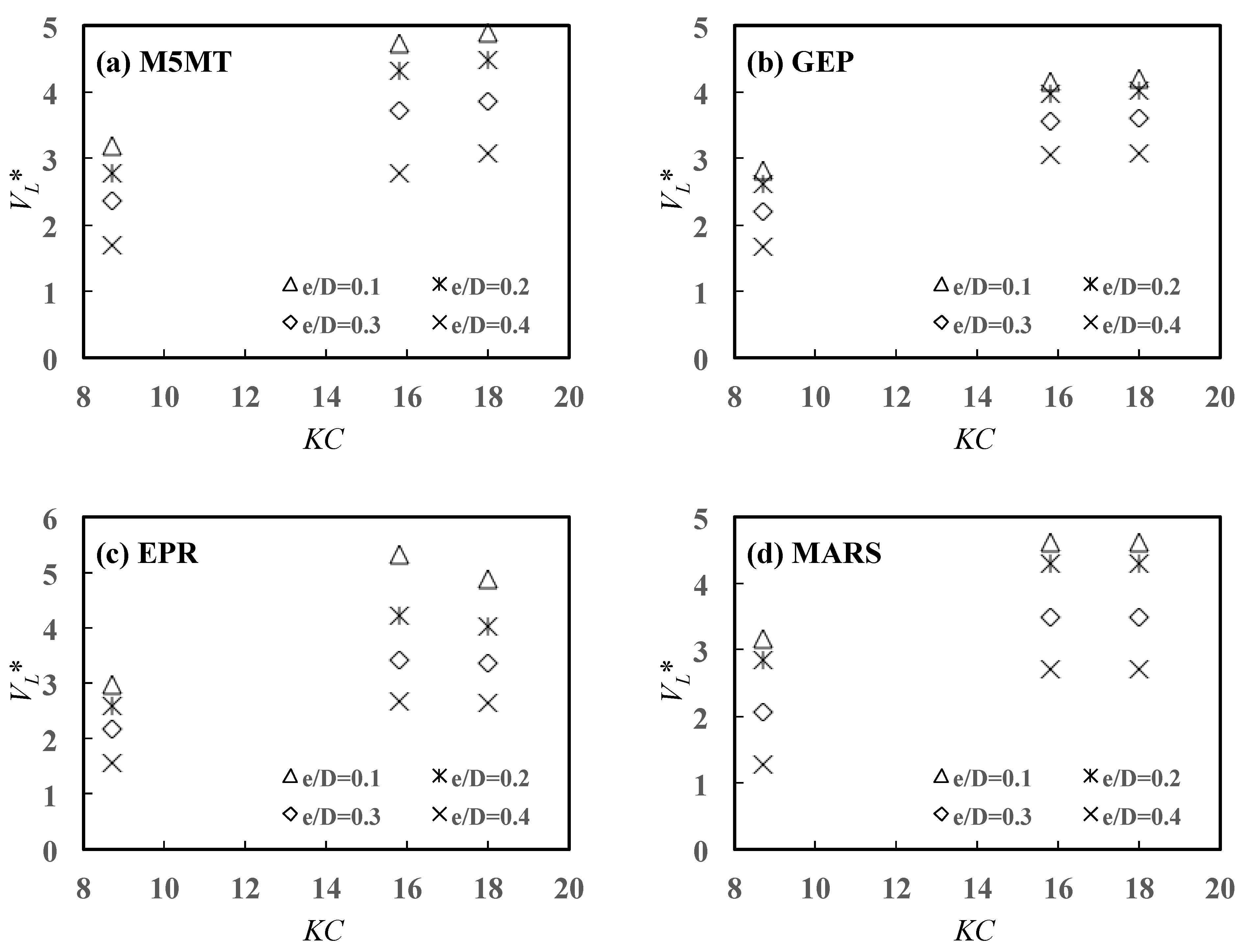
5.3.3. Effects of and on
6. Conclusions
- The considered predictive methodologies indicated two main potentialities: (i) Providing non-linear regression equations with a high degree of complexity (as naturally seen in the scouring process around submarine pipelines) when developed by a limit volume of datasets; (ii) selecting the effective variables (i.e., , , , ) on the scour rates estimation under a full automated manner.
- All AI models applied in this study provided explicit relationships with satisfying performance for the prediction of 3D scour rates. However, the performance indices in the training and testing phases overall revealed that the MARS technique is most the eligible one. Therefore, the scour Equations (A7)–(A9), given in Appendix B, associated with the Basis Functions (BFs) explicitly stated in Table A3, are recommended in the prediction of , , and , respectively.
- The physical consistency of the AI models was controlled by analyzing 3D scour propagation rates versus the normalized embedment depth , the flow incident angle , and Keulegan–Carpenter number . It was confirmed that scour propagation rates decrease with increasing , decrease with increasing the angle of attack , and increase with number. Conversely, it was ascertained the Shields’ parameter does not control, at least significantly, the scour rate propagation at the right- and left-hand pipeline shoulders.
- A comparison with the conventional approach by [9] for the prediction of would prove the superiority of the proposed scour equations. For example, by applying Equation (8) in [9], the performance index IOA is 0.842, significantly lower than the values of IOA for all the considered AI techniques (i.e., 0.9670 for MARS, 0.9435 for M5MT, 0.9356 for EPR, and 0.9329 for GEP).
Author Contributions
Funding
Conflicts of Interest
List of Notations and Acronyms
| Notations | |
| constant coefficient in M5MT model | |
| c | number of elements in input vectors in EPR model |
| D | pipeline diameter |
| median grain size of the seabed sediment | |
| e | pipeline embedment depth |
| ES | exponent range in EPR model |
| acceleration due to gravity | |
| Kelugan -Carpenter number | |
| maximum number of mathematical terms in EPR model | |
| number of experimental observations | |
| number of input variables in MARS model | |
| number of Basis Functions in MARS model | |
| pipeline Reynolds number | |
| T | wave period |
| wave orbital velocity at the seabed | |
| scour propagation velocity along the longitudinal (axial) direction of the pipeline | |
| scour propagation velocity at the left-hand shoulder of the pipeline | |
| scour propagation velocity at the right-hand shoulder of the pipeline | |
| computed scour rate value | |
| dimensionless scour propagation velocity | |
| observed scour rate value | |
| average value for computed scour rate values | |
| average value for observed scour rate values | |
| i-th input variable in MARS model | |
| X | vector of input variables in MARS model |
| z | specific function in EPR model |
| flow incident angle to the pipeline (or angle of attack) | |
| angle of repose of the seabed sediment | |
| Γ | output vector in EPR model |
| i-th input vector in EPR model | |
| Shields’ parameter | |
| dynamic viscosity of water | |
| i-th non-dimensional parameter | |
| density of water | |
| density of sediment | |
| ω | set of weighting coefficients in MARS model |
| i-th weighting coefficient in MARS model | |
| constant coefficient in MARS model | |
| Ω | approximation function in MARS model |
| bias term in EPR model | |
| j-th coefficient in EPR model | |
| Acronyms | |
| ADR | Average Discrepancy Ratio |
| AI | Artificial Intelligence |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ANN | Artificial Neural Network |
| BP | Back Propagation |
| CART | Classification and Regression Tree |
| CBO | Colliding Bodies’ Optimization |
| CW | Clear-Water regime |
| EPR | Evolutionary Polynomial Regression |
| GEP | Gene-Expression Programming |
| GMDH | Group Method of Data Handling |
| GP | Genetic Programming |
| IOA | Index Of Agreement |
| LB | Live-Bed regime |
| LGP | Linear Genetic Programming |
| MAE | Mean Absolute Error |
| MARS | Multivariate Adaptive Regression Splines |
| MNLR | Multivariate Non-Linear Regression |
| MSE | Mean Square Error |
| cMT | Model Tree |
| PSO | Particle Swarm Optimization |
| SI | Scatter Index |
| SSE | Sum of Squared Errors |
| SVM | Support Vector Machine |
| WA | Wale Algorithm |
Appendix A. Experiments by Cheng et al. (2014): Test Conditions and Main Results
| Test# | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [-] | [°] | [-] | [m] | [s] | [m/s] | [-] | [-] | [mm/s] | [mm/s] | [mm/s] |
| w15t15e1 | 0° | 0.1 | 0.13 | 1.5 | 0.29 | 8.7 | 0.18 | 3.5 | 3.6 | 3.4 |
| w15t15e2 | 0° | 0.2 | 0.13 | 1.5 | 0.29 | 8.7 | 0.18 | 3.8 | 4.8 | 2.8 |
| w15t15e3 | 0° | 0.3 | 0.13 | 1.5 | 0.29 | 8.7 | 0.18 | 2.6 | 2.6 | 2.6 |
| w15t15e4 | 0° | 0.4 | 0.13 | 1.5 | 0.29 | 8.7 | 0.18 | 1.9 | 2.0 | 1.8 |
| w16t18e1 | 0° | 0.1 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 5.7 | 6.3 | 5.1 |
| w16t18e2 | 0° | 0.2 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 4.9 | 5.4 | 4.4 |
| w16t18e3 | 0° | 0.3 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 4.3 | 4.6 | 4.0 |
| w16t18e4 | 0° | 0.4 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 3.2 | 3.7 | 2.8 |
| w16t20e1 | 0° | 0.1 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 6.1 | 6.5 | 5.7 |
| w16t20e2 | 0° | 0.2 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 5.4 | 5.3 | 5.5 |
| w16t20e3 | 0° | 0.3 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 4.7 | 4.7 | 4.7 |
| w16t20e4 | 0° | 0.4 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 3.4 | 3.0 | 3.7 |
| a15w15t15e3 | 15° | 0.3 | 0.13 | 1.5 | 0.29 | 8.7 | 0.18 | 2.2 | 1.6 | 2.7 |
| a15w15t15e4 | 15° | 0.4 | 0.13 | 1.5 | 0.29 | 8.7 | 0.18 | 1.5 | 1.6 | 1.5 |
| a15w16t18e1 | 15° | 0.1 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 5.4 | 5.2 | 5.6 |
| a15w16t18e2 | 15° | 0.2 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 4.3 | 4.1 | 4.5 |
| a15w16t18e3 | 15° | 0.3 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 4.2 | 4.0 | 4.4 |
| a15w16t18e4 | 15° | 0.4 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 2.8 | 2.6 | 3.1 |
| a15w16t20e2 | 15° | 0.2 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 4.8 | 4.4 | 5.2 |
| a15w16t20e3 | 15° | 0.3 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 4.0 | 3.7 | 4.3 |
| a15w16t20e4 | 15° | 0.4 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 3.2 | 3.4 | 3.0 |
| a30w15t15e1 | 30° | 0.1 | 0.13 | 1.5 | 0.29 | 8.7 | 0.18 | 2.6 | 2.2 | 3.0 |
| a30w15t15e2 | 30° | 0.2 | 0.13 | 1.5 | 0.29 | 8.7 | 0.18 | 1.8 | 2.2 | 1.4 |
| a30w16t18e1 | 30° | 0.1 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 3.9 | 3.9 | 4.0 |
| a30w16t18e2 | 30° | 0.2 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 3.4 | 3.2 | 3.6 |
| a30w16t18e3 | 30° | 0.3 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 2.9 | 2.7 | 3.1 |
| a30w16t18e4 | 30° | 0.4 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 2.5 | 2.3 | 2.6 |
| a30w16t20e1 | 30° | 0.1 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 3.8 | 3.4 | 4.1 |
| a30w16t20e2 | 30° | 0.2 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 3.2 | 3.1 | 3.4 |
| a30w16t20e3 | 30° | 0.3 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 2.7 | 2.3 | 3.1 |
| a30w16t20e4 | 30° | 0.4 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 2.3 | 2.3 | 2.3 |
| a45w15t15e1 | 45° | 0.1 | 0.13 | 1.5 | 0.29 | 8.7 | 0.18 | 1.8 | 1.9 | 1.7 |
| a45w15t15e2 | 45° | 0.2 | 0.13 | 1.5 | 0.29 | 8.7 | 0.18 | 1.6 | 1.8 | 1.4 |
| a45w16t18e1 | 45° | 0.1 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 2.7 | 2.8 | 2.7 |
| a45w16t18e2 | 45° | 0.2 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 2.2 | 2.5 | 1.9 |
| a45w16t18e3 | 45° | 0.3 | 0.17 | 1.8 | 0.44 | 15.8 | 0.30 | 1.8 | 2.0 | 1.6 |
| a45w16t20e1 | 45° | 0.1 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 2.8 | 2.4 | 3.1 |
| a45w16t20e2 | 45° | 0.2 | 0.15 | 2.0 | 0.45 | 18.0 | 0.29 | 2.3 | 2.3 | 2.3 |
Appendix B. Implementation of the Intelligent Computing Methods: Tables and Equations
- GEP-derived equations
| Parameters | Description of Parameters | Setting of Parameters |
|---|---|---|
| P1 | Function set | +,−,·,/, Power (x2), min(x1, x2), (1−x), ln(x), average(x1, x2), arctan(x), tanh(x) |
| P2 | Linking function | Addition |
| P3 | Mutation rate | 0.003 |
| P4 | Inversion rate | 0.00546 |
| P5 | One-point and two-point recombination rates | 0.00277 |
| P6 | Gene recombination rate | 0.00277 |
| P7 | Permutation | 0.00546 |
| P8 | Maximum tree depth | 6 |
| P9 | Number of genes | 3 |
| P10 | Number of chromosomes | 30 |
| P11 | Best fitness values | 773.67 (), 763.76 (), 761.35 () |
- EPR-derived equations
- MARS-derived equations
| Prediction | |
| BF1 | |
| BF2 | |
| BF3 | |
| BF4 | |
| BF5 | |
| BF6 | |
| Prediction | |
| BF1 | |
| BF2 | |
| BF3 | |
| BF4 | |
| BF5 | |
| BF6 | |
| BF7 | |
| Prediction | |
| BF1 | |
| BF2 | |
| BF3 | |
| BF4 | |
- M5MT-derived equations
| If 1+ sinα <= 1.379: |
| | If 1 e/D <= 0.75: |
| | | If KC <= 12.25: LM#1 |
| | | If KC > 12.25: |
| | | | If 1 e/D <= 0.65: LM#2 |
| | | | If 1 e/D > 0.65: LM#3 |
| | If 1 e/D > 0.75: |
| | | If 1+ sinα <= 1.129: |
| | | | If θw <= 0.295: LM#4 |
| | | | If θw > 0.295: LM#5 |
| | | If 1+ sinα > 1.129: LM#6 |
| If 1+ sinα > 1.379: |
| | If KC <= 12.25: |
| | | If 1+ sinα <= 1.603: LM#7 |
| | | If 1+ sinα > 1.603: LM#8 |
| | If KC > 12.25: |
| | | If 1-e/D <= 0.65: LM#9 |
| | | If 1- e/D > 0.65: |
| | | | If 1+ sinα <= 1.603: |
| | | | | If 1 e/D <= 0.75: LM#10 |
| | | | | If 1- e/D > 0.75: LM#11 |
| | | | If 1+ sinα > 1.603: LM#12 |
| Linear Equations by M5MT Model | |
|---|---|
| #1 | |
| #2 | |
| #3 | |
| #4 | |
| #5 | |
| #6 | |
| #7 | |
| #8 | |
| #9 | |
| #10 | |
| #11 | |
| #12 |
| Rule#1 |
| IF 1+sinα <= 1.603, 1 e/D <= 0.65, KC > 12.25, 1+ sinα <= 1.379 |
| THEN LM#1 |
| Rule#2 |
| IF 1+ sinα <= 1.603, 1 e/D > 0.65, KC <= 12.25, 1+ sinα <= 1.129 |
| THEN LM#2 |
| Rule#3 |
| IF KC > 12.25, 1+ sinα <= 1.379, 1 e/D <= 0.75 |
| THEN LM#3 |
| Rule#4 |
| IF KC > 12.25, 1+ sinα <= 1.379 |
| THEN LM#4 |
| Rule#5 |
| IF KC > 12.25, 1+ sinα > 1.603, 1 e/D <= 0.85 |
| THEN LM#5 |
| Rule#6 |
| IF KC <= 12.25, 1+ sinα <= 1.603, 1 e/D <= 0.65 |
| THEN LM#6 |
| Rule#7 |
| IF KC <= 12.25, 1+ sinα <= 1.603 |
| THEN LM#7 |
| Rule#8 |
| IF 1+ sinα <= 1.603, 1 e/D <= 0.7 |
| THEN LM#8 |
| Rule#9 |
| IF KC <= 12.25 |
| THEN LM#9 |
| Rule#10 |
| IF 1+ sinα <= 1.603, 1 e/D <= 0.85 |
| THEN LM#10 |
| Rule#11 |
| IF 1+ sinα <= 1.603 |
| THEN LM#11 = 3.7233×(1+ sinα)+8.642 |
| Otherwise |
| Rule#12 LM#12 |
| Linear Equations by M5MT Model | |
|---|---|
| #1 | |
| #2 | |
| #3 | |
| #4 | |
| #5 | |
| #6 | |
| #7 | |
| #8 | |
| #9 | |
| #10 | |
| #11 | |
| #12 |
| If KC <= 12.25: |
| | If 1 e/D <= 0.85: |
| | | If 1+ sinα <= 1.379: LM#1 |
| | | If 1+ sinα > 1.379: LM#2 |
| | If 1 e/D > 0.85: LM#3 |
| If KC > 12.25: |
| | If 1+ sinα <= 1.379: |
| | | If 1 e/D <= 0.75: |
| | | | If 1 e/D <= 0.65: LM#4 |
| | | | If 1 e/D > 0.65: |
| | | | | If 1+ sinα <= 1.129: LM#5 |
| | | | | If 1+ sinα > 1.129: LM#6 |
| | | If 1 e/D > 0.75: |
| | | | If KC <=16.9: LM#7 |
| | | | If KC > 16.9: LM#8 |
| | If 1+ sinα > 1.379: |
| | | If 1+ sinα <= 1.603: |
| | | | If 1 e/D <= 0.85: |
| | | | | If 1 e/D <= 0.75: LM#9 |
| | | | | If 1 e/D > 0.75: LM#10 |
| | | | If 1 e/D > 0.85: LM#11 |
| | | If 1+ sinα > 1.603: |
| | | | If 1 e/D <= 0.85: LM#12 |
| | | | If 1 e/D > 0.85: LM#13 |
| Linear Equations by M5MT Model | |
|---|---|
| #1 | |
| #2 | |
| #3 | |
| #4 | |
| #5 | |
| #6 | |
| #7 | |
| #8 | |
| #9 | |
| #10 | |
| #11 | |
| #12 | |
| #13 |
References
- Xie, L.; Zhu, Y. Scour protection of underwater pipelines. J. Civ. Eng. Constr. 2018, 7, 171–177. [Google Scholar] [CrossRef] [Green Version]
- Sumer, B.M.; Fredsøe, J. The Mechanics of Scour in the Marine Environment; Advanced Series on Ocean Engineering; World Scientific Publishing: Singapore, 2002; Volume 17. [Google Scholar]
- Cevik, E.; Yüksel, Y. Scour under submarine pipelines in waves in shoaling conditions. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 9–19. [Google Scholar] [CrossRef]
- Hansen, E.A. Scour below pipelines and cables: A simple model. In Proceedings of the 11th Offshore Mechanics and Arctic Engineering Conference, ASME, Calgary, AB, Canada, 7–12 June 1992; Volume V-A, pp. 133–138. [Google Scholar]
- Kumar, A.V.; Neelamani, S.; Rao, S.N. Wave pressures and uplift forces on and scour around submarine pipeline in clayey soil. Ocean Eng. 2003, 30, 271–295. [Google Scholar] [CrossRef]
- Cheng, L.; Yeow, K.; Zhang, Z.; Teng, B. Three-dimensional scour below offshore pipelines in steady currents. Coast. Eng. 2009, 56, 577–590. [Google Scholar] [CrossRef]
- Yang, L.; Shi, B.; Guo, Y.; Wen, X. Calculation and experiment on scour depth for submarine pipeline with a spoiler. Ocean Eng. 2012, 55, 191–198. [Google Scholar] [CrossRef]
- Wu, Y.; Chiew, Y.-M. Three-dimensional scour at submarine pipelines. J. Hydraul. Eng. 2012, 138, 788–795. [Google Scholar] [CrossRef]
- Cheng, L.; Yeow, K.; Zang, Z.; Li, F. 3D scour below pipelines under waves and combined waves and currents. Coast. Eng. 2014, 83, 137–149. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Shi, B.; Guo, Y.; Zhang, L.; Zhang, J.; Han, Y. Scour protection of submarine pipelines using rubber plates underneath the pipes. Ocean Eng. 2014, 84, 176–182. [Google Scholar] [CrossRef] [Green Version]
- Yusoff, M.A.M.; Azamathulla, H.M.; Ghani, A.A. Time variations of scour below submerged skewed pipelines. IOP Conf. Series: Mater. Sci. Eng. 2016, 136, 012071. [Google Scholar] [CrossRef] [Green Version]
- Dogan, M.; Aksoy, A.O.; Arisoy, Y.; Guney, M.S.; Abdi, V. Experimental investigation of the equilibrium scour depth below submerged pipes both in live-bed and clear-water regimes under the wave effect. Appl. Ocean Res. 2018, 80, 49–56. [Google Scholar] [CrossRef]
- Yang, S.; Shi, B.; Guo, Y.; Yang, L. Investigation on scour protection of submarine piggyback pipeline. Ocean Eng. 2019, 182, 442–450. [Google Scholar] [CrossRef]
- Zang, Z.; Tang, G.; Chen, Y.; Cheng, L.; Zhang, J. Predictions of the equilibrium depth and time scale of local scour below a partially buried pipeline under oblique currents and waves. Coast. Eng. 2019, 150, 94–107. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Zakaria, N.A. Prediction of scour below submerged pipeline crossing a river using ANN. Water Sci. Technol. 2011, 63, 2225–2230. [Google Scholar] [CrossRef] [PubMed]
- Etemad-Shahidi, A.; Yasa, R.; Kazeminezhad, M. Prediction of wave-induced scour depth under submarine pipelines using machine learning approach. Appl. Ocean Res. 2011, 33, 54–59. [Google Scholar] [CrossRef] [Green Version]
- Zanganeh, M.; Yeganeh-Bakhtiary, A.; Bakhtyar, R. Combined particle swarm optimization and fuzzy inference system model for estimation of current-induced scour beneath marine pipelines. J. Hydroinform. 2010, 13, 558–573. [Google Scholar] [CrossRef]
- Parsaie, A.; Haghiabi, A.H.; Moradinejad, A. Prediction of scour depth below river pipeline using support vector machine. KSCE J. Civ. Eng. 2019, 23, 2503–2513. [Google Scholar] [CrossRef]
- Yasa, R.; Shahidi, A.E. Classification and regression trees approach for predicting current-induced scour depth under pipelines. J. Offshore Mech. Arct. Eng. 2013, 136, 011702. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Yusoff, M.A.M. Soft computing for prediction of river pipeline scour depth. Neural Comput. Appl. 2013, 23, 2465–2469. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Sarkamaryan, S. Extraction of optimal equations for evaluation of pipeline scour depth due to currents. Proc. Inst. Civ. Eng. Mar. Eng. 2018, 171, 1–10. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Ghani, A.A. Genetic programming to predict river pipeline scour. J. Pipeline Syst. Eng. Pract. 2010, 1, 127–132. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Barani, G.-A.; Azamathulla, H.M. Prediction of pipeline scour depth in clear-water and live-bed conditions using group method of data handling. Neural Comput. Appl. 2012, 24, 629–635. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Barani, G.-A.; Kermani, M.R.H. Estimation of pipeline scour due to waves by GMDH. J. Pipeline Syst. Eng. Pract. 2014, 5, 06014002. [Google Scholar] [CrossRef]
- Haghiabi, A.H. Prediction of river pipeline scour depth using multivariate adaptive regression splines. J. Pipeline Syst. Eng. Pract. 2017, 8, 04016015. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Saberi-Movahed, F. GMDH-GEP to predict free span expansion rates below pipelines under waves. Mar. Georesources Geotechnol. 2019, 37, 375–392. [Google Scholar] [CrossRef]
- Ehteram, M.; Ahmed, A.N.; Ling, L.; Fai, C.M.; Latif, S.D.; Afan, H.A.; Banadkooki, F.B.; El-Shafie, A. Pipeline scour rates prediction-based model utilizing a multilayer perceptron-colliding body algorithm. Water 2020, 12, 902. [Google Scholar] [CrossRef] [Green Version]
- Moncada-M, A.T.; Aguirre-Pe, J. Scour below pipeline in river crossings. J. Hydraul. Eng. 1999, 125, 953–958. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Guven, A.; Demir, Y.K. Linear genetic programming to scour below submerged pipeline. Ocean Eng. 2011, 38, 995–1000. [Google Scholar] [CrossRef]
- Sharafati, A.; Yasa, R.; Azamathulla, H.M. Assessment of stochastic approaches in prediction of wave-induced pipeline scour depth. J. Pipeline Syst. Eng. Pract. 2018, 9, 04018024. [Google Scholar] [CrossRef]
- Wu, Y.; Chiew, Y.-M. Mechanics of three-dimensional pipeline scour in unidirectional steady current. J. Pipeline Syst. Eng. Pract. 2013, 4, 3–10. [Google Scholar] [CrossRef]
- Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. Complex Syst. 2001, 13, 87–129. [Google Scholar]
- Giustolisi, O.; Savic, D.A. A symbolic data-driven technique based on evolutionary polynomial regression. J. Hydroinform. 2006, 8, 207–222. [Google Scholar] [CrossRef] [Green Version]
- Berardi, L.; Giustolisi, O.; Kapelan, Z.; Savic, D.A. Development of pipe deterioration models for water distribution systems using EPR. J. Hydroinform. 2008, 10, 113–126. [Google Scholar] [CrossRef] [Green Version]
- Giustolisi, O.; Savic, D.A. Advances in data-driven analyses and modelling using EPR-MOGA. J. Hydroinform. 2009, 11, 225–236. [Google Scholar] [CrossRef]
- Savic, D.A.; Giustolisi, O.; Laucelli, D. Asset deterioration analysis using multi-utility data and multi-objective data mining. J. Hydroinform. 2009, 11, 211–224. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the Australian Joint Conference on Artificial Intelligence (AI ’92), Hobart, Australia, 16–18 November 1992; Adams & Sterling, Ed.; World Scientific: Singapore, 1992; pp. 343–348. [Google Scholar]
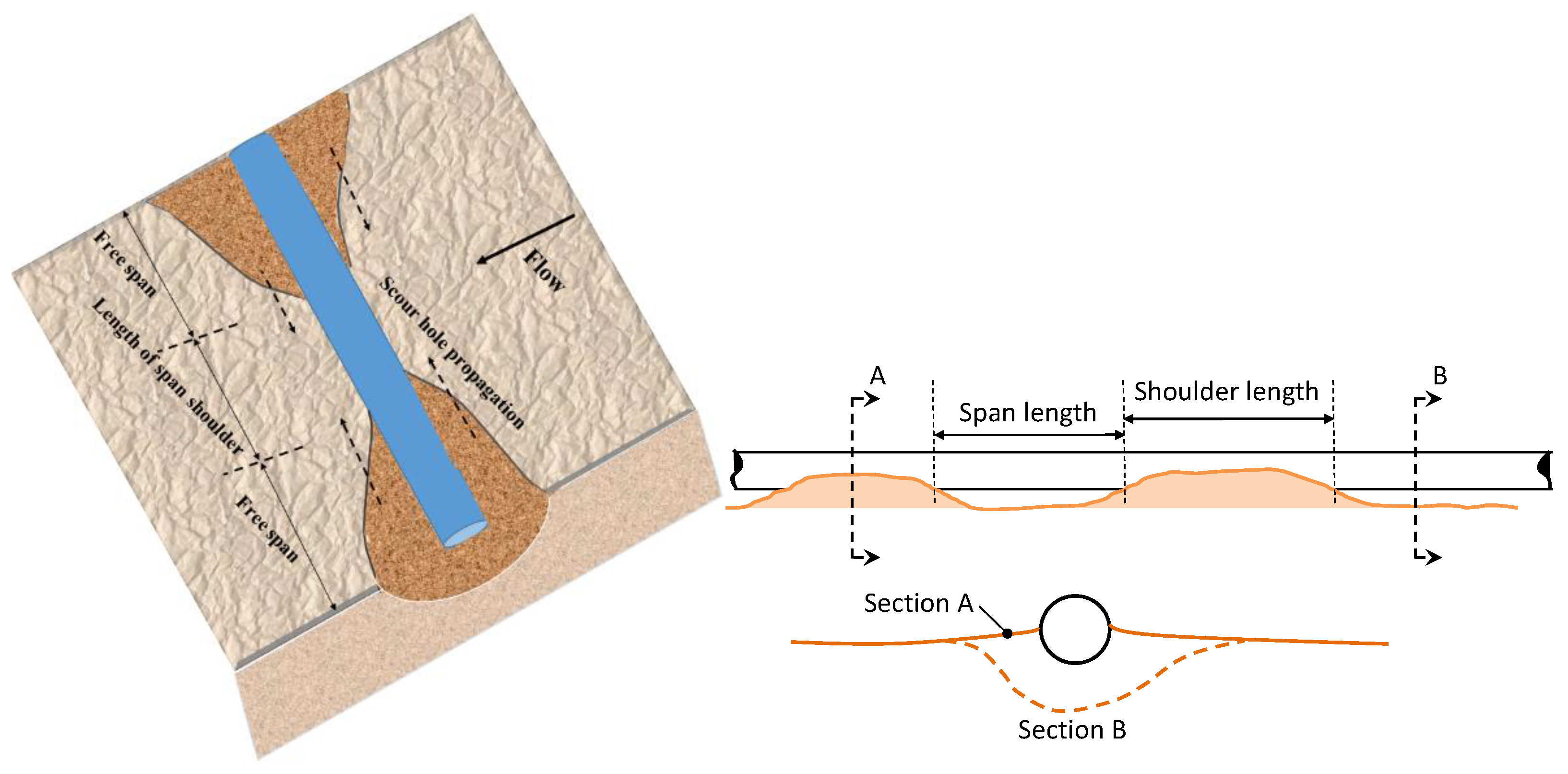
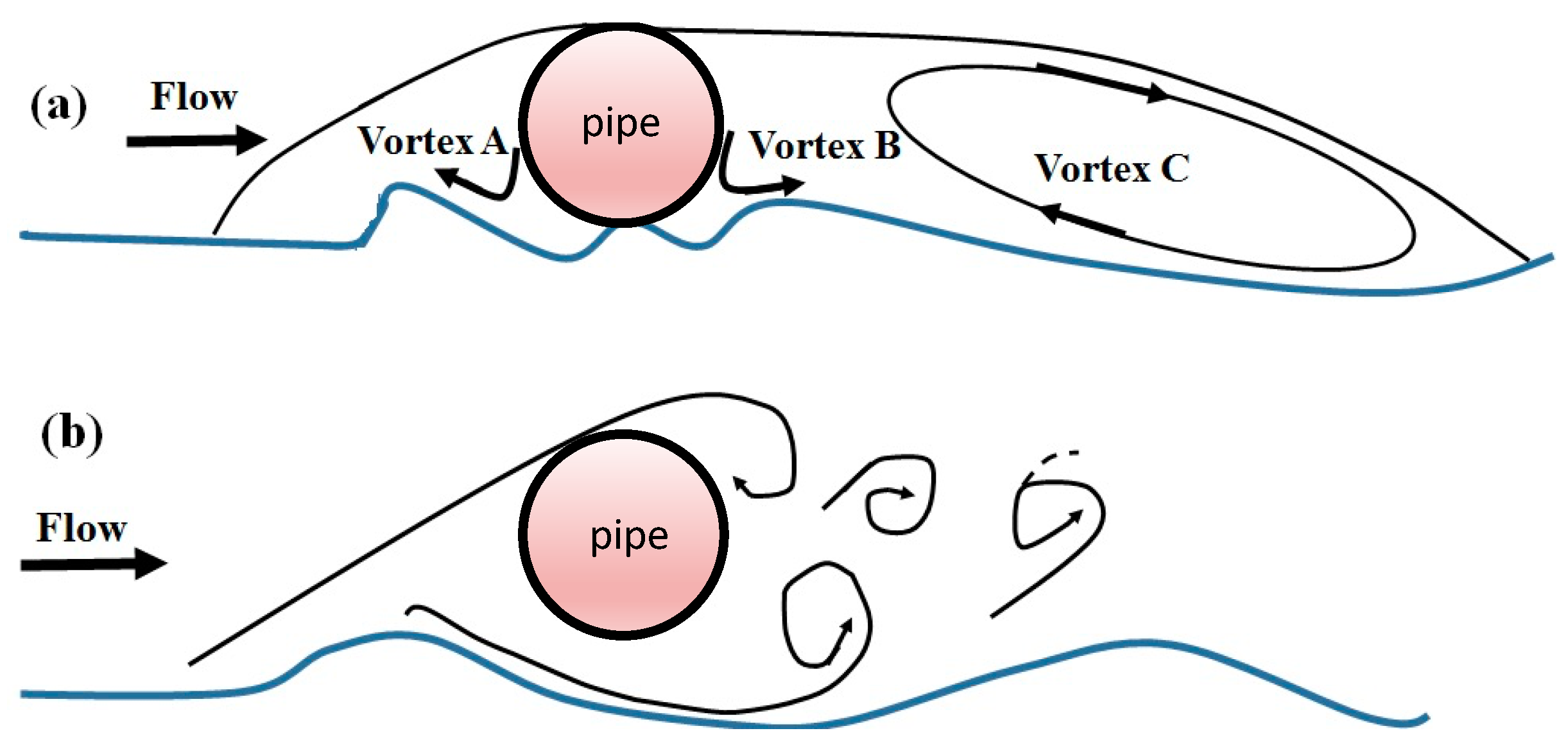
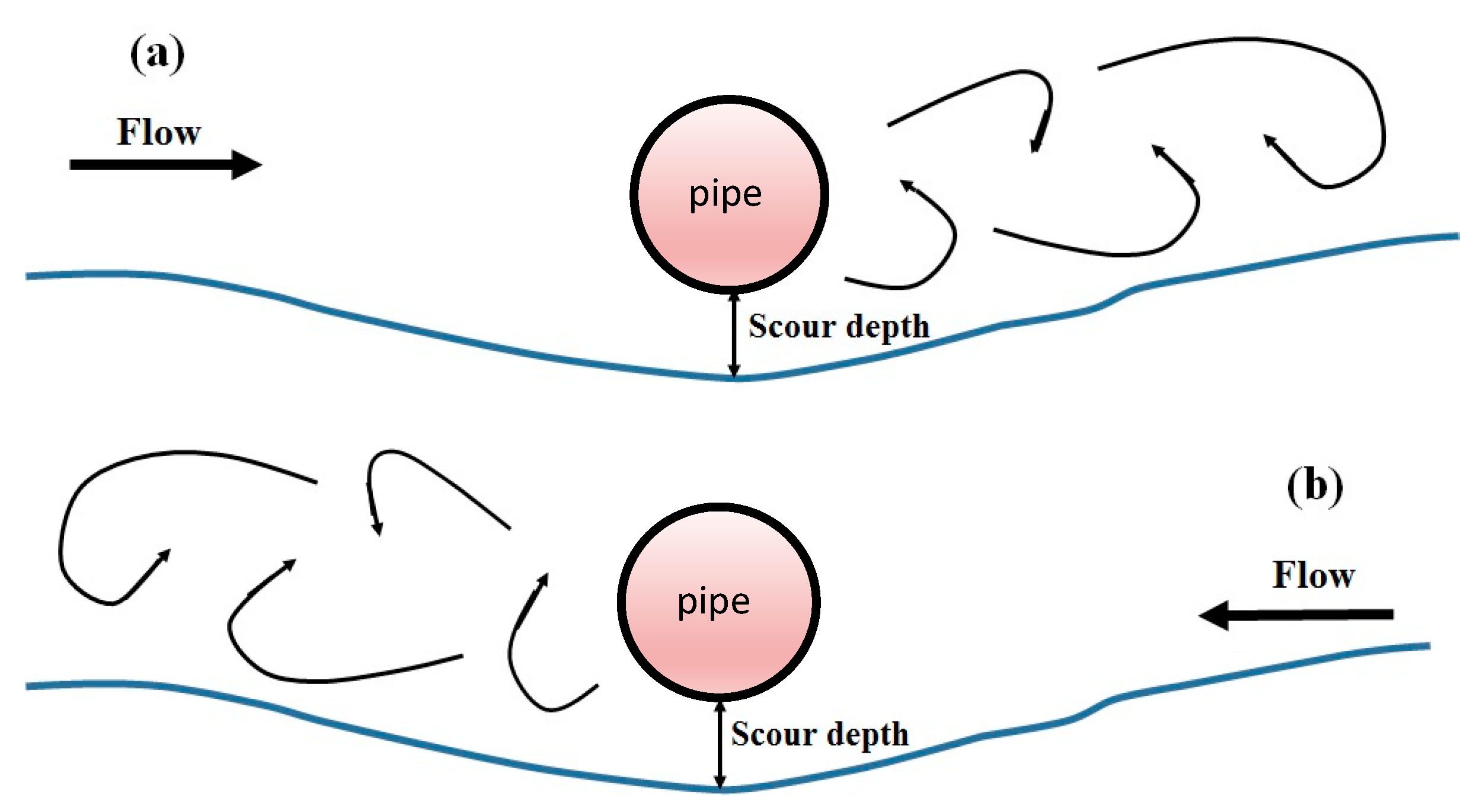

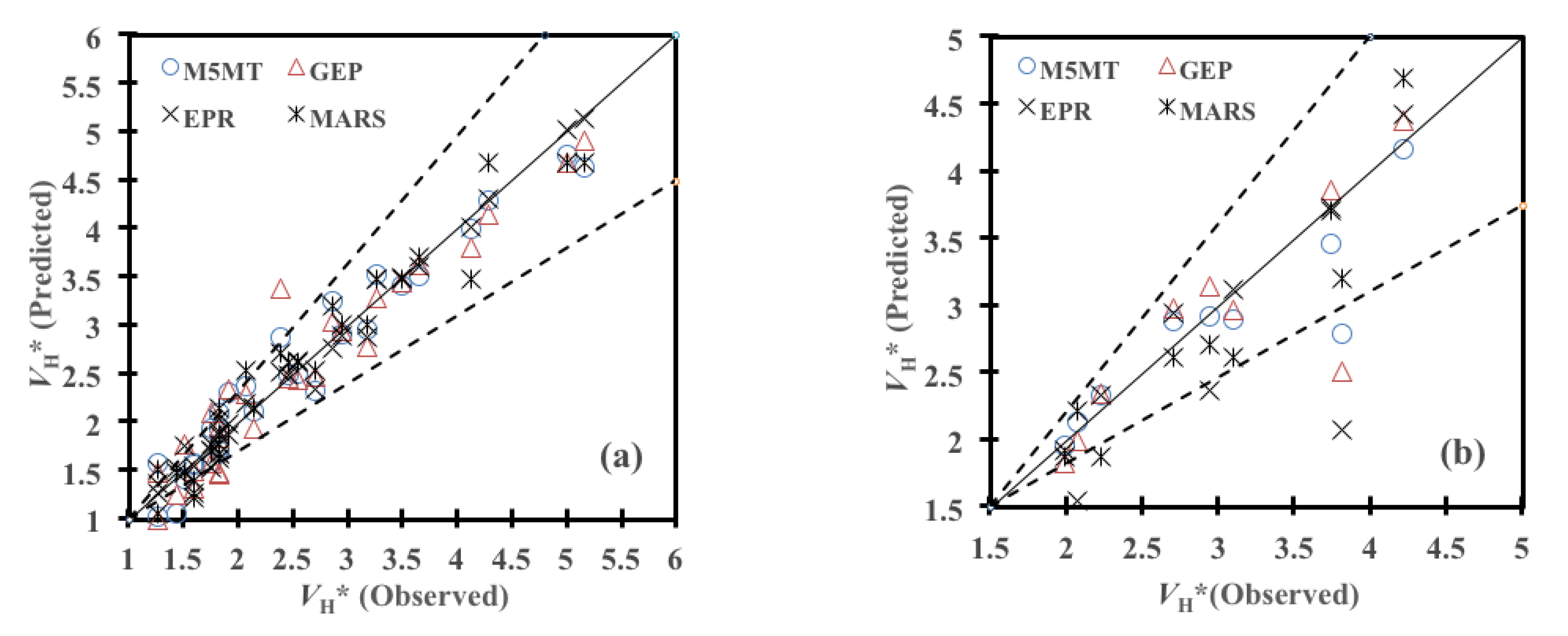

| Dimensional Variables | Minimum | Maximum | Average | Standard Deviation |
| [mm] | 5.0 | 20.0 | 11.97 | 5.445 |
| [m/s] | 0.3 | 0.5 | 0.40 | 0.068 |
| [s] | 1.5 | 2.0 | 1.79 | 0.193 |
| [mm/s] | 1.6 | 6.5 | 3.32 | 1.289 |
| [mm/s] | 1.4 | 5.7 | 3.32 | 1.215 |
| [mm/s] | 1.5 | 6.1 | 3.32 | 1.210 |
| Dimensionless Variables | Minimum | Maximum | Average | Standard Deviation |
| [-] | 0.10 | 0.71 | 0.32 | 0.263 |
| [-] | 0.10 | 0.2143 | 0.0893 | 0.0893 |
| [-] | 8.70 | 18.00 | 14.68 | 3.698 |
| [-] | 0.18 | 0.30 | 0.27 | 0.051 |
| [-] | 1.27 | 5.16 | 2.64 | 1.025 |
| [-] | 1.19 | 4.85 | 2.64 | 0.961 |
| [-] | 1.11 | 4.53 | 2.64 | 0.965 |
| AI Models | Training Stage | ||||
| IOA | SSE | MAE | SI | ADR | |
| M5MT | 0.9468 | 0.0612 | 0.0886 | 0.0974 | 1.0090 |
| GEP | 0.9244 | 0.0111 | 0.1056 | 0.1158 | 1.0039 |
| EPR | 0.9799 | 0.0030 | 0.0550 | 0.0599 | 1.0026 |
| MARS | 0.9468 | 0.0068 | 0.0826 | 0.1016 | 1.0068 |
| AI Models | Testing Stage | ||||
| IOA | SSE | MAE | SI | ADR | |
| M5MT | 0.9430 | 0.1323 | 0.0644 | 0.0644 | 0.9682 |
| GEP | 0.9084 | 0.2143 | 0.0893 | 0.0893 | 0.9621 |
| EPR | 0.8237 | 0.4124 | 0.1254 | 0.1988 | 0.9260 |
| MARS | 0.9506 | 0.1156 | 0.0912 | 0.1048 | 0.9476 |
| AI Models | Training Stage | ||||
| IOA | SSE | MAE | SI | ADR | |
| M5MT | 0.9877 | 0.0387 | 0.0672 | 0.0772 | 1.0277 |
| GEP | 0.9680 | 0.1001 | 0.1027 | 0.1274 | 1.0242 |
| EPR | 0.9883 | 0.0369 | 0.0754 | 0.0771 | 1.0085 |
| MARS | 0.9950 | 0.0157 | 0.0374 | 0.0504 | 0.9993 |
| AI Models | Testing Stage | ||||
| IOA | SSE | MAE | SI | ADR | |
| M5MT | 0.9896 | 0.0449 | 0.0644 | 0.0481 | 1.0520 |
| GEP | 0.9911 | 0.0384 | 0.0544 | 0.0611 | 0.9987 |
| EPR | 0.9693 | 0.1322 | 0.0944 | 0.1052 | 1.0624 |
| MARS | 0.9828 | 0.0738 | 0.0870 | 0.0680 | 1.0729 |
| AI Models | Training Stage | ||||
| IOA | SSE | MAE | SI | ADR | |
| M5MT | 0.9801 | 0.0788 | 0.0728 | 0.1046 | 1.0163 |
| GEP | 0.9760 | 0.0953 | 0.1199 | 0.1147 | 1.0294 |
| EPR | 0.9913 | 0.0345 | 0.1030 | 0.0692 | 1.0113 |
| MARS | 0.9831 | 0.0670 | 0.1030 | 0.0964 | 1.0050 |
| AI Models | Testing Stage | ||||
| IOA | SSE | MAE | SI | ADR | |
| M5MT | 0.9435 | 0.1581 | 0.1356 | 0.1601 | 0.9955 |
| GEP | 0.9329 | 0.1892 | 0.1525 | 0.1755 | 1.0020 |
| EPR | 0.9356 | 0.1816 | 0.1500 | 0.1713 | 1.0503 |
| MARS | 0.9670 | 0.0855 | 0.1086 | 0.1601 | 0.9578 |
| Values | SSE Values for AI Models | |||
|---|---|---|---|---|
| M5MT | GEP | EPR | MARS | |
| and | 0.300 | 0.435 | 0.843 | 0.161 |
| and | 0.018 | 0.040 | 0.081 | 0.078 |
| and | 0.147 | 0.276 | 0.018 | 0.142 |
| and | 0.049 | 0.018 | 0.040 | 0.010 |
| and | 0.011 | 0.047 | 0.003 | 0.063 |
| and | 0.031 | 0.054 | 0.028 | 0.040 |
| and | 0.005 | 0.035 | 0.006 | 0.054 |
| AI Models | Varying | |||||
| M5MT | 0.0388 | 0.2038 | 0.0271 | |||
| GEP | 0.0622 | 0.2602 | 0.0827 | |||
| MARS | 0.0483 | 0.0844 | 0.1490 | |||
| EPR | 0.0168 | 0.0132 | 0.0969 | |||
| AI Models | Varying | |||||
| M5MT | 0.0480 | 0.0948 | 0.0244 | 0.1924 | ||
| GEP | 0.0349 | 0.1298 | 0.0416 | 0.3338 | ||
| MARS | 0.0629 | 0.1662 | 0.0544 | 0.0920 | ||
| EPR | 0.0355 | 0.0106 | 0.0035 | 0.1197 | ||
| AI Models | Varying | |||||
| M5MT | 0.0874 | 0.0958 | 0.0488 | |||
| GEP | 0.0502 | 0.1037 | 0.1627 | |||
| MARS | 0.0618 | 0.1847 | 0.0563 | |||
| EPR | 0.0606 | 0.0494 | 0.0272 | |||
| AI Models | Varying | |||||
| M5MT | 0.0725 | 0.0959 | 0.0658 | 0.0751 | ||
| GEP | 0.1804 | 0.0803 | 0.0188 | 0.1425 | ||
| MARS | 0.2189 | 0.1260 | 0.0526 | 0.0063 | ||
| EPR | 0.0720 | 0.0617 | 0.0207 | 0.0286 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najafzadeh, M.; Oliveto, G. Exploring 3D Wave-Induced Scouring Patterns around Subsea Pipelines with Artificial Intelligence Techniques. Appl. Sci. 2021, 11, 3792. https://doi.org/10.3390/app11093792
Najafzadeh M, Oliveto G. Exploring 3D Wave-Induced Scouring Patterns around Subsea Pipelines with Artificial Intelligence Techniques. Applied Sciences. 2021; 11(9):3792. https://doi.org/10.3390/app11093792
Chicago/Turabian StyleNajafzadeh, Mohammad, and Giuseppe Oliveto. 2021. "Exploring 3D Wave-Induced Scouring Patterns around Subsea Pipelines with Artificial Intelligence Techniques" Applied Sciences 11, no. 9: 3792. https://doi.org/10.3390/app11093792
APA StyleNajafzadeh, M., & Oliveto, G. (2021). Exploring 3D Wave-Induced Scouring Patterns around Subsea Pipelines with Artificial Intelligence Techniques. Applied Sciences, 11(9), 3792. https://doi.org/10.3390/app11093792







