Experimental Investigation and Numerical Modeling of Elastic Modulus Variation with Stress during Hydration and Expansion Process of Static Cracking Agent
Abstract
:1. Introduction
2. Materials and Method
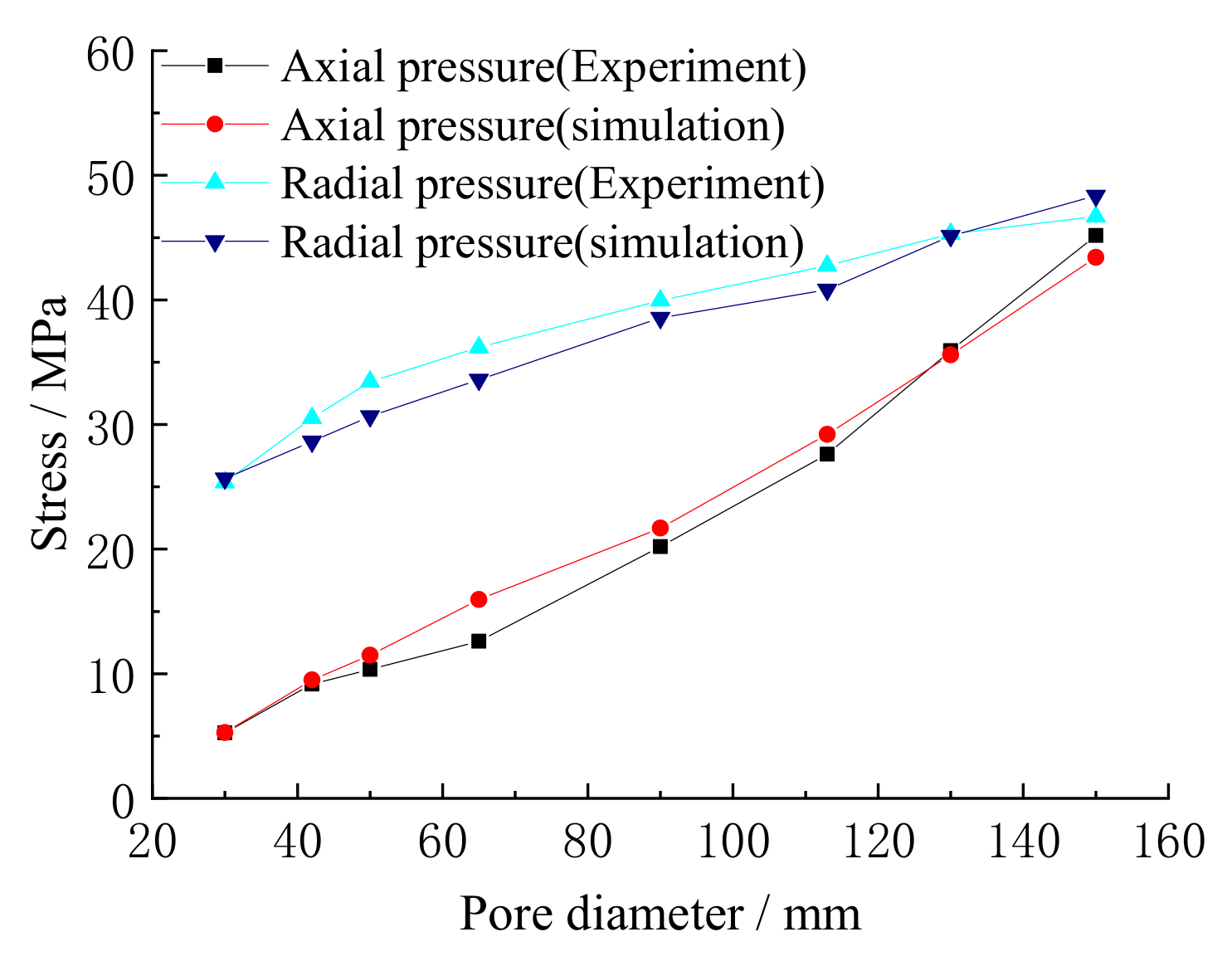
2.1. Model Experiments
2.2. Numerical Experiments
3. Discussion
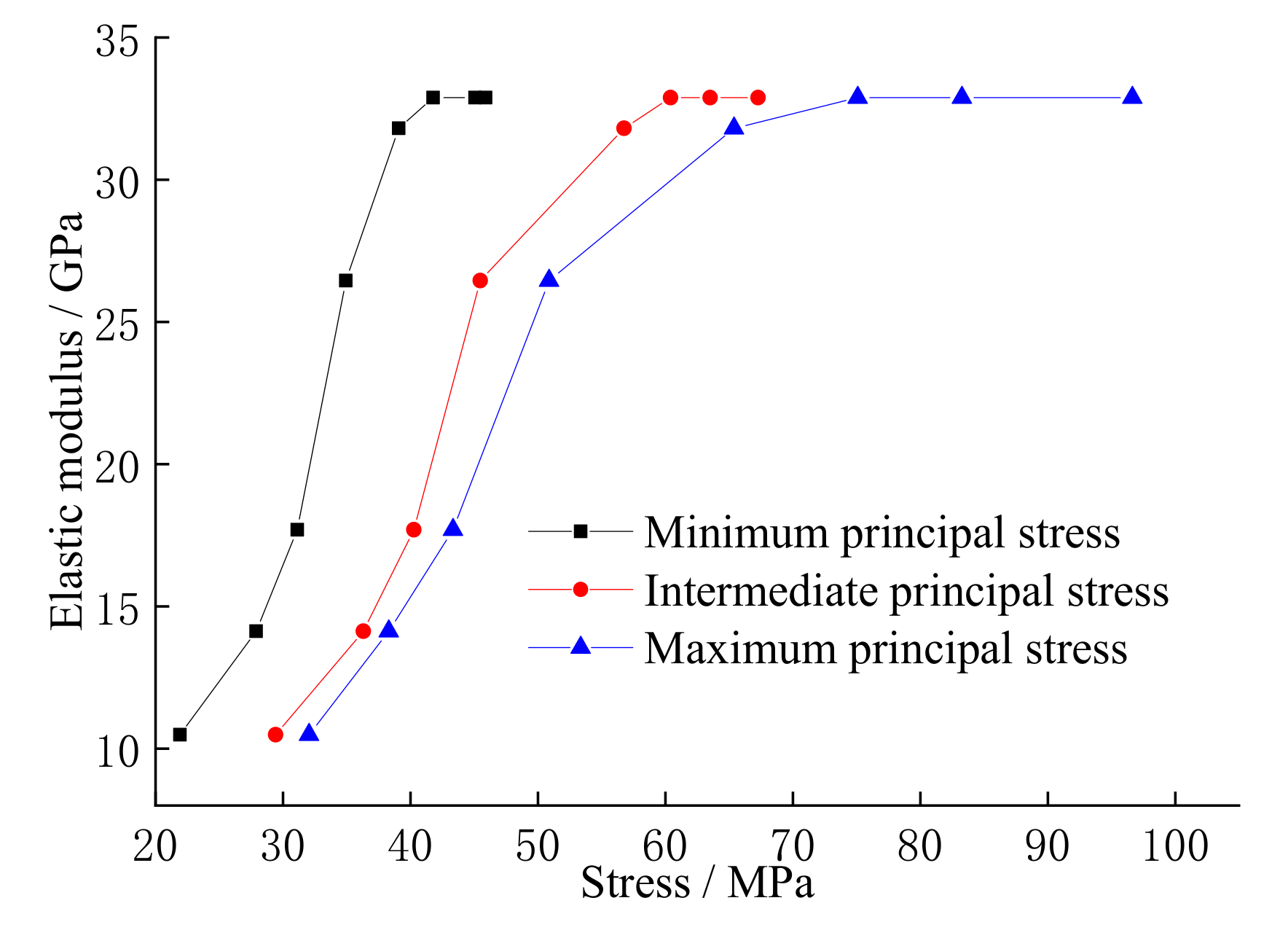
3.1. Effect of Elastic Modulus on Axial and Radial Pressures
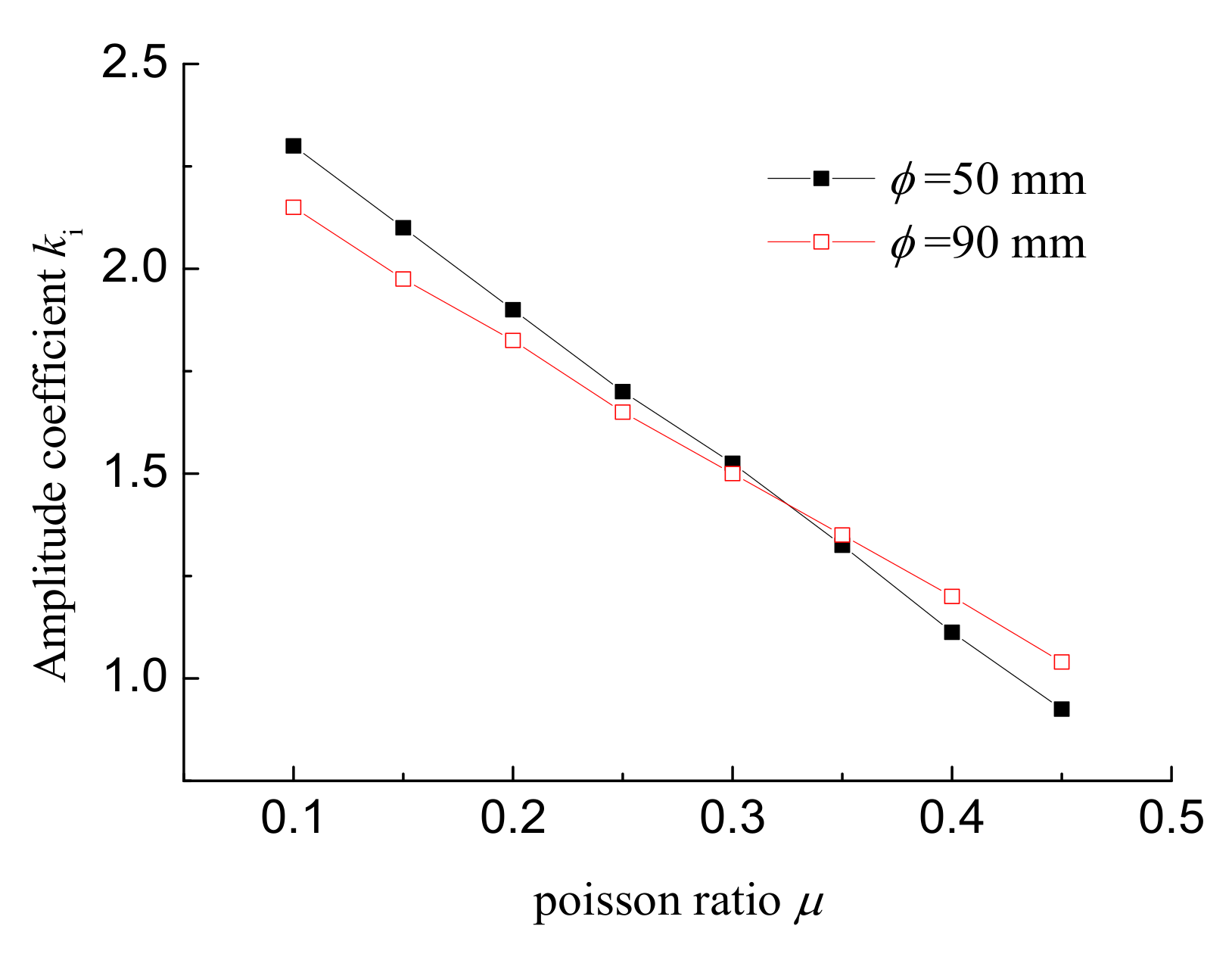
3.2. Effect of Poisson’s Ratio
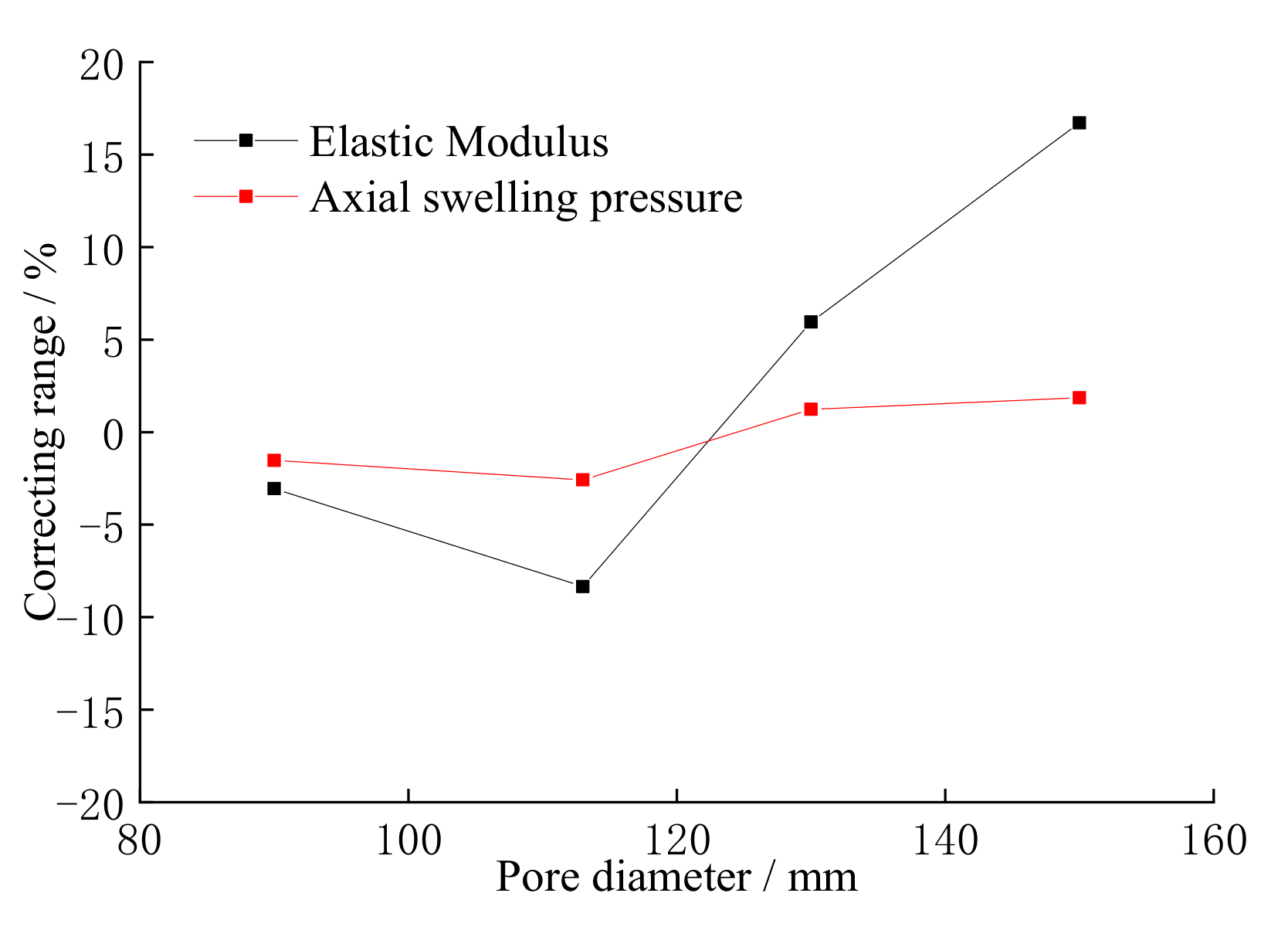
3.3. Comparison of Results Obtained with Literature
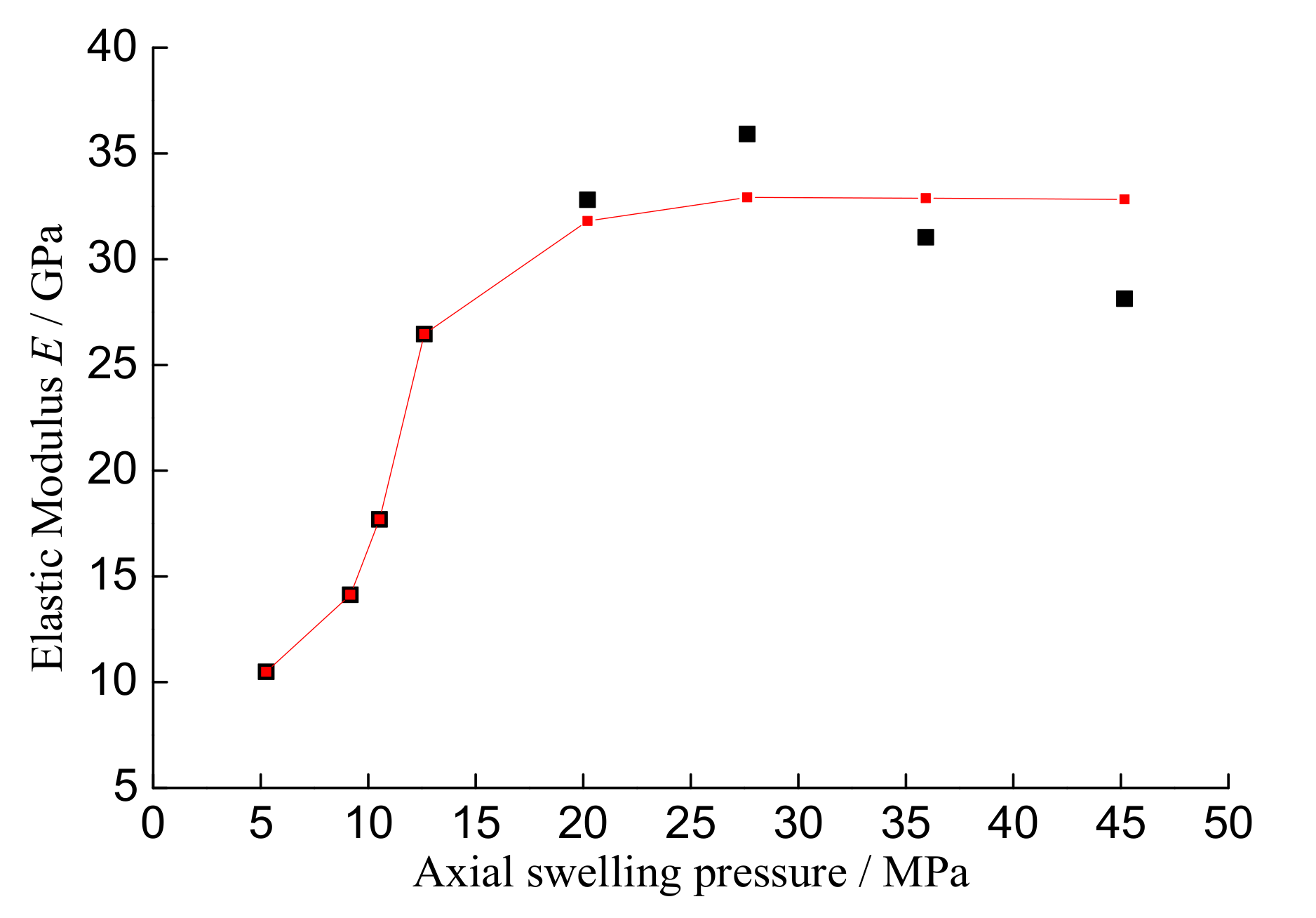
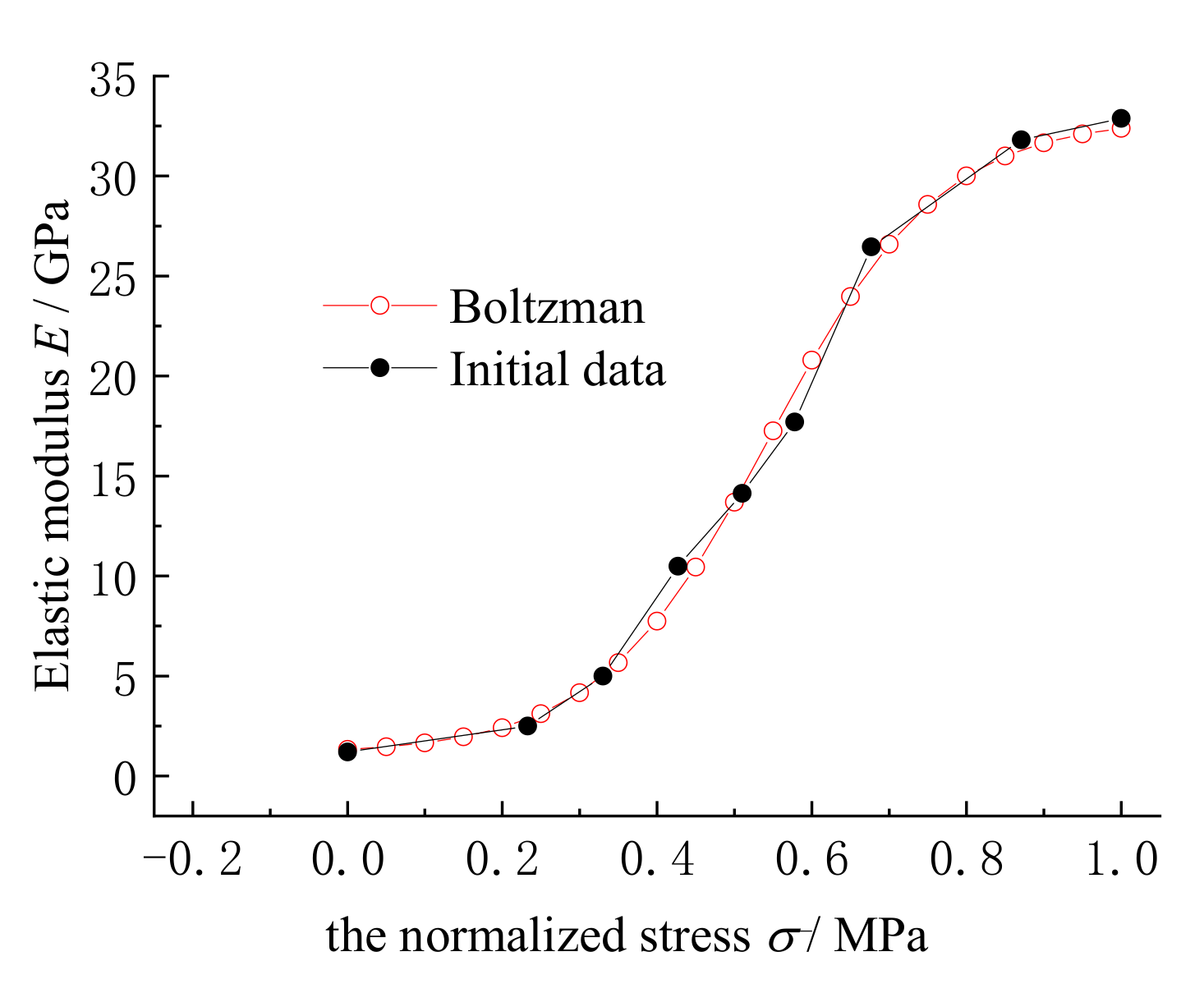
4. Mathematical Model for Variation of Elastic Modulus
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
List of Symbols
| i | Number of steel cylinder |
| t | Time (hour) hydration and expansion of static cracking agent |
| Normalized radial pressure at different time | |
| Radial pressure at different time | |
| Maximum radial pressure, which is taken as σmax = σ(65 h) | |
| Minimum radial pressure, which taken as σmin = 0 | |
| Φ | Cylinder diameter |
| Amplitude coefficient | |
| Normalized temperature. | |
| E | Elastic modulus |
| μ | Poisson’s ratio |
| a1, a2, a3 | Constants |
| σN0 | Normalized stress |
References
- Tang, L.X.; Tang, C.A.; Tang, S.B.; Cui, Y.H.; Song, L. Physical experiment and numerical simulation on effect of soundless cracking agent. Chin. J. Geotech. Eng. 2005, 27, 437–441. [Google Scholar]
- Swanson, D.; Labuz, J. Behavior of a calcium oxide-based expansive cement. Concr. Sci. Eng. 1999, 1, 166–172. [Google Scholar]
- Guo, R.P.; Yang, Y.Q. Swelling mechanism and controllability of SCA. J. China Coal Soc. 1994, 19, 478–485. [Google Scholar]
- Laefer, D.F.; Ambrozevitch-Cooper, N.; Huynh, M.; Midgette, J.; Ceribasi, S.; Wortman, J. Expansive fracture agent behaviour for concrete cracking. Mag. Concr. Res. 2010, 62, 443–452. [Google Scholar] [CrossRef] [Green Version]
- Schram, C.M.; Hinze, J. Fracturing of rock using expansive soundless chemical demolition agents. In Proceedings of the Foundation Engineering: Current Principles and Practices, Evanston, IL, USA, 25–29 June 1989; pp. 447–458. [Google Scholar]
- Arshadnejad, S.; Goshtasbi, K.; Aghazadeh, J. A model to determine hole spacing in the rock fracture process by non-explosive expansion material. Int. J. Miner. Metall. Mater. Struct. 2011, 18, 509–514. [Google Scholar] [CrossRef]
- Xu, S.; Hou, P.Y.; Li, R.R.; Cai, M. An Experimental Study on the Mechanical Properties and Expansion Characteristics of a Novel Self-Swelling Cartridge for Rock Breakage. Rock Mech. Rock Eng. 2021, 54, 819–832. [Google Scholar] [CrossRef]
- Xu, S.; Hou, P.Y.; Cai, M.; Li, Y.H. An experiment study on a novel selfswelling anchorage bolt. Rock Mech. Rock Eng. 2019, 52, 4855–4862. [Google Scholar] [CrossRef]
- Natanzi, A.S.; Laefer, D.F.; Zolanvari, S.M.I. Selective demolition of masonry unit walls with a soundless chemical demolition agent. Constr. Build. Mater. 2020, 248, 118635. [Google Scholar] [CrossRef]
- Li, K.M.; Li, Y.H.; Jing, H.D. Evaluation of the Active Support and Yielding Bearing Properties of Artificial Pillars Supporting a Stope Roof Using 3DEC Numerical Simulation. Adv. Civ. Eng. 2019, 2, 1–7. [Google Scholar] [CrossRef]
- Shang, J.; Hencher, S.R.; West, L.J.; Handley, K. Forensic Excavation of Rock Masses: A Technique to Investigate Discontinuity Persistence. Rock Mech. Rock Eng. 2017, 50, 2911–2928. [Google Scholar] [CrossRef] [Green Version]
- Shang, J.; West, L.J.; Hencher, S.R.; Zhao, Z. Tensile strength of large-scale incipient rock joints: A laboratory investigation. Acta Geotech. 2018, 13, 869–886. [Google Scholar] [CrossRef] [Green Version]
- Inada, Y.; Matsuki, S.; Yokota, K. Basic research on static crushing by utilizing expansive agents. Min. Metall. Inst. Jpn. 1988, 104, 337–344. [Google Scholar] [CrossRef] [Green Version]
- Fukui, H.; Tsukada, K. Static demolition agent by calcium oxide. Sci. Technol. Energ. Mater. 2003, 64, 25–31. [Google Scholar]
- Ishibashi, K.; Watanabe, A.; Harada, T.; Idemitsu, T. Design method for demolition of concrete with non-explosive demolition agent. Trans. Jpn. Concr. Inst. 1985, 119–126. [Google Scholar]
- Fukui, H.; Matsumoto, K.; Tsukada, K.; Hansaki, K. Stress analysis by finite element method around parallel holes occurred by static demolition agent. Sci. Technol. Energ. Mater. 2005, 66, 255–259. [Google Scholar]
- Cho, H.; Nam, Y.; Kim, K.; Lee, J.; Sohn, D. Numerical simulations of crack path control using soundless chemical demolition agents and estimation of required pressure for plain concrete demolition. Mater. Struct. 2018, 51, 169.1–169.13. [Google Scholar] [CrossRef]
- Arshadnejad, S.; Niu, J. Birth of the first crack and its growth under incremental static loading between two holes in brittle rocks. J. Earth Eng. 2014, 1, 1–15. [Google Scholar]
- Shang, J.; Zhao, Z.; Aliyu, M.M. Stresses induced by a demolition agent in non-explosive rock fracturing. Int. J. Rock Mech. Min. Sci. 2018, 107, 172–180. [Google Scholar] [CrossRef]
- Harada, T.; Soeda, K.; Idemitsu, T.; Watanabe, A. Characteristics of expansive pressure of an expansive demolition agent and the development of new pressure transducers. Proc. Jpn. Soc. Civ. Eng. 1993, 478, 91–100. [Google Scholar]
- Soeda, K.; Harada, T.; Kanbayashi, M.; Hosono, K. Measuring method of expansive pressure of expansive demolition agent using flush diaphragm type pressure transducer. Proc. Jpn. Soc. Civ. Eng. 1993, 478, 145–148. [Google Scholar]
- Tang, Y.B.; Yuan, L.; Xue, J.H.; Duan, C.R. Experimental study on fracturing coal seams using cao demolition materials to improve permeability. J. Sustain. Min. 2017, 16, 47–54. [Google Scholar] [CrossRef]
- Gambatese, J.A. Controlled concrete demolition using expansive cracking agents. J. Constr. Eng. Manag. 2003, 129, 98–104. [Google Scholar] [CrossRef]
- Hinze, J.; Nelson, A. Enhancing performance of soundless chemical demolition agents. J. Constr. Eng. Manag. 1996, 122, 193–195. [Google Scholar] [CrossRef]
- Hinze, J.; Brown, J. Properties of soundless chemical demolition agents. J. Constr. Eng. Manag. 1994, 120, 816–827. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Q.Y. Test and analysis on reaction temperature variation of static cracking agent. Chin. J. Undergr. Space Eng. 2013, 9, 1289–1292. [Google Scholar]
- Natanzi, A.S.; Laefer, D.F.; Connolly, L. Cold and moderate ambient temperatures effects on expansive pressure development in soundless chemical demolition agents. Constr. Build. Mater. 2016, 110, 117–127. [Google Scholar] [CrossRef] [Green Version]
- Silva, V.R.S.D.; Ranjith, P.G.; Perera, M.S.A.; Wu, B.; Rathnaweera, T.D. The influence of admixtures on the hydration process of soundless cracking demolition agents (SCDA) for fragmentation of saturated deep geological reservoir rock formations. Rock Mech. Rock Eng. 2019, 52, 435–454. [Google Scholar] [CrossRef]
- Silva, V.R.S.D.; Ranjith, P.G.; Perera, M.S.A.; Wu, B.; Rathnaweera, T.D. Investigation of the mechanical, microstructural and mineralogical morphology of soundless cracking demolition agents during the hydration process. Mater. Charact. 2017, 130, 9–24. [Google Scholar] [CrossRef]


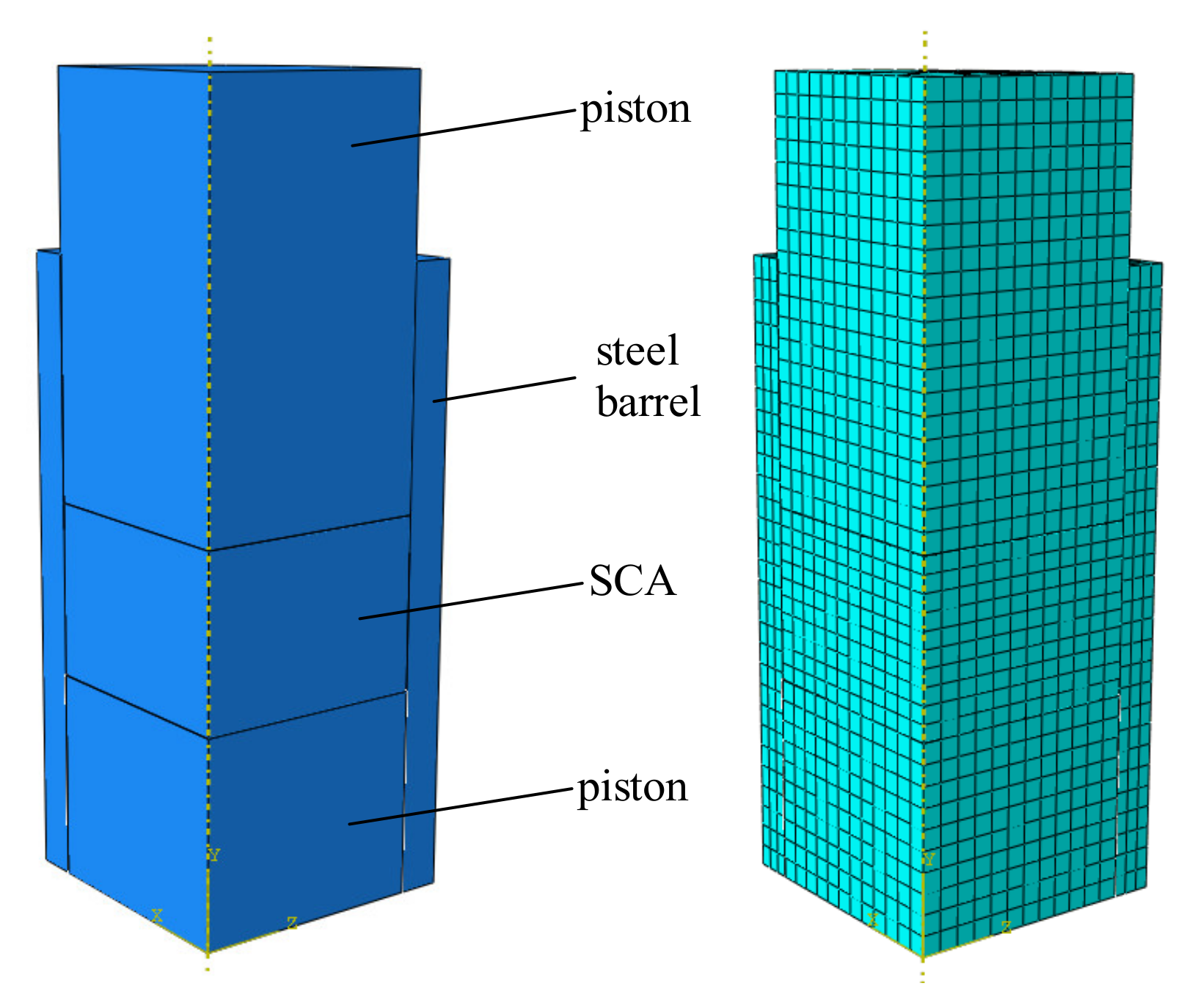
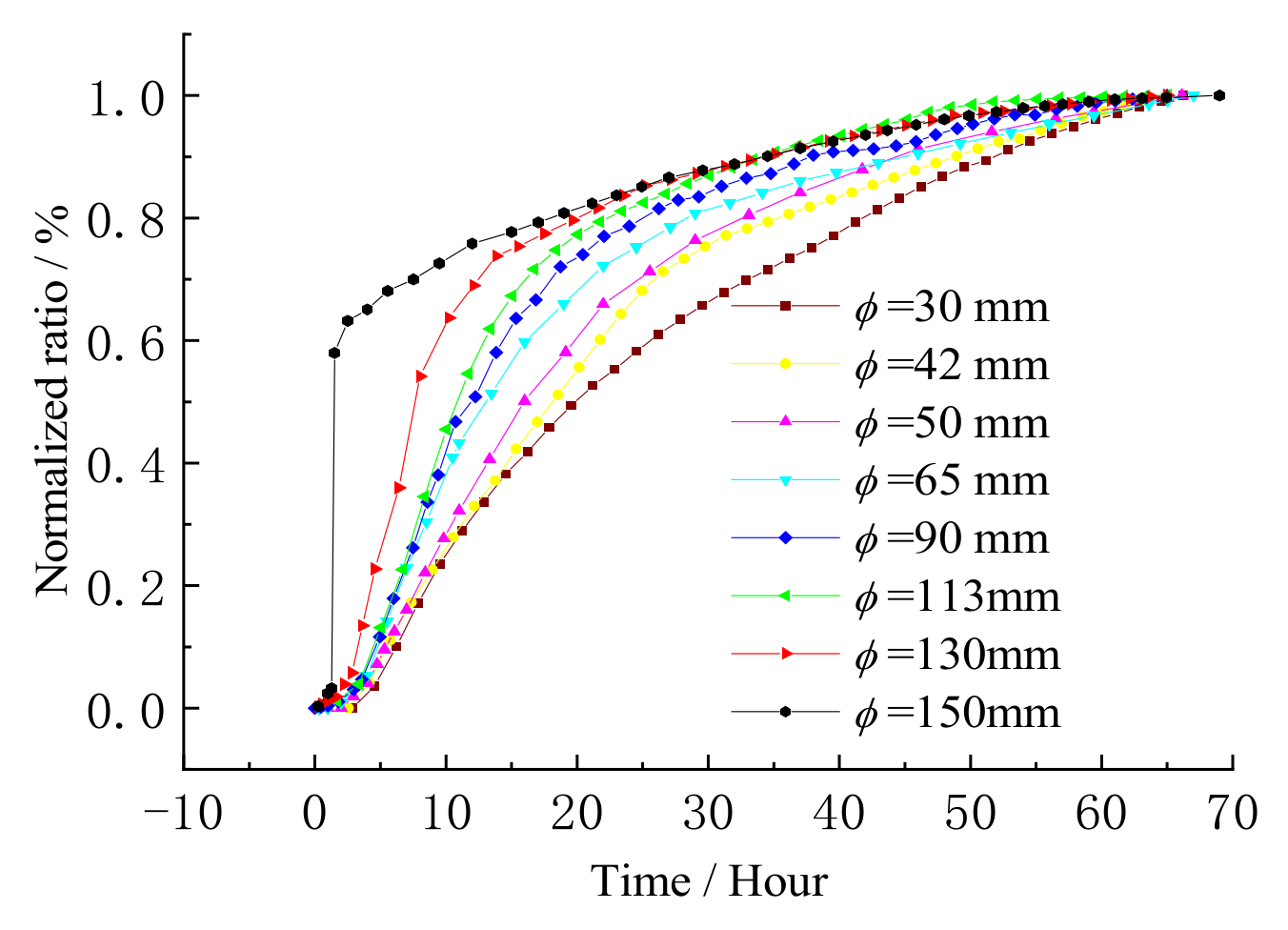



| Cylinder No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Inner diameter of cylinder (mm) | 30 | 42 | 50 | 65 | 90 | 113 | 130 | 150 |
| Piston area (cm2) | 7.065 | 13.847 | 19.625 | 33.166 | 63.585 | 100.237 | 132.665 | 176.625 |
| Slurry height (cm) | 1.1 | 1.6 | 1.9 | 2.4 | 3.4 | 4.2 | 4.9 | 5.6 |
| Slurry volume (cm3) | 7.772 | 22.155 | 37.288 | 79.598 | 214.599 | 420.995 | 650.059 | 989.100 |
| Slurry mass (g) | 18 | 52 | 87 | 185 | 499 | 980 | 1510 | 2300 |
| Normalized Stress σN0 | 0 | 0.233 | 0.33 | 0.427 | 0.51 | 0.578 | 0.677 | 0.871 | 1 |
| Elastic modulus (GPa) | 1.2 | 2.5 | 5.0 | 10.49 | 14.13 | 17.695 | 26.457 | 31.807 | 32.885 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Z.; Ji, Y.; Zhang, F.; Yan, G. Experimental Investigation and Numerical Modeling of Elastic Modulus Variation with Stress during Hydration and Expansion Process of Static Cracking Agent. Appl. Sci. 2021, 11, 3955. https://doi.org/10.3390/app11093955
Qiu Z, Ji Y, Zhang F, Yan G. Experimental Investigation and Numerical Modeling of Elastic Modulus Variation with Stress during Hydration and Expansion Process of Static Cracking Agent. Applied Sciences. 2021; 11(9):3955. https://doi.org/10.3390/app11093955
Chicago/Turabian StyleQiu, Zhaoguo, You Ji, Fengpeng Zhang, and Guangliang Yan. 2021. "Experimental Investigation and Numerical Modeling of Elastic Modulus Variation with Stress during Hydration and Expansion Process of Static Cracking Agent" Applied Sciences 11, no. 9: 3955. https://doi.org/10.3390/app11093955
APA StyleQiu, Z., Ji, Y., Zhang, F., & Yan, G. (2021). Experimental Investigation and Numerical Modeling of Elastic Modulus Variation with Stress during Hydration and Expansion Process of Static Cracking Agent. Applied Sciences, 11(9), 3955. https://doi.org/10.3390/app11093955





