Simultaneous Measurement Method and Error Analysis of Six Degrees of Freedom Motion Errors of a Rotary Axis Based on Polyhedral Prism

Abstract

A novel method is proposed for measuring the six degrees-of-freedom (DOF) geometric motion errors of a rotary axis based on a polyhedral prism. An error-sensitive unit which consists of a polyhedral prism and a planar reflector, is designed to carry out measurement of all six DOF errors, including the angular positioning error, the tilt motion error around the Y axis, the tilt motion error around the X axis, the radial motion error along the X and Y axes, and the axial motion error along the Z axis. The mathematical error model, including the six DOF geometric motion errors of the rotary axis, the installation errors between the polyhedral prism and the rotary axis, the manufacturing errors of the polyhedral prism, and the position errors of the sensors, are established. The effectiveness of the proposed method and the compensation model was simulated and experimentally verified.

1. Introduction

Because they possesses the advantages of high efficiency and strong capability in machining complex surfaces [1], multi-axis computerized numerical control (CNC) machine tools are widely used in industrial production such as in the automobile, ship manufacturing, and aerospace industries. Rotary axes are important moving parts of a multi-axis CNC machine tool, which has six degrees-of-freedom (DOF) geometric motion errors when it moves. The geometric motion errors of a rotary axis are important factors affecting the accuracy of the machined parts [2]. In order to improve the machining accuracy of multi-axis CNC machine tools and machining centers, scholars worldwide have conducted a considerable amount of research to compensate the geometric motion errors of the rotating shaft [3,4,5,6]. Geometrical error compensation technology is generally divided into three steps: error measurement, error model establishment, and error compensation [5]. Therefore, error measurement is the basis of improving the motion accuracy of a rotary axis. This paper focuses on precisely measuring the geometric motion errors of a rotary axis.

Compared to the linear axis, research on the measurement of multi-DOF geometric errors of a rotary axis is relatively late [6]. At present, the main measurement methods are divided into contact measurement and noncontact measurement.

The contact measurement methods include two kinds of methods based on capacitance sensor and circular trajectory, respectively. Both of them cannot measure the angular positioning error which is the most important parameter of a rotary axis. Ahn et al. used a built-in capacitance sensor to measure radial motion error [7]. Kim et al. used a cylindrical capacitance sensor to measure motion error of milling machine spindle. The sensing range would be ±30 μm [8]. Xiang et al. used T-type capacitive sensor to measure five DOF motion errors [9]. The contact measurement method, based on capacitive sensors, has the advantages of compact structure and low cost, but its measurement range is small. The measurement methods of a circular trajectory include the ball-bar and R-test. Bryan et al. put forward the measuring principle of measuring the motion error of rotary axis by using the ball-bar in 1982, and it has been used to measure the geometric error of three-coordinate machine and CNC machine tools [10]. Lei et al. use a double ball-bar clockwise and anticlockwise measured rotary axis and obtained five DOF motion errors [11]. Hong et al. used an R-test to measure the trajectories of the rotary axis at different positions and heights, and the five DOF motion errors were obtained [12]. The measurement methods of a circular trajectory have the advantages of using simple instruments, convenient portability, and low system costs; however, error decoupling is complex, the measurement of angle positioning error cannot be realized, and the measurement results are not given in real time. Moreover, because the length of the ball bar and R-test measuring rod is short and can only vary according to limited spacing, there are great limitations in measuring large CNC machine tools and compensating spatial errors.

There are many kinds of noncontact optical measurement methods, including interferometry-based, laser tracker-based, diffraction-based, laser collimation-based, and polyhedral prism-based methods. The interference method usually uses a single-frequency or dual-frequency laser interferometer as the core device, and its measurement has the advantage of high precision. Yao et al. used two laser interferometers to measure the six DOF motion errors in three steps [13]. Pi et al. used laser interferometers to measure two rotary axis Angular position error in 5-axis CNC machine tool in two steps [14]. In most cases, the laser interferometer can only measure a single parameter. If multi-DOF motion errors are being measured, other auxiliary optical devices and measurement steps are needed, which increases costs and difficulty and has low efficiency. Zhang et al. used Laser Tracker System to measure the six DOF motion errors by tracking three noncollinear points on the axis of rotation at different spatial positions, accuracy was 0.9 μm [15]. The laser tracking method has the advantages of simplicity, high efficiency, and not requiring complex equipment installation and alignment, but its accuracy is relatively low [13]. Liu et al. used diffraction grating and position sensitive detectors to measure motion errors, the resolution is 0.2″ [16]. The diffraction method, which takes the high-precision diffraction grating as the sensitive unit, requires high installation accuracy and high maintenance costs. Park et al. used laser collimation method to measure the six DOF motion errors in two steps [17]. Gao et al. used two-dimensional slope sensors to measure the six DOF motion errors [18]. Murakami et al. used a ball lens and rod lens to measure the five DOF motion errors [19]. Bao et al. used a laser collimation method to measure the five DOF motion errors simultaneously [20]. The laser collimation method has the advantages of high precision and fast speed, but most existing methods cannot simultaneously measure all six DOF geometric motion errors of a rotary axis; in addition, the measurement device is usually complex and difficult to install, and takes a long time to calibrate. Many studies used a polyhedral prism to measure angular position error. To our knowledge, no method based on polyhedral prisms has been proposed which can simultaneously measure the six DOF motion errors. Suh et al. proposed a measurement method of angular position error based on autocollimation and polyhedral prisms [21]. This method has been recommended by ISO230-1 as one of the standard measurement methods of angular position error [22]. Qiu et al. used polygonal prism and precise angle dividing table accomplish mutual check of angular deviation [23].

A novel method based on polyhedral prisms is proposed for simultaneously measuring the six DOF motion errors in this paper. A high-precision polyhedral prism and a plane mirror are designed to be the sensitive unit that can carry all six DOF motion errors of a rotary axis. By using photoelectric autocollimators and laser displacement sensors, the full-circle and simultaneous measurement of all six DOF motion errors of a rotary axis can be realized. This has the advantages of simple structure, fast measurement speed, and convenient installation.

An error model is established, including the six DOF geometric motion errors of a rotary axis, installation errors between the polyhedral prism and rotary axis, manufacturing errors of the polyhedral prism, and the position errors of photoelectric autocollimators and laser displacement sensors. This model can accurately calculate the six DOF geometric motion errors of a rotary axis and provide technical support for compensating the geometric motion errors of a rotary axis and improving its motion accuracy.

2. Measuring Principle

As shown in Figure 1, the measuring device includes a polyhedral prism, two autocollimators, and three laser displacement sensors. The polyhedral prism is fixed with the target rotary axis to be measured and has a plane reflector in the center of the top surface. The polyhedral prism synchronously rotates with the target rotary axis.

The laser displacement sensors are placed in the X, Y, and Z directions of the target rotary axis to measure the radial motion error of the rotary axis along the X and Y directions and the axial motion error along the Z direction. The autocollimators are placed in the X and Y directions to measure the angular positioning error and the tilt motion error around the Y axis and X axis of the target rotary axis.

The specific measurement principle is this: The autocollimator beam placed in the X-axis direction is reflected along the X-axis incident polyhedral prism working surface, and then enters the autocollimator to obtain the angular positioning error around the Z-axis and the tilt motion error around the Y-axis. The autocollimator beam placed in the Y-axis direction is reflected along the working surface of the polyhedral prism, and then enters the autocollimator to obtain the tilt motion error of the target rotary axis around the X-axis. The radial motion error of the target axis along the X axis can be obtained by the laser displacement sensor which is placed in the direction of the X axis after the ray of the laser displacement sensor is reflected along the working surface of the X-axis incident polyhedral prism. Similarly, the radial motion error along the Y axis and the axial motion error along the Z axis can be measured by the other two laser displacement sensors. The whole measuring device can simultaneously measure all six DOF geometric motion errors of a rotary axis.

3. Establishment and Simulation of the Error Model

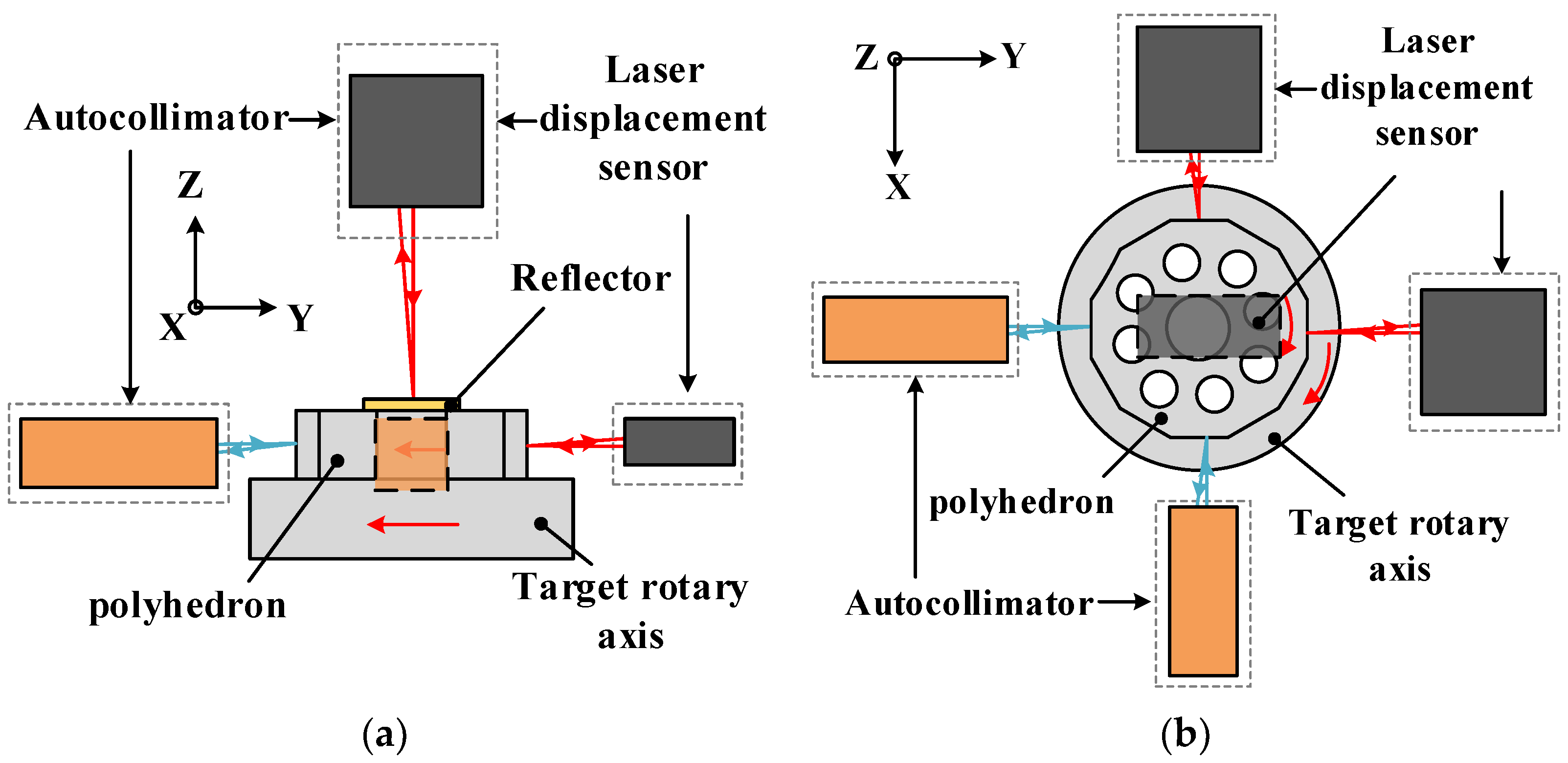
The measurement results of the six DOF geometric motion errors of a rotary axis are affected by the installation errors, manufacturing errors, and crosstalk errors of each component. In order to improve measurement accuracy, we analyzed the influence of various errors on the measurement results and established the error compensation model.

The main processes include the following: (1) Establish the coordinate system of each component: the stationary world coordinate system “0” (CS0); the coordinate system “1” (CS1), fixed on the target axis C and moving with the axis; the coordinate systems “2” (CS2) and “3” (CS3), fixed on the polyhedral prism B and moving with the polyhedral prism; the coordinate systems “4” (CS4) and “5” (CS5), fixed on autocollimators AC1 and AC2; the coordinate systems “6” (CS6), “7” (CS7), and “8” (CS8), fixed on laser displacement sensors LDS1, LDS2, and LDS3, as shown in Figure 2. (2) According to the principle of rigid body kinematics, establish the homogeneous transformation matrix $T_n^m$ ($T_n^m$ represents the transformation matrix from coordinate m to coordinate n) between each coordinate system to describe the relative motion between adjacent components. (3) Establish the equations of the rays. The ray is tracked by the homogeneous coordinate transformation matrix, and the six DOF geometric motion errors of the target rotary axis are obtained by the spatial coordinate change of the returned ray.

3.1. Matrix Description of Relative Motion

The origin of CS0 is located at the center of the top surface of the target rotary axis measured at the initial timepoint, which represents the position-pose of the initial timepoint and without errors of the target rotary axis. The origin of CS1 is the center of the top surface of axis C, which coincides with CS0 at the initial timepoint.

In the movement process of the axis, there are two tilt errors, ${\epsilon }_x$ and ${\epsilon }_y$, one angular positioning error, ${\epsilon }_z$, two radial motion errors, ${\delta }_x$, ${\delta }_y$, and one axial motion error, ${\delta }_z$. The theoretical angle of rotation is $\theta$, and the coordinate transformation matrix when CS1 is reached is this:

$$T_0^1=\left[\begin{array}{cc}\begin{array}{cc}\cos \left(\theta +{\epsilon }_z\right)& -\sin \left(\theta +{\epsilon }_z\right)\\ \sin \left(\theta +{\epsilon }_z\right)& \cos \left(\theta +{\epsilon }_z\right)\end{array}& \begin{array}{cc}{\epsilon }_y& {\delta }_x\\ -{\epsilon }_x& {\delta }_y\end{array}\\ \begin{array}{cc}-{\epsilon }_y\cos \left(\theta +{\epsilon }_z\right)+{\epsilon }_x\sin \left(\theta +{\epsilon }_z\right)& {\epsilon }_{y}sin\left(\theta +{\epsilon }_z\right)+{\epsilon }_x\cos \left(\theta +{\epsilon }_z\right)\\ 0& 0\end{array}& \begin{array}{cc}1& {\delta }_z\\ 0& 1\end{array}\end{array}\right]$$

(1)

CS2 is fixed at the center of the bottom surface of the polyhedral prism and moves with that. There are five installation errors between the initial coordinate system and CS1, excluding the positioning error. The installation error between them is expressed in pairwise lowercase letters. For example, ${\delta }_{zbc}$ represents the position error between B and C in the Z direction. Therefore, the transformation matrix from CS2 to CS1 is this:

$$T_1^2=\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}{\epsilon }_{ybc}& {\delta }_{xbc}\\ -{\epsilon }_{xbc}& {\delta }_{ybc}\end{array}\\ \begin{array}{cc}-{\epsilon }_{ybc}& {\epsilon }_{xbc}\\ 0& 0\end{array}& \begin{array}{cc}1& {\delta }_{zbc}\\ 0& 1\end{array}\end{array}\right]$$

(2)

CS3 and CS2 have the same origin of coordinates, and its X-axis direction is constantly perpendicular to the current working surface of the polyhedral prism. Therefore, CS3 and CS2 have an angular difference, $\theta +{\epsilon }_{pz}$, around the Z axis (manufacturing errors of the working angle of the polyhedral prism) and angular error ${\epsilon }_{py}$ around the Y axis or angular error ${\epsilon }_{px}$ around the X axis (${\epsilon }_{px}$ and ${\epsilon }_{py}$ are perpendicularity errors between the working surface and datum plane, and change with the $\theta$ angle). When the target rotary axis rotates θ, the transformation matrix from CS3 to CS2 is as follows: (This matrix is for measuring the error ${\epsilon }_y$. For measuring the error ${\epsilon }_x$, the variables in the matrix should be changed accordingly).

$$T_2^3=\left[\begin{array}{cc}\begin{array}{cc}\cos \left(\theta +{\epsilon }_{pz}\right)& \sin \left(\theta +{\epsilon }_{pz}\right)\\ -\sin \left(\theta +{\epsilon }_{pz}\right)& \cos \left(\theta +{\epsilon }_{pz}\right)\end{array}& \begin{array}{cc}{\epsilon }_{py}& 0\\ 0& 0\end{array}\\ \begin{array}{cc}-{\epsilon }_{py}\cos \left(\theta +{\epsilon }_{pz}\right)& -{\epsilon }_{py}\sin \left(\theta +{\epsilon }_{pz}\right)\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right]$$

(3)

The original point P of CS4 is at the center of the front surface of autocollimator AC1, and the P point in CS0 is ${\left(\begin{array}{cc}\begin{array}{cc}{P}_x& P_y\end{array}& \begin{array}{cc}{P}_z& 1\end{array}\end{array}\right)}^T$. The angle installation errors between CS4 and CS0 are expressed as ${\epsilon }_{xl}$, ${\epsilon }_{yl}$, and ${\epsilon }_{zl}$. The transformation matrix from CS4 to CS0 is this:

$$T_0^4=\left[\begin{array}{cc}\begin{array}{cc}1& -{\epsilon }_{zl}\\ {\epsilon }_{zl}& 1\end{array}& \begin{array}{cc}{\epsilon }_{yl}& P_x\\ -{\epsilon }_{xl}& P_y\end{array}\\ \begin{array}{cc}-{\epsilon }_{yl}& {\epsilon }_{xl}\\ 0& 0\end{array}& \begin{array}{cc}1& P_z\\ 0& 1\end{array}\end{array}\right]$$

(4)

The position of the exit light $P^4$ is ${\left(\begin{array}{cc}\begin{array}{cc}0& P_y^4\end{array}& \begin{array}{cc}{P}_z^4& 1\end{array}\end{array}\right)}^T$ and the direction is parallel to the X axis. The light vector is ${\left[\begin{array}{cc}\begin{array}{cc}x& 0\end{array}& \begin{array}{cc}0& 0\end{array}\end{array}\right]}^T$. Therefore, the ray equation $L^4$ is this:

$$\left[\begin{array}{cc}\begin{array}{cc}0& 1\end{array}& \begin{array}{cc}0& -P_y^4\end{array}\\ \begin{array}{cc}0& 0\end{array}& \begin{array}{cc}1& -P_z^4\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{x}^4\\ y^4\end{array}\\ \begin{array}{c}{z}^4\\ 1\end{array}\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$

(5)

The original point Q of CS5 is at the center of the front surface of autocollimator AC2, and the Q point in CS0 is ${\left(\begin{array}{cc}\begin{array}{cc}{Q}_x& Q_y\end{array}& \begin{array}{cc}{Q}_z& 1\end{array}\end{array}\right)}^T$. The angle installation errors between CS5 and CS0 are expressed as ${\epsilon }_{xm}$, ${\epsilon }_{ym}$, and ${\epsilon }_{zm}$. The position of the exit light $Q^5$ is ${\left(\begin{array}{cc}\begin{array}{cc}{Q}_x^5& 0\end{array}& \begin{array}{cc}{Q}_z^5& 1\end{array}\end{array}\right)}^T$, and the light vector is ${\left[\begin{array}{cc}\begin{array}{cc}0& y\end{array}& \begin{array}{cc}0& 0\end{array}\end{array}\right]}^T$.

Similarly, the position coordinate of the original point K of CS6 in CS0 is ${\left(\begin{array}{cc}\begin{array}{cc}{K}_x& K_y\end{array}& \begin{array}{cc}{K}_z& 1\end{array}\end{array}\right)}^T$, and the angular installation errors relative to CS0 are expressed as ${\epsilon }_{xn}$, ${\epsilon }_{yn}$, and ${\epsilon }_{zn}$. The position of the exit light $K^6$ is ${\left(\begin{array}{cc}\begin{array}{cc}0& K_y^6\end{array}& \begin{array}{cc}{K}_z^6& 1\end{array}\end{array}\right)}^T$, and the light vector is ${\left[\begin{array}{cc}\begin{array}{cc}x& 0\end{array}& \begin{array}{cc}0& 0\end{array}\end{array}\right]}^T$.

The position coordinate of the original point U of CS7 is ${\left(\begin{array}{cc}\begin{array}{cc}{U}_x& U_y\end{array}& \begin{array}{cc}{U}_z& 1\end{array}\end{array}\right)}^T$, and the angular installation errors are expressed as ${\epsilon }_{xu}$, ${\epsilon }_{yu}, \mathrm{and} {\epsilon }_{zu}$. The position of the exit light $U^7$ of the light is ${\left(\begin{array}{cc}\begin{array}{cc}{U}_x^7& 0\end{array}& \begin{array}{cc}{U}_z^7& 1\end{array}\end{array}\right)}^T$, and the light vector is ${\left[\begin{array}{cc}\begin{array}{cc}0& y\end{array}& \begin{array}{cc}0& 0\end{array}\end{array}\right]}^T$.

The position coordinate of the original point V of CS8 is ${\left(\begin{array}{cc}\begin{array}{cc}{\mathrm{V}}_x& {\mathrm{V}}_y\end{array}& \begin{array}{cc}{\mathrm{V}}_z& 1\end{array}\end{array}\right)}^T$, and the angular installation errors are expressed as ${\epsilon }_{xv}$, ${\epsilon }_{yv}$, and ${\epsilon }_{zv}$. The position of the exit light $V^8$ of the light is ${\left(\begin{array}{cc}\begin{array}{cc}{V}_x^8& V_y^8\end{array}& \begin{array}{cc}0& 1\end{array}\end{array}\right)}^T$, and the light vector is ${\left[\begin{array}{cc}\begin{array}{cc}0& 0\end{array}& \begin{array}{cc}z& 0\end{array}\end{array}\right]}^T$. According to the above definition, the corresponding equations of light rays $L^5$, $L^6$, $L^7$, and $L^8$ and coordinate transformation matrix $T_0^5$, $T_0^6$, $T_0^7$, and $T_0^8$ can be obtained, respectively.

The above homogeneous coordinate transformation matrix describes the relative motion relationship between each component, which not only includes the six DOF motion errors of the target rotary axis, but also includes the installation errors of each component. Through ray tracing, the six DOF geometric motion errors of the rotary axis can be obtained by using the spatial coordinate change of the returned ray.

3.2. Ray Tracing and Error Representation

The core of ray tracing is the light reflection process on the working surface of the polyhedral prism. When the coordinate of the incident light point is the origin of the coordinate system in CS3, the reflection matrix of the reflecting surface is this:

$$R_P^0=\left[\begin{array}{cccc}-1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

(6)

The position of the actual incident light P is ${\left(\begin{array}{cc}\begin{array}{cc}Pi{n}_x^3& Pi{n}_y^3\end{array}& \begin{array}{cc}Pi{n}_z^3& 1\end{array}\end{array}\right)}^T$. The reflection matrix of the point P can be obtained by using the translation transformation of the matrix: $R_P=Trans{\left(Pi{n}_y^3,Pi{n}_y^3,Pi{n}_z^3\right)}^{-1}{R}_P^{0}Trans\left(Pi{n}_y^3,Pi{n}_y^3,Pi{n}_z^3\right)$.

3.2.1. Angular Positioning Error and Tilt Motion Error around Y Axis

When calculating the six DOF motion errors of a rotary axis according to the relationship between the ray tracing method and the spatial geometric coordinates, it is necessary to transform all rays, reflection surfaces, and receiving surfaces into the same coordinate system by using the matrix coordinate transformation. The exit light of autocollimator AC1 is defined in CS4, and its reflection surface of the polyhedral prism is defined in CS3. The incident light of AC1 can be obtained by converting the outgoing light of AC1 to the reflection in CS3, and then converting the reflected light to CS4. The coefficient matrix of the incident light is shown in Equation (7).

$$LoutLP=LP{T}_4^0{T}_0^1{T}_1^2{T}_2^3{R}_P{T}_3^2{T}_2^1{T}_1^0{T}_4^3$$

(7)

The plane where the incident light is received by AC1 is x = L_r. The coordinate SC$\left(X_{SC},Y_{SC},Z_{SC}\right)$ of the autocollimator’s incident point can be obtained from the incident ray and the receiving surface. The reflection surface of the polyhedral prism is defined $\mathrm{x}=Pi{n}_x^3$ in CS3, which can be transformed into CS4 and expressed as shown in Equation (8).

$$\left[\begin{array}{cc}\begin{array}{cc}1& 0\end{array}& \begin{array}{cc}0& -Pi{n}_x^3\end{array}\end{array}\right]T_3^4\left[\begin{array}{c}\begin{array}{c}{X}^4\\ Y^4\end{array}\\ \begin{array}{c}{Z}^4\\ 1\end{array}\end{array}\right]=0$$

(8)

In CS4, the coordinates of the reflection point PH can be obtained from the incident light and the reflector. The rotation angle around the Z axis measured by AC1 is denoted as ${\theta }_{SCz}$. According to the geometric position relationship, ${\theta }_{SCz}$=$\frac{\left|Y_{SC}-P_y^4\right|}{2\left|X_{PH}^4-X_{SC}^4\right|}$.

The rotation angle $\theta$ is zero at the initial timepoint. We can eliminate some of the system errors by setting all errors’ initial values to zero, so as to obtain the rotation angular positioning error:

$${\epsilon }_z={\theta }_{SCz}-{\theta }_{SCz\left(t=0\right)}+{\epsilon }_{pz}-{\epsilon }_{pz\left(t=0\right)}$$

(9)

${\theta }_{SCz\left(t=0\right)}$ is the value of the autocollimator AC1 at the initial timepoint; ${\epsilon }_{pz\left(t=0\right)}$ is the manufacturing error of the first working surface of the polyhedral prism.

Only the manufacturing error ${\epsilon }_{pz}$ will affect the angular positioning error, and the influences of the installation errors and manufacturing errors of other components can be neglected. The manufacturing errors of each working surface of the polyhedral prism are constant values, which does not affect repeatability. The measurement data can be compensated by measuring the manufacturing errors of each working surface.

Similarly, the tilt motion error of a rotary axis around the Y-axis can be obtained:

$${\epsilon }_y={\theta }_{SCy}-{\theta }_{SCy\left(t=0\right)}-{\epsilon }_{py}cos\theta +{\epsilon }_{py\left(t=0\right)}-{\epsilon }_{xbc}sin\theta -{\epsilon }_{ybc}cos\theta +{\epsilon }_{ybc}$$

(10)

In the formula, ${\theta }_{SCy}$ is the angle value of the Y direction measured by the AC1.

The perpendicularity error ${\epsilon }_{py}$ and the installation errors ${\epsilon }_{xbc}$ and ${\epsilon }_{ybc}$ have an effect on the measurement of the tilt motion error around the Y axis and are related to the rotation angle of the target rotary axis. Among them, ${\epsilon }_{py}cos\theta$, ${\epsilon }_{xbc}sin\theta$, and ${\epsilon }_{ybc}cos\theta$ are trigonometric function terms, and ${\epsilon }_{py\left(t=0\right)}$ and ${\epsilon }_{ybc}$ are constant terms. These errors can be compensated by the triangular fitting method.

3.2.2. Tilt Motion Error around X Axis

Similar to the calculation process of the tilt motion error around the Y axis, the tilt motion error around the X axis can be obtained by the following equation:

$${\epsilon }_x={\theta }_{SCx}-{\theta }_{SCx\left(t_1=0\right)}-{\epsilon }_{px}cos\theta +{\epsilon }_{px\left(t=0\right)}-{\epsilon }_{ybc}sin\theta -{\epsilon }_{xbc}cos\theta +{\epsilon }_{xbc}$$

(11)

The perpendicularity error ${\epsilon }_{px}$ and the installation errors ${\epsilon }_{xbc}$ and ${\epsilon }_{ybc}$ have an effect on the measurement of the tilt motion error around the X axis and are related to the rotation angle of the target rotary axis. Among them, ${\epsilon }_{px}cos\theta$, ${\epsilon }_{ybc}sin\theta$, and ${\epsilon }_{xbc}cos\theta$ are trigonometric function terms, and ${\epsilon }_{px\left(t=0\right)}$ and ${\epsilon }_{xbc}$ are constant terms. These errors can be compensated by the triangular fitting method.

3.2.3. The Radial Motion Error along X Axis

The output surface and incident surface of laser displacement sensor LDS1 are defined in CS6. The output surface is expressed as x = 0. The light receiving plane of LDS1 is x = $L_r$. We can obtain the reflected light of the polyhedral prism from the output light of LDS1 and the reflection matrix of the reflector.

The coordinate LDSX$\left(X_{LDSX},Y_{LDSX},Z_{LDSX}\right)$ of the incident point of LDS1 can be obtained from the reflected light of the polyhedral prism and the receiving surface of the LDS1. The coordinate PHLX$\left(X_{PHLX},Y_{PHLX},Z_{PHLX}\right)$ of the reflection point on the polyhedral prism can be obtained according to the incident light and the reflection surface. The measured value of the LDS1 is expressed as ${\mathrm{LX}}_{lds}$. Using the spatial geometric relationship, ${\mathrm{LX}}_{lds}=\sqrt{X_{PHLS}^6{}^2+{\left(Y_{PHLS}^6-K_y^6\right)}^2+{\left(X_{PHLS}^6-K_x^6\right)}^2}$. Because the values of $Y_{PHLS}^6-K_y^6$ and $X_{PHLS}^6-K_x^6$ are first order infinitesimal, ${\mathrm{LX}}_{lds}\approx X_{PHLS}^6$. Some system errors can be eliminated by reducing the initial value. Then, the radial motion error along the X axis is obtained:

$$\begin{array}{cc}\hfill {\delta }_x={\mathrm{LX}}_{lds}-& {\mathrm{LX}}_{lds\left(t=0\right)}-cos\theta \left({\delta }_{xbc}+\left(K_z+K_z^6\right)\left({\epsilon }_{py}+{\epsilon }_{ybc}\right)\right)+sin\theta \left({\delta }_{ybc}-\left(K_z+K_z^6\right){\epsilon }_{xbc}\right)\hfill \\ & +{\delta }_{xbc}+\left(K_y+K_y^6\right){\epsilon }_{pz\left(t=0\right)}+\left(K_z+K_z^6\right)\left({\epsilon }_{py\left(t=0\right)}+{\epsilon }_{ybc}\right)-\left(K_y+K_y^6\right){\epsilon }_{pz}+\left(K_y+K_y^6\right){\epsilon }_z\hfill \\ & -\left(K_z+K_z^6\right){\epsilon }_y\hfill \end{array}$$

(12)

The main factors affecting the measurement of the radial motion error along the X axis include the following: installation errors ${\delta }_{xbc}$, ${\delta }_{ybc}$, ${\epsilon }_{xbc}$, and ${\epsilon }_{ybc}$; perpendicularity error ${\epsilon }_{py}$; working angle manufacturing error ${\epsilon }_{pz}$; the coordinates $K_y+K_y^6$ and $K_z+K_z^6$ of the light emission point in CS0. Where $cos\theta \left({\delta }_{xbc}+\left(K_z+K_z^6\right)\left({\epsilon }_{py}+{\epsilon }_{ybc}\right)\right)$, $sin\theta \left({\delta }_{ybc}-\left(K_z+K_z^6\right){\epsilon }_{xbc}\right)$, ${\delta }_{xbc}$, $\left(K_y+K_y^6\right){\epsilon }_{pz\left(t=0\right)}$, $\left(K_z+K_z^6\right)\left({\epsilon }_{py\left(t=0\right)}+{\epsilon }_{ybc}\right)$ are constants and can be compensated by triangular fitting, $\left(K_y+K_y^6\right){\epsilon }_{pz}$ can be compensated by measuring the spatial coordinates of the LDS1 and the manufacturing errors of the polyhedral prism working surface. ${\epsilon }_z$ and ${\epsilon }_y$ in $\left(K_y+K_y^6\right){\epsilon }_z-\left(K_z+K_z^6\right){\epsilon }_y$ can be calculated by the method mentioned above.

3.2.4. The Radial Motion Error along Y Axis

Similar to the derivation process of radial runout error along the X axis, the radial motion error along the Y axis is this:

$$\begin{array}{cc}\hfill {\delta }_y={\mathrm{LY}}_{lds}& -{\mathrm{LY}}_{lds\left(t=0\right)}+{\delta }_{ybc}\left(1-cos\theta \right)+{\delta }_{xbc}sin\theta -\left(U_x+U_x^7\right)\left({\epsilon }_z-{\epsilon }_{pz}+{\epsilon }_{pz\left(t=0\right)}\right)\hfill \\ & +\left(U_z+U_z^7\right)\left({\epsilon }_{px}cos\theta +{\epsilon }_x+{\epsilon }_{ybc}sin\theta +{\epsilon }_{xbc}cos\theta -{\epsilon }_{px\left(t=0\right)}-{\epsilon }_{xbc}\right)\hfill \end{array}$$

(13)

The main factors affecting the radial motion error along the Y axis include the following: the installation errors ${\delta }_{xbc}$, ${\delta }_{ybc}$, ${\epsilon }_{xbc}$, and ${\epsilon }_{ybc}$; the perpendicularity error ${\epsilon }_{py}$; the working angle manufacturing error ${\epsilon }_{pz}$; the position coordinates of the laser exit point $U_x+U_x^7$ and $U_z+U_z^7$. The error compensation method is the same as the radial motion error along the X axis.

3.2.5. The Axial Motion Error along Z Axis

The outgoing light $L^8$ of the LDS3 along the Z direction can be expressed as this:

$$\left[\begin{array}{cc}\begin{array}{cc}1& 0\end{array}& \begin{array}{cc}0& -V_x^8\end{array}\\ \begin{array}{cc}0& 1\end{array}& \begin{array}{cc}0& -V_y^8\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{x}^8\\ y^8\end{array}\\ \begin{array}{c}{z}^8\\ 1\end{array}\end{array}\right]$$

(14)

The top surface matrix of the polyhedral prism is $\left[\begin{array}{cc}\begin{array}{cc}0& 0\end{array}& \begin{array}{cc}1& 0\end{array}\end{array}\right]$, and the reflection surface matrix of the plane reflector is $\left[\begin{array}{cc}\begin{array}{cc}0& 0\end{array}& \begin{array}{cc}1& -H_b\end{array}\end{array}\right]$; $H_b$ is the sum of the thickness of the polyhedral prism and the plane reflector. Considering the parallel error of the polyhedral prism, the bottom surface of the plane reflector can be expressed as this:

$$\left[\begin{array}{cc}\begin{array}{cc}0& 0\end{array}& \begin{array}{cc}1& -H_b\end{array}\end{array}\right]\left[\begin{array}{cccc}1& 0& {\epsilon }_{yb}& 0\\ 0& 1& -{\epsilon }_{xb}& 0\\ -{\epsilon }_{yb}& {\epsilon }_{xb}& 1& 0\\ 0& 0& 0& 1\end{array}\right]=\left[\begin{array}{cc}\begin{array}{cc}-{\epsilon }_{yb}& {\epsilon }_{xb}\end{array}& \begin{array}{cc}1& -H_b\end{array}\end{array}\right]$$

(15)

The ${\epsilon }_{xb}$ and ${\epsilon }_{yb}$ are the parallel errors between the top surface and the bottom surface. In CS8, the reflection surface of the plane reflector can be expressed as this:

$$\left[\begin{array}{cc}\begin{array}{cc}-{\epsilon }_{yb}& {\epsilon }_{xb}\end{array}& \begin{array}{cc}1& -H_b\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{X}^2\\ Y^2\end{array}\\ \begin{array}{c}{Z}^2\\ 1\end{array}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{cc}-{\epsilon }_{yb}& {\epsilon }_{xb}\end{array}& \begin{array}{cc}1& -H_b\end{array}\end{array}\right]T_2^1{T}_1^0{T}_0^8\left[\begin{array}{c}\begin{array}{c}{X}^8\\ Y^8\end{array}\\ \begin{array}{c}{Z}^8\\ 1\end{array}\end{array}\right]$$

(16)

The coordinates of the reflection points that can be obtained from the incident light and the reflection surface are as follows:

$$\begin{array}{cc}\hfill X^8=V_x^8, Y^8& =V_y^8,Z^8\hfill \\ & =V_x^8\left(-{\epsilon }_{yb}cos\theta -{\epsilon }_{xb}sin\theta +{\epsilon }_y-{\epsilon }_{yv}\right)+V_y^8\left(-{\epsilon }_{yb}sin\theta +{\epsilon }_{xb}cos\theta +{\epsilon }_x+{\epsilon }_{xv}\right)\hfill \\ & -{\epsilon }_{yb}\left(cos\theta V_x+sin\theta V_y\right)+{\epsilon }_{xb}\left(-sin\theta V_x+cos\theta V_y\right)+{\epsilon }_y{V}_x-{\epsilon }_x{V}_y+V_z-{\delta }_z-H_b\hfill \end{array}$$

(17)

The measurement value of the LDS3 is ${\mathrm{LZ}}_{lds}$. We can use the spatial geometric position relationship to obtain ${\mathrm{LZ}}_{lds}=\sqrt{{Z^8}^{{}^2}+{\left(X^8-V_x^8\right)}^2+{\left(Y^8-V_y^8\right)}^2}\approx Z^8$. Because the values of $X^8-V_x^8$ and $Y^8-V_y^8$ are first order infinitesimal, ${\mathrm{LZ}}_{lds}\approx Z^8$. Some system errors can be eliminated by reducing the initial value. The axial motion error along the Z direction is this:

$$\begin{array}{cc}\hfill {\delta }_z={\mathrm{LZ}}_{lds}& -{\mathrm{LZ}}_{lds\left(t=0\right)}–\left(V_y+V_y^8\right){\epsilon }_x+\left(V_x+V_x^8\right){\epsilon }_y\hfill \\ & -\left(cos\theta -1\right)\left[\left(V_x+V_x^8\right)\left({\epsilon }_{yb}-{\epsilon }_{ybc}\right)+\left(V_y+V_y^8\right)\left({\epsilon }_{xbc}-{\epsilon }_{xb}\right)\right]\hfill \\ & -sin\theta \left[\left(V_x-V_x^8\right)\left({\epsilon }_{xb}-{\epsilon }_{xbc}\right)+\left(V_y+V_y^8\right)\left({\epsilon }_{yb}-{\epsilon }_{ybc}\right)\right]\hfill \end{array}$$

(18)

The main factors affecting the axial motion error along Z axis include the following: the parallel errors ${\epsilon }_{xb}$ and ${\epsilon }_{yb}$; the perpendicularity error ${\epsilon }_{py}$; the working angle manufacturing error ${\epsilon }_{pz}$; the position coordinates $V_x$ and $V_y$ of the origin of CS8 in CS0. The position of LDS3 outgoing light is the coordinates $V_x^8$ and $V_y^8$ in CS8. The error compensation method is the same as the radial motion error along X axis.

The effects of the polyhedral prism’s manufacturing errors on the measurement of the six DOF motion errors are shown in

Table 1. The effects of the polyhedral prism’s manufacturing errors on the measurement of the six DOF motion errors.

	${\mathit{\epsilon }}_{\mathit{x}}$	${\mathit{\epsilon }}_{\mathit{y}}$	${\mathit{\epsilon }}_{\mathit{z}}$	${\mathit{\delta }}_{\mathit{x}}$	${\mathit{\delta }}_{\mathit{y}}$	${\mathit{\delta }}_{\mathit{z}}$
${\epsilon }_{px}$	√	×	×	×	√	×
${\epsilon }_{py}$	×	√	×	√	×	×
${\epsilon }_{pz}$	×	×	√	√	√	×
${\epsilon }_{xb}$	×	×	×	×	×	√
${\epsilon }_{yb}$	×	×	×	×	×	√

.

The above model includes forty-six errors: the six DOF motion errors of the rotary axis, the installation errors of each component, and the manufacturing errors. Because the complete expansion of the model is rather complex, the above model ignores the influence of the second or higher order infinitesimals.

3.3. Model Simulation Analysis

MATLAB matrix calculation software was used to simulate the proposed error model for verification. By introducing certain installation errors and manufacturing errors, the model compensation calculation results of the six DOF motion errors of a rotary axis are compared with the preset values.

Setting of the simulation parameters: the six DOF motion errors of the target rotary axis are set to zero at the initial timepoint. Thirteen measurement points are set from 0° to 360° with intervals of 30°, corresponding to the twelve faces of the polyhedral prism. Except for the 0° and 360° points, the ${\epsilon }_Z$, ${\epsilon }_Y$, and ${\epsilon }_X$ values of other points are set to 100″; the ${\delta }_X$ and ${\delta }_Y$ values are set to 100 μm, and the ${\delta }_Z$ value is set to 10 μm.

The diameter of the polyhedral prism is 100 mm, its thickness is 17 mm, the distance from the reflection surface to the center is 48.3 mm, and the width of each surface is 12.94 mm. Assuming that the distance from the light point position of the autocollimators and the laser displacement sensors on the reflection surface of the polyhedral prism to the axis in X and Y directions is 100 μm, the installation errors of the polyhedral prism around the X and Y axes are 50″, the radial installation errors along the X direction and Y direction are 10 μm, and the axial installation error along the Z direction is 10 μm. Because the manufacturing errors of the working angle of the 0-level polyhedral prism in practical application are within 1″, the manufacturing errors of the working angle of each surface are set to a random number within 1″. The perpendicularity error between the working surface and the datum plane of the polyhedral prism is ≤5″; subsequently, the perpendicularity errors ${\epsilon }_{px}$ and ${\epsilon }_{py}$ between the working surface and the datum plane of the polyhedral prism are set to be 5″. The parallel error between the top surface and the reference surface is less than 2 μm. Because the diameter of the polyhedral prism is 100 mm, the angle between the top and bottom surfaces around the X axis and the Y axis is less than 4.13″; therefore, the angle between the two surfaces around the X and Y directions is 4.13″. The maximum distance between the origin coordinates of the measurement unit coordinate systems 4, 5, 6, and 7 and the origin coordinates of the world coordinate system is 100 mm. The angle installation errors of the autocollimators and laser displacement sensors are set to 100″. The positions of the emitted light of the autocollimators and the laser displacement sensors are located at 100 μm deviation from the X axis and Y axis of their respective coordinate centers. The specific simulation results are shown in Figure 3.

According to the simulation results, the proposed error model is able to compensate the installation errors and manufacturing errors for measuring all six DOF geometric motion errors of a rotary axis. The differences between the compensated measurement results and the errors’ set values are 0.0509″, 0.0003″, 0.0003″, 0.084 μm, 0.036 μm, and 0.028 μm, respectively. The compensation effect is significant, which verifies the accuracy and effectiveness of the compensation model.

4. Measurement Experiment

In order to verify the proposed measurement method and error model, an experimental device was designed and built. As shown in Figure 4, all components were installed on the optical platform. The target rotary axis was an SKQ-12200 numerically controlled rotary table made by Yiliya Company. The angular positioning accuracy is about 40″ and repeatability precision is about 20″. The polyhedral prism adopted the 0-level 12-face prism from Hongce Company. The manufacturing error of the working surface was ≤±1″, and the perpendicularity between the working face and the datum plane was ≤±5″. The Collapex-EXP photoelectric autocollimator was used as the rotation angular error measurement unit. An ILD2300-2LL laser displacement sensor from Micro-Epsilon, Germany, was used as the measurement unit of the radial and axial motional errors of the target rotary axis. The specific parameters of the autocollimator and laser displacement sensor are shown in

Table 2. The specific parameters of the autocollimator and laser displacement sensor.

Autocollimator	Range	Maximum Error	System Accuracy	Resolution
	±300″	±0.05″	±0.2″	±0.01″
laser displacement sensor	Wavelength	range	absolute error	resolution
	670 nm	2 mm	0.6 μm	0.03 μm

.

The laboratory environment temperature was about 25 ± 1 °C. The measurement angle interval was 30° (determined by the number of polygon faces), and the rotation speed of the target rotary axis was 0.57°/s. Limited by laboratory conditions, one laser displacement sensor and one autocollimator were used to carry out the experiment step by step.

The specific steps were as follows: Firstly, the autocollimator was installed in the X direction of the target rotary axis to measure the angular positioning error and the tilt motion error around the Y axis. The laser displacement sensor was installed in the Y direction to measure the radial motion error of the rotary axis along the Y axis, as shown in Figure 4. The second step was to install the autocollimator in the Y direction to measure the tilt error of the target rotary axis around the X axis. The laser displacement sensor was installed in the X direction to measure the radial motion error of the target rotary axis along the X direction. Finally, the axial motion error along the Z direction was measured by a laser displacement sensor placed on the target rotary axis through a fixed device.

The SKQ-12200 numerically controlled rotary table was measured ten times with the above measuring device, and errors were compensated by the proposed model. The measurement results before and after the compensation of the six DOF motion errors of the rotary axis are shown in

Table 3. The measurement results before and after the compensation of the six DOF motion errors of the rotary axis.

Motion Errors	Before Compensation	After Compensation
${\epsilon }_x$	26.15″	15.93″
${\epsilon }_y$	33.36″	16.69″
${\epsilon }_z$	27.28″	27.38″
${\delta }_x$	37.65 μm	12.74 μm
${\delta }_y$	53.09 μm	11.12 μm
${\delta }_z$	2.66 μm	2.57 μm

. The motion error of a certain DOF is the maximum absolute value of the motion errors of all measurement points. According to the compensation results, ${\epsilon }_x$, ${\epsilon }_y$, ${\delta }_x$ and ${\delta }_y$ are significantly reduced after compensation. The maximum reduction is 79.1%. According to Equation (9), ${\epsilon }_z$ is only affected by the manufacturing errors of the polyhedral prism’s working surface, and the values of manufacturing errors of the polyhedral prism is small (≤±1″). It can be seen that the other error terms have small influence on the measurement of ${\delta }_z$.

The measurement results after compensated and the repeatability values of the six DOF geometric motion errors are shown in Figure 5. The repeatability of each measurement point is half of the peak-to-peak value of the ten measurements, and the repeatability of the motion error of a certain degree of freedom is the maximum value of the repeatability of all measurement points.

The experimental results show that after error model compensation, the repeatability deviation of the angular positioning error is 15.13; the repeatability deviation of the tilt motion error around the Y axis is reduced from 1.35 to 1.28″; the repeatability deviation of the tilt motion error around the X axis is reduced from 1.92 to 0.87″; the repeatability deviation of the radial motion error along the X axis is reduced from 1.12 to 0.74 μm; the repeatability deviation of the radial motion error along the Y axis is reduced from 1.36 to 0.87 μm; the repeatability deviation of the axial motion error along the Z axis is reduced from 0.53 to 0.34 μm; the maximum reduction is 54.69%. According to Equation (9), the angular positioning error is only affected by the manufacturing error of the polyhedral prism working surface, and the manufacturing error of the polyhedral prism is determined as a fixed value. Therefore, the model’s compensation does not affect the measurement repeatability of the angular positioning error. The measurement repeatability of the angular position error is determined by the repeatability of the target rotary axis itself, and the measurement results are essentially consistent with the nominal repeatability of the target rotary axis.

5. Conclusions

A new method based on a polyhedral prism is proposed to simultaneously measure the six DOF geometric motion errors of a rotary axis by using autocollimators and laser displacement sensors. An analysis model of 46 errors was established, which included the motion errors of the target rotary axis and the manufacturing errors and installation errors of each component. The results simulated by the professional matrix analysis software show that the six DOF motion errors of the target rotary axis after being compensated by our model are essentially equal to the preset errors. This provides a theoretical basis for the high precision of this method. The six DOF geometric motion errors of a rotary axis were measured ten times by the measurement device built on the optical platform. After compensation, the motion errors of the target rotary axis, ${\epsilon }_Z$, ${\epsilon }_Y$, ${\epsilon }_X$, ${\delta }_X$, ${\delta }_Y$, and ${\delta }_Z$, were, 27.38″, 16.69″, 15.93″, 12.74 μm, 11.12 μm, and 2.57 μm, respectively. The maximum reduction is 79.1%. The repeatability values were 15.13″, 1.28″, 0.87″, 0.74 μm, 0.89 μm, and 0.34 μm, respectively. Repeatability was significantly improved, with a maximum of up to 54.69%. The results verified the effectiveness of our method and error model. It can be used as a new reliable measurement method of six DOF geometric motion errors of a rotary axis. Subsequently, by analyzing the influence of the higher order errors on the geometric motion errors of the six DOF rotary axis, measurement accuracy and the repeatability can be further improved.