Health Indicators Construction and Remaining Useful Life Estimation for Concrete Structures Using Deep Neural Networks
Abstract
1. Introduction
- A health indicator (HI) constructor based on a SAE-DNN is developed. No manually extracted features are used in the construction of the SAE-DNN-based HI constructor. The SAE-DNN automatically extracts representative features during the training process.
- The constant false-alarm rate (CFAR) algorithm is used to capture the AE hits in every degradation cycle; the number of AE hits in each cycle is considered the label to train the DNN.
- The LSTM-RNN is investigated to learn the long-term dependencies of HI curves constructed in an offline process and is then used to predict the RUL of a concrete structure in an online process.
2. Experimental Setup
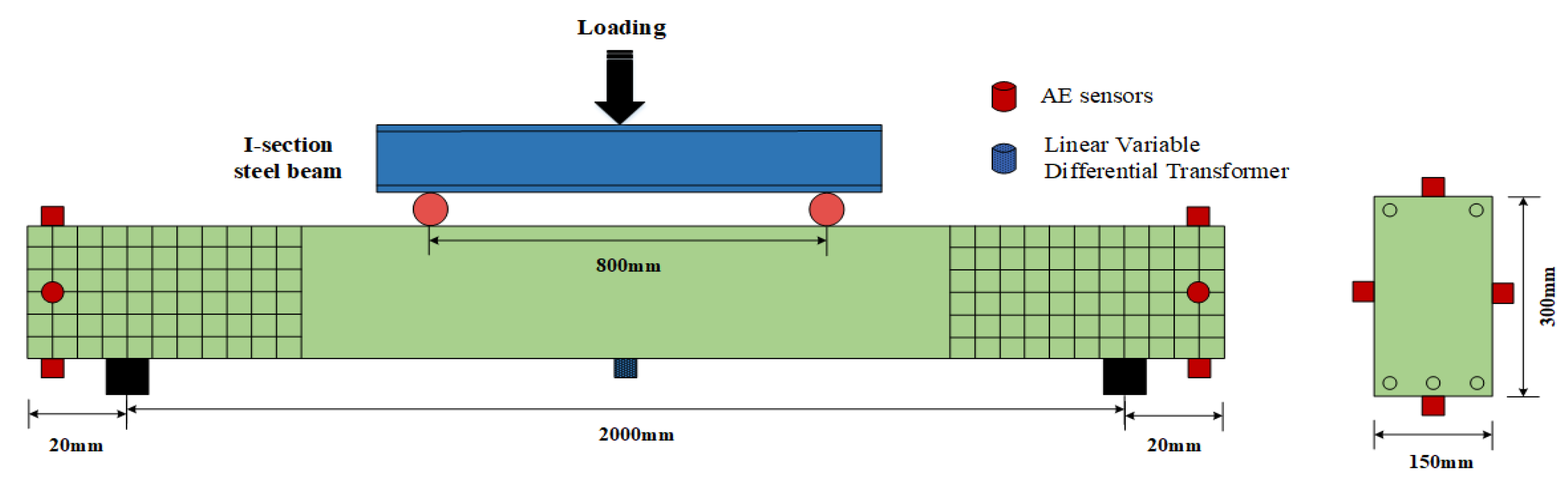
2.1. Experimental Specimens and Data Acquisition System
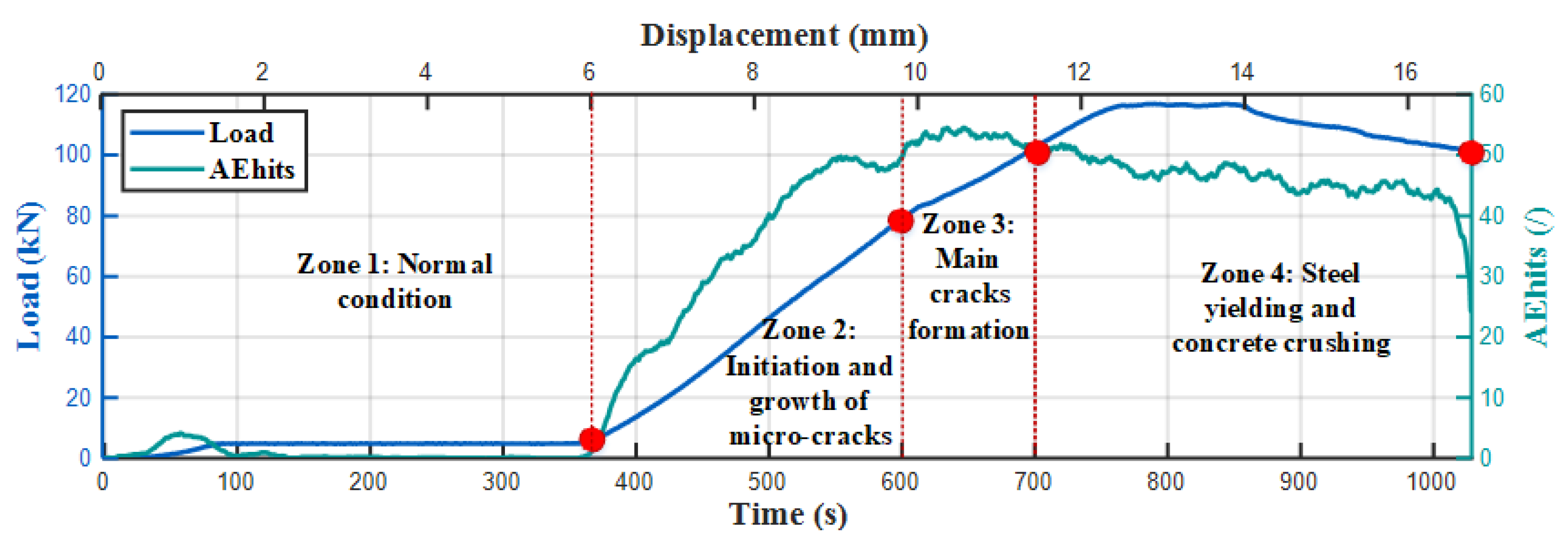
2.2. Separation of Destructive Processes
- Stage 1: The RC specimen deteriorates from its normal condition to a damaged state. Micro-cracks start at the end of this stage.
- Stage 2: Hairline cracks appear on the surface, which soon develop into macro-cracks.
- Stage 3: Main cracks form. Distributed flexure appears along with shear cracks, which soon lead to steel yielding.
- Stage 4: The steel yielding intensifies and shear cracks ultimately culminate in concrete crushing.
3. Methodologies
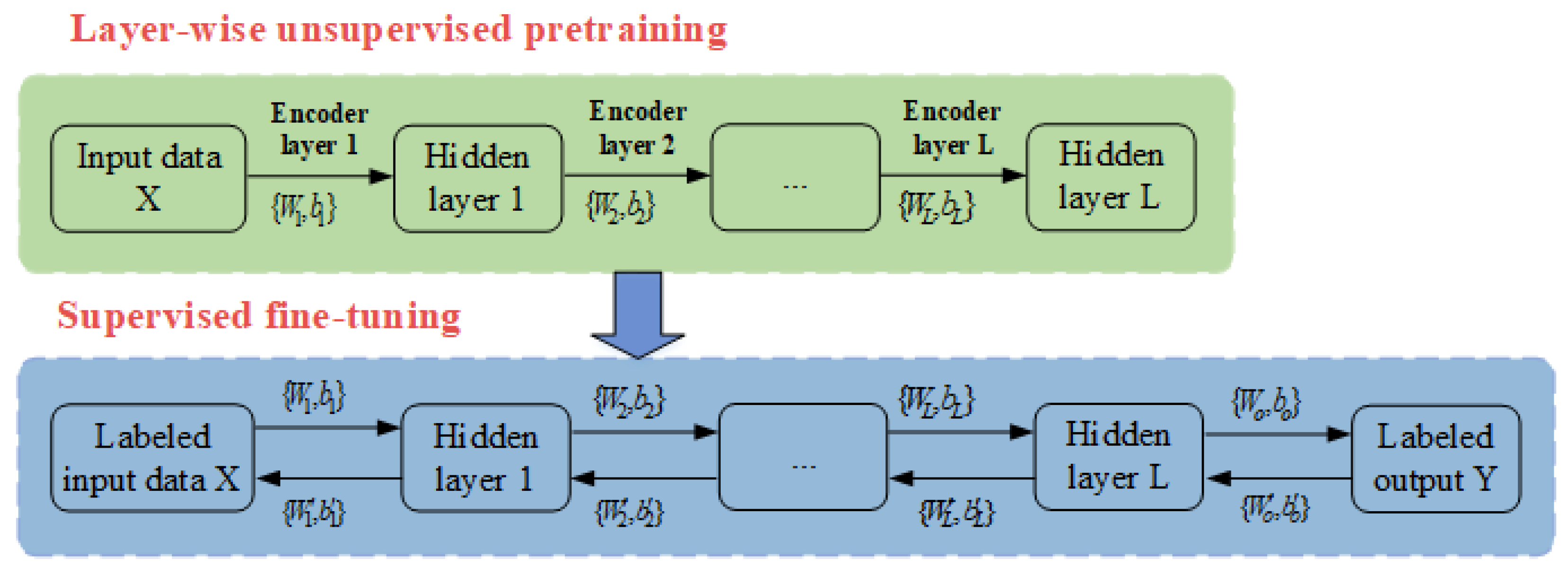
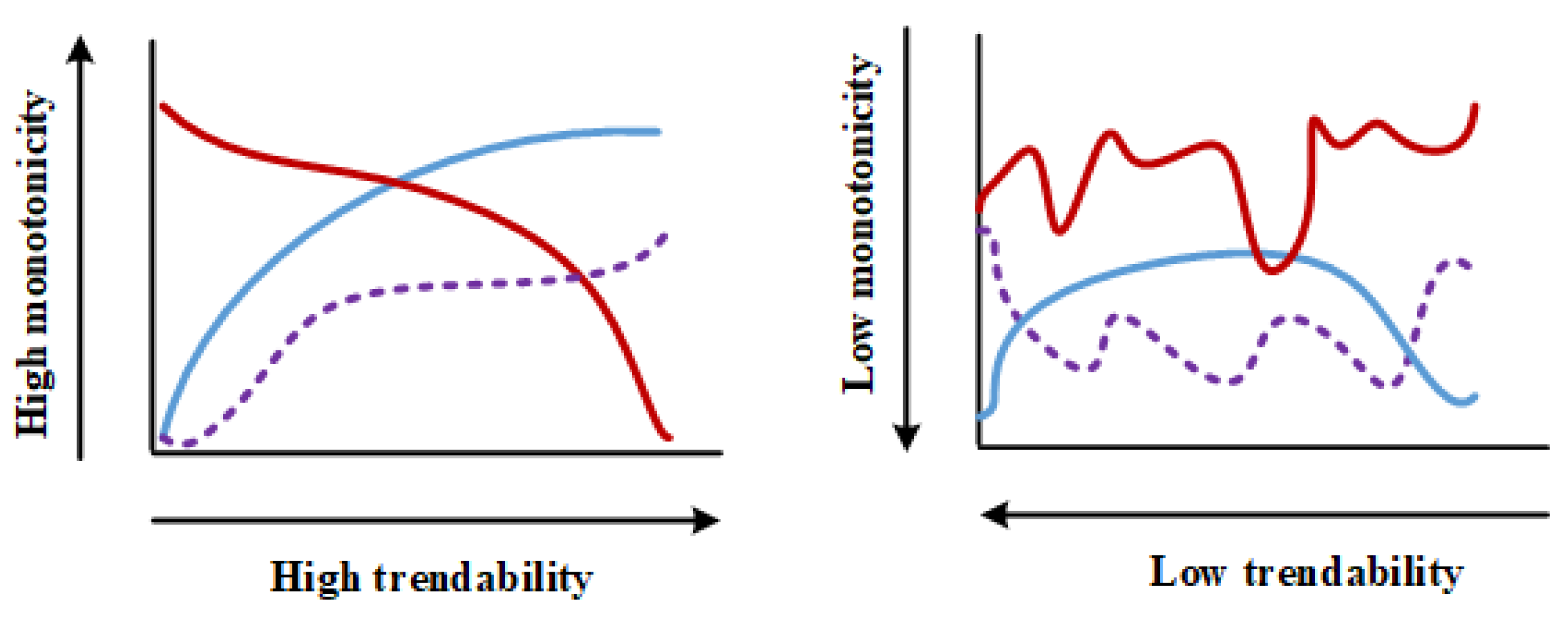
3.1. SAE-DNN-Based HI Constructor
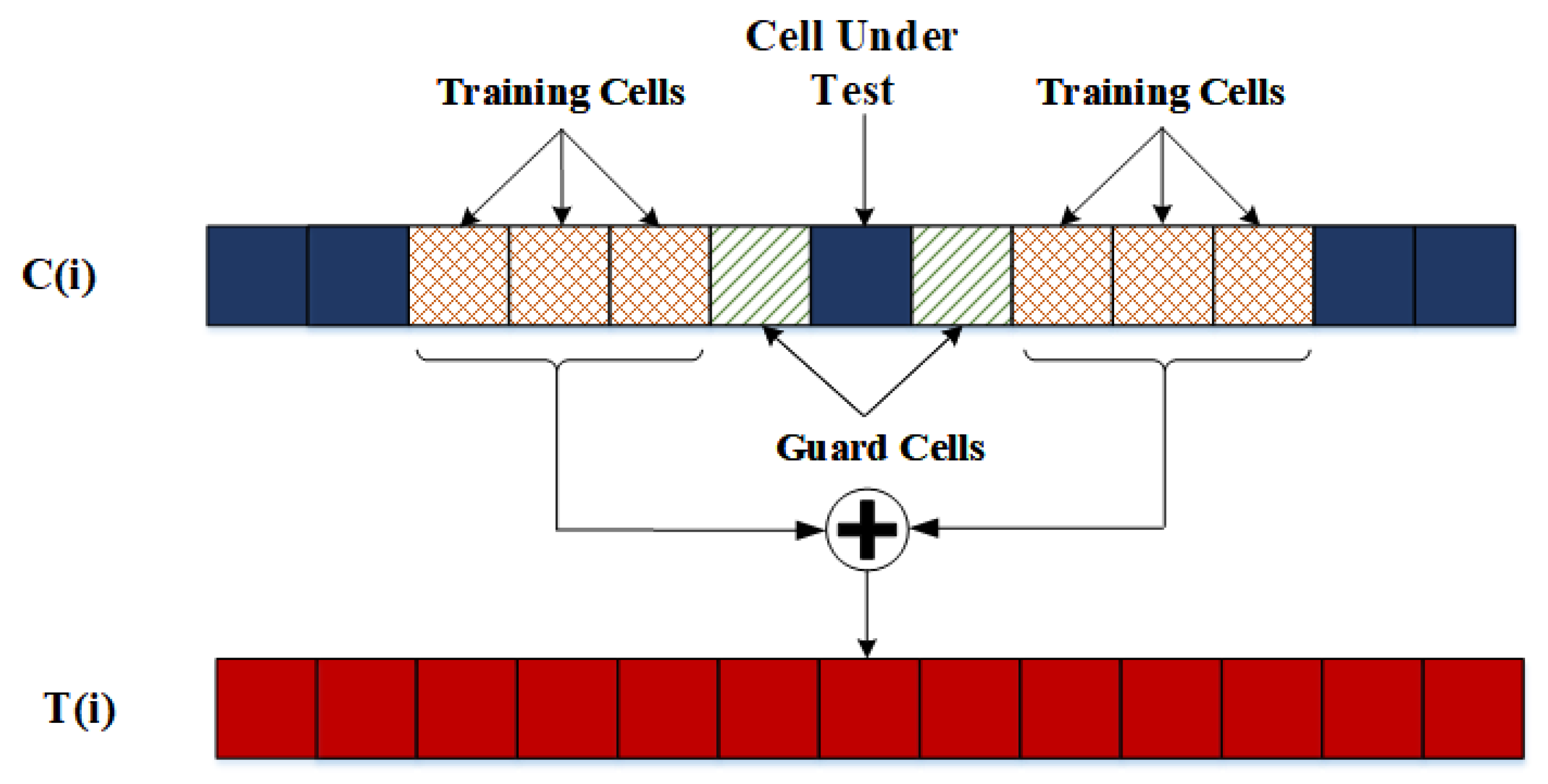
3.2. Impulse Detection Using the Constant False Alarm Rate (CFAR) Algorithm
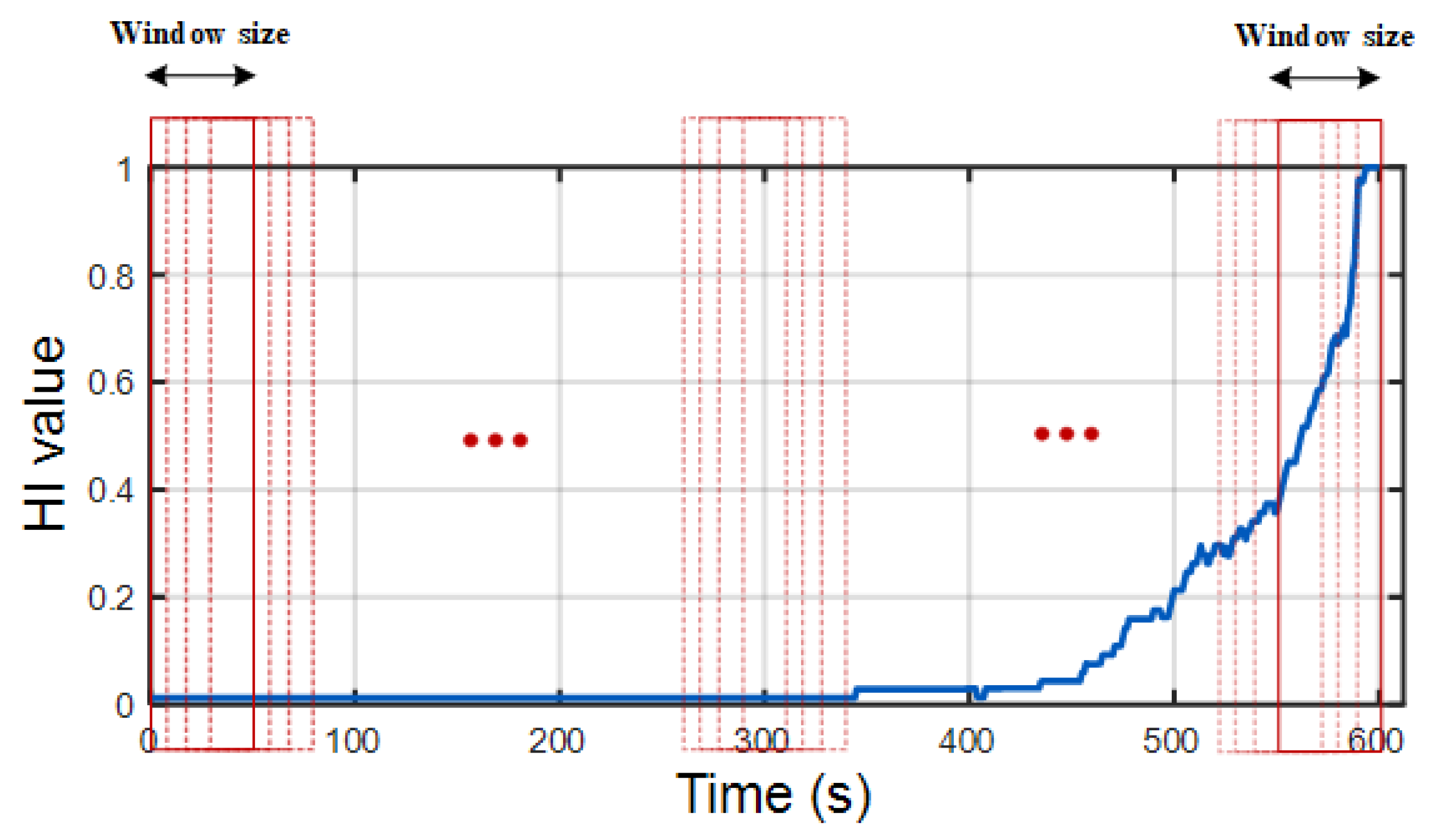
3.3. LSTM-RNN-Oriented RLU Prediction
4. Experimental Validation
4.1. Dataset Description
4.2. The Efficacy of an SAE-DNN-Based HI Constructor
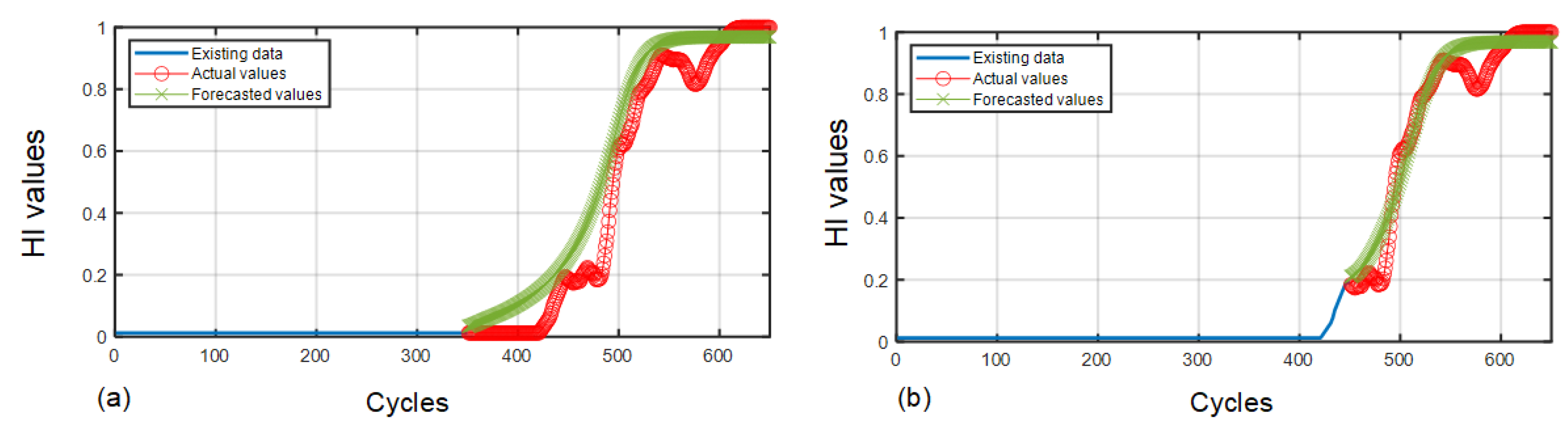
4.3. The Efficacy of the LSTM-RNN-Oriented RLU Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ohno, K.; Ohtsu, M. Crack classification in concrete based on acoustic emission. Construct. Build. Mater. 2010, 24, 2339–2346. [Google Scholar] [CrossRef]
- Aggelis, D.G. Classification of cracking mode in concrete by acoustic emission parameters. Mechan. Res. Commun. 2011, 38, 153–157. [Google Scholar] [CrossRef]
- Aggelis, D.; Mpalaskas, A.; Matikas, T. Investigation of different fracture modes in cement-based materials by acoustic emission. Cement Concr. Res. 2013, 48, 1–8. [Google Scholar] [CrossRef]
- Tra, V.; Kim, J.-Y.; Jeong, I.; Kim, J.-M. An acoustic emission technique for crack modes classification in concrete structures. Sustainability 2020, 12, 6724. [Google Scholar] [CrossRef]
- Fan, S.-K.S.; Hsu, C.-Y.; Tsai, D.-M.; He, F.; Cheng, C.-C. Data-driven approach for fault detection and diagnostic in semiconductor manufacturing. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1925–1936. [Google Scholar] [CrossRef]
- Fan, S.-K.S.; Hsu, C.-Y.; Jen, C.-H.; Chen, K.-L.; Juan, L.-T. Defective wafer detection using a denoising autoencoder for semiconductor manufacturing processes. Adv. Eng. Inf. 2020, 46, 101166. [Google Scholar] [CrossRef]
- Park, Y.-J.; Fan, S.-K.S.; Hsu, C.-Y. A Review on Fault Detection and Process Diagnostics in Industrial Processes. Processes 2020, 8, 1123. [Google Scholar] [CrossRef]
- Phi Duong, B.; Kim, J.-M. Prognosis of remaining bearing life with vibration signals using a sequential Monte Carlo framework. J. Acoust. Soc. Am. 2019, 146, EL358–EL363. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Shu, T.; Wan, J.; De Silva, C.W.; Wang, Z. A two-stage approach for the remaining useful life prediction of bearings using deep neural networks. IEEE Trans. Ind. Inf. 2018, 15, 3703–3711. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, Y.; Zi, Y.; Jin, X.; Tsui, K.-L. A two-stage data-driven-based prognostic approach for bearing degradation problem. IEEE Trans. Ind. Inf. 2016, 12, 924–932. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electr. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Xie, X.; Luo, H. A review on basic data-driven approaches for industrial process monitoring. IEEE Trans. Ind. Electr. 2014, 61, 6418–6428. [Google Scholar] [CrossRef]
- Tra, V.; Khan, S.A.; Kim, J.-M. Diagnosis of bearing defects under variable speed conditions using energy distribution maps of acoustic emission spectra and convolutional neural networks. J. Acoust. Soc. Am. 2018, 144, EL322–EL327. [Google Scholar] [CrossRef]
- Tra, V.; Kim, J. Pressure Vessel Diagnosis by Eliminating Undesired Signal Sources and Incorporating GA-Based Fault Feature Evaluation. IEEE Access 2020, 8, 134653–134667. [Google Scholar] [CrossRef]
- Tra, V.; Kim, J.; Khan, S.A.; Kim, J.-M. Incipient fault diagnosis in bearings under variable speed conditions using multiresolution analysis and a weighted committee machine. J. Acoust. Soc. Am. 2017, 142, EL35–EL41. [Google Scholar] [CrossRef] [PubMed]
- Williams, T.; Ribadeneira, X.; Billington, S.; Kurfess, T. Rolling element bearing diagnostics in run-to-failure lifetime testing. Mechan. Syst. Sig. Proc. 2001, 15, 979–993. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Sig. Proc. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Bozchalooi, I.S.; Liang, M. A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection. J. Sound Vib. 2007, 308, 246–267. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Wang, D.; Peter, W.T.; Guo, W.; Miao, Q. Support vector data description for fusion of multiple health indicators for enhancing gearbox fault diagnosis and prognosis. Meas. Sci. Technol. 2010, 22, 025102. [Google Scholar] [CrossRef]
- Tra, V.; Kim, J.; Khan, S.A.; Kim, J.-M. Bearing fault diagnosis under variable speed using convolutional neural networks and the stochastic diagonal levenberg-marquardt algorithm. Sensors 2017, 17, 2834. [Google Scholar] [CrossRef] [PubMed]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and Tensor Flow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Newton, MA, USA, 2019. [Google Scholar]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Wang, J.; Mao, K. Learning to monitor machine health with convolutional bi-directional LSTM networks. Sensors 2017, 17, 273. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Song, S.; Li, S.; Ma, L.; Pan, S.; Han, L. Research on gas concentration prediction models based on LSTM multidimensional time series. Energies 2019, 12, 161. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, T.; Han, G.; Gou, Y. TD-LSTM: Temporal dependence-based LSTM networks for marine temperature prediction. Sensors 2018, 18, 3797. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, L.; Hou, C.; Han, H.; Liu, Z.; Sun, Y.; Zheng, M. Wind power short-term prediction based on LSTM and discrete wavelet transform. Appl. Sci. 2019, 9, 1108. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Yuan, X.; Huang, B.; Wang, Y.; Yang, C.; Gui, W. Deep learning-based feature representation and its application for soft sensor modeling with variable-wise weighted SAE. IEEE Trans. Ind. Inf. 2018, 14, 3235–3243. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing; Tata McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]


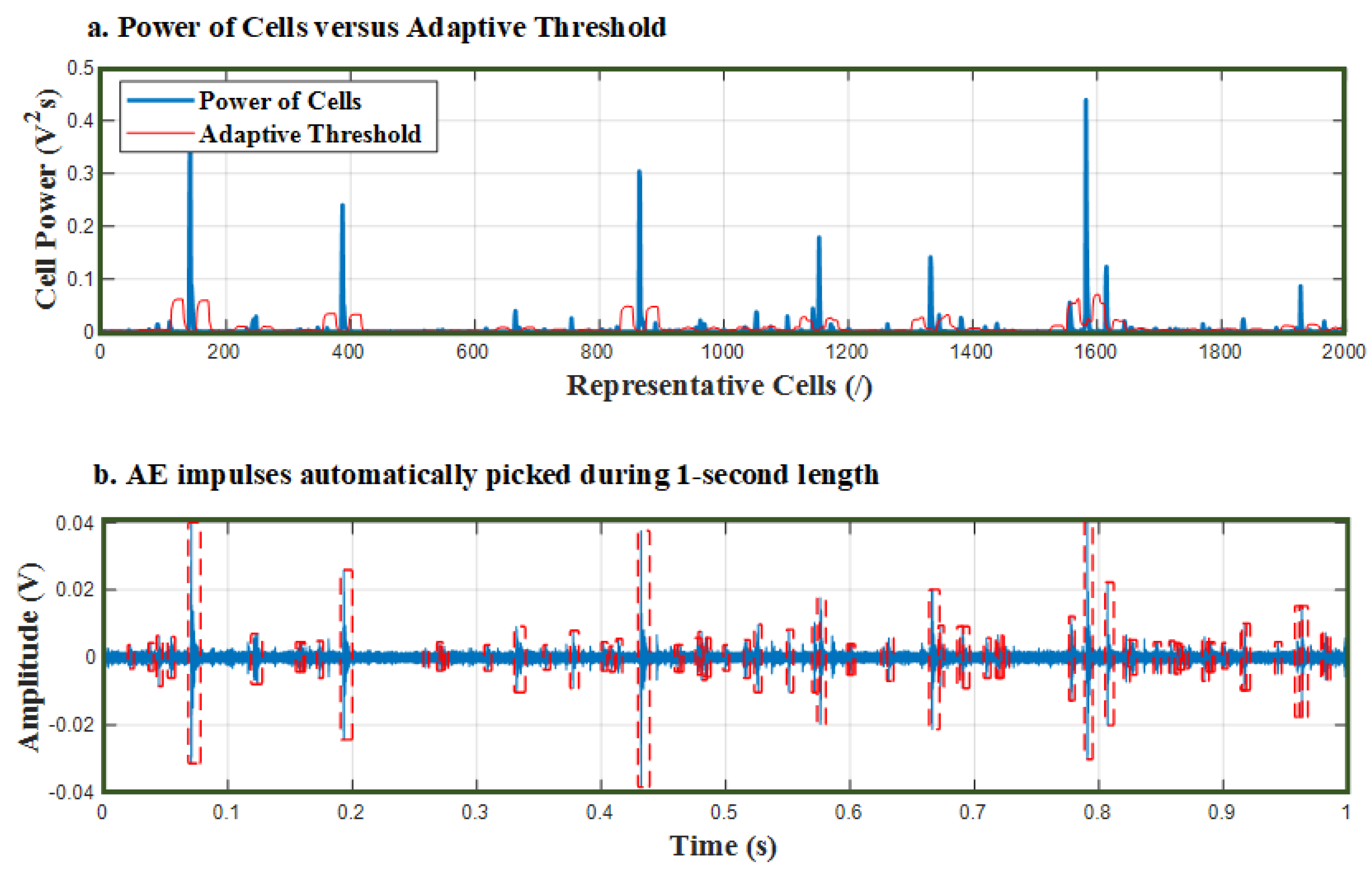


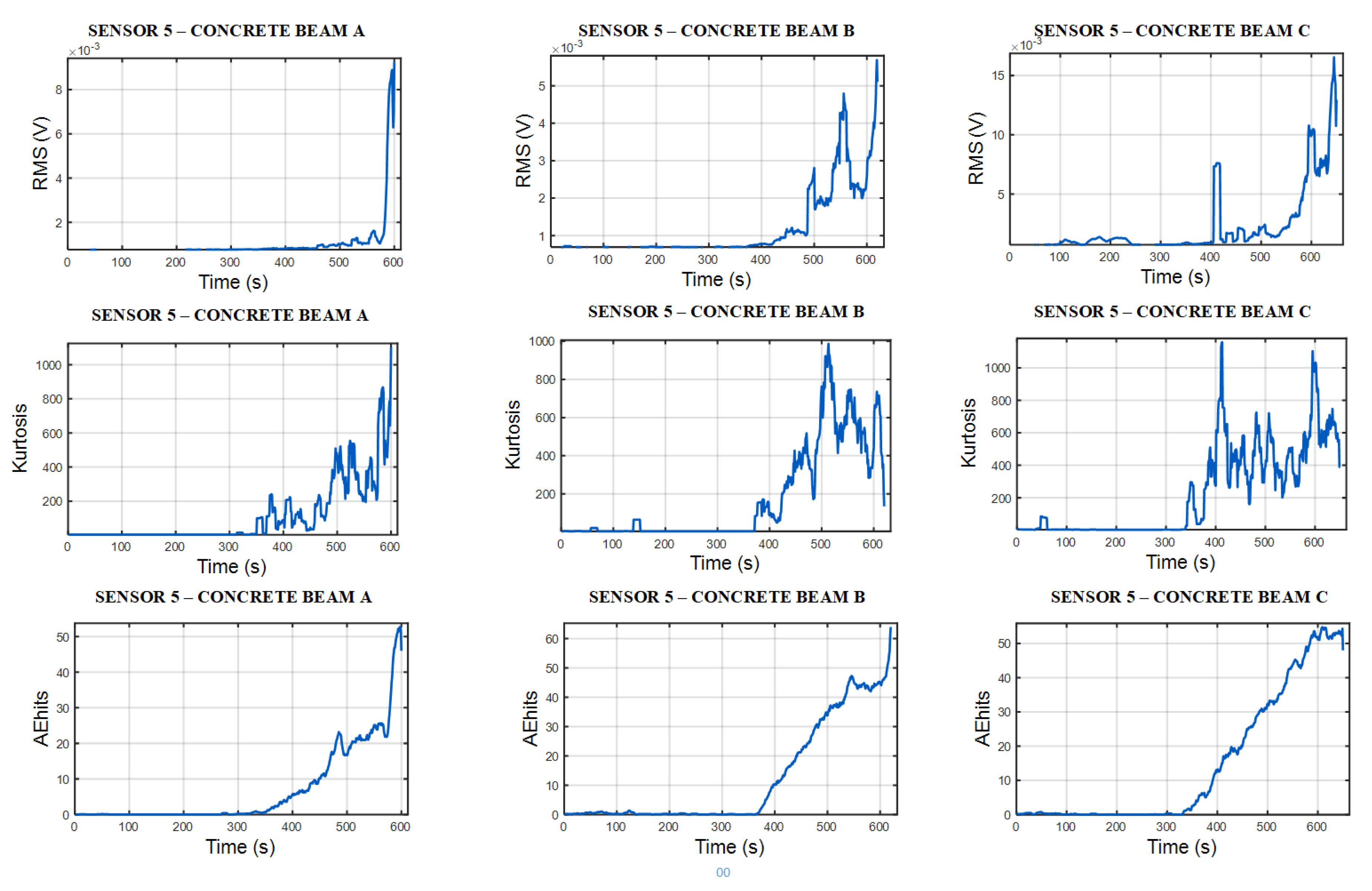



| Dataset | Bending Test | Concrete Beam | No. Sensors (Run-to-Fail Signals) | Signal Length (s) |
|---|---|---|---|---|
| Training dataset | 1 | A | 4 | 600 |
| 2 | B | 4 | 650 | |
| 3 | C | 4 | 620 | |
| Test dataset | 1 | A | 4 | 600 |
| 2 | B | 4 | 650 | |
| 3 | C | 4 | 620 |
| Type of HI | Min Value | Max Value | M | R |
|---|---|---|---|---|
| RMS | 0.0005 | 0.1529 | 0.037 ± 0.022 | 0.347 ± 0.064 |
| Kurtosis | 2.7496 | 5629.1 | 0.004 ± 0.021 | 0.458 ± 0.050 |
| Crest factor | 3.0803 | 145.91 | 0.0013 ± 0.183 | 0.7416 ± 0.024 |
| Skewness | −19.279 | 10.855 | 0.0102 ± 0.0215 | 0.1077 ± 0.1020 |
| Entropy | 0.0883 | 4.8324 | 0.0019 ± 0.0234 | 0.1886 ± 0.1740 |
| SAE-DNN | 0.0125 | 1 | 0.6788 ± 0.079 | 0.6801 ± 0.0489 |
| Fault-to-Failure Signals | Method | Prediction Error Cycles (at Cycle 350) | Prediction Error Cycles (at Cycle 450) |
|---|---|---|---|
| Concrete beam A | LSTM-RNN | 32 ± 3 | 21 ± 4 |
| GRU-RNN * | 36 ± 4 | 32 ± 5 | |
| Simple RNN | 81 ± 6 | 61 ± 8 | |
| Concrete beam B | LSTM-RNN | 41 ± 7 | 34 ± 5 |
| GRU-RNN * | 43 ± 6 | 37 ± 7 | |
| Simple RNN | 95 ± 11 | 89 ± 8 | |
| Concrete beam C | LSTM-RNN | 36 ± 3 | 24± 3 |
| GRU-RNN * | 39 ± 7 | 32 ± 3 | |
| Simple RNN | 88 ± 4 | 68 ± 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tra, V.; Nguyen, T.-K.; Kim, C.-H.; Kim, J.-M. Health Indicators Construction and Remaining Useful Life Estimation for Concrete Structures Using Deep Neural Networks. Appl. Sci. 2021, 11, 4113. https://doi.org/10.3390/app11094113
Tra V, Nguyen T-K, Kim C-H, Kim J-M. Health Indicators Construction and Remaining Useful Life Estimation for Concrete Structures Using Deep Neural Networks. Applied Sciences. 2021; 11(9):4113. https://doi.org/10.3390/app11094113
Chicago/Turabian StyleTra, Viet, Tuan-Khai Nguyen, Cheol-Hong Kim, and Jong-Myon Kim. 2021. "Health Indicators Construction and Remaining Useful Life Estimation for Concrete Structures Using Deep Neural Networks" Applied Sciences 11, no. 9: 4113. https://doi.org/10.3390/app11094113
APA StyleTra, V., Nguyen, T.-K., Kim, C.-H., & Kim, J.-M. (2021). Health Indicators Construction and Remaining Useful Life Estimation for Concrete Structures Using Deep Neural Networks. Applied Sciences, 11(9), 4113. https://doi.org/10.3390/app11094113









