Evaluation of Design Provisions for Horizontal Shear Strength in Composite Precast Concrete Beams with Different Interface Conditions
Abstract
1. Introduction
2. Research Significance
3. Design Code Provisions and Previous Test Results
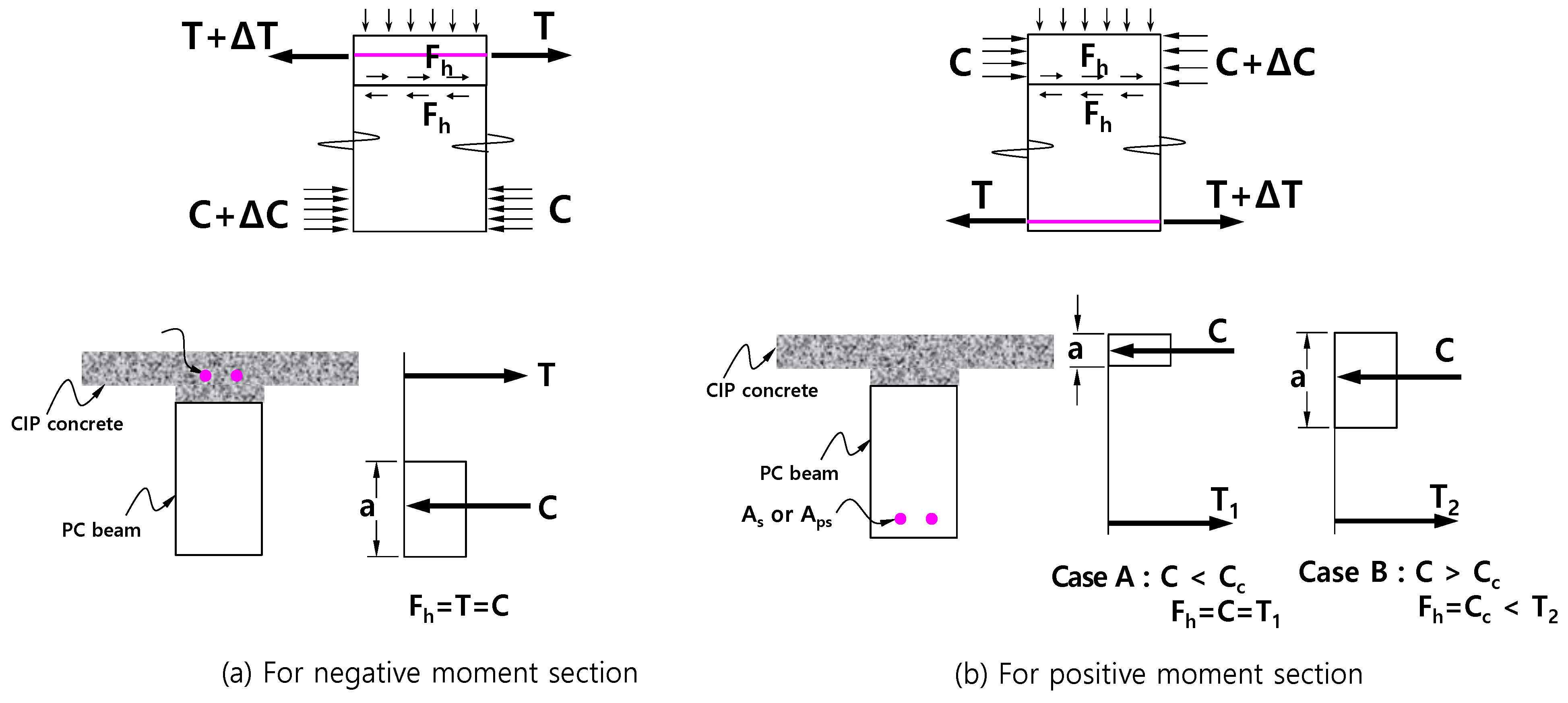
- Case 1: horizontal shear transfer in composite members (ACI 16.4 and PCI 5.3.5)
- Case 2: shear friction (ACI 22.9 and PCI 5.3.4)
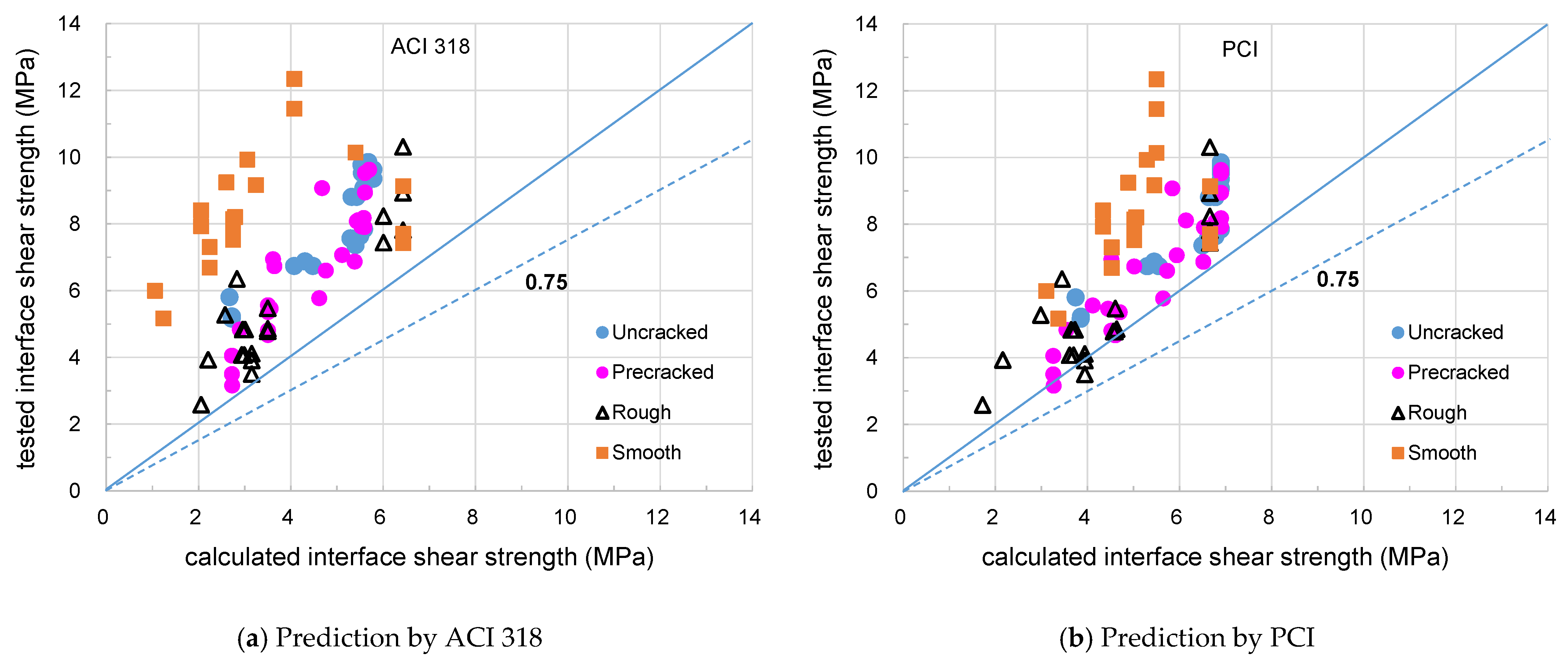
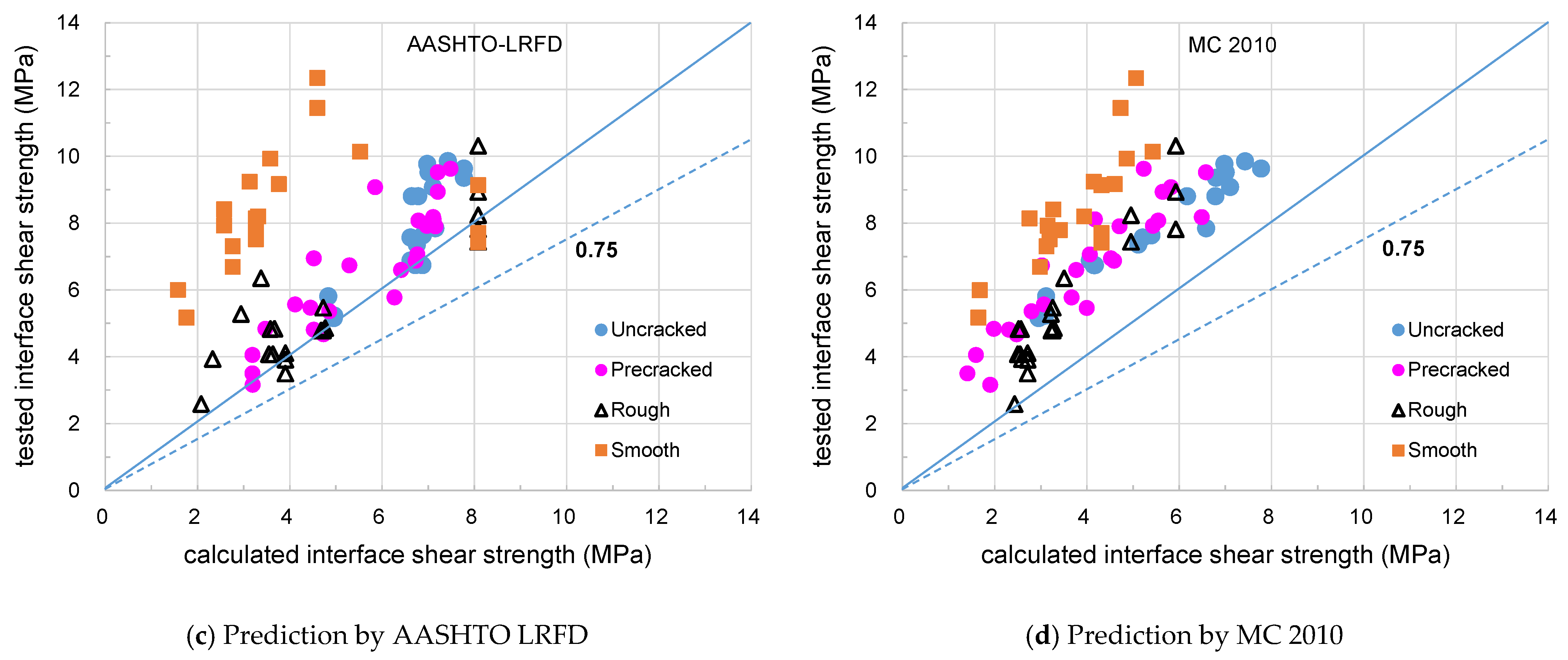
4. Statistical Analysis on Database of Experimental Results
5. Conclusions
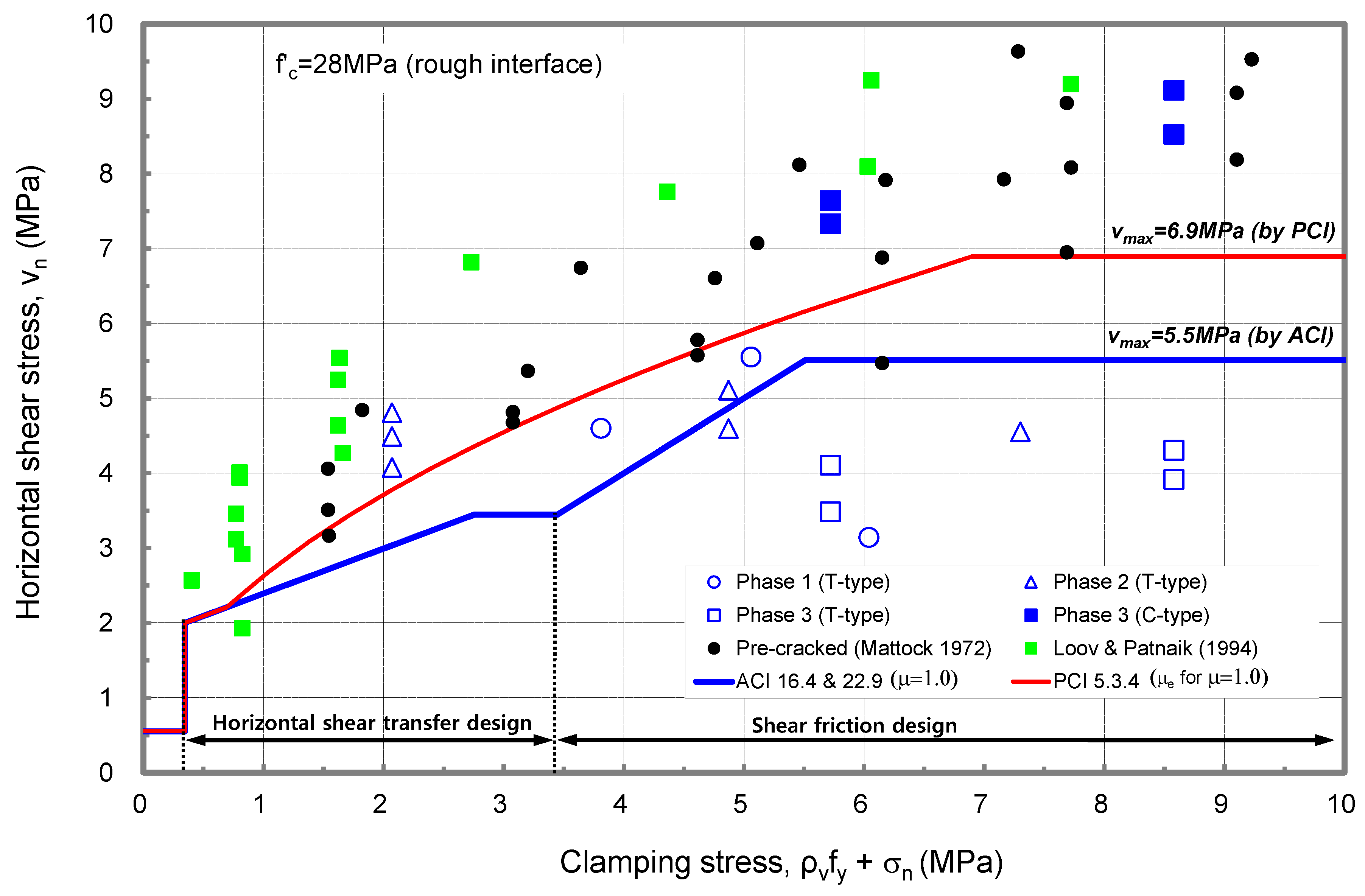
- It was found that the horizontal shear strength equations of the current design codes predict conservatively the horizontal shear strength of push-off specimens regardless of the variables such as the concrete compressive strength and the clamping stress of the shear connector on the interface, as well as surface roughness. However, the push-off tests cannot distinguish the difference from the interface location for either C-type or T-type.
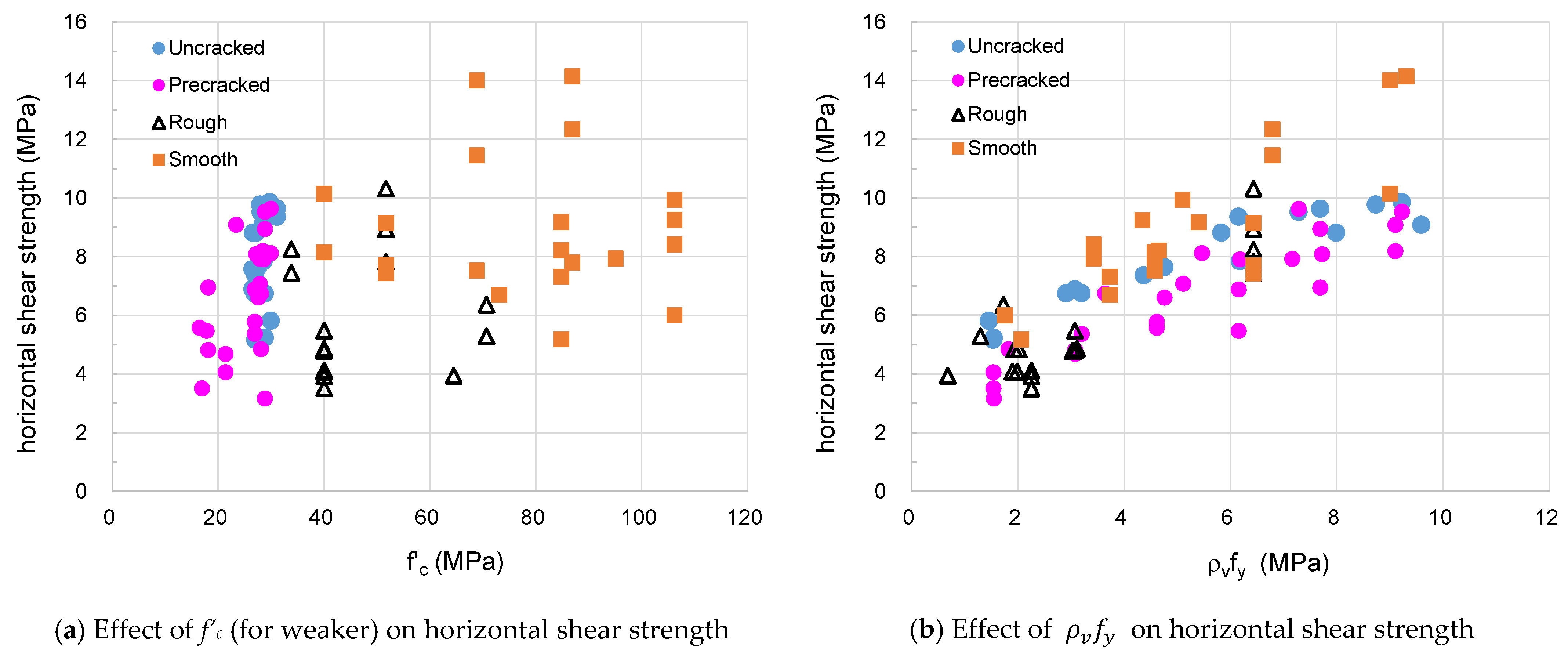
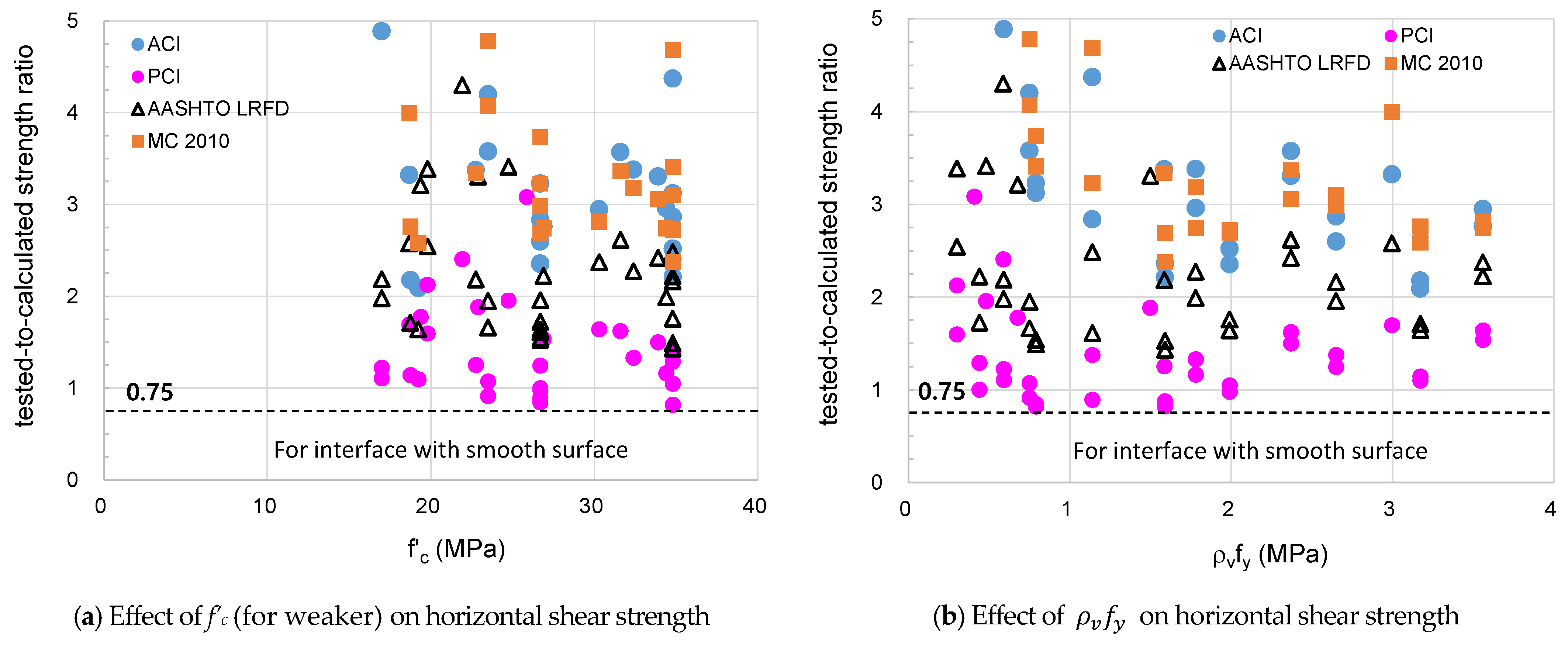
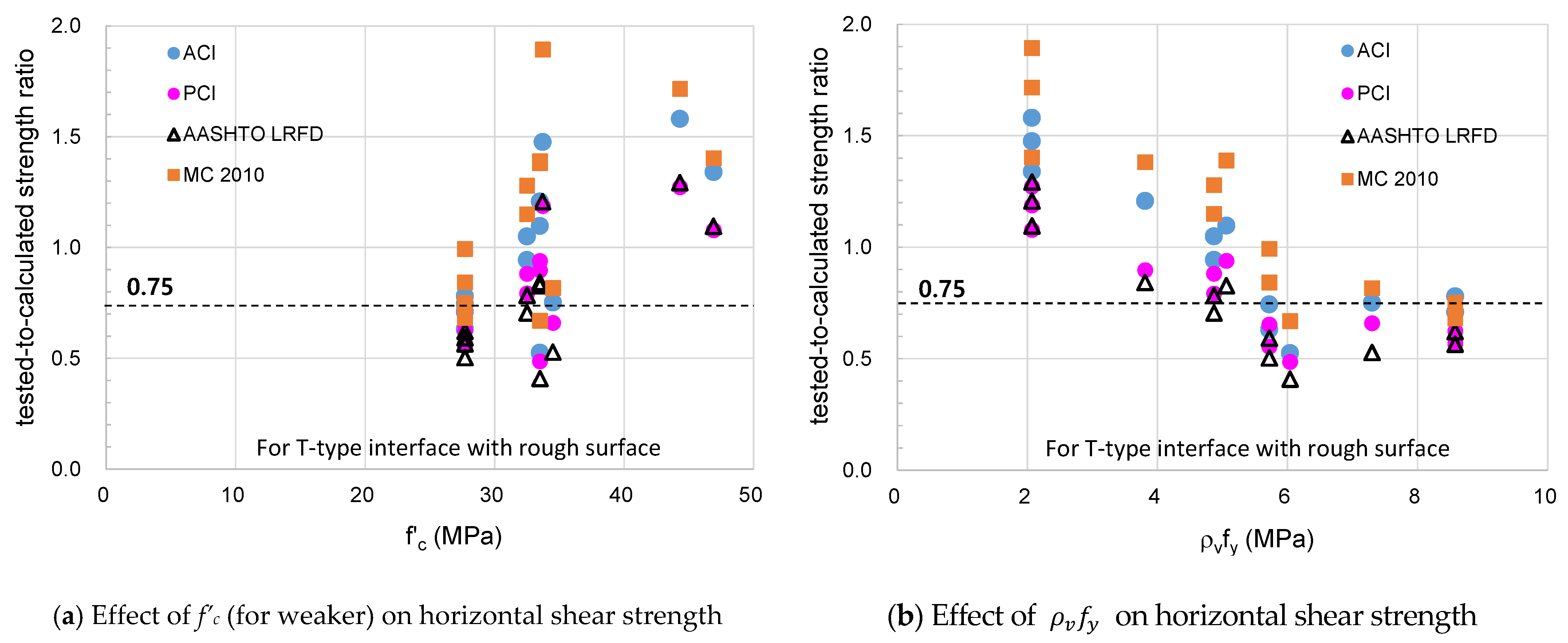
- The horizontal shear strengths by flexure tests were shown to vary greatly depending on the location of the interfaces. In particular, composite beams with roughened T-type interfaces showed a distribution of strength ratios with a minimum value of 0.41 to 0.67 and an average value of 0.77 to 1.15, indicating that horizontal shear strengths are overestimated.
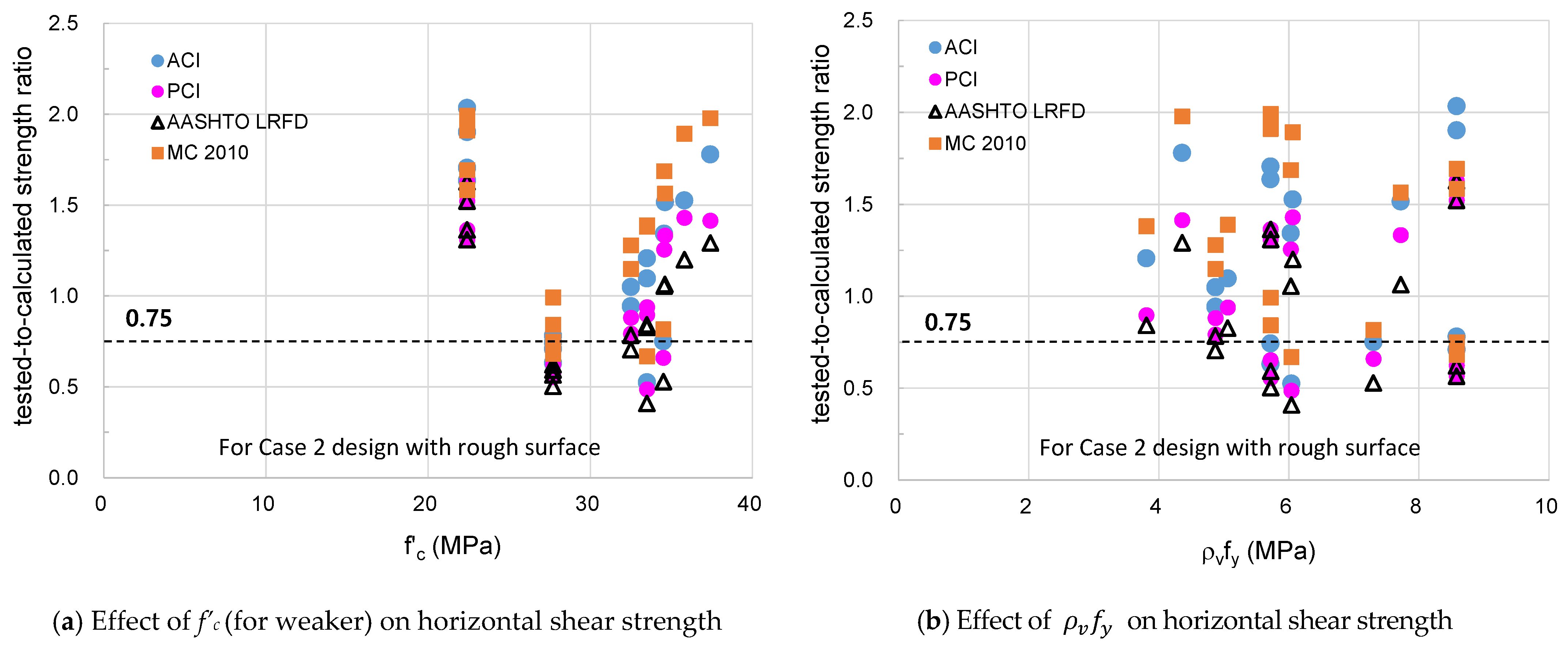
- The horizontal shear strength of the composite beam with roughened T-type interface increased as the compressive strength of concrete increased, but decreased as the clamping stress increased. Based on evaluation, it could be suggested that the shear connector did not operate sufficiently to control the slip deformation at the interface.
- In order to prevent members with roughened T-type interface from brittle failure, it is recommended to use a friction coefficient of 0.7 when using the shear friction method of ACI code.
- It is necessary in the future studies to include the interface location with respect to the neutral axis of composite beam as a variable for the interface shear design equation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, S.J.; Heo, I.; Kim, J.H.; Kim, K.S.; Oh, Y.H. Experimental and Numerical Studies on the Structural Performance of a Double Composite Wall. Appl. Sci. 2021, 11, 506. [Google Scholar] [CrossRef]
- Han, S.J.; Jeong, J.H.; Joo, H.E.; Choi, S.H.; Choi, S.; Kim, K.S. Flexural and Shear Performance of Prestressed Composite Slabs with Inverted Multi-Ribs. Appl. Sci. 2019, 9, 4946. [Google Scholar] [CrossRef]
- Hou, H.; Liu, X.; Qu, B.; Ma, T.; Liu, H.; Feng, M.; Zhang, B. Experimental Evaluation of Flexural Behavior of Composite Beams with Cast-in-place Concrete Slabs on Precast Prestressed Concrete Decks. Eng. Struct. 2015, 126, 405–416. [Google Scholar] [CrossRef]
- Saemann, J.C.; Washa, G.W. Horizontal Shear Connections Between Precast Beams and Cast-in-place Slabs. ACI J. 1964, 61, 1383–1408. [Google Scholar]
- Loov, R.E.; Patnaik, A.K. Horizontal Shear Strength of Composite Concrete Beams with a Rough Interface. PCI J. 1994, 39, 48–69. [Google Scholar] [CrossRef]
- Patnaik, A.H. Behavior of Composite Concrete Beams with Smooth Interface, American Society of Civil Engineers. J. Struct. Eng. 2001, 127, 359–366. [Google Scholar] [CrossRef]
- Kahn, L.F.; Slapkus, A. Interface Shear in High Strength Composite T-beams. PCI J. 2004, 49, 102–110. [Google Scholar] [CrossRef]
- Gohnert, M. Horizontal Shear Transfer Across a Roughened Surface. Cem. Concr. Compos. 2003, 25, 379–385. [Google Scholar] [CrossRef]
- Mattock, A.H.; Hawkins, N.M. Shear Transfer in Reinforced Concrete-Recent Research. PCI J. 1972, 17, 55–75. [Google Scholar] [CrossRef]
- Mattock, A.H. Shear Transfer under Monotonic Loading, across an Interface between Concretes Cast at Different Times; Report SM; University of Washington: Seattle, WA, USA, 1976; p. 62. [Google Scholar]
- Walraven, J.C.; Reinhardt, H.W. Theory and Experiments on the Mechanical Behaviour of Cracks in Plain and Reinforced Concrete Subjected to Shear Loading. Heron 1981, 26, 68. [Google Scholar]
- Hofbeck, J.A.; Ibrahim, I.O.; Mattock, A.H. Shear Transfer in Reinforced Concrete. ACI J. 1969, 66, 119–128. [Google Scholar]
- Kahn, L.F.; Mitchell, A.D. Shear Friction Tests with High-Strength Concrete. ACI J. 2002, 99, 98–103. [Google Scholar]
- Mansur, M.A.; Vinayagam, T.; Tan, K.H. Shear Transfer Across a Crack in Reinforced High-Strength Concrete. J. Mater. Civ. Eng. 2008, 20, 294–302. [Google Scholar] [CrossRef]
- Zeno, G.A. Use of High-Strength Steel Reinforcement in Shear Friction Application; University of Pittsburgh: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Scott, J. Interface Shear Strength in Lightweight Concrete Bridge Girders; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2010. [Google Scholar]
- Harries, K.A.; Zeno, G.; Shahrooz, B. Toward an Improved Understanding of Shear-Friction Behavior. ACI J. 2012, 109, 835–844. [Google Scholar]
- Soltani, M.; Ross, B.E. Database Evaluation of Interface Shear Transfer in Reinforced Concrete Members. ACI J. 2017, 114, 383–394. [Google Scholar] [CrossRef]
- Shaw, D.M.; Sneed, L.H. Interface Shear Transfer of Lightweight-Aggregate Concretes Cast at Different Times. PCI J. 2014, 59, 130–144. [Google Scholar] [CrossRef]
- Mattock, A.H.; Li, W.K.; Wang, T.C. Shear Transfer in Lightweight Reinforced Concrete. PCI J. 1976, 21, 20–39. [Google Scholar] [CrossRef]
- Jiang, H.B.; Fang, Z.C.; Liu, A.R.; Li, Y.H.; Feng, J.H. Interface Shear Behavior Between High-strength Precast Girders and Lightweight Cast-in-place Slabs. Constr. Build. Mater. 2016, 128, 449–460. [Google Scholar] [CrossRef]
- Banta, T.E. Horizontal Shear Transfer Between Ultra High Performance Concrete and Lightweight Concrete. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2005; p. 138. [Google Scholar]
- Hoff, G.C. High Strength Lightweight Aggregate Concrete for Arctic Applications—Part 3: Structural Parameters, Structural Lightweight Aggregate Concrete Performance; SP-136; ACI: Farmington Hills, MI, USA, 1993; pp. 175–246. [Google Scholar]
- Moon, J.H.; Oh, Y.H. Development and Structural Performance Evaluation of Connection Details for the MRS System. Res. Rep. 2008, 337. (In Korean) [Google Scholar]
- Moon, J.H.; Oh, Y.H. Evaluation of Design Method and Shear Transfer Capacity on the Horizontal Interface of PC Composite Beams. J. Korea Concr. Inst. 2013, 25, 81–90. (In Korean) [Google Scholar] [CrossRef]
- Oh, Y.H.; Moon, J.H.; Kim, Y.N. Shear Friction Performance on the Horizontal Interface for PC Composite Beams Subjected to Negative Moment. J. Korea Concr. Inst. 2021, 33, 15–166. (In Korean) [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318–19); ACI: Farmington Hills, MI, USA, 2019. [Google Scholar]
- PCI Industry Handbook Committee. PCI Design Handbook, 8th ed.; Precast/Prestressed Concrete Institute: Chicago, IL, USA, 2017; p. 884. [Google Scholar]
- AASHTO. LRFD Bridge Design Specifications, 4th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2007; p. 1526. ISBN 1-56051-354-3. [Google Scholar]
- Walraven, J.; Frenay, J.; Pruijssers, A. Influence of Concrete Strength and Load History on the Shear Friction Capacity of Concrete Members. PCI J. 1987, 32, 66–84. [Google Scholar] [CrossRef]
- Fédération Internationale du Béton. Model Code for Concrete Structures (MC-2010); Fédération Internationale du Béton: Lausanne, Switzerland, 2010. [Google Scholar]
- Randl, N. Investigations on Transfer of Forces between Old and New Concrete at Different Joint Roughness. Ph.D. Thesis, University of Innsbruck, Innsbruck, Austria, 1997. (In German). [Google Scholar]
- Randl, N. Design Recommendations for Interface Shear Transfer in fib Model Code 2010. Struct. Concr. J. 2013, 14, 230–241. [Google Scholar] [CrossRef]
- Santos, P.M.D.; Julio, E.N.B.S. Factors Affecting Bond between New and Old Concrete. ACI Mater. J. 2011, 108, 449–456. [Google Scholar]
- Randl, N.; Wicke, M. Schubübertragung Zwischen Alt-und Neubeton. Experimentelle Untersuchungen, Theoretischer Hintergrund Und Bemessungsansatz. Beton-und Stahlbetonbau 2000, 95, 461–473. [Google Scholar] [CrossRef]
- Ahmad, S.; Bhargava, P.; Chourasia, A. Shear Transfer Strength of Uncracked Interfaces: A Simple Analytical Model. Constr. Build. Mater. 2018, 192, 366–380. [Google Scholar] [CrossRef]
- Halicka, A. Influence New-to-Old Concrete Interface Qualities on the Behaviour of Support Zones of Composite Concrete Beams. Constr. Build. Mater. 2011, 25, 4072–4078. [Google Scholar] [CrossRef]
- Jabłoński, Ł.; Halicka, A. Influence of the Interface Reinforcement on Static Performance of Concrete Composite T-Shaped Beams. Bud. Archit. 2020, 19, 63–76. [Google Scholar] [CrossRef]
- Júlio, E.N.B.S.; Dias-da-Costa, D.; Branco, F.A.B.; Alfaiate, J.M.V. Accuracy of Design Code Expressions for Estimating Longitudinal Shear Strength of Strengthening Concrete Overlays. Eng. Struct. 2010, 32, 2387–2393. [Google Scholar] [CrossRef]
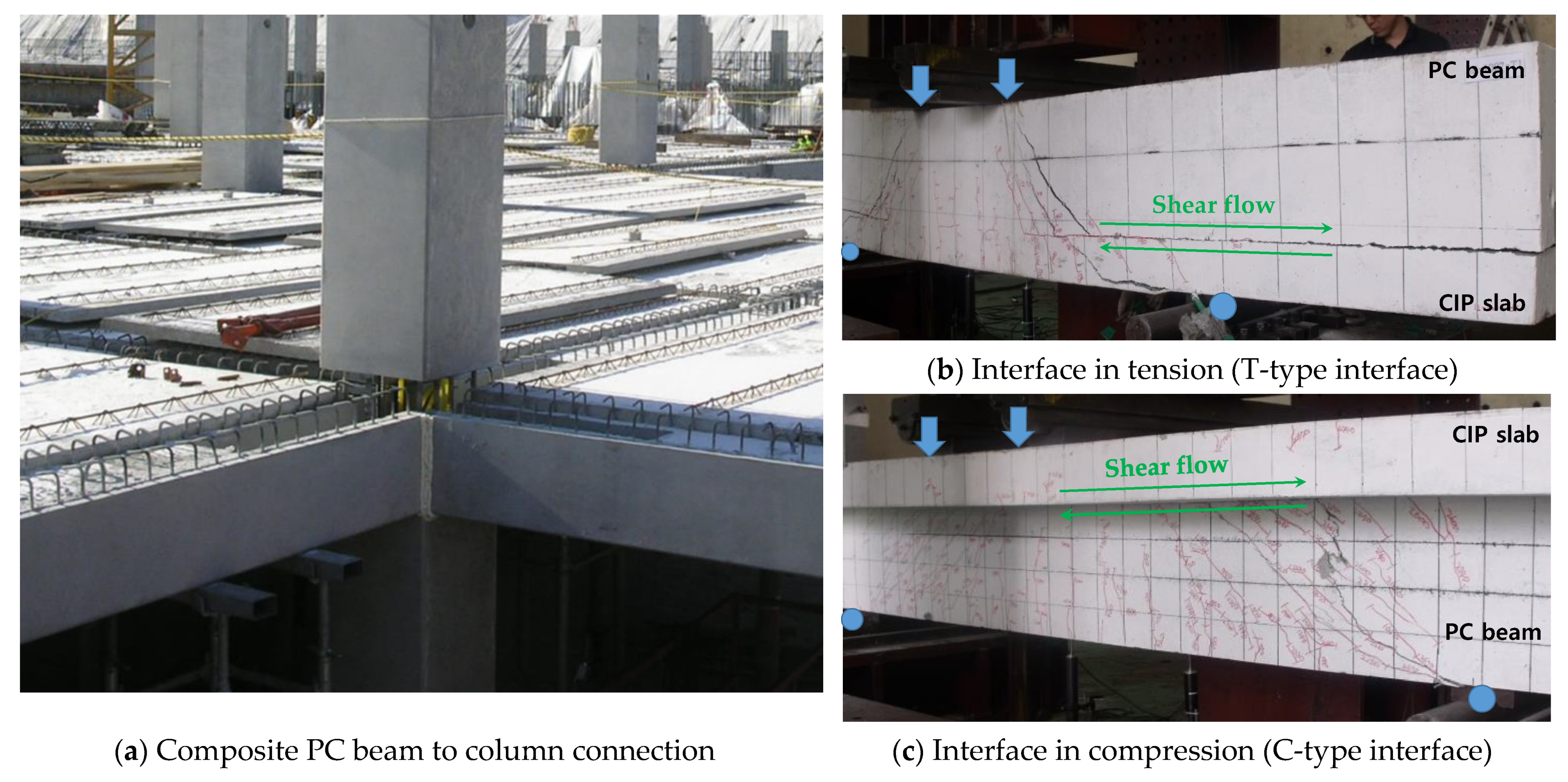




| Stage | Specimen | Interface | d (mm) | f′c (MPa) | Tensile Rebar | Shear Reinforcement | Nominal Strength | Pmax (kN) | Fh (=Max/0.9d) (kN) | vh (MPa) | Failure Mode | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Location | Surface | Width (mm) | PC | CIP | Rebar | fy (MPa) | Rebar | ρv | fy (MPa) | 2Vn (kN) | 2Mn/a (kN) | |||||||
| Phase 1 study [24] | ITB-ST | T-type | medium | 380 | 580 | 43.2 | 33.9 | 10-D22 | 541 | 2-D13@150 | 0.0089 | 568 | 2888 | 1998 | 2170 | 2411 | 5.55 | Flexural Comp. |
| ITB-A1 | medium | 380 | 620 | 43.9 | 33.7 | 14-D22 | 541 | 2-D10@100 | 0.0075 | 510 | 2528 | 2528 | 1949 | 2288 | 4.60 | Interface shear | ||
| ITB-A2 | medium | 500 | 840 | 46.0 | 35.2 | 16-D25 | 543 | D16@100 +D13@100 | 0.013 | 428 519 | 6052 | 3568 | 2374 | 3140 | 3.14 | Interface shear | ||
| Phase 2 study [25] | SF-1027 | T-type | medium | 400 | 520 | 48.5 | 34.5 | 12-D25 | 543 | 9-D16@120 (double) | 0.0171 | 428 | 3435 | 2642 | 1770 | 1986 | 4.55 | Interface shear |
| SF-685-A | medium | 56.6 | 32.5 | 11-D25 | 543 | 6-D16@180 (double) | 0.0114 | 428 | 2490 | 2546 | 1912 | 2145 | 5.11 | Interface shear | ||||
| SF-685-B | medium | 56.6 | 32.5 | 1719 | 1928 | 4.59 | Interface shear | |||||||||||
| SF-291-A | medium | 46.1 | 33.7 | 7-D25 | 543 | 4-D13@200 (double) | 0.0048 | 519 | 1793 | 1757 | 1744 | 1884 | 4.49 | Interface shear | ||||
| SF-291-B | rough | 44.3 | 57.9 | 1784 | 1747 | 1867 | 2017 | 4.81 | Flexural Comp. | |||||||||
| SF-291-C | Keyed | 49.7 | 46.9 | 1812 | 1773 | 1584 | 1711 | 4.08 | Interface shear | |||||||||
| Phase 3 study [26] | SF-6.82-T1 | T-type | rough | 400 | 520 | 31.2 | 27.7 | 12-D25 | 548 | 9-D16@120 (double) | 0.0171 | 503 | 3857 | 2304 | 1612 | 1808 | 4.30 | Interface shear |
| SF-6.82-T2 | rough | 1465 | 1644 | 3.91 | Interface shear | |||||||||||||
| SF-4.55-T1 | rough | 11-D25 | 548 | 6-D16@180 (double) | 0.0114 | 503 | 2701 | 2189 | 1537 | 1724 | 4.10 | Interface shear | ||||||
| SF-4.55-T2 | rough | 1304 | 1463 | 3.48 | Interface shear | |||||||||||||
| SF-6.82-C1 | C-type | rough | 400 | 520 | 36.2 | 22.4 | 12-D25 | 548 | 9-D16@120 (double) | 0.0171 | 503 | 4080 | 2746 | 3412 | 3828 | 9.11 | Flexural Comp. | |
| SF-6.82-C2 | rough | 3191 | 3580 | 8.52 | Flexural Comp. | |||||||||||||
| SF-4.55-C1 | rough | 11-D25 | 548 | 6-D16@180 (double) | 0.0114 | 503 | 2923 | 2560 | 2745 | 3079 | 7.33 | Flexural Comp. | ||||||
| SF-4.55-C2 | rough | 2861 | 3209 | 7.64 | Flexural Comp. | |||||||||||||
| Code | Horizontal Shear Strength | Parameter | Interface Roughness | Limitations | |
|---|---|---|---|---|---|
| Smooth | Rough | ||||
| ACI 318 [27] | c (MPa) | 0.56 | 1.8 | or rough surface | |
| - | 0.6 | ||||
| 0.6 | 1.0 | ||||
| 0.2 | 0.2 | ||||
| (MPa) | 5.5 | ||||
| AASHTO LRFD [29] | c (MPa) | 0.52 | 1.65 | ||
| 0.6 | 1.0 | ||||
| 0.2 | 0.25 | ||||
| (MPa) | 5.52 | 10.34 | |||
| PCI [28] | 0.2 | 0.25 | |||
| (MPa) | 5.5 | 6.9 | |||
| MC 2010 [30] | 0 | 0.1 | |||
| 0.6 | 0.7 | ||||
| 0.5 | 0.5 | ||||
| 1.1 | 0.9 | ||||
| 6.19 | 10.46 | ||||
| Investigator | Quantity | Interface | (mm2) | for Weaker (MPa) | (MPa) |
|---|---|---|---|---|---|
| Hofbeck et al. [12] | 12 | Uncracked | 32,300 | 26~31 | 1.5~9.2 |
| Mattock et al. [20] | 6 | Uncracked | 32,300 | 27~29 | 1.5~9.6 |
| Hofbeck et al. [12] | 19 | Pre-cracked | 32,300 | 16~30 | 1.5~9.2 |
| Mattock et al. [20] | 6 | Pre-cracked | 32,300 | 27~29 | 1.5~9.1 |
| Kahn and Mitchell [13] | 4 | Rough | 92,920 | 65~71 | 0.4~1.7 |
| Shaw and Sneed [19] | 6 | Rough | 31,930 | 34~52 | 6.4 |
| Harries et al. [17] | 4 | Rough | 103,460~106,420 | 40 | 2.0~3.1 |
| Scott [16] | 3 | Rough | 247,740 | 40 | 2.3 |
| Zeno [15] | 4 | Rough | 103,480~106,450 | 40 | 1.9~3.1 |
| Mansur et al. [14] | 18 | Smooth | 35,930 | 40~106 | 1.8~9.3 |
| Shaw and Sneed [19] | 3 | Smooth | 31,930 | 52 | 6.4 |
| Investigator | Quantity | Interface | (mm2) | for Weaker (MPa) | (MPa) | |
|---|---|---|---|---|---|---|
| Location | Surface | |||||
| Saemann and Washa [4] | 32 | C-type | Smooth Intermediated Rough Keyed | 81,290 ~121,935 | 17~34 | 0.2~3.2 |
| Loov and Patnaik [5] | 16 | C-type | Rough | 89,832 ~359,328 | 20~48 | 0.4~7.7 |
| Kahn and Slapkus [7] | 6 | C-type | Rough | 152,903 | 50~78 | 1.0~2.1 |
| Patnaik [6] | 24 | C-type | Smooth | 90,000 ~225,000 | 17~35 | 0.3~3.6 |
| Moon and Oh [24] | 3 | T-type | Intermediated | 440,800 ~1,000,000 | 33 | 3.8~6.0 |
| Moon and Oh [25] | 6 | T-type | Intermediated Rough Keyed | 420,000 | 33~47 | 2.1~7.3 |
| Oh et al. [26] | 8 | T-type C-type | Rough | 420,000 | 22~28 | 5.7~8.6 |
| Interface | Statistics | Experimental-to-Nominal Shear Strength Ratio | |||
|---|---|---|---|---|---|
| ACI | PCI | AASHTO | MC 2010 | ||
| Total specimens | Average | 1.88 | 1.38 | 1.49 | 1.80 |
| Maximum | 5.71 | 2.57 | 3.82 | 3.59 | |
| Minimum | 1.11 | 0.89 | 0.90 | 1.06 | |
| STD | 0.83 | 0.34 | 0.67 | 0.46 | |
| COV (%) | 43.9 | 24.3 | 45.1 | 25.6 | |
| Uncracked interface | Average | 1.65 | 1.30 | 1.18 | 1.47 |
| Maximum | 2.17 | 1.55 | 1.40 | 1.86 | |
| Minimum | 1.36 | 1.13 | 0.98 | 1.19 | |
| STD | 0.21 | 0.12 | 0.13 | 0.19 | |
| COV (%) | 12.4 | 9.0 | 11.2 | 13.1 | |
| Pre-cracked interface | Average | 1.51 | 1.22 | 1.18 | 1.79 |
| Maximum | 1.94 | 1.55 | 1.55 | 2.55 | |
| Minimum | 1.16 | 0.97 | 0.92 | 1.26 | |
| STD | 0.20 | 0.16 | 0.17 | 0.35 | |
| COV (%) | 13.6 | 13.1 | 14.2 | 19.6 | |
| Rough interface | Average | 1.46 | 1.26 | 1.19 | 1.56 |
| Maximum | 2.24 | 1.84 | 1.88 | 1.92 | |
| Minimum | 1.11 | 0.89 | 0.90 | 1.06 | |
| STD | 0.28 | 0.28 | 0.28 | 0.20 | |
| COV (%) | 19.3 | 22.0 | 23.9 | 12.8 | |
| Smooth interface | Average | 2.95 | 1.76 | 2.44 | 2.35 |
| Maximum | 5.71 | 2.57 | 3.82 | 3.59 | |
| Minimum | 1.15 | 1.12 | 0.92 | 1.72 | |
| STD | 1.05 | 0.38 | 0.72 | 0.44 | |
| COV (%) | 35.6 | 21.8 | 29.6 | 18.9 | |
| Interface | Statistics | Experimental-to-Nominal Shear Strength Ratio | |||
|---|---|---|---|---|---|
| ACI | PCI | AASHTO | MC 2010 | ||
| All beam specimens | Average | 2.30 | 1.54 | 1.77 | 3.42 |
| Maximum | 7.15 | 3.91 | 5.24 | 16.64 | |
| Minimum | 0.53 | 0.49 | 0.41 | 0.67 | |
| STD | 0.19 | 0.72 | 0.82 | 2.80 | |
| COV (%) | 52.0 | 46.6 | 46.3 | 81.8 | |
| Case 1: Horizontal shear transfer ( < 3.5 MPa) | Average | 1.90 | 1.87 | 1.71 | 2.85 |
| Maximum | 2.98 | 3.91 | 2.96 | 6.19 | |
| Minimum | 0.84 | 0.81 | 0.78 | 1.40 | |
| STD | 0.56 | 0.80 | 0.59 | 1.26 | |
| COV (%) | 29.4 | 42.7 | 34.7 | 44.2 | |
| Case 2: Shear friction ( > 3.5 MPa) | Average | 1.22 | 1.02 | 0.93 | 1.35 |
| Maximum | 2.03 | 1.63 | 1.63 | 1.99 | |
| Minimum | 0.53 | 0.49 | 0.41 | 0.67 | |
| STD | 0.48 | 0.39 | 0.38 | 0.47 | |
| COV (%) | 39.4 | 37.9 | 40.7 | 34.8 | |
| Interface with smooth surface | Average | 4.86 | 1.38 | 2.32 | 5.31 |
| Maximum | 16.38 | 3.08 | 5.24 | 16.64 | |
| Minimum | 2.09 | 0.82 | 1.43 | 2.38 | |
| STD | 3.43 | 0.50 | 0.85 | 3.77 | |
| COV (%) | 70.5 | 36.1 | 36.4 | 71.0 | |
| Interface | Statistics | Experimental-to-Nominal Shear Strength Ratio | |||
|---|---|---|---|---|---|
| ACI | PCI | AASHTO | MC 2010 | ||
| T-type with rough surface | Average | 0.99 | 0.81 | 0.77 | 1.15 |
| Maximum | 1.58 | 1.27 | 1.29 | 1.89 | |
| Minimum | 0.53 | 0.49 | 0.41 | 0.67 | |
| STD | 0.34 | 0.25 | 0.28 | 0.40 | |
| COV (%) | 34.0 | 31.1 | 36.5 | 34.6 | |
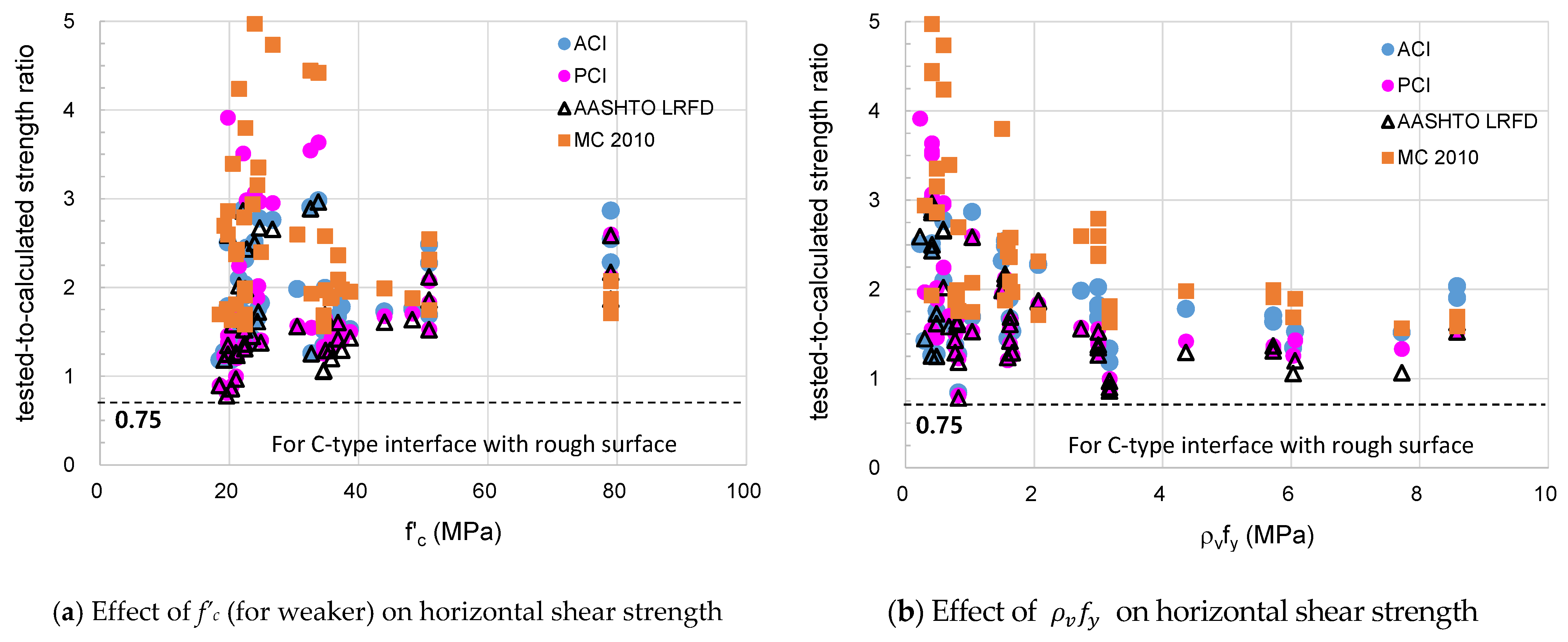
| C-type with rough surface | Average | 1.89 | 1.84 | 1.67 | 2.75 |
| Maximum | 2.98 | 3.91 | 2.96 | 6.19 | |
| Minimum | 0.84 | 0.81 | 0.78 | 1.56 | |
| STD | 0.53 | 0.76 | 0.57 | 1.23 | |
| COV (%) | 28.1 | 41.4 | 34.3 | 44.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, Y.-H.; Moon, J.-H. Evaluation of Design Provisions for Horizontal Shear Strength in Composite Precast Concrete Beams with Different Interface Conditions. Appl. Sci. 2021, 11, 4246. https://doi.org/10.3390/app11094246
Oh Y-H, Moon J-H. Evaluation of Design Provisions for Horizontal Shear Strength in Composite Precast Concrete Beams with Different Interface Conditions. Applied Sciences. 2021; 11(9):4246. https://doi.org/10.3390/app11094246
Chicago/Turabian StyleOh, Young-Hun, and Jeong-Ho Moon. 2021. "Evaluation of Design Provisions for Horizontal Shear Strength in Composite Precast Concrete Beams with Different Interface Conditions" Applied Sciences 11, no. 9: 4246. https://doi.org/10.3390/app11094246
APA StyleOh, Y.-H., & Moon, J.-H. (2021). Evaluation of Design Provisions for Horizontal Shear Strength in Composite Precast Concrete Beams with Different Interface Conditions. Applied Sciences, 11(9), 4246. https://doi.org/10.3390/app11094246






