Abstract
Knowledge bases (KBs) have become an integral element in digitalization strategies for intelligent engineering and manufacturing. Existing KBs consist of entities and relations and deal with issues of newly added knowledge and completeness. To predict missing information, we introduce an expressive multi-layer network link prediction framework—namely, the convolutional adaptive network (CANet)—which facilitates adaptive feature recalibration by networks to improve the method’s representational power. In CANet, each entity and relation is encoded into a low-dimensional continuous embedding space, and an interaction operation is adopted to generate multiple specific embeddings. These embeddings are concatenated into input matrices, and an attention mechanism is integrated into the convolutional operation. Finally, we use a score function to measure the likelihood of candidate information and a cross-entropy loss function to speed up computation by reducing the convolution operations. Using five real-world KBs, the experimental results indicate that the proposed method achieves state-of-the-art performance.
1. Introduction
Recently, knowledge bases (KBs) have become a key component in a variety of applications, including recommendation systems [1,2], engineering technologies [3,4], and intelligent conversation robots [5,6]. To help produce new information for these knowledge-driven applications, researchers have generated a variety of KBs [7,8,9] in the last several decades. KBs are intelligible domain engines that save the structural knowledge of human understanding. Furthermore, they easily integrate various data sources and give a structured semantic representation for computer analysis and knowledge inference.
KBs are multi-relational graphs that depict a large amount of concrete information. Different entities are represented by nodes, and the relations between entities are connected by edges, as seen in Figure 1. All components are grouped in the form of triplets, such as (head entity, relation, tail entity). For example, we know that Mercedes Benz is located in Germany, which can be represented as (Mercedes Benz, Located_in, Germany). Although many KBs now comprise billions of relations, entities, and triplets, they also have to deal with incompleteness and newly acquired real-world information.
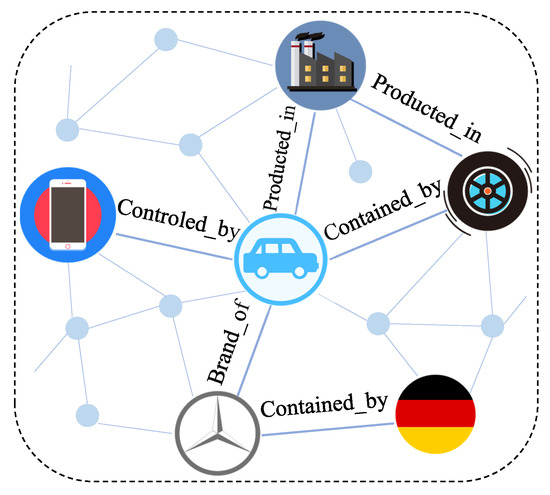
Figure 1.
Illustration of a knowledge base.
To address the above concerns, studies have focused on link prediction, which attempts to forecast missing facts in knowledge bases. Knowledge graph embedding (KGE) [10] is a term used to describe existing link prediction methods. KGE is used to figure out how to represent relations and entities in their embedding representations. Previously, the embedding representation of a relation was mainly seen as a translational distance or semantic matching between entities. They are simple and feasible, and they have been demonstrated to be successful in the field of prediction tasks. However, compared to deep and multi-layer architectures, they learn fewer expressive features, which theoretically restricts their performance.
A typical means of increasing the features and expressiveness of existing methods is that of increasing the embedding size. Thus, the total embedding parameters are proportional to the number of relations and entities. This approach does not scale to large KBs. To increase the method’s expressiveness independently of the embedding size, recent studies have proposed several multi-layer methods [11,12,13] and reported commendable results on established datasets. Having adopted fully connected feature layers, these methods are prone to overfitting. One way to address the scaling and overfitting problems is to use parameter-efficient and fast operators that can be integrated into deep networks.
Convolutional neural networks (CNNs) have grown into a powerful technique among the many available technologies due to their significant performance in speech recognition, computer vision, and natural language processing. Based on the CNN algorithm, artificial intelligence has made significant breakthroughs in many fields [14,15]. The convolution operator is an effective parameter and can achieve rapid computing with highly optimized GPU implementations. Moreover, with the extensive usage of multiple robust methodologies, over-fitting control is efficient in the training of convolutional networks.
To provide a highly articulate link prediction system that effectively converges the advantages of CNNs, this paper proposes a convolutional adaptive network (CANet) method for KGE. First, all entities and relations are embedded into real-valued low-dimensional vectors, and an interaction operation is suggested to convert the initialized embeddings of the head entity and relation into multiple triplet-specific embeddings. Then, the specific embeddings of the head entity and relation are concatenated into 2D input matrices. In the convolution layer, CANet learns features that are different between the input matrices and allows the network to perform feature recalibrations. Finally, the feature map tensors are linearized and converted into the entity embedding space, and an inner product is calculated with the tail entity embedding to evaluate the correct triplet.
The following are the contributions of this paper:
- A new link prediction method called CANet for learning the embedding representation of KBs is proposed. As a multi-layer network method, CANet takes advantage of the parameter-efficient and fast operators of CNNs, thereby generating additional expressive features and addressing the overfitting problem for large KBs.
- An interaction operation is adopted to generate multiple triplet-specific embeddings for relations and entities. Thus, for various triplet predictions, the operation can simulate the selection of different information. Furthermore, multiple interaction embeddings provide rich representations and generalization capabilities.
- To increase the representational capacity of CANet, an attention function is inserted into the convolutional operation. This functionality enables the network to achieve recalibration features adaptively. By learning to use global content, CANet can selectively accentuate features while suppressing pointless ones.
- To test the efficiency of our proposed approach, five real-world datasets were used in our experiments. In comparison to several previous approaches, the results show that CANet achieves state-of-the-art efficiency for general assessment metrics.
The following is how the remainder of the article is structured: In Section 2, we checked and discussed the related works. In Section 3, we defined the research problem systematically, and the CANet is described in detail. The experimental setup and results of the proposed method are detailed in Section 4 and Section 5. Finally, the conclusions and suggestions for future research are presented in Section 6.
2. Related Works
The use of KGE methods to predict incomplete or incorrect triplets in KBs has been extensively studied in recent years. KGE aims to convert relation and entity semantics into continuous low-dimensional embedding spaces. These embeddings are then used to predict links. The previous approaches can be categorized as follows: translational distance methods and semantic matching methods. Over the last several years, there some multi-layer network methods have been proposed, and they achieved impressive link prediction performance.
2.1. Translational Distance Methods
The TransE [16] method is the most well-known translational distance method. For a given triplet (head entity, relation, tail entity), denoted as (h, r, t), TransE regards the relation as a translation from the head entity to the tail entity and assumes that h + r ≈ t, provided that the triplet is correct. The embedding representation is denoted by the bold letters h, r, and t, respectively. Simply and quickly, TransE achieves outstanding performance for link prediction in comparison with previous methods. However, the method has issues when modeling complex relations, including the N–1, 1–N, and N–N relations.
To address this issue, other strategies have been designed to split entities and relations into separate subspaces. For example, TransH [17] posits that entities should exhibit various characteristics in contrast to one another, and it projects the head and tail entities onto a hyperplane that is connected to the relation. Furthermore, TransR [18] considers that the embeddings of relations and entities should be in respective spaces. It projects the entity into the relation space by generating a projection matrix associated with each relation. TransD [19] further learns two projecting matrices to respectively project. Moreover, these matrices are initialized diagonally to reduce the method parameters. TorusE [20] embeds KB relations and entities in a lie group. The method points out that regularization is unnecessary during the training process if the embedding space is in a compact lie group. However, the results on several datasets showed that translational distance methods have weak improvements in terms of modeling complex relations. Furthermore, these methods only learn less expressive features, thus potentially limiting their performance.
2.2. Semantic Matching Methods
By matching the latent semantics, semantic matching methods calculate the likelihood of a triplet. The typical method, DistMult [21], uses a bilinear objective to learn embeddings. It has a bilinear product between the embeddings of a subject, a tail entity, and a diagonal matrix for relations, where and . DistMult is a parameter-efficient method that eliminates redundant operations. However, two triplets of (h, r, t) and (t, r, h) achieve the same product results.
To address this issue, by taking the conjugate of the tail entity’s embedding, ComplEx [22] applies DistMult to complex space and processes asymmetric relations. HolE [23] generates expressive and robust compositional representations by using circular correlations of embeddings. In ANALOGY [24], the analogical properties of relations and entities are further exploited, requiring that linear maps of relations be natural and mutually commutative. However, semantic matching methods have more redundancies compared with translational distance methods. Hence, the former is sensitive to overfitting, which becomes a challenge when KBs have a large number of relations and entities. As a result, a high-dimensional space is needed to completely embed and separate these entities and relations.
2.3. Multi-Layer Network Methods
The usage of a multi-layer network for link prediction has attracted increasing attention in recent studies. ProjE [11] uses brief but effectively shared variable networks to predict entities. Instead of measuring the distance between the components of the input triplet, ProjE projects candidate entities onto a target vector to represent the input data and order the vector value in descending order. R-GCN [12], which can be considered an autoencoder, was proposed for working with highly multi-relational data. The encoder generates latent function representations of relations and entities. To anticipate the named entities, the decoder component uses these representations. The graph convolutional network structure, on the other hand, is restricted to undirected graphs, whereas KBs are inherently oriented. Therefore, by combining the recurrent neural network with residual learning, RSNs [25] can effectively catch long-term relational dependencies within and between KBs. They bridge the gaps between entities by using a skipping mechanism. The experimental results provide some strong evidence that these multi-layer network methods learn more features compared with previous methods and can effectively enhance these methods’ performance.
The convolutional neural network, which is commonly used in computer vision and has the advantages of parameter-efficient and fast operators, can be integrated into deep networks. We present a highly efficient CNN-based approach for relation prediction in KBs in this paper. As a result, we can catch a wide range of possible attributes of entities and relations. When compared to shallow architectures, the proposed approach will greatly boost performance by requiring only a small increase in computing resources.
3. Proposed Method
The majority of the notations and definitions in this paper are presented first, followed by an explanation of the link prediction task. After that, a detailed explanation of the proposed method is given. Finally, the method for training and optimization is discussed.
3.1. Problem Formulation
Formally, the knowledge base can be expressed as
where and denote the set of entities and relations. The numbers of relations and entities are denoted by and , respectively. denotes the set of triplets, and a triplet can be expressed as (h, r, t). The bold symbols represent the d-dimensional vectors of h, r, t. and denote the matrices of relations and entities.
The goal of link prediction is to forecast another entity based on one that has a specific relation; for example, using a head entity and relation (h, r) to predict a tail entity t. A general method for defining a score function for the triplet is used to achieve this purpose. Most optimizations are intended to make a correct triplet outperform false triplets.
3.2. Outline of CANet
As shown in Figure 2, the CANet is a multi-layer convolutional network consisting of embedding combination, encoding, and scoring components. The vector of the embeddings of h and r is extracted by the encoding component. The score function ranks the feature vector and embedding of t in the scoring part. A summary of the details is given in the following.
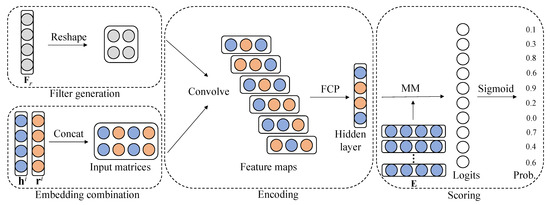
Figure 2.
Illustration of the proposed CANet link prediction model.
Look Up: We must first define the general embeddings of an input triplet (h, r, t) in the matrices of relations R and entities E. Such embeddings can be expressed in the following way:
where , , and are the one-hot index vectors of h, r, and t.
Interaction and Concatenation: To generate multiple triplet-specific embeddings for each relation and entity, we present an interaction embedding , which is connected to the relation. An interaction operation is defined to simulate the interaction effect of entities and relations as follows:
where ∘ is the element-by-element operator. We call and the interaction embeddings of h and r. They can provide generalization capabilities and rich representations. Then, the input matrices M can be obtained as
where ⊕ denotes the concatenation operation.
Convolutional Operation: Then, N separate kernels execute a convolution process on the input layer M. The feature maps are generated as follows:
where ⊛ denotes the action of convolution. To hold the translational property, we set the height h of convolutional kernels to 2 in the experiment.
Attention Mechanism: The local receptive field is then used by each kernel . As a result, outside of the local receptive field, each output function map is unable to use contextual information. We can compact the global spatial information into a series of channel descriptors to solve this problem.
To alleviate this problem, we can compress the global spatial information into a set of channel descriptors as follows:
Then, the weights of each channel are learned through the reduction and expansion operation as
where is a sigmoid function, and represents the rectified linear units [26]. and are the weights of dimensionality increase and reduction, respectively. The is the proportion of the dimension reduction.
Lastly, the remapping of feature maps with channel interdependence can be identified as
The design of the attention mechanism is suggested as a solution to the issue of channel interdependence. It adaptively recalibrates the channel dimension characteristic reaction by specifically modeling channel interdependence and enhancing the network capacity.
Projection and Matrix Multiplication: Then, by flattening and translating the corresponding remapping feature maps into a d-dimensional space, the matrix is allowed to establish the hidden layer. The tail entity embeddings t are multiplied with hidden layer vectors, and the CANet score function can be written as follows:
where vec(x) denotes the flattening operation.
Sigmoid: The plausibility of the triplet (h, r, t) can be written as follows:
where describes a mathematically interpretable prediction of whether the triplet (h, r, t) is valid or not, and b is the bias term. The scoring procedure in our method uses the 1–N scoring strategy to reduce the convolution operations and accelerate the computation. Unlike the 1–1 scoring, the pair (h, r) is scored with respect to all tail entities simultaneously. In addition to the 1–1 scoring, the 1–N scoring allows for a substantial reduction in preparation and training time while still improving accuracy.
3.3. Training Objective
The observed knowledge base and all parameters in CANet were required to optimize the probability function in the following way:
where all parameters in our method are represented by . If the triplet (h, r, t) in is right, we expect it to have a score of 1; otherwise, it will have a score of 0. Then, the Bernoulli distribution is used to describe the probability function:
in which
where is a collection of false triplets collected by disrupting the correct triplet set . Given Equations (11)–(13), the loss function of CANet can be written as follows:
We utilize the dropout [27] technique on many stages to regularize the process, such as the input matrices and the hidden layer. After each layer, the batch normalization [28] technique can be used to stabilize and improve the convergence rate. Furthermore, we adopt the label smoothing [29] technique to improve the generalization and reduce overfitting. Finally, the loss function is optimized by the Adam optimizer [30], which is a computationally effective technique for gradient-based optimization.
4. Experimental Setup
4.1. Evaluation Metrics
The test set can be denoted by . For the i-th test triplet , we created a potentially incorrect (or ) by changing the head (or tail) entity with any other entity. The method was then evaluated to see if it gave a top score to correct triplets and a poor value to incorrect triplets. According to the core function of our method, the left and right ranks of the i-th test triplet were identified with corrupting head or tail entities and denoted as:
where P[x] is just a predictor function that returns to 1 if the hypothesis x is valid and 0 if it is not. To evaluate the prediction performance, two general rating metrics were used. These were MRR and Hits@k, which are described as follows:
where Hits@k is the number of ranks that are smaller than or equal to k, and MRR is the mean reciprocal rank of all test triplets. In all examples, a high MRR or Hits@k provides superior performance.
4.2. Datasets
The extensive evaluation was carried out on the FB15k, FB15k-237, WN18, WN18RR, and YAGO3-10 KB datasets. All of them contain a large number of entities and relations and are composed of training, validation, and test sets. Table 1 shows the details of all of the datasets.

Table 1.
Real-world KB datasets.
- FB15k: FB15k [16] is a large-scale knowledge base containing massive amounts of knowledge and facts; it is a subset of Freebase [7]. It comprises approximately 1345 relations and 14,951 entities. FB15k describes information about awards, athletics, movies, stars, and sports teams, among other things, as part of a broad knowledge base about the human world.
- FB15k-237: FB15k-237 [13] is a subset of FB15k. Due to the inverse relations, it can observe that almost all of the test triplets in FB15k can be predicted easily. Thus, the FB15k-237 dataset was created so that the inverse relations were deleted. There are 14,541 entities in all, with 237 various relations between them.
- WN18: WN18 [16] is a knowledge base featuring lexical relations between words, and it is a subset of WordNet [8]. This dataset also contains massive numbers of inverse relations. There are 18 relations and 40,943 entities in this dataset. Its relations define lexical relationships between entities, while the entities define word senses.
- WN18RR: Similarly to the FB15K-237 dataset, WN18RR [16] is a subset of WN18 and was obtained by removing the inverse relations. It has a total of 40,943 entities and 11 different relations.
- YAGO3-10: YAGO3-10 [13] is a subset of YAGO [9]. There are 37 various relations with 123,182 entities. Each entity has a minimum of 10 relations connected to itself. It defines a person’s characteristics, such as their occupation, ethnicity, and citizenship.
4.3. Comparison Methods
We used many baseline approaches from the area of link prediction to verify the efficiency of the proposed method. Translational distance, semantic matching, and multi-layer network approaches are examples of these methods. The following are the descriptions of these methods:
- TransE: TransE [16] is one of the most common link prediction models for knowledge bases. To model multi-relational data, TransE transforms entities and relations into embedding spaces and regards relations as a translation from the head entity to the tail entity.
- DistMult: DistMult [21] is the most commonly used semantic matching model. By comparing latent semantics in the embedding space, DistMult estimates the possibility of a triplet.
- ComplEx: ComplEx [22] is an extension of DistMult. ComplEx embeds entities and symmetric or antisymmetric relations into the complex space instead of real-valued ones.
- R-GCN: R-GCN [12] is an extension of the graph convolutional network. For working with extremely multi-relational data in KBs, R-GCN proposes a generalization method for graph convolutional networks.
- ConvE: ConvE [13] is the typical convolutional neural network-based model. It is a relatively simple multi-layer convolutional framework for link prediction.
- TorusE: TorusE [20] embeds relations and entities on a compact lie group. It follows the TransE and regards relations as a translation. Because of its flexibility, it can handle large KBs.
- CANet: Convolutional adaptive network (CANet) is the method proposed in this paper. The weights of the convolutional kernels are set to be adaptive.
4.4. Experimental Implementation
The hyper-parameters for the CANet in the experiments were chosen by using a grid search throughout training. The following are the hyper-parameter ranges: input matrices and hidden layer dropout rate [0.1, 0.2, 0.3, 0.4, 0.5], learning rate [0.0001, 0.001, 0.005], relation and entity embedding dimension [50, 100, 200], batch size [64, 128, 256], and label smoothing [0.0, 0.1, 0.2, 0.3]. Different kernel sizes [2 × 3, 2 × 5, 2 × 7, 2 × 9] were tested in the experiments.
Both datasets performed well with the following hyper-parameters: relation and entity dimension sizes of 200, batch size of 128, and label smoothing of 0.1. For FB15k-237 and WN18RR, we set the learning rate to 0.0001, the input matrix dropout rate to 0.4, the hidden layer dropout rate to 0.4, and the kernel size to 2 × 7; for FB15k, WN18, and YAGO3-10, we set the learning rate to 0.001, the input matrix dropout rate to 0.2, the hidden layer dropout rate to 0.3, and the kernel size to 2 × 5. We used the program library PyTorch [31] to apply our methods and reproduce DistMult, ComplEx, and ConvE on the PC with an NVIDIA GTX 2070S.
5. Results and Discussion
5.1. Experimental Results
Table 2, Table 3 and Table 4 present the results of the link prediction tasks. The second-best score is underlined and the best score is in bold. We observed the following:

Table 2.
The MRR and Hits@k of the link prediction results on the WN18 and FB15k datasets.

Table 3.
The MRR and Hits@k of the link prediction results on the WN18RR and FB15k-237 datasets.

Table 4.
The MRR and Hits@k of the link prediction results on the YAGO3-10 dataset.
- The proposed methods surpassed the other baseline methods in most instances. For the majority of the metrics, CANet achieved state-of-the-art results. As a result, the proposed methods could produce impressive link prediction results by using the CNN’s parameter-efficient and fast operators. In comparison to the optimal methods on the WN18RR, FB15k-237, and YAGO3-10 datasets, CANet improved the MRR by 4.3%, 5.8%, and 14.5%, respectively. This proved the efficacy and applicability of our method.
- Semantic matching methods are simple to learn and could be used to represent a knowledge base through the training process. However, because of their redundancy, they were highly susceptible to overfitting, resulting in lower performance than that of the proposed approaches.
- Because the former created the weights of convolutional kernels that were relevant to each reference, CANet surpassed ConvE on all metrics. As a result, multiple relations may be used to obtain various feature maps. As a result, CANet is better at identifying the differences between entities.
To summarize, the proposed link prediction method is highly expressive. The proposed method had considerable improvements for all evaluation metrics in KBs because of its structure. It could also improve the efficiency by generating particular convolutional kernel weights to study different properties with the entity embeddings for each relation.
5.2. Influence of Kernel Size
To see how important multi-scale kernel sizes are, we evaluated the effects of different convolutional kernel sizes on the efficiency of our methods. The performance is depicted in Figure 3. The abscissa represents kernel sizes, with 2D sizes that included 2 × 3, 2 × 5, 2 × 7, and 2 × 9. The ordinate refers to the Hits@10 results. With a kernel size of 2 × 7, excellent results were obtained for the FB15k-237 and WN18RR datasets, with decreasing results for smaller and larger kernel sizes. For a kernel size of 2 × 5, excellent results were obtained for the FB15k and WN18 datasets, with decreasing results for smaller and larger kernel sizes. As a result, a reasonable kernel size normally provides adequate results when convolving the input matrices. The number of interactions can be limited by smaller kernel sizes. Larger kernel sizes, on the other hand, can result in overfitting. As a result, the proposed method convolved the entity and relation embeddings to achieve the experimental results shown in this paper. The appropriate kernel sizes used in this paper were 2 × 5 and 2 × 7.
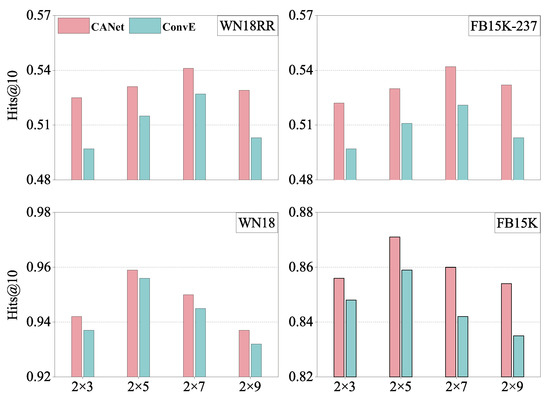
Figure 3.
The Hits@10 performance with various kernel sizes on four datasets.
5.3. Parameter Sensitivity
(1) Label Smoothing: When measuring loss values, overfitting can be avoided by utilizing a method called label smoothing. Accordingly, several comparison experiments on the WN18 and FB15k datasets were extended to reveal the importance of these parameters in the results of CANet. Figure 4 depicts the outcomes. When we set the label smoothing value to 0.1, CANet outperformed both datasets for the Hits@10 results. As a result, label smoothing could increase the efficiency of our method to some degree. Increasing the label smoothing value resulted in underfitting. Thus, it is recommended that the impact of label smoothing should be analyzed on a per-dataset basis.
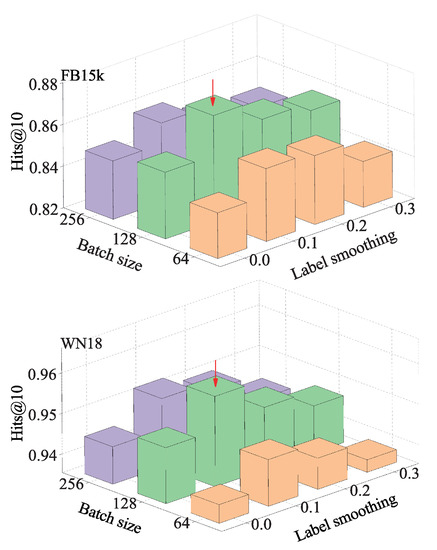
Figure 4.
The Hits@10 performance with various batch sizes and label smoothing on the WN18 and datasets.
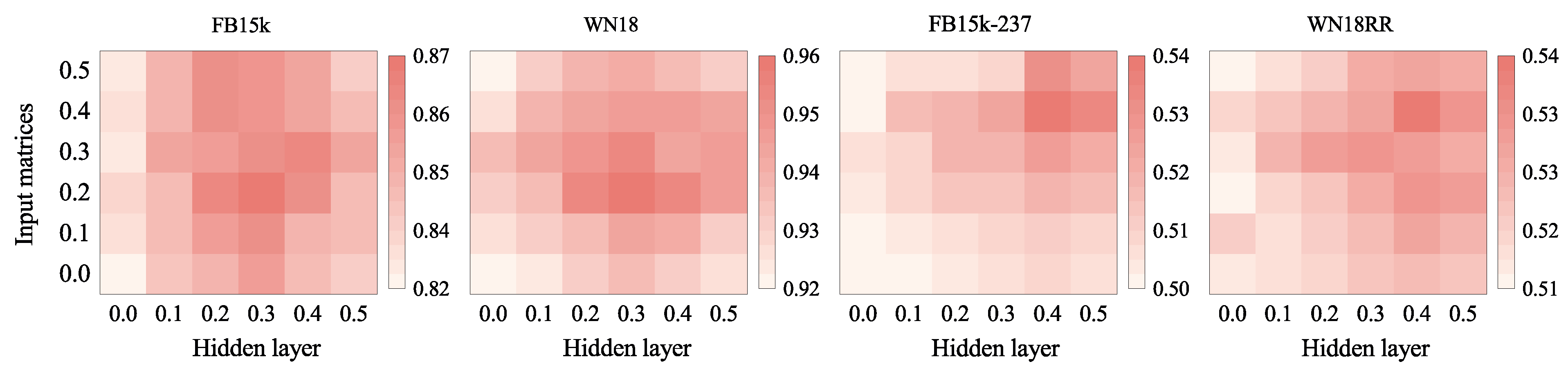
(2) Dropout Rate: To improve the generalization potential of our approaches, we used the dropout strategy. On four datasets, we performed multiple experiments with dropout rates ranging from 0.0 to 0.5 to validate the influence of various dropout rates. The findings of our research are depicted in Figure 5. We focused on how different input matrices and a hidden layer dropout rate affected CANet’s Hits@10 results. The findings show that using the dropout strategy provided better results than those obtained without using it. As a result, the dropout approach has the potential to significantly increase the method’s efficiency. For the FB15k and WN18 datasets, the input matrix dropout rate of 0.2 and hidden layer dropout rate of 0.3 were the highest. However, for the WN18RR and FB15k-237 datasets, the input matrix dropout rate of 0.4 and hidden layer dropout rate of 0.4 were the best. This result could be due to the fact that the first two datasets contained reversible relations, which made prediction easier.
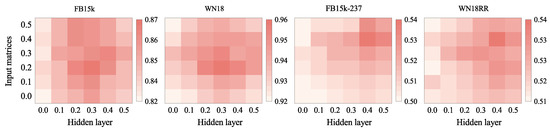
Figure 5.
The Hits@10 performance with various dropout rates for four datasets.
6. Conclusions
In this paper, for link prediction in KBs, we proposed a novel multi-layer convolutional adaptive network method called CANet. CANet makes use of CNN operators that are parameter-efficient and fast. It can also produce additional expressive capabilities and solve the issue of overfitting in large KBs. A scoring technique and an optimizer are used to speed up method training. To reduce overfitting and increase generalization, we use the dropout and label smoothing methods. On several real-world datasets, the proposed method effectively outputted expressive features and obtained new state-of-the-art performance according to the experimental results. We also investigated the responsiveness of various parameters and performed additional research.
In the future, we plan to study link prediction tasks for temporal knowledge bases. As we know, growing knowledge often contains temporal dynamics. This issue requires new methods for modeling such dynamic facts. Furthermore, the applications of knowledge bases are also meaningful. In addition, many industrial applications can be enhanced by knowledge bases, such as in question answering, recommendation systems, and information retrieval.
Author Contributions
Conceptualization, X.H.; methodology, X.H. and Z.L.; software, Z.L.; data curation, X.H.; writing—original draft preparation, X.H.; writing—review and editing, X.H. and Z.L.; visualization, X.H.; supervision, Y.L.; project administration, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities under Grant 2020YBZZ006.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rosa, R.L.; Schwartz, G.M.; Ruggiero, W.V.; Rodríguez, D.Z. A Knowledge-Based Recommendation System That Includes Sentiment Analysis and Deep Learning. IEEE Trans. Inform. 2019, 15, 2124–2135. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, F.; Wang, J.; Zhao, M.; Li, W.; Xie, X.; Guo, M. Exploring High-Order User Preference on the Knowledge Graph for Recommender Systems. ACM Trans. Inf. Syst. 2019, 37, 1–26. [Google Scholar] [CrossRef]
- Schneider, G.F.; Pauwels, P.; Steiger, S. Ontology-Based Modeling of Control Logic in Building Automation Systems. IEEE Trans. Inform. 2017, 13, 3350–3360. [Google Scholar] [CrossRef]
- Engel, G.; Greiner, T.; Seifert, S. Ontology-Assisted Engineering of Cyber–Physical Production Systems in the Field of Process Technology. IEEE Trans. Inform. 2018, 14, 2792–2802. [Google Scholar] [CrossRef]
- Zhou, H.; Young, T.; Huang, M.; Zhao, H.; Xu, J.; Zhu, X. Commonsense Knowledge Aware Conversation Generation with Graph Attention. In Proceedings of the International Joint Conferences on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 4623–4629. [Google Scholar]
- Huang, X.; Zhang, J.; Li, D.; Li, P. Knowledge graph embedding based question answering. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, Melbourne, VIC, Australia, 11–15 February 2019; pp. 105–113. [Google Scholar]
- Bollacker, K.; Evans, C.; Paritosh, P.; Sturge, T.; Taylor, J. Freebase: A collaboratively created graph database for structuring human knowledge. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 9–12 June 2008; pp. 1247–1250. [Google Scholar]
- Miller, G.A. WordNet: A lexical database for English. Commun. ACM 1995, 38, 39–41. [Google Scholar] [CrossRef]
- Suchanek, F.M.; Kasneci, G.; Weikum, G. Yago: A core of semantic knowledge. In Proceedings of the World Wide Web, Banff, AB, Canada, 8–12 May 2007; pp. 697–706. [Google Scholar]
- Wang, Q.; Mao, Z.; Wang, B.; Guo, L. Knowledge Graph Embedding: A Survey of Approaches and Applications. IEEE Trans. Knowl. Data Eng. 2017, 29, 2724–2743. [Google Scholar] [CrossRef]
- Shi, B.; Weninger, T. ProjE: Embedding projection for knowledge graph completion. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1236–1242. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; van den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In Proceedings of the 15th European Semantic Web Conference, Heraklion, Greece, 3–7 June 2018; pp. 593–607. [Google Scholar]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2D Knowledge Graph Embeddings. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 1811–1818. [Google Scholar]
- Gong, J.; Wang, S.; Wang, J.; Feng, W.; Peng, H.; Tang, J.; Yu, P.S. Attentional Graph Convolutional Networks for Knowledge Concept Recommendation in MOOCs in a Heterogeneous View. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 79–88. [Google Scholar]
- Sakurai, R.; Yamane, S.; Lee, J. Restoring Aspect Ratio Distortion of Natural Images With Convolutional Neural Network. IEEE Trans. Inform. 2019, 15, 563–571. [Google Scholar] [CrossRef]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating Embeddings for Modeling Multi-relational Data. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2013; pp. 2787–2795. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge graph embedding by translating on hyperplanes. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; pp. 1112–1119. [Google Scholar]
- Lin, Y.; Liu, Z.; Zhu, X.; Zhu, X.; Zhu, X. Learning entity and relation embeddings for knowledge graph completion. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 2181–2187. [Google Scholar]
- Ji, G.; He, S.; Xu, L.; Liu, K.; Zhao, J. Knowledge Graph Embedding via Dynamic Mapping Matrix. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing, Beijing, China, 26–31 July 2015; pp. 687–696. [Google Scholar]
- Ebisu, T.; Ichise, R. Generalized Translation-based Embedding of Knowledge Graph. IEEE Trans. Knowl. Data Eng. 2020, 32, 941–951. [Google Scholar] [CrossRef]
- Yang, B.; Yih, W.-t.; He, X.; Gao, J.; Deng, L. Embedding Entities and Relations for Learning and Inference in Knowledge Bases. In Proceedings of the 3rd International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014; pp. 1–12. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex embeddings for simple link prediction. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 2071–2080. [Google Scholar]
- Nickel, M.; Rosasco, L.; Poggio, T.A. Holographic Embeddings of Knowledge Graphs. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 1955–1961. [Google Scholar]
- Liu, H.; Wu, Y.; Yang, Y. Analogical inference for multi-relational embeddings. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; pp. 2168–2178. [Google Scholar]
- Guo, L.; Sun, Z.; Hu, W. Learning to Exploit Long-term Relational Dependencies in Knowledge Graphs. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 2505–2514. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the 26th Annual Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 1–4. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).