Experimental Evidence of Specimen-Size Effects on EN-AW6082 Aluminum Alloy in VHCF Regime
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Ultrasonic Fatigue Testing Machine
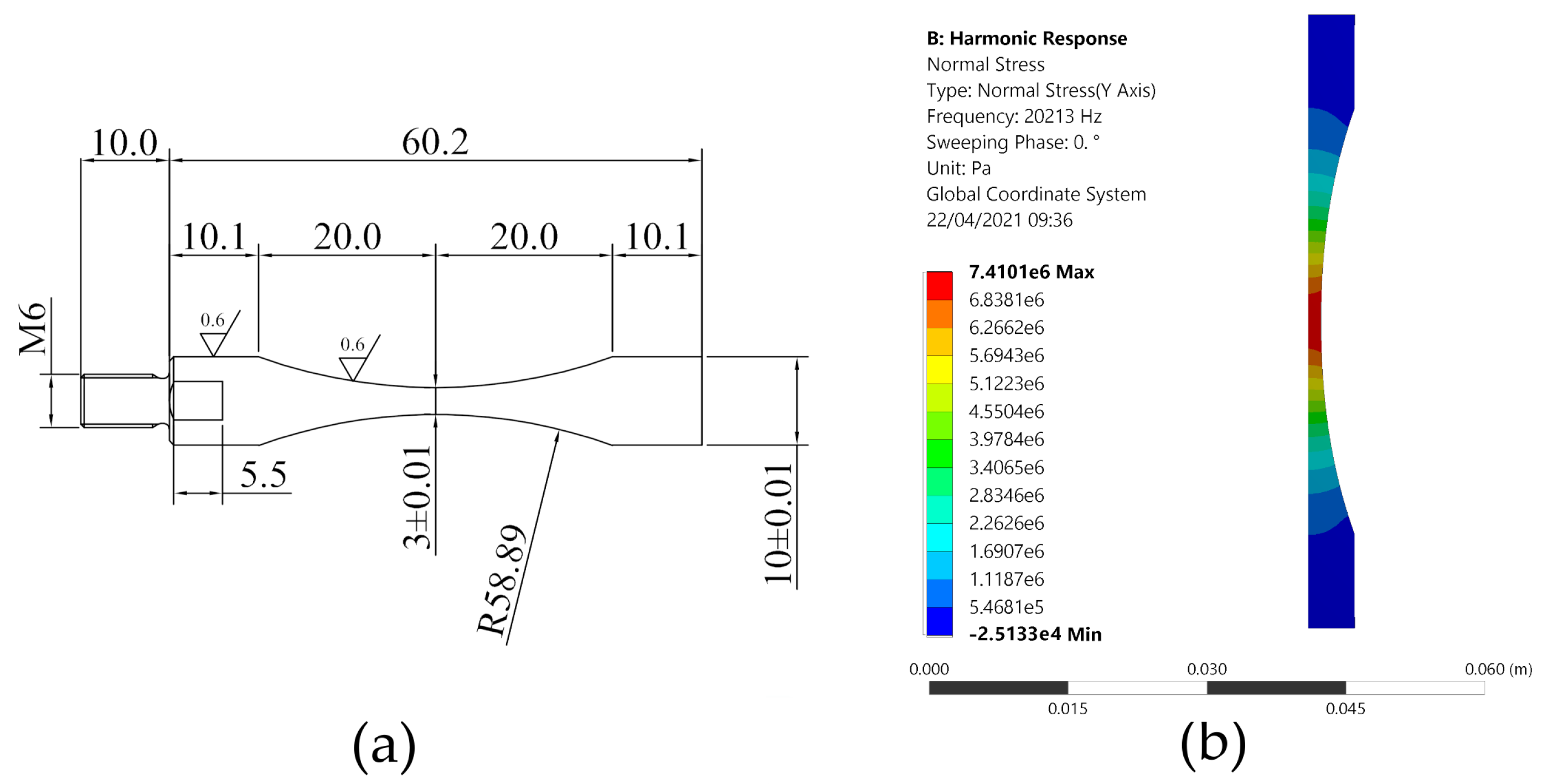
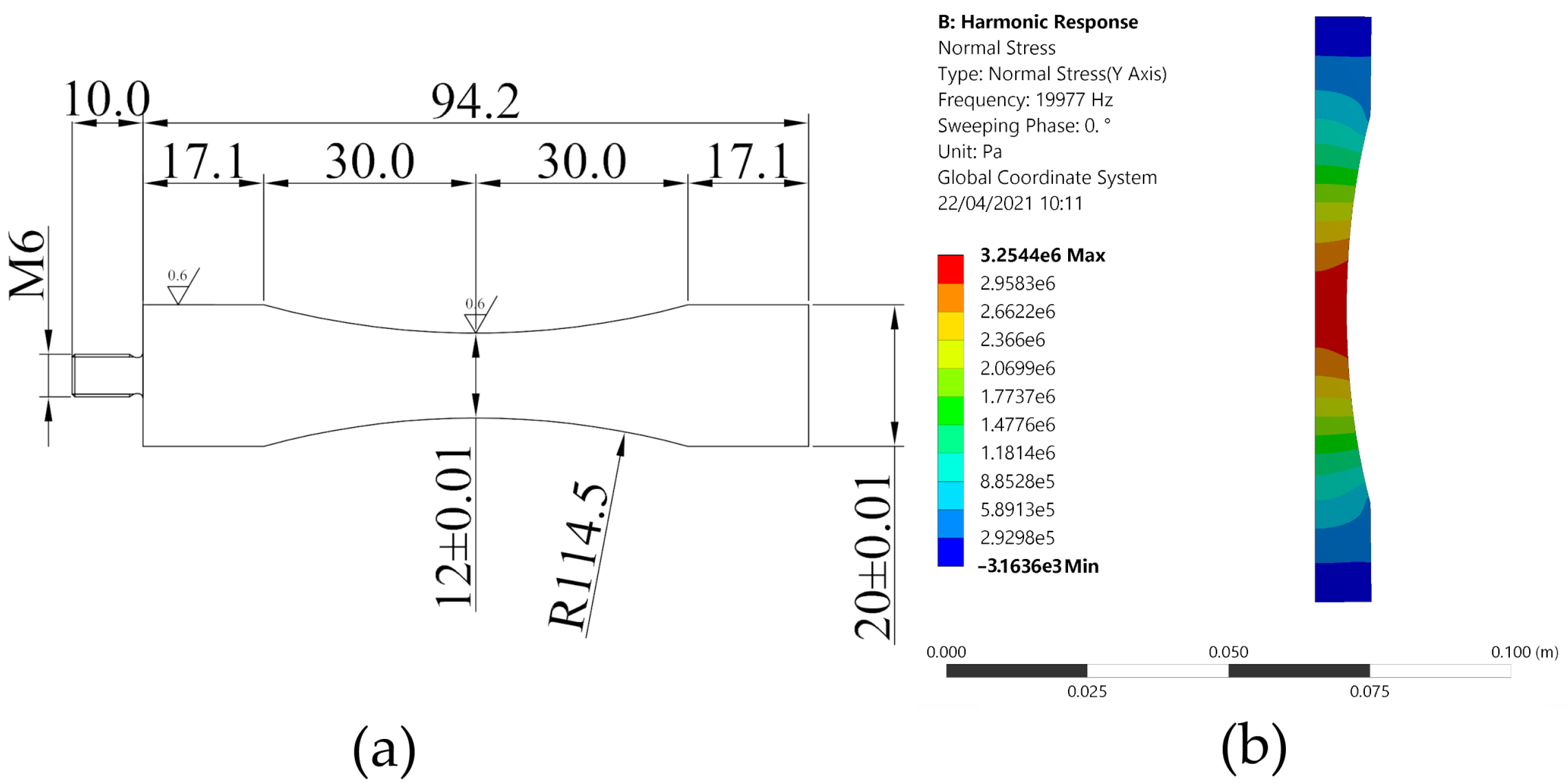
2.3. Specimens Design
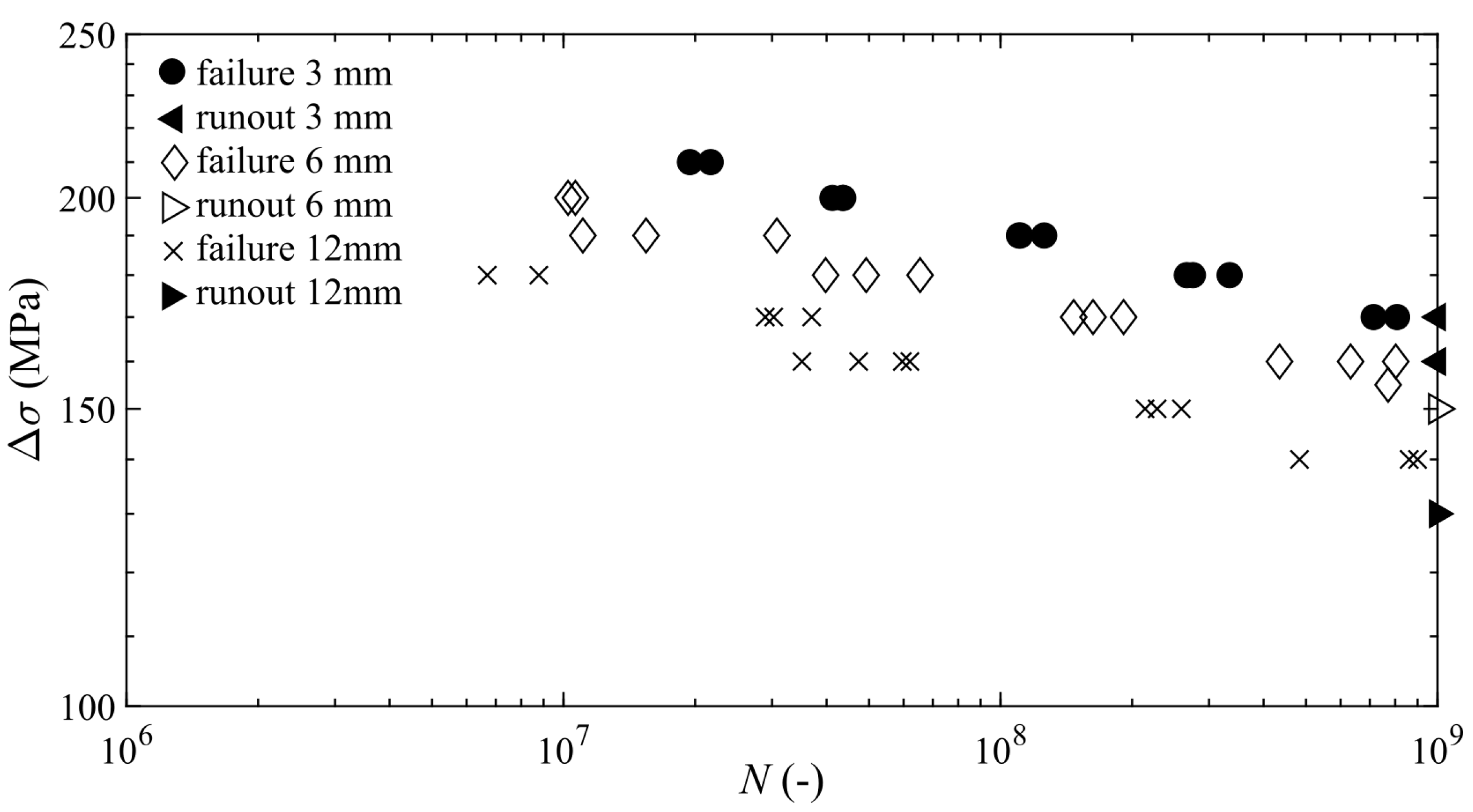
3. Results
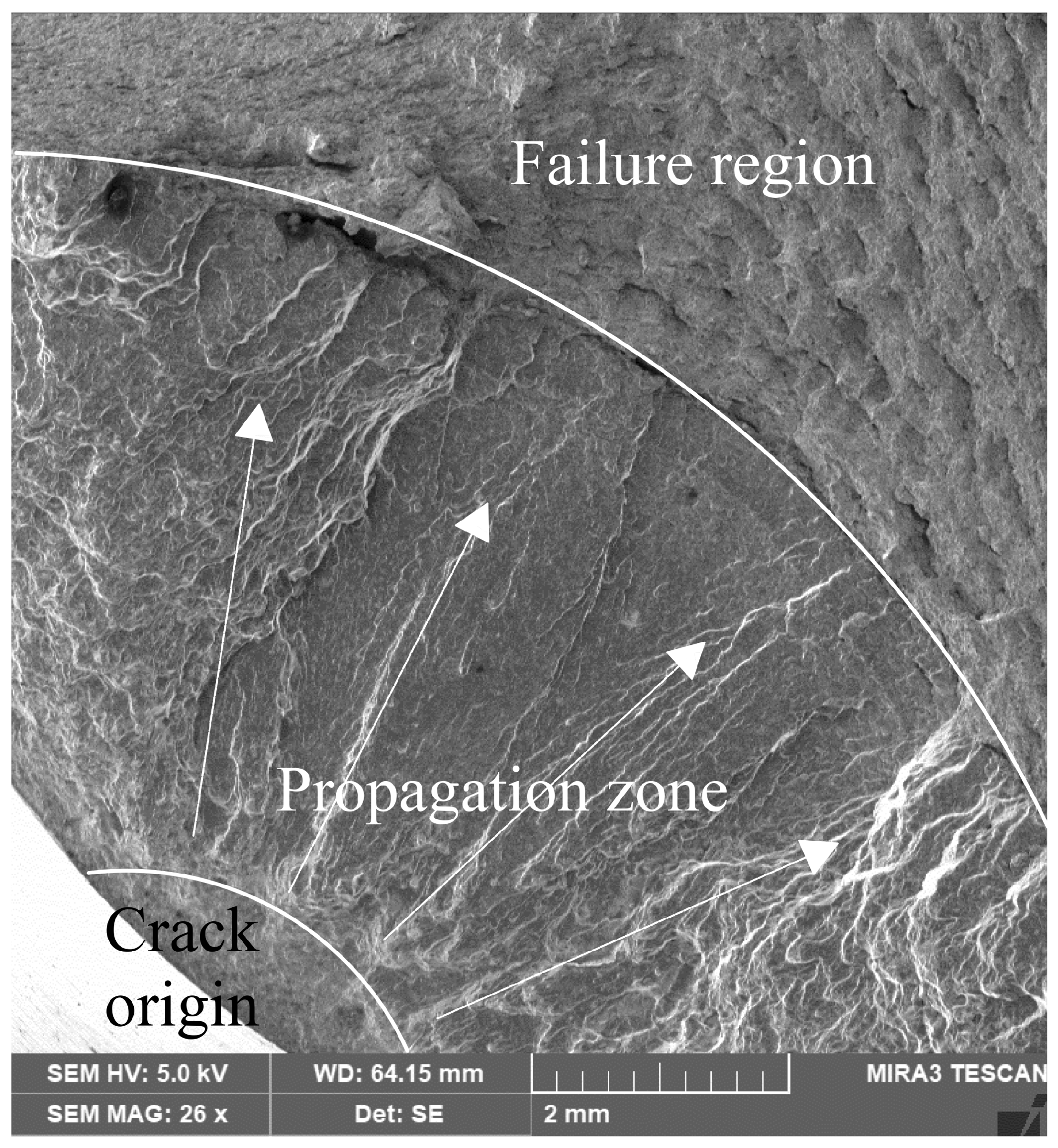
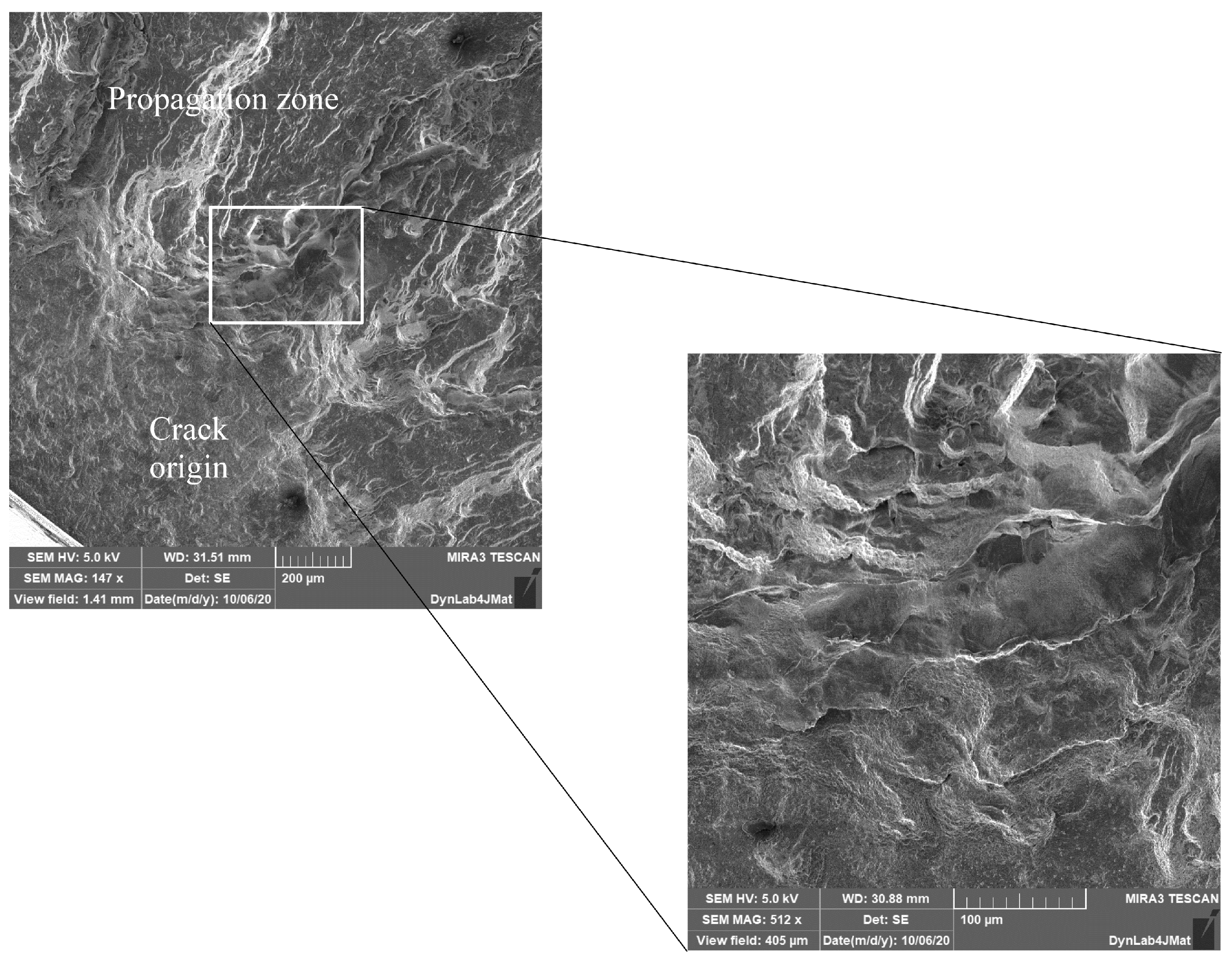
3.1. Experimental Results and Fracture Surface Analysis
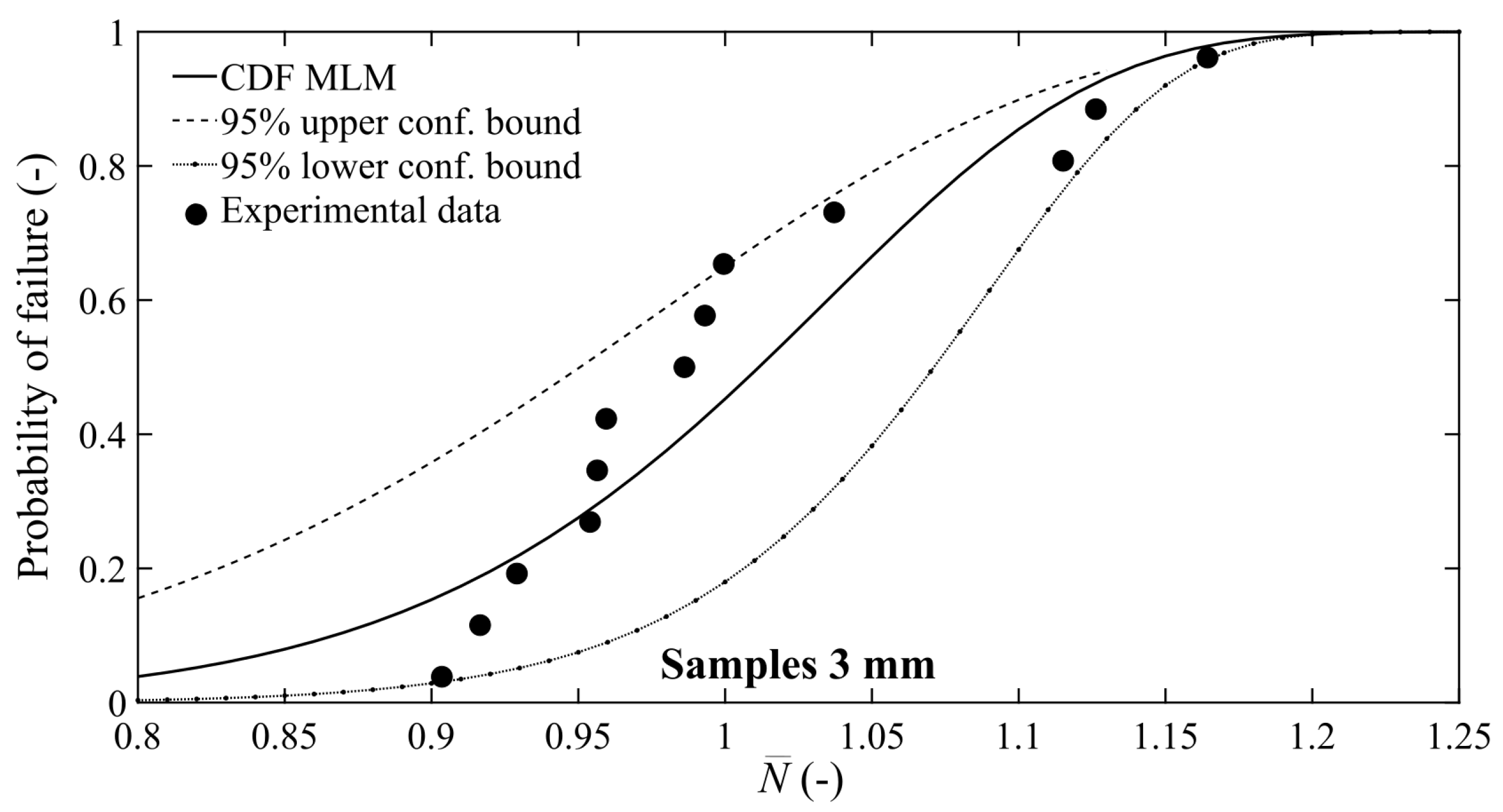
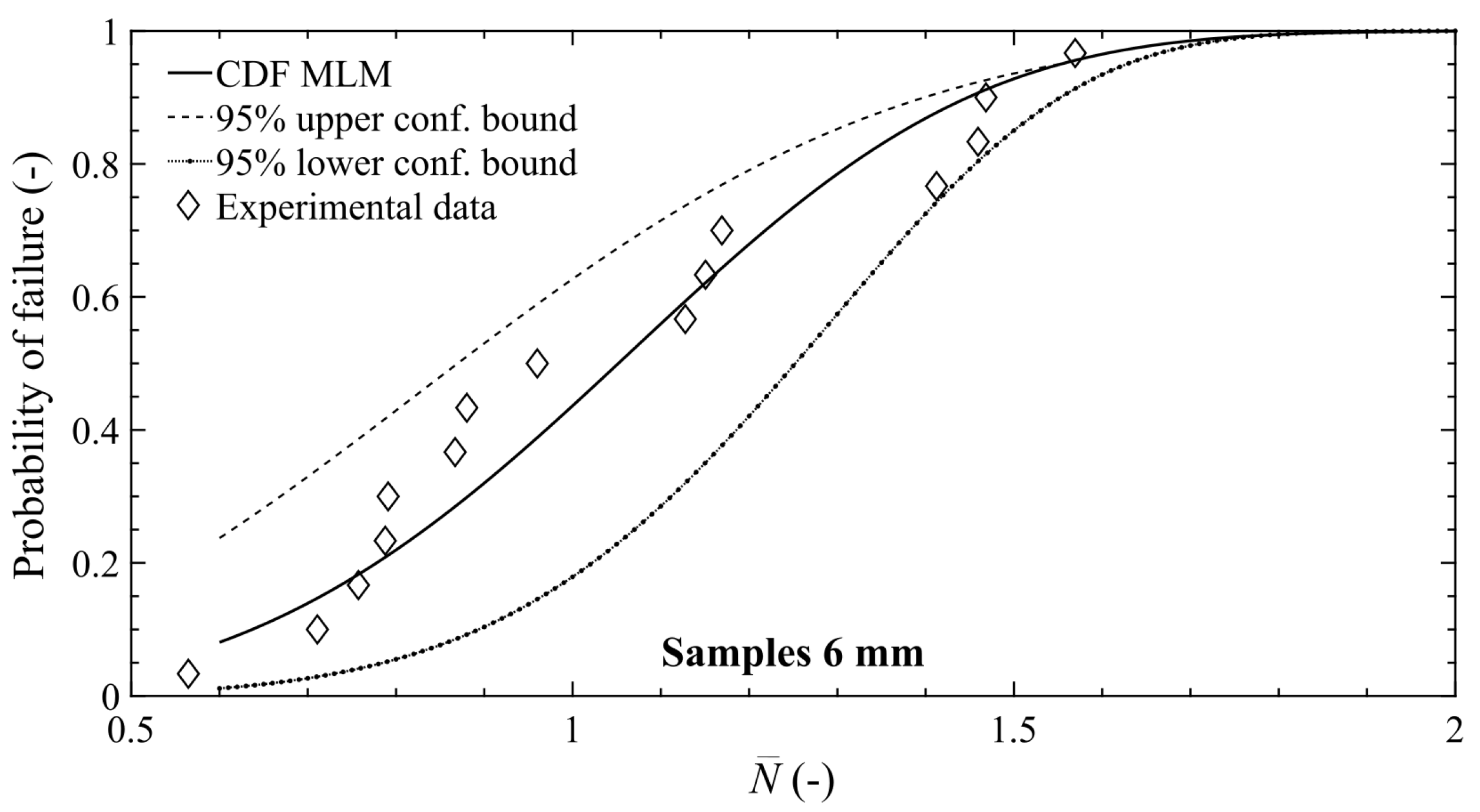
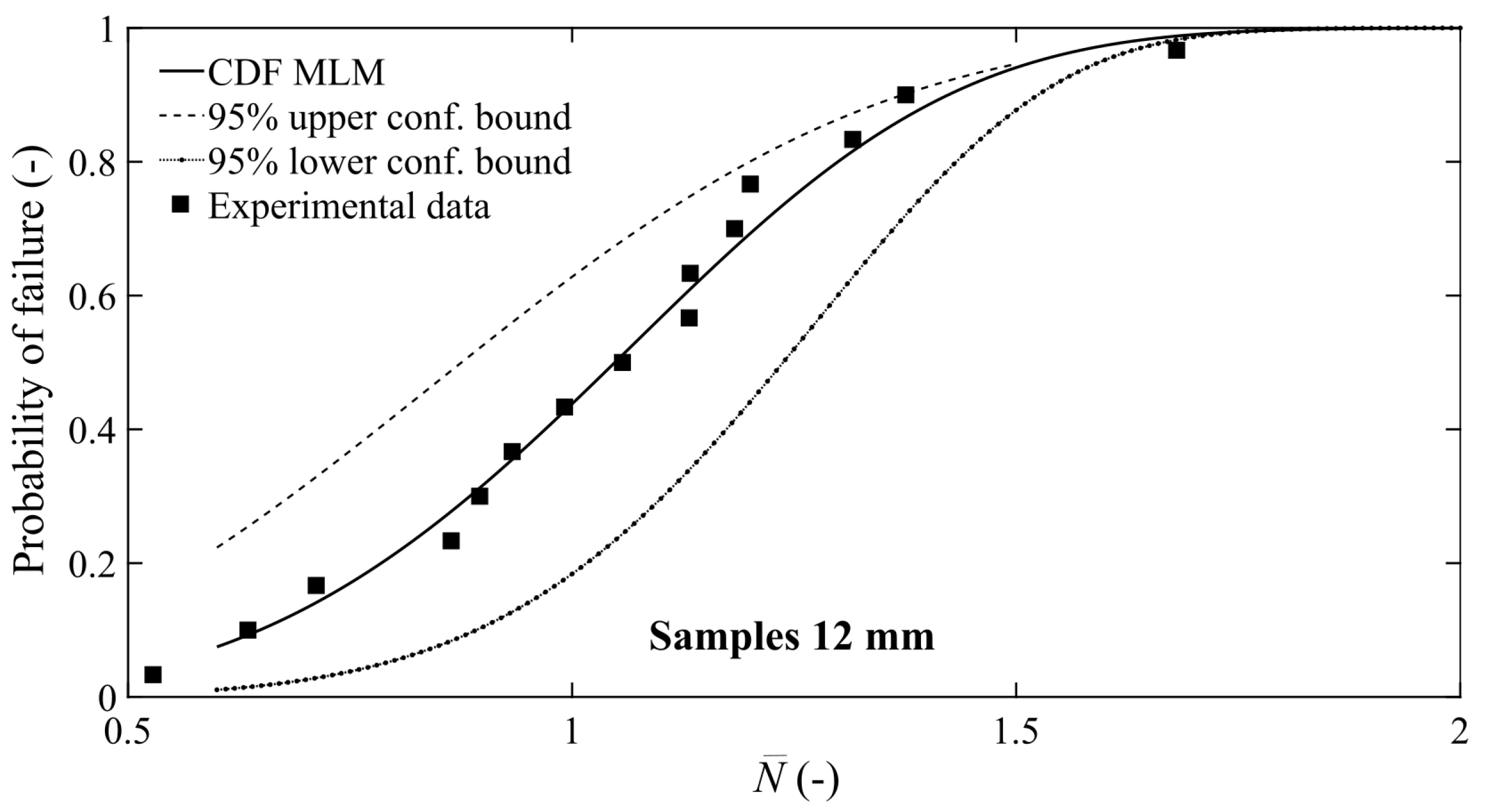
3.2. P-S-N Curves
3.3. Theoretical Interpretation of the Specimen-Size Effect on Fatigue Resistance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VHCF | Very High Cycle Fatigue |
| SLM | Selective Laser Melting |
| AISI | American Iron and Steel Institute |
| P-S-N | Probabilistic Stress-Life |
| UFTM | Ultrasonic Fatigue Testing Machine |
| SEM | Scanning Electron Microscope |
| CDF | Cumulative Distribution Function |
| MLM | Maximum Likelihood Method |
References
- Stanzl-Tschegg, S.E.; Mayer, H. Fatigue and fatigue crack growth of aluminium alloys at very high numbers of cycles. Int. J. Fatigue 2001, 23, 231–237. [Google Scholar] [CrossRef]
- Sharma, A.; Oh, M.C.; Ahn, B. Recent Advances in Very High Cycle Fatigue Behavior of Metals and Alloys—A Review. Metals 2020, 10, 1200. [Google Scholar] [CrossRef]
- Bathias, C.; Paris, P.C. Gigacycle Fatigue in Mechanical Practice; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar] [CrossRef]
- Mayer, H. Recent Developments in Ultrasonic Fatigue. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 3–29. [Google Scholar] [CrossRef]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. Fatigue Assessment of the Collapsed XXth Century Cable-Stayed Polcevera Bridge in Genoa. Procedia Struct. Integr. 2019, 18, 237–244. [Google Scholar] [CrossRef]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. The collapse of the Morandi’s bridge: Remarks about fatigue and corrosion. In Proceedings of the IABSE Symposium, Wroclaw 2020: Synergy of Culture and Civil Engineering—History and Challenges, Wroclaw, Poland, 7–9 October 2020; pp. 1040–1047. [Google Scholar]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. Corrosion Fatigue Investigation on the Possible Collapse Reasons of Polcevera Bridge in Genoa. Lect. Notes Mech. Eng. 2020, 151–159. [Google Scholar] [CrossRef]
- Stanzl-Tschegg, S. Very High Cycle Fatigue Measuring Techniques. Int. J. Fatigue 2014, 60, 2–17. [Google Scholar] [CrossRef]
- Furuya, Y. Specimen Size Effects on Gigacycle Fatigue Properties of High-Strength Steel under Ultrasonic Fatigue Testing. Scr. Mater. 2008, 58, 1014–1017. [Google Scholar] [CrossRef]
- Furuya, Y. Size Effects in Gigacycle Fatigue of High-Strength Steel under Ultrasonic Fatigue Testing. Procedia Eng. 2010, 2, 485–490. [Google Scholar] [CrossRef] [Green Version]
- Furuya, Y. Notable Size Effects on Very High Cycle Fatigue Properties of High-Strength Steel. Mater. Sci. Eng. A 2011, 528, 5234–5240. [Google Scholar] [CrossRef]
- Murakami, Y.; Kodama, S.; Konuma, S. Quantitative Evaluation of Effects of Non-Metallic Inclusions on Fatigue Strength of High Strength Steels. I: Basic Fatigue Mechanism and Evaluation of Correlation between the Fatigue Fracture Stress and the Size and Location of Non-Metallic Inclusions. Int. J. Fatigue 1989, 11, 291–298. [Google Scholar] [CrossRef]
- Murakami, Y.; Usuki, H. Quantitative Evaluation of Effects of Non-Metallic Inclusions on Fatigue Strength of High Strength Steels. II: Fatigue Limit Evaluation Based on Statistics for Extreme Values of Inclusion Size. Int. J. Fatigue 1989, 11, 299–307. [Google Scholar] [CrossRef]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. Comparison between Dog-Bone and Gaussian Specimens for Size Effect Evaluation in Gigacycle Fatigue. Frat. Integrità Strutt. 2013, 26, 49–56. [Google Scholar] [CrossRef] [Green Version]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. Gaussian Specimens for Gigacycle Fatigue Tests: Evaluation of Temperature Increment. Key Eng. Mater. 2015, 627, 85–88. [Google Scholar] [CrossRef]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. Gaussian Specimens for Gigacycle Fatigue Tests: Damping Effects. Procedia Eng. 2014, 74, 113–118. [Google Scholar] [CrossRef]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. VHCF Strength Decrement in Large H13 Steel Specimens Subjected to ESR Process. Procedia Struct. Integr. 2016, 2, 1117–1124. [Google Scholar] [CrossRef] [Green Version]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. VHCF Response of AISI H13 Steel: Assessment of Size Effects through Gaussian Specimens. Procedia Eng. 2015, 109, 121–127. [Google Scholar] [CrossRef] [Green Version]
- Tridello, A.; Paolino, D.S.; Rossetto, M. Ultrasonic VHCF Tests on Very Large Specimens with Risk-Volume up to 5000 mm3. Appl. Sci. 2020, 10, 2210. [Google Scholar] [CrossRef] [Green Version]
- Tridello, A.; Biffi, C.A.; Fiocchi, J.; Bassani, P.; Chiandussi, G.; Rossetto, M.; Tuissi, A.; Paolino, D.S. VHCF Response of As-Built SLM AlSi10Mg Specimens with Large Loaded Volume. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1918–1928. [Google Scholar] [CrossRef]
- Tridello, A.; Fiocchi, J.; Biffi, C.A.; Chiandussi, G.; Rossetto, M.; Tuissi, A.; Paolino, D.S. VHCF Response of Heat-Treated SLM Ti6Al4V Gaussian Specimens with Large Loaded Volume. Procedia Struct. Integr. 2019, 18, 314–321. [Google Scholar] [CrossRef]
- Xue, H.; Sun, Z.; Zhang, X.; Gao, T.; Li, Z. Very High Cycle Fatigue of a Cast Aluminum Alloy: Size Effect and Crack Initiation. J. Mater. Eng. Perform. 2018, 27, 5406–5416. [Google Scholar] [CrossRef]
- Carpinteri, A.; Montagnoli, F.; Invernizzi, S. Scaling and Fractality in Fatigue Resistance: Specimen-Size Effects on Wöhler’s Curve and Fatigue Limit. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1869–1879. [Google Scholar] [CrossRef]
- ASTM E1876-15. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
- ASTM B557M-15. Standard Test Methods for Tension Testing Wrought and Cast Aluminum- and Magnesium-Alloy Products (Metric); ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
- ASTM E10-15. Standard Test Method for Brinell Hardness of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
- Naoe, T.; Xiong, Z.; Futakawa, M. Temperature Measurement for In-Situ Crack Monitoring under High-Frequency Loading. J. Nucl. Mater. 2018, 506, 12–18. [Google Scholar] [CrossRef]
- Furuya, Y. Gigacycle Fatigue Properties of Double-Melted SCM440 Steel and Size Effects. ISIJ Int. 2014, 54, 1436–1442. [Google Scholar] [CrossRef] [Green Version]
- Tridello, A. VHCF Response of Gaussian Specimens Made of High-Strength Steels: Comparison between Unrefined and Refined AISI H13. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1676–1689. [Google Scholar] [CrossRef]
- Krewerth, D.; Weidner, A.; Biermann, H. Application of in Situ Thermography for Evaluating the High-Cycle and Very High-Cycle Fatigue Behaviour of Cast Aluminium Alloy AlSi7Mg (T6). Ultrasonics 2013, 53, 1441–1449. [Google Scholar] [CrossRef] [PubMed]
- Goglio, L.; Rossetto, M. Comparison of Fatigue Data Using the Maximum Likelihood Method. Eng. Fract. Mech. 2004, 71, 725–736. [Google Scholar] [CrossRef]
- Barbosa, J.F.; Correia, J.A.F.O.; Freire Júnior, R.C.S.; Zhu, S.P.; De Jesus, A.M.P. Probabilistic S-N Fields Based on Statistical Distributions Applied to Metallic and Composite Materials: State of the Art. Adv. Mech. Eng. 2019, 11, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Freire Júnior, R.C.S.; Belísio, A.S. Probabilistic S-N Curves Using Exponential and Power Laws Equations. Compos. Part B Eng. 2014, 56, 582–590. [Google Scholar] [CrossRef]
- Pedrosa, B.; Correia, J.A.F.O.; Rebelo, C.A.S.; Veljkovic, M. Reliability of Fatigue Strength Curves for Riveted Connections Using Normal and Weibull Distribution Functions. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2020, 6, 1–8. [Google Scholar] [CrossRef]
- Barbosa, J.F.; Carlos Silverio Freire Júnior, R.; Correia, J.A.F.O.; De Jesus, A.M.P.; Calçada, R.A.B. Analysis of the Fatigue Life Estimators of the Materials Using Small Samples. J. Strain Anal. Eng. Des. 2018, 53, 699–710. [Google Scholar] [CrossRef]
- Carpinteri, A. Scaling Laws and Renormalization Groups for Strength and Toughness of Disordered Materials. Int. J. Solids Struct. 1994, 31, 291–302. [Google Scholar] [CrossRef]
- Carpinteri, A. Fractal Nature of Material Microstructure and Size Effects on Apparent Mechanical Properties. Mech. Mater. 1994, 18, 89–101. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Cornetti, P. A Scale-Invariant Cohesive Crack Model for Quasi-Brittle Materials. Eng. Fract. Mech. 2002, 69, 207–217. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Cornetti, P. On the Mechanics of Quasi-Brittle Materials with a Fractal Microstructure. Eng. Fract. Mech. 2003, 70, 2321–2349. [Google Scholar] [CrossRef]
- Carpinteri, A.; Ferro, G.; Invernizzi, S. The Nominal Tensile Strength of Disordered Materials: A Statistical Fracture Mechanics Approach. Eng. Fract. Mech. 1997, 58, 421–435. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Ferro, G. Size Effects on Nominal Tensile Strength of Concrete Structures: Multifractality of Material Ligaments and Dimensional Transition from Order to Disorder. Mater. Struct. 1995, 28, 311–317. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B. Power Scaling Laws and Dimensional Transitions in Solid Mechanics. Chaos Solitons Fractals 1996, 7, 1343–1364. [Google Scholar] [CrossRef]
- Carpinteri, A.; Montagnoli, F. Scaling and Fractality in Fatigue Crack Growth: Implications to Paris’ Law and Wöhler’s Curve. Procedia Struct. Integr. 2019, 14, 957–963. [Google Scholar] [CrossRef]
- Carpinteri, A.; Spagnoli, A.; Vantadori, S. Size Effect in S-N Curves: A Fractal Approach to Finite-Life Fatigue Strength. Int. J. Fatigue 2009, 31, 927–933. [Google Scholar] [CrossRef]
- Montagnoli, F.; Invernizzi, S.; Carpinteri, A. Fractality and Size Effect in Fatigue Damage Accumulation: Comparison between Paris and Wöhler Perspectives. Lect. Notes Mech. Eng. 2020, 188–196. [Google Scholar] [CrossRef]




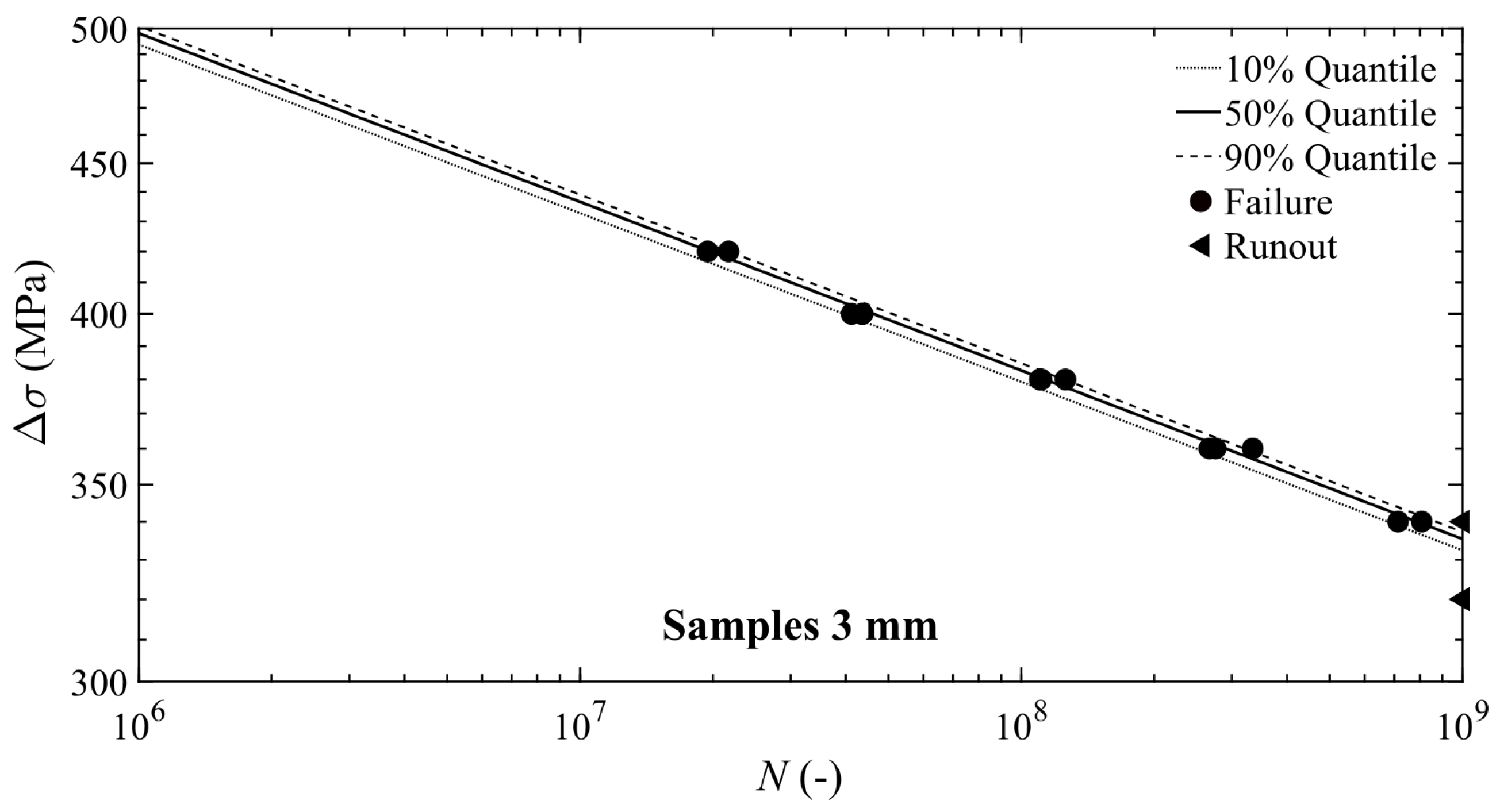
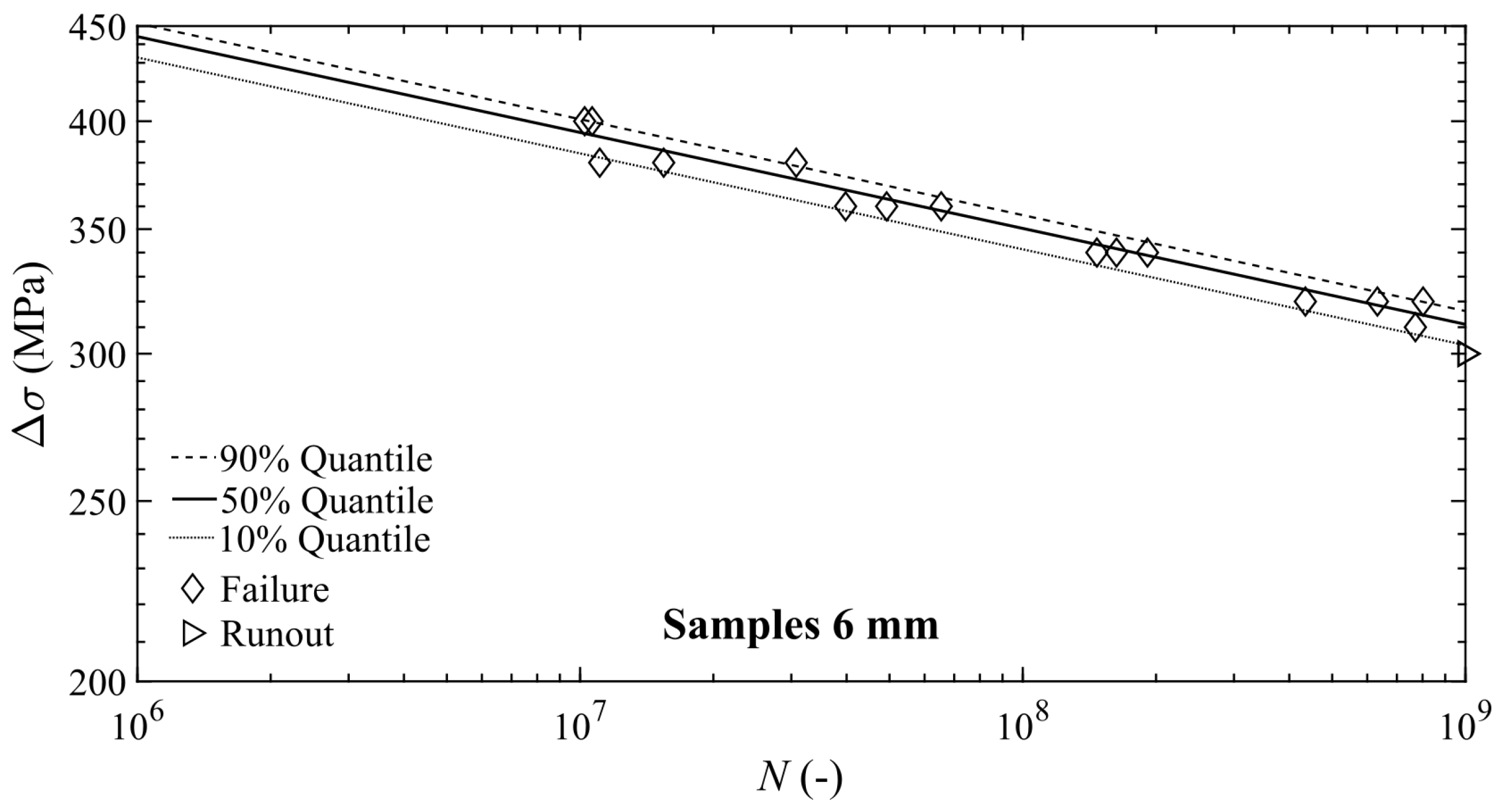

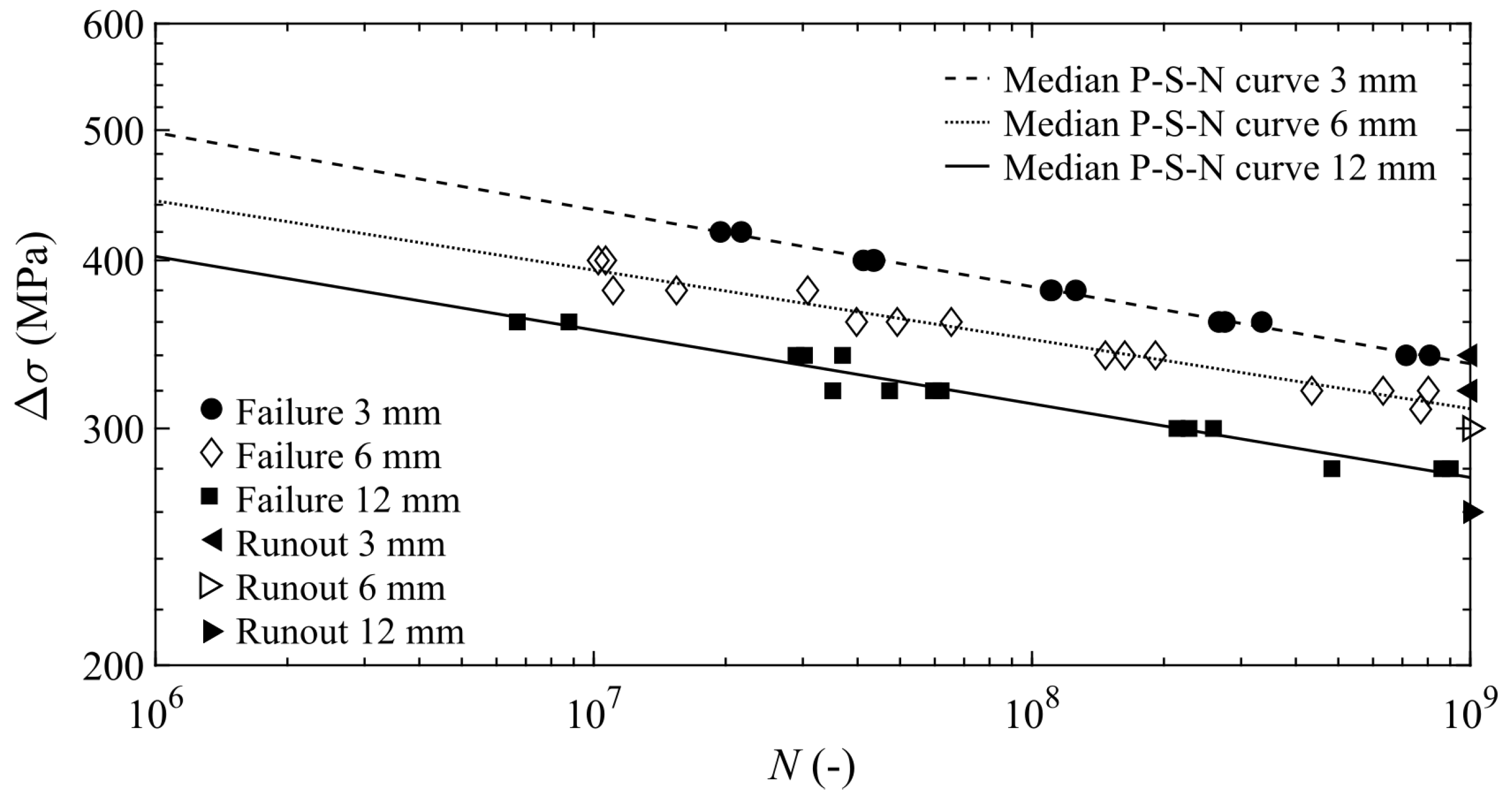
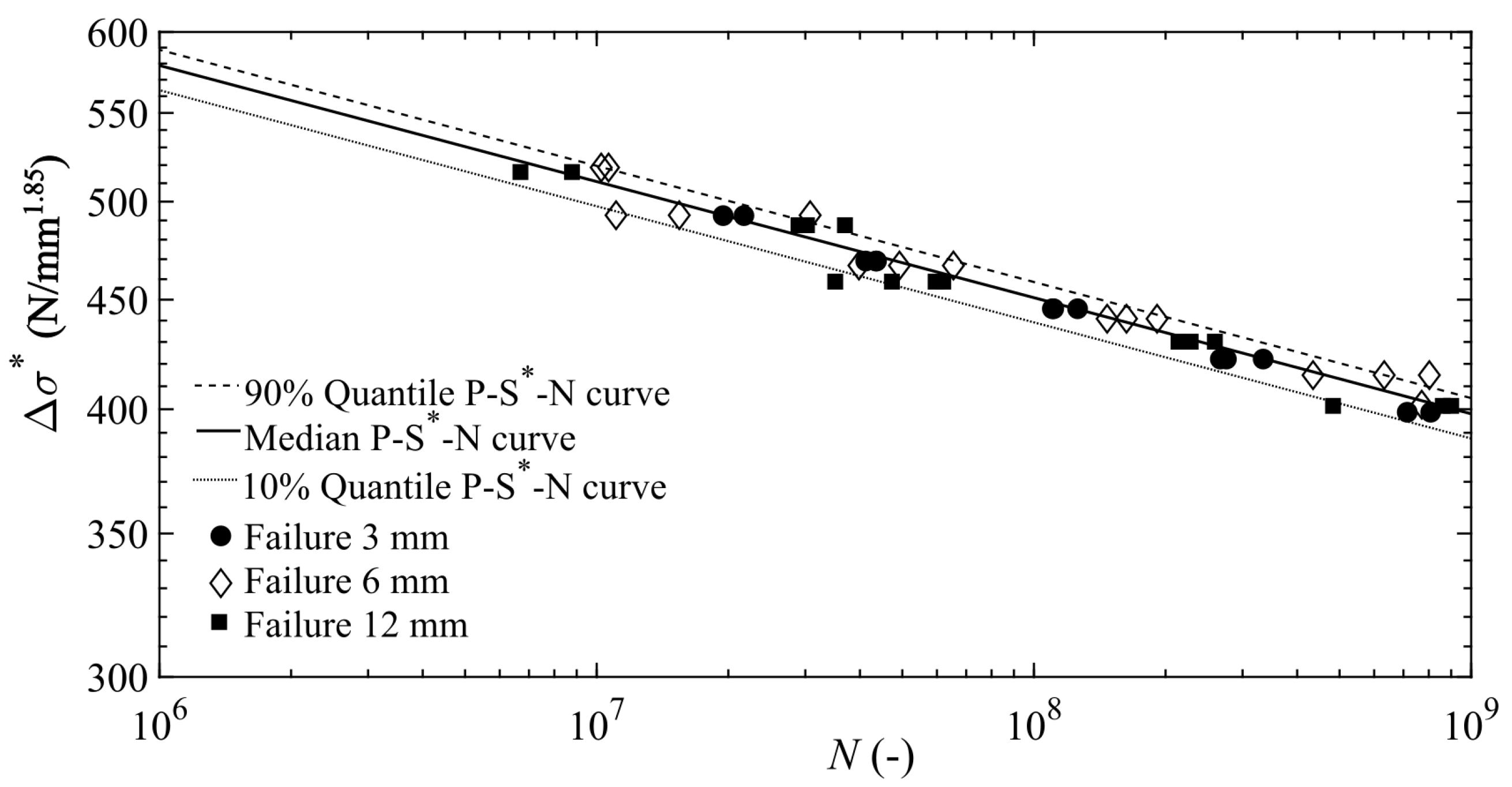
| Element | Si | Mg | Mn | Cu | Fe | Cr | Zi | Ti |
|---|---|---|---|---|---|---|---|---|
| Min% | 0.70 | 0.60 | 0.40 | |||||
| Max% | 1.30 | 1.20 | 1.00 | 0.10 | 0.50 | 0.25 | 0.20 | 0.10 |
| Diameter of Bar | (kg/m) | (GPa) | (MPa) | (MPa) | (%) | Brinnel Hardness (HB) |
|---|---|---|---|---|---|---|
| 20 mm | 2713 | 72.3 | – | – | – | 91 |
| 30 mm | 2700 | 70.1 | 357 | 375 | 11 | 91 |
| Specimen | (MPa/m) | (Hz) | (–) | (mm) |
|---|---|---|---|---|
| 3 mm | 7.474 | 20,213 | 1.021 | 42 |
| 6 mm | 4.233 | 20,047 | 1.025 | 301 |
| 12 mm | 3.350 | 19,947 | 1.046 | 1731 |
| Diameter | ||
|---|---|---|
| 3 mm | 12.2091 | 1.0423 |
| 6 mm | 3.7579 | 1.1596 |
| 12 mm | 3.9214 | 1.1508 |
| GoF Statistics Tests | A-D | C-vM | K-S | |
|---|---|---|---|---|
| Actual values | 7.792 | 0.701 | 0.143 | 0.242 |
| Critical values | 7.815 | 0.728 | 0.214 | 0.316 |
| GoF Statistics Tests | A-D | C-vM | K-S | |
|---|---|---|---|---|
| Actual values | 7.000 | 0.475 | 0.077 | 0.168 |
| Critical values | 7.815 | 0.731 | 0.215 | 0.331 |
| GoF Statistics Tests | A-D | C-vM | K-S | |
|---|---|---|---|---|
| Actual values | 0.600 | 0.156 | 0.019 | 0.107 |
| Critical values | 7.815 | 0.731 | 0.215 | 0.338 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Invernizzi, S.; Montagnoli, F.; Carpinteri, A. Experimental Evidence of Specimen-Size Effects on EN-AW6082 Aluminum Alloy in VHCF Regime. Appl. Sci. 2021, 11, 4272. https://doi.org/10.3390/app11094272
Invernizzi S, Montagnoli F, Carpinteri A. Experimental Evidence of Specimen-Size Effects on EN-AW6082 Aluminum Alloy in VHCF Regime. Applied Sciences. 2021; 11(9):4272. https://doi.org/10.3390/app11094272
Chicago/Turabian StyleInvernizzi, Stefano, Francesco Montagnoli, and Alberto Carpinteri. 2021. "Experimental Evidence of Specimen-Size Effects on EN-AW6082 Aluminum Alloy in VHCF Regime" Applied Sciences 11, no. 9: 4272. https://doi.org/10.3390/app11094272
APA StyleInvernizzi, S., Montagnoli, F., & Carpinteri, A. (2021). Experimental Evidence of Specimen-Size Effects on EN-AW6082 Aluminum Alloy in VHCF Regime. Applied Sciences, 11(9), 4272. https://doi.org/10.3390/app11094272







